最新刚体习题和答案
《大学物理》刚体力学练习题及答案解析
《大学物理》刚体力学练习题及答案解析一、选择题1.刚体对轴的转动惯量，与哪个因素无关 [ C ]（A）刚体的质量（B）刚体质量的空间分布（C）刚体的转动速度（D）刚体转轴的位置2.有两个力作用在一个有固定轴的刚体上. [ B ](1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)这两个力的合力为零时,它们对轴的合力矩也一定是零;(4)当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中,(A)只有(1)是正确的；(B) (1)、(2) 正确, (3)、(4)错误；(C) (1)、(2)、(3)都正确, (4)错误；(D) (1)、(2)、(3)、(4)都正确.3.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动，今使棒从水平位置由静止开始自由下落，在棒摆动到竖立位置的过程中，下述说法哪一种是正确的[ A ](A) 角速度从小到大，角加速度从大到小；(B) 角速度从小到大，角加速度从小到大；(C) 角速度从大到小，角加速度从大到小；(D) 角速度从大到小，角加速度从小到大.4．如图所示，圆锥摆的小球在水平面内作匀速率圆周运动，小球和地球所组成的系统，下列哪些物理量守恒（ C ）（A）动量守恒，角动量守恒（B）动量和机械能守恒（C）角动量和机械能守恒（D）动量，角动量，机械能守恒5.一圆盘绕通过盘心且垂直于盘面的水平轴转动，轴间摩擦不计，如图射来两个质量相同，速度大小相同、方向相反并在一条直线上的子弹，它们同时射入圆盘并且留在盘内，在子弹射入后的瞬间，对于圆盘和子弹系统的角动量L以及圆盘的角速度ω则有（ B ）（A）L不变，ω增大（B）L不变，ω减小（C）L变大，ω不变（D）两者均不变6.一花样滑冰者，开始自转时，其动能为20021ωJ E =。
然后他将手臂收回，转动惯量减少为原来的1/3，此时他的角速度变为ω，动能变为E ，则下列关系正确的是（ D ） （A ）00,3E E ==ωω （B ）003,31E E ==ωω （C ）00,3E E ==ωω （D ）003,3E E ==ωω1C 2.B ，3.A ，4.C ，5.B ，6.D二、填空1.当刚体受到的合外力的力矩为零时，刚体具有将保持静止的状态或_____________状态，把刚体的这一性质叫刚体___________。
大学物理第四章 刚体的转动部分的习题及答案
第四章 刚体的转动一、简答题：1、简述刚体定轴转动的角动量守恒定律并给出其数学表达式?答案：刚体定轴转动时，若所受合外力矩为零或不受外力矩，则刚体的角动量保持不变。
2、写出刚体绕定轴转动的转动定律文字表达与数学表达式?答案：刚体绕定轴转动的转动定律：刚体绕定轴转动时，刚体的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比。
表达式为：αJ M =。
3、写出刚体转动惯量的公式，并说明它由哪些因素确定?答案：dm r J V⎰=2①刚体的质量及其分布；②转轴的位置；③刚体的形状。
二、选择题1、在定轴转动中，如果合外力矩的方向与角速度的方向一致，则以下说法正确的是 ( A )A.合力矩增大时，物体角速度一定增大；B.合力矩减小时，物体角速度一定减小；C.合力矩减小时，物体角加速度不一定变小；D.合力矩增大时，物体角加速度不一定增大2、关于刚体对轴的转动惯量，下列说法中正确的是 ( C ) A.只取决于刚体的质量，与质量的空间分布和轴的位置无关； B.取决于刚体的质量和质量的空间分布，与轴的位置无关； C.取决于刚体的质量，质量的空间分布和轴的位置；D.只取决于转轴的位置，与刚体的质量和质量的空间分布无关；3、有一半径为R 的水平圆转台，可绕通过其中心的竖直固定光滑轴转动， 转动惯量为J ，开始时转台以匀角速度0ω转动，此时有一质量为m 的人站住转台中心，随后人沿半径向外跑去，当人到达转台边缘时，转台的角速度为 ( A ) A.()2mR J J +ω B.()2Rm J J +ω C.20mR J ω D.0ω4、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示。
今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的? ( A )A.角速度从小到大，角加速度从大到小．B.角速度从小到大，角加速度从小到大．C.角速度从大到小，角加速度从大到小．D.角速度从大到小，角加速度从小到大．5、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度( C )A.增大B.不变C.减小 (D) 、不能确定6、在地球绕太阳中心作椭圆运动时，则地球对太阳中心的 ( B ) A.角动量守恒，动能守恒 B.角动量守恒，机械能守恒 C.角动量不守恒，机械能守恒 D.角动量守恒，动量守恒7、有两个半径相同,质量相等的细圆环A 和B ，A 环的质量分布均匀，B 环的质量分布不均匀，它们对通过环心并与环面垂直的轴的转动惯量分别为A J 和B J ，则 ( C )A.B A J J >；B.B A J J <；C.B A J J =；D.不能确定A J 、B J 哪个大。
大学物理(第四版)课后习题及答案 刚体
题4.1：一汽车发动机曲轴的转速在s 12内由13min r 102.1-⋅⨯均匀的增加到13min r 107.2-⋅⨯。
（1）求曲轴转动的角加速度；（2）在此时间内，曲轴转了多少转？题4.1解：（1）由于角速度ω =2πn （n 为单位时间内的转数），根据角加速度的定义td d ωα=，在匀变速转动中角加速度为()200s rad 1.132-⋅=-=-=tn n t πωωα（2）发动机曲轴转过的角度为()t n n t t t 0020221+=+=+=πωωαωθ在12 s 内曲轴转过的圈数为 圈390220=+==t n n N πθ 题4.2：某种电动机启动后转速随时间变化的关系为)1(0τωωte --=，式中10s rad 0.9-⋅=ω，s 0.2=τ。
求：（1）s 0.6=t 时的转速；（2）角加速度随时间变化的规律；（3）启动后s 0.6内转过的圈数。
题4.2解：（1）根据题意中转速随时间的变化关系，将t = 6.0 s 代入，即得100s 6.895.01--==⎪⎪⎭⎫⎝⎛-=ωωωτte（2）角加速度随时间变化的规律为220s 5.4d d ---===tte e t ττωωα（3）t = 6.0 s 时转过的角度为 rad 9.36d 1d 60060=⎪⎪⎭⎫⎝⎛-==⎰⎰-s tst e t τωωθ 则t = 6.0 s 时电动机转过的圈数圈87.52==πθN 题4.3：如图所示，一通风机的转动部分以初角速度0ω绕其轴转动，空气的阻力矩与角速度成正比，比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ，问：（1）经过多少时间后其转动角速度减少为初角速度的一半？（2）在此时间内共转过多少转？题4.3解：（1）通风机叶片所受的阻力矩为ωM C -=，由转动定律αM J =，可得叶片的角加速度为JC t ωωα-==d d （1） 根据初始条件对式（1）积分，有⎰⎰-=ωωω00d d d t t J C t由于C 和J 均为常量，得t JC e-=0ωω当角速度由0021ωω→时，转动所需的时间为2ln CJt = （2）根据初始条件对式（2）积分，有⎰⎰-=tt JC t e00d d ωθθ即CJ 20ωθ=在时间t 内所转过的圈数为 CJ N πωπθ420==题4.4：一燃气轮机在试车时，燃气作用在涡轮上的力矩为m N 1003.23⋅⨯，涡轮的转动惯量为2m kg 0.25⋅。
第四章刚体运动习题详解
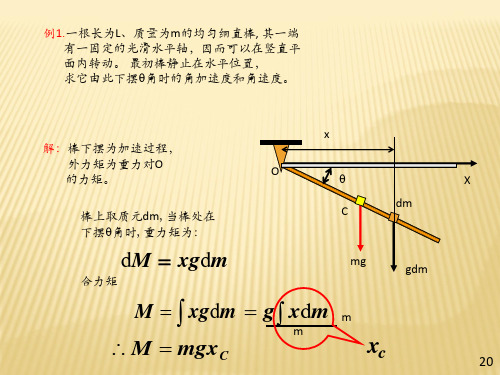
解：棒下摆为加速过程， 外力矩为重力对O 的力矩。
棒上取质元dm,当棒处在 下摆角时,重力矩为：
x
O
X
C
dm
dM xgdm
合力矩
mg
gdm
解：
因摩擦力产生的力矩是恒定的，故角速度均匀 减小。
0
0
t
0
0 t
dt t
0
f dS
r
σ
m πR2
R
dθ o
r
M J 1 mR2
2
dr
t 0mR2 / (2M ) (1) M ?
考虑面元dS对轴的摩擦力矩dM ：
dM r0gdm r0g dS
26
t0mR2/(2M ) (1) dM r0g dS
mg 由(3)(4)(5)得
mgR sin
1 2
J02
1 2
J2
(5)
gh 2R2
cos2
g R
sin
1 2R
.
g 2
(h
4
3R)
M J
mgR 2mR2
g 2R
( 60 )
44
dt
O
X
C
即 d d
3g cos d d
mg
2L
θ
0
3gcos
2L
d
0
d
3g 2L
sin
1 2
2
3g sin
L
22
m 例2.质量为 、长为L的匀质细杆水平放置,一端
刚体定轴转动练习题及答案
刚体定轴转动练习题一、选择题1、一刚体以每分钟60转绕Z 轴做匀速转动（ωϖ沿Z 轴正方向）。
设某时刻刚体上一点P 的位置矢量为k j i r ϖϖϖϖ543++=，其单位为m 210-，若以s m /102-为速度单位，则该时刻P 点的速度为：（ ） A υϖ＝94.2i ϖ+125.6j ϖ+157.0k ϖ； B υϖ=34.4k ϖ； C υϖ=-25.1i ϖ+18.8j ϖ； D υϖ=-25.1i ϖ-18.8j ϖ；2、一均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示。
今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的？（ ）A 角速度从小到大，角加速度从大到小。
B 角速度从小到大，角加速度从小到大。
C 角速度从大到小，角加速度从大到小。
D 角速度从大到小，角加速度从小到大。
3、刚体角动量守恒的充分而必要的条件是：（ ）A 刚体不受外力矩的作用B 刚体所受合外力矩为零C 刚体所受的合外力和合外力矩均为零D 刚体的转动惯量和角速度均保持不变4、某刚体绕定轴做匀变速转动时，对于刚体上距转轴为r 出的任一质元m ∆来说，它的法向加速度和切向加速度分别用n a 和t a 来表示，则下列表述中正确的是 （ ）（A ）n a 、t a 的大小均随时间变化。
（B ）n a 、t a 的大小均保持不变。
（C ）n a 的大小变化, t a 的大小恒定不变。
（D ）n a 的大小恒定不变, t a 的大小变化。
5、有两个力作用在一个有固定转轴的刚体：（1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零；（2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；（3）当这两个力的合力为零时，它们对轴的合力矩也一定是零；（1） 当这两个力对轴的合力矩为零时，它们的合力也一定是零。
A 只有（1）是正确的。
B （1），（2）正确，（3），（4）错误。
刚体结构力学试题及答案
刚体结构力学试题及答案一、选择题（每题4分，共20分）1. 刚体的转动惯量与物体的质量和形状有关，以下说法正确的是（）。
A. 质量越大，转动惯量越大B. 质量分布越集中，转动惯量越小C. 质量分布越分散，转动惯量越大D. 转动惯量与物体的质量无关答案：C2. 刚体在力的作用下发生旋转，下列说法正确的是（）。
A. 力矩的大小与力的大小成正比B. 力矩的大小与力臂的长度成反比C. 力矩的大小与力的大小和力臂的长度都成正比D. 力矩的大小与力的大小和力臂的长度都无关答案：C3. 刚体的角速度与线速度之间的关系是（）。
A. 角速度是线速度的两倍B. 线速度是角速度的两倍C. 角速度与线速度成正比D. 角速度与线速度成反比答案：C4. 在刚体的平移运动中，下列说法正确的是（）。
A. 刚体上任意两点的位移相同B. 刚体上任意两点的速度相同C. 刚体上任意两点的加速度相同D. 以上说法都正确答案：D5. 刚体的转动惯量与物体的转动轴有关，以下说法正确的是（）。
A. 转动轴越靠近物体的重心，转动惯量越小B. 转动轴越远离物体的重心，转动惯量越大C. 转动轴的位置不影响转动惯量D. 转动轴的位置与转动惯量无关答案：A二、填空题（每题4分，共20分）1. 刚体的转动惯量定义为物体的质量与其到转轴的____的乘积。
答案：距离平方2. 刚体在力矩作用下产生的角加速度的大小与力矩成正比，与物体的____成反比。
答案：转动惯量3. 根据牛顿第二定律，刚体的角加速度等于力矩除以物体的____。
答案：转动惯量4. 刚体的角速度和角位移的单位分别是____和____。
答案：弧度每秒，弧度5. 刚体在平面内的运动可以分解为____和____。
答案：平移，旋转三、简答题（每题10分，共30分）1. 请简述刚体的转动惯量与哪些因素有关，并举例说明。
答案：刚体的转动惯量与物体的质量分布和转轴的位置有关。
例如，一个均匀的圆盘绕通过其质心的轴旋转时，其转动惯量较小；而如果绕通过其边缘的轴旋转，其转动惯量则较大。
刚体习题和答案
作业5 刚体力学♫刚体：在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速，t ＝0时角速度为05rad s ω=，t ＝20s 时角速度为00.8ωω=，那么飞轮的角加速度β= -0.05 rad/s 2 ，t ＝0到 t ＝100 s 时间飞轮所转过的角度θ= 250rad ． 【解答】飞轮作匀变速转动，据0t ωωβ=+，可得出：200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律：定轴转动的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2)，如下图．绳与轮之间无相对滑动．假设某时刻滑轮沿逆时针方向转动，那么绳中的力 (A) 处处相等． (B) 左边大于右边． (C) 右边大于左边． (D) 哪边大无法判断． 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1＜m 2)，实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得：21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上，现在在绳端挂一质量为m 的重物，飞轮的角加速度为．如果以拉力2mg 代替重物拉绳时，飞轮的角加速度将(A) 小于． (B) 大于，小于2． (C) 大于2． (D) 等于2． 【解答】设飞轮的半径为R ,质量为m ，根据刚体定轴转动定律M J β=，当挂质量为m 的重物是：mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时，有： '2mgR J β=，2'mgRJβ=，比拟二者可得出结论。
大学物理刚体习题
大学物理刚体习题(总13页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习 题第三章 刚体的转动刚体的定轴转动47. 一定滑轮半径为R ，质量为M ，用一质量不计的绳绕在滑轮上，另一端系一质量为m 的物体并由静止释放，这时滑轮的角加速度为1β，若不系物体而用一力F = mg 拉绳子使滑轮转动，这时角加速度为2β，这时有（）1β2β（）1β2β （C ）1β2β（D ）无法判断 分析由转动定律M I β=本题中I 不变β的大小完全取决于M 的大小而 M TR =系物体m 时 : T mg <不系物体而用一力F = mg 时: TF mg ==因此力矩变大所以有12ββ<mF选49.一飞轮的转动惯量为J ，t = 0时角速度为0ω，轮子在转动过程中受到一力矩2ωk M-=，则当转动角速度为0/3ω时的角加速度β = 从0ω到0/3ω飞轮转动经过的时间t ∆= 解: (1) 求β当0/3ω时, 20()3M k ω=-由 M J β=, 可得此时 209k MJ J ωβ==-(2) d M J J dt ωβ== 2d k J dt ωω-=分离变量，两边积分32td kdt Jωωωω-=⎰⎰解得: 02J t k ω∆=50．长为l 的均匀直棒可绕其下端与棒垂直的水平光滑轴在竖直平面内转动。
抬起一端使与水平夹角为60=θ，棒对轴的转动惯量为231ml J =，由静止释放直棒，则t = 0时棒的β＝？；水平位置时的β＝？这时的ω=（1）求β 据转动定律M J β=, MJβ= 0t =时， cos 602lM mg =︒水平位置时， 2lM mg =代入MJβ=，可别解得034glβ= 和 32g l β= （2）求ωd d d d M J J J J dt d dt d ωωθωβωθθ====将cos 2l M mg θ=和213J ml =代入化简并积分得， 0033cos 2g d d l ωπθθωω=⎰⎰ 60可求得332g l ω=（本题还可用动能定律机械能守恒方便求解ω）2211sin 60223l mg ml ω︒=⋅ 332g lω⇒=51．一飞轮以min /600rev 的转速转动，其转动惯量为25.2m kg J ⋅=，以恒定力矩使飞轮在一分钟内停止转动，求该力矩M 。
刚体的简单运动习题及答案
刚体的简单运动习题及答案刚体的简单运动习题及答案刚体是物理学中的一个基本概念，它指的是在运动过程中形状和大小不发生改变的物体。
在学习刚体的运动时，我们可以通过一些简单的习题来加深对刚体运动的理解。
下面，我将为大家提供一些常见的刚体运动习题及答案。
习题一：平抛运动小明站在一个高处，手中拿着一个小球，以一定的初速度将球水平抛出。
假设空气阻力可以忽略不计，请问球的运动轨迹是什么形状？答案：球的运动轨迹是一个抛物线。
在平抛运动中，刚体在水平方向上做匀速直线运动，在竖直方向上受到重力的作用，所以球的轨迹是一个抛物线。
习题二：滚动运动一个圆柱体沿着水平面滚动，它的质心速度和边缘速度哪个更大？答案：质心速度和边缘速度相等。
在滚动运动中，刚体的质心沿着运动方向做匀速直线运动，而刚体的边缘点则具有线速度和角速度的叠加效果。
由于圆柱体的每个点都有相同的角速度，所以质心速度和边缘速度相等。
习题三：转动惯量一个均匀的圆盘和一个均匀的长方体，它们的质量和半径（或边长）相同，哪个的转动惯量更大？答案：圆盘的转动惯量更大。
转动惯量是刚体旋转时惯性的量度，它与刚体的质量分布有关。
由于圆盘的质量分布更加均匀，所以它的转动惯量更大。
习题四：平衡条件一个悬挂在绳子上的物体处于平衡状态，绳子与竖直方向的夹角是多少？答案：绳子与竖直方向的夹角等于物体所受的重力与绳子张力的夹角。
在平衡状态下，物体所受的重力与绳子张力必须保持平衡，即两者的合力为零。
因此，绳子与竖直方向的夹角取决于物体所受的重力与绳子张力的大小关系。
习题五：平移运动和转动运动一个刚体在平面上做平移运动时，它的转动惯量是多少？答案：在平移运动时，刚体的转动惯量为零。
平移运动是指刚体的质心沿直线运动，此时刚体没有绕任何轴心旋转，所以转动惯量为零。
通过以上习题的解答，我们可以更好地理解刚体的运动特性。
刚体的运动涉及到平抛运动、滚动运动、转动惯量和平衡条件等方面的知识，通过解答这些习题，我们可以加深对刚体运动的理解，提高解题能力。
刚体考试题及答案
刚体考试题及答案一、选择题（每题2分，共20分）1. 刚体的转动惯量是关于旋转轴的（）。
A. 常数B. 函数C. 随机变量D. 无规律变化答案：A2. 刚体绕固定轴的转动惯量I与质量M和半径r的关系是（）。
A. I = Mr^2B. I = 2MrC. I = MrD. I = 1/2Mr^2答案：D3. 刚体的平移运动和转动运动的合成是（）。
A. 平移运动B. 转动运动C. 螺旋运动D. 不确定答案：C4. 刚体的角速度和线速度的关系是（）。
A. 线速度是角速度的两倍B. 线速度是角速度的一半C. 线速度与角速度成正比D. 线速度与角速度无关答案：C5. 刚体的角动量守恒的条件是（）。
A. 外力矩为零B. 外力为零C. 外力矩和外力都为零D. 外力矩和外力都不为零答案：A6. 刚体的动能与（）有关。
A. 质量B. 速度C. 转动惯量D. 所有以上因素答案：D7. 刚体的角加速度与（）有关。
A. 外力矩B. 转动惯量C. 角速度D. 所有以上因素答案：A8. 刚体的进动角速度与（）有关。
A. 外力矩B. 转动惯量C. 角速度D. 所有以上因素答案：D9. 刚体的章动周期与（）有关。
A. 转动惯量B. 外力矩C. 角速度D. 所有以上因素答案：A10. 刚体的自由振动的周期与（）有关。
A. 转动惯量B. 外力矩C. 角速度D. 所有以上因素答案：A二、填空题（每题2分，共20分）1. 刚体的转动惯量是关于旋转轴的________。
答案：常数2. 刚体绕固定轴的转动惯量I与质量M和半径r的关系是I = ________。
答案：1/2Mr^23. 刚体的平移运动和转动运动的合成是________。
答案：螺旋运动4. 刚体的角速度和线速度的关系是线速度与角速度________。
5. 刚体的角动量守恒的条件是外力矩________。
答案：为零6. 刚体的动能与________有关。
答案：所有以上因素7. 刚体的角加速度与________有关。
刚体习题及答案
解法二:
用角动量定理求解
0-10s: 0-90s:
(M M r )t1 J 1 0
(M r t2 ) 0 J1
联立得： Mt1t2 J1 (t1 t2 )
J Mt1t2 / 1 (t1 t2 ) 54kg m2
例4.一圆盘绕过盘心且与盘面垂直的轴 o 以角速度 按图示方 向转动，若射来两颗完全相同的子弹，方向相反并在同一条直 线上，子弹射入圆盘并留在其中，则子弹射入后的瞬间，盘的 角速度 （A）增大;（B）减小; （C）不变;（D）不能确定。
解： (1)dM dm g r
m M dM 2 rdr 1 mgl 0 l 4 (2)由角动量定理：
1 2
m m dr g r rdr l l
Mt J J 0 J 0
J 0 0 l t 3mg M
人: Mg T 2 Ma
1 1 物 : T1 - Mg = Ma 2 2
B
T2
o
T1
2 a g 7
A
Mg
B
a
轮： (T2 T1 ) R J
1 Mg 2
a R
例2.两个匀质圆盘，一大一小，同轴地粘结在一起，构成一个 组合轮。小圆盘的半径为r，质量为m；大圆盘的半径r’＝2r， 质量为m’=2m。组合轮可绕通过其中心且垂直于盘面的光滑水 平固定轴O转动，对O轴的转动惯量J＝9mr2/2。两圆盘边缘上 分别绕有轻质细绳，细绳下端各悬挂质量为m的物体A和B，如 图所示。这一系统从静止开始运动，绳与盘无相对滑动，绳的 长度不变。已知r = 10 cm．求： (1) 组合轮的角加速度； (2) 当物体A上升h＝40 cm时，组合轮的角速度ω。
刚体习题和答案
作业5 刚体力学♫刚体：在力的作用下不发生形变的物体⎰=-⇒=21ttdtdtdωθθθω角速度⎰=-⇒=21ttdtdtdβωωωβ角加速度1、基础训练（8）绕定轴转动的飞轮均匀地减速，t＝0时角速度为5rad sω=，t＝20s时角速度为0.8ωω=，则飞轮的角加速度β=-0.05 rad/s2 ，t＝0到t＝100 s时间内飞轮所转过的角度θ=250rad．【解答】飞轮作匀变速转动，据tωωβ=+，可得出：200.05rad stωωβ-==-据212t tθωβ=+可得结果。
♫定轴转动的转动定律：定轴转动的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比.βJM=质点运动与刚体定轴转动对照[C] 1、基础训练（2）一轻绳跨过一具有水平光滑轴、质量为M的定滑轮，绳的两端分别悬有质量为m1和m2的物体(m1＜m2)，如图所示．绳与轮之间无相对滑动．若某时刻滑轮沿逆时针方向转动，则绳中的张力(A) 处处相等．(B) 左边大于右边．(C) 右边大于左边．(D) 哪边大无法判断．【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m1＜m2)，实际上滑轮在作减速转动,角加速度方向垂直纸面向内,所以,由转动定律21()T T R Jβ-=可得：21T T>[ C] 2、自测提高（2）将细绳绕在一个具有水平光滑轴的飞轮边缘上，现在在绳端挂一质量为m的重物，飞轮的角加速度为．如果以拉力2mg代替重物拉绳时，飞轮的角加速度m2m1O将(A) 小于． (B) 大于，小于2． (C) 大于2． (D) 等于2．【解答】设飞轮的半径为R ,质量为m ，根据刚体定轴转动定律M J β=，当挂质量为m 的重物是：mg T ma TR J a R ββ-===所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时，有： '2mgR J β=，2'mgRJβ=，比较二者可得出结论。
第七章 刚体力学习题及解答
第七章刚体力学习题及解答7。
1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度。
估算地心因公转而具有的线速度和向心加速度（自己搜集所需数据）。
解：7.1.2 汽车发动机的转速在12s内由1200rev/min增加到3000rev/min。
（1）假设转动是匀加速转动,求角加速度.（2）在此时间内,发动机转了多少转？解：（ 1）（ 2)所以转数 =7.1.3 某发动机飞轮在时间间隔t内的角位移为球 t时刻的角速度和角加速度.解：7.1.4 半径为0。
1m的圆盘在铅直平面内转动,在圆盘平面内建立坐标系,原点在轴上。
x和y轴沿水平和铅直向上的方向.边缘上一点A当t=0时恰好在x轴上,该点的角坐标满足求（1）t=0时，(2)自t=0开始转时，（3）转过时，A点的速度和加速度在x和y轴上的投影。
解:（ 1）( 2) 时，由（ 3）当时，由7。
1。
5 钢制炉门由两个各长1.5m的平行臂AB和CD支承，以角速度逆时针转动，求臂与铅直时门中心G的速度和加速度.解:因炉门在铅直面内作平动，门中心 G的速度、加速度与B或D点相同.所以：7。
1.6 收割机拔禾轮上面通常装4到6个压板。
拔禾轮一边旋转，一边随收割机前进。
压板转到下方才发挥作用，一方面把农作物压向切割器，另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反.已知收割机前进速率为 1。
2m/s，拔禾轮直径1.5m，转速22rev/min，求压板运动到最低点挤压作物的速度.解：取地面为基本参考系，收割机为运动参考系。
取收割机前进的方向为坐标系正方向7。
1.7 飞机沿水平方向飞行，螺旋桨尖端所在半径为150cm,发动机转速2000rev/min。
（1)桨尖相对于飞机的线速率等于多少？（2）若飞机以250km/h的速率飞行,计算桨尖相对于地面速度的大小，并定性说明桨尖的轨迹。
刚体试题及答案
刚体试题及答案1.（10分）半径为30cm 的飞轮从静止开始以 0.5 rad/s 2的匀角加速度转动，求飞轮边缘一点在飞轮转过2400时的切向加速度和法向加速度。
解：（1）（2）2.（10分）在质量为 M ，半径为 R 的匀质圆盘上挖出半径为 r 的两个圆孔，圆孔中心在半径 R 的中点，求剩余部分对通过大圆盘中心O 且与盘面垂直的轴线的转动惯量。
解：用填补法。
其中得3.（15分）在倾角为θ的斜面顶端固定一滑轮，用一根绳子缠绕数圈后引出与木块M 连接，M 与斜面摩擦系数为μ（如图），设滑轮质量为m ，半径为R ，轴处无摩擦。
试分析M 作加速运动的条件。
解: 由牛顿第二定律Ma N T M ＝－－ｇμθsinN ’、ｍg 对转轴的力矩为零由转动定律得 αα221R J TR ｍ＝＝平动与转动的关系通过线量与角量联系起来：αR a ＝四个未知量 ()()＋ｍ－ｇ＝得M M a 2cos sin 2θμθM 作加速运动应满足的条件是： 0c o s s i n >θμθ－)/(15.050.030.02s m r a t=⨯==α)/(26.130.018024050.02222s m r r a n =⨯⨯⨯⨯===παθω210J J J J --=22212)2(2,2R m mr J J MR J +===由平行轴定理得：22r R M m =)/2(2122420r R r R M J --=0cos ＝ｇ－θM Nμθ>an 即ｔ4.（15分）一轻绳绕过固定在一起的两个同轴圆柱形刚体，圆柱体可绕OO’ 轴转动，两圆柱体半径分别为R 1 、R 2 （R 2 >R 1），质量分别为M 1 、M 2，绳下连接ｍ1 、ｍ2，求刚体转动时的角加速度。
解：隔离体受力分析如图11112222a T a T ｇ＝ｍ－ｍ＝ｍｇ－ｍ由转动定律得:α21212222111122）＋＝（－R M R M R T R T平动与转动的联系:αα2211R a R a ＝＝222221111122222αR M R M R R ）＋ｍ＋（）＋ｍ（）ｇ－ｍ（ｍ＝讨论：Ⅰ）当ｍ2R 2 >ｍ1R 1时，α>0，则表明圆柱体实际转动方向与所设方向相同，即ｍ2下降，而ｍ1上升。
大学物理第四章-刚体的转动-习题及答案
1．刚体绕一定轴作匀变速转动，刚体上任一点是否有切向加速度？是否有法向加速度？切向和法 向加速度的大小是否随时间变化？
答：当刚体作匀变速转动时,角加速度 不变。刚体上任一点都作匀变速圆周运动，因此该点速
率在均匀变化，v l ，所以一定有切向加速度 at l ，其大小不变。又因该点速度的方向变化，
ω dr
（1）圆盘上半径为r、宽度为dr的同心圆环所受的摩擦力矩
为
dM
m
(
R2
2 rdr)grBiblioteka 2r 2 mgdr/
R2
负号表示摩擦力矩为阻力矩。对上式沿径向积分得圆盘所受
r dF
的总摩擦力矩大小为
M dM R 2r2mgdrdr 2 mgR
0
R2
3
（2）由于摩擦力矩是一恒力矩，圆盘的转动惯量 I 1 mr2 ，由角动量定理可得圆盘停止的 2
度．
解：碰撞过程满足角动量守恒：
2 3
mv0l
1 2
mv0
2 3
l
I
而
I m( 2 l)2 2m(1 l)2 2 ml2
3
33
所以
mv0l
2 3
ml 2
由此得到： 3v0 2l
2m
1 3
l
O⅓l
1 2
v
0
2 3
l
m
⅓l m v0
⅓l
15. 如图所示，A和B两飞轮的轴杆在同一中心线上，设两轮的转动惯量分别为 JA＝10 kg·m2 和 JB
2
2
22
2
2
1 16
( Ld14
1 2
ad24
大学物理-刚体的定轴转动-习题和答案
第4章 刚体的定轴转动 习题及答案1．刚体绕一定轴作匀变速转动，刚体上任一点是否有切向加速度？是否有法向加速度？切向和法向加速度的大小是否随时间变化？答：当刚体作匀变速转动时,角加速度β不变。
刚体上任一点都作匀变速圆周运动，因此该点速率在均匀变化，v l ω=，所以一定有切向加速度t a l β=，其大小不变。
又因该点速度的方向变化，所以一定有法向加速度2n a l ω=，由于角速度变化，所以法向加速度的大小也在变化。
2. 刚体绕定轴转动的转动定律和质点系的动量矩定理是什么关系？答：刚体是一个特殊的质点系，它应遵守质点系的动量矩定理，当刚体绕定轴Z 转动时，动量矩定理的形式为zz dL M dt=，z M 表示刚体对Z 轴的合外力矩，z L 表示刚体对Z 轴的动量矩。
()2z i i L m l I ωω==∑,其中()2i i I m l =∑，代表刚体对定轴的转动惯量，所以()z z dL d d M I I I dt dt dtωωβ====。
既 z M I β=。
所以刚体定轴转动的转动定律是质点系的动量矩定理在刚体绕定轴转动时的具体表现形式，及质点系的动量矩定理用于刚体时在刚体转轴方向的分量表达式。
3．两个半径相同的轮子，质量相同，但一个轮子的质量聚集在边缘附近，另一个轮子的质量分布比较均匀，试问：（1）如果它们的角动量相同，哪个轮子转得快？（2）如果它们的角速度相同，哪个轮子的角动量大？答：(1)由于L I ω=，而转动惯量与质量分布有关，半径、质量均相同的轮子，质量聚集在边缘附近的轮子的转动惯量大，故角速度小，转得慢，质量分布比较均匀的轮子转得快；（2）如果它们的角速度相同，则质量聚集在边缘附近的轮子角动量大。
4．一圆形台面可绕中心轴无摩擦地转动，有一玩具车相对台面由静止启动，绕轴作圆周运动，问平台如何运动？如小汽车突然刹车，此过程角动量是否守恒？动量是否守恒？能量是否守恒？答：玩具车相对台面由静止启动，绕轴作圆周运动时，平台将沿相反方向转动；小汽车突然刹车过程满足角动量守恒，而能量和动量均不守恒。
(完整word版)刚体的平面运动作业习题参考答案1
8-1 图示四杆机构1OABO 中，AB B O OA 211==；曲柄OA 的角速度s rad /3=ω。
求当090=ϕ而曲柄B O 1重合于1OO 的延长线上时，杆AB 和曲柄B O 1的角速度。
参考答案：因OA 杆作定轴转动，故OA v A ⋅=ω。
AB 杆做平面运动其速度瞬心为O 点，s rad OAv AAB /3===ωω，而OA OB v AB B ⋅=⋅=ωω3， 所以s rad s rad BO OAB O v B B O /2.5/3333111≈==⋅==ωωω（逆时针）8-2 四连杆机构中，连杆AB 上固联一块三角板 ABD 。
机构由曲柄A O 1带动。
已知：曲柄的角速度s rad A O /21=ω；曲柄cm A O 101=，水平距离cm O O 521=；AD=5cm ,当A O 1铅垂时，AB 平行于21O O ，且AD 与1AO 在同一直线上；角030=ϕ。
求三角板ABD 的角速度和D 点的速度。
参考答案：三角板 ABD C ，由此可得：s rad ctg O O AO AO AC v A O A/07.121111=⋅+⋅==ϕωωs cm CD v D /35.25=⋅=ω8-7 如图所示，在振动机构中，筛子的摆动由曲柄连杆机构所带动。
已知曲柄OA 的转速cm OA r n 30min,/40==。
当筛子BC 运动到与点O 在同一水平线上时，090=∠BAO ，求此瞬时筛子BC 的速度。
解：由图示机构知BC 作平行移动，图示位置时，B v 与CBO 夹角为30°，与AB 夹角为60°。
Av Bv Dv Av CωAv Bv由题意知 m/s π40.030.03040π=⨯⨯=⋅=OA v A ω 由速度投影定理 AB B AB A v v )()(= 得 ︒=60cos B A v vm/s 2.51π8.060cos ==︒==AB BC v v v8-6 图示机构中，已知cm EF cm DE cm BD cm OA 310,10,10,10==== OA ωs rad /4=，在图示位置，曲柄OA 与水平线OB 垂直，且B 、D 和F 在同一铅直线上。
力学习题-第7章刚体(下含答案)
第七章刚体单元测验题一、选择题1.如图，一个高为h 、底面半径为R 的圆锥体可绕其固定的铅垂轴自由旋转，转动惯量为J 0.在其表面沿母线刻有一条光滑的斜槽.开始时，锥体以角速度ω0旋转，此时，将质量为m 的小滑块从槽顶无初速释放，设在滑块沿槽滑下的过程中始终不脱离斜槽，则当滑块到达底边时，圆锥体的角速度为A.02000+=mR J J ωω;C.2000-=mR J J ωω;D.0=ω答案：B 解：以滑块和圆锥体为研究对象，在转轴方向的外力矩为零，转轴方向角动量守恒：00J ω=20()J mR ω+解得：0020J J mR ωω=+2.如图，质量为m 0、半径为R 的圆盘静止在光滑水平桌面上，一质量为m 的子弹以速度v 0射入圆盘的边缘并留在该处，v 0的方向与入射处的半径垂直.则子弹射入后圆盘系统总动能为A.2=0E K ;B.)+(2=0202m m v m E K ;C.)3+(23=0202m m v m E K ;D.)5+(23=0202m m v m E K 答案：C 解：子弹入射后，子弹和圆盘组成的系统质心与圆盘中心的距离：0c mRr m m=+入射过程动量守恒：()00cmv m m v =+系统对圆盘质心所在的空间固定点角动量守恒：00()c c mv R m m v r J ω=++，其中，222001()2c c J m R m r m R r =++-动能：22021+)+(21=ωJ v m m E c K 联立解得：)3+(23=0202m m v m E K 3.如图，两光滑墙面互相垂直，在墙B 上离墙面A 距离s 处，有一光滑钉子，将一长度为2l 、质量为m 0的均匀杆的一端抵在墙上，杆身斜置在钉子上，使杆位于垂直于墙面A 的竖直平面内，则平衡时杆与水平所成的角θ满足A.l cos θl s =cos 2θ; C.l s =sin 2θ; D.ls=cos 3θ答案：D解：设墙面B 平行于纸面，墙面A 垂直于纸面，以杆为研究对象，静力学平衡。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作业5 刚体力学1 23 ♫刚体：在力的作用下不发生形变的物体4⎰=-⇒=210t t dt dtd ωθθθω角速度5 ⎰=-⇒=210t t dt dtd βωωωβ角加速度6 1、基础训练（8）绕定轴转动的飞轮均匀地减速，t ＝0时角速度为05rad s ω=，7 t ＝20s 时角速度为00.8ωω=，则飞轮的角加速度β= -0.05 rad/s 2 ，t ＝0到 8 t ＝100 s 时间内飞轮所转过的角度θ= 250rad ． 9【解答】10飞轮作匀变速转动，据0t ωωβ=+，可得出：200.05rad s tωωβ-==-11据2012t t θωβ=+可得结果。
12♫定轴转动的转动定律：13 定轴转动的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比.14 βJ M =15 质点运动与刚体定轴转动对照16 17 18 192021 222324 25 262728 2930 [C ] 1、基础训练（2）一轻绳跨过一具有水平光滑轴、质量为M 的31 定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2)，如图所32 示．绳与轮之间无相对滑动．若某时刻滑轮沿逆时针方向转动，则绳33 中的张力34(A) 处处相等． (B) 左边大于右边．35(C) 右边大于左边． (D) 哪边大无法判断． 36【解答】37逆时针转动时角速度方向垂直于纸面向外, 由于(m 1＜m 2)，实际上滑轮在作减38 速转动,角加速度方向垂直纸面向内,所以,由转动定律21()T T R J β-=可得：39 21T T >40 [ C ] 2、自测提高（2）将细绳绕在一个具有水平光滑轴的飞轮边缘上，现41 在在绳端挂一质量为m 的重物，飞轮的角加速度为．如果以拉力2mg 代替重42 物拉绳时，飞轮的角加速度将 43(A) 小于． (B) 大于，小于2． (C) 大于2． (D)44 等于2．45【解答】46m 2m 1O47 484950'2mgR J β=，2'mgRJβ=，比较二者可得出结论。
5152 3、基础训练（9）一长为l ，质量可以忽略的直杆，可绕通53 过其一端的水平光滑轴在竖直平面内作定轴转动，在杆的另一54 端固定着一质量为m 的小球，如图5-12所示．现将杆由水平55 位置无初转速地释放．则杆刚被释放时的角加速度β0= g/l ，杆与水平方向夹56 角为60°时的角加速度β= g/2l ． 57【解答】58由转动定律:M J β=59(1)开始时杆处于水平位置: 0mgl J β=60其中 2J ml =为小球相对于转轴的转动惯量,得：0g lβ=61(2) cos mgl J θβ=, 2glβ=62m4、基础训练（12） 如图5-14所示，滑块A 、重物63 B 和滑轮C 的质量分别为m A 、m B 和m C ，滑轮的半径为R ，64 滑轮对轴的转动惯量J ＝21m C R 2．滑块A 与桌面间、65 滑轮与轴承之间均无摩擦，绳的质量可不计，绳与滑轮之间无相对滑动．滑块A 66 的加速度CB A B m m m gm a ++=)(2267【解答】6869 70 71 72B B B G T m a -= (2) 73A A T m a = (3)74a R β= (4)754个方程,共有4个未知量: A T 、B T 、a 和β。
可求：()22B A B c a m g m m m =++⎡⎤⎣⎦765、基础训练（18）如图5-17所示、质量分别为m 和2m 、半径分别为r 和2r 77 的两个均匀圆盘，同轴地粘在一起，可以绕通过盘心且垂直盘面的水平光滑固78 定轴转动，对转轴的转动惯量为9mr 2/2，大小圆盘边缘都绕有绳子，绳子下端79 都挂一质量为m 的重物，求盘的角加速度的大小． 80【解答】81受力情况如图5-17，'11T T =，'22T T = 82 11mg T ma -= (1) 8322T mg ma -= (2) 84122T r T r J β-= (3)85 12a r β= (4) 86 2a r β= (5)87 联立以上几式解得: 219g r886、自测提高（15）如图5-23所示，转轮A 、B 可分别独立地89 绕光滑的固定轴O 转动，它们的质量分别为m A ＝10 kg 和m B ＝20 90 kg ，半径分别为r A 和r B ．现用力f A 和f B 分别向下拉绕在轮上的91 细绳且使绳与轮之间无滑动．为使A 、B 轮边缘处的切向加速度92 相同，相应的拉力f A 、f B 之比应为多少？(其中A 、B 轮绕O 轴转93 动时的转动惯量分别为221A A A r m J =和221B B B r m J =)94 【解答】95根据转动定律 A A A A f r J β= （1） 96 B B B B f r J r = （2） 97 其中212A A A J m r =212B B B J m r = 98要使A 、B 轮边缘处的切向加速度相同，应有： 99 A A B B a r r ββ== （3）100由（1）、（2）式有A AB A A A AB B A B B B Bf J r m r f J r m r ββββ== （4） 101f B B A f Ar Br A由（3）式有A AB Br r ββ= 102将上式代入（4），得12A AB B f m f m == 103♫转动惯量：104质量非连续分布：22222112j j j j r m r m r m r m J +++=∆=∑ 105质量连续分布：m r r m J j jj d 22⎰∑=∆=1061、基础训练（10）如图5-13所示，P 、Q 、R 和S 是附于刚性轻质细杆上的质107 量分别为4m 、3m 、2m 和m 的四个质点，PQ ＝QR ＝RS ＝l ，则系统对O O '轴的转108 动惯量为 50ml 2 。
109【解答】110据 2i i J m r =∑有：11122224(3)3(2)2050J m l m l ml ml =+++=112113 ♫摩擦力矩：⎰=-=-=-=dMM gdm r dN r rdf dM μμ1141、自测提高（12）一根质量为m 、长为l 的均匀细杆，可在水平桌面上绕通115 过其一端的竖直固定轴转动．已知细杆与桌面的滑动摩擦系数为，则杆转动116 时受的摩擦力矩的大小为=μmgl /2 117【解答】118RPS R Q RO′在细杆长x 处取线元dx ，所受到的摩擦力矩dM=μ(m/l)gxdx ，则119 02lm mgl M gxdx l μμ==⎰120♫121♫定轴转动的角动量定理：1221d d d ωωJ J t M tL M t t -=⇒=⎰122角动量守恒:合外力矩为零。
ωJ L =为常量123[ B ] 1、基础训练（5）如图5-9所示，一静止的均匀细棒，长为L 、质量为124 M ，可绕通过棒的端点且垂直于棒长的光滑固定轴O 在水平面内转动，转动惯量125 为231ML ．一质量为m 、速率为v 的子弹在水平面内沿与棒垂直的方向射出并穿126出棒的自由端，设穿过棒后子弹的速率为v 21127(A)ML mv ． (B) ML m 23v ． (C) ML m 35v ． (D) MLm 47v． 128【解答】129130131132v21v俯视图[ C ] 2、基础训练（7）一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，133 如图5-11射来两个质量相同，速度大小相同，方向134 相反并在一条直线上的子弹，子弹射入圆盘并且留135 在盘内，则子弹射入后的瞬间，圆盘的角速度136(A) 增大． (B) 不变．137(C) 减小． (D) 不能确定． 138 【解答】139把三者看作同一系统时,系统所受合外力矩为零,系统角动量守恒。
140设L 为每一子弹相对与O 点的角动量大小，据角动量守恒定律有：14100()J L L J J J J J ωωωωω+-=+=<+子弹子弹142[ A ] 3、自测提高（7）质量为m 的小孩站在半径为R 的水平平台边缘上．平143 台可以绕通过其中心的竖直光滑固定轴自由转动，转动惯量为J ．平台和小孩开144 始时均静止．当小孩突然以相对于地面为v 的速率在台边缘沿逆时针转向走动145 时，则此平台相对地面旋转的角速度和旋转方向分别为146(A) ⎪⎭⎫⎝⎛=R J mR v 2ω，顺时针． (B) ⎪⎭⎫ ⎝⎛=R J mR v 2ω，逆时针．147(C) ⎪⎭⎫⎝⎛+=R mR J mR v 22ω，顺时针． (D) ⎪⎭⎫⎝⎛+=R mR J mR v 22ω，逆时针． 148【解答】149OMmm图5-11视小孩与平台为一个系统，该系统所受的外力矩为零，系统角动量守恒：1500Rmv J ω=- 可得 2()Rmv mR vJ J R ω==。
151，顺时针． (D) ⎪⎭⎫⎝⎛+=R mR J mR v 22ω，逆时针． 1524、基础训练（16）一转动惯量为J 的圆盘绕一固定轴转动，起初角速度为0ω，153 设它所受阻力矩与转动角速度成正比，即M k ω=- (k 为正的常数)，求圆盘154 的角速度从0ω变为021ω时所需时间．155【解答】156 ωk M -= 157 根据 dtd JJ M ωβ== 158ωJd Mdt = ωκωJd dt =-159 ⎰⎰=-t d J dt 02100ωωωωκ 160所以得 kJ t 2ln =1615、自测提高（16）如图5-24所示，长为l 的轻杆，两端各162 固定质量分别为m 和2m 的小球，杆可绕水平光滑固定轴O 在163 竖直面内转动，转轴O 距两端分别为31l 和32l ．轻杆原来静止164 在竖直位置．今有一质量为m 的小球，以水平速度0v与杆下端165 小球m 作对心碰撞，碰后以021v的速度返回，试求碰撞后轻杆166 所获得的角速度．167【解答】168系统所受的合外力矩为零，角动量守恒： 169 碰前的角动量为： 170171 碰后的角动量为： 172 173 所以174175 得176177 6、自测提高（17）如图5-25所示，一质量均匀分布的圆盘，178 质量为0m ，半径为R ，放在一粗糙水平面上(圆盘与水平面之179 间的摩擦系数为)，圆盘可绕通过其中心O 的竖直固定光滑180 轴转动．开始时，圆盘静止，一质量为m 的子弹以水平速度v 0181 垂直于圆盘半径打入圆盘边缘并嵌在盘边上，如图5-25所示。