刚体部分作业问题全解
合集下载
刚体力学作业解答
1 ( MR 2 − mR 2 )ω 2
EK = 1 1 ( MR 2 − mR 2 )ω 2 2 2
4-11 •
30°
设碰后小球速度为v，受杆平均力f，作用时间∆t，则
小球 f∆t = mv − mv0 棒 − fl∆t = Iω − 0 (1) ( 2)
得
mv0 l − mvl = Iω
(3)
F (l1 + l 2 ) − N ′l1 = 0 (a)
Fy
l1
A
N ′
l2
闸 瓦
F
F r′
x
Fx
题图4-4(b)
N
α
Fr
R
N′ =
l1 + l 2 F l1
mg
⋅
O
ω
题图 4-4(c)
N′ =
l1 + l 2 F l1
N
飞轮受到闸瓦的摩擦力为：
l +l Fr = µN = µN ′ = µ 1 2 F l1
r r
α
r T
F = 98 N
m
mg = 98 N
(b)
T
a m
mg
(c)
(a)
题图4 = Jα
M Fr = = 39.2rad ⋅ s − 2 J J
（2）当绳子拉下l=5 m时，飞轮转过的角度 ω 2 = 2αθ =1960
θ=
l = 25rad r
ω = 44.3rad ⋅ s
θ = ω 0 t + αt 2 = 15 × 2π × 7.07 − × 13.3333 × ( π ) 2 = 53 × 2π (rad )
1 2 1 2 9 4
可知在这段时间里，飞轮转了53转． 53 (2)要求飞轮转速在t=2 s内减少一半，可知 ω0 − ω0 ω0 2 α= =− = −7.5πrad ⋅ s − 2
第四章作业解析
直悬挂时质心为重力势能零点。
初态机械能
E0
1 2
J 棒 2
1 6
Ml 22
末态机械能 E Mg l 2
系统机械能守恒，即 E E0
l2
C
则有 1 Ml22 l Mg
6
2
v0 C v0 2
可得 3g
l
带入（1）式
v0
4M 3m
l，可得
v0
4M 3m
3gl
三 计算题
1.一砂轮直径为1m、质量为50kg，以900r/min
小球这一系统
(A) 只有机械能守恒．(B) 只有动量守恒．
(C) 只有对转轴O的角动量守恒．
(D) 机械能、动量和角动量均守恒．［ C ］
解：将杆、小球与作为一个系统
o
系统不受外力矩作用，因此系统
对转轴O的角动量守恒，故选C。
注：小球与杆的外力矩为零，系统角动
量守恒；为非弹性碰撞，机械能不守恒。
二 填空题
统的角动量守恒。
v0 v0 2
将整个过程分为两个阶段：
第一阶段角动量守恒；第二阶段能量守恒
初态角动量（子弹射击棒前的角动量）
L0
J0
1 2
lmv0
m(
l 2
)2
0
m( l )2 2
v0 l2
末态角动量 L L1 L2
射击棒后子弹的角动量
C
l2
v0 C v0 2
L1
J
m( l )2 2
v0 l
空气的摩擦，当两球都滑至杆端时，杆的角速度
为
(A) 20 (C)0 2
(B) 0 (D)0 4
o
d ld
刚体部分作业问题
促进技术进步
刚体部分作业问题的研究和解决可 以推动相关领域的技术进步和创新， 促进产业的发展和升级。
02
刚体部分作业问题的基本概念
刚体的定义与特性
刚体的定义
刚体是指在运动过程中，其形状 和大小保持不变，内部任意两点 间的距离始终保持不变的物体。
刚体的特性
刚体具有质量、质心、转动惯量 等物理属性，同时还具有不变形 的特性。
刚体部分作业问
• 刚体部分作业问题概述 • 刚体部分作业问题的基本概念 • 刚体部分作业问题的解决方法 • 刚体部分作业问题的实例分析 • 刚体部分作业问题的未来研究方向
01
刚体部分作业问题概述
定义与特点
定义
刚体部分作业问题是指研究刚体在受 到外力作用时，如何通过改变其内部 结构或布局来达到最优性能或特定目 标的问题。
近似法
近似法是一种通过近似计算来求解问题的方法，适用于 数学模型复杂或精度要求不高的简单问题。
近似法的优点是计算速度快、简便易行，适用于对精度 要求不高的问题。
近似法通常需要使用经验公式或近似公式来简化问题， 通过简化计算过程来快速得到近似解。
近似法的缺点是结果可能存在误差较大，不适用于对精 度要求高的问题。
刚体部分作业问题的实际应用拓展研究
总结词
刚体部分作业问题具有广泛的应用前景，未来研究应 加强其在各个领域的拓展和应用。
详细描述
刚体部分作业问题在机械设计、航空航天、交通运输 、船舶制造等领域具有广泛的应用前景。未来应深入 研究这些领域的具体问题，将刚体部分作业问题的研 究成果应用于实际问题的解决中。同时，应关注新兴 领域的发展动态，积极探索刚体部分作业问题在这些 领域的应用可能性。通过实际应用拓展研究，不断完 善和丰富刚体部分作业问题的理论体系和应用实践。
刚体部分作业问题的研究和解决可 以推动相关领域的技术进步和创新， 促进产业的发展和升级。
02
刚体部分作业问题的基本概念
刚体的定义与特性
刚体的定义
刚体是指在运动过程中，其形状 和大小保持不变，内部任意两点 间的距离始终保持不变的物体。
刚体的特性
刚体具有质量、质心、转动惯量 等物理属性，同时还具有不变形 的特性。
刚体部分作业问
• 刚体部分作业问题概述 • 刚体部分作业问题的基本概念 • 刚体部分作业问题的解决方法 • 刚体部分作业问题的实例分析 • 刚体部分作业问题的未来研究方向
01
刚体部分作业问题概述
定义与特点
定义
刚体部分作业问题是指研究刚体在受 到外力作用时，如何通过改变其内部 结构或布局来达到最优性能或特定目 标的问题。
近似法
近似法是一种通过近似计算来求解问题的方法，适用于 数学模型复杂或精度要求不高的简单问题。
近似法的优点是计算速度快、简便易行，适用于对精度 要求不高的问题。
近似法通常需要使用经验公式或近似公式来简化问题， 通过简化计算过程来快速得到近似解。
近似法的缺点是结果可能存在误差较大，不适用于对精 度要求高的问题。
刚体部分作业问题的实际应用拓展研究
总结词
刚体部分作业问题具有广泛的应用前景，未来研究应 加强其在各个领域的拓展和应用。
详细描述
刚体部分作业问题在机械设计、航空航天、交通运输 、船舶制造等领域具有广泛的应用前景。未来应深入 研究这些领域的具体问题，将刚体部分作业问题的研 究成果应用于实际问题的解决中。同时，应关注新兴 领域的发展动态，积极探索刚体部分作业问题在这些 领域的应用可能性。通过实际应用拓展研究，不断完 善和丰富刚体部分作业问题的理论体系和应用实践。
第四章刚体运动习题详解
例1.一根长为L、质量为m的均匀细直棒, 其一端 有一固定的光滑水平轴，因而可以在竖直平 面内转动。 最初棒静止在水平位置， 求它由此下摆角时的角加速度和角速度。
解：棒下摆为加速过程， 外力矩为重力对O 的力矩。
棒上取质元dm,当棒处在 下摆角时,重力矩为：
x
O
X
C
dm
dM xgdm
合力矩
mg
gdm
解：
因摩擦力产生的力矩是恒定的，故角速度均匀 减小。
0
0
t
0
0 t
dt t
0
f dS
r
σ
m πR2
R
dθ o
r
M J 1 mR2
2
dr
t 0mR2 / (2M ) (1) M ?
考虑面元dS对轴的摩擦力矩dM ：
dM r0gdm r0g dS
26
t0mR2/(2M ) (1) dM r0g dS
mg 由(3)(4)(5)得
mgR sin
1 2
J02
1 2
J2
(5)
gh 2R2
cos2
g R
sin
1 2R
.
g 2
(h
4
3R)
M J
mgR 2mR2
g 2R
( 60 )
44
dt
O
X
C
即 d d
3g cos d d
mg
2L
θ
0
3gcos
2L
d
0
d
3g 2L
sin
1 2
2
3g sin
L
22
m 例2.质量为 、长为L的匀质细杆水平放置,一端
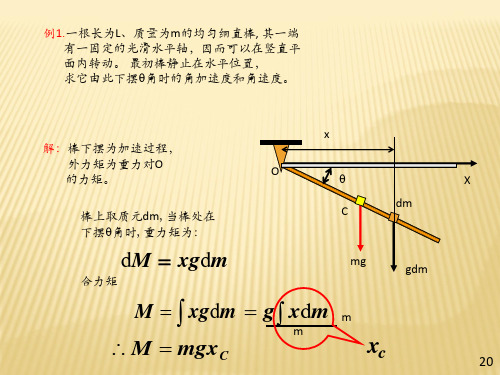
解：棒下摆为加速过程， 外力矩为重力对O 的力矩。
棒上取质元dm,当棒处在 下摆角时,重力矩为：
x
O
X
C
dm
dM xgdm
合力矩
mg
gdm
解：
因摩擦力产生的力矩是恒定的，故角速度均匀 减小。
0
0
t
0
0 t
dt t
0
f dS
r
σ
m πR2
R
dθ o
r
M J 1 mR2
2
dr
t 0mR2 / (2M ) (1) M ?
考虑面元dS对轴的摩擦力矩dM ：
dM r0gdm r0g dS
26
t0mR2/(2M ) (1) dM r0g dS
mg 由(3)(4)(5)得
mgR sin
1 2
J02
1 2
J2
(5)
gh 2R2
cos2
g R
sin
1 2R
.
g 2
(h
4
3R)
M J
mgR 2mR2
g 2R
( 60 )
44
dt
O
X
C
即 d d
3g cos d d
mg
2L
θ
0
3gcos
2L
d
0
d
3g 2L
sin
1 2
2
3g sin
L
22
m 例2.质量为 、长为L的匀质细杆水平放置,一端
大学物理刚体力学中难题及解析
A
B
5
解 设杆的质量为m， 机械能守恒：
l 1 1 2 2 2 mg sin 0 sin m(vCx vCy ) I C 2 2 2 1 2 重力势能转化成质心平动动能和刚体转动动能 I C ml y A 12 l 运动学条件： vCx sin 2 C 质心速度沿 l 水平竖直方 v cos Cy 向分解 2 mg B x
16
正确解法：隔离，分别用角动量定理。 o
R1 f r t J11 J10 J2 R2 2 O2 对轮 2 ： f r fr 1 R 1 R2 fr t J2 2 0 J1 O1
对轮1：
稳定条件：
1 R1 2 R 2
联立可得稳定后的角速度
J1 R J 1 R1 R2 1 0 , 2 0 2 2 2 2 J 1 R2 J 2 R1 J1 R2 J 2 R1 17
N maCt , f maCr
2 2
B
杆无滑动地绕圆环外侧运动，要求
f aCr (l 3r )r 4l ，因 r l 则 。 N f , a 2 R N Ct 24 lR
【9】质量为M，长度为 2l 的梯子上端靠在光 滑墙面上，下端放在粗糙地面上，地面与梯子 的静摩擦系数为 μ，一质量为 m 的人攀登到距 下端 l0 的位置，求梯子不滑动的条件。
0
f
R
vC 0
摩擦力的作用： 对质心的运动 vC
对绕质心的转动
当 vC 0, 而 0 时，乒乓球返回!
3
（2）前进一段后会自动返回的条件：
0
R
•质心运动定理： f maC
vc 0
B
5
解 设杆的质量为m， 机械能守恒：
l 1 1 2 2 2 mg sin 0 sin m(vCx vCy ) I C 2 2 2 1 2 重力势能转化成质心平动动能和刚体转动动能 I C ml y A 12 l 运动学条件： vCx sin 2 C 质心速度沿 l 水平竖直方 v cos Cy 向分解 2 mg B x
16
正确解法：隔离，分别用角动量定理。 o
R1 f r t J11 J10 J2 R2 2 O2 对轮 2 ： f r fr 1 R 1 R2 fr t J2 2 0 J1 O1
对轮1：
稳定条件：
1 R1 2 R 2
联立可得稳定后的角速度
J1 R J 1 R1 R2 1 0 , 2 0 2 2 2 2 J 1 R2 J 2 R1 J1 R2 J 2 R1 17
N maCt , f maCr
2 2
B
杆无滑动地绕圆环外侧运动，要求
f aCr (l 3r )r 4l ，因 r l 则 。 N f , a 2 R N Ct 24 lR
【9】质量为M，长度为 2l 的梯子上端靠在光 滑墙面上，下端放在粗糙地面上，地面与梯子 的静摩擦系数为 μ，一质量为 m 的人攀登到距 下端 l0 的位置，求梯子不滑动的条件。
0
f
R
vC 0
摩擦力的作用： 对质心的运动 vC
对绕质心的转动
当 vC 0, 而 0 时，乒乓球返回!
3
（2）前进一段后会自动返回的条件：
0
R
•质心运动定理： f maC
vc 0
刚体习题和答案
作业5 刚体力学♫刚体：在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速，t ＝0时角速度为05rad s ω=，t ＝20s 时角速度为00.8ωω=，那么飞轮的角加速度β= -0.05 rad/s 2 ，t ＝0到 t ＝100 s 时间飞轮所转过的角度θ= 250rad ． 【解答】飞轮作匀变速转动，据0t ωωβ=+，可得出：200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律：定轴转动的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2)，如下图．绳与轮之间无相对滑动．假设某时刻滑轮沿逆时针方向转动，那么绳中的力 (A) 处处相等． (B) 左边大于右边． (C) 右边大于左边． (D) 哪边大无法判断． 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1＜m 2)，实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得：21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上，现在在绳端挂一质量为m 的重物，飞轮的角加速度为．如果以拉力2mg 代替重物拉绳时，飞轮的角加速度将(A) 小于． (B) 大于，小于2． (C) 大于2． (D) 等于2． 【解答】设飞轮的半径为R ,质量为m ，根据刚体定轴转动定律M J β=，当挂质量为m 的重物是：mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时，有： '2mgR J β=，2'mgRJβ=，比拟二者可得出结论。
刚体部分作业问题全解共33页
46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特
刚体部分作业问题全解
•
6、黄金时代是在我们的前面，而不在 我们的 后面。
•
Hale Waihona Puke 7、心急吃不了热汤圆。•
8、你可以很有个性，但某些时候请收 敛。
•
9、只为成功找方法，不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧，便几乎 能克服 任何恐 惧。因 为，请 记住， 除了在 脑海中 ，恐惧 无处藏 身。-- 戴尔． 卡耐基 。
刚体部分作业问题全解PPT文档33页
60、人民的幸福是至高无个的法。— —西ห้องสมุดไป่ตู้ 罗
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
刚体部分作业问题全解
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益， 而是为 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
刚体部分作业问题全解
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益， 而是为 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
m
m dx g 线元所受重力为：
所以杆转动时线元 所受摩擦力矩大小为
m gdx x
m 1 M xgdx mg 0 2
物理系：凌亚文Leabharlann 大学物理第一学期作业中的问题
3. 一人坐在转椅上，双手各持一哑铃，哑铃与转轴的距 离各为0.6m,先让人体以5rad/s的角速度随转椅旋转。然 后此人将哑铃拉回使之与转轴距离为0.2m。人体和转椅 2 5 kg m ，并视为不变。每一哑铃的 对轴的转动惯量为 质量为 5kg ，可视为质点。哑铃被拉回后，人体的角速度 ω＝_________ 选人、转椅和双手各持的哑铃为系统，系统变化过程中 所受外力矩为零，所以系统的角动量守恒。由角动量守恒 定律有： 初角动量： ( J1 J 2 )1
大学物理第一学期作业中的问题
5. 三个完全相同的轮子绕一公共轴转动，角速度的大小都 相同，但其中一个轮子的转动方向与另外两轮的转动方向 相反。如果使三个轮子靠近并啮合在一起，系统的角速度 大小是原来角速度大小的 (A) 1/9； (B) 1/3； (C) 3 ； (D)9。
解：啮合过程系统外力矩为0，角动量守恒。设一个轮子 转动惯量为 J, 初始角速度位。
由（2）（3）（1）
3T1 2T3 2mg 2T3 T1 4mg
5 T3 mg 4
由（2）（3）（4）
3 T1 mg 2
11 T2 mg 8
物理系：凌亚文
大学物理第一学期作业中的问题
7. 对一个绕固定水平轴O匀速转动的转盘，沿如图所 示的同一水平直线从相反方向射入两颗质量相同、速 率相等的子弹，并留在盘中，则子弹射入后转盘的角 速度为
L J J J J J 总末 3J末 末 3
物理系：凌亚文
大学物理第一学期作业中的问题
6. 如图所示，两个质量均为m，半径均为R的匀质圆盘 状滑轮的两端，用轻绳分别系着质量为m和2m的小木 块。若系统由静止释放，则两滑轮之间绳内的张力为 解：
2mg T1 2ma
(T1 T2 ) R J
(T2 T3 ) R J
T3 mg ma
a R
1 J mR 2 2
T2 ?
物理系：凌亚文
大学物理第一学期作业中的问题
2mg T1 2ma
(T1 T2 ) R J
2mg T1 a 2m
1 T1 T2 ma 2
变慢
M 2m
物理系：凌亚文
大学物理第一学期作业中的问题
二、填空题 1.质量分别为m和2m的两物体(都可视为质点)，用一长为l 的轻质刚性细杆相连，系统绕通过杆且与杆垂直的竖直光 滑固定轴O轴转动，已知轴离质量为2m的质点的距离为l/3， 质量为m的质点的线速度为且与杆垂直，则该系统对转 轴的角动量(动量矩)大小为 。
L J m 2 m 2 3 m l m m 3 2l 2 2 2 1 m 2 l2 J m l 2m l 3 3 3 L J ml
物理系：凌亚文
大学物理第一学期作业中的问题
的均匀细杆，可在水平桌面上绕 、长为 2.一根质量为 通过其一端的竖直固定轴转动。已知杆与桌面的滑动摩 擦系数为 ，则杆转动时受的摩擦力矩的大小为 ____。 x
P m
角动量
L J
质点作匀速率圆周运动所受外力 （向心力）通过圆心，所以产生的 力矩为零则角动量守恒。
物理系：凌亚文
大学物理第一学期作业中的问题
2.人造地球卫星绕地球作椭圆轨道运动，卫星轨道近地 点和远地点分别为A和B。用L和Ek分别表示卫星对地心的 角动量及其动能的瞬时值，则应有 (A) LA> LB， EkA> EkB； (B) LA＝LB， EkA < EkB； dr (C) LA＝LB， EkA > EkB； (D) LA < LB， EkA < EkB。 r m 质点所受外力通过圆心（任意点）， 所以产生的力矩为零则角动量守恒。 万有引力势能
2
子弹和棒为系统系统对转轴的力 矩为零，所以系统角动量守恒。 设所求棒的角速度为ω 初角动量： mL 末角动量： mL 1 ML2 2 3
物理系：凌亚文
大学物理第一学期作业中的问题
由角动量守恒定律：
1 2 mL mL ML 2 3
3m 2 ML
物理系：凌亚文
1 J mR 2 2
质量不变，半径增大了一倍，转动惯量为4J 。
物理系：凌亚文
大学物理第一学期作业中的问题
4.如图所示，一静止的均匀细棒，长为L，质量为M, 可绕通过棒的端点且垂直于棒长的光滑固定轴O在水 平面内转动，转动惯量为 1 ML2 。一质量为m 、速率为 3 的子弹在水平面内沿与棒垂直的方向射入并穿入棒的自 由端，设穿过棒后子弹的速率为 1 ，则此时棒的角速度应为?
1 T2 T3 ma 2
(1)
(T2 T3 ) R J
T3 mg ma
a R
(2)
(3)
1 J mR 2 2
T3 mg a m
(4)
由（1）（4） 由（2）（3）
2T3 T1 4mg
T3 T1 2T2
物理系：凌亚文
大学物理第一学期作业中的问题
GMm r
机械能守恒
物理系：凌亚文
大学物理第一学期作业中的问题
3. 一质量为 m，半径为 R 的匀质圆盘对其中心垂直轴的转 动惯量为 J，若在保持其质量不变的情况下，使之变成半 径为 2R 的匀质圆盘，则其对中心垂直轴的转动惯量的大 小为 (A) 因圆盘的质量不变，所以转动惯量仍为J； (B) 因半径变为2R，所以转动惯量为2J； (C) 转动惯量为3J； (D) 转动惯量为4J。 解： 由圆盘转动惯量公式
大学物理第一学期作业中的问题
刚体定轴转动作业问题
物理系：凌亚文
大学物理第一学期作业中的问题
1.一质点作匀速率圆周运动时， (A) 它的动量不变，对圆心的角动量也不变； (B) 它的动量不变，对圆心的角动量不断改变； (C) 它的动量不断改变，对圆心的角动量不变； (D) 它的动量不断改变，对圆心的角动量也不断改变。 动量