刚体大作业.doc
刚体力学习题答案.docx

连,m1和m2则挂在圆柱体的两侧,如3-8图所示.设R=0.20m,r=0.10m,m=4 kg,M=10
kg,m1=m2=2 kg,且开始时m1,m2离地均为h=2m.求:
(1)柱体转动时的角加速度;
(2)两侧细绳的张力.
2
1( J
2mr
2)
0
2
0
2
2
0
1
1
(5
2 4
0.22)
122
(5 2
4 0.82)
(2 )2
2
2
=183J
3-18如3-20图所示,质量为M,长为l的均匀直棒,可绕垂直于棒一端的水平轴O无摩擦地转动,它原来静止在平衡位置上. 现有一质量为m的弹性小球飞来,正好在棒的下端与棒垂
直地相撞.相撞后,使棒从平衡位置处摆动到最大角度30°处.
L2
m2
vr sin 30
1m1r2
2
2
v
1
2
故有
m2vr sin60 m22r sin30
2m1r
可解得:
(2 3 1)m2v
2m1r
3-16
一人站在一匀质圆板状水平转台的边缘
,转台的轴承处的摩擦可忽略不计
,人的质量
为m',转台的质量为
10m',半径为R.最初整个系统是静止的,这人把一质量为
m的石子
2
mv
6m'R
人的线速度为vR
mv
6m'
其中负号表示转台角速度转向和人的线速度方向与假设方向相反-
3-17一人站在转台上,两臂平举,两手各握一个m
刚体部分作业问题全解共33页

46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
刚体部分作业问题全解
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
Hale Waihona Puke 7、心急吃不了热汤圆。•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
大学物理刚体习题

大学物理刚体习题(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习 题第三章 刚体的转动刚体的定轴转动47. 一定滑轮半径为R ,质量为M ,用一质量不计的绳绕在滑轮上,另一端系一质量为m 的物体并由静止释放,这时滑轮的角加速度为1β,若不系物体而用一力F = mg 拉绳子使滑轮转动,这时角加速度为2β,这时有()1β2β()1β2β (C )1β2β(D )无法判断 分析由转动定律M I β=本题中I 不变β的大小完全取决于M 的大小而 M TR =系物体m 时 : T mg <不系物体而用一力F = mg 时: TF mg ==因此力矩变大所以有12ββ<mF选49.一飞轮的转动惯量为J ,t = 0时角速度为0ω,轮子在转动过程中受到一力矩2ωk M-=,则当转动角速度为0/3ω时的角加速度β = 从0ω到0/3ω飞轮转动经过的时间t ∆= 解: (1) 求β当0/3ω时, 20()3M k ω=-由 M J β=, 可得此时 209k MJ J ωβ==-(2) d M J J dt ωβ== 2d k J dt ωω-=分离变量,两边积分32td kdt Jωωωω-=⎰⎰解得: 02J t k ω∆=50.长为l 的均匀直棒可绕其下端与棒垂直的水平光滑轴在竖直平面内转动。
抬起一端使与水平夹角为60=θ,棒对轴的转动惯量为231ml J =,由静止释放直棒,则t = 0时棒的β=?;水平位置时的β=?这时的ω=(1)求β 据转动定律M J β=, MJβ= 0t =时, cos 602lM mg =︒水平位置时, 2lM mg =代入MJβ=,可别解得034glβ= 和 32g l β= (2)求ωd d d d M J J J J dt d dt d ωωθωβωθθ====将cos 2l M mg θ=和213J ml =代入化简并积分得, 0033cos 2g d d l ωπθθωω=⎰⎰ 60可求得332g l ω=(本题还可用动能定律机械能守恒方便求解ω)2211sin 60223l mg ml ω︒=⋅ 332g lω⇒=51.一飞轮以min /600rev 的转速转动,其转动惯量为25.2m kg J ⋅=,以恒定力矩使飞轮在一分钟内停止转动,求该力矩M 。
大学物理刚体的运动及其习题答案共42页文档

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
大学物理刚体的运动及其习 题答案
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
ห้องสมุดไป่ตู้
谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起而 读书。 ——周 恩来
面向新世纪课程教材大学物理大作业答案——刚体力学作业
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
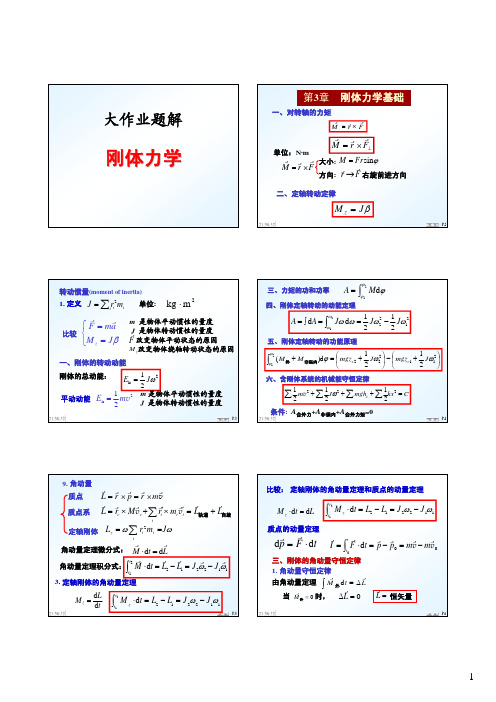
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
多刚体大作业2(maple)

MAPLE理论力学学号:201431206024一、如图1,长0.40m l =、质量 1.00kg M =的匀质木棒,可绕水平轴O 在竖直平面内转动,开始时棒自然竖直悬垂,现有质量8g m =的子弹以200m/s v =的速率从A 点射入棒中,A 、O 点的距离为3/4l ,如图所示。
求:(1)棒开始运动时的角速度; (2)棒的最大偏转角。
解:(1)子弹射入前,子弹角动量为: l L 43mv 1⋅= 子弹射入后,木棒角动量为:ω22M 31l L =子弹射入后,子弹角动量为:ω23)43m(l L =应用角动量守恒定律:321L L L =+22313434mv l Ml m l ωω⎛⎫⋅=+ ⎪⎝⎭解得:3333810200448.9rad/s 191918100.4316310mv M m l ω--⨯⨯⨯===⎛⎫⎛⎫+⨯+⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭(2)子弹射入后,子弹角动能:221M 3121ωl E k ⋅=子弹射入后,木棍角动能:222)43m(21ωl E k =子弹摄入后,子弹重力势能:gl E M 211p -=子弹摄入后,木棍重力势能:gl E m 432p -=最大偏角时,子弹重力势能:θcos M 213p gl E -=最大偏角时,木棍重力势能:θcos m 434p gl E -=应用机械能守恒定律:432121p p p p k k E E E E E E +=+++2211333()cos cos 2342424l l l lMl m l Mg mg Mg mg ωθθ⎡⎤+--=--⎢⎥⎣⎦图1图2解得 2938cos 10.07923M ml M m gθω+=-⋅=-+, 94.5θ=︒答案:(1)8.9rad/s ;(2)94.5︒。
● Maple 程序:> restart: #清零> L[1]:=3/4*m*v*l: #射入前子弹的角动量L1 > L[2]:=1/3*M*omega*l^2: #射入后木棒的角动量L2 > L[3]:=m*(3/4*l)^2*omega: #射入后子弹的角动量L3 > eq1:= L[1]= L[2]+ L[3]: #角动量守恒> Ek[1]:=1/2*1/3*M*l^2*omega^2: #射入瞬间木棒角动能 > Ek[2]:=1/2*1/3*M*l^2*omega^2: #射入瞬间子弹角动能 > Ep[1]:=-1/2*M*g*l: #射入瞬间木棒重力势能 > Ep[2]:=-3/4*m*g*l: #射入瞬间子弹重力势能 > Ep[3]:=-1/2*M*g*l*cos(theta): #最大偏转时木棒重力势能 > Ep[4]:=-3/4*m*g*l*cos(theta): #最大偏转时子弹重力势能 > eq2:= Ek[1]+ Ek[2]+ Ep[1]+ Ep[2]= Ep[3]+ Ep[4]: #角动量守恒 > l:=0.4:M=1:m=0.008:v=200:g=9.8: #已知条件 > solve({eq1,eq2},{omega,theta}): #解方程二、如图3,一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。
大学物理刚体习题

大学物理刚体习题在大学物理的学习中,刚体是一个重要的概念。
刚体是指物体内部各点之间没有相对位移,不发生形变,整体运动状态一致的理想化模型。
在解决物理问题时,刚体的性质为我们提供了极大的便利。
以下是一些常见的大学物理刚体习题。
一、基本概念题1、什么是刚体?列举一些常见的刚体实例。
2、刚体在什么情况下可以被视为刚体?其基本性质是什么?3、描述刚体的运动,并解释相关概念,如转动、角速度、角加速度等。
二、刚体的动力学问题4、一个刚体绕固定轴转动,在某时刻受到一个外力矩的作用,求该刚体接下来的运动状态。
41、一个刚体在平面上做纯滚动,如何计算其加速度和速度?411、一个刚体在重力场中处于平衡状态,求其重心的位置。
三、刚体的静力学问题7、一个刚体受到两个大小相等、方向相反的力作用,求该刚体的平衡状态。
71、一个刚体在平面上受到一个力矩的作用,求该刚体的转动效果。
711、一个刚体在三个不在同一直线上的力作用下处于平衡状态,求该刚体的重心位置。
四、刚体的运动学问题10、一个刚体绕固定轴转动,其角速度与时间成正比,求该刚体的角加速度和转速。
101、一个刚体在平面上做纯滚动,其速度与时间成正比,求该刚体的加速度和转速。
1011、一个刚体受到一个周期性外力矩的作用,求该刚体的运动状态。
以上就是一些常见的大学物理刚体习题。
解决这些问题需要我们深入理解刚体的性质和相关的物理概念,如力、力矩、重心等。
通过这些习题的练习,我们可以更好地掌握刚体的相关知识,提高我们的物理水平。
大学物理刚体力学标题:大学物理中的刚体力学在物理学的研究中,大学物理是引领我们探索自然界规律的重要途径。
而在大学物理中,刚体力学是一个相对独特的领域,它专注于研究物体在受到外力作用时的质点运动规律。
本文将探讨大学物理中的刚体力学。
一、刚体概念及特性刚体是指物体内部各质点之间没有相对位移,形状和体积不发生变化的理想化物体。
在刚体力学中,我们通常将刚体视为一个整体,研究其宏观运动规律。
刚体习题和答案

A
所示,滑块 A、重物 B 和滑轮 C
B
的质量分别为 mA、mB 和 mC,滑
轮的半径为
R
,滑 轮 对 轴 的 转 动 惯 量
J
=
1 2
mC
4
编号 ____________姓名 __________
《大学物理Ⅰ》答题纸
第五 章
R2.滑 块 A 与桌面间、滑轮与轴承之间均无摩
擦,绳的质量可不计,绳与滑轮之间无相对滑
碰前的角mv0动32 l 量为:
碰后的角动量为:
m
1 2
v0
2 3
l
[m( 2 3
l)2
2m(1 l)2 ] 3
所以 mv0
2 3
l
m
1 2
v0
2 3
l
[m( 2 3
l)2
2m(1 l)2 ] 3
得 3v0 2l
6、自测提高(17)如图 5-25 所示,
一质量均匀分布的圆盘,质量为 m0,
O
动.滑块 A 的加速度 a 2mB g 2(mA mB ) mC
【解答】
T
T
由转动定律得:
B
A
TB R TAR J GB TB mBa TA mAa a R
(1)
(2) (3) GB
(4)
4 个方程,共有 4 个未知量: TA 、TB 、 a 和 。可求:
a 2mB g 2mA mB mc
(1 2
mv0 m0 m)R
(2)圆盘的质量面密度 m0 在圆盘上取一 R2
半径为 r,宽为 dr 的小环带,
dM 2rdr 此 环 带 受 到 的 摩 擦 阻 力 矩
dM rgdm rg 2r 2dr
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理( A )大作业(三)刚体定轴转动教学班姓名学号成绩一、选择题【】1. 两个匀质圆盘 A 和 B 的密度分别为A 和B ,若 A > B ,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面的轴的转动惯量各为J AB和 J ,则(A) J A > J B (B) J B >J A (C) J A = J B (D) 不能确定【】 2. 有一根水平杆子,一半是铁,一半是木头,长度、截面均相同,可分别绕 a , b , c 三根竖直轴转动,如图所示。
试问对哪根轴的转动惯量最大(A) a 轴(B) b 轴(C) c 轴(D) 都一样【 】 3. 如图所示,一摆由质量均为 m 的杆与圆盘构成,杆长等于圆盘直径 2 倍,则摆对通过 O 点并与圆盘平面垂直轴的转动惯量为D 的(A) 7 17mD 224(B)17mD 24(C) 5 17mD 224(D)17mD 26【】 4. 刚体绕定轴作匀变速转动时,刚体上距转轴为 r 的任一点的(A) 切向、法向加速度的大小均随时间变化(B) 切向、法向加速度的大小均保持恒定(C) 切向加速度的大小恒定,法向加速度的大小变化(D) 切向加速度的大小变化,法向加速度的大小恒定 【】 5. 在下列说法中错误的是(A) 刚体定轴转动时,各质点均绕该轴作圆周运动(B) 刚体绕定轴匀速转动时,其线速度不变(C) 力对轴的力矩 M 的方向与轴平行(D) 处理定轴转动问题时, 总要取一个转动平面 S ,只有 S 面上的分力对轴产生的力矩才对定轴转动有贡献【】 6. 下列说法中正确的是(A) 作用在定轴转动刚体上的力越大,刚体转动的角加速度越大(B) 作用在定轴转动刚体上的合力矩越大,刚体转动的角速度越大(C) 作用在定轴转动刚体上的合力矩越大,刚体转动的角加速度越大(D) 作用在定轴转动刚体上的合力矩为零,刚体转动的角速度为零【】 7. 均质细杆可绕过其一端且与杆垂直的水平光滑轴在竖直平面内转动。
今使细杆静止在竖直位置,并给杆一个初速度,使杆在竖直面内绕轴向上转动,在这个过程中(A) 杆的角速度减小,角加速度减小 (B) 杆的角速度减小,角加速度增大(C) 杆的角速度增大,角加速度增大(D) 杆的角速度增大,角加速度减小【 】 8. 如图所示, A 、 B 为两个相同的绕着轻绳的定滑轮. A 滑轮挂一质量为 M的物体, B 滑轮受拉力 F ,而且 F = Mg .设 A 、B 两滑轮的角加速度分别为 A 和 B ,不计滑轮轴的摩擦,则有(A)A =BAB(B)A > B(C)A <BMF(D)开始时 A = B ,以后A <B【 】9. 一转动惯量为J 的圆盘绕一固定轴转动,起初角速度为0 。
设它所受阻力矩与转动角速度成正比, 即 Mk ( k 为正的常数),则圆盘的角速度从变为2时所需的时间为(A) J lnkJ(B) ln 2(C) J ln k(D) J ln12k k【】10. 一质量为 m 、半径为 R 的均质圆盘, 绕过其中心的垂直于盘面的轴转动,由于阻力矩存在,角速度由0 减小到 0/ 2 ,则圆盘对该轴角动量的增量为(A) 1mR 20(B)1 mR2 0(C)1 mR2 0(D)1 mR2 02424【】 11. 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 I,开始时转台以匀角速度0 转动,此时有一质量为m 的人站在转台中心.随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A)I ω(B)I ω(C)I ω(D) 0 I mR2 0 I m R2 0 mR2 0【】12. 人造地球卫星,绕地球作椭圆轨道运动,如果地球在椭圆的一个焦点上,则卫星的(A) 动量不守恒,动能守恒(B) 对地心的角动量守恒,动能不守恒(C) 动量守恒,动能不守恒(D) 对地心的角动量不守恒,动能守恒【】13. 一人站在旋转平台的中央,两臂侧平举,整个系统以 2 rad/s 的角速度旋转,转动惯量为kg·m2.如果将双臂收回则系统的转动惯量变为 2.0 kg·m2.此时系统的转动动能与原来的转动动能之比E k / E k0为(A) 2 (B)3 (C) 2 (D) 3【】 14. 一个圆盘在水平面内绕一竖直固定轴转动的转动惯量为J,初始角速度为0 ,后来变为10 .在上述过程中,阻力矩所作的功为2(A)1J42(B)1J82(C)1J42(D)3J82【】15. 有一质量为 m、长为 l 的均匀细棒,静止平放在滑动摩擦系数为的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动,在转动过程中,细棒受到的摩擦力矩为(A) mglmgl mgl 2 mgl(B) (C) (D)2 3 3【】16. 一质量为 m, 长为 l 的均质细杆可在水平桌面上绕杆的一端转动, 杆与桌面间的摩擦系数为, 求摩擦力矩 M . 先取微元细杆dr, 其质量 dm = dr = (m/ l)dr. 它受的摩擦力是df = (dm)g =( mg/l)dr, 再进行以下的计算(A) M = rdf l mg dmgl/ 2=l r r =mg(B) M =( df l)l/ 2=( dr )l/ 2= mgl/ 20 ll mg(C) M =( df )l/ 3=( dr )l/ 3= mgl/ 30 l(D) M =( df )l=( lmg dr )l= mgl0l【】 17. 质量为 m、长为 l 的均质细杆,可绕过其一端,与杆垂直的水平轴在竖直平面内转动。
开始杆静止于水平位置,释放后开始向下摆动,在杆摆过/ 2 的过程中,重力矩对杆的冲量矩为(A) 1 ml2 3g (B) 2 ml2 3g (C) ml23g(D) 4 ml2 3g3 l 3 l l 3 l 【】 18. 一根质量为m,长度为l 的细而均匀的棒,其下端绞接在水平面上,并且竖直的立起,如果让它自由落下,则棒将以角速度撞击地面,如图所示。
如果将棒截去一半,初始条件不变,则棒撞击地面的角速度为(A) 2 (B) 2(C) (D) O2【】19. 一根长为 l、质量为 m 的均匀细杆,可绕距离其一端l的水平轴 O 在竖4直平面内转动,当杆自由悬挂时,给它一个起始角速度,如杆恰能持续转动而不摆动,则3g(A) 4l/47lO 。
g(B)lg(C)l12g(D)l【】 20. 图 (a)为一绳长为l、质量为m 的单摆.图(b)为一长度为l、质量为m 能绕水平固定轴O 自由转动的匀质细棒.现将单摆和细棒同时从与竖直线成角度的位置由静止释放,如果运动到竖直位置时,单摆、细棒角速度分别以1、2 表示.则(A) (C) 11122322(B)(D)1 2 O1 2 / 3 2(a)(b)二、计算题1.计算如图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为M ,半径为r,在绳与轮缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,且m2m1.2. 质量为m,长为l的均匀细棒,可绕垂直于棒的一端的水平轴转动.如将此棒放在水平位置,然后任其落下,求:(1) 当棒转过 60°时的角加速度和角速度; (2) 下落到竖直位置时的动能;(3) 下落到竖直位置时的角速度.3.一质量为 kg,长为 m 的均匀细棒,支点在棒的上端点,开始时棒自由悬挂 .以 100 N 的力打击它的下端点,打击时间为s.(1) 若打击前棒是静止的,求打击时其角动量的变化;(2) 棒的最大偏转角.4.平板中央开一小孔,质量为 m 的小球用细线系住,细线穿过小孔后挂一质量为M 1的重物.小球作匀速圆周运动,当半径为r0时重物达到平衡.今在M 1的下方再挂一质量为M 2的物体,如图所示.试问这时小球作匀速圆周运动的角速度和半径 r 为多少5. 一匀质细棒长度为l ,质量为m ,可绕通过其一端的水平光滑固定轴O 转动,如m 图所示。
当棒自水平位置由静止摆下时,在竖直位置处与放在地面上的质量也是的物体作非弹性碰撞,碰后物体沿地面滑行距离S 而静止,设物体与地面间的摩擦系数为.求与物体相撞后瞬间棒的角速度.6. 如图所示,质量为M,长为l的均匀直棒,可绕垂直于棒一端的水平轴O 无摩擦地转动,它原来静止在平衡位置上.现有一质量为m 的弹性小球飞来,正好在棒的下端与棒垂直地相撞.相撞后,使棒从平衡位置处摆动到最大角度30°处.(1)设碰撞为弹性碰撞,计算小球初速v0的值;(2)相撞时小球受到多大的冲量。
