北京各区初中一模数学分类汇编27题及答案#优选、
2022北京中考数学一模分类《几何综合压轴题》含答案解析

2022北京中考一模数学分类——几何综合压轴题一、倍长八字共5小题1.(2022朝阳一模27题)在ABC △中,D 是BC 的中点,且90BAD ∠≠︒,将线段AB 沿AD 所在直线翻折,得到线段AB ',作//CE AB 交直线AB '于点E . (1)如图,若AB AC >, ①依题意补全图形;②用等式表示线段,,AB AE CE 之间的数量关系,并证明;(2)若AB AC <,上述结论是否仍然成立?若成立,简述理由;若不成立,直接用等式表示线段,,AB AE CE 之间新的数量关系(不需证明).2.(2022顺义一模27题)如图,在Rt ABC △中,90ACB ∠=︒,CD 是斜边AB 上的中线,EF 垂直平分CD ,分别交AC ,BC 于点E ,F ,连接DE ,DF . (1)求∠EDF 的度数;(2)用等式表示线段AE ,BF ,EF 之间的数量关系,并证明.3.(2022平谷一模27题)如图,在△ABC 中,∠ACB =90°,AC =BC ,点D 为AB 边上一点(不与点A ,B 重合),作射线C D ,过点A 作AE ⊥CD 于E ,在线段AE 上截取EF=EC ,连接BF 交CD 于G.(1)依题意补全图形; (2)求证:∠CAE=∠BCD(3)判断线段BG 与GF 之间的数量关系,并证明.4.(2022丰台一模27题)如图,在△ABC 中,∠BAC=α,点D 在边BC 上(不与B,C 重合),连接AD,以点A 为中心,将线段AD 逆时针旋转180°-α得到线段AE,连接BE. (1)∠BAC+∠DAE= °(2)取CD 的中点F ,连接AF ,用等式表示线段AF 与BE 的数量关系,并证明。
5.(2022石景山一模27题)如图,△ACB 中,AC =BC ,∠ACB =90°,D 为边BC 上一点(不与点C 重合),CD <BD ,点E 在AD 的延长线上,且ED =AD ,连接BE ,过点B 作BE 的垂线, 交边AC 于点F . (1)依题意补全图形; (2)求证:BE =BF ;(3)用等式表示线段AF 与CD 的数量关系,并证明.ABCDABCD二、一线三垂直共1小题6.(2022通州一模27题)如图,在Rt ACB △中, 90ACB ∠=︒ ,AC BC =.点D 是BC 延长线上一点,连接AD .将线段AD 绕点A 逆时针旋转90°,得到线段AE .过点E 作//EF BD ,交AB 于点F . (1)①直接写出AFE ∠的度数是____________;②求证:DAC E ∠=∠; (2)用等式表示线段AF 与DC 的数量关系,并证明.三、三线合一共1小题7.(2022大兴一模27题)已知:如图,OB =BA ,∠OBA =150°,线段BA 绕点A 逆时针旋转90°得到线段AC .连接BC ,OA ,OC ,过点O 作OD ⊥AC 于点D .(1)依题意补全图形; (2)求∠DOC 的度数.四、手拉手共5小题8.(2022燕山一模27题)如图,在三角形ABC 中,AB =AC ,∠BAC <60°,AD 是BC 边的高线,将线段AC 绕点A 逆时针旋转60°得到线段AE ,连接BE 交AD 于点F . (1)依题意补全图形,写出∠CAE= ° (2)求∠BAF+∠ABF 和∠FBC 的度数;(3)用等式表示线段AF ,BF ,EF 之间的数量关系,并证明.9.(2022门头沟一模27题)如图,在等边△ABC 中,将线段AC 绕点A 顺时针旋转(060)αα<<,得到线段AD ,连接CD ,作∠BAD 的平分线AE ,交BC 于E . (1)① 根据题意,补全图形;② 请用等式写出∠BAD 与∠BCD 的数量关系,并证明.(2)分别延长CD 和AE 交于点F ,用等式表示线段AF ,CF ,DF 的数量关系,并证明.AB C A B C AB C10.(2022房山一模27题)已知:等边ABC,过点B作AC的平行线l.点P为射线AB上一个动点(不与点,A B重合),将射线PC绕点P顺时针旋转60°交直线l于点D.(1)如图1,点P在线段AB上时,依题意补全图形;∠=∠;①求证:BDP PCBBC BD BP之间的数量关系,并证明;②用等式表示线段,,BC BD BP之间的数量关系.(2)点P在线段AB的延长线上,直接写出线段,,11.(2022海淀一模27题)27.在Rt ABC △中,90ABC ∠=︒,30BAC ∠=︒,D 为边BC 上一动点,点E 在边AC 上, C E CD =.点D 关于点B 的对称点为点F ,连接AD ,P 为AD 的中点,连接,,PE PF EF .(1)如图1,当点D 与点B 重合时,写出线段PE 与PF 之间的位置关系与数量关系;(2)如图2,当点D 与点,B C 不重合时,判断(1)中所得的结论是否仍然成立?若成立,请给出证明,若不成立,请举出反例。
2024年北京海淀区初三一模考试数学及答案

2024北京海淀初三一模数 学2024.04学校________姓名__________准考证号________第一部分 选择题一、迭择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个. 1.下列几何体放置在水平面上,其中俯视图是圆的几何体为2.据报道,2024年春节假期北京接待游客约1750万人次,旅游收入同比增长近四成.将17 500 000用科学记数法表示应为 (A)175×105(B)1.75×106(C)1.75×107(D)0.175×1083.如图,AB ⊥BC ,AD ∥BE ,若∠BAD=28°,则∠CBE 的大小为 (A)66° (B)64° (C)62°(D)60°4.实数a 在数轴上的对应点的位置如图所示,下列结论中正确的是(A)a ≥-2(B)a<-3(C)-a>2(D)-a ≥35.每一个外角都是40°的正多边形是 (A )正四边形(B )正六边形(C )正七边形(D)正九边形6.若关于x 的一元二次方程x 2+2x +m =0有两个相等的实数根,则实数m 的值为 (A)1(B)-1(C)4(D)-47.现有三张背面完全一样的扑克牌,它们的正而花色分别为◆, , ,若将这三张扑克牌背面朝上,洗匀后从中碗机抽取两张,则抽取的两张牌花色相同的概率为(A)16(B)13(C)12(D)238.如图.AB 经过圆心O ,CD 是⊙O 的一条弦,CD ⊥AB ,BC 是⊙O 的切线.再从条件①,条件②,条件③中选择一个作为已知,便得AD=BC. 条件①:CD 平分AB条你②OA 条件③:AD 2=AO ·AB 则所有可以添加的条件序号是 (A) ①(B) ①③(C) ②③(D) ①②③第二部分 非选择题二、填空题(共16分,每题2分)9.x 的取值范围是_______. 10.分解因式:a 3-4a=_______. 11.方程1231x x =− 的解为_______.12.在平面直角坐标系xOy 中,若函数(0)ky k x=≠的图象经过点A (a ,2)和B (b ,-2).则a +b 的值为_______.13.如图,在△ABC 中,∠ACB=90°,AB=5,AC=3.点D 在射线BC上运动(不与点B 重合).当BD 的长为______时, AB=AD. 14.某实验基地为全面掌握“无絮杨”树苗的生长规律,定期对2000棵该品种树苗进行抽测.近期从中随机抽测了100棵树苗,获得了它们的高度x (单位:cm).数据经过整理后绘制的频数分布直方图如右图所示.若高度不低于300cm 的树苗为长势良好,则估计此时该基地培育的2000棵“无絮杨”树苗中长势良好的有_________棵.15.如图,在正方形ABCD 中.点E ,F ,G 分别在边CD ,AD ,BC 上,FD<CG.若FG=AE ,∠1=a ,则∠2的度数为_____(用含a 的式子表示).16.2019年11月,联合国教科文组织将每年的3月14日定为“国际数学日”,也被许多人称为“π节”.某校今年“π节”策划了五个活动,规则见下图:小云参与了所有活动.(1)若小云只挑战成功一个,则挑战成功的活动名称为__________;(2)若小云共挑战成功两个,且她参与的第四个活动成功,则小云最终剩下的“π币”数量的所有可能取值为______.三、解答题(共68分,第17-19题,每题5分,第20-21题,每题6分,第22-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程. 17.计算:112sin 601()2−︒+−+18.解不等式组:435,212.3x x x −<⎧⎪+⎨>−⎪⎩19.已知240b a −=,求代数式241(1)2a b b+−+的值.20.如图,在ABCD 中,O 为AC 的中点,点E ,F 分別在BC ,AD 上,EF 经过点O ,AE=AF.(1)求证:四边形AECF 为菱形;(2)若E 为BC 的中点,AE=3,AC=4.求AB 的长.21.下图是某房屋的平面示意图.房主准备将客厅和卧室地面铺设木地板,厨房和卫生间地面铺设瓷砖.将房间地面全部铺设完预计需要花费10 000元,其中包含安装费1270元.若每平方米木地板的瓷砖的价格之比是5:3,求每平方米木地板和瓷砖的价格.22.在平面直角坐标系xOy 中,函数y =kx +b (k ≠0)的图象经过点A(1,2)和B(0,1). (1)求该函数的解析式;(2)当x <l 时.对于x 的每一个值,函数y =mx -1(m ≠0)的值小于函数y =kx +b (k ≠0)的值,直接写出m 的取值范围.23.商品成本影响售价,为避免因成本波动导致售价剧烈波动,需要控制售价的涨跌幅.下面给出了商品售价和成本(单位:元)的相关公式和部分信息: a.计算商品售价和成本涨跌幅的公式分别为:100%100%−−=⨯⨯当周售价前周售价当周成本前周成本售价涨跌幅,成本涨跌幅=;前周售价前周成本b.规定当周售价涨跌幅为当周成本涨跌幅的一半;c.甲、乙两种商品成本与售价信息如下:根据以上信息,回答下列问题:(1)甲商品这五周成本的平均数为___________,中位数为___________;(2)表中m 的值为____________,从第三周到第五周,甲商品第_______周的售价最高;(3)记乙商品这40周售价的方差为 21S ,若将规定“当周售价涨跌福为当周成本涨跌福的一半”更改为“当周售价涨跌幅为当周成本涨跌辐的四分之一”,重新计算每周售价,记这40周新售价的方差为22S ,则21S ____22S ;(填“>”“=”或“<”).24.如图.AB 、CD 均为⊙O 的直径.点E 在BD ̂上,连接AE ,交CD 于点F,连DE ,∠EDB+∠EAD=45°,点G 在BD 的延长线上,AB=AG. (I)求证:AG 与⊙O 相切;(2)若BG=1tan 3EDB ∠=,求EF 的长.25.某校为培养学生的阅读习惯,发起“阅读悦听”活动,现有两种打卡奖励方式: 方式一:每天打卡可领取60min 听书时长;方式二:第一天打卡可领取5min 听书时长,之后每天打卡领取的听书时长是前一天的2倍. (1)根据上述两种打卡奖励方式补全表二:表一 每天领取听书时长达了变化趋势.其中表示方式二变化趋势的虚线是________(填a 或b ),从第_______天完成打卡时开始,选择方式二累计领取的听书时长超过方式一;(3)现有一本时长不超过60min 的有声读物,小云希望通过打卡领取该有声读物.若选择方式二比选择方式一所需的打卡天数多两天,则这本有声读物的时长t (单位:min )的取值范围是______.26.在平面坐标系xOy 中,点(m ,n )在抛物线2(0)y ax bx a =+>上,其中m ≠0. (1)当m =4,n =0时.求抛物线的对称轴; (2)已知当0<m <4时,总有n <0. ①求证:4a +b ≤0;②点12(,),(3,)P k y Q k y 在该抛物线上,是否存在a ,b ,使得当1<k <2时,都有12y y <?若存在,求出a 与b 之间的数量关系;若不存任,说明理由.27.在△ABC 中.∠ACB=90°,∠ABC=30°,将线段AC 绕点A 顺时针旋转α((0°<α≤60°)得到线段AD.点D 关于直线BC 的对称点为E.连接AE ,DE.(1)如图1,当α=60°时,用等式表示线段AE 与BD 的数量关系,并证明; (2)连接BD ,依题意补全图2.若AE=BD ,求α的大小.28.在平面直角坐标系xOy中,对于图形M与图形N给出如下定义:P为图形N上任意一点,将图形M绕点P顺时针旋转90°得到M’,将所有M’组成的图形记作M’,称M’是图形M关于图形N的“关联图形”.(1)已知A(-2,0),B(2,0),C(2,t),其中t≠0.①若t=1,请在图中画出点A关于线段BC的“关联图形”;②若点A关于线段BC的“关联图形”与坐标轴有公共点.立接写出t的取值范围;(2)对于平面上一条长度为a的线段和一个半径为r的圆,点S在线段关于圆的“关联图形”上,记点S的纵坐标的最大值和最小值的差为d,当这条线段和圆的位置变化时,直接写出d的取值范围(用含a和r的式子表示).海淀区九年级第二学期期中练习数学试卷参考答案第一部分 选择题一、选择题 (共16分,每题2分)第二部分 非选择题二、填空题(共16分,每题2分)9.1x ≥ 10.(2)(2)a a a −+11.1x = 12.0 13.8 14.94015.180α︒−16.(1)鲁班锁;(2)1,2,3三、解答题(共68分,第17-19题,每题5分,第20-21题,每题6分,第22-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 解:原式212=++− 12=+−3=18. 解:原不等式组为435212.3x x x −<⎧⎪⎨+>−⎪⎩,①②解不等式①,得2x <.解不等式②,得1x >. ∴原不等式组的解集为12x <<. 19. 解: 原式241212a b b b +=−++2411a b +=+.∵240b a−=,∴24b a=.∴原式41 41aa+ =+1 =.20.(1)证明:∵四边形ABCD为平行四边形,∴AD // BC.∴AFO CEO∠=∠,FAO ECO∠=∠.∵O为AC的中点,∴AO CO=.∴△AOF≌△COE.∴AF EC=.∵AF//EC,∴四边形AECF为平行四边形.∵AE AF=,∴四边形AECF为菱形.(2)解:∵O为AC的中点,4AC=,∴122OA AC==.∵四边形AECF为菱形,∴AC EF⊥.∴90AOE∠=︒.∴在Rt△AOE中,由勾股定理得OE=.∵E为BC的中点,∴2AB OE==.21. 解:设每平方米木地板的价格为5x元,则每平方米瓷砖的价格为3x元.由题意可得,123(3615)5100001270x x⨯++⨯=−.解得30x=.∴5150x=,390x=.答:每平方米木地板的价格为150元,每平方米瓷砖的价格为90元.22.解:(1)∵函数(0)y kx b k =+≠的图象经过点(1,2)A 和(0,1)B ,∴21.k b b +=⎧⎨=⎩,解得11.k b =⎧⎨=⎩,∴该函数的解析式为1y x =+. (2)13m ≤≤.23.解:(1)32,25;(2) 60,四; (3) >.24.(1)证明:∵BE BE =,∴BAE BDE ∠=∠. ∵45EDB EAD ∠+∠=︒,∴45BAE EAD ∠+∠=︒,即45BAD ∠=︒. ∵AB 为O 的直径, ∴90ADB ∠=︒. ∴AD BG ⊥. ∵AB AG =,∴45BAD GAD ∠=∠=︒. ∴90BAG ∠=︒. ∴AB AG ⊥.∵AB 为O 的直径, ∴AG 与O 相切.(2)解:连接BE ,如图.∵AB AG =,AD BG ⊥,BG =∴12BD BG == 在Rt △ADB 中,90ADB ∠=︒,45BAD ∠=︒,可得AB =∴12OA AB ==. ∵BAE BDE ∠=∠, ∴1tan tan 3BAE BDE ∠=∠=.∵AB 为O 的直径,∴90AEB ∠=︒.在Rt △AEB 中,1tan 3BAE ∠=,可得13BE AE =.由勾股定理得 222BE AE AB +=.∴2221()3AE AE +=.∴6AE =. ∵290BOD BAD ∠=∠=︒. ∴90AOF ∠=︒.在Rt △AOF 中,1tan 3BAE ∠=,OA =OF =.由勾股定理得 103AF =. ∴108633EF AE AF =−=−=. 25.解:(1)60n ,525n ⨯−;(2) a ,7; (3)1535t <≤.26.解:(1)由题意可知,点(40),在抛物线2(0)y ax bx a =+>上,∴1640a b +=. ∴4b a =−. ∴4222b aa a−==−−. ∴抛物线的对称轴为直线2x =.(2)① 法一:令0y =,则20(0)ax bx a +=>. 解得0x =或b x a=−. ∴抛物线2(0)y ax bx a =+>与x 轴交于点(00),,(0)b a−,. ∵0a >,∴抛物线开口向上. (ⅰ)当0b <时,0ba−>.∴当0bx a <<−时,0y <;当0x <或b x a>−时,0y >. ∵当04m <<时,总有0n <. ∴4ba−≥.∵0a >, ∴40a b +≤. (ⅱ)当0b >时,0ba−<. ∴当0bx a −<<时,0y <;当b x a<−或0x >时,0y >. ∴当04m <<时,0n >,不符合题意. 综上,40a b +≤. 法二:∴由题意可知,2am bm n +=.若0n <,则2()0am bm m am b +=+<. ∵0m >, ∴0am b +<. ∵0a >, ∴b m a<−. ∴当0bm a<<−时,0n <. ∵当04m <<时,总有0n <. ∴4ba−≥.∵0a >, ∴40a b +≤. ② 存在.设抛物线的对称轴为x t =,则2b t a=−. ∵,∴当x t ≥时,y 随x 的增大而增大;当x t ≤时,y 随x 的增大而减小. ∵12k <<,∴336k <<,3k k <. (ⅰ)当1t ≤时,∵3t k k ≤<. ∴12y y <,符合题意. (ⅱ)当12t <≤时,当2t k ≤<时, ∵3t k k <<. ∴12y y <. 当1k t <<时,设点1()P k y ,关于抛物线对称轴x t =的对称点为点01'(,)P x y , 则0x t >,0t k x t −=−. ∴02x t k =−. ∵1k t <<,12t <≤, ∴23t k −<. ∴03t x <<. ∵336k <<. ∴03t x k <<. ∴12y y <.∴当12t <≤时,符合题意. (ⅲ)当23t <≤时,令12k t =,332k t =,则12y y =,不符合题意.(ⅳ)当36t <<时,令3k t =,则3k k t <≤. ∴12y y >,不符合题意. (ⅴ)当6t ≥时,∵3k k t <<,∴12y y >,不符合题意. ∴ 当2t ≤,即22ba−≤时,符合题意. ∵0a >, ∴40a b +≥. 由①可得40a b +≤. ∴40a b +=.27.(1)线段AE 与BD的数量关系:AE .证明:连接BE ,如图1.∵点D ,E 关于直线BC 对称, ∴直线BC 是线段DE 的垂直平分线. ∴BD BE =.∴30DBC EBC ∠=∠=. ∴60DBE ∠=.∴△DBE 是等边三角形.∴BD BE DE ==,60BDE BED ∠=∠=. ∵△ABC 中,90ACB ∠=,30ABC ∠=, ∴2AB AC =.依题意,得AD AC =,点D 在AB 上. ∴2AB AD =. ∴.BD AD = ∴.DE AD =∴30.DAE DEA ∠=∠= ∴90.BEA ∠= ∴在Rt △ABE 中,tan tan 60 3.AEABE BE=∠== ∴AE. ∴.AE =(2)依题意补全图2,如图.B图1方法一:解:延长AC 至F ,使CF AC =,连接BF ,BE ,EF ,CD ,CE ,如图2. ∵90ACB ∠=, ∴.AB BF = ∵60BAC ∠=,∴△ABF 是等边三角形. ∴AB AF BF ==,60BFC ∠=. ∵点D ,E 关于直线BC 对称, ∴直线BC 是线段DE 的垂直平分线. ∴BD BE =,CD CE =. ∴DCB ECB ∠=∠. ∵90ACB DCF ∠=∠=, ∴DCA ECF ∠=∠. ∵AC FC =, ∴△DAC ≌△EFC . ∴CAD CFE ∠=∠. ∵AE BD =, ∴BE AE =.∵EF EF =,BF AF =, ∴△BEF ≌△AEF .∴30BFE AFE ∠=∠=. ∴30CAD AFE ∠=∠=. ∴30.α= 方法二:解:如图3,取AB 中点F ,连接DF ,BE ,CD ,CE ,设DBC β∠=.F∵点D ,E 关于直线BC 对称, ∴直线BC 是线段DE 的垂直平分线. ∴BD BE =,CD CE =. ∴DBC EBC β∠=∠=.∴30EBA β∠=︒+,30DBA β∠=︒−. ∵AE BD =, ∴AE BE =.∴30EAB EBA β∠=∠=︒+. ∵90ACB ∠=︒,30ABC ∠=︒, ∴60BAC ∠=︒. ∴30EAC β∠=︒−. ∴EAC DBA ∠=∠. 由(1)可得2.AB AC = ∵F 为AB 中点, ∴22.AB AF BF == ∴.AC AF BF ==∵AC BF =,EAC DBA ∠=∠,AE BD =, ∴△ACE ≌△BFD . ∴CE FD =. ∴CD FD =.∵AD AD =,AF AC =, ∴△ADF ≌△ADC . ∴30FAD CAD ∠=∠=︒. ∴30α=︒.28.(1)①如图,线段B'C'即为所求.②4t ≤−或2t ≥.图3FD≤≤+. (2)d a。
北京市中考数学一模分类27题二次函数及答案

2017年北京中考数学一模 27题“二次函数综合题”西城. 在平面直角坐标系xOy 中,二次函数5)12(2-++-=m x m mx y 的图象与x 轴有两个公共点. (1)求m 的取值范围;(2)若m 取满足条件的最小的整数,①写出这个二次函数的解析式;②当n ≤x ≤1时,函数值y 的取值范围是-6≤y ≤4-n ,求n 的值;③将此二次函数图象平移,使平移后的图象经过原点O . 设平移后的图象对应的函数表达式为k h x a y +-=2)(,当x <2时,y 随x 的增大而减小,求k 的取值范围东城.二次函数2(2)2(2)5y m x m x m =+-+-+,其中20m +>. (1)求该二次函数的对称轴方程; (2)过动点C (0, n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系;② 若抛物线与x 轴有两个交点,将抛物线在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当n =7时,直线l 与新的图象恰好有三个公共点,求此时m 的值; (3)若对于每一个给定的x 的值,它所对应的函数值都不小于1,求m 的取值范围.xy直线lCBA–1–21234–1–2–31234O朝阳.在平面直角坐标系中xOy 中,抛物线2211222y x mx m m =-++-的顶点在x 轴上. (1)求抛物线的表达式;(2)点Q 是x 轴上一点,①若在抛物线上存在点P ,使得∠POQ =45°,求点P 的坐标; ②抛物线与直线y =2交于点E ,F (点E 在点F 的左侧),将此抛物线在点E ,F (包含点E 和点F )之间的部分沿x 轴平移n 个单位后得到的图象记为G ,若在图象G 上存在点P ,使得∠POQ =45°,求n 的取值范围.房山. 在平面直角坐标系xOy 中,直线32-=x y 与y 轴交于点A ,点A 与点B 关于x 轴对称,过点B 作y 轴的垂线l ,直线l 与直线32-=x y 交于点C. (1)求点C 的坐标;(2)如果抛物线n nx nx y 542+-= (n >0)与线段BC 有唯一公共点,求n 的取值范围.顺义.如图,已知抛物线28(0)y ax bx a =++≠与x 轴交于A (-2,0),B 两点,与y 轴交于C点,tan ∠ABC =2.(1)求抛物线的表达式及其顶点D 的坐标;(2)过点A 、B 作x 轴的垂线,交直线CD 于点E 、F ,将抛物线沿其对称轴向上平移m 个单位,使抛物线与线段EF (含线段端点)只有1个公共点.求m 的取值范围.平谷.直线33y x =-+与x 轴,y 轴分别交于A ,B 两点,点A 关于直线1x =-的对称点为点C . (1)求点C 的坐标;(2)若抛物线()230y mx nx m m =+-≠经过A ,B ,C 三点,求该抛物线的表达式;(3)若抛物线()230y ax bx a =++≠ 经过A ,B 两点,且顶点在第二象限,抛物线与线段AC 有两个公共点,求a 的取值范围.yx–2–112345–5–4–3–2–112O门头沟. 在平面直角坐标系xOy 中,抛物线()()13y a x x =+-与x 轴交于A ,B 两点,点A 在 点B 的左侧,抛物线的顶点为P ,规定:抛物线与x 轴围成的封闭区域称为“G 区域”(不包含边界).(1)如果该抛物线经过(1, 3),求a 的值,并指出此时“G 区域”有______个整数点;(整数点就是横纵坐标均为整数的点) (2)求抛物线()()13y a x x =+-的顶点P 的坐标(用含a 的代数式表示); (3)在(2)的条件下,如果G 区域中仅有4个整数点时,直接写出a 的取值范围.海淀.平面直角坐标系xOy 中,抛物线2222y mx m x =-+交y 轴于A 点,交直线x =4于B 点.(1)抛物线的对称轴为x = (用含m 的代数式表示);(2)若AB ∥x 轴,求抛物线的表达式;(3)记抛物线在A ,B 之间的部分为图象G (包含A ,B 两点),若对于图象G 上任意一点P (P x ,P y ),2P y ≤,求m 的取值范围.丰台.在平面直角坐标系xOy 中,抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ,B 两点. (1)求抛物线的对称轴;(2)如果点A 的坐标是(-1,-2),求点B 的坐标;(3)抛物线的对称轴交直线AB 于点C ,如果直线AB 与y 轴交点的纵坐标 为-1,且抛物线顶点D 到点C 的 距离大于2,求m 的取值范围.石景山.在平面直角坐标系xOy 中,抛物线2443(0)y ax ax a a =-+-≠的顶点为A .(1)求顶点A 的坐标;(2)过点(0,5)且平行于x 轴的直线l ,与抛物线 2443(0)y ax ax a a =-+-≠交于B ,C 两点.①当2a =时,求线段BC 的长;②当线段BC 的长不小于6时,直接写出a 的 取值范围.通州.在平面直角坐标系xOy 中,抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A (-3,m ),B (1,m ).(1)求点D 的坐标(用含m 的代数式表示); (2)若该抛物线经过点B (1,m ),求m 的值;(3)若线段AB 与该抛物线只有一个公共点,结合函数的图象,求m 的取值范围.怀柔.已知二次函数122-++=a ax axy (a>0).(1)求证:抛物线与x 轴有两个交点; (2)求该抛物线的顶点坐标;(3)结合函数图象回答:当x ≥1时,其对应的函数值y 的最小值范围是2≤y ≤6,求a 的取值范围.西城.解:(1)∵ 二次函数5)12(2-++-=m x m mx y 的图象与x 轴有两个交点,∴ m ≠0[]054122>)()+(---m m m解得 241->m 且m ≠0. ∴m 的取值范围是241->m 且m ≠0. ·········································· 2分(2)①m 取满足条件的最小的整数,由(1)可知m =1.∴ 二次函数的表达式为234y x x =--. ·································· 3分② 图象的对称轴为直线23=x .当n ≤x ≤1<32时,函数值y∵ 函数值y 的取值范围是-6≤y ≤4-n , ∴ 当x =1时,函数值为- 6. 当x =n 时,函数值为4-n.∴ n 2 – 3n - 4 = 4-n.,解得n = - 2或n = 4(不合题意,舍去). ∴ n 的值为- 2. ③由①可知,a =1. 又函数图像经过原点, ∴k =-h 2,∵当x <2时,y 随x 的增大而减小, ∴h ≥ 2 ∴k ≤-4.············································································································ 7分 东城.解:(1)对称轴方程:2(2)12(2)m x m -+=-=+. …………1分(2)①∵直线l 与抛物线只有一个公共点,∴23n m =-+. …………3分② 依题可知:当237m -+=-时,直线l 与新的图象恰好有三个公共点. ∴5m =. …………5分(3)抛物线2(2)2(2)5y m x m x m =+-+-+的顶点坐标是(1,23)m -+.依题可得 20,23 1.m m +>⎧⎨-+≥⎩解得2,1.m m >-⎧⎨≤⎩∴ m 的取值范围是21m -<≤. …………7分朝阳.解:(1)222111-2()2222y x mx m m x m m =++-=-+-. 由题意,可得m -2=0. ∴2m =. ∴21(2)2y x =-. (2)①由题意得,点P 是直线y x =与抛物线的交点.∴21-222x x x =+. 解得 135x =+,235x =-. ∴P 点坐标为(35,35)++或 (35,35)--.②当E 点移动到点(2,2)时,n =2.当F 点移动到点(-2,2)时,n =-6. 由图象可知,符合题意的n 的取值范围是26-≤≤n .房山解:(1)∵直线y=2x-3与y 轴交于点A (0,-3) ------1分 ∴点A 关于x 轴的对称点为B (0,3),l 为直线y=3 ∵直线y=2x-3与直线l 交于点C ,∴点C 的坐标为(3,3) ------2分(2)∵抛物线n nx nx y 542+-= (n >0) ∴y = nx2-4nx+4n+n = n(x-2)2+n∴抛物线的对称轴为直线x=2,顶点坐标为(2,n ) ------3分 ∵点B (0,3),点C (3,3)①当n >3时,抛物线最小值为n >3,与线段BC 无公共点; ②当n=3时,抛物线顶点为(2,3),在线段BC 上,此时抛物线与线段BC 有一个公共点; ------4分 ③当0<n <3时,抛物线最小值为n ,与直线BC 有两个交点 如果抛物线y=n(x-2)2+ n 经过点B (0,3),则3=5n ,解得53=n由抛物线的对称轴为直线x=2,可知抛物线经过点(4,3)点(4,3)不在线段BC 上,此时抛物线与线段BC 有一个公共点B ------5分如果抛物线y=n(x-2)2+ n 经过点C (3,3),则3=2n ,解得23=n 由抛物线的对称轴为直线x=2,可知抛物线经过点(1,3)点(1,3)在线段BC 上,此时抛物线与线段BC 有两个公共点 ------6分综上所述,当53≤n <23或n=3时,抛物线与线段BC 有一个公共点. ------7分 顺义27.解:(1)由抛物线的表达式知,点C (0,8),即 OC =8;Rt △OBC 中,OB =OC •tan ∠ABC =8×12=4, 则点B (4,0). ………………………… 1分 将A 、B 的坐标代入抛物线的表达式中,得:428016480a b a b -+=⎧⎨++=⎩,解得12a b =-⎧⎨=⎩, ∴抛物线的表达式为228y x x =-++.…… 3分∵2228(1)9y x x x =-++=--+ ,∴抛物线的顶点坐标为D (1,9). ………… 4分(2)设直线CD 的表达式为y =kx +8,∵点D (1,9),∴直线CD 表达式为y =x +8.∵过点A 、B 作x 轴的垂线,交直线CD 于点E 、F , 可得:E (-2,6),F (4,12). ………… 6分 设抛物线向上平移m 个单位长度(m >0),则抛物线的表达式为:2(1)9y x m =--++;当抛物线过E (-2,6)时,m =6,当抛物线过F (4,12)时,m =12, ∵抛物线与线段EF (含线段端点)只有1个公共点,∴m 的取值范围是6<m ≤12. ………………………………………… 7分平谷27.解:(1)令y =0,得x =1.∴点A 的坐标为(1,0). ···································································· 1 ∵点A 关于直线x =﹣1对称点为点C , ∴点C 的坐标为(﹣3,0). ··················· 2 (2)令x =0,得y =3.∴点B 的坐标为(0,3). ∵抛物线经过点B , y 2345B∴﹣3m =3,解得m =﹣1. ····················· 3 ∵抛物线经过点A ,∴m+n ﹣3m =0,解得n =﹣2.∴抛物线表达式为223y x x =--+. (4)(3)由题意可知,a <0.根据抛物线的对称性,当抛物线经过(﹣1,0)时,开口最小,a =﹣3, ·········· 5 此时抛物线顶点在y 轴上,不符合题意.当抛物线经过(﹣3,0)时,开口最大,a =﹣1. (6)结合函数图像可知,a 的取值范围为31a -<≤-. (7)门头沟27. (1)()()3a 1113=+- ……………1分解得:34a =-………………………2分 6个 ………………………3分(2)由()()y a 13x x =+-配方或变形()()()2y a 13=14x x a x a =+--- .所以顶点P 的坐标为(1,-4a ). ……………………………………5分 (3) a <0时, ; 分a >0时, 7分 分 22x +与y 轴交于A 点,分 ∵ AB ∥x 轴,B 点在直线x =4上,∴ B (4,2),抛物线的对称轴为直线x =2. --------------------------------------------- 4分 ∴ m =2.2132a --≤<12≤∴ 抛物线的表达式为2282y x x =-+. --------------------------------------------------- 5分 (3)当0m >时,如图1.∵()02A ,,∴要使04P x ≤≤时,始终满足2P y ≤,只需使抛物线2222y mx m x =-+的对称轴与直线x=2重合或在直线x=2的右侧. ∴2m ≥. -------------------------------------------- 6分当0m <时,如图2,0m <时,2P y ≤恒成立. ------------------- 7分综上所述,0m <或2m ≥.丰台27. 解:(1)∵抛物线()12212422---=-+-=m x m m mx mx y ,∴对称轴为x = 2.…………………………………2分(2)①∵抛物线是轴对称图形,∴点A 点B 关于x = 2轴对称,∵A (﹣1,-2) ,∴B (5,-2).……………………………………………3分 ②∵抛物线()12212422---=-+-=m x m m mx mx y ,∴顶点D (2,﹣2m -1). …………………………………………………4分∵直线AB 与y 轴交点的纵坐标为-1,∴C (2,-1). ……………………………………………………………5分∵顶点D 到点C 的距离大于2,∴﹣2m ﹣1 +1 > 2或﹣1+ 2m +1 > 2,∴m <﹣1或m > 1.………………………………………………………… 7分石景山27.解:(1)解法一: ∵2443y ax ax a =-+-2(2)3a x =--, ………………………………… 1分∴顶点A 的坐标为(2,3)-. ………………………………… 2分图2解法二: ∵244(43)(4)2,324a a a a aa-⨯----==-,∴顶点A 的坐标为(2,3)-. ………………………………… 2分(2)①当2a =时,抛物线为2285y x x =-+,如图. 令5y =,得22855x x -+=, ……………… 3分 解得,1204x x ==,.……………… 4分∴线段BC 的长为4. ……………… 5分② 80<9a ≤. ……………… 7分通州27. 解:(1)D (m ,-m +2) (2)m =3或m =1 ……………………..(5分)(3)1≤m ≤3 ……………………..(7分) 怀柔27.解:(1)令y=0. ∴0122=-++a ax ax .∵△=)1(442--a a a=4a,……………………………1分 ∵a>0,∴4a>0.∴△>0.∴抛物线与x 轴有两个交点. …………………2分 (2)212ax a=-=-.……………………………3分 把x=-1代入122-++=a ax ax y .∴y=-1.∴顶点坐标(-1,-1).…………………4分 (3)①把(1,2)代入122-++=a ax ax y . ∴43=a .……………………………5分 ②把(1,6)代入122-++=a ax axy . ∴74a =.……………………………6分 ∴由图象可知:43≤a ≤74.……………………………7分 y xB x =2–1–2–3–4–512345–1–2–3–41234567CA (2,-3)O。
2024年北京大兴区初三一模考试数学及答案

大兴区2023~2024学年度第二学期初三期中检测数学参考答案及评分标准一、选择题(共16分,每题2分) 题号1 2 3 4 5 6 7 8 答案D B C B C D A D二、填空题(共16分,每题2分) 题号910 11 12 13 14 15 16 答案3x ≥ ()()22a x x +− 1x = -5 45 1 240 60,30三、解答题(共68分,第17-20题,每题5分,第21题6分,第22-23题,每题5分,第24-26题,每题6分,第27,28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17.解:原式=2312222++−⨯························································· 4分 =42+. ··········································································· 5分18. 解:4125213x x x x ⎧⎪⎨⎪⎩-≥+,①-<.②解不等式①,得x ≥3. ································································· 2分解不等式②,得x >-1. ······························································· 4分所以不等式组的解集为x ≥3. ························································ 5分19.解:··························································· 2分. ·········································································· 3分∵,∴. ············································································· 4分∴.∴原式=2-1=1. ················································································ 5分2(1)(4)2a a a +++−222142a a a a =++++−2261a a =+−2310a a +−=231a a +=2262a a +=2261a a =+−原式20.解:设每本A 书籍厚度为x cm ,桌子高度为y cm. ····································· 1分由题意可得37965825,.x y x y ⎧+=⎪⎨⨯+=⎪⎩····································································· 3分 解得176x y ⎧=⎨=⎩,.············································································· 4分 答:每本A 书籍厚度为1cm. ···································································· 5分21. (1)证明:∵四边形ABCD 是正方形,∴AD ∥BC ,AD =BC . …………………………1分∵BE =FD ,∴AD -FD =BC -BE.即AF =CE . …………………………2分又∵AF ∥CE ,∴ 四边形AECF 是平行四边形. ……………………………………3分(2)解:∵四边形ABCD 是正方形,∴AB ∥CD ,∠BCD=∠D =90°,AD =CD. ……………………………4分∴∠BAE=∠G ,∠ECG =90°,∴tan ∠BAE = tan G =. 在Rt △ADG 中,∵ tan G =AD DG =,DG =9, ∴ AD =6.∴ CD =6.…………………………………………………………5分∴ CG =3.在Rt △ECG 中,∵ tan G = =CE CG , ∴ CE=2 . ··········································································· 6分22.解:(1)4; …………………………………………………………………………1分(2)7.55; ……………………………………………………………………………2分(3)①;………………………………………………………………………………4分(4)乙. ………………………………………………………………………………5分23232323. 解:(1)将A (1,3),B (-1,-1)代入0()y kx b k =+≠中,得3 1.,k b k b +=⎧⎨−+=−⎩ ············································································· 1分 解得21.,k b =⎧⎨=⎩∴函数的表达式为21=+y x . ························································ 2分 ∵过点(-2,0)且平行于y 轴的直线交于点C ,∴点C 的横坐标为-2.把x =-2代入,得y =-3.∴点C 的坐标为(-2,-3). ····························································· 3分 (2) 312≤≤n .··············································································· 5分24. (1) ②,①; ···················································································· 2分(2)①不能. ························································································ 3分 理由如下:由题意可得OE =2.6+3=5.6.把x =5.6代入上边缘抛物线表达式,得2156220388()==−−+y ..<0.5 所以绿化带不全在喷头口的喷水区域内.所以洒水车不能浇灌到整个绿化带. ················································· 4分 ②2≤OD ≤231−. ······································································ 6分25. (1)证明:∵AB 为⊙O 的切线,∴∠OBA =90°.∴∠A +∠AEB =90°.∵BC 为⊙O 的直径,∴∠CDB =90°.∴∠CDE +∠BDE =90°.∵BD =BA ,∴∠BDA =∠A .∴∠CDE =∠AEB. ···················································································· 1分又∵∠CDE=∠CBF,∴∠AEB=∠CBF.∴EF=BF. ···························································································2分(2) 解:连接CF.∵AB为⊙O的切线,∴∠OBA=90°.∴∠AEB+∠A=90°,∠EBF+∠FBA=90°.∵∠AEB=∠CBF,∴∠FBA=∠A.∴AF=BF.∴AF=BF=EF. ························································································3分设BF =EF=AF=x,则AE=2x.在Rt△ABE中,∵sin A=13,AE=2x,∴BE=23x. ·····························································································4分∵BC为直径,∴∠CFB=90°.∵∠BCF=∠BDA,∠BDA=∠A,∴∠BCF=∠A. ························································································5分∴sin A=sin∠BCF=1 3 .在Rt△BFC中,∵BF=x,∴BC=3x.∵BC=2OB=2(OE+BE),∴3x=2(52+23x).解得x=3.∴OB=9 2 .∴⊙O半径的长为92. ················································································6分26.解:(1)∵x 2=2,y 2=c ,∴4a +2b +c =c. ………………………………………………………………………………1分 ∴b =-2a .∴12b t .a=−= ························································································ 2分 (2) ∵ 2(0)y ax bx c a =++<,∴抛物线开口向下.∵ 抛物线的对称轴为x =t ,t +1<x 1<t +2,∴点M 在对称轴的右侧. …………………………………………………………………3分 ①当点N 在对称轴上或对称轴右侧时,∵抛物线开口向下,∴在对称轴右侧,y 随x 的增大而减小.由y 1>y 2,∴x 1<x 2.∴424≤≤t ,t .⎧⎨+⎩解得42≤≤t ,t .⎧⎨⎩∴2≤t . ……………………………………………………………………………4分 ②当点N 在对称轴上或对称轴左侧时,设抛物线上的点N (x 2, y 2)关于x =t 的对称点为()2N d ,y ',∴ t - x 2=d -t ,解得d =2t - x 2,∴()222N t x ,y '−.∵4<x 2<5∴2t -5<2t -x 2<2t -4.在对称轴右侧,y 随x 的增大而减小.由y 1>y 2,∴x 1<2t -x 2.∴5225≥≤t,t t .⎧⎨+−⎩解得57≥≥t ,t .⎧⎨⎩∴7≥t .综上所述,t 的取值范围是27≤或≥t t .…………………………………………………6分27. (1)补全图形如下:…………………………………………….1分(2) 解:∵AC= BC ,∠ACB =90°,∴∠A =∠ABC =45°.∴∠CDB =∠A +∠ACD =45°+α. ………………………………………………………….2分 ∵∠CDE =90°,∴∠EDB =∠CDE -∠CDB =45°-α.……………………………………………………….3分(3) 用等式表示线段BE ,BC ,AD 之间的数量关系是BC=AD+BE. ………………………4分 证明:过点D 作DM ⊥AB ,交AC 于点F ,交BC 的延长线于点M .∵∠MDB =∠CDE =90°,∴∠CDM =∠EDB .∵∠MBD =45°,∴∠M =∠MBD =45°.∴DM=DB.又∵DC=DE ,∴△DCM ≌△DEB .∴CM=BE .···························································································· 5分 ∵∠M =45°,∠ACB =90°,∴∠CFM =∠M =45°.∴CF=CM .∴CF=BE. ···························································································· 6分 E CA BD2在Rt △F AD 中,∵∠A =45°,∴cos A =. ∴AF=AD .∵AC=AF+FC ,∴AC=AD+FC.∵CF=BE ,BC=AC ,∴BC=AD+BE.············································································ 7分28.解:(1)① …………………………………………………………………….2分 ②如图1: 设射线与⊙T 相切于点,连接. ∴TM ⊥PM .当∠P =45°时,在Rt △PMT 中,.∴当点在⊙T 外且∠P ≥ 45°时,1<PT . ∴点在以T 为圆心,以为半径的圆上或圆内且在以1为半径的圆外. ············ 3分 如图2:直线上有且只有一个⊙T 的“伴随点”, ∴直线与以为圆心,为半径的圆相切. ∴b ≠0.设直线与轴,轴分别交于点,,与以为圆心,为半径的圆相切于点,连接, ∴.令,则;令,则,.,.在Rt △ATB 中,,90° . , 22AD AF =22223P P ,PM M TM 2222112PT MP MT =+=+=P 12∴<PT ≤P 21:2l y x b =+12y x b =+T 212y x b =+x y A B T 2C TC TC AB ⊥0x =y b =0y =2x b =−2,0),(0,)A b B b ∴−(2AT b ∴=−BT b =1tan 122b BT AT b ∠===−1290∠+∠=TC AB ⊥图2图190°... 在Rt △TCB 中, 1322tan =BC BC .CT ∠== . . . . ···························································································· 5分 (2)或. ································································ 7分 2390∴∠+∠=13∴∠=∠1tan 1tan 32∴∠=∠=22BC ∴=2222210(2)()22BT CT BC ∴=+=+=102b ∴=102b ∴=±213312,2222t t −−−<≤≤<213312,2222t t −−−<≤≤<。
2024北京朝阳区初三一模数学试卷和答案

2024北京朝阳初三一模数 学考生须知1.本试卷共6页,共三道大题, 28道小题, 满分100分.考试时间120分钟.2.在试卷和答题卡上认真填写学校名称、班级、姓名和考号.3.试题答案一律填涂或书写在答题卡上, 在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.5.考试结束, 请将本试卷、答题卡和草稿纸一并交回.一、选择题(共16分,每题2分)第1-8题均有四个选项,其中符合题意的选项只有一个.1. 2024年1月21日北京市第十六届人民代表大会第二次会议开幕,在政府工作报告中提到,2023年北京向天津、河北输出技术合同成交额74870000000元,将74870000000用科学记数法表示应为( )A. 974.8710⨯ B. 107.48710⨯ C. 97.48710⨯ D. 110.748710⨯2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.3. 如图,直线AB ,CD 相交于点O ,若50AOC ∠=︒,15DOE ∠=︒,则∠BOE 的度数为( )A. 15︒B. 30︒C. 35︒D. 65︒4. 如果一个几何体的三视图都是矩形,那么这个几何体可能是( )A. 三棱柱B. 长方体C. 圆柱D. 圆锥5. 若a b <,则下列结论正确的是( )A. a b-<- B. 2a a b<+ C. 11a b-<- D. 2121a b +>+6. 正十边形的内角和为( )A. 144︒B. 360︒C. 1440︒D. 1800︒7. 掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,向上一面的点数为5的概率是( )A.23B. 12C.13D.168. 如图,四边形ABCD 是正方形, 点E F ,分别在AB BC ,的延长线上, 且BE CF =,设AD a AE b AF c ===,,. 给出下面三个结论:①a b c +>;②22ab c <;2a >.上述结论中,所有正确结论的序号是( )A. ①②B. ②③C. ①③D. ①②③二、填空题 (共16分,每题2分)9. x 的取值范围是______.10. 分解因式:3x 2+6xy+3y 2=_____.11. 方程21345x x =-的解为______.12. 关于x 的一元二次方程250x x m ++=有两个不相等的实数根,则实数m 的取值范围是_____.13. 某种植户种植了1000棵新品种果树,为了解这1000棵果树的水果产量,随机抽取了50棵进行统计,获取了它们的水果产量(单位:千克),数据整理如下:水果产量50x <5075x ≤<75100x ≤<100125x ≤<125x ≥果树棵数11520122根据以上数据,估计这1000棵果树中水果产量不低于75千克的果树棵数为_____.14. 在数学活动课上,小南利用镜子、尺子等工具测量学校教学楼高度(如图所示),当他刚好在点C 处的镜子中看到教学楼的顶部D 时,测得小南的眼睛与地面的距离 1.6m AB =,同时测得 2.4m BC =,9.6m CE =,则教学楼高度DE =_____m .15. 如图,O 是Rt ABC △的外接圆,OE AB ⊥于点D ,交O 于点E ,若8AB =,2DE =,则BC 的长为_____.16. 甲、乙两位同学合作为班级联欢会制作A B C D 、、、四个游戏道具,每个道具的制作都需要拼装和上色两道工序,先由甲同学进行拼装,拼装完成后再由乙同学上色.两位同学完成每个道具各自的工序需要的时间(单位:分钟)如下表所示: A B C D 甲9568乙7793(1)如果按照A B C D →→→的顺序制作,两位同学合作完成这四个道具的总时长最少为_______分钟;(2)两位同学想用最短的时间完成这四个道具的制作,他们制作的顺序应该是_______.三、解答题(共68分, 第17-19题, 每题5分, 第20-21题, 每题6分, 第22-23题, 每题5分,第24题6分, 第25题5分, 第26题6分, 第27-28题, 每题7分)解答应写出文字说明、演算步骤或证明过程.17. ()012π2sin45--︒18. 解不等式组:()2431432x x x x ⎧-<-⎪⎨--<⎪⎩,.19. 已知220x y ++=,求代数式 2422yxx x x y ⎛⎫-⋅⎪-⎝⎭的值.20. 如图,在ABCD Y 中,AB AC =,过点D 作AC 的平行线与BA 的延长线相交于点 E .(1)求证: 四边形ACDE 是菱形;(2)连接CE ,若5tan 2AB B ==,,求CE 的长.21. 燕几(即宴几)是世界上最早的一套组合桌,设计者是北宋进士黄伯思.全套燕几一共有七张桌子,每张桌子高度相同.其桌面共有三种尺寸,包括2张长桌、2张中桌和3张小桌,它们的宽都相同.七张桌面可以拼成一个大的长方形,或者分开组合成不同的图形,其方式丰富多样,燕几也被认为是现代七巧板的前身.右图给出了《燕几图》中列出的名称为“函三”和“回文”的两种桌面拼合方式.若全套七张桌子桌面的总面积为61.25平方尺,则长桌的长为多少尺?22. 在平面直角坐标系xOy 中,正比例函数()0y mx m =≠的图象和反比例函数 ()0ky k x=≠的图象都经过点()24A ,.(1)求该正比例函数和反比例函数的解析式;(2)当3x >时, 对于x 的每一个值, 函数()0y mx n m =+≠的值都大于反比例函数 ()0k y k x=≠的值,直接写出n 的取值范围.23. 某广场用月季花树做景观造型,先后种植了两批各12棵,测量并获取了所有花树的高度 (单位:cm ),数据整理如下:a .两批月季花树高度的频数: 131135136140144148149第一批13422第二批12351b .两批月季花树高度的平均数、中位数、众数(结果保留整数): 平均数中位数众数第一批140140n 第二批141m144(1)写出表中m ,n 的值;(2)在这两批花树中,高度的整齐度更好的是 (填“第一批”或“第二批”);(3)根据造型的需要,这两批花树各选用10棵,且使它们高度的平均数尽可能接近.若第二批去掉了高度为135cm 和149cm 的两棵花树,则第一批去掉的两棵花树的高度分别是 cm 和 cm .24. 如图,AB 是O 的直径,点C 在O 上,D 是 BC的中点,AD 的延长线与过点B 的切线交于点E ,AD 与BC 的交点为F .(1)求证:BE BF =;(2)若O 的半径是2,3BE =,求AF 的长.25. 某款电热水壶有两种工作模式:煮沸模式和保温模式,在煮沸模式下将水加热至100C ︒后自动进入保温模式,此时电热水壶开始检测壶中水温,若水温高于50C ︒水壶不加热;若水温降至50C ︒,水壶开始加热,水温达到100C ︒时停止加热……此后一直在保温模式下循环工作.某数学小组对壶中水量a (单位:L ),水温T (单位: C ︒)与时间t (单位:分)进行了观测和记录,以下为该小组记录的部分数据.表1从20C ︒开始加热至100C ︒水量与时间对照表a0.51 1.522.53t4.5811.51518.522表2 1L 水从20C ︒开始加热,水温与时间对照表煮沸模式保温模式t036m 101214161820222426…T 205080100898072666055505560对以上实验数据进行分析后,该小组发现,水壶中水量为1L 时,无论在煮沸模式还是在保温模式下,只要水壶开始加热,壶中水温T 就是加热时间t 的一次函数.(1)写出表中m 的值;(2)根据表2中的数据,补充完成以下内容:①在下图中补全水温与时间的函数图象;②当60t =时,T = ;(3)假设降温过程中,壶中水温与时间的函数关系和水量多少无关.某天小明距离出门仅有30分钟,他往水壶中注入2.5L 温度为 20C ︒的水,当水加热至100C ︒后立即关闭电源.出门前,他 (填“能”或“不能”)喝到低于50C ︒的水.26. 在平面直角坐标系xOy 中,抛物线 ()20y ax bx a =+>上有两点()()1122,,x y x y ,, 它的对称轴为直线x t =.(1)若该抛物线经过点()40,,求t 的值;(2)当()101x <<时,①若1t >, 则1y 0; (填“>”“=”或“<” )②若对于122x x +=,都有120y y >,求t 的取值范围.27. 如图,在菱形ABCD 中,120BAD ∠=︒,E 是CD 边上一点(不与点C ,D 重合).将线段AE 绕点A 逆时针旋转60︒得到线段AF ,连接DF ,连接BF 交AC 于点G .(1)依据题意,补全图形;(2)求证:GB GF =;(3)用等式表示线段BC ,CE ,BG 之间的数量关系.28. 在平面直角坐标系xOy 中,O 的半径为1,对于直线l 和线段PQ ,给出如下定义:若线段PQ 关于直线l 的对称图形是O 的弦P Q ''(P ',Q '分别为P ,Q 的对应点),则称线段PQ 是O 关于直线l 的“对称弦”(1)如图,点1A ,2A ,3A ,1B ,2B ,3B 的横、纵坐标都是整数.线段11A B ,22A B ,33A B 中,是O 关于直线1y x =+的“对称弦”的是 ;(2)CD 是O 关于直线()0y kx k =≠的“对称弦”,若点C 的坐标为()1,0-,且1CD =,求点D 的坐标;(3)已知直线y x b =-+和点(3,M ,若线段MN 是O 关于直线y b =-+的“对称弦”,且1MN =,直接写出b 的值.参考答案一、选择题(共16分,每题2分)第1-8题均有四个选项,其中符合题意的选项只有一个.1. 【答案】B【分析】本题考查了科学记数法的表示方法.科学记数法的表示形式为10n a ⨯的形式,其中110a ≤<,n 为整数,解题的关键要正确确定a 的值以及n 的值.【详解】解:10748700000007.48710=⨯;故选:B .2. 【答案】D【分析】本题考查了中心对称图形以及轴对称图形,根据中心对称图形是指图形绕着某个点旋转180°能与原来的图形重合;轴对称图形是指图形沿一条直线折叠,直线两旁的部分能够完全重合;逐项分析即可得出答案.【详解】解:A 、正三角形是轴对称图形不是中心对称图形,A 不符合题意;B 、等腰直角三角形是轴对称图形不是中心对称图形,B 不符合题意;C 、正五边形是轴对称图形不是中心对称图形,C 不符合题意;D 、正六边形既是轴对称图形又是中心对称图形,D 符合题意;故选:D .3. 【答案】C【分析】本题考查了对顶角相等,角的运算;根据对顶角的性质得50BOD AOC ∠=∠=︒,根据BOE BOD DOE ∠=∠-∠即可求解.【详解】解:∵直线AB ,CD 相交于点O ,50AOC ∠=︒,∴50BOD AOC ∠=∠=︒,∵15DOE ∠=︒,∴501535BOE BOD DOE ∠=∠-∠=︒-︒=︒.故选:C .4. 【答案】B【分析】本题考查了简单几何图的三视图,根据几何体的三视图逐项判断即可求解.【详解】解:三棱柱的两个底面是三角形,所以不可能三视图都是矩形,故选项A 不符合题意;长方体的三视图都是矩形,故选项B 符合题意;圆柱的两个底面是三角形,所以不可能三视图都是矩形,故选项C 不符合题意;正立的圆锥的主视图和左视图都是等腰三角形,俯视图是带圆心的圆,故选项D 不符合题意.故选:B .5. 【答案】B【分析】本题主要考查不等式的基本性质,解题的关键是根据不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变逐项判定.【详解】解:A 、若a b <,则a b ->-,故不合题意;B 、若a b <,则2a a b <+,故符合题意;C 、若a b <,则11a b ->-,故不合题意;D 、若a b <,则2121a b +<+,故不合题意,故选:B .6. 【答案】C【分析】本题主要考查多边形的内角和,解题的关键是利用多边形的内角和公式进行计算即可.【详解】解:正十边形的内角和为180(102)︒⨯-1808=︒⨯1440=︒.故选C .7. 【答案】D【分析】本题主要考查概率公式,解题的关键是根据概率公式求解,随机事件A 的概率()P A =事件A 可能出现的结果数÷所有可能出现的结果数.【详解】解:∵骰子的六个面上分别刻有1到6的点数,∴向上一面的点数为5的概率是16,故选:D .8. 【答案】A【分析】本题考查正方形的性质,全等三角形的判定和性质,勾股定理,证明DAE BAF △≌△,结合三角形的三边关系判断①;完全平方公式结合勾股定理判定②;勾股定理判断③.【详解】解:∵正方形ABCD ,∴,90AD AB BC DAB ABC ==∠=∠=︒,∵BE CF =,∴AE BF =,∴DAE BAF △≌△,∴AF DE c ==,∵AD AE DE +>,∴a b c +>;故①正确;∵222AD AE DE +=,即:222+=a b c ,∴()2222220b a a ab b c ab -=-+=->,∴22ab c <;故②正确;c =,且,E F 为动点,∴无法确定c 和2a 的关系,故③错误;故选A .二、填空题 (共16分,每题2分)9. 【答案】14x ≥【分析】本题考查了二次根式有意义的条件,解一元一次不等式,根据被开方数不小于零列出不等式,解不等式即可.∴140x -≥,解得:14x ≥.故答案为:14x ≥.10. 【答案】3(x+y )2.【分析】先利用提取公因式法提取数字3,再利用完全平方公式继续进行分解.【详解】3x 2+6xy +3y 2=3(x 2+2xy +y 2)=3(x +y )2.故答案为3(x +y )2.【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.11. 【答案】2x =【分析】本题考查了解分式方程,根据去分母,去括号,移项,合并同类项,系数化为1的步骤解方程,然后检验即可得出答案.【详解】解:21345x x =-去分母得:()2453x x -=,去括号得:8103x x -=,移项得:8310x x -=,合并同类项得:510x =,系数化为1得:2x =.检验:当2x =时,()3450x x -≠,∴原分式方程的解为2x =.故答案为:2x =.12. 【答案】254m <【分析】根据有两个不相等的实数根,直接得到判别式>0,即可求解本题.【详解】解:∵方程250x x m ++=有两个不相等的实数根,∴25410>∆=-⨯⨯m ,解得:254m <;故答案为:254m <.【点睛】本题考查的是一元二次方程根的判别式,注意记忆判别式大于0时有两个不相等的实数根,判别式等于0时有两个相等的实数根,判别式小于0时方程无实数根.13. 【答案】680【分析】本题考查了频数(率)分布表和用样本估计总体,解题的关键是利用样本估计总体思想的运用.用1000乘以水果产量不低于75千克的果树的百分比即可求解.【详解】解:估计这1000棵果树中水果产量不低于75千克的果树棵数为20122100068050++⨯=(棵).故答案为:680.14. 【答案】6.4【分析】本题考查了相似三角形的应用,根据相似三角形的判定和性质列出比例式,即可求解.【详解】解:由题意可知,AB DE ∥,∴ABC DEC ∽△△,∴AB BCDE CE=,即1.62.49.6DE =,解得 6.4DE =,则教学楼高度 6.4m DE =,故答案为:6.4.15. 【答案】6【分析】本题考查了垂径定理,勾股定理和中位线定理,由垂径定理得142AD BD AB ===,90ADO BDO ∠=∠=︒,则可得OD 是ABC 的中位线,设半径为r ,由勾股定理得222OA OD AD =+,求出=5r 即可求解,熟练掌握知识点的应用是解题的关键.【详解】解:∵OE AB ⊥,∴142AD BD AB ===,90ADO BDO ∠=∠=︒,∵OA OC =,∴OD 是ABC 的中位线,∴12OD BC =,即2BC OD =,设半径为r ,则2OD OE DE r =-=-,在Rt AOD 中,由勾股定理得:222OA OD AD =+,∴()22224r r =-+,解得=5r ,∴23OD r =-=,∴26BC OD ==.16. 【答案】 ①. 35 ②. B C A D→→→【分析】本题主要考查最优化时间的使用的有理数加减运算,()1根据甲乙各自的拼装和上色所需时间进行分解,求出对应的用时再求得总时长即可;()2由于甲乙开始都需要时间,为甲选择B ,再结合各自所需时间排序即可.【详解】解:(1)甲先拼装A 需9分钟,乙开始上色A ,与此同时甲可以拼装B 和2分钟的C ,乙给B 上色时,甲可以继续拼装C 和3分钟D ,乙为C 上色5分钟时甲可以完成D 的拼装,此时乙还需要4分钟为C 上色,接着为D 上色3分钟,时间分解如图,(其中字母表示制作的游戏道具,数字表示相应的时间)故总时长最少为97754335+++++=分钟,故答案为35;(2)甲先拼装B 需5分钟,乙开始上色B ,与此同时甲可以拼装C 和1分钟的A ,乙给C 上色时,甲可以继续拼装A 和1分钟D ,乙为A 上色7分钟时甲可以完成D 的拼装,此时乙还需要3分钟为D 上色,时间分解如图,选择B C A D →→→这种方案即可用时最少.(其中字母表示制作的游戏道具,数字表示相应的时间)故答案为B C A D→→→.三、解答题(共68分,第17-19题,每题5分,第20-21题,每题6分,第22-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17.【答案】【分析】此题主要考查了实数运算,解题的关键是直接利用二次根式的性质、绝对值的性质、特殊角的三角函数值、零整数指数幂的性质分别化简得出答案.()012π2sin45+---︒112=-+-11=+-+=18. 【答案】12x-<<【分析】本题考查了解一元一次不等式组,分别解出每个不等式的解集,然后确定不等式组的解集即可,熟练掌握不等式组的解法是解题的关键.【详解】解:()2431432x xxx⎧-<-⎪⎨--<⎪⎩①②,解不等式①得,1x>-,解不等式②得,2x<,∴不等式组的解集为12x-<<.19. 【答案】24x y+,4-【分析】本题考查了分式的化简求值,先根据分式的混合运算化简所求式子,再根据220x y++=,可以得到22+=-x y,代入化简后的式子计算即可.【详解】解:2422y xxx x y⎛⎫-⋅⎪-⎝⎭22422x y x x x y -=⋅-()()2222x y x y xxx y-+=⋅-()22x y =+24x y =+,∵220x y ++=,∴22+=-x y ,∴原式()()22422x y ==⨯-=-+.20. 【答案】(1)见解析 (2)【分析】(1)由平行四边形的性质得AB CD =,AB CD ∥,再证明四边形ACDE 是平行四边形,进而证明CD AC =,然后由菱形的判定即可得出结论;(2)设AD 与CE 交于点F ,证明FAC ACB B ∠=∠=∠,再由菱形的性质得AF DF =,CF EF =,AD CE ⊥,进而由锐角三角函数定义得CF 2AF =,设CF x =,则2CF x =,然后在Rt AFC △中,由勾股定理得出方程,解方程即可.【小问1详解】证明: 四边形ABCD 是平行四边形,AB CD ∴=,AB CD ∥,DE AC ∥ ,∴四边形ACDE 是平行四边形,AB AC = ,CD AC ∴=,∴平行四边形ACDE 是菱形;【小问2详解】如图,设AD 与CE 交于点F ,5AB AC == ,B ACB ∴∠=∠,四边形ABCD 是平行四边形,AD BC ∴∥,FAC ACB B ∴∠=∠=∠,由(1)可知,四边形ACDE 是菱形,AB CD AE ∴==,AD BC ∥,AD CE ⊥,90BCE AOE ∴∠=∠=︒,在Rt BCE △中,tan 2CEB BC==,设BC x =,则2CE x =,∵AB =5∴BE =2AB =10∵222BC CE BE += ,222(2)10x x ∴+=,解得12)x x ==-舍即CE 的长为【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质、锐角三角函数定义以及勾股定理等知识.21. 【答案】7【分析】本题考查了一元二次方程的应用,结合图形表示出小桌、中桌、长桌的长是解题的关键.设每张桌面的宽为x 尺,结合图形分别表示出小桌、中桌、长桌的长,根据题意列出方程,解方程即可求解.【详解】解:设每张桌面的宽为x 尺,根据图形可得:小桌的长为2x 尺,中桌的长为3x 尺,长桌的长为4x 尺,故可得22224233261.25x x x ⨯+⨯+⨯=,解得:174x =,274x =-(舍去),∴47x =,答:长桌的长为7尺.22. 【答案】(1)2y x =,8y x=(2)103n ≥-【分析】本题考查了反比例函数与一次函数的交点问题,解题的关键是:(1)将A 点坐标代入两个函数解析式求出,m k 值即可;(2)当3x =时,26y mx n x n n =+=+=+,883y x ==,根据题意863n +>,解出不等式解集即可.【小问1详解】解: 正比例函数(0)y mx m =≠的图象和反比例函数(0)kyk x=≠的图象都经过点(2,4)A ,422m ∴==,428k =⨯=,∴正比例函数解析式为:2y x =;反比例函数解析式为:8y x=;【小问2详解】当3x =时,26y mx n x n n =+=+=+,883y x ==, 当3x >时,对于x 的每一个值,函数(0)ymx n m =+≠的值都大于反比例函数(0)ky k x=≠的值,863n ∴+≥,解得103n ≥-.23. 【答案】(1)140n =,142m = (2)第二批 (3)131,135【分析】本题考查了众数,中位数,平均数等.(1)根据众数和中位数的定义直接进行解答即可;(2)从平均数,众数和中位数三个方面进行分析,即可得出答案;(3)根据表中给出的数据,分别进行分析,即可得出答案.【小问1详解】解:∵在第一批中,140出现了4次,出现的次数最多,∴众数是140cm ,即140n =;把第二批花的高度从小到大排列,中位数是第6、第7个数的平均数,则中位数是1401441422+=(cm ),即142m =;【小问2详解】(2)第一批的方差是:112×[(131-140)2+3×(135-140)2+4×(140-140)2+2×(144-140)2+2×(148-140)2]=793,第二批的方差是:112×[(135-141)2+2×(136-141)2+3×(140-141)2+5×(144-141)2+(149-141)2]=16.5,则在这两批花树中,高度的整齐度更好的是第二批;故答案为:第二批;【小问3详解】解:第二批去掉了高度为135cm 和149cm 的两棵花树后的平均数为:14112135149140.810⨯--=(cm ),第一批花树的平均数为140cm ,去掉的两棵且使高度尽可能接近平均高度,则需要去掉高度最小的两颗,即去掉的两棵花树的高度分别是131cm ,135cm ;故答案为:131,135.24. 【答案】(1)证明见解析 (2)75【分析】(1)根据在同圆中等弧所对的圆周角相等得出BAD CAD ∠=∠,根据直径所对的圆周角是直角可得90C ∠=︒,根据直角三角形中两个锐角互余可得90CAD AFC ∠+∠=︒,根据对顶角相等可得90CAD EFB ∠+∠=︒,根据圆的切线垂直于经过切点的半径可得90ABE ∠=︒,根据直角三角形中两个锐角互余可得90E BAD ∠+∠=︒,根据等角的余角相等可得EEFB ∠=∠,根据等角对等边即可证明;(2)连接BD ,根据直径所对的圆周角是直角可得90ADB ∠=︒,根据直角三角形中两个锐角互余可得90EAB ABD ∠+∠=︒,根据等角的余角相等可得EAB EBD ∠=∠,根据题意可得4AB =,根据直角三角形中两直角边的平方和等于斜边的平方求得5AE =,根据锐角三角形函数的定义可求得95ED =,根据等腰三角形底边上的高与底边上的中点重合可得185EF =,即可求解.【小问1详解】证明:∵D 是 BC的中点,∴ BDCD =,∴BAD CAD ∠=∠,∵AB 是O 的直径,∴90C ∠=︒,∴90CAD AFC ∠+∠=︒,∵AFC EFB ∠=∠,∴90CAD EFB ∠+∠=︒,∵BE 与O 相切于点B ,∴90ABE ∠=︒,∴90E BAD ∠+∠=︒,∴EEFB ∠=∠,∴BE BF =.【小问2详解】解:连接BD ,如图:∵AB 是O 的直径,∴90ADB ∠=︒,∴90EAB ABD ∠+∠=︒,∵90ABE EBD ABD ∠=∠+∠=︒,∴EAB EBD ∠=∠,∵O 的半径是2, ∴4AB =,∵3BE =,在Rt ABE △中,5AE ===,∴3sin sin 5DE BE EBD EAB BE AE ====∠∠,∴39sin 355ED BE EBD =⋅=⨯=∠,∵BE BF =,BD EF ⊥,∴9182255EF DE ==⨯=,∴187555AF AE EF =-=-=.【点睛】本题考查了圆周角定理,直角三角形的性质,切线的性质,等腰三角形的性质,勾股定理,锐角三角形函数的定义,等角的余角相等等,熟练掌握圆周角定理、等腰三角形的性质和勾股定理是解题的关键.25. 【答案】(1)8(2)①图见解析;②60℃ (3)不能【分析】本题考查了一次函数的应用,理解题意并分析表格中数据变化的规律是解题的关键.(1)在煮沸模式下,加热时间每增加3分钟,水温就上升30℃,从而计算出每增加1分钟水上升的温度,据此列方程并求解即可;(2)①描点并连线即可;②当时间从26分开始,设时间为t 时,水温加热到100℃.在这个过程中每2分钟,水温升高5℃,从而求出每增加1分钟水上升的温度,据此列方程求出t ,再计算出剩下的时间,根据表2,得到在剩下的时间内水温可以变化到多少;(3)由表1可知,2.5L 的水从20℃加热到100℃需要18.5分,此时离出门还剩3018.511.5-=(分);根据表2,计算水温从100℃降到50℃需要的时间,将这个时间与21.5分比较,在关闭电源的基础上即可得到结论.【小问1详解】解:在煮沸模式下,加热时间每增加3分钟,水温就上升30℃,30310÷=(℃),∴在煮沸模式下,加热时间每增加1分钟,水温就上升10℃,∴()10610080m -=-,∴8m =.【小问2详解】解:①补全水温与时间的函数图象如图所示:②当时间从26分开始,设时间为t 时,水温加热到100℃.在这个过程中每2分钟,水温升高5℃,则每1分钟水温升高52 2.5÷=(℃),由此得()2.52610060t -=-,解得42t =,604218-=(分),根据表2的数据可知,100T =℃经过18分后水温降到了60℃,∴当60t =时,60T =℃.故答案为:60℃;【小问3详解】解:由表1可知,2.5L 的水从20℃加热到100℃需要18.5分,3018.511.5-=(分),由表2可知,水温从100℃降到50℃需要22814-=(分),∵11.513<,且电源已关闭,∴出门前,他不能喝到低于50℃的水.故答案为:不能.26. 【答案】(1)2t = (2)①<,②1t ≤或0t ≤【分析】本题主要考查二次函数的性质,()1将点代入抛物线求得4b a =-,结合对称轴定义即可求得;()2①根据题意得抛物线开口向上,且过原点,即可得10y<;②由已知求得212x <<,结合120y y >恒成立,则有点()()1122,,x y x y ,在x 的同侧即可.【小问1详解】解:将点()40,代入()20y ax bx a =+>得1640a b +=,解得4b a =-,∴4222b a x a a-=-=-=,则2t =;【小问2详解】①根据题意得抛物线开口向上,且过原点,∵1t >,101x <<,∴10y <;②∵122x x +=, 101x <<,∴212x <<,∵有120y y >恒成立,∴点()()1122,,x y x y ,在x 的同侧,则1t ≤或0t ≤.27. 【答案】(1)图见解析(2)证明见解析 (3)22234BC CE BG +=【分析】(1)根据题意连线即可;(2)连接BD ,与AC 相交于点O ,根据旋转的性质可得60EAF ∠=︒,AE AF =,根据菱形的性质可得AB BC =,1602BAC CAD BAD ∠=∠=∠=︒,BO OD =,根据等边三角形的判定和性质可得AC AD =,60ACD ∠=︒,根据全等三角形的的判定和性质可得60ADF ACD ==︒∠∠,根据平行线的判定得出DF AC ∥,根据平行线分线段成比例定理即可证明;(3)根据勾股定理可得2224BD DF BG +=,根据等边三角形的性质可得30OBC ∠=︒,根据锐角三角函数可求得BC =,推得223BC BD =,即可求解.【小问1详解】解:如图:【小问2详解】证明:连接BD ,与AC 相交于点O ,如图:∵线段AE 绕点A 逆时针旋转60︒得到线段AF ,∴60EAF ∠=︒,AE AF =,∵在菱形ABCD 中,120BAD ∠=︒,∴AB BC =,1602BAC CAD BAD ∠=∠=∠=︒,BO OD =,∴ABC 、ACD 是等边三角形,∴AC AD =,60ACD ∠=︒,∴CAE DAF ∠=∠,∴ACE ADF ≌,∴60ADF ACD ==︒∠∠,∴DF AC ∥,∴BGBOGF OD =,∵BO OD =,∴GB GF =;【小问3详解】解:22234BC CE BG +=,理由如下:∵DF AC ∥,BD AC ⊥,∴DF BD ⊥,在Rt BFD 中,()2222224BD DF BF BG BG +===,∵ABC 是等边三角形,BO AC ⊥,∴1302OBC ABC ==︒∠,cos30cos OB OBC BC ︒===∠,∴BC =,则2243BC BO =,则()2222342BC BO BO BD ===,∴2222234BC CE BD DF BG +=+=,即22234BC CE BG +=.【点睛】本题考查了旋转的性质,菱形的性质,等边三角形的判定和性质,平行线的判定和性质,全等三角形的判定和性质,平行线分线段成比例定理,勾股定理,解直角三角形等,解题的关键是根据全等三角形的性质和平行线的判定推得DF AC ∥.28. 【答案】(1)11A B(2)1,2⎛- ⎝或12⎛- ⎝(3【分析】(1)根据题中定义即可画图得出;(2)根据题意可得直线()0y kx k =≠垂直平分CC ',DD ',结合点C 的坐标,推得点D 在O 上,即可得出点D 是C 与O 交点,根据等边三角形的性质和勾股定理即可求得点1D 、2D 的坐标;(3)结合(2)可得点1N 是点1M 与O 交点,先求出直线y x b =-+与x ,y 轴的交点坐标,结合三角形的面积求得OH 的值,根据锐角三角函数可求得点O '的坐标3,2b ⎫⎪⎪⎭,根据两点间的距离公式即可列出方程,解方程即可.【小问1详解】解:如图所示:∴O 关于直线1y x =+的“对称弦”的是线段11A B ;【小问2详解】解:设点C ,D 关于直线()0y kx k =≠的对称点为C ',D ¢,∴直线()0y kx k =≠垂直平分CC ',DD ',∵CD 是O 关于直线()0y kx k =≠的“对称弦”,∴C ',D ¢在O 上,∵点C 的坐标为()1,0-,即点C 在O 上,∵直线()0y kx k =≠经过圆心O ,∴点D 也在O 上,∵1CD =,故点D 在以点C 为圆心,CD 为半径的圆上,如图:C 与O 交于点1D 与点2D ;∵11OC CD OD ==,即1OCD △是等边三角形,故点1D 的横坐标为12-,点1D同理,点2D 的横坐标为12-,点2D 的纵坐标为-,综上,点D 的坐标为1,2⎛- ⎝或12⎛- ⎝;【小问3详解】解:设点M 关于直线y x b =-+的对称点为1M ,∴直线y x b =-+垂直平分1MM ,∵线段MN 是O 关于直线y x b =-+的“对称弦”, ∴1M 在O 上,由(2)可得点1N 在以点1M 为圆心,MN 为半径的圆上,又∵1MN =,即11OM =;令直线y x b =-+与x ,y 轴交于点P ,Q ,过点O 作OO '⊥直线y x b =-+交于点H ,点O '作O E x '⊥轴交于点E ,如图:令0x =,则y b =,即点()0,Q b ,OQ b =,令0y =,则x =,即点),0P ,OP =,则2PQ b ===,则OQ OP OH PQ ⋅===,∴2OO OH ==',∵90OQP QOH ∠+∠=︒,90OQP QPO ∠+∠=︒,∴QOH QPO ∠=∠,∵OQ O E ' ,∴OO E QOH QPO ∠=∠=∠',∵1sin 2OQ QPO PQ ∠==,cos OP QPO PQ ∠==,∴1sin 2OE OO E OO ∠=='',cos O E OO E OO ''=='∠∴sin OE OO OO E ''=⋅∠=,3cos 2O E OO OO E b ='∠'⋅=',即点O '的坐标为3,2b ⎫⎪⎪⎭,∵(3,M ,11O M OM '==;∴1O M '==,整理得:23200b -+=,解得:b =或b =,故b 的值为【点睛】本题考查了轴对称的性质,一次函数与坐标轴的交点问题,解直角三角形,勾股定理,等边三角形的判定和性质等,正确理解新定义的含义,灵活应用数形结合思想是解题的关键.。
2024北京大兴区初三一模数学试卷和答案

2024北京大兴初三一模数 学考生须知:1.本试卷共6页,共28道题.满分100分.考试时间120分钟.2.在试卷和答题卡上准确填写姓名、准考证号、考场号和座位号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.5.考试结束,将本试卷、答题卡和草稿纸一并交回.一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1. 下面几何体中,是圆锥的为( )A. B. C. D.2. 2024年是京津冀协同发展十周年,高标准建设雄安新区成效显著.从新区设立至2023年底,累计开发面积184平方公里,4017栋楼宇拔地而起,总建筑面积4370万平方米.将43700000用科学记数法表示应为( )A. 643.710⨯B. 74.3710⨯C. 84.3710⨯D. 90.43710⨯3. 五边形的内角和为( )A. 180︒B. 360︒C. 540︒D. 720︒4. 如图,直线AB ,CD 相交于点O ,OE AB ⊥,若30AOC ∠=︒,则EOD ∠的大小为( )A. 30︒B. 60︒C. 120︒D. 150︒5. 实数a ,b ,c 在数轴上的对应点的位置如图所示,下列结论中正确的是( )A. 0b c ->B. 0ac >C. 0b c +<D. 1ab <6. 不透明的盒子中装有3个小球,每个小球上面写着一个汉字分别是“向”、“前”、“冲”,这3个小球除汉字外无其他差别,从中随机摸出一个小球,记录其汉字,放回并摇匀,再从中随机摸出一个小球,记录其汉字,则两次都摸到“冲”字的概率是( )A. 23 B. 13 C. 16 D. 197. 若关于x 的一元二次方程220x x m +-=有两个不相等的实数根,则实数m 的取值范围是( )A. 1m >-B. 1m ≥-C. 1m >D. m 1≥8. 如图,在ABC 中,90BAC ∠=︒,AD BC ⊥于点D ,设BD a =,DC b =,AD c =,给出下面三个结论:①2c ab =;②2a b c +≥;③若a b >,则a c >.上述结论中,所有正确结论的序号是( )A.①②B. ①③C. ②③D. ①②③二、填空题(共16分,每题2分)9. 在实数范围内有意义,则实数x 的取值范围是______.10.分解因式:24ab a -=_______.11. 方程1341x x =-的解为______.12. 在平面直角坐标系xOy 中,若点(5,2)A 和(,2)B m -在反比例函数(0)k y k x=≠的图象上,则m 的值为______.13. 如图,AB 是O 的直径,点C ,D 在O 上,若AC BC =,则D ∠的度数为______︒.14. 如图,在矩形ABCD 中,AC 与BD 相交于点O ,OE BC ⊥于点E .若4AC =,30DBC ∠=︒,则OE 的长为______.15. 某年级为了解学生对“足球”“篮球”“排球”“乒乓球”“羽毛球”五类体育项目的喜爱情况,现从中随机抽取了100名学生进行问卷调查,根据数据绘制了如图所示的统计图.若该年级有800名学生,估计该年级喜爱“篮球”项目的学生有______人.16. 某公园门票价格如下表:某学校组织摄影、美术两个社团的学生游览该公园,两社团的人数分别为a 和()b a b >.若两社团分别以各自社团为单位购票,共需1560元;若两社团作为一个团体合在一起购票,共需1170元,那么这两个社团的人数为=a ______,b =______.购票人数1~4041~8080以上门票价格20元/人16元/人13元/人三、解答题(共68分,第17-20题,每题5分,第21题6分,第22-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 计算:0|3|(2024)2cos 45π-+++-︒18. 解不等式组:4125213x x x x -≥+⎧⎪-⎨<⎪⎩19. 已知2310a a +-=,求代数式2(1)(4)2a a a +++-的值.20. 某学校开展“浸书香校园,品诗词之美”读书活动.现有A ,B 两种诗词书籍整齐地叠放在桌子上,每本A 书籍和每本B 书籍厚度的比为5:6,根据图中所给出的数据信息,求每本A 书籍的厚度.21. 如图,在正方形ABCD 中,点E ,F 分别在BC ,AD 上,BEDF =,连接CF ,射线AE 和线段DC 的延长线交于点G .(1)求证:四边形AECF 是平行四边形;(2)若2tan 3BAE ∠=,9DG =,求线段CE 的长.22. 种子被称作农业的“芯片”,粮安天下,种子为基.农科院计划为某地区选择合适的甜玉米种子,随机抽取20块自然条件相同的试验田进行试验,得到各试验田每公顷产量(单位:t ),并对数据(每公顷产量)进行了整理、描述和分析,下面给出了部分信息:a .20块试验田每公顷产量的频数分布表如下:每公顷产量(t)频数7.407.45x ≤<37.457.50x ≤<27.507.55x ≤<m 7.557.60x ≤<67.607.65x ≤≤5b .试验田每公顷产量在7.557.60x ≤<这一组的是:7.55 7.55 7.57 7.58 7.59 7.59c . 20 块试验田每公顷产量的统计图如下:(1)写出表中m 的值;(2)随机抽取的这20块试验田每公顷产量的中位数为______.(3)下列推断合理的是______(填序号);①20块试验田的每公顷产量数据中,每公顷产量低于7.50t 的试验田数量占试验田总数的25%;②3号试验田每公顷产量在20块试验田的每公顷产量数据中从高到低排第5名.(4)1~10号试验田使用的是甲种种子,11~20号试验田使用的是乙种种子,已知甲、乙两种种子的每公顷产量的平均数分别为7.537t 及7.545t ,若某种种子在各试验田每公顷产量的10个数据的方差越小,则认为这种种子的产量越稳定.据此推断:甲、乙两种种子中,这个地区比较适合种植的种子是______(填“甲”或“乙”).23. 在平面直角坐标系xOy 中,函数(0)y kx b k =+≠的图象经过点(1,3)A 和(1,1)B --,与过点(2,0)-且平行于y 轴的直线交于点C .(1)求该函数的表达式及点C 的坐标;(2)当2x <-时,对于x 的每一个值,函数(0)y nx n =≠的值大于函数(0)y kx b k =+≠的值且小于2-,直接写出n 的取值范围.24. 某洒水车为绿化带浇水,图1是洒水车喷水区域的截面图,其上、下边缘都可以看作是抛物线的一部分,下边缘抛物线是由上边缘抛物线向左平移得到的.喷水口H 距地面的竖直高度OH 为1.5m ,喷水区域的上、下边缘与地面交于A ,B 两点,上边缘抛物线的最高点C 恰好在点B 的正上方,已知6m OA =,2m OB =,2m CB =.建立如图2所示的平面直角坐标系.(1)在①21(2)28y x =-++,②21(2)28y x =--+两个表达式中,洒水车喷出水的上边缘抛物线的表达式为______,下边缘抛物线的表达式为______(把表达式的序号填在对应横线上);(2)如图3,洒水车沿着平行于绿化带的公路行驶,绿化带的横截面可以看作矩形DEFG ,水平宽度3m DE =,竖直高度0.5m DG =.如图4,OD 为喷水口距绿化带底部的最近水平距离(单位:m ).若矩形DEFG 在喷水区域内,则称洒水车能浇灌到整个绿化带.①当 2.6m OD =时,判断洒水车能否浇灌到整个绿化带,并说明理由;②若洒水车能浇灌到整个绿化带,则OD 的取值范围是______.25. 如图,过O 外一点A 作O 的切线,切点为点B ,BC 为O 的直径,点D 为O 上一点,且BD BA =,连接CD ,AD ,线段AD 交直径BC 于点E ,交O 于点F ,连接BF .(1)求证:EF BF =;(2)若1sin 3A =,25OE =,求O 半径的长.26. 在平面直角坐标系xOy 中,()11,M x y ,()22,N x y 是抛物线2(0)y ax bx c a =++<上任意两点.设抛物线的对称轴为直线x t =.(1)若22x =,2y c =,求t 的值;(2)若对于112t x t +<<+,245x <<,都有12y y >,求t 的取值范围.27. 在ABC 中,AC BC =,90ACB ∠=︒,点D 是线段AB 上一个动点(不与点A ,B 重合),()045ACD αα∠=<<︒,以D 为中心,将线段DC 顺时针旋转90︒得到线段DE ,连接EB .(1)依题意补全图形;(2)求EDB ∠的大小(用含α的代数式表示);(3)用等式表示线段BE ,BC ,AD 之间的数量关系,并证明.28. 在平面直角坐标系xOy 中,已知点(,0)T t ,T e 的半径为1,过T e 外一点P 作两条射线,一条是T e 的切线,另一条经过点T ,若这两条射线的夹角大于或等于45︒,则称点P 为T e 的“伴随点”.(1)当0=t 时,①在1(1,0)P ,2P ,3(1,1)P -,4(1,2)P -中,T e 的“伴随点”是______.②若直线12y x b =+上有且只有一个T e 的“伴随点”,求b 的值;(2)已知正方形EFGH 的对角线的交点(0,)M t ,点11,22E t ⎛⎫-+ ⎪⎝⎭,若正方形上存在T e 的“伴随点”,直接写出t 的取值范围.参考答案一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1. 【答案】D【分析】本题考查了常见几何体的识别,观察所给几何体,可以直接得出答案.【详解】解:A 选项为正方体,不合题意;B 选项为球,不符合题意;C 选项为五棱锥,不合题意;D 选项为圆锥,符合题意.故选:D .2. 【答案】B【分析】本题考查科学记数法,科学记数法的表示形式为 10n a ⨯ 的形式,其中 110a ≤<,n 为整数(确定 n 的值时,要看把原数变成 a 时,小数点移动了多少位).【详解】解:43700000=74.3710⨯,故选:B .3. 【答案】C【分析】本题考查了n 边形内角和公式,熟练记忆公式是解题的关键.代入公式即可求解.【详解】解:五边形的内角和为()52180540-⨯︒=︒,故选:C .4. 【答案】B【分析】本题主要考查的是对顶角的性质和垂线,依据垂线的定义可求得90EOB ∠=︒,然后依据对顶角的性质可求得BOD ∠的度数,最后依据EOD EOB DOB ∠=∠-∠求解即可.【详解】解:∵OE AB ⊥,∴90EOB ∠=︒.∵30DOB AOC ∠=∠=︒,∴903060EOD EOB DOB ∠=∠-∠=︒-︒=︒.故选:B .5. 【答案】C【分析】本题考查了根据点在数轴的位置判断式子的正负.熟练掌握根据点在数轴的位置判断式子的正负是解题的关键.由数轴可知,32101a b c -<<-<<-<<<,则0b c -<,0ac <,0b c +<,1ab >,然后判断作答即可.【详解】解:由数轴可知,32101a b c -<<-<<-<<<,∴0b c -<,0ac <,0b c +<,1ab >,∴A 、B 、D 错误,故不符合要求;C 正确,故符合要求;故选:C .6. 【答案】D【分析】本题考查的是列表法或画树状图求解概率,根据题意列出表格即可求解.【详解】解:根据题意列表如下:向前冲向向,向前,向冲,向前向,前前,前前,冲冲向,冲前,冲冲,冲共有9种等可能得情况,其中两次都摸到“冲”字的情况有1种,则两次都摸到“冲”字的概率是:19,故选:D .7. 【答案】A【分析】本题考查了根的判别式:一元二次方程()200ax bx c a ++=≠的根与24b ac ∆=-有如下关系:当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程无实数根.根据判别式的意义得到()22410m ∆=-⨯⨯->,然后求出不等式的解集即可.【详解】解:根据题意得()22410m ∆=-⨯⨯->,解得1m >-.故选:A .8. 【答案】D【分析】由90BAC ∠=︒,AD BC ⊥,得到ABD CAD ∽△△,BD AD AD DC =,将BD a =,DC b =,AD c =代入,即可判断①正确,由()2222a b a b ab -=+-,()2222a b a b ab +=++,将2c ab =代入,整理后即可判断②正确,将2c b a=,代入a b >,即可判断③正确,本题考查了,相似三角形的性质与判定,完全平方公式的应用,解不等式,解题的关键是:熟练掌握完全平方公式的变形及应用.【详解】解:∵90BAC ∠=︒,AD BC ⊥,∴90BAD CAD ∠+∠=︒,90BAD ABD ∠+∠=︒,90BAD ADC ∠=∠=︒,∴CAD ABD ∠=∠,∴ABD CAD ∽△△,∴BD AD AD DC=即:a c c b =,整理得:2c ab =,故①正确,∵()2222a b a b ab -=+-,即:()2222a b a b ab +=-+, ∴()()()222222244a b a b ab a b ab a b c +=++=-+=-+,∵()20a b -≥,∴()224a b c +≥,∵0a >、0b >、0c >,∴2a b c +≥,故②正确,∵a b >,2c b a=,∴2c a a>,∵0a >,∴22a c >,∴a c >,故③正确,综上所述,①②③正确,故选:D .二、填空题(共16分,每题2分)9. 【答案】3x ≥【分析】此题主要考查了分式有意义及二次根式有意义的条件,正确掌握相关定义是解题关键.由分式有意义及二次根式有意义的条件,进而得出x 的取值范围.【详解】由二次根式的概念,可知30x -≥,解得3x ≥.故答案为:3x ≥10. 【答案】()()22a b b +-.【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方公式或平方差公式,若是就考虑用公式法继续分解因式.因此,先提取公因式a 后继续应用平方差公式分解即可【详解】解:()()()224422a a a a b b b b -=-=+-,故答案为:()()22a b b +-.11. 【答案】1x =【分析】本题考查了解分式方程,先将分式方程化为一元一次方程,再解一元一次方程,最后检验即可求解,注意分式的方程需要检验是解题的关键.【详解】解:1341x x =-∴413x x -=,解得:1x =,经检验,1x =是原分式方程的解,∴1x =,故答案为:1x =.12. 【答案】5-【分析】本题考查了反比例函数图象上点的坐标特征,先把(5,2)A 代入(0)k y k x=≠求出10,k =再把(,2)B m -代入10y x=,求出5m =-.【详解】解:把(5,2)A 代入(0)k y k x =≠得:25k =,解得,10,k =∴反比例函数解析式为10y x =,把(,2)B m -代入10y x =,得:102m-=,解得,5m =-,故答案为:5-13. 【答案】45【分析】本题主要考查了圆周角定理,先由直径所对的圆周角为90︒,可得90ACB ∠=︒,然后由AC BC =得:45CAB CBA ∠=∠=︒,然后根据同弧所对的圆周角相等,即可求出D ∠的度数.【详解】解:∵AB 是O 的直径,∴90ACB ∠=︒,∵AC BC =,∴45CAB CBA ∠=∠=︒,∴45D CAB ∠=∠=︒.故答案为:4514. 【答案】1【分析】本题考查矩形的性质,等腰三角形的判定和性质,解直角三角形,根据矩形的性质,得到OB OC =,根据三线合一结合30度角的直角三角形的性质,求解即可.【详解】解:∵矩形ABCD ,∴OB OC =,90BCD ∠=︒,4BD AC ==,∵30DBC ∠=︒,∴122CD BD ==,∴BC =,∵OB OC =,OE BC ⊥,∴12BE BC ==,∴tan 301OE BE =⋅︒==;故答案为:1.15. 【答案】240【分析】本题主要考查了样本估计总体.用800乘以喜爱“篮球”项目所占的百分比,即可.【详解】解:30800240100⨯=人,即该年级喜爱“篮球”项目的学生有240人.故答案为:24016. 【答案】 ①. 60 ②. 30【分析】本题考查了二元一次方程组的应用,由两次门票费用,列出方程组,可求解.【详解】解:∵1170不能整除16,∴两个部门的人数81a b +≥,又1560不能整除16,∴每个部门的人数不可能同时在41~80之间,由于a b >,所以,当140,4180b a ≤≤≤≤,则有:()20161560131170b a a b +=⎧⎨+=⎩解得,6030a b =⎧⎨=⎩故答案为:60,30.三、解答题(共68分,第17-20题,每题5分,第21题6分,第22-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 【答案】4+【分析】本题考查了实数的混合运算,掌握相关运算法则是解题关键.先计算绝对值、零指数幂、二次根式、特殊角的三角函数值,再计算加减法即可.【详解】解:0|3|(2024)2cos 45π-+++-︒312=++-⨯31=++-4=.18. 【答案】3x ≥【分析】本题主要考查了解一元一次不等式组,先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.【详解】解:4125213x x x x -≥+⎧⎪⎨-<⎪⎩①②解不等式①,得3x ≥.解不等式②,得1x >-.∴不等式组的解集为3x ≥.19. 【答案】1【分析】本题考查整式的混合运算、代数式求值,熟练掌握运算法则是解答的关键.先根据整式的混合运算法则结合完全平方公式化简原式,再将已知化为2262a a +=代入求解即可.【详解】解:2(1)(4)2a a a +++-222142a a a a =++++-2261a a =+-.2310a a +-= ,231a a ∴+=.2262a a ∴+=.∴原式2261a a =+-21=-1=.20. 【答案】每本A 书籍厚度为1cm【分析】本题主要考查了二元一次方程的应用,设每本A 书籍厚度为cm x ,桌子高度为cm y ,根据等量关系,列出方程组,解方程组即可.【详解】解:设每本A 书籍厚度为cm x ,桌子高度为cm y ,由题意可得:37965825x y x y +=⎧⎪⎨⨯+=⎪⎩,解得176x y =⎧⎨=⎩,答:每本A 书籍厚度为1cm .21. 【答案】(1)见解析 (2)2CE =【分析】本题考查了平行四边形的判定,正方形的性质,正切的定义;(1)根据正方形的性质得出AD BC ∥,AD BC =.根据题意得出AF CE =,即可得证;(2)根据正方形的性质得出2tan tan 3BAE G ∠==,在Rt ADG 中,得出6CD =则3CG =,根据2tan 3CEG CG ==,即可求解.【小问1详解】证明: 四边形ABCD 是正方形,∴AD BC ∥,AD BC =.BE FD =,∴AD FD BC BE -=-.即AF CE =.又 AF CE ∥,∴四边形AECF 是平行四边形.【小问2详解】解: 四边形ABCD 是正方形,∴AD BC ∥,90BCD D ∠=∠=︒,AD CD =.∴BAE G ∠=∠,90ECG ∠=︒,∴2tan tan 3BAE G ∠==.在Rt ADG 中, 2tan 3ADG DG ==,9DG =,∴6AD =.∴6CD =.∴3CG =.在Rt ECG 中, 2tan 3CEG CG ==,∴2CE =.22. 【答案】(1)4 (2)7.55(3)① (4)乙【分析】本题考查了频数分布表,求中位数,根据方差判断稳定性:(1)运用频数总数减去已知频数即可得出m ;(2)根据中位数的定义可求解;(3)从统计图中可得每公顷产量低于7.50t 的试验田数量有5块,可判断①;3号试验田每公顷产量在20块试验田的每公顷产量数据中从高到低排第4名可判断②.(4)根据图象判断稳定性即可得出结果.【小问1详解】解:2032654m =----=【小问2详解】解:随机抽取的这20块试验田每公顷产量的中位数是7.557.60x ≤<这一组的第1个和第2个数据,即:7.55和7.55,故中位数为:7.557.557.552+=,故答案为:7.55;【小问3详解】解:20块试验田的每公顷产量数据中,每公顷产量低于7.50t 的试验田数量有5块,所以,占试验田总数的百分数为510025%20⨯=,故①正确;3号试验田每公顷产量在20块试验田的每公顷产量数据中从高到低排第4名,故②错误,故答案为:①【小问4详解】解:从20 块试验田每公顷产量的统计图中可看出甲种种子每公顷产量波动大,乙种种子每公顷产量波动小,据此推断:甲、乙两种种子中,这个地区比较适合种植的种子是乙;故答案为:乙23. 【答案】(1)21y x =+;(2,3)--(2)312n ≤≤【分析】本题考查待定系数法求一次函数解析式,一次函数图象及性质,用数形结合思想考虑本题是解答本题的关键.(1)将两点代入函数解析式中即可求得函数解析式,再将2x =-代入解析式即可求出点C 坐标;(2)根据题意将(2,2)--代入(0)y nx n =≠求出n 的最小值,再根据题意将C 代入求出n 的最大值,即为本题答案.【小问1详解】解:∵函数(0)y kx b k =+≠的图象经过点(1,3)A 和(1,1)B --,∴将点(1,3)A 和(1,1)B --代入(0)y kx b k =+≠中,31k b k b +=⎧⎨-+=-⎩,解得:21k b =⎧⎨=⎩,∴该函数的表达式为:21y x =+,∵与过点(2,0)-且平行于y 轴的直线交于点C ,∴将2x =-代入21y x =+中,得=3y -,∴(2,3)C --;【小问2详解】解:∵当2x <-时,对于x 的每一个值,函数(0)y nx n =≠的值大于函数(0)y kx b k =+≠的值且小于2-,,通过图象可知,当(0)y nx n =≠的函数值小于2-时,即将(2,2)--H 代入(0)y nx n =≠中,1n =,当(0)y nx n =≠的函数值大于函数(0)y kx b k =+≠的值将(2,3)C --代入(0)y nx n =≠中,32n =,∴n 的取值范围为:312n ≤≤.24. 【答案】(1)②,① (2)①不能;理由见解析;②21OD ≤≤-【分析】本题考查了二次函数的实际应用,(1)由题意可知:顶点坐标()2,2C ,()0,1.5H ,利用待定系数法即可求出函数解析式为:()21228y x =--+,利用()0,1.5H 关于对称轴2x =的对称点为:()4,1.5,可知下边缘抛物线是由上边缘抛物线向左平移4个单位得到,求出下边缘抛物线为:()21228=-++y x ;(2)①根据 2.6m OD =,将 5.6x =代入上边缘抛物线的函数解析式得出0.380.5y =<,即可求解;②当点B 和点D 重合时,d 有最小值,此时2d =;当上边缘抛物线过点F 时,d 有最大值,231=+-=-d ;所以21d ≤≤-.【小问1详解】解:由题意可知:()2,2C ,故设上边缘抛物线的函数解析式为:()222y a x =-+,∵()0,1.5H ,将其代入()222y a x =-+可得:()21.5022=-+a ,解得:18a =-,∴上边缘抛物线的函数解析式为:()21228y x =--+,解:∵()0,1.5H 关于对称轴2x =的对称点为:()4,1.5,∴下边缘抛物线是由上边缘抛物线向左平移4个单位得到,∴下边缘抛物线为:()21228=-++y x ,故答案为:②,①.【小问2详解】①不能,理由如下,依题意, 2.63 5.6OE =+=将 5.6x =代入上边缘抛物线的函数解析式()21228y x =--+得()215.6220.380.58y =--+=<∴绿化带不全在喷头口的喷水区域内,∴洒水车不能浇灌到整个绿化带;②解:设灌溉车到绿化带的距离OD 为d ,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,则当点B 和点D 重合时,d 有最小值,此时2d =;当上边缘抛物线过点F 时,d 有最大值,3m DE =,0.5m EF =.∴令()21220.58=--+=y x ,解得:2x =+2x =-,结合图像可知:()2+Fd ∴的最大值为:231=+-=-d ;∴21d ≤≤-.故答案为:21OD ≤≤-.25. 【答案】(1)证明见解析(2)92【分析】(1)由切线的定义可得出90A AEB ∠+∠=︒,由直径所对的圆周角等于90︒得出90CDE BDE ∠+∠=︒,由等边对等角得出BDA A ∠=∠,等量代换得出CDE AEB ∠=∠,由同弧所对的圆周角相等得出C D E C B F ∠=∠, 进而可得出AEB CBF ∠=∠ ,由等角对等边得出EF BF =.(2)连接CF ,先证明==AF BF EF ,设BF EF AF x ===,则2AE x =,解直角三角形Rt ABE 得出23BE x =,再证明BCF A ∠=∠,得出1sin sin 3A BCF =∠=,进一步得出22()BC OB OE BE ==+,即523223x x ⎛⎫=+ ⎪⎝⎭,解出x 即可求解.【小问1详解】证明: AB 为O 的切线,∴90OBA ∠=︒.∴90A AEB ∠+∠=︒.BC 为O 的直径,∴90CDB ∠=︒.∴90CDE BDE ∠+∠=︒.BD BA =,∴BDA A ∠=∠.∴CDE AEB ∠=∠.又CDE CBF ∠=∠ ,AEB CBF ∴∠=∠.EF BF ∴=.【小问2详解】连接CF .AB 为O 的切线,∴90OBA ∠=︒.∴90AEB A ∠+∠=︒,90EBF FBA ∠+∠=︒.AEB CBF ∠=∠,∴FBA A ∠=∠.∴AF BF =.∴==AF BF EF .设BF EF AF x ===,则2AE x =.在Rt ABE 中, 1sin 3A =,2AE x =,∴23BE x =.BC 为直径,∴90CFB ∠=︒.BCF BDA ∠=∠,BDA A ∠=∠,∴BCF A ∠=∠.∴1sin sin 3A BCF =∠=.在Rt BFC △中,BF x =,∴3BC x =.22()BC OB OE BE ==+,∴523223x x ⎛⎫=+⎪⎝⎭.解得3x =.∴92OB =.∴O 半径的长为92.【点睛】本题主要考查了切线的定义,直径所对的圆周角等于90︒,同弧所对的圆周角相等,解直角三角形的相关计算,等角对等边等知识,掌握这些性质是解题的关键.26. 【答案】(1)1t =(2)2t ≤或7t ≥【分析】本题主要考查了二次函数的图象和性质等知识,(1)将22x =,2y c =代入解析式,得出2b a =-即可得解;(2)分①当点N 在对称轴上或对称轴右侧时,②当点N 在对称轴上或对称轴左侧时两种情况讨论组成不等式组即可得解;解题的关键是理解题意,灵活运用所学知识解决问题.【小问1详解】22x =,2y c =,42a b c c ∴++=,2b a ∴=-,12bt a ∴=-=,【小问2详解】2(0)y ax bx c a =++<,∴抛物线开口向下,抛物线的对称轴为x t =,112t x t +<<+,∴点M 在对称轴的右侧,①当点N 在对称轴上或对称轴右侧时,抛物线开口向下,∴在对称轴右侧,y 随x 的增大而减小.由12y y >,∴12x x <,∴4,24t t ≤⎧⎨+≤⎩,解得42t t ≤⎧⎨≤⎩,∴2t ≤,②当点N 在对称轴上或对称轴左侧时,设抛物线上的点()22,N x y 关于x t =的对称点为()2,N d y ',2t x d t ∴-=-,解得22d t x =-,∴()222,N t x y '-,245x <<,∴225224t t x t -<-<-,在对称轴右侧,y 随x 的增大而减小,由12y y >,∴122x t x <-,∴5225t t t ≥⎧⎨+≤-⎩,解得57t t ≥⎧⎨≥⎩,∴7t ≥,综上所述,t 的取值范围是2t ≤或7t ≥.27. 【答案】(1)补全图形见解析(2)45α︒-(3)BC BE =+;证明见解析【分析】本题主要考查旋转的性质,全等三角形的性质与判定,三角形外角的性质,勾股定理等:(1)根据题目叙述作图即可;(2)由三角形外角性质得45CDB A ACD α∠=∠+∠=︒+,根据90CDE ∠=︒可得结论; (3)过点D 作DM AB ⊥,交AC 于点F ,交BC 的延长线于点M .证明DCM DEB △≌△,得出CM BE =,再证明CF CM =,CF BE =,在Rt FAD △中,由勾股定理得出AF =,得出AC FC =+,由CF BE =,BC AC =可得出结论【小问1详解】补全图形如下:【小问2详解】解: AC BC =,90ACB ∠=︒,∴45A ABC ∠=∠=︒.∴45CDB A ACD α∠=∠+∠=︒+.90CDE ∠=︒,∴45EDB CDE CDB α∠=∠-∠=︒-.【小问3详解】解:用等式表示线段BE ,BC ,AD 之间的数量关系是BC BE =+.证明:过点D 作DM AB ⊥,交AC 于点F ,交BC 的延长线于点M .90MDB CDE ∠=∠=︒,∴CDM EDB ∠=∠.45MBD ∠=︒,∴45M MBD ∠=∠=︒.∴DM DB =.又 DC DE =,∴DCM DEB △≌△.∴CM BE =.45M ∠=︒,90ACB ∠=︒,∴45CFM M ∠=∠=︒.∴CF CM =.∴CF BE =.在Rt FAD △中,45A ∠=︒,∴45AFD A ∠=∠=︒,∴,AD FD =AF ∴==.AC AF FC =+ ,AC FC ∴=+.CF BE = ,BC AC =,BC BE ∴=+.28. 【答案】(1)①2P ,3P ;②b =(232t <≤或32t -≤<【分析】(1)①设射线PM 与T e 相切于点M ,连接TM ,根据题目中的定义得出1PT <≤,分别求出四个点与()0,0T 间的距离,然后进行判断即可;②根据直线12y x b =+上有且只有一个T e 的“伴随点”,得出直线12y x b =+与以()0,0T为半径的圆相切,设直线12y x b =+与x 轴,y 轴分别交于点A 、B ,与以()0,0T 为半径的圆相切于点C ,连接TC ,求出BT ===,得出b =,即可求出结果;(2)分两种情况进行讨论:当0t >时,当0t <时,分别画出图形,列出不等式组,解不等式组即可.【小问1详解】解:①如图1,设射线PM 与T e 相切于点M ,连接TM ,∴TM PM ⊥,当45P ∠=︒时,PTM △为等腰直角三角形,∴1PM TM ==,PT ===,∴当点P 在T e 外,45P ≥︒∠时,1PT <≤,当0=t 时,点()0,0T ,∵11PT =,2PT =,3PT ==4PT ==>∴在1(1,0)P ,2P ,3(1,1)P -,4(1,2)P -中,T e 的“伴随点”是2P ,3P ;故答案为:2P ,3P②∵当点P 在T e 外,45P ≥︒∠时,1PT <≤∴点P 在以T 为半径的圆上或圆内且在以1为半径的圆外,如图2:∵直线12y x b =+上有且只有一个T e 的“伴随点”,∴直线12y x b =+与以()0,0T 为圆心,为半径的圆相切,∴0b ≠,设直线12y x b =+与x 轴,y 轴分别交于点A 、B ,与以()0,0T 为半径的圆相切于点C ,连接TC ,∴TC AB ⊥,令0x =,y b =,令0y =,2x b =-,∴()2,0A b -,()0,B b ,∴2AT b =-,BT b =,在Rt ATB △中,1tan 122bBTAT b ∠===-,1290∠+∠=︒,∵TC AB ⊥,∴2390∠+∠=︒,∴13∠=∠,∴1312tan tan ==∠∠,在Rt TCB 中132tan BC CT ===∠,∴BC =∴BT ===,∴b =∴b =;【小问2详解】解:∵正方形EFGH 的对角线的交点(0,)M t ,点11,22E t ⎛⎫-+ ⎪⎝⎭,∴点11,22G t ⎛⎫- ⎪⎝⎭,11,22F t ⎛⎫+ ⎪⎝⎭,11,22H t ⎛⎫-- ⎪⎝⎭,当0t >时,如图所示:此时正方形EFGH 上的点到圆心T 的最大距离为ET ,最小距离为GT ,∵正方形上存在T e 的“伴随点”,且点P 在以T为圆心,以为半径的圆上或圆内且在以1为半径的圆外,∴1ET >,GT ≤,∵12ET t ⎫==+⎪⎭,12GT ==-,∴11212t ⎫+>⎪⎭-≤,32t <≤;当0t <时,如图所示:此时正方形EFGH 上的点到圆心T 的最大距离为GT ,最小距离为ET ,∵正方形上存在T e 的“伴随点”,且点P 在以T为圆心,以为半径的圆上或圆内且在以1为半径的圆外,∴ET ≤,1GT >,∵12ET ==+,12GT t ⎫==-⎪⎭,∴12112t +≤⎫->⎪⎭,解得:32t -≤<;综上分析可知:t 32t <≤或32t -≤<.【点睛】本题主要考查了切线的性质,解直角三角形,勾股定理,两点间距离公式,等腰直角三角形的性质,解不等式组,解题的关键是数形结合,注意进行分类讨论.。
2024年北京西城区九年级初三一模数学试卷及答案

北 京 市 西 城 区 九 年 级 统 一 测 试 试 卷数 学 2024.4考生须知1. 本试卷共7页,共两部分, 28道题。
满分 100分。
考试时间120分钟。
2. 在试卷和草稿纸上准确填写姓名、准考证号、考场号和座位号。
3. 试题答案一律填涂或书写在答题卡上, 在试卷上作答无效。
4. 在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5. 考试结束, 将本试卷、答题卡和草稿纸一并交回。
第一部分 选择题一、选择题 (共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.右图是某几何体的展开图,该几何体是 (A) 圆锥 (B)三棱柱 (C)三棱锥 (D)四棱锥2. 2024年5.5G 技术正式开始商用,它的数据下载的最高速率从5G 初期的1Gbps 提升到10Gbps,给我们的智慧生活“提速”.其中10Gbps 表示每秒传输10000000000 位(bit)的数据. 将 10000000000用科学记数法表示应为(A )0.1×10¹¹ (B )1×10¹⁰ (C )1×10¹¹ (D) 10×10⁹3.下列图形中,既是中心对称图形也是轴对称图形的是4. 直尺和三角板如图摆放,若∠1=55°,则∠2的大小为 (A)35° (B)55° (C) 135° (D) 145°北京市西城区九年级统一测试试卷 数学2024.4 第1页 (共7页)15.如图,两个边长相等的正六边形的公共边为BD,点A,B,C在同一直线上, 点O₁, O₂分别为两个正六边形的中心. 则tan∠O₂AC的值为.16. 将1, 2, 3, 4, 5, …, 37这37个连续整数不重不漏地填入37个空格中. 要求: 从左至右,第1个数是第2个数的倍数,第1个数与第2个数之和是第3个数的倍数,第1,2,3个数之和是第4个数的倍数,…,前36个数的和是第37个数的倍数.若第 1 个空格填入 37,则第 2 个空格所填入的数为,第 37 个空格所填入的数为 .37三、解答题(共68分,第17-22题,每题5分,第23-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 计算:|−3|−+2sin60∘−12.18.解不等式组: 2(+1)<x+5, x+23≥x−12.19. 已知x²−x−4=0,求代数式 (x−2)²+(x−1)(x+3)的值.20. 如图,点E在▱ABCD的对角线DB的延长线上,AE=AD.AF⊥BD于点F,EG∥BC交AF的延长线于点G, 连接DG.(1) 求证: 四边形AEGD是菱形;(2)若AF=BF,tan∠AEF=12,AB=4,求菱形AEGD的面积.21.某学校组织学生社团活动,打算恰好用1000元经费购买围棋和象棋,其中围棋每套40元,象棋每套30元.所购买围棋的套数能否是所购买象棋套数的2倍?若能,请求出所购买的围棋和象棋的套数,若不能,请说明理由.22. 在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象经过点A(3,5), B(-2,0), 且与y轴交于点 C.(1)求该函数的解析式及点C的坐标;(2)当x<2时, 对于x的每一个值, 函数y=-3x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.北京市西城区九年级统一测试试卷 数学2024.4 第3页 (共7页)24. 如图, AB 为⊙O 的直径, 弦CD⊥AB 于点H, OO 的切线CE 与BA 的延长线交于点E, AF∥CE, AF 与⊙O 的交点为F.(1) 求证: AF=CD;(2) 若⊙O 的半径为6, AH=2OH,求AE 的长.25. 如图,点O 为边长为1的等边三角形ABC 的外心. 线段PQ 经过点O,交边AB 于点P, 交边AC 于点Q. 若 AP =x,AQ =y 1,S APQ :S ABC =y 2,下表给出了x, y ₁, y ₂的一些数据 (近似值精确到0.0001).x 0.50.550.60.650.70.750.80.850.90.951y ₁10.84620.750.68420.63640.60.57140.54840.52940.51350.5y ₂0.46540.450.44470.44550.450.45710.46610.47650.48780.5(1)补全表格;(2)在同一平面直角坐标系xOy 中描出了部分点( x ,y ₁,x ,y ₂..请补全表格中数据的对应点,并分别画出y ₁与y ₂关于x 的函数图象;(3)结合函数图象,解决下列问题:①当△APQ 是等腰三角形时, y ₁关于x 的函数图象上的对应点记为(a ,b),请在x轴上标出横坐标为a 的点;C ②当y ₂取最大值时,x 的值为 .北京市西城区九年级统一测试试卷 数学2024.4 第5页 (共7页)5.不透明袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再从中随机摸出一个小球,则两次都摸到蓝球的概率为(A) 14(B) 13(C) 12(D)236. 已知-2<a<-1, 则下列结论正确的是(A) a<1<-a<2 (B) 1<a<-a<2 (C) 1<-a<2<a (D) -a<1<a<27.若关于x 的一元二次方程 lnx²+x−2=0有两个实数根,则实数k 的取值范围是(A )k ≤−18 (B )k >−18且k≠0 (C )k ≥−18且k≠0 (D )k ≥−14且k≠08. 如图, 在Rt△ABC 中, ∠ACB=90°, BC=a, AC=b(其中a<b). CD⊥AB 于点D,点E 在边AB 上, BE=BC. 设CD=h, AD=m, BD=n, 给出下面三个结论:①n²+h²<(m+n)²;②2h²>m²+n²;③AE 的长是关于 x 的方程 x²+2ax−b²=0的一个实数根.上述结论中,所有正确结论的序号是(A)① (B) ①③ (C) ②③ (D) ①②③第二部分 非选择题二、填空题 (共16分,每题2分)9. 若 x−3在实数范围内有意义,则实数x 的取值范围是 .10. 分解因式:x²y-12xy+36y= .11. 方程43x−1=3x−2的解为 .12.在平面直角坐标系xOy 中,若函数 y =kx(k ≠0)的图象经过点(-1,8)和(2,n), 则n 的值为.13. 如图, 在▱ABCD 中, 点E 在边AD 上, BA, CE 的延长线交于点F. 若AF=1, AB=2, 则 AEED =¯.14. 如图, 在⊙O 的内接四边形ABCD 中, 点A 是 ⌢BD 的中点,连接AC, 若∠DAB=130°, 则∠ACB= °.北京市西城区九年级统一测试试卷 数学2024.4 第2页 (共7页)23.某学校组织学生采摘山楂制作冰糖葫芦(每串冰糖葫芦由5颗山楂制成).同学们经过采摘、筛选、洗净等环节,共得到7.6kg的山楂.甲、乙两位同学各随机分到了15颗山楂,他们测量了每颗山楂的重量(单位:g),并对数据进行整理、描述和分析.下面给出了部分信息.a.甲同学的山楂重量的折线图:b.乙同学的山楂重量:8, 8.8, 8.9, 9.4, 9.4, 9.4, 9.6, 9.6, 9.6, 9.8, 10, 10, 10, 10,10c.甲、乙两位同学的山楂重量的平均数、中位数、众数:平均数中位数众数甲9.5m9.2乙9.59.6n根据以上信息,回答下列问题:(1)写出表中m, n的值;(2)对于制作冰糖葫芦,如果一串冰糖葫芦中5颗山楂重量的方差越小,则认为这串山楂的品相越好.①甲、乙两位同学分别选择了以下5颗山楂制作冰糖葫芦.据此推断:品相更好的是(填写“甲”或“乙”);甲9.29.29.29.29.1乙9.49.49.48.98.8②甲同学从剩余的 10颗山楂中选出5颗山楂制作一串冰糖葫芦参加比赛,首先要求组成的冰糖葫芦品相尽可能好,其次要求冰糖葫芦的山楂重量尽可能大.他已经选定的三颗山楂的重量分别为9.4,9.5,9.6,则选出的另外两颗山楂的重量分别为和 ;(3)估计这些山楂共能制作多少串冰糖葫芦.北京市西城区九年级统一测试试卷 数学2024.4 第4页 (共7页)26. 在平面直角坐标系xOy中,点A−2y₁,B2y₂,C m y₃在抛物线y=ax²+bx+3(a⟩0)上.设抛物线的对称轴为直线x=t.(1)若y₁=3,,求t的值;(2) 若当t+1<m<t+2时,都有y₁>y₃>y₂,求t的取值范围.27. 在△ABC中,∠ABC=∠ACB=45°,AM⊥BC于点M.D是射线AB上的动点 (不与点 A, B重合), 点 E 在射线 AC 上且满足.AE=AD,,过点D 作直线 BE 的垂线交直线BC于点F, 垂足为点 G, 直线BE交射线AM于点P.(1) 如图1, 若点D在线段AB上, 当AP=AE时,求∠BDF的大小;(2)如图2,若点D在线段AB的延长线上,依题意补全图形,用等式表示线段CF,MP, AB的数量关系, 并证明.北京市西城区九年级统一测试试卷 数学2024.4第6页 (共7页)28.在平面直角坐标系xOy 中,已知⊙O 的半径为1.对于⊙O 上的点 P 和平面内的直线l:y =ax 给出如下定义:点P 关于直线l 的对称点记为 P¹,,若射线OP 上的点Q 满足 OQ =PP ′,则称点Q 为点P 关于直线l 的“衍生点”.(1)当a=0时,已知⊙O 上两点 PP 2−22,在点Q ₁(1,2), QQ 3(−1,−1),Q 4(−2,−2)中,点P ₁关于直线l 的“衍生点”是 ,点P ₂关于直线l 的“衍生点”是 ;(2) P 为⊙O 上任意一点, 直线y=x+m (m≠0)与x 轴, y 轴的交点分别为点 A,B.若线段AB 上存在点S ,T ,使得点S 是点P 关于直线l 的“衍生点”,点T 不是点P 关于直线l 的“衍生点”,直接写出m 的取值范围;(3) 当-1≤a≤1时,若过原点的直线s 上存在线段 MN,对于线段 MN 上任意一点R,都存在⊙O 上的点P 和直线l ,使得点R 是点P 关于直线l 的“衍生点”. 将线段MN 长度的最大值记为D(s),对于所有的直线s ,直接写出D(s)的最小值.北京市西城区九年级统一测试试卷 数学2024.4 第7页 (共7页)北 京 市 西 城 区 九 年 级 统 一 测 试 试 卷数学答案及评分参考 2024.4一、选择题(共16分,每题2分)题号12345678答案C B D D A A C B二、填空题(共16分,每题2分)9. x≥3 10.y(x−6)² 11. x=-1 12. -413.1214. 25 15.3516. 1, 19三、解答题(共68分, 第17-22题, 每题5分, 第23-26题, 每题6分, 第27-28题,每题7分)17. 解: |−3|−+2sin60∘−12=3−5+2×32−23 4分 =-5 . 5分18.解:原不等式组为2(x+1)<x+5, x+23≥x−12.解不等式①, 得x<3. ·2分 解不等式②, 得x≤7. 4分 ∴ 原不等式组的解集为x<3. 5分19. 解: (x−2)²+(x−1)(x+3)=(x²−4x+4)+(x²+2x−3)=2x²−2x+1.…… 3分∵x²−x−4=0,∴x²−x=4.∴原式=2(x²−x)+1=9. ·5分20. (1) 证明: 如图1.∵ AE=AD, AF⊥BD于点F,∴ ∠EAG=∠DAG, EF=DF.∵ 四边形 ABCD 是平行四边形,北京市西城区九年级统一测试试卷 数学答案及评分参考 2024.4 第1页(共6页)①②∴ AD∥BC.∵ EG∥BC,∴ AD∥EG.∴ ∠AGE=∠DAG.∴ ∠EAG=∠AGE.∴ AE=EG.∴ AD=EG.∴ 四边形AEGD 是平行四边形.又∵ AE=AD,∴四边形AEGD是菱形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分(2) 解: 在Rt△ABF中, ∠AFB=90°, AF=BF, AB=4,∴ ∠ABF=45° , AF=AB·sin45°=22.在Rt△AEF中,∠AFE=90∘,tan∠AEF=12,AF=22,∴EF=AFtan∠AEF=4 2.∵ 四边形 AEGD 是菱形,∴AG=2AF=42,DE=2EF=8 2.∴S差πAEGD =12AG×DE=12×42×82=32. …5分21.解:设购买x套围棋,y套象棋 (1)假设所购买围棋的套数能是所购买象棋套数的2倍,①则40x+30y=1000,x=2y.② 3分解得y=10011. 4分此时 y不为正整数,不合题意.答:所购买围棋的套数不能是所购买象棋套数的2倍.⋯⋯⋯⋯⋯⋯⋯⋯5分22. 解: (1) ∵ 函数y=kx+b (k≠0) 的图象经过点 A(3,5), B(-2,0),∴3k+b=5,−2k+b=0.解得k=1,b=2.∴该函数的解析式为y=x+2,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分点C的坐标为C(0,2).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分(2)n≥10.……………………………………………………………………………5分北京市西城区九年级统一测试试卷 数学答案及评分参考 2024.4 第2页 (共6页)23.解:(1)9.4,10;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)①甲;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分②9.3,9.6;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分(3)76009.5×5=160(串).答:估计这些山楂共能制作160串糖葫芦.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分24. (1) 证明: 如图2, 连接OC, OC与AF交于点 G.∵ CE 与⊙O 相切, 切点为C,∴CE⊥OC.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴ ∠OCE=90° .∵ AF∥CE,∴ ∠OGA=∠OCE=90° .∴ OC⊥AF于点 G.∴ AF=2AG.∵ CD⊥AB 于点 H,∴ ∠OHC=90° , CD=2CH .∴ ∠OGA=∠OHC.又∵ ∠AOG=∠COH, OA=OC,∴ △OAG≌△OCH.∴ AG=CH.∴AF=CD.…………………………………………………… 3分(2) 解: ∵ ⊙O的半径为6, AH=2OH,∴ OH=2, AH=4.在Rt△OCH中,∠OHC=90∘,cos∠COH=OHOC =13.在Rt△OCE中,∠OCE=90∘,cos∠COE=13,OC=6,∴OE=OCcos∠COE=18.∴AE=OE-OA=18-6=12.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分北京市西城区九年级统一测试试卷 数学答案及评分参考 2024.4 第3页(共6页)25. 解: (1)0.5; ……………………… 1分(2)3分(3)①见图3; ·4分 ②0.5, 1. …6分26. 解: (1) 抛物线 y =ax²+bx +3与y 轴的交点的坐标为(0,3).∵ 抛物线. y =ax²+bx +3过A(-2,y ₁), y ₁=3,∴ A(-2,3)与(0,3)关于直线x=t 对称.∴t =−2+02=−1. 2分(2) ∵ a>0,∴ 当x≤t 时, y 随x 的增大而减小; 当x≥t 时, y 随x 的增大而增大.A(-2,y ₁), B(2,y ₂), C(m,y ₃).①当t≤-2时,∵ t≤-2<2,|.y₁<y₂,不合题意.②当-2<t<2时, A(-2,y ₁)关于对称轴x=t 的对称点为 A ′(2t +2,y ₁).∵ 当t+1<m<t+2时, 都有 y₁>y₃>y₂,∴t +1≥2,t +2≤2t +2.解得 t≥1.∴ 1≤t<2.③当t≥2时,A(-2,y ₁),B(2,y ₂)关于对称轴x=t 的对称点分别为 A ′(2t +2,y ₁), B ′(2t−2,y ₂).北京市西城区九年级统一测试试卷 数学答案及评分参考 2024.4 第4页(共6页)∵当t+1<m<t+2时, 都有. y₁>y₃>y₂,∴t +1≥2t−2,t +2≤2t +2.解得 0≤t≤3.∴ 2≤t≤3.综上所述,t 的取值范围是1≤t≤3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分27. 解: (1) 如图4.∵在△ABC 中, ∠ABC=∠ACB=45° ,∴ AB=AC, ∠BAC=90° , ∠1+∠2=90°.∵ AM⊥BC 于点 M,∴∠3=∠BAC 2=45∘,BM =CM.∵ AP=AE, ∴∠2=180∘−∠32=180∘−45∘2=67.5∘.∵ DF⊥BE 于点 G,∴ ∠1+∠BDF=90°.∴∠BDF=∠2=67.5°.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)补全图形见图5.CF =2MP +2AB.证明: 如图4, 作 CQ∥AP 交BE 于点 Q.∵ CQ∥AP, BM=CM, AM⊥BC, ∴MP CQ =BM BC =12,∠BCQ =∠AMC =90∘ ∴CQ =2MP,∠5=180°−∠ACB−∠BCQ =45°.∵∠4=∠ABC =45°,∴ ∠4=∠5.北京市西城区九年级统一测试试卷 数学答案及评分参考 2024.4 第5页 (共6页)∵∠DBG=∠ABE,DG⊥BE于点 G,∠BAC=90°,∴ ∠D=∠E.∵AD=AE,AB=AC,∴AD−AB=AE−AC, 即BD=CE.∴△BDF≅△CEQ.:.BF=CQ.∵CF=BF+BC,BC=2AB,∴CF=CQ+2AB=2MP+2AB. ……………… 7分28. 解: (1)Q₂,Q₃; · ·2分(2)−22≤m≤−2或 2≤m≤22; ·5分(3)2−2. 7分北京市西城区九年级统一测试试卷 数学答案及评分参考 2024.4 第6页(共6页)。
北京市各区2022届中考数学一模试题分类汇编 几何综合
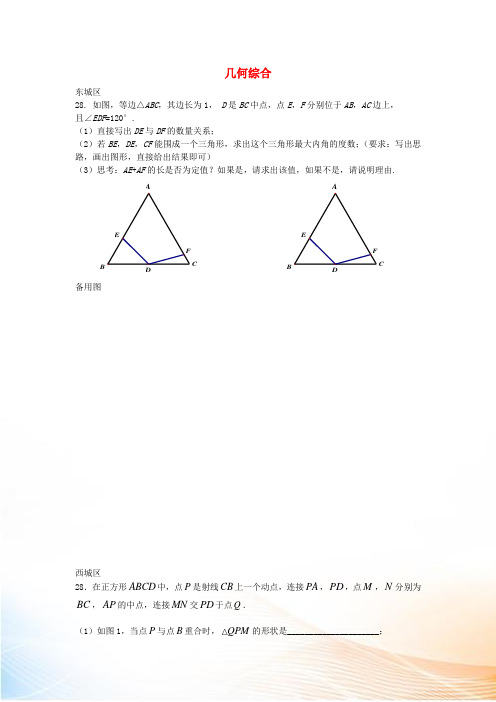
∠CBE的数量关系并证明;
(3)在(2)的条件下,若点E为边CD的三等分点,且CE<DE,请写出求
cos∠FED的思路.(可以不写出计算结果).
图1图2备用图
顺义区
28.已知:在△ABC中,∠BAC=60°.
如图1,若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP
图1图2
图1图2图3
朝阳区
28.在等腰三角形ABC中,AC=BC,点P为BC边上一点(不与B、C重合),连接PA,以P为旋转中心,将线段PA顺时针旋转,旋转角与∠C相等,得到线段PD,连接DB.
(1)当∠C=90º时,请你在图1中补全图形,并直接写出∠DBA的度数;
(2)如图2,若∠C=α,求∠DBA的度数(用含α的代数式表示);
(2)判断AE与BD的数量关系与位置关系并加以证明;
(3)若0°<α≤64°,AB=4,AE与BD相交于点G,求点G到直线AB的距离的最大值.请写出求解的思路(可以不写出计算结果).
房山区
28.如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD.
(1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
(3)连接AD,若∠C =30º,AC=2,∠APC=135º,请写出求AD长的思路.(可以不写出计算结果)
海淀区
28.在△ABC中,AB=AC,∠BAC= ,点D在射线BC上(与B、C两点不重合),以
AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018北京各区初中一模数学分类汇编27题及答案 平谷27.在△ABC 中,AB=AC ,CD ⊥BC 于点C ,交∠ABC 的平分线于点D ,AE 平分∠BAC 交BD 于点E ,过点E 作EF ∥BC 交AC 于点F ,连接DF . (1)补全图1;(2)如图1,当∠BAC =90°时,①求证:BE=DE ;②写出判断DF 与AB 的位置关系的思路(不用写出证明过程); (3)如图2,当∠BAC=α时,直接写出α,DF ,AE 的关系.西城27.正方形ABCD 的边长为2,将射线AB 绕点A 顺时针旋转α,所得射线与线段BD 交于点M ,作CE AM ⊥于点E ,点N 与点M 关于直线CE 对称,连接CN . (1)如图,当045α︒<<︒时, ①依题意补全图.②用等式表示NCE ∠与BAM ∠之间的数量关系:__________.(2)当4590α︒<<︒时,探究NCE ∠与BAM ∠之间的数量关系并加以证明. (3)当090α︒<<︒时,若边AD 的中点为F ,直接写出线段EF 长的最大值.CDBA图1备用图C DBAM图1BB 图2延庆27.如图1,正方形ABCD 中,点E 是BC 延长线上一点,连接DE ,过点B 作BF ⊥DE于点F ,连接FC .(1)求证:∠FBC =∠CDF .(2)作点C 关于直线DE 的对称点G ,连接CG ,FG .①依据题意补全图形;②用等式表示线段DF ,BF ,CG 之间的数量关系并加以证明.海淀27.如图,已知60AOB ∠=︒,点P 为射线OA 上的一个动点,过点P交OB 于点E ,点D 在AOB ∠内,且满足DPA OPE ∠=∠,6DP PE +=.(1)当DP PE =时,求DE 的长;(2)在点P 的运动过程中,请判断是否存在一个定点M ,使得DMME的值不变?并证明你的判断.图1备用图FDEC BA FDEC BA大兴27.如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥C F于点G,连接AG.(1)求证:∠ABG=∠ACF;(2)用等式表示线段C G,AG,BG之间的等量关系,并证明.怀柔27.如图,在△ABC中,∠A=90°,AB=AC,点D是BC上任意一点,将线段AD绕点A 逆时针方向旋转90°,得到线段AE,连结EC.(1)依题意补全图形;(2)求∠ECD的度数;(3)若∠CAE=7.5°,AD=1,将射线DA绕点D顺时针旋转60°交EC的延长线于点F,请写出求AF长的思路.顺义27. 如图,在正方形ABCD中,E是BC边上一点,连接AE,延长CB至点F,使BF=BE,过点F作FH⊥AE于点H,射线FH分别交AB、CD于点M、N,交对角线AC于点P,连接AF.(1)依题意补全图形;(2)求证:∠FAC=∠APF;(3)判断线段FM与PN的数量关系,并加以证明.门头沟27.如图,在△ABC中,AB=AC,2Aα∠=,点D是BC的中点,DE AB E⊥于点,DF AC F⊥于点.(1)EDB∠=_________°;(用含α的式子表示)(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转1802α︒-,与AC边交于点N.①根据条件补全图形;②写出DM与DN的数量关系并证明;③用等式表示线段BM CN、与BC之间的数量关系,(用含α的锐角三角函数表示)并写出解题思路.FE丰台27.如图,Rt △ABC 中,∠ACB = 90°,CA = CB ,过点C 在△ABC 外作射线CE ,且∠BCE = α,点B 关于CE 的对称点为点D ,连接AD ,BD ,CD ,其中AD ,BD 分别交射线CE 于点M ,N .(1)依题意补全图形; (2)当α= 30°时,直接写出∠CMA 的度数; (3)当0°<α< 45°时,用等式表示线段AM ,CN 之间的数量关系,并证明.ABCE东城27. 已知△ABC 中,AD 是BAC ∠的平分线,且AD =AB , 过点C 作AD 的垂线,交 AD的延长线于点H . (1)如图1,若60BAC ∠=︒①直接写出B ∠和ACB ∠的度数; ②若AB =2,求AC 和AH 的长;(2)如图2,用等式表示线段AH 与AB +AC 之间的数量关系,并证明.房山27. 如图,已知Rt △ABC 中,∠C =90°,∠BAC =30°,点D 为边BC 上的点,连接AD ,∠BAD =α,点D 关于AB 的对称点为E ,点E 关于AC 的对称点为G ,线段EG 交AB 于点F ,连接AE ,DE ,DG ,AG . (1)依题意补全图形;(2)求∠AGE 的度数(用含α的式子表示);(3)用等式表示线段EG 与EF ,AF 之间的数量关系,并说明理由.燕山28.在Rt △ABC 中, ∠ACB =90°,CD 是AB 边的中线,DE ⊥BC 于E , 连结CD ,点P 在射线CB 上(与B ,C 不重合).(1)如果∠A =30°①如图1,∠DCB =°②如图2,点P 在线段CB 上,连结DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连结BF ,补全图2猜想CP 、BF 之间的数量关系,并证明你的结论;( 2 )如图3,若点P 在线段CB 的延长线上,且∠A =α (0°<α<90°) ,连结DP , 将线段DP 绕点逆时针旋转 α2得到线段DF ,连结BF , 请直接写出DE 、BF 、BP 三者的数量关系(不需证明).αD CB A平谷27.解:(1)补全图1; (1)B(2)①延长AE ,交BC 于点H . ················· 2 ∵AB=AC , AE 平分∠BAC ,∴AH ⊥BC 于H ,BH=HC .∵CD ⊥BC 于点C , ∴EH ∥CD . ∴BE=DE . (3)②延长FE ,交AB 于点G .由AB=AC ,得∠ABC =∠ACB . 由EF ∥BC ,得∠AGF =∠AFG . 得AG=AF .由等腰三角形三线合一得GE=E F . ······· 4 由∠GEB =∠FED ,可证△BEG ≌△DEF .可得∠ABE =∠FDE . (5)从而可证得DF ∥AB . ························ 6 (3)tan 2DF αAE =. (7)西城27. (1)①补全的图形如图所示:NEMABDC②2NCE BAM ∠=∠.BB(2)1902MCE BAM ∠+∠=︒,连接CM ,NQM ABDC EDAM DCM ∠=∠,DAQ ECQ ∠=∠,∴2NCE MCE DAQ ∠=∠=∠,∴12DCM NCE ∠=∠,∵BAM BCM ∠=∠, 90BCM DCM ∠+∠=︒,∴1902NCE BAM ∠+∠=︒. (3)∵90CEA ∠=︒, ∴点E 在以AC 为直径的圆上,E∴max 1EF FO r =+=+延庆27.(1)证明:∵四边形ABCD 是正方形,∴∠DCB =90°. ∴∠CDF +∠E =90°. ∵BF ⊥DE , ∴∠FBC +∠E =90°.图1FDEC BA∴∠FBC =∠CDF .……2分(2)① ……3分②猜想:数量关系为:BF =DF +CG .证明:在BF 上取点M 使得BM =DF 连接CM .∵四边形ABCD 是正方形, ∴BC =DC .∵∠FBC =∠CDF ,BM =DF , ∴△BMC ≌△DFC . ∴CM =CF ,∠1=∠2. ∴△MCF 是等腰直角三角形.∴∠MCF =90°,∠4=45°. ……5分 ∵点C 与点G 关于直线DE 对称, ∴CF =GF ,∠5=∠6. ∵BF ⊥DE ,∠4=45°, ∴∠5=45°, ∴∠CFG =90°, ∴∠CFG =∠MCF , ∴CM ∥GF . ∵CM =CF ,CF =GF , ∴CM =GF ,∴四边形CGFM 是平行四边形, ∴CG =MF .∴BF =DF +CG . ……7分海淀27..解:(1)作PF ⊥DE 交DE 于F .∵PE ⊥BO ,60AOB ∠=,∴30OPE ∠=.∴30DPA OPE ∠=∠=.∴120EPD ∠=.…1分 ∵DP PE =,6DP PE +=,∴30PDE ∠=,3PD PE ==.∴cos30DF PD =⋅︒=∴2DE DF ==……3分 (2)当M 点在射线OA 上且满足OM =DMME的值不变,始终为1.理由如下:…………4分当点P 与点M 不重合时,延长EP 到K 使得PK PD =.GFDECBA∵,DPA OPE OPE KPA ∠=∠∠=∠,∴KPA DPA ∠=∠. ∴KPM DPM ∠=∠.∵PK PD =,PM 是公共边, ∴KPM △≌DPM △.∴MK MD =. ………………5分作ML ⊥OE 于L ,MN ⊥EK 于N . ∵23,60MO MOL =∠=,∴sin 603ML MO =⋅=. ………………6分∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ,∴四边形MNEL 为矩形.∴3EN ML ==. ∵6EK PE PK PE PD =+=+=,∴EN NK =.∵MN ⊥EK ,∴MK ME =.∴ME MK MD ==,即1DMME=. 当点P 与点M 重合时,由上过程可知结论成立. ………………7分 大兴27.(1)证明 :∵ ∠CAB=90°. ∵ BG ⊥CF 于点G , ∴ ∠BGF =∠CAB =90°.∵∠GFB =∠CFA . ………………………………………………1分 ∴ ∠ABG =∠ACF . ………………………………………………2分(2)CG =2AG +BG . …………………………………………………3分证明:在CG 上截取CH =BG ,连接AH , …………………………4分 ∵ △ABC 是等腰直角三角形, ∴ ∠CAB =90°,AB =AC . ∵ ∠ABG =∠ACH .∴ △ABG ≌△ACH . …………………………………………………… 5分 ∴ AG =AH ,∠GAB =∠HAC . ∴ ∠GAH =90°.∴ 222AG AH GH +=.∴ GH =2AG . ………………………………………………………6分 ∴ CG =CH +GH =2AG +BG . ………………………………………7分NMD KOBA PB怀柔27. (1)如图 …………………………………………………………………………………………1分 (2) ∵线段AD 绕点A 逆时针方向旋转90°,得到线段AE. ∴∠DAE=90°,AD=AE. ∴∠DAC+∠CAE =90°.∵∠BAC=90°, ∴∠BAD+∠DAC =90°.∴∠BAD=∠CAE . …………………………………………………………………………2分 又∵AB=AC,∴△ABD ≌△ACE. ∴∠B=∠ACE.∵△ABC 中,∠A=90°,AB=AC, ∴∠B=∠ACB=∠ACE=45°.∴∠ECD=∠ACB+∠ACE=90°. ……………………………………………………………4分(3)Ⅰ.连接DE,由于△ADE 为等腰直角三角形,所以可求DE=2;……………………5分 Ⅱ.由∠ADF=60°,∠CAE=7.5°,可求∠EDC 的度数和∠CDF 的度数,从而可知DF 的长; …………………………………………………………………………………………………6分Ⅲ.过点A 作AH ⊥DF 于点H ,在Rt △ADH 中, 由∠ADF=60°,AD=1可求AH 、DH 的长; Ⅳ. 由DF 、DH 的长可求HF 的长;Ⅴ. 在Rt △AHF 中, 由AH 和HF,利用勾股定理可求AF 的长.…………………………7分顺义27.(1)补全图如图所示. ………………………………………………………… 1分 (2)证明∵正方形ABCD , ∴∠BAC =∠BCA =45°,∠ABC =90°, ∴∠PAH =45°-∠BAE . ∵FH ⊥AE .∴∠APF =45°+∠BAE . ∵BF=BE ,∴AF=AE ,∠BAF =∠BAE . ∴∠FAC =45°+∠BAF .∴∠FAC =∠APF .…………………………… 4分(3)判断:FM =PN . …………………………………… 5分 证明:过B 作BQ ∥MN 交CD 于点Q ,∴MN =BQ ,BQ ⊥AE .∵正方形ABCD,∴AB=BC,∠ABC=∠BCD=90°.∴∠BAE=∠CBQ.∴△ABE≌△BCQ.∴AE=BQ.∴AE=MN.∵∠FAC=∠APF,∴AF=FP.∵AF=AE,∴AE=FP.∴FP=MN.∴FM=PN.……………………………………………………………8分门头沟27.(本小题满分7分)(1)EDBα∠=……………………………………………1分(2)①补全图形正确……………………………………2分②数量关系:DM DN=…………………………………3分∵,AB AC BD DC==∴DA平分BAC∠∵DE AB E⊥于点,DF AC F⊥于点∴DE DF=,MED NFD∠=∠……………………4分∵2Aα∠=∴1802EDFα∠=︒-∵1802MDNα∠=︒-∴MDE NDF∠=∠∴MDE NDF△≌△……………………5分∴DM DN=③数量关系:sinBM CN BCα+=⋅……………………6分证明思路:a.由MDE NDF△≌△可得EM FN=b. 由AB AC=可得B C∠=∠,进而通过BDE CDF△≌△,可得BE CF=进而得到2BE BM CN=+c.过BDERt△可得sinBEBDα=,最终得到sinBM CN BCα+=⋅……………7分丰台27.解:(1)如图;…………………1分(2)45°;…………………2分(3)结论:AMCN.…………………3分证明:作AG⊥EC的延长线于点G.∵点B与点D关于CE对称,∴CE是BD的垂直平分线.∴CB=CD.∴∠1=∠2=α.∵CA=CB,∴CA=CD.∴∠3=∠CAD.B87654321GNMCEB ∵∠4=90°,∴∠3=12(180°-∠ACD )=12(180°-90°-α-α)=45°-α.∴∠5=∠2+∠3=α+45°-α=45°.…………………5分 ∵∠4=90°,CE 是BD 的垂直平分线, ∴∠1+∠7=90°,∠1+∠6=90°. ∴∠6=∠7. ∵AG ⊥EC , ∴∠G =90°=∠8.∴在△BCN 和△CAG 中, ∠8=∠G , ∠7=∠6, BC =CA ,BCN ≌△CAG .∴CN =AG . ∵Rt △AMG 中,∠G =90°,∠5=45°, ∴AM 2.∴AM 2. …………………7分东城27. (1)①75B ∠=︒,45ACB ∠=︒;--------------------2分②作DE ⊥AC 交AC 于点E .Rt △ADE 中,由30DAC ∠=︒,AD =2可得DE =1,AE 3=. Rt △CDE 中,由45ACD ∠=︒,DE=1,可得EC =1. ∴AC 31.Rt △ACH 中,由30DAC ∠=︒,可得AH 33+=; --------------4分(2)线段AH 与AB +AC 之间的数量关系:2AH =AB +AC证明: 延长AB 和CH 交于点F ,取BF 中点G ,连接GH .易证△ACH ≌△AFH .∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =,∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. --------------7房山27. 解(1)G………………………………………………1分(2)由轴对称性可知,AB 为ED 的垂直平分线,AC 为EG 的垂直平分线.∴AE =AG =AD .∴∠AEG =∠AGE ,∠BAE =∠BAD =α ∴∠EAC =∠BAC +∠BAE =30°+α ∴∠EAG =2∠EAC =60°+2α∴∠AGE =12(180°-∠EAG ) =60°-α………………………………………………3分或:∠AGE =∠AEG =90°-∠EAC =90°-(∠BAC +∠EAB )=90°-(30°+α)=60°-α……………………………………………………………………3分(3)EG =2EF +AF ……………………………………………………………………………4分 法1:设AC 交EG 于点H ∵∠BAC =30°,∠AHF =90°∴FH =12AF …………………………5分∴EH =EF +FH =EF +12AF …………6分又∵点E ,G 关于AC 对称 ∴EG =2EH∴EG =2(EF +12AF )=2EF +AF ………………………………………………………7分法2:在FG 上截取NG =EF ,连接AN. 又∵AE =AG , ∴∠AEG =∠AGE ∴△AEF ≌△AGNH∴AF=AN∵∠EAF=α,∠AEG=60°-α∴∠AFN=60°…………………………………………………………………………6分∴△AFN为等边三角形∴AF=FN∴EG=EF+FN+NG=2EF+AF…………………………………………………………7分燕山28.解:(1) ①∠DCB=60°…………………………………1′②补全图形CP=BF …………………………………3′△DCP≌△DBF …………………………………6′(2)BF-BP=2DE⋅tanα…………………………………8′最新文件仅供参考已改成word文本。
