方波信号f展开为傅里叶级数
合集下载
方波信号的傅里叶变换
例4―3 求矩形脉冲信号gτ(t)的频谱。
g (t) F()
1
－ 2/
2/
－/ 2 0 / 2
(a)
t
0 (b )
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
1 g r (t ) 0 gτ(t)的傅里叶变换为 t t
f (t ) 1
t
F ( j ) 1 e jt dt
单位直流信号的频谱
例4―6 求单位直流信号的频谱。 解 幅度为1的单位直流信号可表示为 f(t)=1,-∞<t<∞ (4―44) 它可以看作是双边指数信号在α取极限趋近0时的一个 特例,即
1 lim e
0
t
u (t ), 0 u( t )] lim[ e
0
t
(4―45)
[1] [lim e
0
t
2a u( t )] lim 2 0 a 2
(4―46)
0 0 0
lim
0
2 2 d lim d( ) 2 2 0 1 ( )2
(4―50)
f (t)
F()
1
0 －1 (a )
t
0
(b )
图4.10 符号函数及其频谱
符号函数sgn(t)也可看作是下述函数在α取极限趋近0时的一 个特例: t e t0 (其中α>0) f ( t ) t t0 e
F [ f (t )]
F(j ) 1
f (t )
g (t) F()
1
－ 2/
2/
－/ 2 0 / 2
(a)
t
0 (b )
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
1 g r (t ) 0 gτ(t)的傅里叶变换为 t t
f (t ) 1
t
F ( j ) 1 e jt dt
单位直流信号的频谱
例4―6 求单位直流信号的频谱。 解 幅度为1的单位直流信号可表示为 f(t)=1,-∞<t<∞ (4―44) 它可以看作是双边指数信号在α取极限趋近0时的一个 特例,即
1 lim e
0
t
u (t ), 0 u( t )] lim[ e
0
t
(4―45)
[1] [lim e
0
t
2a u( t )] lim 2 0 a 2
(4―46)
0 0 0
lim
0
2 2 d lim d( ) 2 2 0 1 ( )2
(4―50)
f (t)
F()
1
0 －1 (a )
t
0
(b )
图4.10 符号函数及其频谱
符号函数sgn(t)也可看作是下述函数在α取极限趋近0时的一 个特例: t e t0 (其中α>0) f ( t ) t t0 e
F [ f (t )]
F(j ) 1
f (t )
方波信号的傅里叶变换_图文
(4―45)
(4―46)
(4―47)
(4―48) (4―49)
图4.9 单位直流信号及其频谱
符号函数Sgn(t)的频谱函数
例 3.4-7 求符号函数Sgn(t)的频谱函数。
考察例 3.4-4 所示信号f(t)
当α→0时，其极限为符号函数Sgn(t)。因而可以用求f(t)的频 谱函数F(jω)当α→0的极限的方法来求得Sgn(t)的频谱函数。
图 3.8-2 例 3.8-2 (a) 系统组成； (b) s(t)的波形
先求f(t)的傅里叶变换F(jω)，由于
再求s(t)的傅里叶变换S(jω)。由于s(t)为周期信号，T=1ms，则 , 因而有
图 3.8-3 y(t)的求解
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
解 图示信号f(t)可表示为
(a>0)
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
Байду номын сангаас
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
gτ(t)的傅里叶变换为
(4―36)
(4―37) (4―38) (4―39)
δ(t)的频谱函数
例 3.4-5 求单位冲激函数δ(t)的频谱函数。
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
常见波形的傅里叶级数展开
常见波形的傅里叶级数展开一、正弦波的傅里叶级数展开正弦波是一种最简单的周期性波形，可以通过傅里叶级数展开来表示。
傅里叶级数展开是将一个周期性函数表示为一组正弦函数的和的形式。
二、方波的傅里叶级数展开方波是一种周期为T的波形，它在一个周期内由两个不同幅值的水平线段组成。
方波可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
三、三角波的傅里叶级数展开三角波是一种周期为T的波形，它在一个周期内由连续的线性上升和下降线段组成。
三角波可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
四、锯齿波的傅里叶级数展开锯齿波是一种周期为T的波形，它在一个周期内由连续的线性上升和突然下降的线段组成。
锯齿波可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
五、矩形波的傅里叶级数展开矩形波是一种周期为T的波形，它在一个周期内由连续的水平线段组成。
矩形波可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
六、脉冲波的傅里叶级数展开脉冲波是一种非周期性的波形，它在一个有限时间内只有一个脉冲信号。
脉冲波可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
七、高斯波包的傅里叶级数展开高斯波包是一种非周期性的波形，它的振幅随时间按高斯分布变化。
高斯波包可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
八、噪声信号的傅里叶级数展开噪声信号是一种随机的信号，它包含了各种频率的谐波分量。
噪声信号可以通过傅里叶级数展开来表示，展开系数中包含各个谐波分量的幅值和相位。
以上是常见波形的傅里叶级数展开的简要介绍。
傅里叶级数展开是一种将周期性信号表示为谐波分量的和的方法，可以用来分析和合成各种复杂的波形。
通过傅里叶级数展开，我们可以更好地理解和描述各种波形的性质和特征。
傅里叶级数展开在信号处理、通信系统、音乐合成等领域具有广泛的应用。
方波信号f(t)展开为傅里叶级数.ppt
(j)
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
F() f (t)e jtdt eat e jtdt
1
j
2 T
2
f (t)cos(2nft)dt
2 T
0 T
2
(1)cos(2nft)dt 2
T
T 2 0
1 cos(2nft)dt
2 T
1
2 nf
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2nft)dt
2 T
o 2
τ 2
t
(a )
F(j )
2
－
4
－
2
o
4
(b )
F( )
( )
－
4
－
2
o
2 4
－
4
－
2
o 2 4
－
(c)
(d )
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
F() f (t)e jtdt eat e jtdt
1
j
2 T
2
f (t)cos(2nft)dt
2 T
0 T
2
(1)cos(2nft)dt 2
T
T 2 0
1 cos(2nft)dt
2 T
1
2 nf
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2nft)dt
2 T
o 2
τ 2
t
(a )
F(j )
2
－
4
－
2
o
4
(b )
F( )
( )
－
4
－
2
o
2 4
－
4
－
2
o 2 4
－
(c)
(d )
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
方波信号的傅里叶变换
CATALOGUE
方波信号的傅里叶变换原理
傅里叶变换的定义
01
02
03
04
05
傅里叶变换的性质
方波信号的傅里叶变换
CATALOGUE
方波信号的频谱分析
频谱的概念与计算
频谱定义
01
频谱计算
02
离散频谱
03
方波信号的频谱特点
基本频率分量
方波信号可以分解为一系列不同 频率的正弦波和余弦波的叠加， 这些正弦波和余弦波的频率即为
方波信号的傅里叶 变换
• 方波信号概述 • 方波信号的傅里叶变换原理 • 方波信号的频谱分析 • 方波信号的滤波处理 • 方波信号的合成与调制 • 方波信号的傅里叶变换实例分析
CATALOGUE
方波信号概述
方波信号的定 义
• 方波信号是一种常见的周期性信号，其特点是信 号在一定周期内以矩形波的形式重复。方波信号 在时间轴上的一个周期内，波形的最大值为1，最 小值为-1，波形在最大值和最小值之间以线性方 式变化。
CATALOGUE
方波信号的滤波处理
滤波器的基本概念
线性时不变系统
滤波器属于线性时不变系统，对输入信号的响应是线性的，并且 不随时间改变。
传递函数
滤波器的传递函数表示系统输入与输出之间的数学关系。
频率响应
滤波器的频率响应描述了系统对不同频率信号的增益或抑制程度。
方波信号的滤波处理方法
理想滤波器
感谢观看
方波信号的基本频率分量。
谐波分量
除了基本频率分量外，方波信号 还包含一系列谐波分量，它们的 频率是基本频率分量的整数倍。
频谱对称性
方波信号的频谱具有对称性，即 正弦波和余弦波的幅度随着频率 的增加而逐渐减小，且正弦波和
方波信号的傅里叶变换
信号的滤波
滤波器设计
通过傅里叶变换，可以将信号分解为 不同频率的分量，从而根据需要设计 滤波器，滤除特定频率范围的分量。
噪声抑制
在信号中混入噪声时，傅里叶变换可 以帮助识别和分离噪声分量，从而降 低噪声对信号的影响。
信号的压缩与扩展
压缩编码
通过对方波信号进行傅里叶变换，可 以将信号压缩为较小的数据量，便于 存储和传输。
方波信号的性质
01
方波信号具有明确的频率成分，其傅里叶变换可以 解析为简单的正弦和余弦函数。
02
方波信号的频率成分与其周期T有关，可以通过傅里 叶变换得到。
03
方波信号的波形因子a决定了其频谱的宽度和峰值。
方波信号的应用
1
方波信号在通信、控制、测量等领域有广泛应用 。
2
方波信号可以用于产生电磁波、调制载波等。
方波的频谱幅度随着谐波次数增 加而减小，呈现快速衰减的趋势 。
方波信号的频域特性周期性来自方波信号在频域内表现为一系列离散的谐波分量，这 些分量具有周期性重复的特点。
带宽有限
方波信号的频域特性表明其带宽是有限的，即其最高 频率分量是有限的。
能量集中
方波信号的能量主要集中在基频和较低次谐波上，高 次谐波携带的能量逐渐减少。
3
方波信号在数字电路中常被用作时钟信号。
02
CATALOGUE
傅里叶变换基础
傅里叶变换的定义
01
傅里叶变换是一种将时域信号转换为频域信号的方法。
02
对于给定的时域信号，通过傅里叶变换，可以得到该信号的频
谱。
傅里叶变换的基本公式为：(X(f) = int_{-infty}^{infty} x(t)
方波信号的傅里叶变换
方波信号傅里叶变换
从频谱函数的定义式出发
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
f(t) 1
e－t ＞0)
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
(b)
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
g r (t)
1
0
t 2
t 2
gτ(t)的傅里叶变换为
[ g r (t)]
2
A2 2
1 0 1 10 2 20
A3 0.4
3 45
A6 0.8
6 30
其余 An 0
An 3 3
2 2
1
0.8
0.4
o
2 3 4 5 6
(a )
n
45 °
45 °
30 ° 30 °
20 °
15 °
10 °
o
2
3
4
5
6
(b )
图 3.3-1 例 3.3-1
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
f(t) 1
e－t ＞0)
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
(b)
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
g r (t)
1
0
t 2
t 2
gτ(t)的傅里叶变换为
[ g r (t)]
2
A2 2
1 0 1 10 2 20
A3 0.4
3 45
A6 0.8
6 30
其余 An 0
An 3 3
2 2
1
0.8
0.4
o
2 3 4 5 6
(a )
n
45 °
45 °
30 ° 30 °
20 °
15 °
10 °
o
2
3
4
5
6
(b )
图 3.3-1 例 3.3-1
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o
方波信号的傅里叶变换课件
傅里叶变换定义
将时间域的信号转换为频域的表示，通过将信号拆分为不同频率 的正弦波和余弦波的叠加。
方波信号的频谱计算
通过对方波信号进行傅里叶变换，可以得到其频谱，即各个频率分 量的幅度和相位。
频谱分析
通过分析方波信号的频谱，可以了解该信号在不同频率下的表现和 特征。
方波信号的频域分析
频域分析方法
在频域中，通过观察信号的频谱，可以分析信号的频率成分、能 量分布以及频率变化规律等信息。
方波信号的频域特性
方波信号在频域中表现出较为突出的离散性，即主要集中在某些 特定的频率分量上。
频域分析的应用
通过频域分析，可以对方波信号进行滤波、调制和解调等操作， 实现信号处理和通信系统的应用。
方波信号的逆变换结果
01
02
03
逆变换的概念
将经过傅里叶变换得到的 频域表示重新变换回时间 域，恢复原始信号的过程 。
时移性质
若f(t)是函数，则f(t+a)的 傅里叶变换为F(ω)e^(iωa)。
频移性质
若f(t)是函数，则f(at)的傅 里叶变换为|a|F(|a|ω)。
对偶性
若f(-t)=f*(t)，则 F(ω)=F*(-ω)。
帕斯瓦尔定理
f(t)的能量等于其傅里叶变 换在无穷大频率域上的积 分。
离散傅里叶变换（DFT）与快速傅里叶变换（FFT）
方波信号的傅里叶变 换课件
目录
• 方波信号简介 • 傅里叶变换基础 • 方波信号的傅里叶变换 • 方波信号的傅里叶逆变换 • 方波信号的傅里叶变换实例
01
方波信号简介
方波信号的定义
方波信号是一种常见的周期信号，其在一个周期内取值 为+1或-1，且在半个周期内从+1跳变到-1或从-1跳变 到+1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
f (t)sin(2nft)dt
2
T
0 T
2
(1)sin(2nft)dt 2
T
T 2 0
1 sin(2nft)dt
2 T
1 [cos(2nft)] 2 nft
0 T
2
2 T
1
2 nf
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,
2
－4
－
2
o
4
(b )
F( )
( )
－4 －2 o
2 4
－4 －2
o 2 4
－
(c)
(d )
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
15 °
10 °
o
2
3
4 5
6
(b )
图 3.3-1 例 3.3-1
(a) 振幅谱； (b) (b) 相位谱
|F n |
2
1 .5
1 .5
1
1
1
0 .4 0 .2
0 .4 0 .2
－ 6－ 5 － 4－ 3－ 2 － o
2 3 4 5 6
(a )
n 45°
li m0 a2
2a
2
0
0 0
(4―45) (4―46)
lim
0
2
d lim
2 2
0
1
2
(
)2
d
(
)
lim 2 arctan
0
2
[1] 2 ( )
1 2 ( )
t 0
(0)
e at t 0
当α→0时，其极限为符号函数Sgn(t)。因而可以用求f(t)的频
谱函数F(jω)当α→0的极限的方法来求得Sgn(t)的频谱函数。
例 3.4-4
所示信号的频谱函数为
j
2 2 2
，从而有
Sgn(t) 1
X()
o
t
o
－1
(a) (b)
图 3.4-7 符号函数Sgn(t) (a)Sgn(t)的波形； (b) 频谱
f(t) 1
e－t ＞0)
X( )
1
o
t
－ et
o
－1 (a)
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
－
1
(b)
解 图示信号f(t)可表示为
f
(t)
e at
e at
t 0
(a>0)
t 0
F(j) 0eaet jtdt etejtdt
e((jj )t ) 01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
例 3.4-2 求指数函数f(t)的频谱函数。
f
(t)
e at
t 0
0
t 0
f (t)
1 e－t (＞0)
(0)
F()
1
o
t
o
(a)
(b)
图 3.4-2 单边指数函数e-αt
(a) 单边指数函数e-αt; (b) e-αt的幅度谱
解
F(j) f(t)ejtdt etejtdt
方波信号f(t)展开为傅里叶级数
例4―1 试将图4.2所示的方波信号f(t)展开 为傅里叶级数。
f (t)
1
－T T
0T T
2T
t
2
－1 2
图4.2 方波信号的傅里叶级数
解 我们将信号按式(4―6)分解成傅里叶级数,
并按式(4 及c。
―
7)、(4―8)、(4―9)分别计算an,
bn
an
2 T
F() f (t)e jtdt eat e jtdt
1
0
j
(4―40) (4―41)
F()
1
12
－ 0
(a)
argF()
2 4
－ 0
－
4
－
2
(b)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
4
n
n 2,4,6, n 1,3,5,
c2 T
T
2 T
2
f(t)dt0
f(t)4[sin2ft13sin6ft15sin10f
1sin2ft]
n
n1,3,5,
振幅谱和相位谱例题
例 3.3-1 f(t)13cots1 (0 )2co2st (20 ) 0.4co3st (45 )0.8co6st (30 ),
试画出f(t)的振幅谱和相位谱。 解 f(t)为周期信号，题中所给的f(t)表达式可视为f(t)的傅里
叶级数展开式。据
f(t)A 20n 1Ancon st(n)
可知，其基波频率Ω=π(rad/s)，基本周期T=2 s，ω=2π、3π、 6 π分别为二、 三、六次谐波频率。且有
A0 1 2
45°
30° 30°
20°
15° 10°
－ 6－ 5 － 4－ 3 － 2 － o
2 3 4 5 6
－ 10° － 15°
－ 30°
－ 20°
－ 30°
－ 45°
－ 45° (b )
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱； (b) 相位谱
单边指数函数f(t)的频谱函数
从频谱函数的定义式出发
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
(4―75)
直流信号1的频谱函数
例 3.4-6 求直流信号1的频谱函数。
f (t) 1
F(j) 2()
o
o
(a)
(b)
图 3.4-6 直流信号f(t) (a) 直流信号f(t); (b) 频谱
解 直流信号1可表示为
f (t) 1
t
F(j) 1ejtdt
解
尺度变换求频谱
例4―11 已知
gr(t)
Sa(
2
)
求gτ(2t)的频谱函数
解 根据傅里叶变换的尺度变换性 质,gτ(2t)的频谱函数为
[gr(2t)]1 2Sa(4)
f (t) 1
0
t
22
f (2t)
1
0
t
44
F()
2π
2π
0
1 F( )
22
4π
0
1 1
j j
j
2 a2 2
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
g (t ) 1
－τ 2o
τ 2
t
(a )
F(j )
1
t
0
(b)
图4.5 冲激信号及其频谱
移位冲激函数δ(t-t0)的频谱函数
例4―12求移位冲激函数δ(t-t0)的频谱函数。
解 由于已知冲激函数δ(t)的频谱函数为1, 求移位冲激函数δ(t-t0)的频谱函数，此时可利 用傅里叶变换的时移特性式(4―74)。
[ (t t0 )] e jt0 1 (t t0 ) e jt0
2
j
0
0 0
F [sgn(t)] 2 j
(4-51)
阶跃函数ε(t)的频谱函数
例 3.4-8 求阶跃函数ε(t)的频谱函数。 解 由阶跃函数ε(t)的波形容易得到
(t)11Sg(nt)
22
从而就可更为方便地求出ε(t)的频谱函数， 即
(t)
1
o
(a)
X() R()
o
(b)
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
解
F(j) (t)ejtd t1
可见，冲激函数δ(t)的频谱是常数1。也就是说，δ(t)中包含了 所有的频率分量， 而各频率分量的频谱密度都相等。 显然， 信号δ(t)实际上是无法实现的。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
f (t)sin(2nft)dt
2
T
0 T
2
(1)sin(2nft)dt 2
T
T 2 0
1 sin(2nft)dt
2 T
1 [cos(2nft)] 2 nft
0 T
2
2 T
1
2 nf
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,
2
－4
－
2
o
4
(b )
F( )
( )
－4 －2 o
2 4
－4 －2
o 2 4
－
(c)
(d )
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
15 °
10 °
o
2
3
4 5
6
(b )
图 3.3-1 例 3.3-1
(a) 振幅谱； (b) (b) 相位谱
|F n |
2
1 .5
1 .5
1
1
1
0 .4 0 .2
0 .4 0 .2
－ 6－ 5 － 4－ 3－ 2 － o
2 3 4 5 6
(a )
n 45°
li m0 a2
2a
2
0
0 0
(4―45) (4―46)
lim
0
2
d lim
2 2
0
1
2
(
)2
d
(
)
lim 2 arctan
0
2
[1] 2 ( )
1 2 ( )
t 0
(0)
e at t 0
当α→0时，其极限为符号函数Sgn(t)。因而可以用求f(t)的频
谱函数F(jω)当α→0的极限的方法来求得Sgn(t)的频谱函数。
例 3.4-4
所示信号的频谱函数为
j
2 2 2
，从而有
Sgn(t) 1
X()
o
t
o
－1
(a) (b)
图 3.4-7 符号函数Sgn(t) (a)Sgn(t)的波形； (b) 频谱
f(t) 1
e－t ＞0)
X( )
1
o
t
－ et
o
－1 (a)
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
－
1
(b)
解 图示信号f(t)可表示为
f
(t)
e at
e at
t 0
(a>0)
t 0
F(j) 0eaet jtdt etejtdt
e((jj )t ) 01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
例 3.4-2 求指数函数f(t)的频谱函数。
f
(t)
e at
t 0
0
t 0
f (t)
1 e－t (＞0)
(0)
F()
1
o
t
o
(a)
(b)
图 3.4-2 单边指数函数e-αt
(a) 单边指数函数e-αt; (b) e-αt的幅度谱
解
F(j) f(t)ejtdt etejtdt
方波信号f(t)展开为傅里叶级数
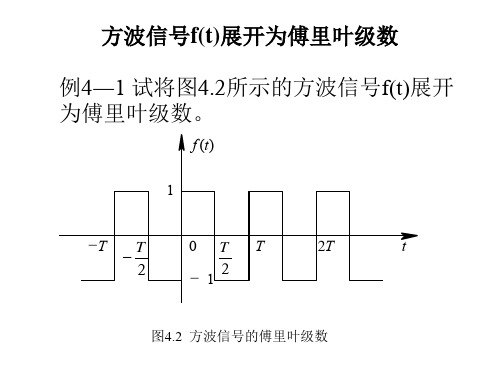
例4―1 试将图4.2所示的方波信号f(t)展开 为傅里叶级数。
f (t)
1
－T T
0T T
2T
t
2
－1 2
图4.2 方波信号的傅里叶级数
解 我们将信号按式(4―6)分解成傅里叶级数,
并按式(4 及c。
―
7)、(4―8)、(4―9)分别计算an,
bn
an
2 T
F() f (t)e jtdt eat e jtdt
1
0
j
(4―40) (4―41)
F()
1
12
－ 0
(a)
argF()
2 4
－ 0
－
4
－
2
(b)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
4
n
n 2,4,6, n 1,3,5,
c2 T
T
2 T
2
f(t)dt0
f(t)4[sin2ft13sin6ft15sin10f
1sin2ft]
n
n1,3,5,
振幅谱和相位谱例题
例 3.3-1 f(t)13cots1 (0 )2co2st (20 ) 0.4co3st (45 )0.8co6st (30 ),
试画出f(t)的振幅谱和相位谱。 解 f(t)为周期信号，题中所给的f(t)表达式可视为f(t)的傅里
叶级数展开式。据
f(t)A 20n 1Ancon st(n)
可知，其基波频率Ω=π(rad/s)，基本周期T=2 s，ω=2π、3π、 6 π分别为二、 三、六次谐波频率。且有
A0 1 2
45°
30° 30°
20°
15° 10°
－ 6－ 5 － 4－ 3 － 2 － o
2 3 4 5 6
－ 10° － 15°
－ 30°
－ 20°
－ 30°
－ 45°
－ 45° (b )
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱； (b) 相位谱
单边指数函数f(t)的频谱函数
从频谱函数的定义式出发
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
(4―75)
直流信号1的频谱函数
例 3.4-6 求直流信号1的频谱函数。
f (t) 1
F(j) 2()
o
o
(a)
(b)
图 3.4-6 直流信号f(t) (a) 直流信号f(t); (b) 频谱
解 直流信号1可表示为
f (t) 1
t
F(j) 1ejtdt
解
尺度变换求频谱
例4―11 已知
gr(t)
Sa(
2
)
求gτ(2t)的频谱函数
解 根据傅里叶变换的尺度变换性 质,gτ(2t)的频谱函数为
[gr(2t)]1 2Sa(4)
f (t) 1
0
t
22
f (2t)
1
0
t
44
F()
2π
2π
0
1 F( )
22
4π
0
1 1
j j
j
2 a2 2
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
g (t ) 1
－τ 2o
τ 2
t
(a )
F(j )
1
t
0
(b)
图4.5 冲激信号及其频谱
移位冲激函数δ(t-t0)的频谱函数
例4―12求移位冲激函数δ(t-t0)的频谱函数。
解 由于已知冲激函数δ(t)的频谱函数为1, 求移位冲激函数δ(t-t0)的频谱函数，此时可利 用傅里叶变换的时移特性式(4―74)。
[ (t t0 )] e jt0 1 (t t0 ) e jt0
2
j
0
0 0
F [sgn(t)] 2 j
(4-51)
阶跃函数ε(t)的频谱函数
例 3.4-8 求阶跃函数ε(t)的频谱函数。 解 由阶跃函数ε(t)的波形容易得到
(t)11Sg(nt)
22
从而就可更为方便地求出ε(t)的频谱函数， 即
(t)
1
o
(a)
X() R()
o
(b)
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
解
F(j) (t)ejtd t1
可见，冲激函数δ(t)的频谱是常数1。也就是说，δ(t)中包含了 所有的频率分量， 而各频率分量的频谱密度都相等。 显然， 信号δ(t)实际上是无法实现的。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0