Buffon投针实验的理论证明
Buffon掷针实验的计算机模拟实验的设计与实现

Buffon 掷针实验的计算机模拟实验的设计与实现收稿日期:2018-12-05基金项目:长沙理工大学大学生研究性学习与创新性实验项目(1203058);长沙理工大学教研教改项目(CNJG201808)作者简介:周浙泉,王志宇,张棣妍(女),隆超怡(女),长沙理工大学信息与计算科学专业2014级学生;万勇(1963-),硕士研究生,教授,研究方向:几何分析与偏微分方程。
一、研究背景18世纪,蒲丰(Buffon )提出Buffon 投针问题:(1)取一张白纸,在上面画上许多条间距为a 的平行线。
(2)取一根长度为l (l ≤a/2)的针,随机地向画有平行直线的纸上掷n 次,观察针与直线相交的次数,记为m 。
(3)计算针与直线相交的概率。
蒲丰证明了这个概率是:p=2l πa。
因为它与π有关,人们想到利用投针实验来估计圆周率的值。
历史上,有不少人做过蒲丰掷针实验:这个问题十分有趣,只是人工实验往往耗时、耗力,而用计算机模拟实验,却能迅速获得结果。
自从20世纪90年代美国率先开始数学实验以来,数学实验改变了人们传统的数学思维方式,人们发现数学是可以借助计算机去探索和发现的。
近十年来,国内外已有不少的数学实验教材和一些好的数学实验范例,但是这需要一定的计算机编程能力,如math-ematica 编程、matlab 编程等,才能实现人机对话,因此数学实验只能在具有一定数学知识和较高计算机编程能力的特定人群中使用,不能“飞入寻常百姓家”。
二、系统的设计本系统研发工具为Java 语言。
Java 是一门面向对象编程语言,不仅吸收了C++语言的各种优点,还作为静态面向对象编程语言的代表,极好地实现了面向对象理论,允许程序员以优雅的思维方式进行复杂的编程。
Java 看起来设计得很像C++,但是能够自动处理对象的引用和间接引用,实现自动的无用单元收集,使用户不必为存储管理问题烦恼,能将更多的时间和精力花在研发上。
Java 是一个面向对象的语言。
蒲丰(Buffon)投针试验

一、利用Matlab计算机语言验证蒲丰(Buffon)投针试验问题给定a=10,b=5时,模拟100万次投针实验的Matlab程序如下:a=10;b=5;n=1000000;p=10; % a为平行线间距,b为针的长度,n为投掷次数,p为有效数字位数x=unifrnd(0,a/2,[n,1]);phi=unifrnd(0,pi,[n,1]); % 产生均匀分布的随机数,分别模拟针的中点与最近平行线的距离和针的倾斜角y=x<0.5*b*sin(phi); m=sum(y); % 计数针与平行线相交的次数PI=vpa(2*b*n/(a*m),p)运行结果PI =3.138919145二、利用C++计算机语言编程通过大量重复实验验证以下结论:三个阄,其中一个阄内写着“有”字,两个阄内不写字,三人依次抓取,各人抓到“有”字阄的概率均为1/3。
程序如下:#include<stdio.h>#include<stdlib.h>#include<time.h>void main(){int n=500000;int i,a[3]={0};srand(time(NULL));for(i=0;i<n;i++)a[rand()%3]++;printf("共测试%d次,其中有字事件有%d次, 占%.2f%%\n""抓到无字事件1有%d次,占%.2f%%\n""抓到无字事件2有%d次,占%.2f%%\n""抓到无字事件共%d次,占%.2f%%",n,a[0],a[0]*100.0/n,a[1],a[1]*100.0/n,a[2],a[2]*100.0/n,a[1]+a[2],(a[1]+a[2])*100.0/n);return 0;}。
Buffon's needle problem

d ℓ
2 2
) − arcsin
d ) ℓ
以上公式告诉我们在ℓ = d时得出p= 时的概率趋于1。
2
π
,概率依ℓ严格递增,而且当
ℓ→∞
2
π /2
π
∫
0
ℓ sin α 2 ℓ 2 ℓ π /2 dα = [ − cos α ] 0 = d π d π d
d 对于长针,只要 ℓ sin α ≤,即角度在 0 ≤ α ≤ arcsin ℓ 内变化,我们得 到相同的概率。但是,对于更大的角 α ,针就必定穿过横线,于 是其概率一定为1,因此对于 ℓ ≥ d 我们计算可得:
E ( P n ) ≤ E (C ) ≤ E ( P )
n
n
现在 P n和 P 都是多边形,因此两者与直线交叉点的期望均 为“c倍的长度”,又对于圆C的交叉点为2,因此 n c ℓ ( P) <= 2 <=c ℓ ( P )。 (1) n n n lim ℓ ( P n ) = dπ = lim ℓ ( P ) n 其中, → ∞ 时, Pn 和 P 与圆C近似。特别是,→ ∞ n n→∞ n → ∞ 时, cdπ ≤ 2 ≤ cdπ ,得 因此根据(1)可推出当 到c = 2 1 π d
记投掷一根长度为ℓ的直针产生的交叉点的期望个数记 为E(ℓ),若ℓ=x+y,x和y可分别看作是针的前端和后端, 则有E(x+y)=E(x)+E(y),因为交点数总是恰好等于前端 产生的加上后端产生的那些。 由期望的线性性,我们可得到E(rx)=rE(x)对所有的 有理数 r ∈ Q 成立
此外,,E(x)显然在 其中c=E(1)
Buffon’s needles problem 蒲丰投针问题
Buffon投针试验

a
M x
m(G ) G的面积 P ( A) m( S ) S的面积
b 0 2 sin d a π 2 b 2b . a π aπ 2
π
蒲丰投针试验的应用及意义
根据频率的稳定性, 当投针试验次数n很大时, m 算出针与平行直线相交的次数m, 则频率值 即可 n 作为P( A)的近似值代入上式, 那么
定义 当随机试验的样本空间是某个区域,并且任 意一点落在度量 (长度, 面积, 体积) 相同的子区域 是等可能的,则事件 A 的概率可定义为
m( A) P( A) m( S )
(其中m( S ) 是样本空间的度量, m( A) 是构成事件 A 的子区域的度量 ) 这样借助于几何上的度量来合理 规定的概率称为几何概率.
投针试验的所有可能结果 与矩形区域 a S {( x, ) | 0 x , 0 } 2 中的所有点一一对应. 由投掷的任意性可知, 这是一个几何概型问题. 所关心的事件
A {针与任一平行直线相交} 发生的充分必要条件为S中的点满足
b 0 x sin , 0 π 2
蒲丰投针试验
例 1777年,法国科学家蒲丰(Buffon)提出了投针 试验问题.平面上画有等距离为a(>0)的一些平行直 线,现向此平面任意投掷一根长为b(<a)的针,试求 针与任一平行直线相交的概率.
解: 以x表示针投到平面上时, a 针的中点M 到最近的一条平行
M x
直线的距离, 表示针与该平行直线的夹角. 那么针落在平面上的位置可由( x, )完全确定.
几何概型
古典概型是关于试验的结果为有限且每个结果出现的 可能性相同的概率模型。一个直接的推广是:保留等 可能性,而允许试验的所有可能结果为直线上的一线 段,平面上的一区域或空间中的一立体等具有无限多 个结果的情形,称具有这种性质的试验模型为几何概 型.
Buffon投针实验报告

Buffon投针实验一、实验目的:在计算机上用试验方法求圆周率的近似值。
二、实验原理:假设平面上有无数条距离为1的等距平行线,现向该平面随机投掷长度为L(L≤1)的针,则针与平行线相交的概率 P=。
设针的中心M与最近一条平行线的距离为x,则x~U(0,1);针与平行线的夹角为(不管相交与否),则~U(0,)如图:()在矩阵上均匀分布,且针与平行线相交的充要条件为x≤=;P=P{ x=}。
记录≤成立的次数,记为由-大数定理:≈,则=2。
在计算机上产生则=~U(0,),i=1,2,…,n;再产生,则, i=1,2,…,n三、实验方法及代码:在计算机上进行模拟实验,求出的实验值。
给定L,在计算机上利用MFC独立随机产生x和,然后判断≤是否成立.代码如下:#include "stdafx.h"#include "buffon.h"#include "ChildView.h"#include "ChoiceDlg.h"#include <ctime>#include <cmath>#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif// CChildViewCChildView::CChildView(){Trynum=1000;}CChildView::~CChildView(){}BEGIN_MESSAGE_MAP(CChildView,CWnd )//{{AFX_MSG_MAP(CChildView)ON_WM_PAINT()ON_COMMAND(ID_TOOL_NUM, OnToolNum)ON_COMMAND(ID_TOOL_RETRY, OnToolRetry)//}}AFX_MSG_MAPEND_MESSAGE_MAP()// CChildView message handlersBOOL CChildView::PreCreateWindow(CREATESTRUCT& cs){if (!CWnd::PreCreateWindow(cs))return FALSE;cs.dwExStyle |= WS_EX_CLIENTEDGE;cs.style &= ~WS_BORDER;cs.lpszClass = AfxRegisterWndClass(CS_HREDRAW|CS_VREDRAW|CS_DBLCLKS,::LoadCursor(NULL, IDC_ARROW), HBRUSH(COLOR_WINDOW+1), NULL);return TRUE;}void CChildView::OnPaint(){CPaintDC dc(this),*pDC;pDC=&dc;CFont font, *pOldFont;font.CreatePointFont(200,"宋体");pOldFont=pDC->SelectObject(&font);pDC->SetTextColor(RGB(255,0,0));pDC->TextOut(100,5,"蒲丰投针试验");pDC->SelectObject(pOldFont);CPen myPen1,myPen2, *pOldPen1,*pOldPen2;CRect rect1(30,30,920,620);pDC->Rectangle(rect1);myPen1.CreatePen(PS_SOLID, 1, RGB(0,0,255));pOldPen1=pDC->SelectObject(&myPen1);for(int i=100;i<600;i+=50){pDC->MoveTo(50,i);pDC->LineTo(900, i);}pDC->SelectObject(pOldPen1);myPen2.CreatePen(PS_SOLID, 1, RGB(0,255,0));pOldPen2=pDC->SelectObject(&myPen2);srand(time(0));int a,b,q,a1,b1,su,flag;np=0;for(int j=0;j<Trynum;j++){a=rand()%850+50;b=rand()%450+100;q=rand()%180;a1=25*cos(q);b1=25*sin(q);su=pow(-1,rand()%2);pDC->MoveTo((a-su*a1),(b-su*b1));pDC->LineTo((a+su*a1),(b+su*b1));if( (b%50) >= 25 )flag =50-b%50;elseflag = b%50;if( 25*sin(q) >= flag )np++;}pDC->SelectObject(pOldPen2);CString str;int c=Trynum/(np*1.0);int d=(int)((Trynum/(np*1.0)*100000))%100000;str.Format("投针次数:%d;\n相交次数:%d;\nπ的估算值:%d.%d",Trynum,np,c,d);MessageBox(str,"实验数据信息");}void CChildView::OnToolNum(){CChoiceDlg mydlg;if(mydlg.DoModal()==IDOK){this->Trynum = mydlg.m_Trynum ;this->RedrawWindow();}}void CChildView::OnToolRetry(){// TODO: Add your command handler code herethis->RedrawWindow();}四、实验数据处理与分析:根据实验数据,得到近似值为3.2313,可得相对误差为δ=(3.2313-π)/π≈0.02856;运行截图:五、实验小结:本次实验,通过MFC进行模拟投针,模拟效果较好,随着投针次数模拟的增多,实验结果逼近于π的真实值,但是实验程序有待优化,在较多投针次数的模拟中,实验程序运行速度较慢,可以改进相关算法来做适当调节。
蒲丰投针原理
/4.因为对于每一个z,这个概率都为(π-2)/4,因此对于任意的正数x,y,z,有P=(π-2)/4,命题得证。
为了估算π的值,我们需要通过实验来估计它的概率,这一过程可交由计算机编程来实现,事实上x+y>z,x²+y²;﹤z²;等价于(x+y-z)(x²+y²-z²;)﹤0,因此只需检验这一个式子是否成立即可。
若进行了m 次随机试验,有n次满足该式,当m足够大时,n/m趋近于(π-2)/4,令n/m=(π-2)/4,解得π=4n/m+2,即可估计出π值。
值得注意的是这里采用的方法:设计一个适当的试验,它的概率与我们感兴趣的一个量(如π)有关,然后利用试验结果来估计这个量,随着计算机等现代技术的发展,这一方法已经发展为具有广泛应用性的蒙特卡罗方法。
计算π最稀奇方法之一计算π的最为稀奇的方法之一,要数18世纪法国的博物学家C·布丰和他的投针实验:在一个平面上,用尺画一组相距为d的平行线;一根长度小于d的针,扔到画了线的平面上;如果针与线相交,则该次扔出被认为是有利的,否则则是不利的.布丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于d,那么有利扔出的概率为2/π.扔的次数越多,由此能求出越为精确的π的值.公元1901年,意大利数学家拉兹瑞尼作了3408次投针,给出π的值为3.1415929——准确到小数后6位.不过,不管拉兹瑞尼是否实际上投过针,他的实验还是受到了美国犹他州奥格登的国立韦伯大学的L·巴杰的质疑.通过几何、微积分、概率等广泛的范围和渠道发现π,这是着实令人惊讶的!证明下面就是一个简单而巧妙的证明。
找一根铁丝弯成一个圆圈,使其直径恰恰等于平行线间的距离d。
可以想象得到,对于这样的圆圈来说,不管怎么扔下,都将和平行线有两个交点。
蒲丰投针问题_概率论论文

Buffon投针问题摘要本文讨论了Buffon投针问题的解法及其不同解法之间的内在联系,同时从投针到投平面图形对Buffon投针问题给出了一些推广,并得到一般的结论,指出了其概率在探矿、近似计算中的应用。
关键词蒲丰投针概率随机试验近似计算一、引言蒲丰投针问题是由法国科学家蒲丰(Buffon)在1777年提出的,它是概率中非常有代表性的问题,它是第一个用几何形式表达概率问题的例子,其结论具有很强的理论与实际意义。
蒲丰针问题的解决不仅较典型的反应了集合概率的特征及处理方法,而且还可以由此领略到从“概率土壤”上开出的一朵瑰丽的鲜花——蒙特卡洛(Monte-Carlo)方法。
二、Buffon投针问题及其解法Buffon投针问题:平面上画有等距离的平行线,每两条平行线之间的距离为2a,向平面任意投掷一枚长为2l(l<a)的针,试求针与平行线相交的概率。
解:以x表示针的中点M到最近一条平行线的距离,以φ表示该针与平行线的夹角。
针与平行线的关系见图1.则有:0≤x≤a,0≤φ≤π,由它们所围成的矩形区域记为G1。
针与平行线相交的充要条件是:0≤x≤lsinφ,记满足这个关系的区域为g1(图2中的阴影部分)。
则所求概率为P1=g1的面积G1的面积=∫lsinφdφπaπ=2laπ三、Buffon投针问题不同解法及其内在联系上述解法是常见解法之一(记为解法一),这里讨论一下蒲丰针问题的其他解法及其之间的联系。
1.其他解法解法二:以x表示针的重点M到最近一条平行线的距离,y表示该针在此平行线上投影和长度,如图3所示。
易知x和y的取值范围是0≤x≤a,0≤y≤2l,这两个不等式确定了xOy平面上的矩形区域G2,针与平行线相交的充要条件是(y2)2+x2≤l2,该不等式确定了矩形区域G2(如图4所示)中的区域g2,从而所求概率为P2=g2的面积G2的面积=14·l·2l·π2l·a=lπ4a解法三:作垂直于平行线的直线,在该直线上选定一方向为正向,用z1,z2分别表示针头与针尾关于某平行线的纵坐标(如图5所示),该平行线的选取应使|z1+z2|≤2a。
蒲丰投针与蒙特卡洛(MonteCarlo)方法

蒲丰投针与蒙特卡洛(Monte —Carlo)方法1777年法国科学家蒲丰(Buffon )提出并解决了如下的投针问题:桌面上画有一些平行线,它们之间的距离都是,一根长为a )(a l l ≤的针随机地投在桌面上。
问:此针与任一直线相交的概率是多少?设表示针的中点到最近的一条平行线的距离,Y 表示针与平行线的夹角(如图),如果X 2sin l Y X <, 或Y lX sin 2<时,针与一条直线相交。
由于向桌面投针是随机的,所以用来确定针在桌面上位置的是二维随机向量。
并且在),(Y X X ⎟⎠⎞⎜⎝⎛2,0a 上服从均匀分布,在Y ⎟⎠⎞⎜⎝⎛2,0π上服从均匀分布,与Y 相互独立。
由此可以写出的联合概率密度函数:X ),(Y X⎪⎩⎪⎨⎧<<<<=其它20,204),(ππy ax ay x f 于是,所求概率为:∫∫∫∫===⎭⎬⎫⎩⎨⎧<<20sin 20sin 224),(sin 2πππal dxdy adxdy y x f Y l X P y ly lx ①由于最后的结果与π有关,因此有些人想利用它来计算π的值。
其方法是向桌面投针次,若针与直线相交次,则针与直线相交的频率为n k n k ,以频率代替概率,则有al n k π2=,所以aknl2=π。
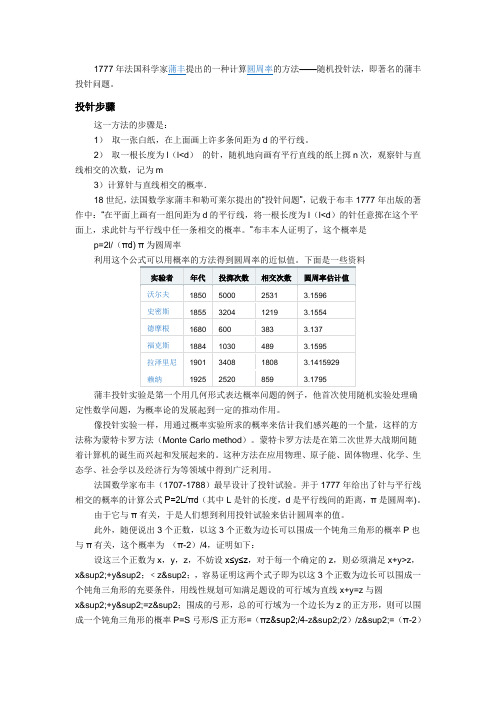
下表列举了这些试验的有关资料。
投针试验的历史资料(折算为1)a 试验者 年份 针长投针次数n 相交次数k π的试验值Wolf 1850 0.85000 2532 3.1596 Smith1855 0.63204 1219 3.1554 De.Morgan 1860 1600 383 3.137 Fox 1884 0.751030 489 3.1595 Lazzerini 1901 0.833408 1801 3.1415929 Reina1925 0.5425208593.1795这个思路已被人们发展成为统计学的一个分支—随机试验法或称为蒙特卡洛(Monte—Carlo )方法,其中随机试验可借助计算机大量重复,以致结果更接近真值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Buffon投针实验的理论证明
我们知道,当正多边形的边数无限增多时,它的极限是圆。
所以“圆”这种图形可以代表弯曲得最厉害的小针。
现在假定圆形小针的直径恰好与纸上两条相邻的平行线间的距离相等,那末这个圆形小针投掷下来时,不是和一条直线相交两次,就是和两条相邻的平行线相切。
不管怎样,它的相交次数是2。
因此,当投掷的次数为n时,碰线的次数便是2n。
现在小针的长度只有两条相邻平行线间距离的一半,所以针的长度只有上述圆形小针长度(即圆周长)的。
但是可能碰线的次数是与针的长度成正比的,因此小针的可能碰线的次数k就必须满足下面的比例式:
1:(1/2π) =2n: k
于是就得到π=n/k,也就是
π=投掷总次数/碰线次数
这就是上面“投针实验”的理论根据。
它又叫莆丰氏实验,在概率论中是很出名的,也可以说是近代的“统计试验法”(又叫“蒙特卡罗法”)的滥觞。
蒲丰(Buffon)投针求π
蒲丰(Buffon)投针问题:在平面上画有等距离的一些平行线,平行线间的距离为a(a>0),向平面上随机投一长为l (l<a)的针,针与平行线相交的概率P,结果发现π=2*l/(a*p)。
一、实验目的
蒲丰实验是采用投针来计算π的值,历史上也有许多的学者曾亲自做过这个实验,如下表:
我们也可以来做这个实验,而且希望做更多次,但是投针又比较费时费力,于是,可以采用另一种设计随机实验的方法,随机模拟的办法来模拟蒲丰投针实验。
从而求得π的近似值。
二、实验方法
可以采用MatLAB软件进行模拟实验,即用MATLAB编写程序来进行“蒲丰投针实验”。
1.基本原理:由于针投到纸上的时候,有各种不同的方向和位置(图a),但是,每一次投针时,其位置和方向都可以由两个量唯一确定,那就是针的中点和偏离水平的角度(图b)。
随机投针图
针的某一特定位置
于是,我们可以生成两个n*1随机矩阵,分别设为x和y,x 表示此时针的中点的位置,y表示此时针偏离水平方向的角度。
如图b,当x< 0.5*l*sin(y)的时候,即可认为此时的针与横线相交;只要随机生成n对这样的x和y,就可以模拟n次的投针实验,然后统计满足x< 0.5*l*sin(y)的x的个数,就可以认为这是相交的次数。
然后利用公式求得π值。
2.MATLAB编程
这是名字为P_Buffon的m文件:…………………………………………………………………………function PI=P_Buffon(a,l,n,p) %蒲丰投针实验求π,其中a 为横线间距,l为针的长度,n为投掷次数,p为有效位数
if l>a
error('针的长度不能超过横线间距,请确定l<a');
return;end
x=unifrnd(0,a/2,[n,1]);
f=unifrnd(0,pi,[n,1]);
y=x<0.5*l*sin(f);
m=sum(y) %显示相交次数
PI=vpa(2*l*n/(a*m),p); …………………………………………………………………………
三、实验数据(见附表)
四、数据分析
1)由数据可以看出,当l和a为定值,而次数改变时,相交次数也会改变,相交次数与投掷次数有个近似的线性关系,这个关系就是P,即相交的概率,但是n越大,对结果只是变化减小,n越大,并不会使得结果越准确。
2)由上面的实验数据第二部分可知,当间距和n(投掷次数)不变时,针长越大或是越小,都会越偏离π的真实值,一般来说,a可能在[0.6*l,0.8*l]之间时,会接近真实结果一些。
