常见分布的测量不确定度置信因子的计算
测量不确定度的计算公式

测量不确定度的计算公式测量不确定度这东西,在很多科学和工程领域那可是相当重要!咱先来说说啥是测量不确定度。
简单来讲,它就是对测量结果可能存在的误差范围的一种描述。
比如说,你测量一个物体的长度,得到的结果是 10 厘米,但实际上,由于各种因素的影响,它真正的长度可能在 9.8 厘米到 10.2 厘米之间波动,这个波动范围就是测量不确定度。
那测量不确定度的计算公式是啥呢?常见的有 A 类评定和 B 类评定两种方法。
先来说说 A 类评定。
这就好比你多次测量同一个量,然后通过对这些测量数据的统计分析来估算不确定度。
比如说,你测量一个房间的温度,测了 10 次,分别是 25.1℃、25.3℃、24.9℃、25.0℃、25.2℃、24.8℃、25.1℃、25.3℃、24.9℃、25.0℃。
那首先要算这 10 个数的平均值,(25.1 + 25.3 + 24.9 + 25.0 + 25.2 + 24.8 + 25.1 + 25.3 + 24.9 + 25.0)÷ 10 = 25.0℃。
然后算每个测量值与平均值的差值,再平方。
比如第一个 25.1℃与平均值 25.0℃的差值是 0.1℃,平方就是 0.01。
把这 10 个平方差加起来,除以测量次数减 1(也就是 9),得到的就是实验标准偏差。
最后再乘以一个包含因子(通常根据测量次数和置信水平来确定),就得到了 A 类评定的不确定度。
再讲讲 B 类评定。
这通常是基于经验、信息或者其他非统计的方法来估算不确定度。
比如说,你用的测量仪器的说明书上说,它的精度是 ±0.5℃,那这 ±0.5℃就是一个 B 类不确定度的来源。
然后把 A 类和 B 类评定得到的不确定度合成,这就用到了合成不确定度的公式。
合成不确定度等于根号下(A 类评定的不确定度的平方 + B 类评定的不确定度的平方)。
举个我自己经历过的事儿吧。
有一次学校组织科学实验比赛,我们小组要测量一个小金属块的密度。
测量不确定度计算

附件:高效液相色谱/串联质谱法测定硝基呋喃代谢物残留量的测量不确定度计算一、检测流程称样+5mL 0.2M HCL+50μL 100mM 2-NBA震荡30min37℃过夜+0.5mL 0.3M Na3PO4+2M NaOH调pH7.4+2×5mL乙酸乙酯震荡20min乙酸乙酯层40℃ N2吹干1mL流动相溶解+2×1.5mL正己烷震荡1min4000r/m离心3 min下层溶液0.20μm过滤HPLC/MS/MS检测二、 建模分析残留量检测公式:内标法定量WV P V V C P X ⨯⨯⨯⨯⨯=标标终样标样 (1)式中:X —试样中目标化合物含量,μg/kgP 样-试样中目标化合物峰面积/内标化合物峰面积 P 标-标准溶液中标准化合物峰面积/内标化合物峰面积C 标-标准溶液浓度(ng/mL ) V 标-标准溶液进样体积(μL) V 终-样品溶液最终定容体积(mL) V 样-样品溶液进样体积(μL) W -样品称样量(g )充分考虑样品检测过程中的各种不确定性因素,建立不确定性评估模型:rec ll ext mon f f f f WV P V V C P X ⨯⨯⨯⨯⨯⨯⨯⨯⨯=标标终样标样 (2)式中: m o n f -均匀化因子ext f -提取因子 ll f -液-液萃取因子rec f -回收率校正因子三、不确定度计算表1 计算硝基呋喃多残留不确定度的有关量值 项目 量值 标准不确定度 相对标准不确定度PAOZ0.983 0.0058 0.0058 AMOZ 0.990.0058 0.0058 SEM0.999 0.0058 0.0058 AHD 0.9990.0058 0.0058 M standard 100mg 0.216mg 0.0022 C 标 0.01ppm 0.000029 ppm 0.0029 W 2.004g 0.00204g 0.0010 V 样 20μl 0 0 V 标 20μl 0 0 V 终 1ml 0.0098 0.0098 f mon 1.0 0.02 0.02 f ext 1.0 0.005 0.005 f ll 1.0 0.030 0.030f recAOZ1.0 0.0220 0.0220 AMOZ 1.00.0370 0.0370 SEM1.0 0.0423 0.0423 AHD 1.00.0494 0.0494 E’spe 1.0μg/kg1 AOZ (呋喃唑酮代谢物)标准品纯度的不确定度u[P (AOZ)]按供应商目录所给纯度(所用标准品的纯度不确定度为0.5~1%,此处取最大值1%)为98.3±1%,即0.983±0.01,按均匀分布转换成标准偏差为:0058.03/01.0][)(==EPTC P u2标准品称量称量不确定度来自两个方面: 第一,称量变动性,根据历史记载,在50g 以内,变动性标准偏差为0.07 mg ;第二,天平校正产生的不确定度,按国家标准物质研究中心校准证书给出的在95%置信概率时为0.4mg ,换算成标准偏差为0.4/1.96=0.204mg 。
测量不确定度 (2)
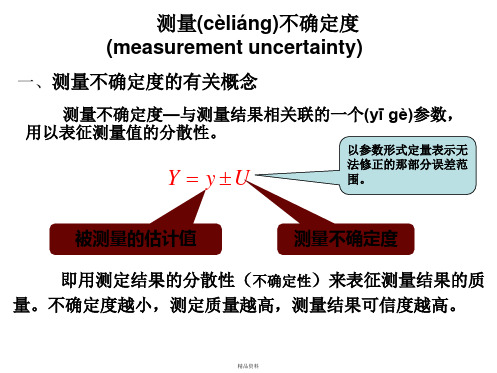
标准不确定(quèdìng)度B类评定的信息来源
1.以前的观测数据; 2.对有关技术资料的测量仪器特性的了解和经验; 3.生产企业提供的技术说明文件; 4.校准证书(检定证书)或其他文件提供的数据、准确 度的等别或级别,包括目前仍在使用的极限误差、最大 允许误差等; 5.手册或某些资料给出的参考数据及其不确定(quèdìng) 度; 6.规定试验方法的国家标准或类似技术文件中给出的重 复性限 或复现性。
4)当x受到两个独立且皆满足均匀分布的因素影响时,则x服
从区间为(x-a,x+a)内的三a角分布 ux 6
5)当x服从区间(x-a,x+a)内的反正弦分布时,则其标
准不确定度为
ux
a 2
精品资料
B类评定一般(yībān)步 骤 根据(gēnjù)有关信息或经验,判断被测量的可能值区间(-a,a)
为自由度,由下式给定 简易法:一般可取k=2~3。
uc 4 n ui4
i1 i
精品资料
测量(cèliáng)不确度的评定流程
建立(jiànlì)数学模型
求最佳值
列出各不确定度分量的表达式
A类评定
B类评定
求出合成不确定度 评定扩展不确定度 不确定度精品报资料 告
例:用最小分度为0.01mm千分尺多次测量某圆柱体的直 径(zhíjìng) D,得到数据4.552mm、4.570mm、4.564mm、 4.578mm、4.574mm,写出测量结果。
精品资料
非正态分布置信水平与包含因子(yīnzǐ)对应表
分布类型 P=1 P=0.9973 P=0.99 P=0.95
均匀分布 3
1.73
1.71
1.65
测量不确定度的实际计算

测量不确定度的实际计算肖懿群王丽君一、直接测量、间接测量与合成不确定度直接测量法是指不必测量与被测量有函数关系的其它量,而能直接得到被测量值的测量方法(见《JJG1001-1991通用计量名词及定义》以下简称《1001》)。
也就是说由一组操作即可获得被测量值,而不论这组操作复杂程度如何,也不论为了消除或减小影响量的影响而作的其它补充测量或多次测量。
直接测量法的特点是被测量值可以直接从计量器具中得出。
例如用游标卡尺测量工件长度;用天平称量物体的质量等。
间接测量法是指通过测量与被测量有函数关系的其它量,而得到被测量值的测量方法(见《1001》)。
与直接测量法不同,有些量不能直接测量以得到测量结果,而必须先逐个测量与该量有关的量,然后再根据该量的定义公式计算出测量结果。
例如通过测量矩形的长与宽而确定矩形的面积;通过测量管道中孔板两侧的差压而计算出管道中液体的流量等。
设被测量Y根据下列函数由直接测量法测得的量X1、X2、…、Xi、…、Xm计算得出:Y=f(X1、X2、…、Xi、…、Xm) ①由①式可知,直接测量法实际上是间接测量法的特例,即:Y=X ②因此,研究了间接测量法测量不确定度的计算,也就研究了所有测量方法测量不确定度的计算。
所以当X1、X2、…、Xi、…、Xm的测量值x1、x2、…、xi、…、x m 彼此独立时,间接测量的合成标准不确定度uc由下式计算得出:其中:1.Si是用A类评定法评定的第i个可直接测量的量Xi的不确定度分量。
也就是通过n次直接测量xi所得到数据列xi1、xi2、…、xil、…、xin,用统计方法计算出的不确定度分量。
通常用该数据列均值的标准差表示,即:(1)对直接测量而言,i=1,则Si=S。
而对于间接测量而言,直接测量了几个X i 就有几个Si。
Si与Xi是对应的。
(2)既然Si是通过数据列计算出的,那么Si中就免不了包含有计量器具、人员、环境条件等误差源的影响,所以Si是多个误差源影响的综合反映。
测量不确定度的两种计算方法
6、测量结果报告
测量结果为5.3±0.1cm,其中 v=8,P=95%
4
测量不确定度的计算
A类不确定度的统计学原理:
本质:总体均值在一定置信概率下的置信区间。Fra bibliotek理论依据:
5
测量不确定度的计算
B类不确定度的计算:
定义:用不同于对观测列进行统计分析的方法,进行不确定度的估算。 B类不确定度的计算步骤:
➢确认影响测量结果的因素 ➢各影响因素和测量结果之间的关系
Y=a1x1+a2x2+a3x3
➢计算个影响因素的标准确定度 依据:以往测量数据、检定证书、校准证书、设备厂家出厂说明书 ➢合成出测量值的不确定度
6
测量不确定度的计算
灵敏系数p
Y=a1x1+a2x2+a3x3
Y=a1X1X2+a2X2X3+a3X3X1
不确定度计算的应用:
建立国家计量基准、计量标准及其国际比对; 标准物质、标准参考数据; 测量方法、检定规程、检定系统、校准规范等; 科学研究及工程领域的测量; 计量认证、计量确认、质量认证以及实验室认可; 测量仪器的校准和检定; 生产过程的质量保证以及产品的检验和测试; 贸易结算、医疗卫生、安全防护、环境监测及资源测量。
12
测量不确定度的计算
维氏硬度不确定度的计算 GB/T 4340.1
UE:最大允许误差下的不确定度 UCRM:标准硬度块的标准不确定度 UH:用标准硬度块检定的标准不确定度 UX:重复性的标准不确定度 Ums:压痕测量分辨率的标准不确定度
13
测量不确定度的计算
14
测量不确定度的计算
测量不确定度的计算方法

测量不确定度的计算方法哎呀,说到测量不确定度的计算方法,这事儿可真是让人头疼,但也挺有意思的。
就像你做菜时,盐放多了还是少了,那味道可就差远了。
不过,别担心,我今天就用大白话给你讲讲这事儿。
首先,你得知道,测量不确定度,就是说,你测出来的数,可能不是那么准,就像你用尺子量东西,尺子上的小刻度可能有点磨损,或者你眼睛有点近视,看不太清楚。
所以,测量不确定度,就是告诉你,你的测量结果可能在哪个范围内。
举个例子,比如说你今天去超市买了一袋大米,上面写着5公斤。
但是,你回家一称,发现只有4.9公斤。
这时候,你就得考虑不确定度了。
你可能会想,这袋大米的重量可能在4.9公斤到5.1公斤之间,因为你的秤可能有点误差,或者大米在运输过程中可能有点水分蒸发。
那么,怎么计算这个不确定度呢?首先,你得知道,不确定度有几种类型,比如A类不确定度和B类不确定度。
A类不确定度,就是通过测量数据的统计分析得到的,比如你多次测量大米的重量,然后计算平均值和标准差。
B类不确定度,就是你根据经验或者别的信息估计出来的,比如你根据秤的说明书,知道秤的误差范围。
现在,我们来详细说说怎么计算。
假设你用秤称了大米10次,每次的重量分别是4.91公斤,4.92公斤,4.93公斤,4.94公斤,4.95公斤,4.96公斤,4.97公斤,4.98公斤,4.99公斤,5.00公斤。
你把这些数加起来,然后除以10,得到平均值是4.95公斤。
接下来,你计算标准差。
标准差就是测量值和平均值差的平方的平均值的平方根。
你把每次测量值和平均值的差的平方加起来,然后除以9(因为这是样本标准差),最后开方,得到标准差是0.03公斤。
然后,你把标准差乘以一个叫做“t分布”的值,这个值取决于你的测量次数和置信水平。
假设你想要95%的置信水平,那么t值大概是2。
所以,你的A类不确定度就是0.03公斤乘以2,等于0.06公斤。
至于B类不确定度,假设你根据秤的说明书,知道秤的误差范围是±0.05公斤。
测量不确定度评定与表示中常见概率分布包含因子k值的计算
其方差为
于是
k=
2.4 梯形分布
对于梯形分布,若其上底和下底之比为β=,b和a分别为上底和下底的半宽。若设梯形的高为h,则由于梯形的面积S应为1,即
S=h×(a+b)=1
故梯形的高h为
h==
图4 梯形分布
于是其概率密度函数可以表示为:
y= p(x)=
其方差为
=
=
=
=
于是
k=
2.5 反正弦(U形)分布
2 常见概率分布包含因子k值的计算
2.1 正态(xx)分布
图1 正态分布
正态分布的概率密度函数p(x)为:
对上式作变换u=,得dx=σdu,故有
=
其中,
关于一般正态分布,以下几个概率是经常用到的。
P (μ-0.676σ≤x<μ+0.676σ)=0.50
P(μ-σ≤x<μ+σ)=0.6827
P (μ-1.645σ≤x<μ+1.645σ)=0.90
50%
68.27%
90%
95%
95.45%
99%
99.73%
包含因子k
0.676
1
1.645
1.960
2
2.576
3
2.2 矩形(均匀)分布
图2 矩形(均匀)分布
对于数学期望为µ,分布区间半宽为a的矩形分布的概率密度函数p(x)为:
y=p(x)=
其方差为
于是
k=
2.3 三角分布
图3 三角分布
对于分布区间半宽为a的三角分布,其概率密度函数p(x)为:
图5 反正弦(U形)分布
对于数学期望为µ,分布区间半宽为a的反正弦分布的概率密度函数p(x)为 结束语
置信度置信区间计算方法-置信区间公式表
置信度置信区间计算方法-置信区间公式表置信度置信区间计算方法置信区间公式表在统计学中,置信度和置信区间是非常重要的概念。
它们帮助我们在对总体参数进行估计时,给出一个可能包含真实参数值的范围,以及我们对这个范围的确定程度,也就是置信度。
首先,让我们来理解一下什么是置信度。
置信度通常用百分数表示,比如 95%或 99%。
它反映了我们在多次重复抽样和估计的过程中,得到的置信区间能够包含真实总体参数值的比例。
比如说,95%的置信度意味着如果我们进行 100 次抽样和估计,大约有 95 次得到的置信区间能够包含真实的总体参数值。
而置信区间则是一个可能包含总体参数真实值的范围。
这个范围的宽窄取决于我们所选择的置信度、样本数据的特征以及样本量的大小。
接下来,我们重点介绍几种常见的置信区间计算方法和相应的公式。
对于正态总体均值的置信区间计算,当总体方差已知时,我们使用的公式是:\\bar{X} \pm Z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\其中,\(\bar{X}\)是样本均值,\(Z_{\alpha/2}\)是标准正态分布的双侧分位数(对应于置信度\(1 \alpha\)),\(\sigma\)是总体标准差,\(n\)是样本量。
例如,如果我们有一个样本均值为 50,总体标准差为 10,样本量为 100,并且想要计算 95%置信度下的置信区间,那么首先找到\(Z_{\alpha/2}\),对于 95%的置信度,\(\alpha = 005\),\(\alpha/2 = 0025\),对应的\(Z_{\alpha/2} \approx 196\)。
然后代入公式计算:\50 \pm 196 \times \frac{10}{\sqrt{100}}= 50 \pm 196\得到的置信区间就是 4804, 5196。
当总体方差未知时,我们用样本方差\(s\)来代替总体方差\(\sigma\),此时使用的是\(t\)分布,公式变为:\\bar{X} \pm t_{\alpha/2}(n 1) \frac{s}{\sqrt{n}}\其中,\(t_{\alpha/2}(n 1)\)是自由度为\(n 1\)的\(t\)分布的双侧分位数。
测量结果的不确定度及其计算
讲座测量结果的不确定度及其计算周舜元(卫生部工业卫生实验所,北京100088)1 概述随着生产和科学技术的进步,对检测数据的准确可靠性提出了更高的要求。
过去通常用测量误差即测量结果与真值的差异来表示测量结果的准确可靠程度,但由于真值通常是未知的,所以误差常常也无法知道,只能用约定真值代替真值来求误差。
在实际工作中更多遇到的应该是测量的不准确度,这已逐渐成为人们的共识。
特别是由于国际贸易的发展,检测数据的质量高低需要在国际间得到评价和承认,由此开展的国际间的验证比对试验、实验室认可等活动,越来越重视对测量结果不确定度的分析和表达。
国家标准校准和检验实验室能力的通用要求!(GB/T15481-1995,等同采用ISO导则25)中就要求实验室的每个证书或报告,均应对估算的校准和测试结果的不确定度作出说明:ISO9001也规定,应保证所用设备的测量不确定度已知。
在1993年,由BIPM(国际计量局)、IEC(国际电工委员会)、IFCC(国际临床化学联合会、ISO(国际标准化组织)、IUPAC(国际理论与应用化学联合会)、IUPAP(国际理论与应用物理联合会)和OIML(国际法制计量组织)等7个国际机构共同发起,ISO公布了∀测量不确定度表示指南#,从而形成了共同的基础。
2 基本概念2.1 测量不确定度它是一个与测量结果相关的参数,用以表征可以合理赋予被测量值的分散性。
该参数可以用标准偏差或其给定倍数来表示,也可以用置信水平的区间半宽度来表示。
测量不确定度通常由其所有的不确定度分量构成,其中有些分量可以用测量结果的统计分析来加以评定,有些分量则基于统计分析以外的方法或信息来评定。
测量不确定度一般来源于随机性和模糊性,前者来自一些主客观条件不充分,后者归因于事物本身概念不明确。
在具体实践中,可能包括的来源如下:(1)对被测量的定义不完善;(2)实现被测量的定义的方法不理想;(3)被测量的样本(抽样)不能代表所定义的被测量;(4)环境条件的测量不完善,或对测量受环境条件影响的认识不周全;(5)人员对模拟仪器的读数有偏差;(6)测量仪器的分辨力和鉴别阈不够;(7)赋予计量标准的值和标准物质的值不准;(8)从外部来源取得,并用于数据计算的常数和其他参数不准;(9)与测量方法和测量程序相关联的近似性和假定性;(10)在表面上完全相同的条件下,被测量重复观测值的变化。
测试方法不确定度计算公式
测试方法不确定度计算公式在科学研究和工程实践中,测试方法的不确定度是一个非常重要的概念。
不确定度可以理解为测量结果的不确定程度,它反映了测量结果的可靠性和精确度。
因此,正确计算测试方法的不确定度对于保证实验结果的准确性和可靠性至关重要。
测试方法的不确定度计算涉及到许多因素,包括仪器的精度、环境条件、人为误差等。
为了正确计算测试方法的不确定度,我们需要使用一些数学公式和统计方法。
本文将介绍一些常用的测试方法不确定度计算公式,并对其进行详细的解释和应用。
首先,我们需要了解一些基本的统计概念。
在统计学中,方差是衡量一组数据离散程度的指标,它表示了数据点与数据集平均值之间的差异程度。
方差的计算公式如下:\[ \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i \bar{x})^2 \]其中,\( \sigma^2 \) 表示方差,\( N \) 表示数据点的个数,\( x_i \) 表示第 \( i \)个数据点,\( \bar{x} \) 表示数据集的平均值。
在实际的测试方法中,我们通常无法获取全部数据点的数值,而是通过多次重复测量得到一组数据。
因此,我们需要使用样本方差来估计总体方差。
样本方差的计算公式如下:\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i \bar{x})^2 \]其中,\( s^2 \) 表示样本方差,\( n \) 表示样本数据点的个数,\( x_i \) 表示第\( i \) 个样本数据点,\( \bar{x} \) 表示样本数据集的平均值。
在计算测试方法的不确定度时,我们通常使用标准偏差来表示数据的离散程度。
标准偏差是方差的平方根,它的计算公式如下:\[ s = \sqrt{s^2} \]现在,我们来看一些常用的测试方法不确定度计算公式。
首先是直接测量法的不确定度计算公式。
直接测量法是指通过一次测量得到测试结果的方法,其不确定度计算公式如下:\[ U = k \cdot s \]其中,\( U \) 表示不确定度,\( k \) 表示覆盖因子,通常取 2,表示置信水平为95%,\( s \) 表示样本标准偏差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N
N
直 角 分 布
( p x) =
{ {
1
a+x , \ x \Sa 2 a2 0, \x\ > a
a 3
2 N a 3
pa =
{
e , 0 e>a a S 1, aS e
I=
3 3 pa = (1 -!) 2 2 N N
双 三 角 分 布
( p x) =
\x\ , \ x \Sa a2 0, \x\ > a
-1 -x
+
该对象 x 与概率分布 p ( x) 及置信水平 p ! = 1 -! 所 对应的置信因子为 (3) k = e /" 对于 B 类不确定度, 其标准不确定度为 u 时则有 (4) k= e/u 三、 常见分布所对应的置信因子 鉴于上述原因, 有必要给出常见分布在不同置
参考文献
[1]李慎安 . 测量不确定度的定义及其有关问题 . 计量技术, 1999.6 [2]林奎明 . B 类不确定度计算方法的探讨 . 计量技术, 2000.3 [3]费业泰 . 误差理论与数据处理 (第三版) . 机械工业出版社, 1997 [4]中山大学数学力学系 . 概率论及数理统计 . 人民教育出版社, 1980
2 " = e
信水平下所对应的置信因子函数 k = k (p 。本文 !) 推导了均匀分布等 10 种常见分布的置信水平、 置信 因子及数学期望、 标准差的值或其计算公式, 为简便 起见, 在此将不同概率分布以式 (1) (2) 、 (3) 、 计算所 得结果以列表方式给出结论, 而略去所有具体计算
一、 引言 文 [I] 讨论了测量不确定度的定义, 给出了 “测 量不确定度为与测量结果一起, 用以表征合理赋予 被测量之值的分散性” 这一较为准确的定义。无论 是 A 类不确定度还是 B 类不确定度, 在进行讨论 时, 往往都要涉及相应置信水平。如当要求表明真 值所处的范围时, 有必要引入测量结果, 此时应给出
本文读者也读过(10条) 1. 朱爱民.张建志.贾克军 测量不确定度的实际应用[期刊论文]-计量技术2005(5) 2. 李树波 测量不确定度计算中的一点注意事项[期刊论文]-计量技术2000(10) 3. 王维龙 实际计量测试中不确定度评定的一些探讨[期刊论文]-计量技术2001(7) 4. 李慎安 JJF1059-1999《测量不确定度评定与表示》讨论之三十二关于不确定度合成中较小分量的忽略问题[期 刊论文]-工业计量2011,21(1) 5. 余学锋.张红清.李培 二维随机变量扩展不确定度置信因子的确定与分析[期刊论文]-计量技术2006(7) 6. 李树波 A类不确定度评定时几点注意事项[期刊论文]-计量技术2001,1(3) 7. 基于Taylor展开式的测量系统不确定度分析[期刊论文]-计量学报2005,26(4) 8. 王正武.张瑞平 最短置信区间的近似计算[期刊论文]-高等数学研究2006,9(2) 9. 李庆忠.李宇红 计量不确定度评估要点[期刊论文]-计量技术2003(1) 10. 王立吉.Wang Liji 测量误差与不确定度表述中的若干问题[期刊论文]-计量学报1998,19(2)
0
a 2 N
e2 , 2 0S e < a a pa = 1, aS e
{
2 1 -!) I = N2 p ! = N(
反 正 弦 分 布
( p x) =
{
2 2 # Na - x 0, \ x \Za
, \x\ < a
0
a 2 N
{
1
p != e 2 , arcsin 0 e<a a S # 1, aS e
2sin I =N
#p ! 2
( p x, 1) = t 分 布
N
(1 + x 1 \x\ < +
2
1 +1 ) ( ! 2 1 ( ) #1! 2
1 +1 )2
0 1 >1
1 -2 N 1 >2
pa = 2
f x, 1) cx I(
0
t !
( 1) I= t ! (查表)
椭 圆 分 布
( p x) = 2 2 2 , 2 Na - x \ x \ S a #a 0, \x\ > a
耐电压仪输出高压的测量不确定度
王 英
(江苏省电子产品监督检验所, 无锡市 214073)
摘 要 本文主要论述了耐电压仪输出高压误差的表达、 检定方法及其测量不确定度的分析与评定。 耐电压仪 高压 检定方法 不确定度
关键词
耐电压仪是指对各种电器装置、 绝缘材料和绝 缘结构的耐电压能力进行测试的仪器。该仪器能调 整输出需要的交流 (或直流) 试验电压和设定击穿 (保护) 电流。在试验中, 样品在要求的试验电压作 用之下达到规定时间时, 耐电压测试仪自动或被动 切断试验电压, 一旦出现击穿, 电流超过设定的击穿 (保护) 电流, 能够自动切断输出电压并同时报警, 以 确定样品能否承受规定的绝缘强度试验。本文将对 该仪器输出高压的测量不确定度的评定进行研讨。 一、 测量方法 本文 以 耐 压 仪 TOS8750 为 例, 依据检定规程 《耐电压测试仪》 , 采用直接测量法检定, JJG795 - 92 按图 1 连接测量电路。对其 5kV 输出电压的检定进 行讨论。 二、 数学模型 设被检耐压仪的输出电压为 Vx , 标准表上实际 读数为 V , 且由技术说明书及其有关资料可得, 对 于数字高压表 ( JSGB - 50) 和耐压仪 ( TOS8750) , 在标 准条件下, 温度、 湿度、 磁场和电源变化等带来的影 响可忽略。 则测量结果误差为:
1 过程。表 中 # - ( 为# ( x) 的 反 函 数, ($)= x) !
"
-
+
( x) x2 p dx -
[ "
+ -
"
-e
( p x) d x (1)
( x) xp dx
]
2பைடு நூலகம்
(2)
( , 且与正态分布及 I 分布对应 "0 x" e d x $ > 0) 的置信因子可查相应分布表 (如文 [3] ) 。
{
0
a 2
pa = e 4[ N a2 - e2 a2 2 " a2 e , + 2 arcsin a ] 0S e < a 1, aS e
2a ( "p !Na - e2 I = 2arcsin e ) , a 0S e < a 2, aS e
偏 心 分 布
引用本文格式:孙川 常见分布的测量不确定度置信因子的计算[期刊论文]-计量技术 2002(7)
{
a - IxI , I x I"a a2 0, IxI > a
0
a 6 !
P O=
{
(2 a - e) e , 0" e < a a2 I, a" e
( 6 I-! I =! O)
・ 46 ・
计量技术 2002 NO 7
误差与数据处理
分 布 图形 分布密度函数 ( p x) 数学 期望 标准差 置信水平 p ! = 1 -! = p{\ x \ S e} I = ( p x) = 1 , \x\ < 6 a+ 6 a - \x\ , 6S \ x \ S a a2 - 62 0, a > \ x \ 置信因子 I = e /"
I=
!
-I ( c) ) @ (p @ O ( ) c I - c$ ( c) @
均 匀 分 布
( p x) =
{
I , I x I" O 2a 0, I x I > a
0
O 3 !
P O=
{
e , 0" e < a a I, a" e
I =! 3p O ( =! 3 I -O)
三 角 分 布
( p x) =
梯 形 分 布
{
0
N
p != 2e , 0 e< 6 a+ 6 S 1 2 2 (a + 6 ) 2 ( a - e) 6 , 1- 2 2 6S e < a a -6 1, aS e
{
6 a + 6 (1 - !) , a2 + 62 2 0 S e < 6 26 2 a +6 [ a - N ( a2 - 62) !] , 6 < e
{
1 $
1 2 $
- e $ p !=1- e
(1 - p = -$ln I = -$ln ! !)
计量技术 2002 NO 7
・ 47 ・
误差与数据处理
二、 置信因子与概率分布及置信水平的关系 设已知讨论对象 x 服从分布密度函数为 p ( x) 则置信水平与方 的概率分布, 置信区间的半宽为 e , 差分别为 {\ x \ ! e }= p ! = 1 -! = p
0
6N
e ( ) p @ O = 2 6N = 2 !2 T
I I = @ -(
#
e 6 N exp 0
-
x dx 2
2
I p) 2 O
(查表)
双 截 尾 正 态 分 布
{
0
6N
IxI > a
!
( c) p = I - c$ ( c) O @
{
e ( ) @ 6N , ( c) 0" e < a @ I, a" e
标准差 置信水平 p O = I -O = p{I x I " e} 置信因子 I = e /6
根据经验或 I 亦不同。特别是对于 B 类不确定度,
