六年级奥数综合题型训练(二)
小学六年级数学思维能力(奥数)《抽屉原理》训练题(二)

小学六年级数学思维能力(奥数)《抽屉原理》训练题(二)1、礼堂里有253人开会,这253人中至少有多少人的属相相同?2、一兴趣小组有10名学生,他们都订阅甲、乙两种杂志中的一种或两种。
问:至少有多少名学生订阅的杂志种类相同?3、把130件玩具分给幼儿园小朋友,如果不管怎样分,都至少有一位小朋友分得4件或4件以上的玩具,那么这个幼儿园最多有多少个小朋友?5、体育组有足球、篮球和排球,上体育课前,老师让一班的41名同学往操场拿球,每人最多拿两个。
问:至少有几名同学拿球的情况完全一样?5、口袋里放有足够多的红、白两种颜色的球,有若干人轮流从袋中取球,每人取三个球。
要保证有4人取出的球的颜色完全相同,至少应有多少人取球?6、10个足球队之间共赛了11场,赛得最多的球队至少赛了几场?7、抽屉里有4枝红铅笔和3枝蓝铅笔,如果闭着眼睛摸,一次必须拿多少枝才能才能保证至少有1枝蓝色铅笔?8、盒子里有5个红球,6个蓝球和7个白球,一次拿出多少个球才能保证至少有1个白球?9、有红、黄、蓝、白四色球各10个,一次摸出5个球,至少有多少个球的颜色是相同的?10、有红、黄、蓝3种颜色的小珠子各4颗混放在口袋里,为了保证一次能取出2颗颜色相同的珠子,一次至少取多少颗?11、一只袋子里有许多规格相同但颜色不同的玻璃球,颜色有红黄绿三种,至少取出多少个球才能保证有2个球的颜色相同?12、某班学生去买语文书、数学书和英语书。
买书的情况是:有买一本的,有买两本的,有买三本的,至少要去多少人才能保证一定有两位同学买到相同的书?(每种书最多买一本)13、某班学生去买数学书、语文书、美术书、自然书,买书的情况是:有买一本的、两本的、三本的和四本的。
至少去多少人才能保证一定有两人买的书是相同的。
(每种书最多买一本)14、学校图书室有历史、文艺、科普三种图书。
每个学生从中任意借两本,至少要多少个同学才能保证一定有两人所借的图书属于同一种?15、学校买来红、黄、蓝、绿四种颜色的球,每个学生最多只能借2个球,至少要有多少个学生借球,才能保证其中必然有两个学生所借的球一样?16、某班学生去买书,A、B、C、D四种,每人可买一本,二本,三本或四本.至少有( )位同学才能保证一定有两位同学买到相同的书?(每种书最多买一本)。
六年级下册奥数专题训练-钟表问题(二)

六年级下册奥数专题训练-钟表问题(二)【例题分析】例1. 早晨晓龙看到镜中的表指针指在6时20分,他赶快起床出去跑步,可跑回来妈妈告诉他刚到6点20分,问晓龙起床时实际是什么时刻?分析与解:造成晓龙与妈妈看到的钟面为同一时刻的原因在于:晓龙看到的是反射在镜面上的钟面,时针、分针经过镜面的反射其位置改变了。
反射前后钟面左右位置互换,也就是说表盘右边的刻度其指针经反射后变到左边了,相反,表盘左边的刻度其指针经过镜面反射后变到右边了。
如下图例2. 不难看出:这一时刻时针与分针应分别在8、9之间和1、2之间。
设这一时刻的时针位置在8点过x 格,则分针应走格。
那么时针经过的时间为,分针经过的时间为,因为经过的时间相同,则有下面的方程: 解:设该时刻时针的位置在8点过x 格(分钟)答:当时针与分针的位置与5的距离相等时为8时分。
()2-x x ÷160()215-÷x x x x ÷=-÷=160215213()……602139313⨯=9313例3. 小明晚上9点将手表对准,可早晨8点到校时却迟到10分钟,那么,小明的手表每小时慢几分钟?分析与解:这实际是一个分数应用题或者可以看作是一个比例应用题,从晚上9点至第二天早晨8点,小明的手表时针共转动11个格,而实际准确时间为11小时+10分钟小时。
即每小时少转格,所以小明的手表每小时比实际慢:(分钟)答:小明的手表每小时慢分钟。
例4. 有甲、乙两只手表,甲表每小时比乙表快2分钟,乙表每小时比标准时间慢2分钟,请问甲表是否准确?分析与解:通过“乙表比标准时间慢2分钟”可知:标准时间1小时走60分,而乙表只走60-2=58分,乙表的速度是标准时间的。
用,以“标准时间”为单位“1” 又通过“甲表比乙表快2分钟”可知:乙表走1小时(60分),而甲表却走了60+2=62分钟,甲表的速度是乙表的。
用,以“乙表速度”为单位“1” 所以甲表是标准时间的,比标准时间慢,每小时慢:(秒)例5. 某人下午6点多外出,看手表上两指针的夹角为,下午7点前回家时发现两指针夹角=11161111166667÷=167601676067⨯=606729306026058602930-==31306026062603130+==29303130899900⨯=360018999004⨯-=()110仍为设他 了。
六年级奥数训练第2讲比例解应用题

六年级奥数训练第2讲比例解应用题内容概述涉及两个或多个量之闻比例的应用题.熟练掌握比的转化和运算;对条件较多的应用题,学会通过列表的方法逐步分析求解;了解正比例与反比例的概念,掌握行程问题和工程问题中的正反比例关系.典型问题兴趣篇1.圆珠笔和铅笔的价格比是4:3,20支圆珠笔和21支铅笔共用71.5元.问:圆珠笔的单价是每支多少元?2.一段路程分为上坡和下坡两段,这两段的长度之比是4:3.已知阿奇在上坡时每小时走3千米,下坡时每小时走4.5千米.如果阿奇走完全程用了半小时.请问:这段路程一共有多少千米?3.加工一个零件,甲要2分钟,乙要3分钟,丙要4分钟,现有1170个零件,甲、乙、丙三人各加工几个零件,才能使得他们同时完成任务?4.有两块重量相同的铜锌合金.第一块合金中铜与锌的重量比是2:5,第二块合金中铜与锌的重量比是1:3.现在把这两块合金合铸成一块大的.求合铸所成的合金中铜与锌的重量之比.5.已知甲、乙、丙三个班总人数的比为3:4:2,甲班男、女生的比为5:4,丙班男、女生的比为2:1,而且三个班所有男生和所有女生的比为13:14.请问: (1)乙班男、女生人数的比是多少?(2)如果甲班男生比乙班女生少12人,那么甲、乙、丙三个班各有多少人?6.甲、乙两包糖的重量比是5:3,如果从甲包取出10克放入乙包后,甲、乙两包糖的重量比变为7:5.请问:这两包糖重量的总和是多少克?7.小明从甲地到乙地,去时每小时走5千米,回来时每小时走7千米,来回共用了4小时.问:小明去时用了多长时间?8.冬冬从家去学校,平时总是7:50到校,有一天他起晚了,结果晚出发了10分钟,为了不至于迟到,他将速度提高了五分之一,跑步前往学校,最后在7:55到校,请问:冬冬这天是几点出发的?9.一项工程,由若干台机器在规定时间内完成.如果增加2台机器,只需用规定时间的87就可完成;如果减少2台机器,就要推迟32小时才能完成.请问:(1)在规定时间内完成需几台机器?(2)由1台机器去完成这工程,需要多少小时?10.康师傅加工一批零件,加工720个之后,他的工作效率提高了20%,结果提前4天完成任务;如果康师傅从一开始就把工作效率提高12.5%,那么也可以提前4天完成任务.这批零件共有多少个?拓展篇1.学校组织体检,收费标准如下:老师每人3元,女生每人2元,男生每人1元,已知老师和女生的人数比为2:9,女生和男生的人数比为3:7,共收体检费945元.那么老师、女生和男生各有多少人?2.徐福记的巧克力糖每6块包成一小袋,水果糖每15块包成一大袋.现有巧克力糖和水果糖各若干袋,而且巧克力糖比水果糖多30袋.如果巧克力糖的总块数与水果糖的总块数之比为7:10,那么它们各有多少块?3.甲、乙、丙三人合买一台电视机,甲付的钱数等于乙付的钱数的2倍,也等于丙付的钱数的3倍.已知甲比丙多付了680元,请问:(1)甲、乙、丙三人所付的钱数之比是多少? (2)这台电视机售价多少钱?4.一把小刀售价3元,如果小明买了这把小刀,那么小明与小强剩余的钱数之比是2:5;如果小强买了这把小刀,那么两人剩余的钱数之比变为8:13.小明原来有多少钱?5.两根粗细相同、材料相同的蜡烛,长度比为29:26,燃烧50分钟后,长蜡烛与短蜡烛的长度比为11:9,那么较长的那根还能燃烧多少分钟?6.某俱乐部男、女会员的人数比是3:2,分为甲、乙、丙三组.已知甲、乙、丙三组的人数比是10:8:7,甲组中男、女会员的人数比是3:1,乙组中男、女会员的人数比是5:3.求丙组中男、女会员的人数比.7.某次数学竞赛设一、二、三等奖,已知:①甲、乙两校获一等奖的人数比为1: 2,但它们一等奖人数占各自获奖总人数的百分数之比为2:5;②甲、乙两校获二等奖人数占两校获奖人数总和的25%,其中乙校是甲校的3.5倍;③甲校三等奖获奖人数占该校获奖人数的80%.请问:乙校获三等奖人数占该校获奖人数的百分比是多少?8.如果单独完成某项工作,甲需24天,乙需36天,丙需48天,现在甲先做,乙后做,最后由丙完成.甲、乙工作的天数比为1:2,乙、丙工作的天数比为3:5.问:完成这项工作一共用了多少天?9.已知猫跑5步的路程与狗跑3步的路程相同,猫跑7步的路程与兔跑5步的路程相同.而猫跑3步的时间与狗跑5步的时间相同,猫跑5步的时间与兔跑7步的时间相同,求猫、狗和兔的速度之比.10.星期天早晨,哥哥和弟弟都要到奶奶家去,弟弟先走5分钟,哥哥出发25分钟后追上了弟弟,如果哥哥每分钟多走5米,出发20分钟后就可以追上弟弟.问:弟弟每分钟走多少米?11.一支解放军部队从驻地乘车赶往某地抗洪抢险,如果行驶1个小时后,将车速提高五分之一,就可比预定时间提前20分钟赶到;如果先按原速度行驶72千米,再将车速提高三分之一,就可比预定时间提前30分钟赶到,问:这支解放军部队一共需要行多少千米?12.一项工作由甲、乙两人合作,恰可在规定时间内完成,如果甲效5即可完成;如果乙效率降低率提高三分之一,则只需用规定时间的6四分之一,那么就要推迟75分钟才能完成,请问:规定时间是多少小时?超越篇1.甲、乙两人分别同时从A、B两地开始,修建一条连接A、B两地的公路,并按修路的距离分配240万元工程款.如果按原计划,甲应分得100万元.而在实际施工的时候,乙每天比原计划多修l千米,结果乙实际分得了150万元,那么乙队实际施工时,每天修多少千米?2.孙悟空有仙桃、机器猫有甜饼、米老鼠有泡泡糖,他们按下面比例互换:仙桃与甜饼为3:5,仙桃与泡泡糖为3:8,甜饼与泡泡糖为5:8.现在孙悟空共拿出39个仙桃分别与其他两位互换,机器猫共拿出甜饼90个与其他两位互换,米老鼠共拿出88个泡泡糖与其他两位互换.请问:米老鼠与孙悟空和机器猫各交换泡泡糖多少个?3.有两包糖,每包糖内装有奶糖、水果糖和巧克力糖.已知:2;②在第一包糖中,奶糖占25%,①第一包糖的粒数是第二包糖的3在第二包糖中,水果糖占50%;③巧克力糖在第一包糖中所占的百分比是在第二包糖中所占的百分比的两倍,当两包糖混合在一起时,巧克力糖占28%.求第一包与第二包中水果糖占所有糖的百分比.4.某工地用三种型号的卡车运送土方.已知甲、乙、丙三种卡车载重量之比为10:7:6,速度比为3:4:5,运送土方的路程之比为15:14:14,三种车的辆数之比为10:5:7.工程开始时,乙、丙两种车全部投入运输,但甲种车只有一半投入,直到10天后,另一半甲种车才投人工作,又干了15天才完成任务.求甲种车完成的工作量与总工作量之比.5.在一个490米长的圆形跑道上,甲、乙两人从相距50米的A、B 两地,相背出发,相遇后,乙返回,甲方向不变,继续前进,甲的速度提高五分之一,乙的速度提高四分之一.当乙回到B地时,甲刚好回到A地,此时他们都按现有速度与方向前进.请问:当甲再次追上乙时,甲(从开始出发算起)一共走了多少米?6.将A、B两种细菌分别放在两个容器里.在光线亮时A细菌需12小时分裂完毕,B细菌需15小时分裂完毕;在光线暗时,A细菌的分裂速度要下降40%,B细菌的分裂速度反而提高10%.现在两种细菌同时开始分裂并同时分裂完毕,试问:在分裂过程中,光线暗的时间有多少小时?7.某大学本科共有四个年级,男生总人数和女生总人数的比为7:5.又已知:①一年级男生和二年级女生的比是3:2,二年级男生和一年级女生的比也是3:2;②三年级和四年级的人数相等,且三年级男生比四年级女生多100人;③三、四年级男生与女生的比为6:5;④二年级的男生占学生总数的24%.请问:一年级男生和女生的人数分别是多少?8.如图2-1所示,A、B、C、D、E、F是六个齿轮.其中A和B相互咬合,B和C相互咬合,D和E、E和F也都相互咬合;而C和D是同轴的两个齿轮,也就是说C和D转动的圈数始终相同.当A转了7圈时,B恰好转了5圈;当E转了8圈时,F恰好转了9圈;当C转了5圈时,B和E恰好共转了28圈.请问:(1)如果A、E转的总圈数总是和B、F转的总圈数相同,那么当A、F共转了100圈时,D转了多少圈?(注:图片只是示意图,并不代表实际齿数)(2)如果A、E的总齿数和B、F的总齿数相等,D的齿数是C的齿数的2倍,那么当A转了210圈时,D和F分别转了多少圈?。
六年级奥数专题 数论综合二(学生版)

学科培优数学“数论综合二”学生姓名授课日期教师姓名授课时长知识定位在整个数学领域,数论被当之无愧的誉为“数学皇后”。
翻开任何一本数学辅导书,数论的题型都占据了显著的位置。
在小学各类数学竞赛和小升初考试中,我们系统研究发现,直接运用数论知识解题的题目分值大概占据整张试卷总分的30%左右,而在竞赛的决赛试题和小升初一类中学的分班测试题中,这一分值比例还将更高。
知识梳理涉及知识点多、解题过程比较复杂的整数综合题,以及基本依靠数论手段求解的其他类型问题.例题精讲【试题来源】【题目】一台计算器大部分按键失灵,只有数字“7”和“0”以及加法键“+”尚能使用,因此可以输入77,707这样只含数字7和0的数,并且进行加法运算.为了显示出222222,最少要按“7”键多少次?【试题来源】【题目】有一批图书总数在1000本以内,若按24本书包成一捆,则最后一捆差2本;若按28本书包成一捆,最后一捆还是差2本书;若按32本包一捆,则最后一捆是30本.那么这批图书共有本.【试题来源】【题目】一个五位数恰好等于它各位数字和的2007倍,则这个五位数是 .【试题来源】【题目】在纸上写着一列自然数1,2,…,98,99.一次操作是指将这列数中最前面的三个数划去,然后把这三个数的和写在数列的最后面.例如一次操作后得到4,5,…,98,99,6;而两次操作后得到7,8,…,98,99,6,15.这样不断进行下去,最后将只剩下一个数,则最后剩下的数是 .【试题来源】【题目】有两种规格的9箱钢珠,每箱300个,甲种钢珠每个10克,乙种钢珠每个11克,将这9箱钢珠编为1~9号,然后依次从1~9号箱中取出20,21,22,23,24,25,26,27,28,个钢珠,这些钢珠共重5555克。
问:哪几箱是甲种钢珠?【试题来源】【题目】把除1外的所有奇数依次按一项,二项,三项,四项循环的方式进行分组:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,3l,33),(35,37,39,41),(43),…….那么,第1994个括号内的各数之和是多少?【试题来源】【题目】2001个球平均分给若干人,恰好分完。
六年级奥数综合练习二

六年级奥数综合练习二1、 若a ,b 是非0的自然数,并且a <b ,则a+b b的值 。
A. 0和1之间的数B. 1和2之间的数C. 可以是2D. 可以大于22、满足38<n18<1112的自然数n 有 个。
3、求三个分数2012201220132013,2013201320142014,2014201420152015中值最大的是 。
4、若p ,q 是非0的自然数,并且p <q ,则四个式子:pq ,q−p p,q+p p,q+p q中,值在1和2之间的是 。
5、计算:1)11×2×3+12×3×4+13×4×5+…+18×9×10 2)2016×334×1.3+3÷223(1+3+5+7+9)×20+46、计算:52+15−1+72+17−1+92+19−1+…+992+199−17、计算:(1+0.2%+2%+20%)×(0.2%+2%+20%+200%)-(1+0.2%+2%+20%+200%)×(0.2%+2%+20%)8、计算:11−1311×12×13+12−1412×13×14+13−1513×14×15+⋯+12014−1201612014×12015×120169、112016+12015+12014+12013+12012+12011的整数部分是_______。
10、已知a=2015×2017,b=2014×2018,c=2016×2016,将a 、b 、c 从大到小排列。
11、A 、B 、C 、D 四个数的平均数是150,A 与B 的平均数是200,B 、C 、D 的平均数是160,求B.12、若P=2015201520162016−2014201420152015,Q= 2014201420152015−2013201320142014,R= 12015−12016,比较P 、Q 、R 的大小。
六年级奥数专题 行程综合二(学生版)

学科培优 数学 “行程综合二” 学生姓名授课日期 教师姓名授课时长 知识定位 通常我们所接触的行程问题可以称作为“参考系速度为0”的行程问题,例如当我们研究甲乙两人在一段公路上行走相遇时,这里的参考系便是公路,而公路本身是没有速度的,所以我们只需要考虑人本身的速度即可。
但是在流水行船问题中,我们的参考系将不再是速度为0的参考系,因为水本身也是在流动的,所以这里我们必须考虑水流速度对船只速度的影响.重难点在于1.流水行船中的相遇与追击2.火车问题知识梳理知识点:行程综合(二)流水问题:顺水速度=船速+水速, 逆水速度=船速-水速. ( 其中为船在静水中的速度,为水流的速度)由上可得:船速=(顺水速度+逆水速度)÷2;水速=(顺水速度-逆水速度)÷2.流水行船中的相遇与追击:水船顺V V V +=水船逆V V V -=船V 水V(1)两只船在河流中相遇问题.当甲、乙两船(甲在上游、乙在下游)在江河里相向开出,它们单位时间靠拢的路程等于甲、乙两船速度和.这是因为:甲船顺水速度+乙船逆水速度=(甲船速+水速)+(乙船速-水速)=甲船船速+乙船船速.这就是说,两船在水中的相遇问题与静水中的及两车在陆地上的相遇问题一样,与水速没有关系.(2)同样道理,如果两只船,同向运动,一只船追上另一只船所用的时间,也只与路程差和船速有关,与水速无关.这是因为:甲船顺水速度-乙船顺水速度=(甲船速+水速)-(乙船速+水速)=甲船速-乙船速.也有:甲船逆水速度-乙船逆水速度=(甲船速-水速)-(乙船速-水速)=甲船速-乙船速.这说明水中追及问题与在静水中追及问题一样.由上述讨论知,解流水行船问题,更多地是把它转化为已学过的相遇和追及问题来解答火车问题⑴火车过桥时间是指从车头上桥起到车尾离桥所用的时间,因此火车的路程是桥长与车身长度之和.⑵火车与人错身时,忽略人本身的长度,两者路程和为火车本身长度;火车与火车错身时,两者路程和则为两车身长度之和.⑶火车与火车上的人错身时,只要认为人具备所在火车的速度,而忽略本身的长度,那么他所看到的错车的相应路程仍只是对面火车的长度.对于火车过桥、火车和人相遇、火车追及人、以及火车和火车之间的相遇、追及等等这几种类型的题目,在分析题目的时候一定得结合着图来进行.例题精讲【试题来源】【题目】两港相距 120 千米,甲船往返两港需 60 小时,逆流航行比顺流航行多用了 20 小时.乙船的静水速度是甲船的静水速度的 3 倍,那么乙船往返两港需要多少小时?【试题来源】【题目】一艘轮船顺流航行 120 千米,逆流航行 80 千米共用 16 时;顺流航行 60 千米,逆流航行 120 千米也用 16 时。
六年级奥数 几何;第5讲;几何综合题_二_;学生版
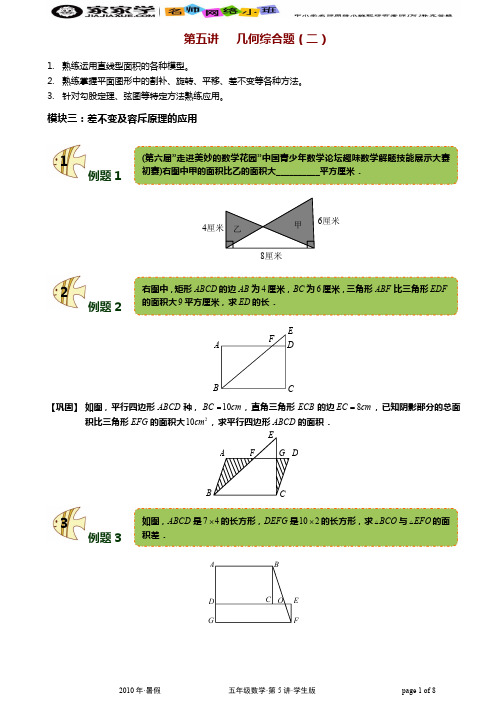
1. 熟练运用直线型面积的各种模型。 2. 熟练掌握平面图形中的割补、旋转、平移、差不变等各种方法。 3. 针对勾股定理、弦图等特定方法熟练应用。
模块三:差不变及容斥原理的应用
1
例题 1
(第六届”走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛 初赛)右图中甲的面积比乙的面积大__________平方厘米.
4cm
1cm
【巩固】 如图,阴影部分四边形的外接图形是边长为12 厘米的正方形,则阴影部分四边形的面积是多少平方 厘米?
2010 年·暑假
五年级数学·第 5 讲·学生版
page 2 of 8
4cm
2cm
板块四、弦图及勾股定理
8
例题 8
从一块正方形的玻璃板上锯下宽为 0.5 米的一个长方形玻璃条后,剩下的长方形的 面积为 5 平方米,请问锯下的长方形玻璃条的面积等于多少?
方厘米,FB 为 8 厘米.那么,正方形 ABCD 的面积是
平方厘米.
例题 11
B 8F A
48
C
D
E
如图,一个正方形被分成 4 个小长方形,它们的面积分别是 1 平方米、 1 平方
10
5
1
米、 3 平方米和 2 平方米.已知图中的阴影部分是正方形,那么它的面积是多
例题 12
10
5
少平方米?
1
如图所示,直角三角形 PQR 的直角边分别为 5 厘米和 9 厘米.问:图中 3 个正方
A
F
GD
3
例题 3
B
C
如图,ABCD 是 7 × 4 的长方形,DEFG 是10 × 2 的长方形,求 +BCO 与 +EFO 的面 积差.
2019年春小学六年级奥数奖学金班数学综合检测(2)

2019年春小学六年级奥数奖学金班数学综合检测(二)学校姓名一、计算下列各题(1)256255128127646332311615874321(2)17591915017167995二、填空题1、有两堆河沙,第一堆比第二堆重60%,那么第二堆比第一堆轻%.2、10条直线最多有个交点.3、桌面上有10元、5元、1元的纸币12张,共72元,三种纸币张数的比为.4、有200个连续自然数(按照从小到大的顺序排列)的和是23900,那么这200个数中从小到大第108个数是.5、在189至495的整数中,数字1出现了次.6、在天平秤的一边放上砝码,要秤出1至2019之间所有整数克重量,至少要个砝码.7、有甲、乙、丙三种盐水,按照甲与乙数量比为1:2混合,得到浓度为13%的盐水,按照甲与:1混合得到浓度为14%的盐水,如果甲、乙、丙数量的比为3:1:1混合成的盐乙的数量比为2水浓度为10.2%,那么丙的浓度为.8、1999、2009、2019这三个数减去同一个四位数时,得到的差刚好是三个质数,这个四位数是.9、一个长方形,如果长减少5厘米,宽减少2厘米,面积就减少66平方厘米,这时剩下部分恰好是一个正方形,原来长方形的面积是.10、已知下图是边长为10cm和8cm的两个正方形,则MN的长是cm .11、若,23y x 则yx 25.075.02019.12、3个非0的不同数字可以组成一些不重复的三位数,所有这些三位数之和如果是3774,则其中最大三位数最大可以是,最小可以是.13、一位便衣警察刚好坐上了公共汽车,忽然发现一个小偷向相反的方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,比汽车速度慢54,则追上小偷需要秒.三、解答题1、某人以每小时3千米的速度沿着环城汽车道旁前进,每7分钟有一辆汽车从他后面追上他,每5分钟又与迎面开来的汽车相遇一次。
汽车间隔时间相同,速度也相同。
汽车每小时行多少千米?2、有甲、乙两项工程,现在分别由A,B 两个施工队完成.在晴天,A 施工队完成工程要8天,B施工队完成工程要12天。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数综合题型训练(二)
题型二解题技巧
一、画图解应用题技巧
【例1】甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘。
到现在为止,甲已经赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘。
问:小强已经赛了几盘?分别与谁赛过?
【例2】一群人在两片草地上割草,大的一片草地比小的正好大1倍。
他们先全体在大的一片草地干了半天,下午留下一半人在大草地上继续干,收工时正好把草割完;另一半人到小草地上干,收工时还余下一块地,这块地再用1人经1天也可以割完。
问:这群干活的人共有多少位?
【例3】把一笔22500元的科研奖金发给一、二、三等奖获奖者,每个一等奖的奖金是每个二等奖奖金的2倍多500元,每个二等奖的奖金是每个三等奖的2倍,一、二、三等奖的获奖者各是3人,那么每个一等奖的奖金是多少元呢?【例4】两名运动员在长为50米的游泳池里来回游泳。
甲运动员的速度是1米/秒,乙运动员的速度是0.5米/秒,他们同时分别在游泳池的两端出发,来回共游了5分钟,如果不计转向时间,那么这段时间里共相遇了几次?
练习
1.三年级一班有42人,全班都订了杂志。
订“少年文艺”的有38人,订“少年科学画报”的有24人。
两种杂志都订的有多少人?
2.有三堆围棋子,每堆棋子数相等。
第一堆中的黑子与第二堆中的白子一样多,第三堆中的黑子占全部黑子的
2
5,那么三堆棋子中,白子占全部棋子的几分之几?
3.甲、乙两辆汽车同时从东、西两城相向而行,甲车每小时行42千米,乙车每小时行35千米,经过若干小时后,两车在离中点14千米处相遇。
两城之间的路程是多少千米?
4.甲、乙两车同时从A、B两地出发相向而行,两车在离B地64千米处第一次相遇。
相遇后两车仍以原速继续行驶,并且在到达对方出发点后,立即沿原路返回,途中两车在距A地48千米处第二次相遇,问两次相遇点相距多少千米?
二、用方程解应用题技巧
【例1】某县农机厂加工车间有77个工人。
已知每个工人平均每天加工甲种零件5个或乙种零件4个或丙种零件3个。
但加工3个甲种零件、1个乙种零件和9个丙种零件才恰好配成一套。
问:应安排生产甲、乙、丙种零件各多少人时,才能使生产的三种零件恰好配套。
【例2】某建筑公司有红、灰两种颜色的砖,红砖量是灰砖量的2倍,计划修建住宅若干座。
若每座住宅使用红砖80立方米,灰砖30立方米,那么,红砖缺40立方米,灰砖剩40立方米。
问:计划修建住宅多少座?【例3】两个数的和是100,差是8,求这两个数。
练习:
1.两个缸内共有48桶水,甲缸给乙缸加水一倍,然后乙缸又给甲缸加甲缸剩余水的一倍,则两缸的水量相等,求两个水缸原来各有多少桶水?
2.早晨6点多钟有两辆汽车先后离开学校向同一目的地开去,6点32分时,第一辆汽车离开学校的距离是第二辆汽车的3倍。
到6点39分的时候,第一辆汽车离开学校的距离是第二辆汽车的2倍,求第一辆汽车是6点几分离开学校的?
3.一人乘竹排沿江顺水漂流而下,迎面遇到一艘逆流而上的快艇,他问快艇驾驶员:“你后面有轮船开过来吗?”快艇驾驶员回答:“半小时前我超过一艘轮船。
”竹排继续顺水漂流了1小时遇到了迎面开来的这艘轮船。
那么快艇静水速度是轮船静水速度的多少倍?
4.丢番图是古希腊著名的数学家,他的墓志铭与众不同,碑文是:“过路人!这里埋葬着丢番图,他一生的六分之一是幸福的童年;又活了一生的十二分之一,面部长起了胡须;随后是一生的七分之一的单身汉生活;婚后五年,他有了一个儿子;可是,儿子活到丢番图一生年龄一半时,不幸夭折;儿子死后,父亲在深深的悲哀中又过了4年也与世长辞……”你能计算出他一生中经历的主要年龄吗?
三、等差数列求和技巧
【例1】求123+++…+1998+1999的和。
【例2】求111112113+++…+288+289的和。
【例3】求246+++…+196+198的和。
【例4】计算:25811141720++++++
【例5】小红读一本长编小说,第一天读了30页,从第二天起,每天读的页数都比前一天4页,最后一天读了70页,刚好读完。
问:这本小说共多少页?
练习:
1.求297294291+++…9+6+3的和。
2.求8000124128132
----…-272-276的值。
三、解定义新运算的技巧
【例1】我们规定符号“○”表示选择两数中较大数的运算。
例如:3○2=2○3=3。
符号“△”表示选择两数中较小数的运算,例如:3△2=2△3=2。
请计算:[(625△630)]+(370○375)]÷(130△125)
【例2】以a※b表示
1
2
a b
b a
++,计算:(1992996)
※※(996※498)
【例3】若对所有a、b,a b a x
=⨯
△,x是一个与b无关的常数;
()2
a b a b
=+÷
▽,且(13)3=1
△▽△(3▽3)。
求(13)
△▽2的值。
【例4】规定43
a b a b
⊗=⨯-⨯,已知8(1)5
x
⊗⊗=,求x。
【例5】设a b
※表示a的3倍减去b的2倍,即=32
a b a b
-
※。
例如,当6
a=,
5
b=时,6536258
=⨯-⨯=
※。
(1)计算:(1.60.8)0.75
※※;
(2)已知:41=7
x※(※)
练习:
1.如果:2→(3)表示2+3+4=9;5→(4)表示5+6+7+8=26,那么6→(100)为( )。
A .5000
B .5550
C .5500
D .5555
2.如果“△◎□”表示△乘以△,再乘以□,那么下列数中,表示“4◎3”所得结果的数是( )。
A .12
B .27
C .36
D .48
E .64
3.x 、y 表示两个数,规定两个新运算“※”及“△”:
x y mx ny =+※,x y kxy =△,其中m 、n 、k 都是自然数。
已知1※2=5,(2※3)△4=64,求(1△2)※3的
值。
4.对于两个数a 、b ,a △b=a +b -1。
(1)计算(7△8)△6=?
(2)已知(5△x )△x =84,求x 。
5.对于两个数x 、y ,x ⊙y 表示y ×A -x ×2,并且已知82⊙65=31,计算29⊙57的值。
6.我们规定符号“⊕”表示选择两数中较大数的运算,符号“⊗” 表示选择两数中较小数的运算,例如5⊕3=3⊕5=5,5⊗3=3⊗5=3,试计算: [(0.6⊕0.8)+(3⊗3.1)]× [(2.1⊗2.11)-(0.21⊕2.10)]。
