实验1 贝叶斯分类实验
实验一贝叶斯决策教材

实验一贝叶斯决策一、 实验原理1. 最小错误率贝叶斯决策规则:对于两类问题,最小错误率贝叶斯决策有以下裁决规则:P( 1 | x) P( 2 | x),则 x 1 ; 反之,则 x 2。
因为先验概率 P( i )可以确立,与当前样本 x 没关,因此决策规则也可整理成下边的形式:若l (x) P( x | 1 ) P( 2 ) ,则 x1 ,不然 x 。
P(x |2 ) P( 1) 22. 均匀错误率决策界限把 x 轴切割成两个地域,分别称为第一类和第二类的决策地域 .样本在中但属于第二类的错误概率和样本在中但属于第一类的错误概率就是出现错误的概率, 再考虑到样本自己的分布后就是均匀错误率:t P( 2 | x) p( x)dx P( 1 | x) p( x)dxP(e)t tp( x | 2 ) P( 2 )dx p( x | 1 ) P( 1 )dx t3. 此实验中的裁决门限和均匀错误率(1)裁决门限假设随机脉冲信号 f 中 0 的概率为 ,高斯噪声信号 n 服从,信号叠加时的放大倍数为 a ,叠加后的信号为s f * a n 。
由最小错误率贝叶斯决策可得:P( 1 ) p( x | 1 )P( 2 ) p( x |2)a2 2a2 2 (ln(1 p0 ) ln p0 )化简计算得: t2a(2)均匀错误率由上述积分式可计算。
二、实验内容1、已知均值和方差,产生高斯噪声信号,计算其统计特征实验中利用 MATLAB产生均值为 0,方差为 1 的高斯噪声信号,信号统计分布的程序和结果以下:%产生高斯噪声并统计其特征x=0;%均值为 0y=1;%方差为 1n=normrnd(x,y,[1 1000000]);%产生均值为 0,方差为 1 的高斯噪声m1=mean(n);%高斯噪声的均值v1=var(n); %高斯噪声的方差figure(1)plot(n(1:400)); title( '均值为 0,方差为 1 的高斯噪声 ');figure(2)hist(n,10000); title('高斯噪声的统计特征 ');获得 m1=-4.6534e-005 ;v1= 0.9971 。
模式识别实验一

, n 是 n 维均值
向 量 , C i 是 n n 协 方 差 矩 阵 ; Ci 为 矩 阵 Ci 的 行 列 式 。 且 i Ei x ,
Ci Ei
x
i
x
i , Ei x 表示对类别属于 i 的模式作数学期望运算。
T
因此判别函数可表示为 J i ( x) P( x | i ) P(i ) 对判别函数取自然对数
1 1 J i ( x) ( x i ) Ci1 ( x i ) ln P(i ) ln Ci 2 2
然后根据(1)中所述最大后验准则判断样本所属类别。 三、实验过程 实验数据: IRIS 数据集 实验假设: 各类数据服从正态分布 实验方法: 最大后验概率 实验环境: MATLAB 2010b (1)数据导入
A , B 可设置每种类型的先验概率 P A , P B 。针对某一训练数据 x 计
算其判别函数 J A x , J B x ,比较两个值的大小,哪个最大,就可判断该数据 属于哪一类。最后统计分类器判决结果,设置矩阵存储被错误分类的数据,统计 A,B 两类测试数据的误判数,计算误判率。 %---------分类器测试----------% %选择分类组(w1,w2)(w1,w3)(w2,w3) %test = 1代表(w1,w2)分类 %test = 2代表(w1,w3)分类 %test = 3代表(w2,w3)分类 test = 1; if test==1 avr_A = avr_w1';var_A = var_w1'; avr_B = avr_w2';var_B = var_w2'; %合并待测数据 data_test = [data_test_w1;data_test_w2]; end if test==2 avr_A = avr_w1';var_A = var_w1'; avr_B = avr_w3';var_B = var_w3'; %合并待测数据 data_test = [data_test_w1;data_test_w3]; end if test==3 avr_A = avr_w2';var_A = var_w2'; avr_B = avr_w3';var_B = var_w3'; %合并待测数据 data_test = [data_test_w2;data_test_w3]; end %s设置先验概率 P_wA = 1/2; P_wB = 1/2;
实验一贝叶斯分类实验

实验一:贝叶斯分类实验学时:4学时实验目的:设计简单的线性分类器,了解模式识别的基本方法。
掌握利用贝叶斯公式进行设计分类器的方法。
实验内容:(1) 简单分类:有两类样本(如鲈鱼和鲑鱼),每个样本有两个特征(如长度和亮度),每类有若干个(比如20个)样本点,假设每类样本点服从二维正态分布,自己随机给出具体数据,计算每类数据的均值点,并且把两个均值点连成一线段,用垂直平分该线段的直线作为分类边界。
再根据该分类边界对一随机给出的样本判别类别。
画出如下图形。
提示:1.可以入下产生第一类数据:% x1是第一类数据,每一行代表一个样本(两个特征)x1(:,1) = normrnd(10,4,20,1);x1(:,2) = normrnd(12,4,20,1);% 第2类数据x2(:,1) = normrnd(15,4,20,1);x2(:,2) = normrnd(13,4,20,1);2.可假设分类边界为kx-y+b=0,根据垂直平分的条件计算出k和b。
3.如果新的样本点代入分类边界方程的值的符号和第一类样本均值代入分类边界方程的符号相同,则是判断为第一类。
(2) 贝叶斯分类:根据贝叶斯公式,给出在类条件概率密度为正态分布时具体的判别函数表达式,用此判别函数设计分类器。
数据随机生成,比如生成两类样本(如鲈鱼和鲑鱼),每个样本有两个特征(如长度和亮度),每类有若干个(比如20个)样本点,假设每类样本点服从二维正态分布,随机生成具体数据,然后估计每类的均值与协方差,在下列各种情况下求出分类边界。
先验概率自己给定,比如都为0.5。
如果可能,画出在两类协方差不相同的情况下的分类边界。
提示:若第一类的样本为{}12,,n x x x ,则第一类均值的估计为11ˆnk k x n μ==∑,协方差的估计为11ˆˆˆ()()nT k kk x x n μμ=∑=--∑。
若若第一类的样本为:则均值的估计为:332431ˆ486664μ⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++= ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭协方差的估计为:[][][][]330111ˆ02021010462004⎛⎫⎛⎫-⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤∑=--++-+ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭000010101/201ˆ04040000024⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤∑=+++= ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭ 分类边界0()0t w x x -=可用专门绘制隐函数的ezplot 来绘制。
《模式识别》实验报告-贝叶斯分类

《模式识别》实验报告---最小错误率贝叶斯决策分类一、实验原理对于具有多个特征参数的样本(如本实验的iris 数据样本有4d =个参数),其正态分布的概率密度函数可定义为112211()exp ()()2(2)T d p π-⎧⎫=--∑-⎨⎬⎩⎭∑x x μx μ 式中,12,,,d x x x ⎡⎤⎣⎦=x 是d 维行向量,12,,,d μμμ⎡⎤⎣⎦=μ是d 维行向量,∑是d d ⨯维协方差矩阵,1-∑是∑的逆矩阵,∑是∑的行列式。
本实验我们采用最小错误率的贝叶斯决策,使用如下的函数作为判别函数()(|)(),1,2,3i i i g p P i ωω==x x (3个类别)其中()i P ω为类别i ω发生的先验概率,(|)i p ωx 为类别i ω的类条件概率密度函数。
由其判决规则,如果使()()i j g g >x x 对一切j i ≠成立,则将x 归为i ω类。
我们根据假设:类别i ω,i=1,2,……,N 的类条件概率密度函数(|)i p ωx ,i=1,2,……,N 服从正态分布,即有(|)i p ωx ~(,)i i N ∑μ,那么上式就可以写为1122()1()exp ()(),1,2,32(2)T i i dP g i ωπ-⎧⎫=-∑=⎨⎬⎩⎭∑x x -μx -μ对上式右端取对数,可得111()()()ln ()ln ln(2)222T i i i i dg P ωπ-=-∑+-∑-i i x x -μx -μ上式中的第二项与样本所属类别无关,将其从判别函数中消去,不会改变分类结果。
则判别函数()i g x 可简化为以下形式111()()()ln ()ln 22T i i i i g P ω-=-∑+-∑i i x x -μx -μ二、实验步骤(1)从Iris.txt 文件中读取估计参数用的样本,每一类样本抽出前40个,分别求其均值,公式如下11,2,3ii iii N ωωω∈==∑x μxclear% 原始数据导入iris = load('C:\MATLAB7\work\模式识别\iris.txt'); N=40;%每组取N=40个样本%求第一类样本均值 for i = 1:N for j = 1:4w1(i,j) = iris(i,j+1); end endsumx1 = sum(w1,1); for i=1:4meanx1(1,i)=sumx1(1,i)/N; end%求第二类样本均值 for i = 1:N for j = 1:4 w2(i,j) = iris(i+50,j+1);end endsumx2 = sum(w2,1); for i=1:4meanx2(1,i)=sumx2(1,i)/N; end%求第三类样本均值 for i = 1:N for j = 1:4w3(i,j) = iris(i+100,j+1); end endsumx3 = sum(w3,1); for i=1:4meanx3(1,i)=sumx3(1,i)/N; end(2)求每一类样本的协方差矩阵、逆矩阵1i -∑以及协方差矩阵的行列式i ∑, 协方差矩阵计算公式如下11()(),1,2,3,41i ii N i jklj j lk k l i x x j k N ωωσμμ==--=-∑其中lj x 代表i ω类的第l 个样本,第j 个特征值;ij ωμ代表i ω类的i N 个样品第j 个特征的平均值lk x 代表i ω类的第l 个样品,第k 个特征值;iw k μ代表i ω类的i N 个样品第k 个特征的平均值。
实验一图像的贝叶斯分类一、实验目...

实验一图像的贝叶斯分类一、实验目的将模式识别方法与图像处理技术相结合,掌握利用最小错分概率贝叶斯分类器进行图像分类的基本方法,通过实验加深对基本概念的理解。
二、实验仪器设备及软件HP D538、MATLAB三、实验原理1 基本原理阈值化分割算法是计算机视觉中的常用算法,对灰度图象的阈值分割就是先确定一个处于图像灰度取值范围内的灰度阈值,然后将图像中每个像素的灰度值与这个阈值相比较。
并根据比较的结果将对应的像素划分为两类,灰度值大于阈值的像素划分为一类,小于阈值的划分为另一类,等于阈值的可任意划分到两类中的任何一类。
此过程中,确定阈值是分割的关键。
对一般的图像进行分割处理通常对图像的灰度分布有一定的假设,或者说是基于一定的图像模型。
最常用的模型可描述如下:假设图像由具有单峰灰度分布的目标和背景组成,处于目标和背景内部相邻像素间的灰度值是高度相关的,但处于目标和背景交界处两边的像素灰度值有较大差别,此时,图像的灰度直方图基本上可看作是由分别对应于目标和背景的两个单峰直方图混合构成。
而且这两个分布应大小接近,且均值足够远,方差足够小,这种情况下直方图呈现较明显的双峰。
类似地,如果图像中包含多个单峰灰度目标,则直方图可能呈现较明显的多峰。
上述图像模型只是理想情况,有时图像中目标和背景的灰度值有部分交错。
这时如用全局阈值进行分割必然会产生一定的误差。
分割误差包括将目标分为背景和将背景分为目标两大类。
实际应用中应尽量减小错误分割的概率,常用的一种方法为选取最优阈值。
这里所谓的最优阈值,就是指能使误分割概率最小的分割阈值。
图像的直方图可以看成是对灰度值概率分布密度函数的一种近似。
如一幅图像中只包含目标和背景两类灰度区域,那么直方图所代表的灰度值概率密度函数可以表示为目标和背景两类灰度值概率密度函数的加权和。
如果概率密度函数形式已知,就有可能计算出使目标和背景两类误分割概率最小的最优阈值。
假设目标与背景两类像素值均服从正态分布且混有加性高斯噪声,上述分类问题可以使用模式识别中的最小错分概率贝叶斯分类器来解决。
朴素贝叶斯实验

朴素贝叶斯实验实验算法朴素贝叶斯分类器实验【实验名称】朴素贝叶斯实验【实验要求】掌握朴素贝叶斯分类模型应用过程,根据模型要求进行数据预处理,建模,评价与应用;【背景描述】贝叶斯分类是一类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。
而朴素贝叶斯分类是分类中最简单的,也是常见的一种分类方法。
【知识准备】了解贝叶斯分类器模型的使用场景,数据标准。
了解Python/Spark数据处理一般方法。
了解spark 模型调用,训练以及应用方法【实验设备】Windows或Linux 操作系统的计算机。
部署Spark,Python,本实验提供centos6.8环境。
【实验说明】采用UCI机器学习库中的wine数据集作为算法数据,把数据集随机划分为训练集和测试集,分别对模型进行训练和测试。
【实验环境】Spark2.3.1,Pyrhon3.X,实验在命令行pyspark中进行,或者把代码写在py脚本,由于本次为实验,以学习模型为主,所以在命令行中逐步执行代码,以便更加清晰地了解整个建模流程。
【实验步骤】第一步:启动pyspark:命令行中键入pyspark--masterlocal[4],本地模式启动spark与python:第二步:导入用到的包,并读取数据,数据源地址为/opt/algorithm/naiveBayes/wine.txt,具体命令如下所示:frompysparkimportSparkContext,SQLContextimportp yspark.ml.featureaspmfimportpyspark.ml.classificati onaspmcfrompyspark.sql.functionsimportcolimportpysp ark.sql.functionsasfunsqlContext=SQLContext(sc)df_w ine=sc.textFile(ufile:/opt/algorithm/naiveBayes/win e.txt).map(lambdax:str(x).split(,)).map(lambdax:[fl oat(z)forzinx])df_wine_rdd=sqlContext.createDataFra me(df_wine)df_wine_rdd.show()第三步:数据预处理(1).数据集划分(df_wine_rdd_train,df_wine_rdd_test)=df_wine_rdd.ra ndomSplit([7.0,3.0])(2).数据聚合,按ml贝叶斯模型,需要输入label|vos(data)cols=df_wine_rdd.columnsmodel_VA=pmf.VectorAssembler().setInputCols(cols[1:]).setOutput Col(F)VA_train=model_VA.transform(df_wine_rdd_train)VA_test=model_VA.transform(df_wine_rdd_test)VA_tra in.show(20,False)(3).类型编码,把类别变量编码为double型,实际上是让spark明白这是个类别变量,因为ml模型需要以Double作为输入model_lable=pmf.StringIndexer().setInputCol(cols[0] ).setOutputCol(label).fit(VA_train)VA_lable_train=m odel_lable.transform(VA_train)VA_lable_test=model_l able.transform(VA_test)VA_lable_train.show(20,False )第四步:构建模型并进行预测(1).建立模型model=pmc.NaiveBayes(featuresCol="F",labelCol="labe l",predictionCol="pred",probabilityCol="prob",rawPr edictionCol=rawpred,smoothing=1.0).fit(VA_lable_tra in)(2).模型预测prob=model.transform(VA_lable_test)prob.select(labe l,pred,prob,rawpred).show(20,False)第五步:构建模型评估方法arr=prob.select(col(label),col(pred),col(prob),col( rawpred),(col(label)==col(pred)).alias(check)).filt er(col(check)).count()*1.0/prob.count()第六步:输出模型效果print(模型准确率+str(arr*100)+%)第七步:通过Spark-Submit直接提交整个python文件,进行运算/opt/spark-2.3.1/bin/spark-submit/opt/algorithm/nai veBayes/NaiveBayes.py【问题与回答】1、Q:朴素贝叶斯分类器与一般的贝叶斯分类器有什么区别?A:最大的不同是朴素贝叶斯假设特征之间是独立,互不影响。
贝叶斯中文文本分类案例

贝叶斯中文文本分类案例咱来说说贝叶斯中文文本分类这个超有趣的事儿哈。
想象一下,你有一堆中文文章,有讲科技的、娱乐的、美食的啥啥的,你想把它们自动分类。
这时候贝叶斯就像一个超聪明的小助手来帮忙啦。
首先呢,贝叶斯定理就像是一个魔法公式。
咱简单说啊,就是根据一些已经知道的情况,去推测某个新的东西的可能性。
比如说,你已经知道了在很多科技文章里经常出现“芯片”“算法”这些词,在娱乐文章里经常出现“明星”“电影”这些词。
那对于一篇新的文章,贝叶斯就开始工作啦。
它会先把这篇文章拆成一个个的词,就像把一个大蛋糕切成好多小块。
然后呢,它会看这些词在不同类型文章(像之前说的科技类、娱乐类等)里出现的概率。
比如说这篇新文章里有“芯片”这个词,那根据之前统计的结果,这个词在科技文章里出现的概率很大。
贝叶斯就会想:“哟呵,这篇文章很可能是科技类的呢。
”但是呢,如果这篇文章里既有“芯片”又有“明星”,那它就得综合考虑这两个词在不同类型文章里的概率啦。
打个比方,就像你在猜一个人来自哪里。
如果他穿着苏格兰裙,那他可能是苏格兰人,但如果他又戴着牛仔帽,那就得再好好想想啦,说不定他是个很有个性,既喜欢苏格兰风格又喜欢西部牛仔风格的家伙,不过呢,还是得根据之前看到的苏格兰人和牛仔的各种特点的比例来判断他到底更可能是哪里人。
再具体一点哈。
假设我们有一个小小的文本库,里面有10篇科技文章和20篇娱乐文章。
在科技文章里,“算法”这个词出现了8次,在娱乐文章里“算法”只出现了1次。
现在有一篇新文章里有“算法”这个词,那贝叶斯就会这么算:这篇文章是科技文章的概率就会比较高,因为“算法”在科技文章里出现的次数相对娱乐文章来说多很多。
贝叶斯分类器就这么一点点地分析每个词,然后算出这篇文章属于各个类型(科技、娱乐、美食等)的概率,最后把这篇文章分到概率最高的那个类型里去。
就像把一群小动物分别赶到它们自己的小窝里一样。
这样就完成了中文文本分类啦,是不是还挺酷的呢?。
山东大学计算机学院机器学习实验一贝叶斯分类
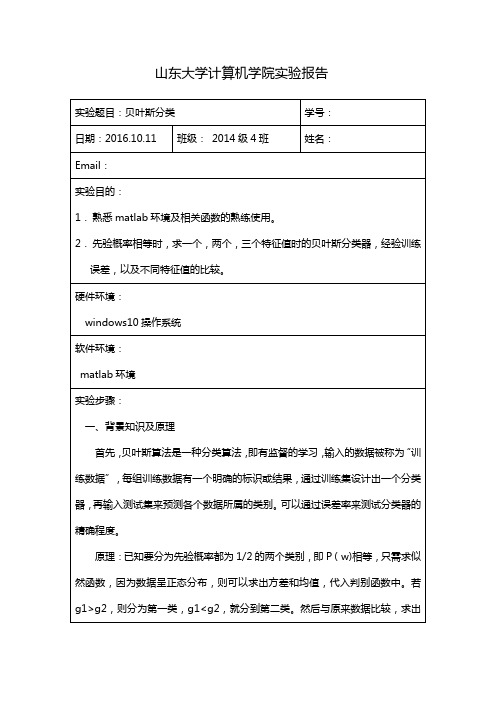
公式:
二、实验步骤
1.因为以前经常使用微软的Azure平台,这次仍然想用这个平台实验一下。分别测试使用一个,两个,三个特征值时用贝叶斯算法求出的准确率和召回率等。
1.熟悉matlab环境及相关函数的熟练使用。
2.先验概率相等时,求一个,两个,三个特征值时的贝叶斯分类器,经验训练误差,以及不同特征值的比较。
硬件环境:
windows10操作系统
软件环境:
matlab环境
实验步骤:
一、背景知识及原理
首先,贝叶斯算法是一种分类算法,即有监督的学习,输入的数据被称为“训练数据”,每组训练数据有一个明确的标识或结果,通过训练集属的类别。可以通过误差率来测试分类器的精确程度。
三、实验结果
1.一个特征值:分类错误率为0.3,界定误差0.473999
2.两个特征值:分类误差率0.45,界定误差为0.460466
3.三个特征值:分类误差率0.15,界定误差为0.411926
4.讨论:对于一有限的数据集,是否有可能在更高的数据维数下经验误差会增加
——我觉得如果数据维数高的话,误差是有可能相对于低维数的反而增加的。因为可能会产生比如这次实验的情况,两维数据的时候第二个特征值特别乱,误差很大,结果误差率比一个特征值的时候还要高了。
结论分析与体会:
刚开始感觉这个题无从下手,不知道要做出来的分类器是个什么样子,虽然知道该怎么在纸上计算后验概率,但是拿到matlab上面编写程序就不会了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一:贝叶斯分类实验
学时:4学时
实验目的:设计简单的线性分类器,了解模式识别的基本方法。
掌握利用贝叶斯公式进行设计分类器的方法。
实验内容:
(1)
简单分类:有两类样本(如鲈鱼和鲑鱼),每个样本有两个特征(如长度和亮度),每类有若干个(比如20个)样本点,假设每类样本点服从二维正态分布,自己随机给出具体数据,计算每类数据的均值点,并且把两个均值点连成一线段,用垂直平分该线段的直线作为分类边界。
再根据该分类边界对一随机给出的样本判别类别。
画出如下图形。
提示:
1.可以入下产生第一类数据:
% x1是第一类数据,每一行代表一个样本(两个特征)
x1(:,1) = normrnd(10,4,20,1);
x1(:,2) = normrnd(12,4,20,1);
% 第2类数据
x2(:,1) = normrnd(15,4,20,1);
x2(:,2) = normrnd(13,4,20,1);
2.可假设分类边界为 kx-y+b=0,根据垂直平分的条件计算出k和b。
3.如果新的样本点代入分类边界方程的值的符号和第一类样本均值代入分类边界方程的符号相同,则是判断为第一类。
(2)
贝叶斯分类:根据贝叶斯公式,给出在类条件概率密度为正态分布时具体的判别函数表达式,用此判别函数设计分类器。
数据随机生成,比如生成两类样本(如鲈鱼和鲑鱼),每个样本有两个特征(如长度和亮度),每类有若干个(比如20个)样本点,假设每类样本点服从二维正态分布,随机生成具体数据,然后估计每类的均值与协方差,在下列各种情况下求出分类边界。
先验概率自己给定,比如都为0.5。
如果可能,画出在两类协方差不相同的情况下的分类边界。
提示:
若第一类的样本为{}12,,n x x x ,则第一类均值的估计为1
1ˆn k k x n μ==∑,协方差的估计为1
1ˆˆˆ()()n T k k k x x n μμ=∑=--∑。
若若第一类的样本为:
则均值的估计为:
134x ⎡⎤=⎢⎥⎣⎦238x ⎡⎤=⎢⎥⎣⎦326x ⎡⎤=⎢⎥⎣⎦446x ⎡⎤=⎢⎥⎣⎦
332431ˆ486664μ⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤
=+++= ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦
⎝⎭ 协方差的估计为: [][][][]330111ˆ02021010462004⎛⎫⎛⎫-⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤∑=--++-+ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎪⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭ 000010101/201ˆ04040000024⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤∑=+++= ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦
⎝⎭ 分类边界0()0t w x x -=可用专门绘制隐函数的ezplot 来绘制。
若求出了w 和0x ,如: w = [ -0.4127, -0.1641]’; x0=[12.2197, 12.5141]’; 则可用:
fh=@(x,y)w*([x,y]'-x0); %判别函数表达式
ezplot(fh,[0,20]) %画出判别边界
情况1. 两类协方差相同且和单位阵成比例的情况下的分类边界为:
0()0t w x x -=
其中 i j w μμ=-,2
02()1()()ln 2()i i j i j j i j
P x P ωσμμμμωμμ=+--- 判别边界是一条直线,且垂直于均值的连线,但不一定通过连线的中点。
如下图:
情况2. 两类协方差相同且和单位阵不成比例的情况下的判别函数为:
0()0t w x x -=
其中 1
()i j w μμ-=∑-,01ln ()/()1().()2()()i j i j i j t i j i j P P x ωωμμμμμμμμ-⎡⎤⎣⎦=+---∑-。
判别边界仍是一条直线,但不垂直于均值的连线。
情况3. 两类协方差不相同的情况下的判别函数为:
判别边界为g1(x)-g2(x)=0,是一条一般二次曲线(可能是椭圆、双曲线、抛物线等)。
可用ezplot来绘制隐函数:
% 情况3. 两类协方差e1和e2不相同的情况下:
W1=-1/2*inv(e1);
w1=inv(e1)*u1;
w10=-1/2*u1'*inv(e1)*u1-1/2*log(det(inv(e1)))+log(2/5);%假设w1的先验概率为2/5
W2=-1/2*inv(e2);
w2=inv(e2)*u2;
w20=-1/2*u2'*inv(e2)*u2-1/2*log(det(inv(e2)))+log(3/5);% 假设w2的先验概率为3/5
fh=@(x,y)[x,y]*(W1-W2)*[x,y]'+(w1-w2)'*[x,y]'+w10-w20;% 判别函数表达式ezplot(fh,[0,20]) %画出判别边界。
