黄昆固体物理习题-第三章 晶体的热性质
《固体物理·黄昆》第三章
氢键结合的情况可写成通式:
X－H…Y。 式中 X 、 Y 代表 F 、 O 、 N 等电负 性大而原子半径较小的非金属原 子， X 和 Y 可以是两种相同的元 素，也可以是两种不同的元素。 d F l H F H F
归纳起来，氢键形成的条件是：
A)有与电负性大（X）的原子相结合的氢原子；
B) 有一个电负性也很大，含有孤对电子并带有部分负 电荷的原子（Y）； C)X与Y的原子半径都要较小。
氯化钠型 —— NaCl、KCl、AgBr、PbS、MgO (配位数6) 氯化铯型 —— CsCl、 TlBr、 TlI（配位数8）
离子结合成分较大的半导体材料ZnS等（配位数4）
2. 离子晶体结合的性质
1) 系统内能的计算 晶体内能 : 1)所有离子库仑相互作用能(吸引作用)
2) 和重叠排斥能之和(排斥作用)
具体晶体的内聚能(晶格能)参见周期表,有一定的规律性: 惰性气体晶体<碱金属<过渡族金属(共价晶体)
两粒子间的相互作用 相互作用能.
f(r) 和u(r)分别表示相互 作用力和相互作用势 则:
u (r ) f (r ) r
U 排斥 r
f (r )
B rn
u (r )
pij A12= j'
12
12.13188
pij A6= j'
6
14.45392
物理意义:
晶体总的势能:
—— 非极性分子晶体的晶格常数、结合能和体变模量 晶格常数
平衡状态体变模量
晶体的结合能
分子晶体: 常温下是气态的物质如:Cl2,SO2,HCl, H2, O2, He, Ne, Ar, Xe等在低温下依靠范德瓦耳斯力结合成的晶体.
固体物理习题与答案
《固体物理学》习题解答黄昆 原著 韩汝琦改编 （志远解答，仅供参考）第一章 晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。
因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= （4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
固体物理第三章
固体物理第三章班级成绩学号Chapter 3 晶格振动与晶体的热学性质姓名(lattice vibration and its heat characteristics)⼀、简要回答下列问题(answer the following questions):1、在晶格常数为a 的⼀维单原⼦晶格中，波长λ=8a 和波长λ=8a/5的格波所对应的原⼦振动状态有⽆不同? 试画图加以说明。
［答］对于⼀维单原⼦链，由q=2π／λ知，λ＝8a 时，q ＝π／4a ，λ＝8a ／5时，q ＝5π／4a ，⼆者的aq 相差π，不是2π的整数倍，因此，两个格波所对应的原⼦振动状态不同。
如上图，当两个格波的位相差为2π的整数倍时，则它们所对应的原⼦的振动状态相同。
2、什么叫简正振动模式？简正振动数⽬、格波数⽬或格波振动模式数⽬是否是⼀回事？［答］在简谐振动下，由N 个原⼦构成的晶体的晶格振动，可等效成3N 个独⽴的谐振⼦的振动，每⼀个谐振⼦的振动模式称为简正振动模式。
格波振动通常是这3N 个简正振动模式的线性叠加。
简正振动数⽬、格波数⽬或格波振动模式数⽬是是⼀回事，其数⽬等于晶体中所有原⼦的⾃由度之和，即等于3N 。
3、晶体中声⼦数⽬是否守恒？在极低温下，晶体中的声⼦数与温度T 之间有什么样的关系？［答］频率为ωi 的格波的平均声⼦数为： 11)(/-=Tk i B en ωω即每⼀个格波的声⼦数都与温度有关，因此晶体中的声⼦数⽬不守恒，它随温度的改变⽽改变。
以德拜模型为例。
晶体中的声⼦数⽬为ωωωωd g n N D)()('0=其中令 T k x B ω= 则 123'2/033233-=x TB e dxx C T k V N D θπ在极低温度下，θD ／T →∞，于是 331332332033233)2(23123'T nC T Vk e dx x C T k V N n B x B ∑∞=∞=-=ππ即在温度极低时，晶体中的声⼦数⽬与T 3成正⽐。
黄昆固体物理习题-第三章_晶体的热性质
第三章习题参考解答3.1已知一维单原子链，其中第j 个格波，在第n 个格点引起的位移μnj 为：δj 为任意位相因子。
并已知在较高温度下每个格波的平均能量为kT ，具体计算每个原子的平方平均位移。
)sin(j j j j nj naq t δωαμ++=21)(sin 102=++⎰dt q n t T j j j Tδαω根据=2nj μ22221)(sin j j j j j q n t αδαωα=++解：其中T =2π/ωj 为振动周期，所以：格波的平均动能：∑∙=n njm E 221μN m j j 2241ωα=一维单原子链可以认为是经典的简谐运动，因此有：)(cos 21222j j j j n j q n t m δαωωα++=∑平均动能=平均势能= 格波平均能量=kT 2121其中：M =ρL其中振幅222j j Nm kT ωα=得：kT N m E j j 214122==ωα所以有：22221jj nj Nm kT ωαμ==所以，每个原子的平方平均位移：∑∑∑===222121j j njn Nm kT ωαμμ其中：M =ρL3.2 讨论N个原胞的一维双原子链(相邻原子间距为a)，其2N个格波解，当M=m时与一维单原子链结果一一对应。
解：质量为M的原子位于2n-1，2n+1，2n+3……。
质量为m的原子位于2n，2n+2，2n+4 ……。
牛顿运动方程体系有N个原胞，有2N个独立的方程方程的解：A,B有非零解可以得到：两种不同的格波的色散关系为：对应一个q有两支格波：一支声学波和一支光学波，总的格波数目为2N。
当M=m时,色散关系简化为：长波极限情况下与一维单原子晶格格波的色散关系一致3.3质量相同两种原子形成一维双原子链，最近邻原子间的力常数交错等于c和10c，令两种原子的质量相等，并且最近邻间距是a/2，试求在k=0和k=π/a处的ω(k)。
并粗略。
画出色散关系。
固体物理基础第3章-晶格振动与晶体的热学性质
3-2 一维单原子链模型
格波的色散关系 4 2 2 aq sin ( )
m 2 • ω取正值，则有 (3)
(q)
aq 2 sin( ) m 2 • 频率是波数的偶函数
• 色散关系曲线具有周期性， 仅取简约布里渊区的结果即可 • 由正弦函数的性质可知，只有满足 0 2 / m 的格波 才能在一维单原子链晶体中传播，其它频率的格波将被强
原子n和原子n+1间的距离
非平衡位置
原子n和原子n+1间相对位移
a n1 n
n1 n
3-2 一维单原子链模型
• 忽略高阶项，简谐近似考虑原子 振动，相邻原子间相互作用势能 1 d 2v v(a ) ( 2 ) a 2 2 dr • 相邻原子间作用力 dv d 2v f , ( 2 )a d dr • 只考虑相邻原子的作用，第n个原 子受到的作用力
• 连续介质中的波（如声波）可表示为 Ae ，则可看出 • 格波和连续介质波具有完全类似的形式 • 一个格波表示的是所有原子同时做频率为ω的振动 • 格波与连续介质波的主要区别在于(2)式中，aq取值任意加减 2π的整数倍对所有原子的振动没有影响，所以可将波数q取值 限制为 q a a
V
O
a
r
• 第n个原子的运动方程
(n1 n ) (n n1 ) (n1 n1 2n )
(1)
平衡位置
d 2 n m 2 ( n1 n 1 2n ) dt
非平衡位置
——牛顿第二定律F=ma
3-2 一维单原子链模型
• 上述(1)式的解（原子振动位移）具有平面波的形式
a
)
黄昆版固体物理学课后答案解析答案 (2)
《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。
因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π=（2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。
证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
固体物理课后习题解答（黄昆版）第三章
固体物理课后习题解答（黄昆版）第三章黄昆固体物理习题解答第三章晶格振动与晶体的热学性质3.1 已知⼀维单原⼦链，其中第j个格波，在第个格点引起的位移为，µ= anj j sin(ωj_j+ σj) ，σj为任意个相位因⼦，并已知在较⾼温度下每个格波的平均能量为，具体计算每个原⼦的平⽅平均位移。
解：任意⼀个原⼦的位移是所有格波引起的位移的叠加，即µn= ∑ µnj=∑ a j sin(ωj t naq j+σj)j j（1）µ2 n =∑µjnj∑µj*nj=µj2nj+ µ µnj*nj′j j′由于µ µnj?nj数⽬⾮常⼤的数量级，⽽且取正或取负⼏率相等，因此上式得第2 项与第⼀项µ相⽐是⼀⼩量，可以忽略不计。
所以2= ∑ µ 2njn j由于µnj是时间的周期性函数，其长时间平均等于⼀个周期内的时间平均值为µ 2 = 1 T∫0 2 ω+σ 1 2 j aj sin( t naqjj j)dt a=j（2）T0 2已知较⾼温度下的每个格波的能量为KT，µnj的动能时间平均值为1 L T ?1 ?dµ 2 ?ρw a2 T 1= ∫∫dx0?ρnj?= j j∫0 2 ω+ σ= ρ 2 2 T??dt L a sin( t naq)dt w Lanj T0 0 0 ? 2 ?dt??2T0 j j j j 4 j j其中L 是原⼦链的长度，ρ使质量密度，T0为周期。
1221所以Tnj= ρ w La j j=KT（3）4 2µKT因此将此式代⼊（2）式有nj2 = ρωL 2 jµ所以每个原⼦的平均位移为2== ∑ µ 2= ∑KT= KT∑1n njρωL2ρLω2j j j j j3.2 讨论N 个原胞的⼀维双原⼦链（相邻原⼦间距为a），其2N 格波解，当M=m 时与⼀维单原⼦链的结果⼀⼀对应.解答（初稿）作者季正华- 1 -黄昆固体物理习题解答解：如上图所⽰，质量为M 的原⼦位于2n-1，2n+1，2n+3 ……质量为m 的原⼦位于2n，2n+2，2n+4 ……⽜顿运动⽅程：..mµ2n= ?βµ(22n?µ2n+1 ?µ2n?1)..Mµ2n+1 = ?βµ(22n+1 ?µ2n+2 ?µ2n)体系为N 个原胞，则有2N 个独⽴的⽅程i na q⽅程解的形式：iµ2n=Ae[ωt?(2 ) ] µ2n+1=Be[ω?(2n+1)aq]na qµ=将µ2n=Ae[ωt?(2 ) ]2n+1 Be i[ωt?(2n+1) aq]代回到运动⽅程得到若A、B 有⾮零的解，系数⾏列式满⾜：两种不同的格波的⾊散关系：——第⼀布⾥渊区解答（初稿）作者季正华- 2 -第⼀布⾥渊区允许 q 的数⽬黄昆固体物理习题解答对应⼀个 q 有两⽀格波：⼀⽀声学波和⼀⽀光学波。
黄昆版固体物理习题课_03
01/34
设试探解： 将试探解代入方程得到： 由线性齐次方程组有非零解的条件得到：
习题问题讨论三 ——晶格振动与晶体的热力学性质
02/34
当：
代入原方程组得到： 光学支：
声学支：
当：
光学支：B=0 声学支：A=0
习题问题讨论三 ——晶格振动与晶体的热力学性质
03/34
补充题二、设有一纵波：
沿着一维单原子链传播，原子间距为a，最近邻忽作用的恢复 力常数为 试证明：每个原子对时间平均的总能量为：
考虑到晶体中存在有许多不同频率、不同模式的格波，因此总 的均方位移应对所有不同格波进行求和。又由于各振动模式间 是相互独立的，因此有：
当N足够大时，振动频率趋于连续，求和可以用积分代替
习题问题讨论三 ——晶格振动与晶体的热力学性质
11/34
将德拜模型的频率分布函数及最大频率代入得：
（2）非零温度下相应于某频率的格波的平均能量应为格波能 量和该温度下该格波的平均声子数之积，即：
红色标记原子位于2n， 2n+2， 2n+4 ……
习题问题讨论三 ——晶格振动与晶体的热力学性质
19/34
—— 第2n个原子和第2n＋1个原子的运动方程
—— 体系N个原胞，有2N个独立的方程 —— 方程的解
令
习题问题讨论三 ——晶格振动与晶体的热力学性质
20/34
—— A、B有非零的解，系数行列式满足
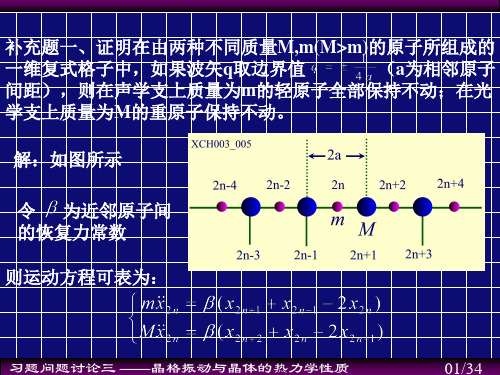
补充题一、证明在由两种不同质量M,m(M>m)的原子所组成的
一维复式格子中，如果波矢q取边界值
（a为相邻原子
间距），则在声学支上质量为m的轻原子全部保持不动；在光
学支上质量为M的重原子保持不动。
解：如图所示
固体物理第三章 晶格振动与晶体热学性质
固体物理第三章晶格振动与晶体热学性质第三章晶格振动与晶体的热学性质晶格振动是描述原子在平衡位置附近的振动，由于晶体内原子间存在着相互作用力，各个原子的振动也不是孤立的，而是相互联系的，因此在晶体内形成各种模式的波。
只有当振动微弱时，原子间非谐的相互作用可以忽略，即在简谐近似下，这些模式才是独立的。
由于晶格的周期性条件，模式所取的能量值不是连续的而是分立的。
对于这些独立而又分立的振动模式，可以用一系列独立的简谐振子来描述。
和光子的情形相似，这些谐振子的能量量子称为声子。
这样晶格振动的总体就可以看成声子系综。
若原子间的非谐相互作用可以看作微扰项，则声子间发生能量交换，并且在相互作用过程中，某些频率的声子产生，某些频率的声子湮灭。
当晶格振动破坏了晶格的周期性，使电子在晶格中的运动受到散射而电阻增加，可以看作电子受到声子的碰撞，晶体中的光学性质也与晶格振动有密切关系，在很大程度上可以看作光子与声子的相互作用乃至强烈耦合。
晶格振动最早是用于研究晶体的热学性质，其对晶体的电学性质、光学性质、超导电性、磁性、结构相变等一系列物理问题都有相当重要的作用，是研究固体宏观性质和微观过程的重要基础。
ωη§3-1 简谐近似和简正坐标由原子受力和原子间距之间的关系可以看出，若离开平衡位置的距离在一定限度，原子受力和该距离成正比。
这时该振动可以看成谐振动.用n μϖ表示原子偏离平衡位置（格点）位移矢量，对于三维空间，描述N 个原子的位移矢量需要3N 个分量，表为)3,,2,1(N i i Λ=μ将体系的势函数在平衡位置附近作泰勒展开:高阶项+∑⎪⎪⎭⎫ ⎝⎛∂∂∂+∑∂∂+===j i N j i j i i N i i V V V V μμμμμμ031,2031021)(第一项为平衡位置的势能，可取为零，第二项为平衡位置的力，等于零。
若忽略高阶项，因为势能仅和位移的平方成正比，即为简谐近似。
23121i N i i m T μ&∑==引入合适的正交变换，将动能和势能用所谓的简正坐标表示成仅含平方∑==N j j ij i i Q a m 31μ项而没有交叉项，即：由分析力学，基本形式的拉格朗日方程为：)32,1(,N i q Q T Q T dt d i i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂其中)32,1(,1N i q f q i j N j j i Λϖϖ=∂∂⋅∑==μ朗日方程：)32,1(,0N i Q L Q L dt d i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂则正则方程为：)3,2,1(,02N i Q Q i i i Λ&&==+ω其解为：)sin(δω+=t A Q i i 当考察某一个j Q 时，则：)sin(δωμ+=t A m a j i iji 晶体参与的振动，且它们的振动频率相同。
黄昆版固体物理学课后答案解析答案 (3)
《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。
因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。
证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r 同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
固体物理(黄昆)
PART ONE 填空问题Q01_01_001 原胞中有p 个原子。
那么在晶体中有3支声学波和33p −支光学波？Q01_01_002 按结构划分，晶体可分为7大晶系, 共14布喇菲格子?Q01_01_004 面心立方原胞的体积为314a Ω=；其第一布里渊区的体积为334(2)*a πΩ= Q01_01_005 体心立方原胞的体积为32a Ω=；第一布里渊区的体积为332(2)*a πΩ= Q01_01_006 对于立方晶系，有简单立方、体心立方和面心立方三种布喇菲格子。
Q01_01_007 金刚石晶体是复式格子，由两个面心立方结构的子晶格沿空间对角线位移 1／4 的长度套构而成，晶胞中有8个碳原子。
Q01_01_008 原胞是最小的晶格重复单元。
对于布喇菲格子，原胞只包含1个原子；Q01_01_009 晶面有规则、对称配置的固体，具有长程有序特点的固体称为晶体；在凝结过程中不经过结晶（即有序化）的阶段，原子的排列为长程无序的固体称为非晶体。
由晶粒组成的固体，称为多晶。
Q01_01_010 由完全相同的一种原子构成的格子，格子中只有一个原子，称为布喇菲格子。
满足ij j i b a πδ2=⋅G G ⎩⎨⎧≠===)(0)(2j i j i π 关系的1b G ,2b G ,3b G 为基矢，由322211b h b h b h G h K K K K ++=构成的格子，称作倒格子。
由若干个布喇菲格子相套而成的格子，叫做复式格子。
其原胞中有两个以上的原子。
Q01_03_001 由N 个原胞构成的晶体，原胞中有l 个原子，晶体共有3lN 个独立振动的正则频率。
Q01_03_002 声子的角频率为ω，声子的能量和动量表示为ω=和q K =。
Q01_03_003 光学波声子又可以分为纵光学波声子和横光学波声子，它们分别被称为极化声子和电磁声子Q01_03_004 一维复式原子链振动中，在布里渊区中心和边界，声学波的频率为 ⎪⎩⎪⎨⎧→±==0,02,)2(211q a q M πβω；光学波的频率⎪⎪⎩⎪⎪⎨⎧±=→=a q m q 2)2(0)2(21212πβµβωQ01_04_001 金属的线度为L ，一维运动的自由电子波函数ikx e Lx 1)(=ψ；能量m k E 222==；波矢的取值Ln k π2= Q01_04_002 电子在三维周期性晶格中波函数方程的解具有()()ik r kr e u r k ψ⋅=K K K K K K 形式？式中()k u r K K 在晶格平移下保持不变。
固体物理基础学：第3章 晶格振动与晶体的热学性质
晶格振动在晶体中形成了各种模式的波（格波），这些模式 是相互独立的，各模式的波所取的能量是分立的 简谐近似下，通过一些数学手段处理，可以用一系列独立的 简谐振子来描述这些相互独立、能量分立的振动模式 这些谐振子的能量量子，成为声子 晶格振动的总体可看做是声子的系宗
3-0 本章导读
热容量 热运动在宏观性 质的表现
v f （ n1 - n） （ n - n 1） n
平衡位置
牛顿第二定律 F=ma
力与两个原 子的位移有关
d 2 n （ n1 - n） （ n - n 1） m dt 2
(1)
非平衡位置
这即是第n个原子的运动方程！
3-2 一维单原子链模型
dv f d
d 2v 其中 ( 2 )a dr
3-1 一维单原子链模型
现考虑第n-1和第n+1个原子对第n个原子的双重作用 同样，写出简谐近似后的相互作用势v，如下：
v
1 2 2 （ ） （ ） n n 1 n 1 n 2
对位移求偏导，得到力：
杜隆－珀替经验规律： 一摩尔固体有N个原子，有3N个振动自由度，按能量均分 定律，每个自由度平均热能为kT，摩尔热容量 3Nk＝3R
—— 实验表明在较低温度下，热容量随着温度的降低而下降 爱因斯坦模型与德拜模型
研究晶格振动的意义远不限于热学性质。晶格振动是 研究固体 宏观性质和微观过程的重要基础。对晶体的热学性质、电学性 质、光学性质、超导电性、磁性、结构相变有密切关系。
其中任意一个简正坐标方程解
Qi Asin(it )
可化为 i
—— ωi是振动的圆频率，当只考察某一个 的振动时：
方程
固体物理第三章 晶格振动与晶体的热学性质.
方程了，方程解为： nq Aei( tnaq )
2. 格波—解的物理意义 连续介质波的解：
i (t 2
Ae
x)
Ae i(t qx )
格波：上述原子振动方程的解与一般连续介质的波有完全类似
的形式，所不同的是只在格点位置上有原子的振动。我们称原
子振动的波为“格波”。
格波与连续介质波的区别：
（1）连续介质中x表示空间任意一点，而格波中空间位置只能取
将包含N个原胞的有限原子链首位相连， 呈封闭环，使链上所有原（胞）子等价。
第n个原（胞）子与第n+N个原子情况完 全相同。B-K边界条件也
称周期性边界条件。nq Aei(tnaq)
边界条件要求：eiNaq 1 即：Nqa=2 π h， q 2 h (h为 整 数)
Na
q
a
a
N h N , h取N个整数值 2 / a N
(Qi
)
i (Qi
)
解出：
i
(ni
1 2
)hi
ni
i
h
exp(
22)Hni来自()其中
i
h
Qi
系统的本征能量：
，Hni(ξ)是厄米尔多项式。
E
3N i 1
(ni
1 2
)hi
3N
系统的本征函数：
(Q1 ,Q2 ...Q3N )
ni (Q1 )
i 1
只要找出系统的简正坐标，或说是振动模, 晶格振动问题就解决
4. 简正坐标代表所有原子的一种集体运动(而不是哪个原子的位移) 因为原子位移和简正坐标之间存在正交变换关系：
mi i
aij Q j
假设只存在某一个Qi，j 其它的都为0 (即只考察一个Qj振动)，那么，
固体物理 课后习题解答(黄昆版)第三章
•
w
M M
将
us −1
d 2us = C (Vs −1 − us ) + 10C (Vs − us ) ， dt 2 d 2Vs = 10C ( us − Vs ) + C ( us +1 − Vs ) , dt 2
w
a/2
o
vs −1
. e h c 3 . w
c 10c
m o c
o
•
o
•
us
vs
当 当
k = k x ，且 k y = 0 时的 ω − k 图，和 kx = k y
时的 ω − k 图，如右图所示。
3.5 已知 Nacl 晶体平均每对离子的相互作用能为 U (r ) = −
马德隆常数 α ＝1.75，n＝9，平均离子间距 r0 = 2.82 Å 。 （1）试求离子在平衡位置附近的振动频率
(b)根据题意，
μl ,m = μ (0) exp[i (lk x a + mk y a − ωt )]
) = c[( μl +1,m + μl −1,m − 2μl ,m ) 的解， dt 2 + ( μl ,m +1 + μl ,m −1 − 2μl ,m )] M(
因为
d 2 μl , m
μl ,m = μ (0) exp[i (lk x a + mk y a − ωt )]
代回到运动方程得到
若 A、B 有非零的解，系数行列式满足：
w
两种不同的格波的色散关系：
w
. e h c 3 . w
-2-
m o c
——第一布里渊区
解答（初稿）作者 季正华
03_11_晶格的热传导
203_11 晶格的热传导非简谐效应 —— 简谐近似下，原子之间的作用力与原子的位移成正比晶格的原子振动可以描述成为一系列线性独立的谐振子 ——声子—— 声子之间不发生作用，因而不能交换能量晶体中，某种声子一旦被激发出来，其数目就一直保持不变，它既不能把能量传递给其它频率的声子，也不能处于热平衡分布状态。
原来处于非平衡状态的系统永远不能变成平衡系统 —— 与实际物理过程不相符此外理想晶体的声子态是稳态，携带热流的声子一旦建立起来，就不随时间变化，热流将永不衰减，晶体的导热率为无穷大 —— 和实际物理过程不相符原子间的相互作用力并非严格地与原子的位移成正比。
当考虑到原子的相互作用势能泰勒级数展开中含有高次项，晶格的原子振动就不能描述成为一系列严格线性独立的谐振子。
如果原子的位移还相当小，可将高次项看成微扰。
由于微扰项的存在，这些振子不再是相互独立的，相互间要发生作用，则声子与声子之间发生能量交换。
如果开始时只存在某种频率的声子，由于声子间的互作用，这种频率的声子转换成另一种频率的声子，即一种频率的声子要湮灭．而另一种频率的声子会产生。
经过一定的弛豫时间后，各种声子的分布就能达到热平衡。
这些高次项 —— 使晶格振动达到热平衡的最主要原因两个声子通过非简谐项的作用，产生第三个声子，可以看成是两个声子碰撞，变成为第三个声子。
物理图像 —— 一个声子的存在将在晶体中引起周期性的弹性应变，由于非简谐项的影响，晶体的弹性模量不是常数，而受到弹性应变的调制，由于弹性模量的变化，将使第二个声子受到散射而产生第三个声子。
声子之间的相互作用，必须遵守能量守恒定律和动量守恒定律。
设两个相互碰撞的声子的频率和波矢分别为：112,,q andq ωωK K 第三个声子的频率和波矢为：33,q ωK三个声子之间满足：123123()()a q q q b ωωω+=⎧⎨+=⎩===K K K —— 晶格中的波矢具有平移周期性，波矢q K 和波矢h q K +KK 描写的振动状态完全一样 所以存在关系： 123()nq q q G c +=+K K K K 满足：关系的两个声子的碰撞过程 123123()()a q q q b ωωω+=⎧⎨+=⎩===K K K N 过程（正常过程）—— Normal Process满足：关系的两个声子的碰撞过程123123()()n a q q q G c ωωω+=⎧⎨+=−+⎩===K K K K U 过程（叫倒逆过程） —— Umklapp Process如果在晶体中存在温度梯度：dT dx能流密度：dT j dxθκ=− —— 单位时间内通过单位面积的热能 κ —— 晶体的导热系数存在温度梯度时，“声子气体”的密度分布是不均匀的。
黄昆固体物理解答
由上式可得 ε 23 = 0, ε 32 = 0, ε11 = 0
0 ⎞ ⎛ ε11 0 ⎜ 可得六角晶系的介电常数为 ε = ⎜ 0 ε 22 0 ⎟ ⎟ ⎜ 0 ⎟ 0 ε 33 ⎠ ⎝ ⎛ ε1 0 0 ⎞ ⎟ 选择相应的坐标变换即可得到 ε = ⎜ ⎜ 0 ε 2 0 ⎟ ，原命题得证。 ⎜0 0 ε ⎟ 2⎠ ⎝
(2) 体心立方（书P3，图1-3）
r 取 原 子 球 相 切 时 的 半 径 （ 体 对 角 线 的 1/4 ） ， r= 3a / 4 ,n=2, V ＝ a 3 所 以
ρ=
n 4π r 3 3 = 3π / 8 V
(3) 面心立方（书P4，图1-7）
r 取 原 子 球 相 切 时 的 半 径 （ 面 对 角 线 的 1/4 ） r= 2a / 4 ,n=4, V ＝ a 3 ， 所 以
r
r
0 ⎞ ⎛ ε11 0 ⎜ ε = ⎜ 0 ε 22 ε 23 ⎟ ⎟ ⎜ 0 ε ε 33 ⎟ 32 ⎝ ⎠
将上式代入 ε = Az T ε Az 得
⎛ ⎜ 0 ⎞ ⎜ ⎜ ε 23 ⎟ = ⎟ ⎜− ⎜ ε 33 ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ 1 3 ε11 + ε 22 4 4 3 3 ε11 + ε 22 4 4 3 − ε 32 2 − 3 3 ε11 + ε 22 4 4 3 1 ε11 + ε 22 4 4 1 − ε 32 2 − 3 ⎞ ε 23 ⎟ 2 ⎟ ⎟ 1 − ε 23 ⎟ 2 ⎟ ⎟ ε 33 ⎟ ⎟ ⎠
A
D
C
设想一个由正负两种离子相间排列的无限长的离子键取任一负离子作参考离子这样马德隆常数中的正负号可以这样取即遇正离子取正号遇负离子取负号用表示相邻离子间的距离于是有前边的因子2是因为存在着两个相等距离的离子一个在参考离子左面一个在其右面故对一边求和后要乘2马德隆常数为22讨论使离子电荷加倍所引起的对nacl晶格常数及结合能的影响排斥势看作不变ncdr于是当e变为2e23若一晶体两个离子之间的相互作用能可以表示为平衡间距r0解答初稿作者固体物理习题解答1003的计算晶体内能dudr为常数n为原胞数目固体物理习题解答1003109510191024经过sp杂化后形成的共价的方向求共价键之间的夹sp轨道杂键其方向沿着立方体的四条对角线化过程形成的共体结构容价键如右图所示
固体物理--第三章 晶格振动
三、周期性边界条件 周期性边界条件：
N n n
e
iNaq
1
2 q h Na
q的分布密度：
h =整数， N：晶体链的原胞数
Na L q const. 2 2
{
简约区中q的取值总数 ＝ q
2 N ＝晶体的原胞数 a 晶格振动的格波总数＝2N＝晶体的自由度数
2 1
两个色散关系即有两支格波：（＋：光学波； －：声学波）
简约区：
a
q
a
π a
π a
对于不在简约区中的波数q’ ，一定可在简约区中 找到唯一一个q，使之满足：
2 q q G a
G 为倒格矢
二、光学波和声学波的物理图象 第n个原胞中P、Q两种原子的位移之比
n m M n q0
离子晶体在某种光波的照射下，光波的电场可以激发这 种晶格振动，因此，我们称这种振动为光学波或光学支。
对于单声子过程（一级近 似），电磁波只与波数相同的格
(q)
=c0q +
+(0)
波相互作用。如果它们具有相同
的形式在整个晶体中传播，称为格波。
q取不同的值，相邻两原子间的振动位相差不同，则 晶格振动状态不同。 2 则 q 与 q描述同一晶格振动状态 若 q q a
1 4a
例：
q1
q2
2
1
2 a
5
4
2
2a 5
2a
2
2 q2 q1 a
三、周期性边界条件（Born－Karman边界条件）
N+1
黄昆版固体物理学课后答案解析答案 (1)
《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。
因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。
证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
《固体物理学》房晓勇主编教材-习题解答参考03第三章 晶体振动和晶体的热学性质
⎧ d 2 xn m = β 2 ( xn +1 − xn ) − β1 ( xn − xn −1 ) ⎪ ⎪ dt 2 ⎨ 2 ⎪m d xn +1 = β ( x − x ) − β ( x − x ) 1 2 n n+2 n +1 n +1 ⎪ dt 2 ⎩
设格波的解分别为
n i [( ) aq −ωt ] ⎧ ⎪ xn = Ae 2 ⎨ n ⎪ x = Bei[( 2 ) aq + qb −ωt ] ⎩ n +1
A 2β cos qa / m = =0 B 2β / m − 2β / M
由此可知，声学支格波中所有轻原子 m 静止。 而在光学支中，重原子 M 与轻原子 m 的振幅之比为
B 2β cos qa / M = =0 A 2β / M − 2β / m
由此可知，光学支格波中所有重原子 M 静止。 此时原子振动的图像如下图 3.6 所示：
v弹 =
ω
q
=
c
ρ
，c = βa ， ρ =
1
⎡ ⎢ v弹 = ⎢ β a ⎛ m+M ⎢ ⎜ ⎢ ⎝ 2a ⎣
⎤2 1 ⎥ ⎛ 2β ⎞ 2 ⎥ =⎜ ⎟ a ⎞⎥ ⎝m+M ⎠ ⎟ ⎠⎥ ⎦
由此可以看出，弹性波的波速与长声学波的波速完全相等，即长声学波与弹性波完全一样。 长声学波，格波可以看成连续波，晶体可以看成连续介质。 3.5 设有一维原子链 （如图） ， 第 2n 个原子与第 2n + 1 个原子之间的力常数为 β ； 而第 2n 个原子与第 2n − 1 个原子的力常数为 β ' （ β ' < β ） 。设两种原子的质量相等，最近邻间距均为 a，试求晶格振动的振动谱以 及q = 0 和q = ±
黄昆固体物理习题解答
因此只要先求出倒格点 Ghkl ，求出其大小即可。
由正格子基矢 a = ai ， b = bj ， c = ck ，可以马上求出：
a∗ = 2π i ， b ∗ = 2π j ， c∗ = 2π k
a
b
c
因为倒格子基矢互相正交，因此其大小为
Ghkl =
(ha∗ )2 + (kb∗ )2 + (lc∗ )2 = 2π
(h)2 + (k )2 + ( l )2 abc
则带入前边的关系式，即得晶面族的面间距。 1.7 写出体心立方和面心立方晶格结构的金属中，最近邻和次近邻的原子数。若立方边长为
a ，写出最近邻和次近邻的原子间距。
答：体心立方晶格的最近邻原子数（配位数）为 8，最近邻原子间距等于 3 a ，次近邻原 2
=V0
∂2U ( ∂r2
)r0
=
N 2
[−
m(m +1)α r m+2
0
+
n(n +1)β r n+2
0
=
N 2
{−
1 r02
m2α [( r0m
−
n2β r0n
)
+
(
mα r0m
−
nβ r0n
)]}
=
N 2
[−
1 r02
m2α ( r0m
−
n2β r0n
)]
=
N 2
[−
1 r m+2
0
(m2α
−
n2β nβ
AB = a (i − j − k ) 2
c
B
b
C
O
a
OB ⋅ AB =| OB || AB | cosθ = a2 (−1) 4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(10 eiaq ) 2M 11
解之得：
2
M
11
121
20(1
c
os
aq)
1 2
当 q 时，cos 1
a
可得
2
M
1
2
1
20
M
2
当q=0时,则有：
0
1
22
M
2
色散关系如图所示：
22
M
20
M
2
M
3.4题目：
略。
系。
3.4 解：(1)设μl,m代表第（l,m）个原子，即第l
要激发的声子所用的电磁波波长在近红外线波段
2k mM
mM
其中，mNa=23 kg
代入数计算，可得： 11.11013 Hz
计算波长，可得：
2
q
2
c
2c
代入数据，计算波长，可得：
17m
与实测同数量级。因为得到的色散关系存在近似。
3.6 计算一维单原子链的频率分布函数 解： 设单原子链长度
2
2
所以有：
E
1 4
m
2j
2 j
N
1 2
kT
其中振幅
2 j
2kT
Nm
2 j
得：
2 nj
1 2
2 j
kT
Nm
2 j
所以，每个原子的平方平均位移：
n
2 nj
1
2
2 j
kT Nm
1
2 j
其中：M=rL
3.2 讨论N个原胞的一维双原子链(相邻原子间距为a)，其 2N个格波解，当M=m时与一维单原子链结果一一对应。
j
)dt
1 2
其中T=2π/ωj为振动周期，所以：
2 nj
2 j
sin
2
(
jt
nq
j
j
)
1 2
2 j
格波的平均动能：
E
n
1 2
m
•
2 nj
1m 2
n
2j
2 j
cos
2
(
jt
nq
j
j)
1 4
m
2j
2 j
N
其中：M=rL
一维单原子链可以认为是经典的简谐运动，因此有：
平均动能=平均势能= 1 格波平均能量= 1 kT
cos aky )
这就是色散关系。
（c）k=kx，ky=0， kx=ky的-k图像为：
由（c）的结果代入可得到
3.5题：已知NaCl晶体平均每对离子的相互作用能为：
U (r) q2 / r / r n
其中马德龙常数α=1.75, n=9，平均离子间距为
r0=2.82Å。
（1）试求离子在平衡位置附近的振动频率； （2）计算与频率相当的电磁波的波长，并与NaCl红 外吸收频率的测量值61μm进行比较。
系是：ω=vq，在二维波矢空间内，格波的等频面是一个园， 如图所示，在q—q+dq区间内波速为v的格波数目为：
qy dq
dz
S
(2 )2
,
2qdq
Sd 2v 2
q
o
qx 式中S为二维晶格的总面积，由此可以得
到波速为v的格波的模式密度为：
g ( )
dz
d
S 2v2
由此可以得E为：
3.9题: 写出量子谐振子系统的自由能，证明在经典 极限，自由能为：
解：绿色标记的原子位于2n-1， 2n+1， 2n+3 …… 红色标记原子位于 2n， 2n+2， 2n+4 ……
第2n个原子和第2n＋1个原子的运动方程可以写为： 体系N个原胞，有2N个独立的方程 方程的解：
令
A、B有非零的解，系数行列式满足
两种色散关系
—— 两种色散关系
色散关系(2--k)图如 右，这是一个双原子 （例如H2）晶体。
解: 1)光学波的最大频率
光学波的最小频率 声学波的最大频率
2）相应声子的能量
3) 某一特定谐振子具有激发能
的几率
归一化常数
—— 归一化条件
频率为谐振子的平均能量 频率为谐振子的能量
第i个q态的平均数声子
声子数目为:
4）如果用电磁波激发光学波 要激发 的声子所用的电磁波波长在什么波段？ 对应电磁波的能量和波长
将上式代入F式中，便得到
F U0 kBT
q
ln( q )
kBT
3.10题：设晶体中每个振子的零点振动能为：1 ，
试用德拜模型求晶体的零点振动能。
2
解：根据量子力学，零点能是谐振子所固有的，与温
度无关，故T =0 K时的振动能E0就是各振动模零点能
之和:
E0
D 0
E0
()g()d
将
E0
1 ,
解：质量为M的原子位于 2n-1， 2n+1， 2n+3 ……。 质量为m的原子位于 2n， 2n+2， 2n+4 ……。
牛顿运动方程 体系有N个原胞，有2N个独立的方程 方程的解：
A , B有 非零解
可以得到： 两种不同的格波的色散关系为：
对应一个q有两支格波：一支声学波和一支光学波， 总的格波数目为2N 。
(,m1 ,m1 2,m )]
设试探解的形式为：
(0)ei[t( akx maky )] ,m
代入运动方程，消去公因子后，得：
M 2 c(eiakx eiakx eiaky eiaky 4)
2c(2 cos akx cos aky )
据此得色散关系 ：
2
2c M
(2
cos akx
2
g()
3V 2 2 2C 3
代入上式，
E0
3V
2 2 C 3
. 2
m 3d
0
3Vm4 16 2 C 3
其中V是晶体的体积
由
CV
(T )
d E(T ) dT
3Vk
2 2 C 3
.
m 0
k
T
2
e
k
T
e
k
T
2
1
2d
式给出ωm
1
m
C 6 2
N V
3
把 m 代入上式，便可得到晶体的零点能：
行 m列的原子垂直于晶格平面的位移，当只考虑最 近邻原子间的相互作用时，由于（l +1,m）原子对 它的作用力：
f1 c( 1,m ,m )
第l-1,m原子对它的作用力：
f2 c( ,m ) 1,m
而f1于f2 方向是相反的。同样处理（ l，m+1）原 子和（ l，m-1）原子对（l,m）原子的作用力f3，f4， 于是得到第（l，m）个原子所受的力：
3.5解：由 U (r) q2 / r / r n
dU 0 dr
可以得到β：
1 n
q
2
r0n1
利用题目所给条件（1），可知：
f
k
dU dr
dU
d
d 2U dr 2
计算、简化，代入β，可得回复力系数k：
k
(n
1)q2
r03
=143N/m
对于NaCl晶体，可以认为是一维双原子晶体，由 黄昆教材p96-97分析可以知道，对于离子晶体只有长 光学波可以和电磁波发生相互作用。所以有
E0
3
16 2
V
3
C
(6 2
N
)
4 3
C
4
V
9 8
NkB (6
2
N V
1
)3
C kB
9 8
R D
3.11题: 一维复式格子中，如果
计算
1) 光学波频率的最大值
的最大值
；
和最小值 ，声学波频率
2) 相应声子的能量 , 和
；
3) 在
下，三种声子数目各为多少？
4) 如果用电磁波激发光学波
要激发的声子所用的电磁波波长在什么波段？
F U0 kBT
q
ln( q )
kBT
解：已知晶体自由能可以表示为
F U0
q
1 2
q
kBT
ln(1
q
e
kBT
)
量子谐振子的自由能为：
F U kBT
q
1 2
q
kBT
ln(1 eq kBT )
对于经典极限，kBT q ，因而有
1 q 0
2 kBT
eq kBT 1 q
kBT
4
F fi c ( 1,m ,m ) ( ,m 1,m ) i 1
c ( ,m1 ,m ) ( ,m ,m1)
c[( 1,m 1,m 2 ,m )
(,m1 ,m1 2,m )]
根据运动方程形式：
M, m
M
d
2l,
dt 2
m
F
c[( 1,m 1,m 2 ,m )
两边微分
将dq和
代入
得到 时
为虚数，有
解方法 2:
振动模式密度函数 已知三维色散关系
q空间的等频率面是球面，q为常数
对于光学波，在
处振动频率具有最大值
频率分布函数
3.8 有N各相同原子组成面积为S的二维晶格，在德拜 近似下计算比热，并论述在低温极限比热正比于T2。
解：德拜模型考虑的格波是弹性波,波速为v的格波的色散关
ei(t naq) n
ei(t naq) n
代入到运动方程，得：
2Mn (10 n neiaq 11n )