2020数学实验任务书 - 360文档中心

数学活动实验报告

一、实验目的本次数学活动实验旨在通过实践活动，培养学生的动手操作能力、观察分析能力和创新思维，提高学生对数学知识的理解和运用能力。

同时，通过实验活动，激发学生对数学的兴趣，培养学生的团队合作精神。

二、实验内容本次实验内容为“探究三角形的稳定性”。

三角形是数学中常见的几何图形，具有稳定性强的特点。

通过实验，让学生了解三角形稳定性的原因，并运用所学知识解决实际问题。

三、实验步骤1. 实验准备（1）实验器材：铁丝、剪刀、胶带、直尺、三角板、钩码、支架等。

（2）实验分组：将学生分成若干小组，每组4-6人。

2. 实验过程（1）观察三角形的稳定性：引导学生观察生活中常见的三角形结构，如桥梁、建筑等，感受三角形稳定性的重要性。

（2）制作三角形框架：每组学生根据所学知识，利用铁丝和剪刀制作一个三角形框架。

要求三角形框架的边长满足一定条件，如边长比例为1:1:√2。

（3）测试三角形稳定性：将三角形框架固定在支架上，逐渐增加钩码的重量，观察三角形框架的变形情况。

（4）分析实验结果：引导学生分析实验结果，总结三角形稳定性的原因。

3. 实验总结（1）各小组汇报实验结果，分享实验心得。

（2）教师点评各小组的实验过程和结果，总结三角形稳定性的原因。

四、实验结果与分析1. 实验结果在实验过程中，大部分小组制作的三角形框架在增加钩码重量时，能够保持较好的稳定性，只有少数小组的框架发生了较大变形。

2. 实验分析（1）三角形稳定性原因：三角形具有稳定性强的特点，主要原因是三角形的内角和为180°，当外力作用于三角形时，三个角能够均匀分担外力，使三角形保持稳定。

（2）影响三角形稳定性的因素：边长比例、材料强度、受力方式等。

五、实验结论通过本次实验，学生掌握了三角形稳定性的基本原理，了解了三角形在实际生活中的应用。

同时，培养了学生的动手操作能力、观察分析能力和创新思维，提高了学生对数学知识的理解和运用能力。

六、实验反思1. 实验过程中，部分学生动手能力较差，需要教师在实验过程中给予指导和帮助。

数学实验课程实验指导书Word版

《数学实验》课程实验指导书2006-4-29目录实验一、微积分基础 3实验二、怎样计算 5实验三、最佳分数近似值 6实验四、数列与级数 7实验五、素数 8实验六、概率 9实验七、几何变换 11实验八、天体运动 13实验九、迭代（一）——方程求解 15实验十、寻优 16实验十一、最速降线 18实验十二、迭代（二）——分形 20实验十三、迭代（三）——混沌 21实验十四、密码 22实验十五、初等几何定理的机器证明 23附表（实验报告） 24实验一、微积分基础一、实验目的及意义：1、熟悉Mathematic软件常见函数图形2、通过作图，进一步加深对函数的理解，观察函数的性质3、构造函数自变量与因变量的对应表，观察函数的变化。

二、实验内容：1．1函数及其图象1．2数e1．3 积分与自然对数1．4调和数列1．5双曲函数三、实验步骤1.开启软件平台——Mathematics ，开启Mathematics编辑窗口；2.根据各种问题编写程序文件3.保存文件并运行；4.观察运行结果(数值或图形)；5.根据观察到的结果写出实验报告，并浅谈学习心得体会四、实验要求与任务根据实验内容和步骤，完成以下具体实验，要求写出实验报告（实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论→心得体会）1、1函数及图形(1)在区间[-0.1,0.1]上作出 y = sin(x)/x 的图象,观察图象在 x = 0 附近的形状(2)在同一坐标系内作出函数y = sin(x) 和它的展开式的前几构成的多项式函数y = x-x^3/3!,y = x-x^3/3!+x^5/5! . . . 的图象,观察这些多项式函数图象对 y = sin x 的图象逼近的情况.(3)分别取n =10,20,画出函数 y = sin(2k-1)x/(2k-1),k=1,2,...,n求和} 在区间[-3PI,3PI]上的图象.当N 趋向无穷时函数趋向什麽函数?(4)别取n = 5,10,15, 在同一坐标系内作出函数f(x) = sin x 与p(x) = x * (1-x^2/PI^2)*(1-x^2/(2^2*PI^2))*...*(1-x^2/n^2*PI^2))在区间[-2PI,2PI]上的图象,观察 p(x) 图象对 y = sin x的图象逼近的情况.1、2数e观察当n趋于无穷大时数列a n=(1+1/n)n和A n=(1+1/n)n+1的变化趋势:（1）n=10m,m=1,2,. . . ,7时的值,a n,A n观察变化趋势.（2）在同一坐标系内作出三个函数地图象y=(1+1/10x)10^x , y=(1+1/10x)10^x , y=e观察当 x 增大时图象变化趋势（3）计算 e 的精确值.1.3积分与自然对数1）计算1/x的大和及小和以及两者的平均，观察变化趋势。

数学实验任务书x

15 10.58
16 10.6
10、在排污管道设计中，工程师最关心管道坡度、管子直径和污水流量之间的关系。经验表明对于圆截面的排污管道，这些量之间有如下的经验公式
Q D1 S 2
3 其中 Q 代表流量( m / s ),S 代表管道坡度(m/m)、代表管道直径(m), , 1 , 2 是 3 个需要通过实 D
验测定的经验参数。现有一组实验数据如下：
实验序号 D(m) 1 2 3 4 5 6 7 8 9 0.302 0.604 0.906 0.302 0.604 0.902 0.302 0.604 0.906
S 0.001 0.001 0.001 0.01 0.01 0.01 0.05 0.05 0.05
8、某农场饲养的动物所能达到的最大年龄为 15 岁，将其分为三个年龄组：第一组，0——5 岁；第二组 6——10 岁；第三组成 11——15 岁。动物从第二年龄组起开始繁殖后代，经过长期统计，第二年龄组的动物在其年龄段平均繁殖 4 个后代，第三组在其年龄段平均繁殖 3 个后代，第一年龄组和第二年龄组的动物能顺利进入下一个年龄组的存活率分别是 1/2 和 1/4。假设农场现有三个年龄段的动物各 1000 头， 15 年后农场饲养的动物总数及农场三个年龄段的动物各将达到多少头？指出 15 年间，问动物总增长多少头及总增长率。
五、综合分析题目（3 选 1） 16、 (1) 炼钢是个氧化脱碳的过程.因为钢液含碳量 x 与精炼时间 y 有一定的关系，现将某平炉共炼 34 炉钢
记录下来的含碳量 x 与精炼时间 y 的数据列如下表：编 1 2 3 号含碳量 x(％) 1.80 1.04 1.34 精炼时间 y(分) 200 100 135

数学实验报告单

（3）构造线段 CD，选中 CD 所在的直线、点 A 和点 B，单击“显示”
/“隐藏对象”。
（4）在直线上任取一点 E（除 D 点外），连接 CE。
（5）选中线段 CD、CE，点击“度量”菜单中的“长度”，量出 CD 和
CE 的长，依次选中点 C、E、D，点击“度量”/“角度”，测量∠CED
实
的大小。
数学实验报告单
实验名称实验目的实验要求实验工具
垂线段最短
设计人唐晓霞
通过用刻度尺测量和几何画板软件两种方式经理“垂线段最短”的发现过程。经历实践活动的过程，学会寻找思考问题的着眼点，掌握研究问题的方法，领悟数学思想。
刻度尺、三角尺、装有几何画板软件的计算机等。
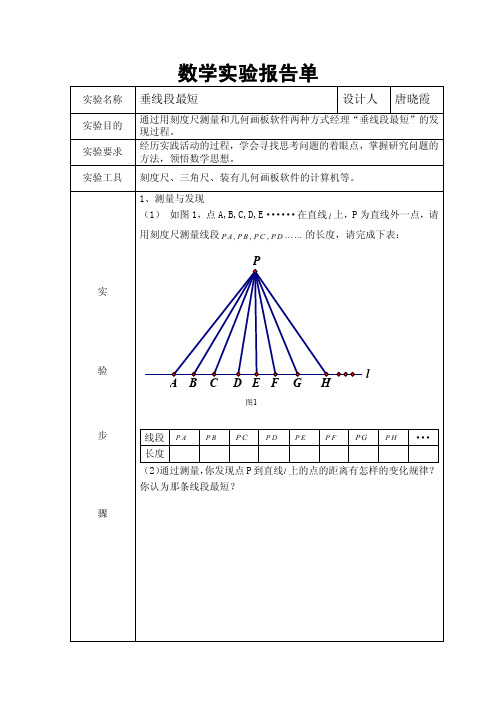
1、测量与发现（1）如图 1，点 A,B,C,D,E······在直线 l 上，P 为直线外一点，请用刻度尺测量线段 P A , P B , P C , P D 的长度，请完成下表：
CE = 4.73厘米
C
CED = 65.87°
A
B DE
图2
1、独立猜想、操作； 2、学生交流、小组合作； 3、学生汇报、上台演示
实验结论
实验收获
P
实
验
l
A B C DEF G H
图1
步
线段 P A
PB
PC
PD PE
PF
P G P H ···
长度
（2）通过测量，你发现点 P 到直线l 上的点的距离有怎样的变化规律？你认为那条线段最短？
骤
2、操作与验证
（1）打开几何画板软件，画直线 AB、直线 AB 外的点 C。
（2）选中点 C 和直线 AB，点击“构造”/“垂线”，交直线 AB 于点 D。

数学实验课程实验指导书Word版

《数学实验》课程实验指导书2006-4-29目录实验一、微积分基础 3实验二、怎样计算 5实验三、最佳分数近似值 6实验四、数列与级数 7实验五、素数 8实验六、概率 9实验七、几何变换 11实验八、天体运动 13实验九、迭代（一）——方程求解 15实验十、寻优 16实验十一、最速降线 18实验十二、迭代（二）——分形 20实验十三、迭代（三）——混沌 21实验十四、密码 22实验十五、初等几何定理的机器证明 23附表（实验报告） 24实验一、微积分基础一、实验目的及意义：1、熟悉Mathematic软件常见函数图形2、通过作图，进一步加深对函数的理解，观察函数的性质3、构造函数自变量与因变量的对应表，观察函数的变化。

二、实验内容：1．1函数及其图象1．2数e1．3 积分与自然对数1．4调和数列1．5双曲函数三、实验步骤1.开启软件平台——Mathematics ，开启Mathematics编辑窗口；2.根据各种问题编写程序文件3.保存文件并运行；4.观察运行结果(数值或图形)；5.根据观察到的结果写出实验报告，并浅谈学习心得体会四、实验要求与任务根据实验内容和步骤，完成以下具体实验，要求写出实验报告（实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论→心得体会）1、1函数及图形(1)在区间[-0.1,0.1]上作出 y = sin(x)/x 的图象,观察图象在 x = 0 附近的形状(2)在同一坐标系内作出函数y = sin(x) 和它的展开式的前几构成的多项式函数y = x-x^3/3!,y = x-x^3/3!+x^5/5! . . . 的图象,观察这些多项式函数图象对 y = sin x 的图象逼近的情况.(3)分别取n =10,20,画出函数 y = sin(2k-1)x/(2k-1),k=1,2,...,n求和} 在区间[-3PI,3PI]上的图象.当N 趋向无穷时函数趋向什麽函数?(4)别取n = 5,10,15, 在同一坐标系内作出函数f(x) = sin x 与p(x) = x * (1-x^2/PI^2)*(1-x^2/(2^2*PI^2))*...*(1-x^2/n^2*PI^2))在区间[-2PI,2PI]上的图象,观察 p(x) 图象对 y = sin x的图象逼近的情况.1、2数e观察当n趋于无穷大时数列a n=(1+1/n)n和A n=(1+1/n)n+1的变化趋势:（1）n=10m,m=1,2,. . . ,7时的值,a n,A n观察变化趋势.（2）在同一坐标系内作出三个函数地图象y=(1+1/10x)10^x , y=(1+1/10x)10^x , y=e观察当 x 增大时图象变化趋势（3）计算 e 的精确值.1.3积分与自然对数1）计算1/x的大和及小和以及两者的平均，观察变化趋势。

数学实验报告单范文

数学实验报告单范文实验名称：探究平面中的几何变换实验目的：通过实验，探究平面中的几何变换，加深对平移、旋转和尺缩变换的理解。

实验器材：1.平面图形模型（如纸片或木板）2.直尺3.量角器4.尺子实验原理：平移变换：平面上的任意一点通过平行移动一定距离，得到该点的平移变换。

平行移动的方向和距离决定了平移的效果。

旋转变换：平面上的任意一点围绕一些旋转中心旋转一定角度，得到该点的旋转变换。

旋转中心和旋转角度决定了旋转的效果。

尺缩变换：平面上的任意一点距离一些固定点的距离乘以一个倍数，得到该点的尺缩变换。

倍数决定了尺缩的效果。

实验步骤：1.准备平面图形模型，可以使用纸片或木板规划图形。

2.使用直尺和量角器测量选定图形的各个重要点和线段的坐标和角度。

3.进行平移变换：a.选定一个平移向量，使用尺子和直尺对图形上的每一个点进行平行移动。

b.测量并记录移动后的图形的各个点和线段的坐标和角度。

4.进行旋转变换：a.选定一个旋转中心和旋转角度，使用量角器和直尺对图形上的每一个点进行旋转变换。

b.测量并记录旋转后的图形的各个点和线段的坐标和角度。

5.进行尺缩变换：a.选定一个固定点和一个倍数，使用尺子对图形上的每一个点进行尺缩变换。

b.测量并记录尺缩后的图形的各个点和线段的坐标和角度。

6.分析实验结果，总结平移、旋转和尺缩变换对图形的影响。

实验结果：经过实验，我们观察到以下现象：1.平移变换：图形上的点整体移动了一段距离，但相对位置仍保持不变。

2.旋转变换：图形上的点绕着旋转中心旋转了一定角度，但相对距离和相对位置仍保持不变。

3.尺缩变换：图形上的点距离固定点乘以一个倍数，使得图形整体扩大或缩小。

实验结论：通过本次实验，我们加深了对平移、旋转和尺缩变换的理解。

平移、旋转和尺缩变换是平面中常见的几何变换，它们能够改变图形的位置、方向和大小。

在实际应用中，我们可以利用这些变换来解决各种几何问题，例如图像处理、计算机图形学和建筑设计等领域。

数学教学实验工作计划及安排

数学教学实验工作计划及安排一、实验名称：“超越和三角函数图像的绘制”二、实验目的：通过完成实验，使学生掌握“超越和三角函数图像的绘制”技能，加深对函数图像的认识和理解，提高数学思维能力和解决实际问题的能力。

三、实验内容：1、超越函数：正弦函数、余弦函数、正切函数、反正切函数等。

2、三角函数：指数函数、对数函数、幂函数、多项式函数等。

3、函数图像绘制的基本方法。

四、实验设备与材料：1、黑板或白板2、画板、画笔、尺子、三角板3、计算器或电脑软件五、实验教学方法：1、讲解+练习相结合，重点是绘制函数图像的方法和步骤。

2、通过小组合作、自主探究、互动交流等形式，提高学生的参与度和思考能力。

3、课堂上不断加强交流和互动，促进学生对课程内容的深入理解和掌握。

六、实验步骤：1、介绍函数的概念、域、值域、奇偶性、周期等数学概念及其在超越和三角函数中的应用。

2、介绍函数图像的基本要素、思路和方法，重点是绘图的基本技巧和注意事项。

4、讲解指数函数、对数函数、幂函数、多项式函数等函数的图像绘制方法和特点，着重介绍它们的单增性、严格单增性等数学性质。

5、教师讲解后，学生板书并练习一些例题，加深对函数图像的理解和掌握。

七、实验效果评估及注意事项：1、在教学过程中，要加强教学评价，及时对学生的掌握情况进行检测和培养，使学生能够充分理解课程内容和掌握实验操作技能。

2、实验过程中，学生要保持注意力集中，按时按要求完成实验，避免实验材料的浪费和损坏。

3、实验结束后，要及时统计学生表现情况和总结实验经验，为教学改进提供参考依据。

4、实验结束后，学生要及时清理教室和实验设备，保持教室和设备的整洁和完好。

5、教师要根据实验效果，适时进行教学调整和改进，以提高教学与实验的质量和深度。

数学实验基础实验报告

实验名称：线性方程组的求解实验目的：1. 理解线性方程组的基本概念和解法。

2. 掌握高斯消元法和矩阵运算的基本方法。

3. 培养学生运用数学软件进行实验的能力。

实验器材：1. 计算机2. 数学软件（如MATLAB、Mathematica等）3. 纸和笔实验时间：2023年X月X日实验内容：一、实验背景线性方程组是数学中常见的一类问题，它在工程、物理、经济学等领域有着广泛的应用。

本实验旨在通过计算机软件，解决线性方程组的求解问题，并加深对线性代数知识的理解。

二、实验原理线性方程组的求解方法有很多，如高斯消元法、克拉默法则等。

本实验主要介绍高斯消元法。

高斯消元法是一种通过行变换将系数矩阵化为上三角矩阵，从而求解线性方程组的方法。

三、实验步骤1. 准备实验数据：根据题目要求，准备一个线性方程组，如：\[ \begin{cases}2x + 3y - z = 8 \\x - 2y + 3z = 4 \\3x + 2y - 4z = 0\end{cases} \]2. 使用数学软件编写程序，实现高斯消元法。

以下为MATLAB代码示例：```matlab% 定义系数矩阵和常数项A = [2 3 -1; 1 -2 3; 3 2 -4];b = [8; 4; 0];% 高斯消元法r = size(A, 1);for i = 1:r% 寻找主元[~, maxIndex] = max(abs(A(i:r, i)));maxIndex = maxIndex + i - 1;% 交换行A([i maxIndex], :) = A([maxIndex i], :);b([i maxIndex]) = b([maxIndex i]);% 消元for j = i+1:rfactor = A(j, i) / A(i, i);A(j, i:r) = A(j, i:r) - factor A(i, i:r);b(j) = b(j) - factor b(i);endend% 输出结果x = A \ b;disp('方程组的解为：');disp(x);```3. 运行程序，观察输出结果，验证方程组的解是否正确。

数学实践活动实验方案

一、实验目的1. 提高学生对数学知识的实际应用能力。

2. 培养学生的创新思维和团队合作精神。

3. 激发学生对数学学科的兴趣，增强学习动力。

4. 帮助学生将数学知识运用到实际生活中，提高综合素质。

二、实验内容1. 实验一：生活中的数学（1）收集生活中与数学相关的问题，如购物、烹饪、旅游等。

（2）运用所学数学知识解决这些问题。

（3）撰写实验报告，总结经验。

2. 实验二：数学建模（1）选择一个实际问题，如环保、交通、经济等。

（2）分析问题，建立数学模型。

（3）运用数学方法求解模型，得到结果。

（4）撰写实验报告，分析结果。

3. 实验三：数学竞赛（1）组织学生参加数学竞赛，如奥数、数学建模等。

（2）辅导学生准备竞赛，提高解题技巧。

（3）总结竞赛经验，提高学生的数学素养。

4. 实验四：数学实验（1）设计数学实验方案，如几何实验、概率实验等。

（2）实施实验，观察现象，记录数据。

（3）分析实验结果，得出结论。

（4）撰写实验报告，总结实验过程和结果。

三、实验方法1. 实验一：观察法、调查法、分析法（1）观察法：观察生活中与数学相关的问题，记录下来。

（2）调查法：通过访谈、问卷调查等方式，了解问题背景和需求。

（3）分析法：运用数学知识，分析问题，提出解决方案。

2. 实验二：建模法、分析法、求解法（1）建模法：根据实际问题，建立数学模型。

（2）分析法：分析模型，找出关键因素。

（3）求解法：运用数学方法，求解模型，得到结果。

3. 实验三：辅导法、竞赛法、总结法（1）辅导法：针对竞赛内容，辅导学生解题技巧。

（2）竞赛法：组织学生参加竞赛，提高解题能力。

（3）总结法：总结竞赛经验，提高学生的数学素养。

4. 实验四：设计法、观察法、分析法（1）设计法：设计实验方案，确定实验步骤。

（2）观察法：观察实验现象，记录数据。

（3）分析法：分析实验结果，得出结论。

四、实验步骤1. 实验一：（1）收集生活中与数学相关的问题。

（2）运用所学数学知识解决这些问题。

《数学实验》课程教学大纲

《数学实验》课程教学大纲课程编号： 90907012学时：32学分：2适用专业：本科各专业开课部门：各学院一、教学的目的和要求数学实验是借助数学软件,结合所学的数学知识解决实际问题的一门实验课。

数学实验分基础实验和建模实验。

基础实验要求学生熟悉MATLAB软件环境，熟悉软件库函数，比较熟练地运用MATLAB常用工具箱函数。

建模实验要求学生能用高等数学知识建立简单模型，并会用MA TLAB求解。

通过数学实验课程的教学，培养学生熟练地应用MA TLAB解决相关课程中的复杂数学计算的能力和建立简单数学模型的能力。

二、实验名称与学时分配三、实验的目的、内容、方法及要求实验（一）MA TLAB入门1.实验目的熟悉MATLAB，掌握矩阵输入与矩阵运算实现。

2.实验内容MATLAB的工作环境，MATLAB帮助文档的使用，MATLAB矩阵输入和运算。

3.实验方法观察推演法。

4.实验要求熟悉MATLAB的工作环境，掌握MATLAB帮助文档的使用，掌握MA TLAB的矩阵输入和运算。

实验（二）程序设计基础1.实验目的掌握MATLAB的简单编程方法。

2.实验内容MATLAB的基本程序设计原则，常量和变量，程序的运算符，数据类型，程序流程控制语句以及各数组的运算。

3.实验方法观察推演法。

4.实验要求理解MATLAB的基本程序设计原则，掌握常量和变量，程序的运算符，数据类型，会设计简单程序。

实验（三）MA TLAB数值计算1.实验目的掌握矩阵的数值计算、多项式的拟合和插值运算。

2.实验内容矩阵的定义和函数定义，矩阵的数值计算方法，多项式基本运算及多项式拟和和多项式的插值运算3.实验方法观察推演法。

4.实验要求理解矩阵的定义和函数定义，掌握矩阵的数值计算方法，掌握多项式基本运算及多项式拟和和多项式的插值运算。

实验（四）MA TLAB符号计算1.实验目的会用MATLAB符号进行微积分，线性代数运算，方程求解。

2.实验内容在线帮助和系统演示，创建和使用符号对象，微积分、线性代数的运算，方程求解。

学期实验教学任务书模板

比例
例：20L162Q 机械原理
64
必修
张英
机构简图测绘与分析实验
2
机电10 级
400
第四周周三第 1、2节
15
1
15
26.7 53.33
自然班
综合
Z405
洪建平徐双满
高工
50% 50%
注：若实验时间一旦确定或有变化，请务必至少提前1-2天报教学科。
任课教师：
实验教师：
说明：1、课程属性为必修或限选； 2、实验组织方式分为自然班或教学班； 3、实验轮次为根据实验组织方式而确定的实验轮数； 4、实验性质分为综合、设计、自主研究和验证； 4、实验教师工作量分配比例为各实验教师分配工作量占总工作量的百分比； 5、实验教学任务书为工作量计算依据，请仔细填写。
20 -20 （）学期实验教学任务书
课程号
课程名称
课程总学
时
课程属性
任课教师
实验名称
实验计划学时
参加实验的班
级
实Hale Waihona Puke 人数实验时间一次实验台套
数
实验人数/1台
套
实验人数 /轮次
实验总轮
次
实验总学
时
实验已认定组织实验性方式质
实验地点
实验教师
实验教师职称
实验教师工作量分配
实验中心主任：

数学教学实验工作计划及安排

数学教学实验工作计划及安排一、背景介绍数学教学实验是为了探索新的教学方法和手段，提高数学教学效果，培养学生的数学思维能力和解决问题能力而进行的一种实践活动。

本次数学教学实验旨在通过引入创新的教学策略和新颖的教学资源，提升学生的学习兴趣和水平。

以下是本次数学教学实验的工作计划及安排。

二、工作目标1. 提高学生的数学学习兴趣和主动性；2. 培养学生的数学思维能力和解决问题能力；3. 探索适合本班学生的数学教学模式。

三、工作计划与安排1. 教学内容的选择根据学生的学习情况和实际需求，选择合适的数学教学内容。

优先选择与学生生活相关、具有实际应用意义的数学知识，增强学生对数学的兴趣。

2. 教学策略的确定结合教学内容与学生的特点，确定适合本班学生的教学策略。

采用探究式教学、合作学习、项目学习等多种教学方法，激发学生的学习兴趣和积极性。

3. 教学资源的准备收集和准备适合本次实验的教学资源，包括教材、习题集、教学工具、多媒体课件等。

积极利用互联网资源，寻找适合本次实验的在线学习平台和数学教育应用程序。

4. 教学环境的改善改善教学环境，创设良好的学习氛围。

调整教室布局，使学生能够进行合作学习和小组讨论。

创建数学角，展示学生的作品与成果，鼓励他们分享数学学习的心得体会。

5. 教学进度的安排结合实际情况，合理安排教学进度。

根据学生的学习情况和理解程度，灵活调整教学进度，确保每个学生都能跟上教学进度。

6. 评价与总结定期进行学生学习情况的评估，记录学生的学习表现和成绩，及时给予反馈和指导。

每周进行一次教学总结，反思教学过程中的问题和不足，及时进行改进和调整。

《数学实验》报告册(华南农业大学)

《数学实验》报告册(华南农业大学)
一、实验目的
本实验的目的是通过实践来深入学习高中数学中的函数、极限、导数等概念和运算，掌握一些应用技巧，加深对数学知识的理解和应用，提高数学思维能力和创新意识。

二、实验过程
本次实验共包括函数的变化趋势、导数与函数的性质、曲线的相关概念与方法、等差数列与等比数列等。

在实验中，我们用数学软件Geogebra进行数学模拟，还使用了一些工具在纸上进行计算和绘图。

1.函数的变化趋势
实验中，我们首先通过Geogebra绘制出一个函数图像，然后利用函数的导数等工具和知识，分析函数图像的运动变化趋势，并进行比较和总结。

2.导数与函数的性质
在这一部分中，我们通过对导数的定义和性质，结合具体的函数图像，来分析函数的性态变化趋势，并对函数的极值、最值、单调性、凸凹性等进行分析。

3.曲线的相关概念与方法
在这一部分中，我们通过曲线的方程和图像，来学习曲线的一些基本概念，如切线、法线、弧长、曲率半径等，同时还进行了一些曲线变换的操作，如平移、翻转、放缩等。

4.等差数列与等比数列
这一部分中，我们学习了等差数列和等比数列的基本概念和特点，掌握了求这些数列的和、通项公式等应用技巧。

三、实验收获
此外，我还学会了如何使用数学软件Geogebra，在使用过程中，我体会到了数学计算和思考的乐趣，并发现了数学工具的优越性，感受到了在数学实践中使用现代科技手段的重要性。

总之，本次实验使我更加熟练地掌握了高中数学中的一些基本概念和运算，提高了我的数学能力和综合素质，也拓展了我的视野和思考方式，使我更加自信地面对数学学习和应用。

高中数学实验教学计划书

高中数学实验教学计划书一、教学主题本次实验教学的主题是“应用数学的探索与实践”。

通过实验教学的方式，让学生能够亲自参与数学实践活动，在实际应用中提高数学思维能力和解决问题的能力。

本次实验教学将涉及几个与实际生活紧密相关的数学应用领域，包括统计分析、数据处理、几何推理等。

二、活动安排1. 实验教学目标本次实验教学的主要目标是让学生掌握统计调查方法和数据处理技能，培养学生分析和解读数据的能力；培养学生的几何推理能力，让他们能够运用几何知识解决实际问题。

2. 实验准备在实验开始之前，教师需要准备相关的实验器材和材料，包括统计调查表、测量工具、数据处理软件等。

同时，教师还需对实验过程进行详细的规划和安排，确保实验的顺利进行。

3. 实验活动（1）统计调查实验通过设计实际调查问题，让学生进行统计调查，收集数据，并利用所学知识进行数据处理和分析。

例如，可以设计一个调查问题：“你所在班级的学生喜欢的体育项目有哪些？”，学生可以制作调查表，收集数据，并用统计图表展示结果。

（2）数据处理实验将学生收集到的数据进行整理和处理，教师可以教授学生如何使用Excel等数据处理软件进行数据整理和分析，例如制作各种图表展示数据分布、计算中心位置和散布情况等。

（3）应用几何实验通过实际应用场景，让学生运用几何知识解决问题。

例如，可以设计一个问题：“如何确定一个三角形的面积？”，学生可以利用所学的几何知识设计实验方法，并进行实际测量和计算。

三、教材使用本次实验教学主要使用教材中的统计与概率、几何推理等相关章节内容。

教师可以结合实际应用场景对教材中的知识点进行深入讲解，并引导学生进行实际操作和实践。

四、教学评估在实验教学结束后，教师需要对学生的实验过程和结果进行评估。

评估方法可以包括学生实验报告的撰写和展示、实际操作的评判等。

通过评估结果，教师可以了解学生的实际掌握情况，并对教学过程进行反思和优化。

五、总结与展望通过本次实验教学活动，学生能够亲自参与数学实践活动，提高数学思维能力和解决问题的能力。

数学教学实验计划

数学教学实验计划1.引言为了提高学生数学学习的兴趣和效果，我制定了一项数学教学实验计划。

这个计划将通过丰富的内容形式和结构，以及一定的长度和深度，来帮助学生更好地理解和应用数学知识。

2.设定目标首先，我将明确本次实验的目标。

我希望通过这个实验，让学生在数学学习中发展出自主学习和合作学习的能力。

同时，我希望他们不仅掌握数学的基本概念和技巧，还能培养数学思维和解决问题的能力。

3.实验内容本次实验将涵盖多个数学领域的内容，如代数、几何、概率等。

我计划设计一系列的任务和习题，让学生通过完成这些任务和习题来学习和巩固数学知识。

我会选择一些贴近学生实际生活和感兴趣的题材，以增加他们的学习动力。

4.多样化教学方法为了提高学生的学习效果，我将采用多样化的教学方法。

除了传统的课堂讲解和演示外，我还会使用互动教学、小组合作学习、实践探究等方式。

例如，在学习几何时，我将鼓励学生通过实地观察和测量来发现几何形状的特征，以提高他们的直观理解能力。

5.个性化学习在实验中，我将注重学生的个性化学习。

每个学生的数学理解和能力都有所不同，我会根据他们的水平和需求，分别安排不同难度和类型的任务。

同时，我也会鼓励学生自主选择学习内容，并提供个性化的指导和批判性反馈。

6.评估方式为了评估学生的学习效果，我计划采用形成性评价和终结性评价相结合的方式。

形成性评价将在课堂中进行，包括小组合作任务的表现和课堂练习的成绩。

而终结性评价将通过考试和综合作业来完成，以全面评估学生对数学知识的掌握和应用能力。

7.实施过程我计划将实验计划分为若干个单元，在每个单元内设置相应的任务和习题。

每个单元将包括引入新知识、实践探索和巩固练习三个环节。

我将根据学生的进展和反馈，调整课堂进度和内容，确保每个学生都能达到预期的学习目标。

8.资源和工具在实验中，我将提供多种资源和工具来支持学生的学习，如教科书、课件、实验器材等。

此外，我还会鼓励学生利用互联网资源，如在线学习平台和数学学习网站，来拓宽知识面和解决问题。

人教版2022--2023学年度第一学期初中数学实验计划

人教版2022--2023学年度第一学期初中数学实验计划人教版2022-2023学年度第一学期初中数学实验计划简介该数学实验计划旨在提高学生对数学的兴趣，培养他们的数学思维能力和解决问题的能力。

通过实际操作和探究，让学生在数学中享受研究的乐趣，并提升他们的研究效果。

目标1. 激发学生研究数学的兴趣和热情。

2. 提升学生的数学知识与技能。

3. 培养学生的数学思维和解决问题的能力。

4. 增强学生的自主研究和合作研究能力。

实施内容1. 数学实验课程设计：通过设计不同主题和内容的数学实验课程，激发学生的探究欲望，培养他们的实验能力和总结能力。

2. 教师引导和学生探究：教师应扮演引导者的角色，在学生的实验过程中提供指导和帮助，鼓励学生自主探究和合作研究。

3. 实验报告和展示：学生应在每次实验结束后完成实验报告，并在班级内展示实验结果。

通过报告和展示，培养学生的表达能力和分享能力。

4. 评价和反馈：教师应定期进行评价和反馈，鼓励学生不断改进和提高。

实施步骤1. 制定实验计划：根据学校课程要求和学生需求，制定符合教学目标的实验计划。

2. 实施实验课程：安排时间和场地，实施数学实验课程。

3. 学生实验报告：要求学生在每次实验后完成实验报告，包括实验目的、过程、结果和总结。

4. 实验展示：安排学生在班级内展示实验结果，通过口头陈述和展示板等方式展示。

5. 评价和反馈：定期对学生的实验报告和实验展示进行评价，给予积极的反馈和建议。

期望效果通过实施该数学实验计划，我们期望学生能够更加主动地研究数学，提高数学知识与技能的掌握程度，培养数学思维和解决问题的能力。

同时，期望学生能够在实验中锻炼自主研究和合作研究的能力，提高表达和分享能力，形成良好的研究惯和研究动力。

结束语本实验计划旨在为学生提供更有趣、更实践、更探究的数学研究方式，希望通过实验的方式能够激发学生的兴趣，提高研究效果。

希望通过实施该实验计划，能够为学生的数学研究和发展提供有效的支持和帮助。

小学数学实验活动计划方案

一、活动背景随着新课程改革的不断深入，小学数学教学越来越注重培养学生的动手操作能力、实践能力和创新精神。

为了提高学生的数学素养，激发学生的学习兴趣，我校特制定本次数学实验活动计划方案。

二、活动目标1. 培养学生的动手操作能力，让学生在实践中学习数学知识。

2. 培养学生的观察、分析、归纳能力，提高学生的数学思维能力。

3. 激发学生的学习兴趣，培养学生对数学学科的热情。

4. 培养学生的合作精神，提高学生的团队协作能力。

三、活动内容1. 实验一：测量物体的长度（1）学生分组，每组选用不同的测量工具（尺子、卷尺等）。

（2）学生在教师指导下，测量教室内的物体长度。

（3）学生记录测量数据，分析测量结果，总结测量方法。

2. 实验二：探究图形的面积（1）学生分组，每组选用不同的图形（长方形、正方形、三角形等）。

（2）学生在教师指导下，用不同的方法计算图形的面积。

（3）学生比较不同方法的优缺点，总结计算面积的方法。

3. 实验三：探索分数的意义（1）学生分组，每组选用不同的分数（1/2、1/3、1/4等）。

（2）学生在教师指导下，用图形表示分数的意义。

（3）学生比较不同分数的大小，总结分数的性质。

4. 实验四：探究数字的规律（1）学生分组，每组选用不同的数字（1、2、3等）。

（2）学生在教师指导下，观察数字的规律，找出数字之间的联系。

（3）学生总结数字的规律，用数学语言表达规律。

四、活动安排1. 活动时间：每周一、三、五下午第三节课。

2. 活动地点：学校实验室、教室。

3. 活动对象：三年级至六年级全体学生。

五、活动评价1. 教师评价：观察学生在活动中的表现，记录学生的实验成果，评价学生的动手操作能力、观察分析能力和创新能力。

2. 学生评价：学生之间互相评价，互相学习，共同进步。

3. 家长评价：邀请家长参与活动，了解学生的表现，共同关注学生的成长。

六、活动总结1. 活动结束后，组织学生进行总结，分享实验心得，总结实验成果。