云南大学软件学院大物实验磁场
磁场研究实验报告

一、实验目的1. 理解并掌握磁场的基本概念和基本定律,如毕奥-萨伐尔定律、安培环路定理等。
2. 学习使用各种实验仪器测量磁场,包括数字式毫特斯拉计、霍尔传感器等。
3. 掌握磁场分布的实验方法,通过实验验证磁场叠加原理和毕奥-萨伐尔定律。
4. 分析实验数据,加深对磁场理论的理解。
二、实验原理1. 毕奥-萨伐尔定律:载流线圈在空间某点产生的磁感应强度与电流强度、线圈半径、距离和角度有关。
2. 安培环路定理:闭合路径上的磁场与电流的乘积在路径上的积分等于穿过路径的电流乘以真空磁导率。
3. 磁场叠加原理:多个磁场在同一空间内叠加时,磁场强度等于各单个磁场在该点的矢量和。
三、实验仪器1. 圆线圈和亥姆霍兹线圈实验平台2. 高灵敏度三位半数字式毫特斯拉计3. 三位半数字式电流表4. 直流稳流电源组合仪5. 传感器探头(2只配对的95A型集成霍尔传感器)6. 探头盒7. 大理石台面四、实验步骤1. 搭建实验平台:将圆线圈和亥姆霍兹线圈固定在实验平台上,确保线圈与台面平行。
2. 连接仪器:将毫特斯拉计、电流表和直流稳流电源连接到相应的线圈上。
3. 设置参数:调节电流强度和线圈半径,记录实验数据。
4. 测量磁场:将传感器探头放置在圆线圈和亥姆霍兹线圈轴线上不同位置,测量磁感应强度。
5. 数据分析:使用MATLAB等软件对实验数据进行处理和分析,绘制磁场分布图。
五、实验结果与分析1. 圆线圈磁场:实验结果显示,圆线圈轴线上的磁感应强度与理论计算值基本一致。
在圆线圈中心处,磁感应强度达到最大值。
2. 亥姆霍兹线圈磁场:实验结果显示,亥姆霍兹线圈轴线上的磁感应强度在中心位置达到最大值,且磁场分布较为均匀。
这与理论计算结果相符。
3. 磁场叠加原理:通过实验验证了磁场叠加原理,即多个磁场在同一空间内叠加时,磁场强度等于各单个磁场在该点的矢量和。
六、实验结论1. 本实验成功验证了毕奥-萨伐尔定律和安培环路定理的正确性。
2. 通过实验测量了圆线圈和亥姆霍兹线圈轴线上磁场的分布,加深了对磁场理论的理解。
载流圆线圈的磁场分布研究

载流圆线圈的磁场分布研究杜珊;王琼辉;王婧;项云钏【摘要】利用毕奥-萨伐尔定律计算出载流圆线圈平面内和轴线上磁场分布的数学表达式,并结合实验数据分析研究载流圆线圈平面内部分场点的磁场分布情况以及轴线上磁感应强度的大小.结果表明,载流圆线圈平面内任意点的磁感应强度的大小与线圈半径和该点到圆心的距离有关,而载流圆线圈轴线上的磁场随场点到圆心距离的增大而逐渐减弱,且与轴线两端成对称分布.从而进一步加深了对毕奥-萨伐尔定律的认识.此外,采用软件Mac Os Grapher辅助处理实验数据,使结论更具直观性.【期刊名称】《昆明学院学报》【年(卷),期】2017(039)006【总页数】5页(P94-97,100)【关键词】载流圆线圈;毕奥-萨伐尔定律;磁感应强度;磁场分布【作者】杜珊;王琼辉;王婧;项云钏【作者单位】昆明学院物理科学与技术系,云南昆明650214;昆明学院物理科学与技术系,云南昆明650214;昆明学院物理科学与技术系,云南昆明650214;昆明学院物理科学与技术系,云南昆明650214【正文语种】中文【中图分类】O441.2在大学物理教学中讨论载流圆线圈产生的磁场时,通常只给出圆线圈轴线上任意点和圆心处的磁感强应度.本文试图从更一般的角度来探讨这个问题,即运用毕奥-萨法尔定律计算载流圆线圈平面内任意一点及轴线上的磁感应强度的大小,然后再结合实验数据进行综合性讨论.如图1所示,半径为R的圆线圈中流有电流I,O为圆心,P为圆线圈平面内任意一点,P与圆心的距离为a.在圆线圈上任一点A处取电流元则根据毕奥-萨伐尔定律可得在P点产生的磁感应强度为[1]:的方向由右手螺旋定则确定,为垂直于纸面指向外.因为圆线圈上每一个电流元在P点的磁感应强度方向相同,所以由磁场的叠加原理可得P点的磁感应强度大小:为了计算方便,连接OP并取它与X轴重合,其垂直方向为Y轴,在OXY坐标系中,圆的方程是[2]:令与X轴之间的夹角为θ,则有:因为P是圆内任意一点,所以r的值不会小于零,由此可求得r与θ之间的函数关系式为:在图1中作AC⊥DP,并令AC与AD之间的夹角为β,则可得dlsinα=dlsin=dlcosβ=rdθ.顺便指出,在图1中与之间的夹角α>π/2.如果α﹤π/2,则有dlsinα=dlsin(π/2-β)=dlcosβ=rdθ;当α=π/2时,dlsinα=dl=rdθ.因为0﹤α﹤π/2.因此,总有关系式dlsinα=rdθ成立.把(2)式和(3)式带入(1)式,得:因为[3]:()2-()2-…],()-…],=,B== .因为P点是圆线圈平面内的任意一点,过任意点都可以作出一个过圆心的x轴线,所以上式对圆线圈平面内的所有点都适用.下面对一些特殊点进行讨论,由(6)式得出不同的点B与a的关系,并画出B随a的变化关系曲线.1)当a=0(即圆心处),B0=μ0I/2R;2)当a=±R/4时,B=1.05B0;3)当a=±2R/4时,B=1.25B0;4)当a=±3R/4时,B=1.96B0;5)当a=±R时,B=∞.此种情况在物理上没有意义.根据以上讨论可得载流圆线圈平面内B~a关系曲线,如图2所示.为了验证上述理论的正确性,可利用亥姆赫兹线圈磁场实验仪(HZDH)测量载流圆线圈平面内不同点的磁感应强度数值,同时利用(6)式计算其理论值,并将理论值和实验值进行比较分析.有关参数、实验数据见表1和表2.取圆线圈平面上一直径为横坐标,表 2中各场点a分布在该坐标轴上,以与它们所对应的磁感应强度B为纵坐标,根据表2的数据,画出各场点的磁感应强度B与a的关系曲线,如图3所示.为了更全面、直观地反映载流圆线圈平面内其他场点磁场的分布情况,借助Mac Os Grapher软件,并参照表2的数据作出平面内不同直径轴线上各点的磁感应强度B与a的关系曲线,以便理解不同角度的磁场分布情况,进一步验证(6)式对圆线圈平面内的所有点都适用,如图4所示.上述实验中,通过线圈的电流是直流电流,主要测量的是磁感应强度的大小.从B 随a的变化关系曲线(图3和图4)可以看出,它们符合相同的规律,即圆心处磁感应强度B值最小.随着a的增大,B也增大.且任意直径上点的磁感应强度大小相对圆心处呈对称性分布,这样就验证了(6)式的正确性,即在载流圆线圈平面内,磁场分布是不均匀的,同时也进一步加深了对毕奥-萨伐尔定律的认识.对于上述分析,图4看到的结论更具普遍性和直观性.如图5所示,半径为R的圆线圈,在线圈中通上电流时,则通电线圈就会在其周围空间激发磁场[4].设线圈上某点A处的电流元在线圈轴线上任意点P产生了元磁场它的方向垂直于PA联线并和POA面处于同一面内,且与轴线OP的夹角α=∠PAO.根据毕奥-萨伐尔定律dB=sinθ,对于轴线上的点P,θ=π/2,sinθ=1.设r0为P点到线圈中心的距离,则r0=rsinα,r=,dB = sin2 α.由磁场的叠加原理得B=dBcosα = sin2 αcosαdl .由于cosα = ,sinα = ,(8)式有以下两种特殊情况[5]:1)在圆心处,r0=0,B=μ0I/2R;2)当r0>>R时下面采用实验的方法研究载流圆线圈轴线上的磁感强度分布.取电流I=500 mA,线圈平均半径R=11.00 cm,线圈匝数N=500匝,并且真空磁导率μ0=4π×10-7 N/A-2.载流圆线圈轴线上不同位置磁感应强度B的测量结果见表3.以r为横坐标,B为纵坐标画出载流圆线圈轴线上磁场分布情况,如图6所示(坐标原点在圆心处).同样,也可应用Mac Os Grapher软件画出上图,该图能更直观地反映载流圆线圈轴线上磁场的分布情况,如图7所示.根据(6)式,1)在圆心处磁感应强度的理论计算值为:B=B(0)=μ0NI/2R=1.43 mT;而实验测得的圆心处磁感应强度值:B′(0)=1.45 mT.百分误差:ε=×100%=×100%≈1.4%.2)r0=5 cm时,可得此时的理论值为:B(5) = = = 1.077 mT;实验中测得的值:B′(5)=1.048 mT.则百分误差:ε==×100%≈2.7%.实验中,我们采用霍耳元件测出磁场中不同点的磁感应强度B,取代了传统的线圈感应法测磁场,即不必靠人为缓慢转动线圈平面与磁场垂直,通过判断感应电动势的“极大值”来测B的大小,大大提高了实验的精度,有效地减小了系统误差.此外,从图6可看出,当载流圆线圈轴线上的点在圆心处时,磁感应强度为最大,并且圆线圈轴线上的磁感应强度随x与圆心距离的增大而逐渐减小[5].轴线两边的磁场以轴线中心为原点成对称性分布,说明实验和理论能很好地契合.综上所述,本文利用毕奥-萨伐尔定律分别对载流圆线圈平面内任意一点和轴线上任意点的磁感应强度进行了理论推导,并进行了实验研究,进一步验证了理论推导的正确性,从而揭示了载流圆线圈平面内及轴线上的磁场分布规律.此外,在上述研究中我们使用了软件Mac Os Grapher辅助处理实验数据,使得结论更具直观性,如果把此方法运用到教学中,则能够激发学生的好奇心,调动学生的学习积极性,使学生更好地理解磁场的分布情况,从而提高教学质量.【相关文献】[1]赵凯华,陈熙谋.电磁学[M].北京:高教出版社,2003:94-98.[2]沈犁理,钟寿仙.圆电流所包围的平面内磁感应强度的分布[J].昆明师专学报,1997,12(2):46-47.[3]胡邵宗.椭圆积分的计算及其应用[J].大学数学,2013,29(1):111-113.[4]张玉明,威博云.电磁学[M].合肥:中国科学技术大学出版社,2008:213-226.[5]杨述武,赵立竹,沈国土.普通物理实验2:电磁学部分[M].4版.北京:高等教育出版社,2011:126-132.。
大学磁场测量实验报告

一、实验目的1. 理解磁场的基本概念和特性。
2. 掌握利用不同方法测量磁场的方法和原理。
3. 通过实验加深对电磁学基本定律的理解。
4. 培养实验操作能力和数据处理能力。
二、实验原理磁场是描述磁力作用的空间状态,其基本单位是特斯拉(T)。
本实验主要涉及以下几种磁场测量方法:1. 螺线管磁场测量:利用安培力定律,通过测量电流和螺线管几何尺寸来计算磁场强度。
2. 霍尔效应磁场测量:利用霍尔效应,通过测量霍尔电压和霍尔系数来计算磁场强度。
3. 地磁场测量:利用磁针或磁强计测量地磁场的水平分量和垂直分量。
三、实验器材1. 螺线管实验装置:螺线管、电流表、安培计、尺子等。
2. 霍尔效应实验装置:霍尔元件、稳压电源、毫伏表、导线等。
3. 地磁场测量装置:磁针或磁强计、指南针、水平仪等。
四、实验步骤1. 螺线管磁场测量:1.1. 将螺线管连接到稳压电源和电流表上。
1.2. 通过调节稳压电源,使电流表显示一定电流值。
1.3. 使用尺子测量螺线管的长度、直径和匝数。
1.4. 根据安培力定律计算螺线管内的磁场强度。
2. 霍尔效应磁场测量:2.1. 将霍尔元件连接到稳压电源和毫伏表上。
2.2. 调节稳压电源,使电流表显示一定电流值。
2.3. 使用指南针或磁强计确定磁场方向。
2.4. 通过测量霍尔电压和霍尔系数,计算磁场强度。
3. 地磁场测量:3.1. 将磁针或磁强计放置在水平面上。
3.2. 使用水平仪调整磁针或磁强计,使其水平。
3.3. 使用指南针确定磁场方向。
3.4. 记录磁针或磁强计的读数,计算地磁场的水平分量和垂直分量。
五、实验结果与分析1. 螺线管磁场测量:1.1. 通过实验数据,计算得到螺线管内的磁场强度为X特斯拉。
1.2. 对比理论计算值,分析误差来源。
2. 霍尔效应磁场测量:2.1. 通过实验数据,计算得到磁场强度为Y特斯拉。
2.2. 对比理论计算值,分析误差来源。
3. 地磁场测量:3.1. 通过实验数据,计算得到地磁场的水平分量和垂直分量分别为Z特斯拉和W特斯拉。
云南大学大学物理实验6-实验报告模板

云南大学软件学院 实验报告课程: 大学物理实验 学期: 2012-2013学年 第一学期 任课教师: 专业: 学号: 姓名: 成绩:实验6 示波器一、实验目的1.了解示波器的主要结构和显示波形的基本原理。
2.学会使用信号发生器。
3.学会用示波器观察波形以及测量电压、周期和频率。
二、实验内容1.观察信号发生器波形 2.测量正弦波电压在示波器上调节出大小适中、稳定的正弦波形,选择其中一个完整的波形,先测算出正弦波电压峰—峰值U p-p ,即:U p-p =(垂直距离DIV )×(档位V/DIV )×(探头衰减率)= 20V然后求出正弦波电压有效值U 为2U 71.0U pp -⨯== 7.1V3.测量正弦波周期和频率在示波器上调节出大小适中、稳定的正弦波形,选择其中一个完整的波形,先测算出正弦波的周期T ,即T =(水平距离DIV )×(档位t/DIV )= 1s然后求出正弦波的频率T f 1== 1Hz 。
4.利用李萨如图形测量频率设将未知频率f y 的电压U y 和已知频率f x 的电压U x(均为正弦电压),分别送到示波器的Y 轴和X 轴,则由于两个电压的频率、振幅和相位的不同,在荧光屏上将显示各种不同波形,一般得不到稳定的图形,但当两电压的频率成简单整数比时,将出现稳定的封闭曲线,称为李萨如图形。
根据这个图形可以确定两电压的频率比,从而确定待测频率的大小。
图4-15-8列出各种不同的频率比在不同相位差时的李萨如图形,不难得出:yx xy N N f X f Y 点数垂直直线与图形相交的点数水平直线与图形相交的轴电压的频率加在轴电压的频率加在=所以未知频率xyx y f NN f =但应指出水平、垂直直线不应通过图形的交叉点。
测量方法如下:(1)将一台信号发生器的输出端接到示波器Y 轴输入端上,并调节信号发生器输出电压的频率为50Hz ,作为待测信号频率。
把另一信号发生器的输出端接到示波器X 轴输入端上作为标准信号频率。
磁力仿真分析实验报告

磁力仿真分析实验报告1. 引言磁力仿真分析是一种通过计算机模拟磁场行为的方法,可以用于各种应用场景,如电机设计、传感器优化等。
本实验旨在通过使用磁力仿真软件来模拟磁力场行为,并对其进行分析和评估。
2. 实验目的- 了解磁力场仿真原理和方法- 学习使用磁力仿真软件进行磁力场仿真- 分析和评估不同磁力场设计方案的优缺点3. 实验步骤3.1 实验准备- 下载并安装磁力仿真软件(例如Comsol Multiphysics)- 准备实验所需材料,如磁铁、线圈等3.2 建立模型在磁力仿真软件中,根据实验需求和要模拟的现象建立相应的模型。
例如,如果要研究磁铁与线圈间的磁力作用,可以在软件中创建一个磁铁和线圈的模型。
3.3 设置仿真参数根据实验需求和模型特性,设置仿真参数,如磁场强度、电流大小等。
这些参数可以根据已知的物理特性或者实验要求来确定。
3.4 运行仿真在完成建立模型和设置参数后,开始运行仿真。
磁力仿真软件将计算模型中的磁场分布,并根据设定的仿真参数生成相应的结果。
3.5 分析结果根据仿真结果,我们可以获得研究对象在不同条件下的磁场分布、力的大小和方向等信息。
这些结果可以帮助我们了解物理现象,并优化设计方案。
4. 实验结果与讨论在实验中,我们以磁铁和线圈的相互作用为例,进行了磁力仿真分析。
通过改变磁场强度和电流大小等参数,我们观察到以下现象:1. 磁场变化:随着磁铁与线圈间的距离增加,磁场强度逐渐减小,符合磁场衰减规律。
2. 力的大小和方向:根据模拟结果,我们可以确定磁铁和线圈间的作用力大小和方向。
在不同条件下,作用力大小和方向有所变化。
根据实验结果,我们可以得出以下结论:1. 通过磁力仿真分析,我们可以快速了解不同条件下磁力场的行为,避免实验耗时和成本。
2. 磁力仿真分析结果可以为磁场设计和优化提供指导,帮助我们更好地理解和改进现有设计。
5. 结论通过本次实验,我们初步了解了磁力仿真分析的原理和方法,学会了使用磁力仿真软件进行磁场行为模拟,并分析了实验结果。
大学物理实验报告

大学物理实验指导书云南大学软件学院目录1.课程基本信息 (2)2.课程简介 (2)3.教学目的与基本要求 (2)4.考核方式和成绩评定办法 (3)5.参考文献 (3)6.实验指导 (4)6.1测量及误差分析 (4)6.2质点运动学 (9)6.3质点动力学 (11)6.4静电场 (13)6.5磁场 (18)6.6电量测量.................................. 错误!未定义书签。
6.7波的叠加.................................. 错误!未定义书签。
6.8示波器.................................... 错误!未定义书签。
6.9传感器.................................... 错误!未定义书签。
6.10光的干涉与衍射.......................... 错误!未定义书签。
1. 课程基本信息名称:大学物理实验/College Physics Lab课程性质:学科基础总学时/学分: 32/12. 课程简介本实验课程根据教育部《非物理类理工学科大学物理实验课程教学基本要求》并结合软件学院人才培养目标开展教学。
本实验课程内容包括:•测量误差的基础知识、用计算机处理实验数据的基本方法,以及基本物理量的测量方法,并加强数字化测量技术的应用。
•结合软件学院的专业特点,通过计算机模拟和实际操作掌握误差分析方法、质点运动学、质点动力学、振动与波、电场、磁场、光的干涉与衍射等基本原理。
•学习常用物理实验方法,实验室常用仪器的性能,常用实验操作技术及仪器正确调节,学习简单的计算机模拟。
3. 教学目的与基本要求本实验课培养学生初步掌握实验科学的思想和方法,提高其分析能力和创新能力;培养理论联系实际的科学作风,认真严谨的科学态度,积极主动的探索精神,团结协作的职业素养。
使之加深对物理学基本概念、基本理论的理解,掌握运用物理学基本原理分析和解决问题的科学方法。
大学物理实验8-实验报告

云南大学软件学院实验报告
课程:大学物理实验学期:2014-2015学年第一学期任课教师:朱艳萍专业:学号:姓名:成绩:
实验8 光的干涉
一、实验目的
1.了解迈克耳逊干涉仪的结构,掌握调节方法;
2、观察光的干涉条纹。
二、实验步骤(用截图来表示)
1、调整干涉仪,为实验做好准备。
2、测量He-Ne激光的波长。
波长经计算得:631nm
3、测量钠光波长、波长差及相干长度。
缓慢转动微动手轮,移动M1,中心每生出或吞进n个条纹,几下移动的距离,用公式2h/n求出波长调节过程中发现钠光条纹的清晰度会产生变化。
4、测量透明薄片的折射率。
换用白光光源。
在d=0的附近可看到白色的干涉花纹:中央是直线黑纹,即中央花纹;两旁是对称分布的彩色花纹。
D稍大时,显不出条纹,当视场中出现中央花纹后,在M1与G1之间放入折射率为n,厚度为l的透明薄片,则此时光程差要比原来增大2l(n-1),中央花纹既移出视场范围,如果将M1向G1前移动d,使d=l(n-1) ,则中央花纹重新出现,测出d,则可由d=l(n-1)求出折射率n.。
大学物理实验5 磁场
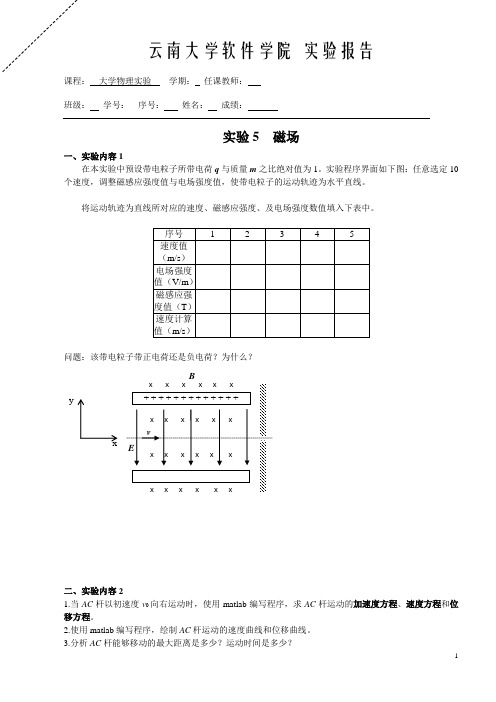
云南大学软件学院 实验报告课程: 大学物理实验 学期: 任课教师:班级: 学号: 序号: 姓名: 成绩:实验5 磁场一、实验内容1在本实验中预设带电粒子所带电荷q 与质量m 之比绝对值为1。
实验程序界面如下图:任意选定10个速度,调整磁感应强度值与电场强度值,使带电粒子的运动轨迹为水平直线。
将运动轨迹为直线所对应的速度、磁感应强度、及电场强度数值填入下表中。
问题:该带电粒子带正电荷还是负电荷?为什么?B x y二、实验内容21.当AC 杆以初速度v 0向右运动时,使用matlab 编写程序,求AC 杆运动的加速度方程、速度方程和位移方程。
2.使用matlab 编写程序,绘制AC 杆运动的速度曲线和位移曲线。
3.分析AC 杆能够移动的最大距离是多少?运动时间是多少?syms B L m R B v F v0F=sym((-(B*L).^2*v)/R);a=F/mu=dsolve('Dv=(-(B*L)^2*v)/(R*m)','v(0)=v0')x=dsolve('Dx=v0*exp(-B^2*L^2/R/m*t)','x(0)=0') t=0:0.01:5;u=1.*exp(-t);x=-1./exp(t)+1;subplot(2,1,1);plot(t,u);title('AC杆运动的速度');xlabel('t/s');ylabel('v/m*s^-^1');grid on;subplot(2,1,2);plot(t,x);title('位移');xlabel('t/s');ylabel('x/m');grid on;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 云南大学软件学院 实验报告
课程: 大学物理实验 学期: 2013-2014学年 第一学期 任课教师: 专业: 学号: 姓名: 成绩:
实验5 磁场
一、实验目的
通过计算机模拟速度选择器,研究恒稳磁场和静电场性质,验证速度、电场强度、磁感应强度 的关系。
二、实验内容
在本实验中预设带电粒子所带电荷q 与质量m 之比绝对值为1。
实验程序界面如下图:任意选 定10个速度,调整磁感应强度值与电场强度值,使带电粒子的运动轨迹为水平直线。
将运动轨迹为直线所对应的速度、磁感应强度、及电场强度数值填入下表中。
问题:
1、 该带电粒子带正电荷还是负电荷?为什么?
答:该粒子带正电;因为当磁场强度为0T 时,该粒子向下偏转,电场强度方向为y 轴负向。
2、 简要讨论速度值的大小对磁感应强度和电场强度的要求。
答:该带电粒子在复合场中运动时,所受合力为:qvB qE F F F m e +-=+=,所以当该粒子穿过恒稳磁场与静电场的复合场时,若要受力平衡,根据牛顿定律要求加速度为0,即)(E vB m q m F a -==,所以在受力平衡的时候,速度对于磁感应强度和电场强度的要求为:B E v =。
