浅基础地基承载力
浅谈浅基础地基承载力的确定

浅谈浅基础地基承载力的确定摘要:地基承载力是土力学的三大经典问题之一。
天然地基承载力是岩土工程勘察文件中不可缺少的一个内容,也是天然地基浅基础设计的基本依据。
在承受基础以及上部建筑物的所有荷载作用下,地基中的应力状态会发生改变。
一方面附加应力引起地基内土体变形,导致建筑物沉降,另一方面,当土中一点的某一面上的剪应力等于该点地基土的抗剪强度时,该点就达到极限平衡,发生剪切破坏。
在确定地基承载力时,必须满足上述两个条件,即变形与强度两个指标同时满足规范允许值,才能达到规范对建筑物地基承载力的要求。
关键词:地基承载力;原位试验;临塑荷载;临界荷载;极限承载力;静止侧压力系数。
1.1 浅基础地基承载力概述地基承载力问题是土力学中的一个重要的研究课题,其目的是为了掌握地基的承载规律,发挥地基的承载能力,通过合理确定地基承载力确保地基不致因荷载作用而发生剪切破坏,产生过大变形而影响建筑物或土工建筑物的正常使用。
为此,地基基础设计一般都限制基底压力最大不超过地基容许承载力。
地基承载力计算方法的合理确定,对工程的经济性和安全性影响极大。
在规范中涉猎了五个不同的承载力概念:地基容许承载力、地基承载力基本值、地基承载力标准值、地基承载力设计值和地基承载力特征值。
地基容许承载力([f]):在保证地基稳定性和建筑物的沉降量不超过容许值的的条件下,地基土体所能承受的最大压力;地基承载力基本值(f0):根据土的室内试验或原位测试物理力学指标的平均值,按经验公式计算或查经验表格得到,相当于标准基础宽度和深度时的地基容许承载力值;地基承载力标准值(fk):考虑了土性指标变异影响后,相当于标准基础宽度和埋深时地基容许承载力代表值,可通过承载力基本值乘以回归修正系数得到,也可通过野外鉴别结果、标准贯入试验、轻便触探试验锤击数查表获得;地基承载力设计值(f):地基承载力标准值经基础宽度和埋深修正后的值,或直接用地基强度指标按承载力理论公式计算得到的地基承载力。
简述浅基础地基承载力的计算理论及方法

简述浅基础地基承载力的计算理论及方法1 地基承载力的理论计算方法1.1根据刚塑性理论确定的极限承载力地基极限承载力理论公式首先是由朗肯于1857年提出的,Prandtl(1920)和Reissner(1924)根据塑性理论,导出了刚性基础压入无重力土中的滑动面形状及其相应的承载力公式.不少学者在Pran<="" p="">1. 2 根据弹塑性理论确定的承载力根据弹塑性理论,埋深为 D 的条形基础地基中任意点M 的应力,由计算点以上土层自重引起的应力和基底附加压力引起的应力两部分叠加组成. 当M 点的应力达到极限平衡状态时,该点的应力满足MohrCoulomb 强度条件. 通过分析即可得容许塑性区最大深度Zmax处的承载力计算公式. 当土的物理力学指标已知,地基承载力就取决于塑性区容许开展的深度Zmax及基础埋深 D. 若允许地基中塑性区开展深度达1/ 4基础宽度B,令Zmax= 1/ 4B ,则PV 4= Mb+ MdVDD +MCC . 目前,我国勘察设计规范中多采用其作为地基允许承载力的计算公式. 需要指出的是,在推导公式过程中,假定土的自重应力在各个方向相等(即η = 1),由于M 点的自重应力在各个方向实际上是不等的,因此严格地讲,以上两项在M 点处产生的应力在数值上是不能叠加的,这是此理论公式在推导过程中最大的不足之处. 另外,在临塑荷载的推导中采用弹性力学的解答,对于已出现塑性区的塑性变形阶段,该公式的推导是不够严格的[ 2]。
1. 3 总应力法确定地基承载力土体稳定分析成果的可靠性在很大程度上决定于对抗剪强度试验方法和强度指标的正确选择. 抗剪强度总应力法是用试验方法模拟原位土体的工作条件,其依据有以下两个公式在地基土的承载力计算中,若建筑物的施工速度快,地基土的性大,透水性小,排水差,宜采用不排水强度指标进行计算,以确保工程安全. 在不排水试验中φu= 0,将其代入 A. S. Vesic 公式计算得地基极限承载力[ 3]:P u= 5. 14c + q.. 2 软土地基承载力计算中应考虑的问题2. 1 考虑变形的地基承载力的确定承载力极限状态是在刚塑性或弹塑性假定的基础上推导出来的一系列计算公式,在推导过程中未考虑变形. 将地基强度与变形割裂开来考虑,不仅是目前我国在地基承载力理论上存在的缺陷,而且也是工程设计施工中经常出现事故的原因之一. 从表面上看,浅基础地基承载力的设计似乎比深基础容易,由于土体是一种非均匀各向异性的介质,其土性非常复杂,很难用单一的土体本构关系来精确地确定地基土的地基承载力. 在软土地区以变形为控制因素来决定地基承载力设计应是解决问题的途径之一.。
天然地基上浅基础的设计例题(zhang)

天然地基上浅基础的设计例题一、地基承载力计算【例题3-1】某粘土地基上的基础尺寸及埋深如例图3-1所示,试按强.7=035+=+⨯20+061675.kPa.15112.3.35二、地基承载力验算(基底尺寸确定)【例题3-2】试确定例图3-2所示某框架柱下基础底面积尺寸。
212~5.90.22075.2241600)4.1~1.1()4.1~1.1(75.22475.24200)5.02(5.160.1200)5.0(mdf F A kPa d f f G a k m d ak a =⨯-⨯=-==+=-⨯⨯+=-+=γγη由于力矩较大,底面尺寸可取大些,取b=3.0m ,l =4.0m 。
(2)计算基底压力kPaWM P P kPad blF P kk k G k k 8.358.3106/4321208603.1733.1732204316002minmax =⨯⨯+±=±==⨯+⨯=+=γ(3)验算持力层承载力不满足KPaKPa f KPa P KPaf KPa P a k a k 8.2698.2242.12.18.3108.2243.173max =⨯=>==<=(4)重新调整基底尺寸,再验算,取=l 4.5mkPaf kPa P P kPa f KPa P a k k a k 2.2692.11.2676.1085.1586/5.4321208608.2245.1582205.4316002max =<=+=⨯⨯++==<=⨯+⨯=则所以 取b=3.0m ,l =4.5m ,满足要求。
对带壁柱的条形基础底面尺寸的确定,取壁柱间距离l 作为计算单元长度(图3-16)。
通常壁柱基础宽度和条形基础宽度一样,均为b ;壁柱基【例题3-3】 某仓库带壁柱的墙基础底面尺寸如例图3-3所示,作用于基底形心处的总竖向荷载kNG F k k 420=+,总力矩mkN M k⋅=30,持力层土修正后的承载力特征值kPaf a120=,试复核承载力是否满足要求。
浅基础地基承载力基础工程

注意:①成层土γm=σcd/d;
.
13
fa fak b(b3)dm(d 0.5) (7.9) 注意: ②埋深d的取法,见教材。一般从室外地面算起。 超载q=γmd
滑动面 室内外埋深不同时
B. 确定基础及其上土的重力Gk,d要考虑室内与室外地坪标高的不同,取平均高 程计算。
A Fk fa G d
.
36
例题2–2
某粘性土重度γm为18.2kN/m3 ,孔隙比e=0.7,液性指数IL=0.75,地基承载 力特征值fak为220kPa。现修建一外柱基础,作用在基础顶面的轴心荷载Fk= 830kN,基础埋深(自室外地面起算)为1.0m,室内地面高出室外地面0.3m, 试确定方形基础底面宽度。
△≤ [△]
(2–15)
.
24
2.4 浅基础的地基承载力
地基变形按其特征可分为四种: 沉降量——独立基础中心点的沉降值或整幢建筑物基础的平均沉降值; 沉降差——相邻两个柱基的沉降量之差;
.
25
2.4 浅基础的地基承载力
倾 斜——基础倾斜方向两端点的沉降差与其距离的比值; 局部倾斜——砌体承重结构沿纵向6~10m内基础两点的沉降差与其距离的比 值
持力层土的承载力特征值
fa 170 17.7 1.0 (1.0 0.5) 178.9kPa
3.取1m长的条基作计算单元
基础宽度
b Fk
195
1.23m 3.0m
fa Gd 178.9 20 1.0
.
34
取该承重墙下条形基础宽度b=1.25m。 4.验算:
关于浅基础地基承载力的有限元分析

关于浅基础地基承载力的有限元分析摘要:本文运用有限元数值分析方法将地基的沉降及承载力分析结合起来。
根据极限平衡理论,沿方形浅基础表面的对角线切出四分之一进行分析,在考虑自重、黏聚力和过载的同时,又考虑切割体侧面受到侧向土压力的影响,采用整体分析法,可求得各级荷载下地基的非线性沉降变形、地基土体塑性区的开展情况和地基的极限承载力,能反映竖向荷载作用下浅基础地基的实际工作机理。
关键词:地基承载力;有限元数值分析法;浅基础1概述Abaqus是一套功能强大的工程有限元分析软件,作为通用的模拟计算工具,ABAQU能解决结构(应力/位移)的许多问题。
本文以工程实例形象的描述了地基承载力理论分析过程和与实际工程中的偏差,运用有限元的方法对地基进行了分析,用ABAQUS得出了地基变形图和应力应变图。
通过数值方法即有限元一无限元藕合的方法的运用,结合土的非线性、弹塑性本构模型对浅基础地基进行三维分析,把浅基础地基的强度及沉降变形发展联系在一起来研究,从而得到考虑土体非线性、弹塑性的地基沉降曲线以及基底土体塑性区的渐进性开展情况,并据此来获得合理的地基承载力值。
2 ABAQUS有限元分析2.1 模型介绍及参数设置方形浅基础边长,土体重度。
计算影响深度取5m,宽度取4m,基础计算边长取0.5m。
土体采用莫尔一库仑(Mohr-Coufomb)准则模拟。
二次分析时,取一高0.2m,底面边长0.5m的正方形作为方形基础,不计其重度,直接在基础顶面施加均布竖向荷载。
基础为混凝土或钢筋混凝土结构,刚度相对土体刚度无限大,故采用弹性材料模拟本文取十组土样,各组土样及基础的计算参数取值见下表1-1:表1-1土样及地基的计算参数土样编号密度/kg/m³ 压缩模量/MPa 泊松比/粘聚力/KPa 内摩擦角1 1900 25 0.35 35 202 1950 28 0.3 30 163 1920 32 0.32 31 184 1780 27 0.33 32 205 1850 38 0.25 33 226 1800 32 0.28 34 247 1820 25 0.26 28 268 1750 35 0.36 25 219 2000 18 0.34 27 1910 1980 24 0.32 29.4 23基础2500 30000 0.22.2 约束设置本文的方形浅基础地基模型只取三个自由度,在ABAQUSE Edit Boundary Condition中选择Displacement/Rotation后,其中:CSYS:用于选择坐标系,默认为整个坐标系(Global);Method:用于选择施加边界条件的方式。
2017第3讲浅基础-地基承载力-基础工程001

2.4 浅基础的地基承载力
地基变形按其特征可分为四种:
沉降量——独立基础中心点的沉降值或整幢建筑物基础的平均沉降值; 沉降差——相邻两个柱基的沉降量之差;
2.4 浅基础的地基承载力
倾 斜——基础倾斜方向两端点的沉降差与其距离的比值;
局部倾斜——砌体承重结构沿纵向6~10m内基础两点的沉降差与其距离的比 值
f ak 和 f a 的区别
f a ——地基承载力特征值:
由理论公式法、岩石地基的现场和室内试验法直接取得。
f ak ——未经深宽修正的地基承载力特征值:
由土质地基的现场载荷试验和静力触探、动力触探、标准贯入试验 fa 等原位测试法取得,经深宽修正后方得到 。
(25页)某场地地表土层为中砂,厚度2m,γ =18.7kN/m3,标准贯入锤击 数N=13;中砂层之下为粉质粘土,γ =18.2kN/m3,γ sat=19.1kN/m3,抗剪 强度指标标准值φ k=21,ck=10kPa,地下水位在地表下2.1m处。若修建的基 础底面尺寸为2×2.8m,试确定基础埋深分别为1m和2.1m处时持力层的承载 力特征值。
f a ——修正后的地基承载力特征值(kPa) ;
f ak ——地基承载力特征值(kPa) ;
(7.9)
b——基础底面宽度(m);b取值范围3~6 m d——基础埋置深度(m);
修正原因 : 考虑增加基础宽度和埋置深度时,地基承载力也将随之提高,应将地基承 载力对不同的基础宽度和埋置深度进行修正,才能供设计使用。
Fk 6M G d w hw 2k bl bl 6e p k 1 l pk max
单向偏心荷载作用下的基础
②e>l/6
pk max
条形浅基础极限承载力
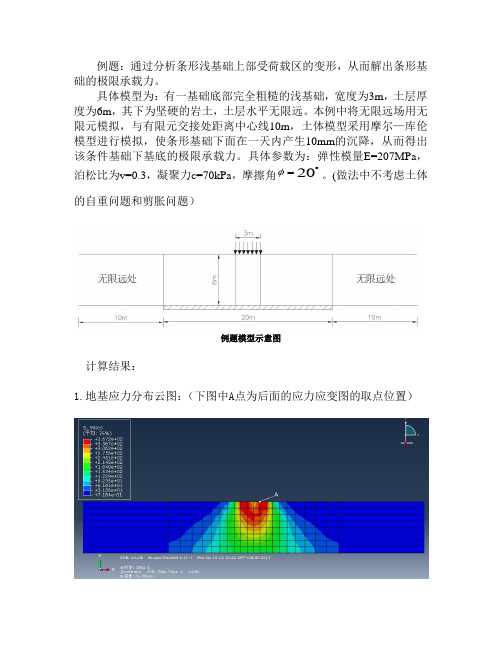
例题:通过分析条形浅基础上部受荷载区的变形,从而解出条形基础的极限承载力。
具体模型为:有一基础底部完全粗糙的浅基础,宽度为3m ,土层厚度为6m ,其下为坚硬的岩土,土层水平无限远。
本例中将无限远场用无限元模拟,与有限元交接处距离中心线10m ,土体模型采用摩尔—库伦模型进行模拟,使条形基础下面在一天内产生10mm 的沉降,从而得出该条件基础下基底的极限承载力。
具体参数为:弹性模量E=207MPa ,泊松比为v=0.3,凝聚力c=70kPa ,摩擦角20o
=φ。
(做法中不考虑土体的自重问题和剪胀问题)
例题模型示意图
计算结果:
1.地基应力分布云图:(下图中A 点为后面的应力应变图的取点位置)
2.地基位移云图:
3.等效塑性应变云图:
4.A点的应力(y方向)随时间的变化图:(A点的位置见图1)
5.A点的应变(y方向)随时间的变化图:
从上图中的应变曲线中可以看出,此条形基础的极限承载力约为460kpa。
深浅基础的定义

深浅基础的定义
深浅基础是建筑工程中的一个重要概念,它指的是建筑物的地基深度和地基承载力。
深浅基础的选择对于建筑物的稳定性和安全性有着至关重要的影响。
深基础是指地基深度超过一定深度的基础,一般用于建造高层建筑、大型桥梁、大型水利工程等。
深基础的优点是承载力大、稳定性好,但是建造成本高,施工难度大,需要考虑地下水位、地质条件等因素。
浅基础是指地基深度较浅的基础,一般用于建造低层建筑、小型桥梁、小型水利工程等。
浅基础的优点是建造成本低、施工简单,但是承载力较小,稳定性差,需要考虑地基土壤的承载能力。
在选择深浅基础时,需要考虑多种因素,如建筑物的高度、重量、地质条件、地下水位等。
一般来说,建筑物高度超过三层时,应选择深基础;建筑物高度在三层以下时,可以选择浅基础。
但是在实际工程中,还需要根据具体情况进行综合考虑。
除了深浅基础的选择,还需要注意地基的处理。
地基处理包括地基加固、地基改良等,可以提高地基的承载能力和稳定性。
地基处理的方法包括灌注桩、钻孔灌注桩、挖孔桩等,需要根据具体情况选择合适的方法。
深浅基础是建筑工程中的重要概念,选择合适的基础类型和地基处理方法对于建筑物的稳定性和安全性至关重要。
在实际工程中,需要根据具体情况进行综合考虑,选择最合适的方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
地基极限承载力理论研究与分析 摘 要:分析了常用的几种地基极限承载力理论和计算公式的优缺点及其适用范围,并提出了具体的改进设想,为今后的理论研究和工程实体的运用提供了借鉴和参考。
关键词:地基极限承载力;改进设想;岩土工程
Abstract:Analysis of the advantages and disadvantages as well as the scope of application of the used several foundation ultimate bearing capacity theory and calculation formulas ,And made specific improvements envisaged to provide a reference for future theoretical research and engineering entities use and reference.
Keywords:Ultimate bearing capacity; For Improvement; Geotechnical Engineering
一、引言
用于浅基础的地基极限承载力计算的理论主要有普朗德尔(Prandtl )极限承载力理论、太沙基(Terzaghi )承载力理论、魏锡克(Vesic )极限承载力公式等。
这些理论的基本出发点都是按整体剪切破坏模式,在条形荷载作用下,假设滑裂面,由静力平衡条件推导出浅基础的地基极限承载力Pu 的表达式。
在假设滑裂面、形成计算模式过程中,这些理论都对实际复杂的地基问题作出了不少相应的假设、简化。
由于这些假设的存在,使得这些理论在实际应用中都存在着一定的局限性,往往与实际偏离的较大,下面对这些理论做一些初步的探讨。
二、地基极限承载力理论分析与研究
1 普朗德尔理论
普朗德尔根据塑性平衡的观点,研究了坚硬物体压入较软的、均匀的、各向同性材料的过程,导出了下列公式:
—材料内聚力
——材料内摩擦角
——极限压应力—式中:)—(———c q e c e c q f f ϕϕϕϕϕ
πϕϕπϕπ1]1)sin 1/sin 1[(cot ]1)2
4([tan tan /tan tan 2--+⋅=-+=
该公式构造简单,不需复杂、高深的数学微分就可求解。
在该理论中,假设了承压板底面与土之间是光滑的,GECDF 面以上的土体处于塑性平衡状态,而其余部位的土则处于弹性平衡状态。
根据假定的条件,普朗德尔理论的不足表现在以下几个方面:
(1)该理论只适用于无重量的介质的极限平衡平面课题,由公式(1)可知,当00==f q c 时,。
由于假定了承压板下的土的容重等于零而引起的误差,这个结果与实际试验结果不相符合。
(2)该理论把地基土看作是不可变形的刚塑性材料,基于这种假定所导出的公式(1)只能适用于地基土整体剪切破坏的情况。
(3)为了方便起见,该理论不计地表面GF 以上土的抗剪强度,而只将这部分土作为超载,以压力f D q γ=加在GF 面上,没有考虑地基土的内聚力,这与实际情况显然不符。
(4)普朗德尔的极限承载力公式与条形基础的宽度无关,这一点也与实际不符。
2 太沙基理论
太沙基根据普朗德尔相似的假定,导出了地基的极限承载力公式如下:
—地基土的内摩擦角
——基础的宽度——基础埋置深度
——地基土的容重
——地基土的内聚力
—的函数数,为—均为无因次承载力系—式中:)—(———ϕγϕγγB D c N N N N B N D cN q f r q c r q f f ,,22
1+
+=
太沙基理论的优点在于:它考虑了地基土的内摩擦、土的容重以及覆土压力的影响,用三个作为土的内摩擦角函数的承载力系数表示出来。
由于其假定条件的局限性,太沙基理论的不足之处存在于以下几个方面:
(1)太沙基所导得的公式(2)中虽然计及了地基土的容重,但他忽略了土的容重对滑线形状的影响。
另外,他假定基础底面不是光滑的,而是与土之间具有相当大的摩擦,因此沿着AB 面不发
生剪切位移,这与实际情况是有区别的。
(2)在该理论中,假定了滑动面CDF 是已知的。
实际上,真正的滑动面必须用试算法求出,也就是假定不同的对数螺线的中心点,试算若干个滑动面,求出最小的f q 值,才是所需的极限承载力f q 值。
(3)太沙基公式只适用于地基土的整体剪切破坏的情况,因为在地基破坏前并没有考虑土体的变形。
其计算结果往往过高地估计了地基的承载力。
(4)太沙基理论一方面忽略了覆土的抗剪强度,另一方面滑动面被假定与基础底面水平线相交为止,没有延伸到地表面上去。
因此所假定的破坏机理与实际观测的土体移动一般是不符合的。
3 魏西克理论
ϕ
ϕ
ϕπγγϕπtan )1(2cot )1()2
4(tan 32
12tan +=-=+=++=q r q c q r q c f N N N N e N bN dN cN q 式中:)—(———
魏西克理论的优点:魏西克所提出的地基极限承载力的计算,是把地基土的破坏机理分为三种不同的模式:整体剪切破坏、局部剪切破坏以及刺入剪切破坏。
与此同时,他提出了判定地基土破坏模式的刚度指标。
在该理论中,他假定了介质体积变化的影响。
其解不仅能应用到浅基础和深基础的地基承载力的计算方面,而且在许多地质问题上都可以得到实际的应用。
这里必须指出,近年来对于浅基础和深基础的破坏机理的研究结果表明:在浅基础的情况下,地基沿着滑动面所发生的平均抗剪强度将随着基础尺寸的增大而降低;这种强度降低是由于三种互不相关的因素引起的:1)摩尔圆包络线的非线性;2)沿着滑动面的剪切破坏的发展;3)地基土中存在着较弱的区或薄层。
目前还没有精确的公式计及这些影响因素。
为了考虑这些因素,引入了压缩性系数。
这种计算方法至今还仅仅在不多的模型试验中得到验证,还有待于今后在工程实践中加以检验。
三、改进设想
改进设想一:现有的地基极限承载力公式:如普朗德尔、太沙基、梅耶霍夫等极限承载力公式大多都是基于Tresca 准则或Mohr-Coulomb 准则推导而得。
而Tresca 准则、Mohr-Coulomb 准则并没有考虑中间主应力的影响。
实验证明:中间主应力对土体的屈服和破坏有影响。
由Mohr-Coulomb 或Tresca 强度准则推导的地基极限承载力公式并不能完全反映地基实际情况,且所得的结果是偏于保守的,不能充分发挥土体的强度潜能。
基于以上缺点及局限性,设想研究三向应力状态下的地基极限承载力问题具有重要的理论和实际意义。
改进设想二:地基极限承载力分析经常采用极限平衡方法和滑移线场理论。
经典的极限平衡方法不能考虑材料的本构关系,只能适用于各向同性材料,而岩土材料由于受诸多地质因素的影响,常表现出各向异性。
因此,设想在采用各向异性不排水抗剪强度或各向异性的本构关系基础上进行分析。
四、结语
(1)研究和分析了常用地基极限承载力理论和公式,指出了各种理论和公式的局限性及其适用范围,为今后实体工程中计算地基极限承载力提供有力的参考和依据。
(2)根据各种地基极限承载力理论和公式的缺点及局限性,提出了两种改进设想,以期在今后的学习和工作中做更近一步的研究。
