建筑力学电子压杆稳定
合集下载
压杆稳定—提高压杆稳定性的措施(建筑力学)
2.采用合理的截面形状： (1)各方向约束相同时： 1)各方向惯性矩I相等—采用正方形、圆形截面； 2)增大惯性矩I—采用空心截面。 (2)压杆两方向约束不同时： 使两方向柔度接近相等 可采用两个主惯性矩不同的截面，如矩形、工字形等。 3.减少压杆支承长度： (1)直接减少压杆长度； (2)增加中间支承； (3)整体稳定性与局部稳定性相近。 4.加固杆端约束：尽可能做到使压杆两端部接近刚性固接。
提高压杆稳定性的措施
1.合理选择材料 细长压杆：
ห้องสมุดไป่ตู้ cr
2E 2
采用E值较大的材料可提高压杆的稳定性 由于各种钢材的E值大致相同，所以对大柔度钢压杆不宜选用优质钢材，以避 免造成浪费。
中粗压杆
cr a b
短粗压杆
cr u
采用强度较高的材料能够提高其临界应力，即能提高其稳定性。
提高压杆稳定性的措施
提高压杆稳定性的措施
1.合理选择材料 细长压杆：
ห้องสมุดไป่ตู้ cr
2E 2
采用E值较大的材料可提高压杆的稳定性 由于各种钢材的E值大致相同，所以对大柔度钢压杆不宜选用优质钢材，以避 免造成浪费。
中粗压杆
cr a b
短粗压杆
cr u
采用强度较高的材料能够提高其临界应力，即能提高其稳定性。
提高压杆稳定性的措施
压杆稳定—细长压杆的临界力(建筑力学)
2
（μl）
式中，μl为计算长度，μ称为长度系数。
不同支承下的计算长度及长度系数见下表。
压杆稳定
临界力的影响因素
临界力Fcr的大小反映了压杆失稳的难易，而压杆失稳
就是直杆变弯，发生弯曲变形，因此临界力的大小与影响
直杆弯曲变形的因素有关：
杆的长度l
抗弯刚度EI
杆端支承
l越大
EI越大
越牢固
抵抗变形的能力越小
弹性模量E＝200GPa。试计算其临界力。
解 查型钢表得Iz=2370cm4，Iy=158cm4，应取小值。
π 2 EI π 2 200 103 158 10 4
Fcr 2
N 346kN
2
l
3 103
压杆稳定
二、其他支承情况下细长压杆的临界力的欧拉公式
π 2 EI
Fcr
a）；在最小刚度平面
内弯曲时为两端固定（
图b）。木材的弹性模
量E=10GPa，试求木柱
的临界力。
解 由于最大刚度平面与最小刚度平面内的支承
情况不同，所以需分别计算。
Fcr
（1）计算最大刚度平面内的临界力
截面的惯性矩为
两端铰支，长度系数μ=1
2 EI y 3.14 2 10 109 8 10 5
12
2.88 107 mm 4
2.88 10 m
z
4
y
两端固定，长度系数μ=0.5
EI Z 3.14 10 10 2.88 10
Fcr
N
2
2
( l )
(0.5 8)
2
2
177 103 N 177 kN
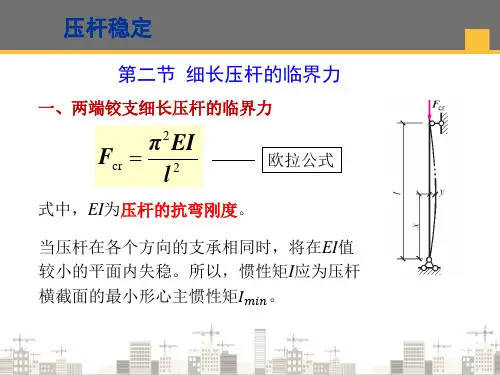
（μl）
式中，μl为计算长度，μ称为长度系数。
不同支承下的计算长度及长度系数见下表。
压杆稳定
临界力的影响因素
临界力Fcr的大小反映了压杆失稳的难易，而压杆失稳
就是直杆变弯，发生弯曲变形，因此临界力的大小与影响
直杆弯曲变形的因素有关：
杆的长度l
抗弯刚度EI
杆端支承
l越大
EI越大
越牢固
抵抗变形的能力越小
弹性模量E＝200GPa。试计算其临界力。
解 查型钢表得Iz=2370cm4，Iy=158cm4，应取小值。
π 2 EI π 2 200 103 158 10 4
Fcr 2
N 346kN
2
l
3 103
压杆稳定
二、其他支承情况下细长压杆的临界力的欧拉公式
π 2 EI
Fcr
a）；在最小刚度平面
内弯曲时为两端固定（
图b）。木材的弹性模
量E=10GPa，试求木柱
的临界力。
解 由于最大刚度平面与最小刚度平面内的支承
情况不同，所以需分别计算。
Fcr
（1）计算最大刚度平面内的临界力
截面的惯性矩为
两端铰支，长度系数μ=1
2 EI y 3.14 2 10 109 8 10 5
12
2.88 107 mm 4
2.88 10 m
z
4
y
两端固定，长度系数μ=0.5
EI Z 3.14 10 10 2.88 10
Fcr
N
2
2
( l )
(0.5 8)
2
2
177 103 N 177 kN
建筑力学 第十三章 压杆稳定
受干扰前杆的直线形状的平衡状态称为临界平衡状态，压
力Fcr称为压杆的临界力。 临界平衡状态实质上是一种不稳定的平衡状态，因为此时
杆一经干扰后就不能维持原有直线形状的平衡状态了。 压杆从稳定的平衡状态转变为不稳定的平衡状态,这种现象称
为丧失稳定性，简称失稳。
（3）压力F超过Fcr后
杆的弯曲变形将急剧增大，甚至最
因为临界力是使压杆产生失稳所需要的最小压力，而钢压杆在 各纵向平面内的弯曲刚度EI相同，所以公式中的μ应取较大的值， 即失稳发生在杆端约束最弱的纵向平面内。
由已知条件，钢压杆在xy平面内的杆端约束为两端铰支， μ=1；在xz平面内杆端约束为一端铰支、一端固定，μ=0.7。故 失稳将发生在xy平面内，应取μ=1进行计算。 临界力为
2
2 10 109 597.3 104 1012
1 3
2
N
655 102 N 65.5kN
在临界力Fcr作用下，木柱将在弯曲刚度最小的xz平面内发 生失稳。
F<Fcr
变形，在干扰撤去后，杆经若干次振动后仍会回到
原来的直线形状的平衡状态。
压杆原有直线形状的平衡状态称为稳 定的平衡状态。
（2）压力F增至某一极限值Fcr时
给杆一微小的横向干扰，使杆发
F=Fcr
生微小的弯曲变形，则在干扰撤去后，
杆不再恢复到原来直线形状的平衡状
态，而是仍处于微弯形状的平衡状态。
O
【解】 由于木柱两端约束为球形铰支，故木柱两端 在各个方向的约束都相同（都是铰支）。因为临界力是 使压杆产生失稳所需要的最小压力，所以公式中的I应 取Imin。由图知，Imin 104 mm4
O
故临界力为
《建筑力学》第九章压杆稳定
cr 为临界应力的许用值，其值为：
（9－13）
cr
cr
K
（9－14）
式中 K 称为稳定安全系数。稳定安全系数一般都大于强度计算时的安全系数，这是因为在
确定稳定安全系数时，除了应遵循确定安全系数的一般原则以外，还必须考虑实际压杆并 非理想的轴向压杆这一情况。比如，在制造过程中杆件不可避免地存在微小的弯曲(即存在 初曲率)；外力的作用线也不可能绝对准确地与杆件的轴线相重合(即存在初偏心)；还必需 考虑杆件的细长程度等等，这些都应在稳定安全系数中加以考虑。
d=20mm，材料的许用应力 =170MPa，已知 h=0.4m，作用力 F=15kN。试在计算平面内校核
二杆的稳定。
图 9-3
解：(1)计算各杆承受的压力 取结点 A 为研究对象，根据平衡条件列方程
x 0 FAB cos 450 FAC cos 300 0 Y 0 FAB sin 450 FAC sin 300 F 0
压杆的临界应力。
5、临界应力总图 综上所述，压杆按照其柔度的不同，可以分为三类，计算各自临界应力的方法也不相
同。当 ≥ p 时，压杆为细长杆(大柔度杆)，其临界应力用欧拉公式来计算；当 s < < p 时，压杆为中长杆(中柔度杆)，其临界应力用直线经验公式来计算； s 时，压杆为短
4 1 0.566 103 20
113
4
AC
lAC i
4 1 0.8 103 20
160
(3)由表 9－3 查得折减系数为：
AC 0.272
AB
0.536
(0.536
最新完美版建筑力学第八章压杆稳定
y
y
d y EI 2 M x Fcr y dx
2
Fcr (b)
目录
第八章 压杆稳定\压杆的临界力与临界应力
上两边同除以EI，并令
Fcr k EI
M (x) =Fcry x O
x Fcr
d2 y 2 k y 0 移项后得到 2 dx 解此微分方程，可以得到两端铰 支细长压杆的临界力为
目录
第八章 压杆稳定\压杆的临界力与临界应力
§8－2 压杆的临界力与临界应力
8－2－l 细长压杆的临界力 临界力Fcr也是压杆处于微弯形状的平衡状态所需的 最小压力，由此我们得到确定压杆临界力的一个方法：假 定压杆处于微弯形状的平衡状态，求出此时所需的最小压 力即为压杆的临界力。
目录
第八章 压杆稳定\压杆的临界力与临界应力
故临界力为：
Fcr π 2 EI y (l )2
2 10 109 Pa 597.3 10-8 m4
(1 3)2 m2
655 102 N 65.5 kN
在临界力Fcr作用下，木柱将在弯曲刚度最小的xz平 面内发生失稳。
目录
第八章 压杆稳定\压杆的临界力与临界应力
目录
第八章 压杆稳定\压杆的临界力与临界应力
表8－1 四种典型细长压杆的临界力
目录
第八章 压杆稳定\压杆的临界力与临界应力
例8－1 一长l = 4 m，直径d = 100 mm的细长钢压杆， 支承情况如图所示，在xy平面内为两端铰支，在xz平面内 为为一端铰支、一端固定。已知钢的弹性模量E = 200 GPa，试求此压杆的临界力。
目录
第八章 压杆稳定\压杆的临界力与临界应力
将欧拉公式改写为
建筑力学压杆稳定课件
E c 0.57 s
0.43，
E c 0.57 s
对Q235钢：
s 235MP ， a
cr 235 0.00668 2
c 123
(MPa)
第10章 压杆稳定 2、临界应力总图
商丘职业技术学院汽车建筑工程系
第10章 压杆稳定
商丘职业技术学院汽车建筑工程系
不能保持原有的直 线平衡状态的平衡。
压力Fcr称为压杆的临界力或称为临界荷载（Critical loads）。 压杆的失稳现象是在纵向力的作用下，使杆发生突然 弯曲，所以称为纵弯曲。这种丧失稳定的现象 也称为 屈曲。
第10章 压杆稳定
商丘职业技术学院汽车建筑工程系
压杆由直线形状的稳定的平衡过渡到不稳定的 平衡时所对应的轴向压力， 称为压杆的临界压力或临界力，用Fcr表示
上述说明有、无扫地杆的脚手架搭设是完 全不同的情况，在施工过程中要注意这一 类问题。
cr1 cr 2 196.5 37.94 100% 80.6% cr1 196.5
第10章 压杆稳定
10.3 压杆的稳定计算
一、安全系数法 压杆稳定条件为：
商丘职业技术学院汽车建筑工程系
l
i
0.7 1800 79.85 ＜ 15.78
c 123
2
所以压杆为中粗杆，其临界应力为
cr1 240 0.00682 196.5MPa
（2）第二种情况的临界应力 一端固定一端自由 因此 μ=2 计算杆 长l=1.8m
第10章 压杆稳定
i
商丘职业技术学院汽车建筑工程系
欧拉公式的适用范围
1、临界应力（ critical stress ）和柔度
压杆的稳定性
在理论分析中首先找出每一具体情况下杆的 挠曲线方程，而方程成立时的荷载就是所求的临 界荷载。
建筑力学
x
δ
Fcr
l
w
x
o
y
z y
压杆的稳定性
9
考虑下图细长压杆
M ( x) Fcr (d w)
在线弹性、小变形情况下，且 不考虑剪切对于变形的影响， 则其挠曲线近似微分方程为
EIzw M ( x) Fcr (d w)
建筑力学
压杆的稳定性
16
§7-3 欧拉公式的适用范围·临界应力总图
应注意：
求压杆临界荷载的欧拉公式Fcr= p2EI /( l )2只
适用于压杆失稳时仍在线弹性范围内工作的情况。 按失稳的概念，在临界荷载作用下尽管压杆的
直线状态的平衡是不稳定的，但如果不受干扰，杆 仍可在直线状态下保持平衡。
建筑力学
Fcr
Fcr x
A l
B
Fcr
π2EI y l2
1
A l
B
Fcr
π2EI y (0.7l )2
0.7
y
建筑力学
Fcr
压杆的稳定性
A l
Fcr
π2EI y (0.5l )2
l
0.5
B
15
Fcr
v
Fcr
π2EI y (2l )2
2
从上述分析可知,中心受压直杆的临界力Fcr 与杆端的约束情况有关，杆端的约束越强，临界 力越大。
建筑力学
压杆的稳定性
§7-1 关于稳定性的概念
实际压杆存在的情况：
(1) 本身不可能绝对地直； (2) 材质不可能绝对地均匀； (3) 轴向压力也会有偶然偏心。
建筑力学
x
δ
Fcr
l
w
x
o
y
z y
压杆的稳定性
9
考虑下图细长压杆
M ( x) Fcr (d w)
在线弹性、小变形情况下，且 不考虑剪切对于变形的影响， 则其挠曲线近似微分方程为
EIzw M ( x) Fcr (d w)
建筑力学
压杆的稳定性
16
§7-3 欧拉公式的适用范围·临界应力总图
应注意：
求压杆临界荷载的欧拉公式Fcr= p2EI /( l )2只
适用于压杆失稳时仍在线弹性范围内工作的情况。 按失稳的概念，在临界荷载作用下尽管压杆的
直线状态的平衡是不稳定的，但如果不受干扰，杆 仍可在直线状态下保持平衡。
建筑力学
Fcr
Fcr x
A l
B
Fcr
π2EI y l2
1
A l
B
Fcr
π2EI y (0.7l )2
0.7
y
建筑力学
Fcr
压杆的稳定性
A l
Fcr
π2EI y (0.5l )2
l
0.5
B
15
Fcr
v
Fcr
π2EI y (2l )2
2
从上述分析可知,中心受压直杆的临界力Fcr 与杆端的约束情况有关，杆端的约束越强，临界 力越大。
建筑力学
压杆的稳定性
§7-1 关于稳定性的概念
实际压杆存在的情况：
(1) 本身不可能绝对地直； (2) 材质不可能绝对地均匀； (3) 轴向压力也会有偶然偏心。
建筑力学 第11章 压杆稳定
第11章压杆稳定[内容提要]稳定问题是结构设计中的重要问题之一。
本章介绍了压杆稳定的概念、压杆的临界力-欧拉公式，重点讨论了压杆临界应力计算和压杆稳定的实用计算，并介绍了提高压杆稳定性的措施。
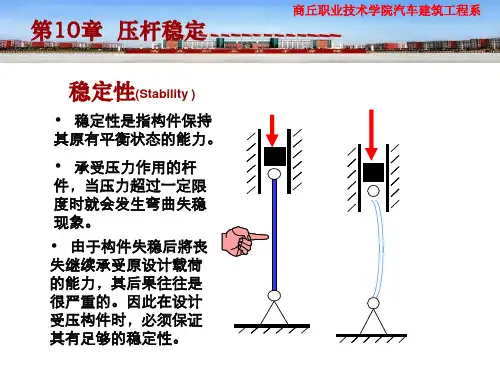
11.1 压杆稳定的概念工程中把承受轴向压力的直杆称为压杆。
前面各章中我们从强度的观点出发，认为轴向受压杆，只要其横截面上的正应力不超过材料的极限应力，就不会因其强度不足而失去承载能力。
但实践告诉我们，对于细长的杆件，在轴向压力的作用下，杆内应力并没有达到材料的极限应力，甚至还远低于材料的比例极限σP时，就会引起侧向屈曲而破坏。
杆的破坏，并非抗压强度不足，而是杆件的突然弯曲，改变了它原来的变形性质，即由压缩变形转化为压弯变形（图11-1所示），杆件此时的荷载远小于按抗压强度所确定的荷载。
我们将细长压杆所发生的这种情形称为“丧失稳定”，简称“失稳”，而把这一类性质的问题称为“稳定问题”。
所谓压杆的稳定，就是指受压杆件其平衡状态的稳定性。
为了说明平衡状态的稳定性，我们取细长的受压杆来进行研究。
图11-2(a)为一细长的理想轴心受压杆件，两端铰支且作用压力P，并使杆在微小横向干扰力作用下弯曲。
当P较小时，撤去横向干扰力以后，杆件便来回摆动最后仍恢复到原来的直线位置上保持平衡（图11-2(b)）。
因此，我们可以说杆件在轴向压力P的作用下处于稳定平衡状态。
P，杆件受到干扰后，总能回复到它原来的直线增大压力P，只要P小于某个临界值crP时，杆件虽位置上保持平衡。
但如果继续增加荷载，当轴向压力等于某个临界值，即P=cr然暂时还能在原来的位置上维持直线平衡状态，但只要给一轻微干扰，就会立即发生弯曲并停留在某一新的位置上，变成曲线形状的平衡（图11-2(c)）。
因此，我们可以认为杆件在P的作用下处在临界平衡状态，这时的压杆实质上是处于不稳定平衡状态。
P=cr(a) (b) (c)图11-1 图11-2继续增大压力P ，当轴向压力P 略大于cr P 时，由于外界不可避免地给予压杆侧向的干扰作用（例如轻微的振动，初偏心存在，材料的不均匀性，杆件制作的误差等），该杆件将立即发生弯曲，甚至折断，从而杆件失去承载能力。
材料力学课件 第十章压杆稳定
sinkL0
kn P
L EI
临界力 Pcr 是微弯下的最小压力，故，只能取n=1 ；且 杆将绕惯性矩最小的轴弯曲。
Pcr
2
EImin L2
14
Pcr
2
EImin L2
二、此公式的应用条件：
两端铰支压杆临界力的欧拉公式
1.理想压杆； 2.线弹性范围内； 3.两端为球铰支座。
三、其它支承情况下，压杆临界力的欧拉公式
29
我国钢结构柱子曲线
二、 受压构件的稳定公式
利用最大强度准则确定出轴心受压构件的临界应力 cr ，引入抗力分项系数 R ，则轴心受压构件的稳定计算公式如下：
N cr cr f y f A R R fy
f ：钢材的强度设计值
（10.24）
30
例6
如图所示，两端简支，长度l 5m 的压杆由两根槽钢组成，若限定两个槽钢腹板
Iy [73.3 (51.8)2 21.95]2 2176.5cm4
33
若失稳将仍会在 xoy平面内，有
imin iz
Iz A
1732.4 6.28cm 43.9
max
l imin
500 79.6 6.28
查表得2 0.733
此时3 与3 已经很接近，按两个 16a 槽钢计算压杆的许可压力，有
20
[例3] 求下列细长压杆的临界力。
y y
x
z
z
h
L1
L2
解：①绕
y 轴，两端铰支：
=1.0，
I
y
b3h 12
,
②绕 z 轴，左端固定，右端铰支：
b
Pcry
2EI L22
y
=0.7，
建筑力学第十三章 压杆稳定
1）安全系数法
重庆大学精出品版文社档
建筑力学
2）折减系数法
工程中为了简便起见，对压杆的稳定计算还常采 用折减系数法。即将材料的压缩许用应力[ ]乘上 一个小于1的折减系数 作为压杆的许用临界应力， 即：
[cr] = []； < 1，称为折减系数
按折减系数法进行压杆的稳定计算，其稳定条 件为
F A
重庆大学精出品版文社档
建筑力学
解：(a) 杆BD受压，其余杆受拉
BD杆的临界压力:
Pcr
2EI 2EI
2 2a
2a 2
故杆系所能承受的最大载荷
Pmax
Pcr
2EI
2a 2
3Ed 4
128a 2
重庆大学精出品版文社档
建筑力学
(b) 杆BD受拉，其余杆受压
四根受压杆的临界压力：
2EI
Pcr a 2 故杆系所能承受的最大载荷：
Pmax
2 3Ed4
2 Pcr 64a 2
重庆大学精出品版文社档
建筑力学
13.3压杆稳定的临界应力
1 临界应力
2EI Pcr (l )2
cr
Pc r A
2EI (l )2 A
2 E (i 2 A) (l )2 A
2E l 2
i
令 l
i
2
则 E cr
2
重庆大学精出品版文社档
①两个不相等的实根 r1、r2 通解 y C1er1 x C2er2 x
②两个相等的实根 r1 r2 通解 y （C1 C2 x）er1 x
③一对共轭复根 r1,2 i 通解 y e x (C1 cos x C2 sin x)
重庆大学精出品版文社档
重庆大学精出品版文社档
建筑力学
2）折减系数法
工程中为了简便起见，对压杆的稳定计算还常采 用折减系数法。即将材料的压缩许用应力[ ]乘上 一个小于1的折减系数 作为压杆的许用临界应力， 即：
[cr] = []； < 1，称为折减系数
按折减系数法进行压杆的稳定计算，其稳定条 件为
F A
重庆大学精出品版文社档
建筑力学
解：(a) 杆BD受压，其余杆受拉
BD杆的临界压力:
Pcr
2EI 2EI
2 2a
2a 2
故杆系所能承受的最大载荷
Pmax
Pcr
2EI
2a 2
3Ed 4
128a 2
重庆大学精出品版文社档
建筑力学
(b) 杆BD受拉，其余杆受压
四根受压杆的临界压力：
2EI
Pcr a 2 故杆系所能承受的最大载荷：
Pmax
2 3Ed4
2 Pcr 64a 2
重庆大学精出品版文社档
建筑力学
13.3压杆稳定的临界应力
1 临界应力
2EI Pcr (l )2
cr
Pc r A
2EI (l )2 A
2 E (i 2 A) (l )2 A
2E l 2
i
令 l
i
2
则 E cr
2
重庆大学精出品版文社档
①两个不相等的实根 r1、r2 通解 y C1er1 x C2er2 x
②两个相等的实根 r1 r2 通解 y （C1 C2 x）er1 x
③一对共轭复根 r1,2 i 通解 y e x (C1 cos x C2 sin x)
重庆大学精出品版文社档
建筑力学15-压杆稳定
(3) 第三次试算
设 φ3= （φ2+φ2′）/2 = （0.352+0.289）/2 =0.320
则 d3=√4P/πφ3［σ］=103mm i3= d3/4 = 103/4 mm=25.8mm
λ3= μl/i3 = 0.5×5×103/25.8 =97 查表13.2，由直线插入法得φ3′=0.321。φ3′与φ3相差非常小，不 必再选。 (4) 稳定性校核 φ3′［σ］=0.321×12MPa=3.85MPa σ= P/A3 =3.84MPa<φ3′［σ］ 故确定圆柱直径d=103mm。
12.3 压杆的稳定计算
12.3.1 压杆的稳定条件
为了保证压杆具有足够的稳定性，应使 作用在杆上的压力P不超过压杆的临界力Pcr， 而且还应有一定程度的稳定储备。所以，压 杆的稳定条件为 P≤ Pcr/Kw 将式(12.6)两边除以压杆横截面面积A， 可写成以应力表达的形式 σ= P/A ≤［σcr］
I= π/64 (D4-d4)= 262×104mm4
A= π/4 (D2-d2)=23.6×102mm2 i=I/A =262×104/23.6×102mm=33.3mm λ= μl/i = 1×2.2×103/33.3 =66 (2) 计算折减系数 由表12.2查出
12.2.3 欧拉公式的适用范围
欧拉公式是在材料服从虎克定律的条件下导出的， 所以只有在临界应力小于比例极限的条件下才能应用， 即 σcr=π2E/λ2 ≤σp 或改写为以柔度表达的形式 λ≥√π2E/σp =λp 式中λp是与材料比例极限相对应的柔度。 工程中把λ≥λp的压杆称为细长杆或大柔度杆，只有 细长杆才能应用欧拉公式计算临界力或临界应力。
设 φ3= （φ2+φ2′）/2 = （0.352+0.289）/2 =0.320
则 d3=√4P/πφ3［σ］=103mm i3= d3/4 = 103/4 mm=25.8mm
λ3= μl/i3 = 0.5×5×103/25.8 =97 查表13.2，由直线插入法得φ3′=0.321。φ3′与φ3相差非常小，不 必再选。 (4) 稳定性校核 φ3′［σ］=0.321×12MPa=3.85MPa σ= P/A3 =3.84MPa<φ3′［σ］ 故确定圆柱直径d=103mm。
12.3 压杆的稳定计算
12.3.1 压杆的稳定条件
为了保证压杆具有足够的稳定性，应使 作用在杆上的压力P不超过压杆的临界力Pcr， 而且还应有一定程度的稳定储备。所以，压 杆的稳定条件为 P≤ Pcr/Kw 将式(12.6)两边除以压杆横截面面积A， 可写成以应力表达的形式 σ= P/A ≤［σcr］
I= π/64 (D4-d4)= 262×104mm4
A= π/4 (D2-d2)=23.6×102mm2 i=I/A =262×104/23.6×102mm=33.3mm λ= μl/i = 1×2.2×103/33.3 =66 (2) 计算折减系数 由表12.2查出
12.2.3 欧拉公式的适用范围
欧拉公式是在材料服从虎克定律的条件下导出的， 所以只有在临界应力小于比例极限的条件下才能应用， 即 σcr=π2E/λ2 ≤σp 或改写为以柔度表达的形式 λ≥√π2E/σp =λp 式中λp是与材料比例极限相对应的柔度。 工程中把λ≥λp的压杆称为细长杆或大柔度杆，只有 细长杆才能应用欧拉公式计算临界力或临界应力。
材料力学--压杆稳定问题 ppt课件
F
Fcr nst
151.47 3
50.5KN
所以起重机架的最大起重量取决于杆AC的强度，为
Fmax 26.7KN
材料力学
PPT课件
42
例8-4 图示托架结构，梁AB与圆杆BC 材料相同。梁AB为16号工字 钢，立柱为圆钢管，其外径D=80 mm，内径d=76mm，l=6m，a=3 m， 受均布载荷q=4 KN/m 作用；已知钢管的稳定安全系数nw=3,试对立
n Fcr Fp
269 150
1.793 nst 1.8
所以压杆的稳定性是不安全的.
材料力学
PPT课件
38
例8-3 简易起重架由两圆钢杆组成，杆AB：d1 30mm，杆
AC：d2 20mm,两杆材料均为Q235钢, E 200GPa, s 240MPa p 100,0 60 ,规定的强度安全系数ns 2，稳定安全系 数 nst 3，试确定起重机架的最大起重量 Fmax 。
柱进行稳定校核。
l
q
B
A
F
a
C
材料力学
PPT课件
43
压杆稳定问题/提高压杆稳定性的措施
五、提高压杆稳定性的措施
材料力学
PPT课件
44
压杆稳定问题/提高压杆稳定性的措施
1、合理选择材料
细长杆： cr与E成正比。
普通钢与高强度钢的E大致相同，但比铜、铝合金的 高，所以要多用钢压杆。
中长杆： cr随 s 的提高而提高。
压杆稳定问题/细长压杆的临界力
2） 一端固定，一端铰支
C w
BC段,曲线上凸,
1 0;
压杆的稳定计算
③ 确定该支架的许可荷载。
根据外力 F 与 BD 杆所承受压力之间的关系，只要考虑 AC 杆的平衡即可。
由 求得
M A 0,
FBD
l 2
F
3l 2
0
1 F 3 FBD
于是该支架能承受的最大荷载为
Fmax
1 3
FBDmax
1 47.0 103 3
15.7 103
N
最后确定该支架的许可荷载 [F] =15.7 kN。
3. 进行截面设计
已知压杆的长度、所用材料、支承条件以及承受的压力F，按照稳定条件计 算压杆所需的截面尺寸。由于在稳定条件式 (7-12) 中，折减系数 φ 是根据压杆的 柔度 λ 查表得到的，而在压杆的截面尺寸尚未确定之前，压杆的柔度 λ 不能确定， 所以也就不能确定折减系数 φ。因此，这类问题一般采用试算法。
为了计算方便，将临界应力的许用应力写成如下形式
cr
cr kst
(7-10)
式中：[σ] 为强度计算时的许用应力；φ 为折减系数，其值小于1。
由式(7-10) 可知，φ 值为
cr
kst
(7-11)
由式(7-11) 可知， 当[σ] 一定时，φ 取决于σcr 与kst。由于临界应力σcr值随 压杆的柔度而改变，而不同柔度的压杆一般又规定不同的稳定安全系数，所以
【例7-2】如图7-5a 所示，构架由两根直径相同的圆杆构成，杆的材料为 Q235 钢， 直径 d = 20 mm，材料的许用应力 [σ] = 170 MPa，已知 h = 0.4 m，作用力 F = 15 kN。 试校核两杆的稳定。
图7-5a 解：① 计算各杆承受的压力。 取结点 A 为研究对象，画受力分析图，如图7-5b 所示，根据平衡条件列方程
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
( l ) 2
式中 μ 称为长度系数,随杆端约束情况而异；μl 则称为相当长 度，即相当于两端球形铰支压杆的长度。如下各图所示。
Fcr
x Fcr
A l
B
Fcr
π2EI y l2
1
A l
B
Fcr
π2EI y (0.7l ) 2
0.7
y
建筑力学电子教案
Fcr
A l
B
Fcr
π2EI y (0.5l ) 2
Fcr
A
I
l/4
l
2I l/2
BIl/4ຫໍສະໝຸດ w k 2w 0(b)
该二阶常系数线性微分方程(b)的通解为
w Asin kx B coskx
(c)
将边界条件 x=0，w=0 代入式 (c)得 B=0。 利用边界条件 x=l， w=0得到
Asin kl 0
建筑力学电子教案
注意到已有 B=0，故上式中的 A 不可能等于零，否则将有 w≡ 0 而压杆不能保持微弯临界状态。由此可知，欲使(c)成 立，则必须 sinkl=0 。满足此条件的 kl 为
建筑力学电子教案
§13-1 关于稳定性的概念
一根宽30mm，厚5mm的矩形截面松木杆，对其施加轴 向压力，设材料的抗压强度为40MPa， 则当杆很短（如 h=30mm），将杆压坏的压力为：
F c A 40 106 0.005 0.03 6000 N
但如杆长为1m，则不到30N的压力，杆就会突然产生显 著的弯曲变形而失去工作能力。
l
可见此时的挠曲线为半波正弦曲线。但是 是一个无法确 定的值。即不论 为任何微小值，上述平衡都可以维持， 好象压杆受 作用时可以在微弯状态下处于“随遇而安” 的平衡状态。事实上这种平衡状态是不成立的。 值无法
确定的原因是推导采用了挠曲线近似微分方程。如果采用
挠曲线精确微分方程，则可以解出 Fcr ~ 的关系。
可见，研究压杆稳定的关键就是寻找 Fcr 。
建筑力学电子教案
F F（较小） F（较小）
F（特殊值） F（特殊值）
QQ
QQ
轴压
压弯
恢复
直线平衡 曲线平衡 直线平衡
压弯
失稳
曲线平衡 曲线平衡
保持常态、稳定
失去常态、失稳
建筑力学电子教案
§13-2 细长中心受压直杆临界力的欧拉公式
本节以两端球形铰支(简称两 端铰支)的细长中心受压杆件(图a) 为例，按照对于理想中心压杆来说 临界力就是杆能保持微弯状态时的 轴向压力这一概念，来导出求临界 力的欧拉(L.Euler)公式。
建筑力学电子教案
可以用下列模型来说明稳定问题的关键：
在杆上施加一竖向力 F ，再施加一横向力 Q，使杆 发生转动。如果 F 不大，杆能保持平衡，且撤去 Q 后， 杆将恢复到其原来的直线状态。但当 F 大过一个临界值 时，撤去 Q ，杆不再能恢复到原来的状态。前者称为稳 定平衡，后者称为不稳定平衡。这个从稳定平衡转变到 不稳定平衡的压力临界值称为临界力，用 Fcr表示。而Fcr 只与系统本身的性质 l 、EI 有关。
(a)
建筑力学电子教案
(b)
在图a 所示微弯状态下，两 端铰支压杆任意 x 截面的挠度(侧 向位移)为 w，该截面上的弯矩为 M(x)=Fcrw (图b)。杆的挠曲线近 似微分方程为
EIw M x Fcrw (a)
建筑力学电子教案
令 k 2 Fcr ，将挠曲线近似微分方程(a)改写成 EI
截面窄而高的梁，受外压的薄壁容器，都可能发生失 稳现象。
建筑力学电子教案
压杆受压力时弯曲的原因在于：
（1）杆本身不可能绝对地直；
（2）杆的材质不可能绝对地均匀；
F
（3）轴向压力不可能与杆轴线绝对重合。 这些因素使压杆在外加压应力下除了发 生轴向压缩变形外，还发生附加的弯曲 变形。 压杆是在压缩与弯曲组合变形的状 态下工作的。
Fcr
B l
A
建筑力学电子教案
思8-1参考答案 M (x) Fcrv M e
挠曲线近似微分方程
EI z M (x) Fcrv M e
最后得
kl =
挠曲线方程
Fcr
π2EI y l2
v [1 cos(π x / l)]
2
x δ
Me
Fcr B
A
y
Fcr Me
建筑力学电子教案
思考题8-2 推导如图变截面压杆临界力Fcr的欧拉公式。
建筑力学电子教案
细长压杆之所以丧失工作能力，是由于其轴线不能 维持原有直线形状的平衡状态所致，这种现象称为丧失 稳定，简称失稳。
横截面和材料相同的压杆，由于杆的长度不同，其抵 抗外力的性质将发生根本的改变。
粗短的压杆是强度问题，细长的压杆是稳定问题。
建筑力学电子教案
工程中，许多受压构件需要考虑其稳定性，例如：千 斤顶顶杆，托架中的压杆，无缝钢管穿孔机顶杆，采矿工 程中的钻杆等，在轴向压力较大时，就可能丧失稳定而突 然破坏，造成严重事故。
kl 0，π , 2π ，
或即
Fcr l 0，π ， 2π ，
EI
由于
Fcr l 0 EI
意味着临界力
Fcr ＝0，也就是杆根本未
受轴向压力，这不是真实情况。在 kl≠0 的解中，最小解相
应于最小的临界力，这是工程上最关心的临界力。
建筑力学电子教案
由 k l＝ 有
Fcr l π EI
亦即
0.5
Fcr
Fcr
π2EI y (2l ) 2
l
v
2
从上述分析可知,中心受压直杆的临界力 Fcr 与杆端的 约束情况有关，杆端的约束越强，临界力越大。
建筑力学电子教案
思考题8-1 如下图所示两端固定但上端可有水平位移的等截面中
心受压直杆，其长度为 l，横截面对z轴的惯性矩为I。推导 其临界力Fcr的欧拉公式，并求出压杆的挠曲线方程。
12
建筑力学电子教案
§13-3 不同杆端约束下细长压杆临界力的欧
.
拉公式 · 压杆的长度系数
几种理想支端约束条件下的细长压杆
Fcr
x Fcr
Fcr
Fcr
A l
A l
A l
l
v
B
B
y
B
当这些压杆都是等截面杆,且均由同一材料制成时,其 临界荷载 Fcr的计算公式可统一写为
建筑力学电子教案
Fcr＝
π2 EI y
Fcr l 2 π 2 EI
从而得到求两端铰支细长中心压杆临界力的欧拉公式：
Fcr
π
2 EI l2
I 是横截面最小 形心主惯性矩
此时杆的挠曲线方程可取 k l＝ ，代入式(c)得到为：
w Asinπ x l
建筑力学电子教案
注意到当 x=l/2 时 w= ，故有 A= 。从而挠曲线方程为 w sin π x
式中 μ 称为长度系数,随杆端约束情况而异；μl 则称为相当长 度，即相当于两端球形铰支压杆的长度。如下各图所示。
Fcr
x Fcr
A l
B
Fcr
π2EI y l2
1
A l
B
Fcr
π2EI y (0.7l ) 2
0.7
y
建筑力学电子教案
Fcr
A l
B
Fcr
π2EI y (0.5l ) 2
Fcr
A
I
l/4
l
2I l/2
BIl/4ຫໍສະໝຸດ w k 2w 0(b)
该二阶常系数线性微分方程(b)的通解为
w Asin kx B coskx
(c)
将边界条件 x=0，w=0 代入式 (c)得 B=0。 利用边界条件 x=l， w=0得到
Asin kl 0
建筑力学电子教案
注意到已有 B=0，故上式中的 A 不可能等于零，否则将有 w≡ 0 而压杆不能保持微弯临界状态。由此可知，欲使(c)成 立，则必须 sinkl=0 。满足此条件的 kl 为
建筑力学电子教案
§13-1 关于稳定性的概念
一根宽30mm，厚5mm的矩形截面松木杆，对其施加轴 向压力，设材料的抗压强度为40MPa， 则当杆很短（如 h=30mm），将杆压坏的压力为：
F c A 40 106 0.005 0.03 6000 N
但如杆长为1m，则不到30N的压力，杆就会突然产生显 著的弯曲变形而失去工作能力。
l
可见此时的挠曲线为半波正弦曲线。但是 是一个无法确 定的值。即不论 为任何微小值，上述平衡都可以维持， 好象压杆受 作用时可以在微弯状态下处于“随遇而安” 的平衡状态。事实上这种平衡状态是不成立的。 值无法
确定的原因是推导采用了挠曲线近似微分方程。如果采用
挠曲线精确微分方程，则可以解出 Fcr ~ 的关系。
可见，研究压杆稳定的关键就是寻找 Fcr 。
建筑力学电子教案
F F（较小） F（较小）
F（特殊值） F（特殊值）
轴压
压弯
恢复
直线平衡 曲线平衡 直线平衡
压弯
失稳
曲线平衡 曲线平衡
保持常态、稳定
失去常态、失稳
建筑力学电子教案
§13-2 细长中心受压直杆临界力的欧拉公式
本节以两端球形铰支(简称两 端铰支)的细长中心受压杆件(图a) 为例，按照对于理想中心压杆来说 临界力就是杆能保持微弯状态时的 轴向压力这一概念，来导出求临界 力的欧拉(L.Euler)公式。
建筑力学电子教案
可以用下列模型来说明稳定问题的关键：
在杆上施加一竖向力 F ，再施加一横向力 Q，使杆 发生转动。如果 F 不大，杆能保持平衡，且撤去 Q 后， 杆将恢复到其原来的直线状态。但当 F 大过一个临界值 时，撤去 Q ，杆不再能恢复到原来的状态。前者称为稳 定平衡，后者称为不稳定平衡。这个从稳定平衡转变到 不稳定平衡的压力临界值称为临界力，用 Fcr表示。而Fcr 只与系统本身的性质 l 、EI 有关。
(a)
建筑力学电子教案
(b)
在图a 所示微弯状态下，两 端铰支压杆任意 x 截面的挠度(侧 向位移)为 w，该截面上的弯矩为 M(x)=Fcrw (图b)。杆的挠曲线近 似微分方程为
EIw M x Fcrw (a)
建筑力学电子教案
令 k 2 Fcr ，将挠曲线近似微分方程(a)改写成 EI
截面窄而高的梁，受外压的薄壁容器，都可能发生失 稳现象。
建筑力学电子教案
压杆受压力时弯曲的原因在于：
（1）杆本身不可能绝对地直；
（2）杆的材质不可能绝对地均匀；
F
（3）轴向压力不可能与杆轴线绝对重合。 这些因素使压杆在外加压应力下除了发 生轴向压缩变形外，还发生附加的弯曲 变形。 压杆是在压缩与弯曲组合变形的状 态下工作的。
Fcr
B l
A
建筑力学电子教案
思8-1参考答案 M (x) Fcrv M e
挠曲线近似微分方程
EI z M (x) Fcrv M e
最后得
kl =
挠曲线方程
Fcr
π2EI y l2
v [1 cos(π x / l)]
2
x δ
Me
Fcr B
A
y
Fcr Me
建筑力学电子教案
思考题8-2 推导如图变截面压杆临界力Fcr的欧拉公式。
建筑力学电子教案
细长压杆之所以丧失工作能力，是由于其轴线不能 维持原有直线形状的平衡状态所致，这种现象称为丧失 稳定，简称失稳。
横截面和材料相同的压杆，由于杆的长度不同，其抵 抗外力的性质将发生根本的改变。
粗短的压杆是强度问题，细长的压杆是稳定问题。
建筑力学电子教案
工程中，许多受压构件需要考虑其稳定性，例如：千 斤顶顶杆，托架中的压杆，无缝钢管穿孔机顶杆，采矿工 程中的钻杆等，在轴向压力较大时，就可能丧失稳定而突 然破坏，造成严重事故。
kl 0，π , 2π ，
或即
Fcr l 0，π ， 2π ，
EI
由于
Fcr l 0 EI
意味着临界力
Fcr ＝0，也就是杆根本未
受轴向压力，这不是真实情况。在 kl≠0 的解中，最小解相
应于最小的临界力，这是工程上最关心的临界力。
建筑力学电子教案
由 k l＝ 有
Fcr l π EI
亦即
0.5
Fcr
Fcr
π2EI y (2l ) 2
l
v
2
从上述分析可知,中心受压直杆的临界力 Fcr 与杆端的 约束情况有关，杆端的约束越强，临界力越大。
建筑力学电子教案
思考题8-1 如下图所示两端固定但上端可有水平位移的等截面中
心受压直杆，其长度为 l，横截面对z轴的惯性矩为I。推导 其临界力Fcr的欧拉公式，并求出压杆的挠曲线方程。
12
建筑力学电子教案
§13-3 不同杆端约束下细长压杆临界力的欧
.
拉公式 · 压杆的长度系数
几种理想支端约束条件下的细长压杆
Fcr
x Fcr
Fcr
Fcr
A l
A l
A l
l
v
B
B
y
B
当这些压杆都是等截面杆,且均由同一材料制成时,其 临界荷载 Fcr的计算公式可统一写为
建筑力学电子教案
Fcr＝
π2 EI y
Fcr l 2 π 2 EI
从而得到求两端铰支细长中心压杆临界力的欧拉公式：
Fcr
π
2 EI l2
I 是横截面最小 形心主惯性矩
此时杆的挠曲线方程可取 k l＝ ，代入式(c)得到为：
w Asinπ x l
建筑力学电子教案
注意到当 x=l/2 时 w= ，故有 A= 。从而挠曲线方程为 w sin π x