金融工程12-期权的希腊字母
期权希腊字母
期权希腊字母 — 风险度量指标： THETA的说明
如下面例子所示，期权越接近到期，时间价值损失越 快。Theta用以测量每天期权价格大约的下降幅度。在下 面例子中，Theta约等于期权的价格变化。
期权希腊字母 — 风险度量指标： THETA计算器
Theta的数值通常为负值，其绝对值会随时间消逝而 变大， 也就是说愈接近到期日，权证的时间价值消失的 速度会愈快，最后到期时权证的时间价值应等于0。
期权希腊字母 — 风险度量指标： DELTA看跌期权/卖权PUT
对于看跌期权来说，Delta的变动范围为-1至0，而且 标的资产价格越低，Delta就越小。“平值”看跌期权Delta 为-0.5。从另一个角度来说，Delta的绝对值可以被认为是 看跌期权到期时为“实值”的可能性。
期权希腊字母 — 风险度量指标： DELTA的说明
Delta值的运用-Delta中性套期保值 （Delta Hedging）
如果投资者希望对冲期权或期货头寸的风险,Delta 就是套期保值比率。只要使头寸的整体 Delta值保持为0. 就建立了一个中性的套期策略。
期权希腊字母 — 风险度量指标：GAMMA
Gamma是指Delta的变化率，即给定标的资产价格发 生变化时Delta的变化率。(译注：就是为底层资产价格变 动一个单位时Delta的变动量)。Gamma在“平值”的时候最 大，在期权价格向“实值”或“虚值”变化的时候逐渐变小。 如下所示，期权价格的变化（到期之前）用一条曲线表示， 而不是直线。Delta是指曲线上任意一点的变化，而 Gamma则描述了delta的变化或者称之为曲线的曲率。对 于微积分的爱好者来说，Gamma是二阶导数。对于设法 对冲投资组合的交易员来说，理解Gamma至关重要。
「期权系列」期权的风险管理利器—希腊字母
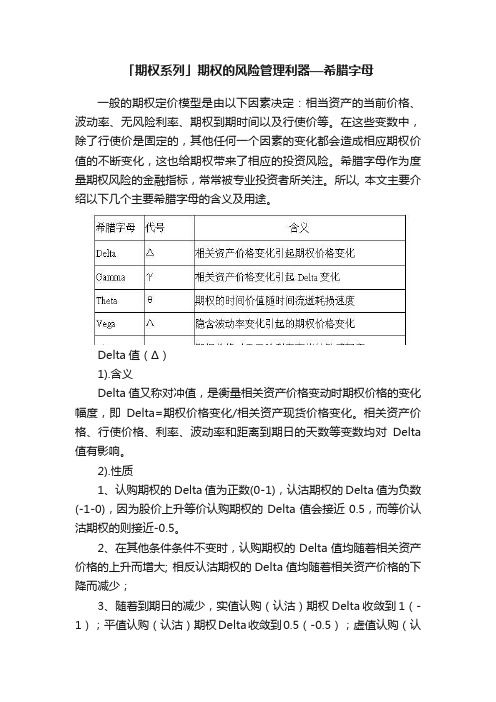
「期权系列」期权的风险管理利器—希腊字母一般的期权定价模型是由以下因素决定：相当资产的当前价格、波动率、无风险利率、期权到期时间以及行使价等。
在这些变数中，除了行使价是固定的，其他任何一个因素的变化都会造成相应期权价值的不断变化，这也给期权带来了相应的投资风险。
希腊字母作为度量期权风险的金融指标，常常被专业投资者所关注。
所以, 本文主要介绍以下几个主要希腊字母的含义及用途。
Delta值（Δ）1).含义Delta值又称对冲值，是衡量相关资产价格变动时期权价格的变化幅度，即Delta=期权价格变化/相关资产现货价格变化。
相关资产价格、行使价格、利率、波动率和距离到期日的天数等变数均对Delta 值有影响。
2).性质1、认购期权的Delta值为正数(0-1)，认沽期权的Delta值为负数(-1-0)，因为股价上升等价认购期权的Delta值会接近0.5，而等价认沽期权的则接近-0.5。
2、在其他条件条件不变时，认购期权的Delta值均随着相关资产价格的上升而增大; 相反认沽期权的Delta值均随着相关资产价格的下降而减少；3、随着到期日的减少，实值认购（认沽）期权Delta收敛到1（-1）；平值认购（认沽）期权Delta收敛到0.5（-0.5）；虚值认购（认沽）期权Delta收敛到0；3).应用Delta均值常用于中性套期保值，如果投资者想要对冲掉期权仓位风险，Delta值就是套期保值比率。
若头寸的Delta值持续为0，就建立了一个中性套期策略。
简单来讲，以做空认购期权为例假设一份长期认购期权的delta是0.8，则卖掉一份认购期权需要买入delta（0.8）份股票来做对冲，达到套期保值的效果。
Gamma 值（γ）1).含义Gamma值反映期权价格对delta值的影响程度，即delta变化量与期货价格变化量之比。
另外的，现在的Delta值将约等于之前的Delta值加上或减去Gamma 值。
2).性质1、对于长仓,无论认购期权或是认沽期权的gamma值均为正值。
详解期权的希腊字母
标的价格变化一单位的时，Delta值变化多少
波动率
Vega
波动率变化一单位间减少一单位时，期权合约的价格减少多少
无风险利率
Rho
无风险利率每变化一单位，期权合约的价格变化多少
期权合约的希腊值
本次内容：
• 为什么期权交易要用到希腊字母？ • 希腊字母体现的是什么关系？ • 希腊字母的取值是什么含义？ • 使用希腊字母时需要注意什么问题？
期权的杠杆率是多少？
• 你问的是哪个合约的杠杆率？ • 你问的是成本杠杆率还是收益杠杆率？ • 你问的是啥时候的杠杆率？ • 你问杠杆率想干啥？
期权价格变化非线性特征
期权价格变化非线性特征
本次内容：
• 为什么期权交易要用到希腊字母？ • 希腊字母体现的是什么关系？ • 希腊字母的取值是什么含义？ • 使用希腊字母时需要注意什么问题？
详解股指期权的希腊字母
本次内容：
• 为什么期权交易要用到希腊字母？ • 希腊字母体现的是什么关系？ • 希腊字母的取值是什么含义？ • 使用希腊字母时需要注意什么问题？
本次内容：
• 为什么期权交易要用到希腊字母？ • 希腊字母体现的是什么关系？ • 希腊字母的取值是什么含义？ • 使用希腊字母时需要注意什么问题？
• 实际使用时，gamma所代表的是 标的价格涨速（真实波动）对期 权价格的影响
期权合约的希腊值
Vega：说不清的价格变化都在这里
• Vega的含义是波动率变化一单 位时，期权合约的价格变化多 少
• 实际使用的时候，波动率用的 是隐含波动率，而隐含波动率 是用市场价反推出来的，其实 隐含波动率不仅仅是波动率
期权合约的希腊值
Theta：时间价值是怎么折损的？
期权风险指标
期权风险指标概述：期权是金融市场中常见的衍生品，它赋予持有者在未来某个时间点以约定价格买入或者卖出标的资产的权利。
然而，期权交易也伴有着一定的风险。
为了匡助投资者更好地评估和管理期权交易的风险，期权风险指标被广泛应用于金融市场。
一、Delta（希腊字母Δ）Delta是期权风险指标中最常用的一个，它衡量了期权价格对标的资产价格变动的敏感程度。
Delta的取值范围是-1到1，对于看涨期权，Delta的取值介于0到1之间，表示期权价格的变动与标的资产价格的变动方向一致；对于看跌期权，Delta的取值介于-1到0之间，表示期权价格的变动与标的资产价格的变动方向相反。
二、Gamma（希腊字母Γ）Gamma是衡量Delta变动速度的指标，它反映了期权价格对标的资产价格变动的敏感程度的变化率。
Gamma的取值范围通常是正数，对于看涨期权和看跌期权来说，Gamma的值越高，表明期权价格对标的资产价格的变动更为敏感。
三、Theta（希腊字母Θ）Theta是衡量期权时间价值衰减速度的指标，它表示每过一天，期权价格将会减少多少。
Theta通常为负数，对于看涨期权和看跌期权来说，Theta的值越高，表明时间价值的衰减速度越快。
四、Vega（希腊字母ν）Vega是衡量期权价格对标的资产价格波动率变动的敏感程度的指标。
Vega的取值通常为正数，表示期权价格对波动率的变动非常敏感。
当波动率上升时，期权价格也会上升，反之亦然。
五、Rho（希腊字母ρ）Rho是衡量期权价格对无风险利率变动的敏感程度的指标。
Rho的取值通常为正数，表示期权价格对无风险利率的变动非常敏感。
当无风险利率上升时，期权价格也会上升，反之亦然。
六、综合风险指标综合风险指标是基于以上各个风险指标的综合评估，用于衡量期权交易的整体风险水平。
常见的综合风险指标包括Delta-Neutral、Vega-Neutral和Gamma-Neutral等。
Delta-Neutral策略通过组合不同的期权合约和标的资产，使得整体Delta值为零，从而实现对标的资产价格变动的中性化。
(2021年整理)期权价值敏感性——希腊字母汇总
(完整版)期权价值敏感性——希腊字母汇总编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)期权价值敏感性——希腊字母汇总）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)期权价值敏感性——希腊字母汇总的全部内容。
（完整版）期权价值敏感性--希腊字母汇总编辑整理：张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望 (完整版)期权价值敏感性--希腊字母汇总这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为 <（完整版）期权价值敏感性——希腊字母汇总> 这篇文档的全部内容。
第三章期权敏感性（希腊字母）顾名思义，期权敏感性是指期权价格受某些定价参数的变动而变动的敏感程度，本章主要介绍期权价格对其四个参数（标的资产市场价格、到期时间、波动率和无风险利率）的敏感性指标，这些敏感性指标也称作希腊值（Greeks）。
每一个希腊值刻画了某个特定风险,如果期权价格对某一参数的敏感性为零，可以想见，该参数变化时给期权带来的价格风险就为零。
实际上，当我们运用期权给其标的资产或其它期权进行套期保值时，一种较常用的方法就是分别算出保值工具与保值对象两者的价值对一些共同的变量（如标的资产价格、时间、标的资产价格的波动率、无风险利率等）的敏感性，然后建立适当数量的证券头寸,组成套期保值组合,使组合中的保值工具与保值对象的价格变动能相互抵消，也就是说让套期保值组合对该参数变化的敏感性变为零,这样就能起到消除相应风险的套期保值的目的。
期权的希腊字母
Gamma——欧式股票期权
Gamma与到期时间的关系
Delta, Theta, Gamma的关系
从BSM方程容易推导出三者的关系
如果投资组合是Delta中性的，则
如果Theta是较大的正数，Gamma就是很大的负数， 因此，Theta可以作为Gamma的替代指标使用
Vega
Vega是期权的价值对标的资产波动率的偏导数，度 量了期权价值对标的资产波动率的敏感性
上图有助于理解动态复制技术
曲线表示卖权与标的股票价格的关系 切线的斜率表示卖权的Delta 截距表示复制投资组合在无风险资产上的投资额
随着股价的涨跌，切线的位置和方向将发生改变，其 斜率与截距都将发生变化
因此，动态复制需要经常性地调整头寸
2. 投资组合保险(股票+卖权)包含两个头寸 • 股票头寸：
股价：Delta, Gamma 到期时间：Theta 波动率：Vega 无风险利率：Rho
Delta
Delta是期权价值对标的资产价格的偏导数，度量了 期权价值对标的资产价格变化的敏感性
图示
Delta——欧式股票期权
利用BS公式，可以推导出 Delta与股价的关系
1
X
Delta——欧式股票期权
动态复制在理论上虽然是“自融资策略”，但是，由于 存在交易成本，实际上不可能是“自融资策略”。基金 经理必须在交易成本与复制效果之间进行平衡
定义：建立对冲工具头寸，使得对冲工具头寸与要保 护的头寸的Delta等于零
Delta中性：资产(或者组合)的Delta等于零
动态对冲
由于资产的Delta通常是时间的函数，因此，为了实现 对冲目标，通常必须动态调整对冲工具头寸的数量
例子：BSM随机微分方程的推导
经济学中的希腊字母
经济学中的希腊字母
1. α（Alpha）：发音为“阿尔法”。
在希腊字母表中是第一个字母，常用于表示角度、系数或参数。
在数学中，α常用于表示一个角度，例如α表示角A；在物理中，α常用于表示角加速度；而在统计学中，α常用于表示显著性水平。
2. β（Beta）：发音为“贝塔”。
在希腊字母表中是第二个字母，通常用于表示系数、参数或某种变量的修正。
在数学中，β经常用于表示函数的参数，如线性回归中的斜率；在物理中，β常用于表示粒子的速度相对于光速的比值；在金融和经济学中，β则表示风险的相关系数。
3. γ（Gamma）：发音为“伽玛”。
在希腊字母表中是第三个字母，主要用于表示某种变化或修正。
在数学中，γ常用于表示伽玛函数，它是一种特殊的函数；在物理学中，γ常用于表示相对论修正因子，它涉及到时间和空间的变形；在金融学和经济学中，γ则表示期权的价格变动对标的资产价格变动的敏感度。
需要注意的是，希腊字母在不同语境中有时会有略微不同的读音，但以上所介绍的读音是最常见和广泛接受的发音方式。
在学术界和专业领域，这些希腊字母常用于表示某种特定的概念或符号，在数学、物理、统计学等领域中使用频繁。
掌握希腊字母的发音和代表的概念，有助于加深对相关学科的理解，并能更准确地进行学术交流。
期权中希腊字母的含义讲解
1. 股指期权
? ? ? c ? e? qT N d1
2. 外汇期权
? ? ? c ? e? rf T N d1
3. 期货期权
? ? ? c ? e? rT N d1
4. 股票远期
? p ? e? qT N ?d1 ?? 1 ? ? ? p ? e? rf T N d1 ? 1 ? p ? e? rT N ?d1 ?? 1
BS 采用Delta 对冲方法，建立起包含期权的 Delta 中性 头寸
Greeks
9
Delta对冲——使用期货
1. 实践中，对冲工具多选用期货
期货流动性好、交易成本低
2. 符号
期货到期时间：T * Delta 对冲需要的标的资产头寸：H A Delta 对冲需要的期货头寸：H F
3. 期货的Delta:
19
Delta, Theta, Gamma的关系
1. 从BSM 方程容易推导出三者的关系
?? ?t
? rS ?? ?S
?
1?
2
2S 2
? 2? ?S 2
?
r?
? ? rS ? ? 1 ? 2S 2? ? r?
2
2. 如果投资组合是Delta 中性的，则
? ? 1 ? 2S 2? ? r?
2
如果Theta 是较大的正数， Gamma 就是很大的负数， 因此， Theta 可以作为 Gamma 的替代指标使用
股价： Delta, Gamma 到期时间： Theta 波动率： Vega 无风险利率： Rho
Greeks
3
Delta
1. Delta 是期权价值对标的资产价格的偏导数，度量了 期权价值对标的资产价格变化的敏感性
期权风险指标--希腊字母
Delta 值一、Delta值概述期权的风险指标通常用希腊字母来表示，包括：delta值、gamma值、theta 值、vega值、rho值等。
Delta值（S）,又称对冲值：是衡量标的资产价格变动时，期权价格的变化幅度。
用公式表示：Delta=期权价格变化/期货价格变化所谓Delta ,是用以衡量选择权标的资产变动时，选择权价格改变的百分比，也就是选择权的标的价值发生变动时，选择权价值相应也在变动。
公式为：Delta =外汇期权费的变化/外汇期权标的即期汇率的变化关于Delta值，可以参考以下三个公式：1•选择权Delta加权部位二选择权标的资产市场价值x选择权之Delta值；2. 选择权Delta加权部位x各标的之市场风险系数=Delta风险约当金额；3. Delta加权部位价值=选择权Delta加权部位价值+现货避险部位价值。
1、Delta值的特性Delta具有以下特性：买权的Delta 一定要是正值；卖权的Delta 一定要是负值；Delta数值的围介乎0到1之间；价平选择权的Delta为0.5; Delta数值可以相加，假设投资组合两个选择权的Delta数值分别为0.5及0.3，整个组合的Delta数值将会是0.8。
对于看涨期权来说，期货价格上涨（下跌），期权价格随之上涨（下跌），二者始终保持同向变化。
因此看涨期权的delta为正数。
而看跌期权价格的变化与期货价格相反，因此，看跌期权的delta为负数。
风险指标的正负号均是从买入期权的角度来考虑的。
［因此,交易者一定要注意期权的指标与部位的指标之区别。
对于delta，期权部位的符号如下表。
表1期权部位的delta值部位看涨期权看跌期权多头+ -空头- +期权的delta值介于-1到1之间。
对于看涨期权，delta的变动围为0到1，深实值看涨期权的delta趋增至1，平值看涨期权delta为0.5，深虚值看涨期权的delta则逼近于0。
对于看跌期权，delta变动围为-1到0,深实值看跌期权的delta趋近-1，平值看跌期权的delta为-0.5，深虚值看跌期权的delta趋近于0。
趣谈期权有关的希腊字母
趣谈期权有关的希腊字母趣谈期权有关的希腊字母！Delta, Gamma, Vega和Theta当我们理解期权价值与其影响因素的敏感性时，可以作这样比喻。
股票期权作为股票的“孩子”，其脾气秉性自然受三方面的影响：一是自身“基因”的制约，比如：权利属性（认购还是认沽）、行权价（K）、到期时间（T）；二是“父母亲”的言传身教：股价（S）、股价的波动率（Sigma）；三是社会大环境的熏陶：无风险收益率（r）。
那么一份股票期权的价格（V）究竟是如何被这些因素所影响的呢？换而言之，股票价格上涨1％，或者股价波动率上升1%，作为孩子的期权的“脾气”变化多少呢？为了回答这个问题，我们就必须认识五个“希腊字母”了。
毫不夸张地说，这五个希腊字母就是期权价格变化的生命源泉，也是“孩子”与“父母”的纽带。
这五个希腊字母就叫做Delta，Gamma，Vega，Theta和Rho。
先让我们来认识第一个希腊字母——Delta。
1． Delta是什么？期权是标的资产的衍生产品。
两者之间就像是“父子”一样，父亲的一举一动无时无刻不在影响着孩子的行为。
父亲的这种影响力就是Delta。
以50ETF为例，当ETF价格发生变化时，期权价格也会随之改变。
ETF与期权之间的价格关系可以用Delta来刻画：当ETF价格变化0.001元时，对期权价格的影响就是0.001*Delta元。
认购期权是“乖孩子”，当“父亲”ETF价格上涨的时候，认购期权价格也会上涨，认购期权的Delta大于零；而“坏孩子”认沽期权则恰恰相反，当ETF 价格上涨时，认沽期权的价格反而是下跌的，它的Delta小于零。
2． Delta在投资中的两个简单应用一个是对冲作用。
如果我们有着如下对冲组合：由Delta份ETF空头和1份期权多头组成。
当ETF价格变化0.001元时，Delta份ETF 空头价格会变化-0.001*Delta元，1份期权合约价格会变化0.001*Delta元。
期权希腊字母-DeltaGammaThetaVegaRho
期权希腊字母-DeltaGammaThetaVegaRho从本⽂开始，我们将开始讲解期权中的希腊字母；本⽂将介绍希腊字母-Delta。
Delta表⽰期权头⼨的波动与标的资产价格波动的关系。
相应的图标给我们展⽰的是期权头⼨相对于价格波动的速度。
因此Delta值为1意味着股票价格每波动1个百分点，期权头⼨也相应变动1个百分点。
Delta值为-1则意味着股票价格每波动1个百分点，期权头⼨则相应波动-1个百分点。
同时Delta是另⼀种表⽰期权到期变成实值的可能性。
平价看涨期权的Delta值为0.5，也就是说，意味着期权有50%的可能性到期时变为实值期权。
⼀份深度实值看涨期权的Delta值接近1，意味着到期时期权有接近100%的可能性变为实值期权。
因此，Delta值可以被解释为头⼨的速度或者⼀份期权到期时变为实值期权的可能性。
⼀些⾼级的交易员喜欢采⽤Delta值总额为0的组合进⾏交易，这种交易类型被认为是Delta中性交易。
这类中性策略也不是没有风险，但是可以保证⽆论市场价格往什么⽅向变化都可以获利。
编辑于 2019-06-26在数学上，Gamma是Delta的⼆阶微分。
Gamma衡量的是Delta随标的价格改变⽽变化的敏感程度，即期货期货价格变动⼀个单位，Delta变动多少个单位。
Gamma就是期权价格随标的价格变化的加速度。
Gamma也可以看做该头⼨到期变为实值的可能性，换句话说，就是Delta 改变符号的可能性。
那么Gamma变化有什么特点吗？看涨期权与看跌期权的多头Gamma值均⼤于0，看涨期权与看跌期权的空⽃Gamma值均⼩于0.平值期权的Gamma值最⼤，即此时Delta值的变化速率最⼤。
深度实值和深度虚值期权的Gamma值接近0.发布于 2019-06-26Theta衡量的是，在期权到期之前，时间每经过⼀天，期权价值会损失多少。
⽐如：某个期权的权利⾦是200，Theta值为7，就表⽰，每过去⼀天，该期权的权利⾦损失是7，也就是说，如果市场其他条件不变的话，权利⾦第⼀天过后变成193，第⼆天变成186，以此类推。
期权价值敏感性——希腊字母汇总
第三章 期权敏感性（希腊字母）顾名思义，期权敏感性是指期权价格受某些定价参数的变动而变动的敏感 程度，本章主要介绍期权价格对其四个参数（标的资产市场价格、到期时间、波动率和无风险利率）的敏感性指标，这些敏感性指标也称作希腊值（Greeks ）。
每一个希腊值刻画了某个特定风险，如果期权价格对某一参数的敏感性为 零，可以想见，该参数变化时给期权带来的价格风险就为零。
实际上，当我们 运用期权给其标的资产或其它期权进行套期保值时，一种较常用的方法就是分 别算出保值工具与保值对象两者的价值对一些共同的变量（如标的资产价格、 时间、标的资产价格的波动率、无风险利率等）的敏感性，然后建立适当数量 的证券头寸，组成套期保值组合，使组合中的保值工具与保值对象的价格变动 能相互抵消，也就是说让套期保值组合对该参数变化的敏感性变为零，这样就 能起到消除相应风险的套期保值的目的。
本章将主要介绍 Delta 、Gamma 、Vega 、Theta 、Rho 五个常用希腊字母。
符号风险因素 量化公式Gamma Γ标的证券价格变化 Delta 变化/标的证券价格变化 Vega ν波动率变化 权利金变化/波动率变化Theta Θ到期时间变化 权利金变化/到期时间变化 本章符号释义：T 为期权到期时间S 为标的证券价格， S 0 为标的证券现价， S T 为标的证券行权时价格K 为期权行权价格σ 为标的证券波动率r 为无风险利率π t 为资产组合在 t 时刻的价值N () 为标准正态分布的累积密度函数，可以查表或用计算机(如 Excel)求得N()为标准正态分布的密度函数，N()=-x2''2第一节Delta（德尔塔，∆）1.1定义Delta衡量的是标的证券价格变化对权利金的影响，即标的证券价格变化一个单位，权利金相应产生的变化。
新权利金=原权利金+Delta×标的证券价格变化1.2公式从理论上，Delta准确的定义为期权价值对于标的证券价格的一阶偏导。
期权对冲中的希腊字母
“希腊字母”期权的风控体系期权产品是目前国际衍生品市场的重要组成部分。
因其独特的优势和丰富的内涵，期权在国际市场上迅猛发展，应用日益广泛，在风险管理、产品构建等方面发挥着举足轻重的作用。
随着投资热情的高涨，期权交易的风险管理问题也日益突出，如何准确地度量和合理控制期权头寸的风险对投资者至关重要。
著名的Black-Scholes期权定价模型中，期权的价格受多种因素影响，包括标的价格、标的波动率、到期时间、行权价格以及无风险利率。
如何量化各类风险，较为准确地估计持仓损益，进行合理有效的风险管理和投资决策非常重要。
由Black-Scholes模型衍生出的希腊字母体系则是这样一套风险管理工具，该体系将期权头寸风险分解成若干风险组成部分，包括标的价格风险、时间风险、波动率风险和利率风险，并用希腊字母估计当其他风险条件不变时，一个单位的某种风险变动所造成的期权的价值变化。
通过量化每一种风险类型的风险暴露，投资者就可以将期权风险管理转化为希腊字母的管理。
Delta看多就买看涨期权，看空就买看跌期权。
这是刚接触期权的投资者的笼统看法。
假设大盘涨了10点，看涨期权价值会涨多少呢，同样是10点吗？ Delta就是用来回答这个问题的。
Delta表示在其他因素保持不变的情况下，一单位标的资产价格的变化所引起的期权价值的变化。
Delta反映了标的价格单位变化给期权投资者带来的收益或亏损。
例如投资者持有一手看涨期权，Delta值为0.5，表示在一定的标的价格变化区间内，期权的价值的变化幅度约为标的价格变化幅度的50%，具体来讲，若标的价格上涨1点，期权价值将上升约0.5点，投资者持有该看涨期权将获利约0.5点，反之若标的价格下降1点，投资者将损失约0.5点。
由Delta的定义可以推导出Delta的一些性质：（1）看涨期权多头的Delta值为正，表示看涨期权价值和标的价格同方向变动；看跌期权多头的Delta值为负，表示看跌期权价值同标的价格反方向变动；期权空头的Delta值与期权多头的Delta值符号相反。
希腊值delta是啥？在期权交易中如何应用？一文详解！
希腊值delta是啥？在期权交易中如何应⽤？⼀⽂详解！前⾔：delta可以告诉我们标的资产是涨了赚钱还是跌了赚钱 delta指的是假设其他因素保持不变的情况下，给定⼀单位标的资产的价格变化所引起的期权价值变化的⼀个估计值。
希腊字母delta在期权交易中有⼴泛的应⽤，尤其是对于复杂的期权组合策略，投资者更需要好好运⽤delta这⼀风险指标。
希腊字母delta在期权操作中⾮常重要。
对⼤多数投资者⽽⾔，期货交易最⼤的风险来⾃于⽅向（多或空），但标的资产的⽅向性变动仅仅是导致期权价格波动的因素之⼀，并且这⼀风险在期权的操作中很容易对冲掉。
期权的各种组合策略⾮常多，了解希腊字母与期权价格的关系对于组合策略⼗分适⽤，也能让投资者很直观地对所持头⼨的⽅向性风险做到⼼中有数。
1什么是期权的deltadelta指的是假设其他因素保持不变的情况下，给定⼀单位标的资产的价格变化所引起的期权价值变化的⼀个估计值。
期权的delta主要回答了⼀个问题：如果标的资产价格上涨或者下跌了1个点，那么期权的涨跌是多少。
数学意义为期权价格对标的资产价格的⼀阶导数，⼏何意义为期权价格曲线上某⼀点的斜率。
本⽂为⽅便起见，将以个股期权为例。
图1为期权delta的⼏何意义例如，⾏权价格为100的某只个股期权，股价为105时，delta为0.63意味着此时股价上涨1元时，期权价格会上涨0.63元。
delta值是个时变的值，并⾮固定不变。
看涨期权delta的取值范围为[0 1]，看跌期权为[-1 0]。
期权delta的⼏条规律delta随标的（股票）价格的变动看涨期权和看跌期权的delta在数值上都会随股票价格的上涨⽽增加，随股票价格的下跌⽽减少。
此处是delta随标的资产价格变动的变动，⽽不是期权价格随标的资产价格的变动。
同⼀⾏权价格的看涨期权和看跌期权（欧式）的delta可以直接从PCP平价关系得到，除delta外，其余的希腊字母（看涨与看跌之间的关系）也均可以通过对PCP平价公式求导直接得到。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• theta（q）度量当生命期减少1天时期权价格的变化。 • rho（r）度量当利率有一个百分点（100个基差点）的增加时
Theta与股价的关系
X
15
Gamma
• Delta对冲，只有在股票价格小幅度变化时才时有 效的.
• 当股票价格出现大幅度变化时，对冲组合就必须考 虑2阶导数, 即Gamma. 否则, 维持原来的Delta就 会出现风险。
• 即:
– Gamma变化较小时，Delta变化变化缓慢，一般不需要 频繁调整头寸。
证明：c S
N (d1) S
N (d1) d1
d1 S
Xer
N (d2 ) d2 d2 S
由于 d1 d2 ,则 S S
Xer N (d2 ) Xer（
1
e ） - d22 2
d2
2
d2 d1
Xer
2
exp(
1 2
(d12
2 d1
2 ))
Xer [ 1
e e ]
1 2
d12
5
Delta
• Delta是期权价值对标的资产价格的偏导数，度量了期权价 值对标的资产价格变化的敏感性
D c S
• 图示
S(0)
6
Delta——无收益资产的欧式股票期权
• 利用BS公式，可以推导出
Dc N d1
D p N d1 1 0
• Delta与股价的关系
1
S(0)
7
• 命题：欧式看涨期权的Delta=N(d1)
化就是0.6DS –如果整个组合的Delta等于0,意味着什么?
• 动态对冲
– 由于资产的Delta通常是时间的函数，因此，为了实现 对冲目标，通常必须动态调整对冲工具头寸的数量
11
Delta对冲
• 例子：BSM随机微分方程的推导
– 1个单位衍生工具空头， f 份股票
S
– BS采用Delta对冲方法，建立起包含期权的Delta中性头 寸
d1
ln( S
/
X
)
(r
T
2
t
/
2)(T
t)
d2
ln( S
/
X
)
(r 2 T t
/
2)(T
t)
4
• 根据泰勒公式对期权价格进行二阶展开，忽略高阶项
Delta
Theta
Vega
Rho
Dc
c s
Ds
c t
Dt
c
D
c r
Dr
1 2
2c S 2
(Ds)2
(3)
这里省略S的下标t
Gamma
D Dt 1 G DS2 2
• Gamma中性与Gamma对冲
– 由于标的资产及其远期、期货合约的Gamma都等于零， 因此，不能用来改变投资组合的Gamma
– 要改变投资组合的Gamma，必须使用那些价格与标的 资产价格呈非线性关系的工具，例如期权
17
Gamma——欧式股票期权
欧式股票期权的Gamma
• 其余支付红利率为q、股指期权、外汇期权、期货期权只要根 据定价公式即可得到其Delta值
• 衍生证券组合的Delta
n
D wiDi
i 1
10
பைடு நூலகம்
Delta对冲
• 定义：建立对冲工具头寸，使得对冲工具头寸与要 保护的头寸的Delta等于零
– Delta中性：资产(或者组合)的Delta等于零 – 如果Delta为0.6,意味着股票价格变化DS,期权价格的变
第十五章 期权的希腊字母
1
15章 期权的希腊字母
• 期权价值的决定因素包括股价、到期时间、波动率、 无风险利率以及执行价格，其中易变的因素有四个：
– 股价：Delta, Gamma – 到期时间：Theta – 波动率：Vega – 无风险利率：Rho
2
期权的希腊字
期权的希腊字是指当公式的一个投入（参数）变化一单位而其它 投入保持不变时期权价值的变化。希腊字度量的重要用途之一 是评估风险的暴露。希腊字度量可以用于计算任何种类在下资 产上的期权，而不仅仅是股票期权上。
d1
2 2
2
8
N (d1)
1
e
1 2
d12
d1
2
d1
ln(S
/
X
)
(r
2
/
2)
d1 2 / 2 ln(S / X ) r
Xer N (d2 ) Xer [
1
e e ]
1 2
d12
d1
2 2
d2
2
Xer N (d1) eln(s / X )r d1
Xer N (d1) S er S N (d1)
– Gamma较大时，对冲组合的Delta对标的资产相当敏感， 若不调整Delta则风险较大。
16
Gamma
• Gamma是期权的Delta对标的资产价格的偏导数，
也是期权价值对标的资产价格的二阶偏倒数
G
D S
2 S 2
• Gamma度量了期权Delta对标的资产价格变化的 敏感性，也度量了期权价值对标的资产价格的凸性
期权价格的变化。
3
回顾：Black-Scholes模型
• 看涨期权的价格（为欧式期权到期时期望值的现值）
c er(T t) E[Max(ST X ,0)]
• 股票价格的概率分布
ln ST
~
ln S
(
2 )(T
2
t),
T t
• 看涨期权价格的解
c S N (d1 ) Xe r(T t) N (d 2 )
d1 X
d1
所以，最后两项相等，则 C S
N (d1)，命题成立。
9
各种产品的Delta
• 远期合约：D=1 X为远期的交割价，当一个远期生效时，远期价 格等于合约规定的交割价格，远期价格F就是f=0
的X值 f (t) S (t) Xerf (T t)
• 无收益资产的欧式期权：买权：N(d1)；卖权- N(-d1)
12
Theta——定义
• Theta是期权价值对时间的偏导数，度量了期权价 值随时间衰减的速度
– 有时也称为证券组合的时间损耗
• 单个期权的Theta几乎总是负值，因为随着到期日 的临近，期权往往是变得越不值钱(若其他因素不 变,而仅仅时间改变)
• 与股价呈随机波动不同，距离到期的时间是一个完 全确定的量，无需进行对冲
– 换句话说，未来股价是不确定的，因而需要对冲；但时 间走向却没有不定性，无需对冲。
13
Theta——欧式股票期权
• 欧式股票期权的Theta
– 买权
c
S0 N (d1 )
2T
rXerT N (d2 )
– 卖权
p
S0 N (d1 )
2T
rXerT N (d2 )
14
Theta——欧式股票期权