温州中学提前招生数学模拟卷精选文档
温州中学提前招生数学模拟试题
7、设y=x4+4x3+8x2+8x+7，其中x为任何实数，则y的取值范围是( )
A、一切正实数B、一切大于或等于7的实数
C、一切大于或等于4的实数D、一切大于或等于3的实数
8、如图,已知Rt△ABC外切于⊙O,E、F、H为切点，∠ABC=90°，直线FE、CB相交于D点，连结AO、HE、HF，则下列结论：①∠EFH=45°；②∠FEH=45°+∠FAO；③BD=AF；④DH2=AO·DF.其中正确结论的个数为（）
自主招生数学试题
一、选择题
1、函数y＝－图象的大致形状是（）
A B C D
2、下列说法中，正确的个数是（）
①到圆心的距离大于半径的点在圆内；②圆的半径垂直于圆的切线；③圆周角等于圆心角的一半；④等弧所对的圆心角相等；⑤平分弦的直径垂直于弦。
A、0个；B、1个C、2个D、3个
3、某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折出售，但要保持利润率不低于5%，则至少可打（）
12、水管的外部需要包扎，包扎时用带子缠绕在管道外部.若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度（指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分）．若带子宽度为2，水管直径为2，则的余弦值为。
13、如图，在扇形纸片AOB中，OA=10，AOB=36，OB在桌面内的直线l上．现将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA落在l上时，停止旋转．则点O所经过的路线长为。
A、6折B、7折C、8折D、9折
4、二次函数 （ ）的图象的顶点在第一象限，且过点（ ， ）.
温州中学自主招生模拟试题数学
温州中学自主招生模拟试题数学试卷（120分） 一试一. 选择题：本大题共8小题，每小题4分，满分32分。
1. 设0a b >>, 那么21()a b a b +-的最小值是（ ）A.2B.3C.4D.52. 已知一组正数12345,,,,x x x x x 的方差为：222222123451(20)5Sx x x x x =++++-，则关于数据123452,2,2,2,2x x x x x + + + + +的说法：①方差为S2；②平均数为2；③平均数为4；④方差为4S2。
其中正确的说法是（ ）A .①②B .①③C . ②④ D.③④3. 已知实数b a ≠，且满足)1(33)1(2+-=+a a ，2)1(3)1(3+-=+b b .则ba aab b+的值为（ ）A.23B.23-C.2-D.13- 4. 如果x 和y 是非零实数，使得3=+y x 和3=+x y x ，那么x+y 等于（ ）A.3B.13C.2131-D.134-5. 如果对于不小于8的自然数n ，当3n+1是一个完全平方数是，n+1都能表示成个k 完全 平方数的和，那么k 的最小值为（ ） A.1 B.2 C.3 D.46. 已知24b ac -是一元二次方程20ax bx c ++= (a ≠0)的一个实数根，则ab 的取值范围为（ ）A.18ab ≥B.18ab ≤C.14ab ≥D.14ab ≤7. 在四边形ABCD 中，边AB=x ，BC=CD=4, DA=5,它的对角线AC=y ，其中x,y 都是整数，∠BAC=∠DAC,那么，x=( )A.4B.5C.4或5D.非以上答案8. 设二次函数()20y ax bx c a =++≠满足:当01x ≤≤时,1y ≤.则a b c ++的最大值是( ).A.3;B.7;C.12;D.17. 二.填空题：本大题共6小题，每小题5分，满分30分。
9. 在边长为2的正方形A B C D 的四边上分别取点E 、F 、G 、H .四边形E F G H 四边的平方和2222EF FG GH HE +++最小时其面积为_____.10. 已知点A ，B 的坐标分别为（1，0），（2，0）． 若二次函数()233y x a x =+-+的图象与线段AB 恰有一个交点，则a 的取值范围是 ．11. △ABC 中，AB ＝7，BC ＝8，CA ＝9，过△ABC 的内切圆圆心I 作DE ∥BC ，分别与AB ，AC 相交于点D ，E ，则DE 的长为 ．12. 关于x ，y 的方程22208()x y x y +=-的所有正整数解为 ． 13. n 个正整数12na a a ，，，满足如下条件：1212009n a a a =<<<= ；且12na a a ，，，中任意n －1个不同的数的算术平均数都是正整数．则 n 的最大值为___________.14. 如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE ，BN 于点F ，C ，过点C 作AM 的垂线CD ，垂足为D ．若CD ＝CF ，A EA D= ．温州中学自主招生模拟试题数学答题卷（120分） 一试一.选择题：本大题共8小题，每小题4分，满分32分。
2019-2020学年浙江省温州中学自主招生九年级数学模拟试卷有标准答案
浙江省温州中学自主招生九年级数学模拟试卷（本卷满分：150分 考试时间：90分钟）一、单项选择题（本大题分5小题，每题4分，共20分）1. 气象台预报：“本市明天降水概率是80%”，但据经验，气象台预报的准确率仅为80%，则在此经验下，本市明天降水的概率为················( ) A 、84% B 、80% C 、68% D 、64%2. 如图，已知A ∠的平分线分别与边BC 、ABC ∆的外接圆交于点D 、M ，过D 任作一条与直线BC不重合的直线l ，直线l 分别与直线MB 、MC 交于点P 、Q ，下列判断不正确的是···········································( ) A ．无论直线l 的位置如何，总有直线PM 与ABD ∆的外接圆相切B ．无论直线l 的位置如何，总有BAC PAQ ∠>∠ C ．直线l 选取适当的位置，可使A 、P 、M 、Q 四点共圆D ．直线l 选取适当的位置，可使APQ S ∆<ABC S ∆3. 欲将正六边形的各边和各条对角线都染为n 种颜色之一，使得以正六边形的任何3个顶点作为顶点的三角形有3种不同颜色的边，并且不同的三角形使用不同的3色组合，则n 的最小值为·········( )A ．6B ．7C ．8D ．9 4. 将一个正11边形用对角线划分为9个三角形，这些对角线在正11边形内两两不相交，则··················································( ) A ．存在某种分法，所分出的三角形都不是锐角三角形 B ．存在某种分法，所分出的三角形恰有两个锐角三角形 C ．存在某种分法，所分出的三角形至少有3个锐角三角形 D ．任何一种分法所分出的三角形都恰有1个锐角三角形5. 已知实系数二次函数()x f 与()x g ，()()x g x f =和()()03=+x g x f 有两重根，()x f 有两相异实根，则()x g ···································( )A ．有两相异实根B ．有两相同实根C ．没有实根D ．没有有理根 二、填空题（本大题分10小题，每题6分，共60分）第2题6. 设正数x 、y 、z 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=+=++.1693253222222x zx z z y y xy x ，，则xy +2yz +3zx 的值为 ．7. 已知ABCD 是一个正方形，点M (异于点B 、C )在边BC 上，线段AM 的垂直平分线l 分别交AB 、CD于点E 、F ．若AB =1，则DF BE -的取值范围为 ．8. 已知实数a ，b ，c ，d 满足2a 2+3c 2=2b 2+3d 2=(ad-bc )2=6，则(a 2+b 2)(c 2+d 2)的值为 ． 9. 由两个不大于100的正整数m ，n 组成的整数对(m ,n )中，满足：2121+<<+m n m 的有 对．10. 甲、乙两人在一个5×5的方格纸上玩填数游戏：甲先填且两人轮流在空格中填数，甲每次选择一个空格写上数字1，乙每次选择一个空格写上数字0，填完后计算每个3×3正方形内9个数之和，并将这些和数中的最大数记为A ，甲尽量使A 增大，乙尽量使A 减小，则甲可使A 获得的最大值是 ．11. 一个锐角ABC ∆，︒=∠60BAC ，三点H 、O 、I 分别是ABC ∆的垂心、外心和内心，若BH=OI ，则ACB ∠= ．12. 设ΔABC 的内切圆⊙O 与边CA 上的中线BM交于点G 、H ，并且点G 在点B 和点H 之间．已知BG =HM ，AB =2．则GH 的最大值为 ．13. 设a 、b 为实数，函数()b ax x f +=满足：对任意x ∈[0,1]，有()1≤x f ，则()()11++=b a S 的取值范围为 ．14. 已知抛物线y 2=6x 上的两个动点A (x 1,y 1)和B (x 2,y 2)，其中x 1≠x 2且x 1+x 2=4．线段AB 的垂直平分线与x 轴交于点C ，则ABC S ∆的最大值为 ．15. 将一个3×3的正方形的四个角上各去掉一个单位正方形所得到的图形称为“十字形”．在一个10×11的棋盘上，最多可以放置 个互不重叠的“十字形”．(每个“十字形”恰好盖住棋盘上的5个小方格)三、解答题（本大题分5小题，16题10分，17~20题每题15分，共70分）16. 三角形的三边之长是某个系数为有理数的三次方程的根．证明：该三角形的高是某个系数为有理数的六次方程的根．第12题17. 已知ΔABC 内有n 个点(无三点共线)，连同A 、B 、C 共n +3个点．以这些点为顶点把ΔABC 分成若干个互不重叠的小三角形．现把A ，B ，C 分别染成红色、蓝色、黄色，而其余n 个点，每个点任意染上红、蓝、黄三色之一．求证：三顶点都不同色的小三角形的总数必是奇数．18. 设奇数a ，b ，c ，d 满足0<a <b <c <d ，ad =bc ，若k d a 2=+，m c b 2=+，其中k ，m 是整数，试证：a =1．19.如图，在锐角ABC∆的外接圆⊙O的切线BD、CE，∆中，∠BAC≠60°，过点B、C分别作ABC且满足BD=CE=BC．直线DE与AB、AC的延长线分别交于点F、G．设CF与BD交于点M，CE与BG 交于点N，证明：AM=AN．第19题20.如图，在ABC中，AB>AC，内切圆⊙I与边BC切于点D，AD与⊙I的另一个交点为E，⊙I的切线EP与BC的延长线交于点P，CF∥PE且与AD交于点F，直线BF与⊙I交于点M、N，M在线段BF上，线段PM与⊙I交于另一点Q．证明：∠ENP=∠ENQ．第20题温州中学自主招生数学模拟试卷参考答案及评分建议一、单项选择题（本大题分5小题，每题4分，共20分）[ 1~5 ] C C B D C二、简答题(本大题分10小题，每空6分，共60分)[本大题评分建议：若数字书写不清晰，不给分]6、 3247、 ⎥⎦⎤⎝⎛410， 8、 6 9、 17110、 6 11、 40° 12、 213、 [-2,49] 14、 7314 15、 15三、分析解答题(本大题分5小题，16题10分，17~20题每题15分，共70分) 16、(10分)(可能有多种解法)(3分)(7分)故得证！ (10分)[证明]17、(15分)(可能有多种解法)[证明]把这些小三角形的边进行赋值：边的端点同色的，赋值0；边的端点不同色的，赋值1．于是每个小三角形的三边之和有如下三种情形：(3分) (1)三顶点都不同色的，和为3； (2)恰有两顶点同色的，和为2； (3)三顶点都同色的，和为0．(6分)设所有小三角形的边赋值之和为S ，上述三种情形的三类小三角形的个数分别为a ，b ，c ，于是S =3a +2b +0c =3a +2b ．(9分)而注意到所有小三角形的边的赋值之和中，除了AB ，BC ，CA 边外，其余的边都被算了两次，所以它们赋值之和为偶数，再加上AB ，BC ，CA 三边赋值之和为3，所以S 是奇数．(14分)因此a 是奇数．即三顶点都不同色的小三角形总数为奇数．(15分)18、(15分)(可能有多种解法)[解]22)(4)(a d ad d a -+=+22)()(4)(4c b b c bc a d bc +=-+>-+=222)()(4)(4c b b c bc a d bc +=-+>-+=． ∴m k 22>．∴k >m ．(2分)把b c a d m k -=-=2,2，代入ad =bc ，有 )2()2(b b a a m k -=-(1)， 由(1)可得2222a b a b k m -=•-•．(4分)即2222a b a b k m -=-，))(()2(2a b a b a b m k m -+=-- (2)(5分)已知a ，b 都是奇数，所以a +b ，a -b 都是偶数，又a b a b a 2)()(=-++是奇数的2倍，故b +a ，b -a 中必有一个不是4的倍数．(7分)由(2)必有⎩⎨⎧=-=+-f a b e a b m 221或⎩⎨⎧=+=--fa b ea b m 221．其中，e ，f 为正整数，且m k a b ef -⋅-=2是奇数．[ef b a b a m 2)()(=-++，与(2)比较可得](9分)由于k >m ，故a b a b ef 22=-<-≤f a b a b ef22=-<-≤．从而e =1，m k a b f -⋅-=2． 考虑前一情况，有⎩⎨⎧⋅-==-=+--)2(2221mk m a b f a b a b (11分) 由第二式可得 a a b m k -+=+12，故 a m k m -+-=1122，所以奇数a =1．(13分)对于后一情况，可作类似的讨论．(15分)19、(15分)(解法可能有多种，给分分为4档：0分、5分、10分、15分，注：学生可能用“易证”、“可证”等词骗取分数，此题需慢改)(5分)(10分)(15分)20、(15分)(解法可能有多种，给分分为4档：0分、5分、10分、15分，注：学生可能用“易证”、“可证”等词骗取分数，此题需慢改)(5分)(10分)(15分)第20题[证明](10分)...(5分)(15分)(5分)略(15分)...。
2020年浙江省温州中学自主招生数学模拟试卷及答案解析
第1页（共16页） 2020年浙江省温州中学自主招生数学模拟试卷一．选择题（共8小题，满分40分，每小题5分）1．（5分）化简代数式√3+2√2+√3−2√2的结果是（ ）A ．3B ．1+√2C ．2+√2D ．2√22．（5分）方程6xy +4x ﹣9y ﹣7＝0的整数解的个数为（ ）A ．1B ．2C ．3D ．43．（5分）在Rt △ABC 中，∠C ＝90°，∠B 是它的一个锐角，若sin B ，cos B 是关于x 的方程4x 2﹣5kx +5k +4＝0的两个实数根，则k 的值为（ ）A ．125B ．−45C ．125或−45D ．以上各项都不对，关于k 无解4．（5分）已知整数a 1、a 2、a 3、a 4、……满足下列条件：a 1＝0，a 2＝﹣|a 1+1|，a 3＝﹣|a 2+2|，a 4＝﹣|a 3+3|，……，a n +1＝﹣|a n +n |（n 为正整数）依此类推，则a 2020值为（ ）A ．﹣1008B ．﹣1009C ．﹣1010D ．﹣10115．（5分）方程3x 2+y 2＝3x ﹣2y 的非负整数解（x ，y ）的组数为（ ）A ．0B ．1C ．2D ．36．（5分）如图，在正方形ABCD 中，AD ＝5，点E 、F 是正方形ABCD 内的两点，且AE＝FC ＝3，BE ＝DF ＝4，则EF 的长为（ ）A ．32B ．23√2 C ．75 D ．√27．（5分）若正实数a 、b 满足ab ＝a +b +3，则a 2+b 2的最小值为（ ）A ．﹣7B ．0C ．9D ．188．（5分）已知x 1，x 2是方程x 2−√5x +1＝0的两根，则x 12+x 22的值为（ ）A ．3B ．5 C．7 D ．4。
温州中学自主招生数学模拟试题
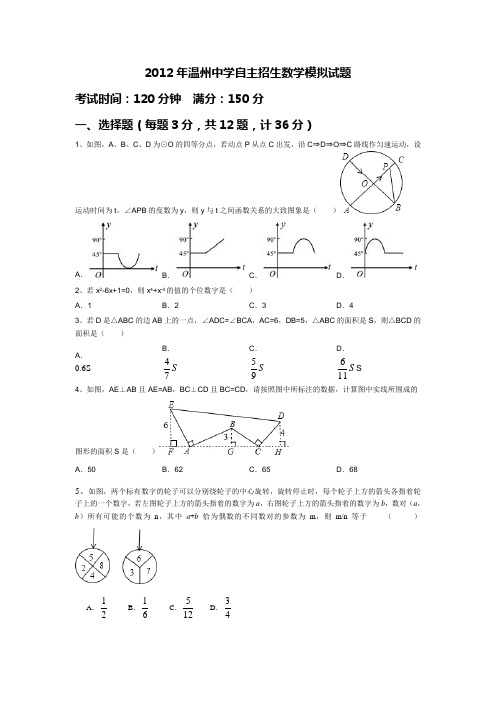
2012年温州中学自主招生数学模拟试题考试时间：120分钟 满分：150分一、选择题（每题3分，共12题，计36分）1、如图，A 、B 、C 、D 为⊙O 的四等分点，若动点P 从点C 出发，沿C ⇒D ⇒O ⇒C 路线作匀速运动，设运动时间为t ，∠APB 的度数为y ，则y 与t 之间函数关系的大致图象是（ ）A ．B ．C ．D ．2、若x 2-6x+1=0，则x 4+x -4的值的个位数字是（ ） A ．1B ．2C ．3D ．43、若D 是△ABC 的边AB 上的一点，∠ADC=∠BCA ，AC=6，DB=5，△ABC 的面积是S ，则△BCD 的面积是（ ） A ．0.6SB ．S 74 C ．S 95 D ．S 116S 4、如图，AE ⊥AB 且AE=AB ，BC ⊥CD 且BC=CD ，请按照图中所标注的数据，计算图中实线所围成的图形的面积S 是（ ）A ．50B ．62C ．65D ．685、如图，两个标有数字的轮子可以分别绕轮子的中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字，若左图轮子上方的箭头指着的数字为a ，右图轮子上方的箭头指着的数字为b ，数对（a ，b ）所有可能的个数为n ，其中a +b 恰为偶数的不同数对的参数为m ，则m/n 等于 （ ）A ．21 B ．61 C ．125 D ．436、某一天的不同时刻老板把信交给秘书打字，每次都将信放在秘书信堆的最上面，秘书有时间就将信堆最上面的那封信取来打．假定共有5封信，且老板以1、2、3、4、5的顺序交来，在下列各顺序中，哪一顺序不可能是秘书打字的顺序？（）A．12345 B．54321 C．23541 D．235147、如图，将△ADE绕正方形ABCD的顶点A顺时针旋转90°，得△ABF，连接EF交AB于H，则下列结论错误的是（）A．AE⊥AFB．EF：AF=1:2C．AF2=FH•FE D．FB：FC=HB：EC8、在△ABC中，点D，E分别在AB，AC上，且CD与BE相交于点F，已知△BDF的面积为10，△BCF 的面积为20，△CEF的面积为16，则四边形区域ADFE的面积等于（）A．22 B．24 C．36 D．449、如图，点A、D、G、M在半⊙O上，四边形ABOC、DEOF、HMNO均为矩形．设BC=a，EF=b，NH=c，则下列各式中正确的是（）A．a＞b＞c B．b＞c＞a C．c＞a＞b D．a=b=c10、如图在梯形ABCD中，AD∥BC，AD⊥CD，BC=CD=2AD，E是CD上一点，∠ABE=45°，则tan ∠AEB的值等于（）A．3 B．2 C．2.5D．1.511、两个不相等的正数满足a+b=2，ab=t-1，设S=（a-b）2，则S关于t的函数图象是（）A．射线（不含端点）B．线段（不含端点）C．直线D．抛物线的一部分A ．60°B ．75°C ．60°或45°D ．15°或75°二、填空题（每空4分，共9空，计36分）13、若关于x 的方程（x-2）（x 2-4x+m ）=0有三个根，且这三个根恰好可以作为一个三角形的三条边的长，则m 的取值范围是____________.14、如图，AB 是⊙O 的直径，AB=10cm ，M 是半圆AB 的一个三等分点，N 是半圆AB 的一个六等分点，P 是直径AB 上一动点，连接MP 、NP ，则MP+NP 的最小值是________cm.15、双曲线y=x1（x ＞0）与直线y=x 在坐标系中的图象如图所示，点A 、B 在直线上AC 、BD 分别平行y 轴，交曲线于C 、D 两点，若BD=2AC 则4OC 2-OD 2的值为_________.16、如图，在坐标平面上，沿着两条坐标轴摆着三个相同的长方形，其长、宽分别为4、2，则通过A ，B ，C 三点的拋物线对应的函数关系式是____________________________.17、设C 1，C 2，C 3，…为一群圆，其作法如下：C 1是半径为a 的圆，在C 1的圆内作四个相等的圆C 2（如图），每个圆C 2和圆C 1都内切，且相邻的两个圆C 2均外切，再在每一个圆C 2中，用同样的方法作四个相等的圆C 3，依此类推作出C 4，C 5，C 6，…，则（1）圆C 2的半径长等于________（用a 表示）；（2）圆C k的半径为_________（k为正整数，用a表示，不必证明）18、已知正数a、b、c满足a2+c2=16，b2+c2=25，则k=a2+b2的取值范围为__________.19、已知x、y均为实数，且满足xy+x+y=17，x2y+xy2=66，则x4+x3y+x2y2+xy3+y4=___________.20、不论m取任何实数，抛物线y=x2+2mx+m2+m-1的顶点都在一条直线上，则这条直线的函数解析式是___________________________.三、简答题（共78分）21、如图1，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若△ABC固定不动，△AFG绕点A旋转，AF、AG与边BC的交点分别为D、E（点D不与点B重合，点E不与点C重合），设BE=m，CD=n．（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明；（2）求m与n的函数关系式，直接写出自变量n的取值范围；（3）以△ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系（如图2）．在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD2+CE2=DE2；（4）在旋转过程中，（3）中的等量关系BD2+CE2=DE2是否始终成立？若成立，请证明；若不成立，请说明理由．，∠BCM=．23、如图，BC是半圆⊙O的直径，D是弧AC的中点，四边形ABCD的对角线AC、BD交于点E．（1）求证：AC•BC=2BD•CD，（2）若AE=3，CD=25，求弦AB和直径BC的长．24、已知二次函数y=x2+bx-c的图象经过两点P（1，a），Q（2，10a）．（1）如果a，b，c都是整数，且c＜b＜8a，求a，b，c的值．（2）设二次函数y=x2+bx-c的图象与x轴的交点为A、B，与y轴的交点为C．如果关于x的方程x2+bx-c=0的两个根都是整数，求△ABC的面积．的坐标；。
温州中学数学提前招模拟卷
2017年温州中学数学提前招模拟卷题号一二三总分1－8 9－14 15 16 17 18得分评卷人复查人答题时注意；1．用圆珠笔或钢笔作答2．解答书写时不要超过装订线3.可以用计算器一、选择题（共8小题，每小题5分，满分40分)．1．已知|a+b|+|a-b|-2b=0，在数轴上给出了如图所示的关于a，b的四种位置关系，则可能成立的有( )A．1种B．2种C．3种D．4种2．已知a是方程3310x x+-=的一个实数根，则直线1y ax a=+-不经过（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3.2612111012111010(2)x x a x a x a x x a--=++++…+a，则12108642a a a a a a+++++=（）（A）64 （B）32 （C）－32 （D）－644.如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是（）A. B. C. D.23-π332-π2332-π3-π第4题5. A 、B 、C 三个足球队举行单循环赛，下表给出了部分比赛信息：则A 、B 两队比赛时，A 队与B 队进球数之比为（ ） ∶0 ∶0 ∶1 ∶16．定义新运算： a ⊕b=，则函数y=3⊕x 的图象大致是( )7．.如图，∠XOY ＝90°，OW 平分∠XOY ，PA ⊥OY ，PB ⊥OX ，PC ⊥OW ． 若OC ＝2－1，则OA ＋OB ＋OC ＝（ ）A ．３B ． ２C ．１D ．218．我们用()f x 代替函数中的变量y ，如：3y x =+可以记作()3f x x =+，“当x =1，y =4”可以记作“(1)4f =”．现有函数1()2f x x =，22()f x x=，3()6(1)(2)f x x x =---，记k I =100(1)99k k f f ⎛⎫-+ ⎪⎝⎭1001019999k k f f ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭197(2)99L k k f f ⎛⎫+- ⎪⎝⎭， 其中k =1，2，3，则下列结论正确的是（ ）A ．123I I I <<B ．213I I I <<C ．231I I I <<D ．321I I I << 二、填空题（共6小题，每小题5分，满分30分）9．有一组数满足, ,2 ,0 ,2 ,0,2,14635241321Λ=-=-=-=-==a a a a a a a a a a按此规律进行下去，则=++++100321a a a a Λ___________.球队 比赛场次 胜 负 平 进球数 失球数 A 2 2场 1 B 2 1场 2 4 C 2 3 7BCOyxP W 第７题图A ABCDO10.如图，菱形ABCD 的边长为a ，点O 是对角线A C 上的一点， 且OA ＝a ，O B ＝OC ＝OD ＝1，则a 的值等于__________．11．直线k x y +=21与x 、y 轴的交点分别为A 、B ，如果S △AOB ≤1， 那么k 的取值范围是 。
【新】2019-2020浙江温州中学初升高自主招生数学【4套】模拟试卷【含解析】
第一套：满分120分2020-2021年浙江温州中学初升高自主招生数学模拟卷一．选择题（共6小题，满分42分）1. （7分）货车和小汽车同时从甲地出发，以各自的速度匀速向乙地行驶，小汽车到达乙地后，立即以相同的速度沿原路返回甲地，已知甲、乙两地相距180千米，货车的速度为60千米/小时，小汽车的速度为90千米/小时，则下图中能分别反映出货车、小汽车离乙地的距离y （千米）与各自行驶时间t （小时）之间的函数图象是【 】A. B. C. D.2. （7分）在平面直角坐标系中，任意两点规定运算：①；②；③当x 1= x 2且y 1=y 2时，A =B.有下列四个命题：（1）若A (1，2)，B (2，–1)，则，； （2）若，则A =C ； （3）若，则A =C ；()()1122,,，A x y B x y ()1212,⊕=++A B x x y y 1212=⊗+A B x x y y (),31⊕= A B 0=⊗A B ⊕=⊕A B B C =⊗⊗A B B C（4）对任意点A 、B 、C ，均有成立. 其中正确命题的个数为（ ）A. 1个B. 2个C. 3个D. 4个 3．（7分）如图，AB 是半圆直径，半径OC ⊥AB 于点O ，AD 平分∠CAB 交弧BC 于点D ，连结CD 、OD ，给出以下四个结论：①AC ∥OD ；②CE=OE ；③△ODE ∽△ADO ；④2CD 2=CE •AB ．正确结论序号是（ ）A ．①②B ．③④C ．①③D ．①④ 4. （7分）如图，在△ABC 中，∠ACB =90º，AC =BC =1，E 、F 为线段AB 上两动点，且∠ECF =45°，过点E 、F 分别作BC 、AC 的垂线相交于点M ，垂足分别为H 、G ．现有以下结论：①；②当点E 与点B 重合时，；③；④MG •MH =，其中正确结论为（ ）A. ①②③B. ①③④C. ①②④D. ①②③④ 5.（7分）在数学活动课上，同学们利用如图的程序进行计算，发现无论x 取任何正整数，结果都会进入循环，下面选项一定不是该循环的是（ ）A. 4，2，1B. 2，1，4C. 1，4，2D. 2，4，1 6. （7分）如图，在矩形ABCD 中，AB =4，AD =5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点，过点D()()⊕⊕=⊕⊕A B C A B C 2AB =12MH =AF BE EF +=12作⊙O 的切线交BC 于点M ，则DM 的长为（ ）A.B. C. D.二．填空题（每小题6分，满分30分）7.（6分）将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为 . 8.（6分）如图，三个半圆依次相外切，它们的圆心都在x 轴上，并与直线3y x =相切．设三个半圆的半径依次为r 1、r 2、r 3，则当r 1＝1时，r 3＝ ．9.（6分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOB=60°，点A 在第一象限，过点A 的双曲线为k y x=．在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ´B ´．（1）当点O ´与点A 重合时，点P 的坐标是 ；（2）设P （t ，0），当O ´B ´与双曲线有交点时，t 的取值范围是 ．1339241332510.（6分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反 比例函数2(0)y x x=>的图象上，顶点A 1、B 1分别在x 轴、y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数2(0)y x x=>的图象上，顶点A 2在x 轴的正半轴上，则点P 3的坐标为 ．11.（6分）如图，在⊙O 中，直径AB ⊥CD ，垂足为E ，点M 在OC 上，AM 的延长线交⊙O 于点G ，交过C 的直线于F ，∠1=∠2，连结CB 与DG 交于点N ．若点M 是CO 的中点，⊙O 的半径为4，cos ∠BOC=41，则BN= ．三．解答题（每小题12分，满分48分）12.（12分）先化简，再求值：， 其中.13.（12分）如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数的图象上．（1）求m ，k 的值；32221052422x x x x x x x x --÷++--+-2022(tan 45cos30)21x =-+︒-︒-xky =xO yAB （2）如果M 为x 轴上一点，N 为y 轴上一点， 以点A ，B ，M ，N 为顶点的四边形是平行四边形，试求直线MN 的函数表达式． （3）将线段AB 沿直线进行对折得到线段，且点始终在直线OA 上，当线段与轴有交点时,则b 的取值范围为 （直接写出答案）14.（12分）如图，在Rt △ABC 中，∠ABC=90°，以AB 为直径作⊙O 交AC 于点D ，DE 是⊙O 的切线，连接DE ．（1）连接OC 交DE 于点F ，若OF=CF ，证明：四边形OECD 是平行四边形； （2）若=n ，求tan ∠ACO 的值b kx y +=11B A 1A 11B A x OFCF15.（12分）如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）。
温州中学九年级提前招生数学模拟卷
68CEABD九年级实验班数学期中考试测试题一、选择题（每小题4分，共40分） 1．若0＜ x ＜1，则x 2，x ，x，x1这四个数中（ ）A ．x1最大，x 2最小 B ．x 最大，x1最小C ．x 2最大，x最小 D ．x 最大，x 2最小2. 将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上．点A 、B 的读数分别为86°、30°，则∠ACB 的大小为（ ）A ．15︒B ．28︒C ．29︒D ．34︒3．直角三角形纸片的两直角边长分别为6，8，现将A B C △如右图那样折叠，使点A 与点B 重合，则折痕D E 的长是（ ）A ．254 B ．154 C ．252D ．1524．已知x 为整数，且分式2364x x +-的值为整数，则x 可取的值有（ ）A ．4个B ．3个C ．2个D ．1个5．若一次函数y kx b =+，当x 得值减小1，y 的值就减小2，则当x 的值增加2时，y 的值是（ ）A ．增加4B ．减小4C ．增加2D ．减小26．已知f (x )＝1－(x －a )(x －b )，并且m ，n 是方程f (x )＝0的两根，则实数a ，b ，m ，n 的大小关系可能是（ ）．A ．m ＜a ＜b ＜nB ．a ＜m ＜n ＜bC ．a ＜m ＜b ＜nD ．m ＜a ＜n ＜b 7、在不等腰A B C △中，90C ∠= ，设sinB n =，当B ∠是最小的内角时，n 的取值范围是（ ）A．02n <<B ．102n <<C．03n <<D．02n <<8.无论m 为何值时,二次函数y=x 2+(2-m)x+m 的图象总过的点是( )9、如图，一次函数122y x =-+的图像上有两点A 、B ，A 点的横坐标为2，B 点的横坐标为(042)a a a <<≠且，过点A 、B 分别作x 的垂线，垂足为C 、D ，AO C BO D ∆∆、的面积分别为12S S 、，则12S S 、的大小关系是( ) A. 12S S > B. 12S S = C. 12S S < D. 无法确定10、．已知函数f (x )＝x 2＋λx ，p 、q 、r 为△ABC 的三边，且p ＜ q ＜r ，若对所有的正整数p 、q 、r 都满足f (p )＜f (q )＜f (r )，则λ的取值范围是（ ）．A ．λ ＞－2B ．λ ＞－3C ．λ ＞－4D ．λ ＞－5 二、填空题（每小题5分，共30分）11、已知a ＝5－1，则2a 3＋7a 2－2a －12 的值等于 ．12、y x ,为实数，且0360tan 0=++-y x ，则=2011)(yx ________________.13、如图1，是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC =6，BC =5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是_______________；14．设()11,A x y ，()22,B x y 为函数21k y x-=图象上的两点，且120x x <<，12y y >，则实数k 的取值范围是15．二次函数a ax x y ++=22在21≤≤-x 上有最小值4-，则a 的值为___________. 图2ABC图1ABC16．如图，CD 是直角三角形ABC 的斜边AD 上的高，I 1、I 2分别是△ADC、△BDC 的内心，若AC ＝3，BC ＝4， 则I1I 2＝__________．三、解答题17. （满分10分）乐清某家俱市场现有大批如图所示的边角余料 (单位：cm)乐清中学数学兴趣小组决定将其加工成等腰三角形， 且方案如下：（1）三角形中至少有一边长为（218. （满分8分）将一个以自由转动的转盘可分成三等分，每一份内标上数字如图所示，第一次转动转盘，当转盘停止后，指针所在的区域的数字记为a ，第二次转动转盘，当转盘停止后，指针所在的区域的数字记为c ，（注意：如果指针恰好指在分割线上，那么重转一次，直到指针指向某一区域为止）用画树状图的方法，求抛物线cx x ay ++=212顶点在第一象限的概率.A BC DI 1I 219、（满分8分）定义{},,a b c 为函数2y ax bx c =++的 “特征数”．如：函数y=x2－2x+3的“特征数”是{1,－2,3}，函数y=2x+3的“特征数”是{0,2,3},函数y=－x 的“特征数”是{0,－1,0}。
2019年浙江省温州市重点高中提前自主招生考试数学模拟试题(Word版含解析答案)
B ．+重点高中提前自主招生选拔考试数 学 试 题（时间：100 分钟满分 120分）2019 年 1 月一、选择题（共 8 小题，每小题 4 分，共 32 分）1．对正整数 n ，记 n !＝1×2×3×…×n ，则 1!+2!+3!+…+10!的末位数为（ ）A ．0B ．1C ．3D ．52．在分别标有号码 2、3、4、…10 的 9 个球中，随机取出两个球，记下它们的标号，则较大标号被较小标号整除的概率是（ ） A ．3．已知关于 x 的方程 为（ ） C． D ．＝ 恰有一个实根，则满足条件的实数 a 的值的个数A ．1B ．2C ．3D ．4 4．函数 y ＝ax +1 与 y ＝ax 2+bx +1（a ≠0）的图象可能是（）A．B．C．D ． 5．十进制数 278，记作 278（10），其实 278（10）＝2×102+7×101+8×100，二进制数 101（2）＝1×22+0×21+1×20．有一个 k （0＜k ≤10 为整数）进制数 165（k ），把它的三个数字顺序颠倒得到的 k 进制数 561（k ）是原数的 3 倍，则 k ＝（ ） A ．10B ．9C ．8D ．76．正方形 ABCD ，正方形 BEFG 和正方形 PKRF 的位置如图所示，点 G 在线段 DK 上，正方形 BEFG 的边长为 2，则△DEK 的面积为（ ） A ．4 B ．2C ．3D ．第6 第7 题7．两个等腰直角△ABC、△ADE 如图放置，AE＝AD，AB＝BC，∠ABC＝∠DAB＝90°，DE 与AC 交于点H，连接BH，若∠BCE＝15°，下列结论错误的是（）3∆EHC S 1 1 113 A ．△ACD ≌△ACE B ．△CDE 为等边三角形 C ． = D ． S ∆AEH 8．如图，在圆内接四边形 ABCD 中，∠A ＝52°，∠B ＝98°，∠AOB ＝120°（O 为圆心），AB＝a ，BC ＝b ，CD ＝c ，DA ＝d ，则此四边形的面积为（ ）（用含 a 、b 、c 、d表示四边形ABCD 的面积）A ． (ab + cd )B ．(ac + bd ) C ． (ad + bc )D ． (ab + bc + cd + ad ) 2 2 2 4第8 题 第 11 题 第14 题二、填空题（共 8 小题，每小题 4 分，共 32 分） 9．已知 a 是 64 的立方根， 2b - 3 是 a 的平方根，则11a - 4b 的算术平方根为 ．410．关于 x 的函数 f (x )符合以下条件：（1）函数 f (x )在 x ＝0 处无意义；（2）当 x 取非零 实数时都有 如当 x ＝1 时，有 f (1)+ 2 f (1) = 3 ，可以求得 f (1) = 1.则f (x )的函数表达式是 f (x )＝.11．如图，在“镖形”ABCD 中，AB = 8，BC=16，∠A =∠B =∠C = 30 ，则点 D到 AB 的距离为 ．12．已知正整数 a 、b 、c 满足 a ＋b 2－2c-2＝0，3a 2－8b ＋c ＝0，则 abc 的最大值为 . 13．AB 为半圆 O 的直径，C 为半圆弧的一个三等分点，过 B ，C 两点的半圆 O 的切线交于 PA 点 P ，则 PC=．14．矩形 ABCD 的边长 AD ＝3，AB ＝2，E 为 AB 的中点，F 在线段 BC 上，F 在线段 BC 上， 且 BF ：FC ＝1：2，AF 分别与 DE ，DB 交于点 M ，N ，则 MN ＝．15．实数a、b、c、d 满足：一元二次方程x2+cx+d＝0 的两根为a、b，一元二次方程x2+ax+b＝0 的两根为c、d，则所有满足条件的数组（a、b、c、d）为．16．小明某天在文具店做志愿者卖笔，铅笔每支售4 元，圆珠笔每支售7 元．开始时他有铅笔和圆珠笔共350 支，当天虽然笔没有全部卖完，但是他的销售收入恰好是2013 元．则他至少卖出了支圆珠笔．三、解答题（共4 小题，共56 分）的图象交于点C 和点D（－1，a）. （1）试求这两个函数的表达式；（2）当x 取何值时，有y1 y2；（3）将△OBC 绕点O 逆时针方向旋转，得到△OB′C′，当点B′第一次落在直线AB 上时，求点C 经过的路线长.第17 题18．（12分）如图，已知AB为圆O的直径，C为圆周上一点，D为线段OB内一点(不是端点)，满足CD⊥AB，DE⊥CO，E 为垂足，若CE=10，且AD 与DB 的长均为正整数，求线段AD 的长．第18 题19．（14 分）如图，抛物线 y 1 = ax 2 + bx + c (a ≠ 0)与 x 轴交于点 A 、B ，与 y 轴交于点 C ， 有 OB=3OA ，抛物线顶点 D 的坐标为( 3,4)．（1）求该抛物线的解析式；（2）构造新函数 y 2 = - y 1 交 y 轴于点 E.①若直线 y ＝x ＋t 与构造的新函数 y 2 有且只有三个交点，试求 t 的值； ②是否存在到直线 BC ，BE ，CE 距离都相等的点？若存在，求出该点的坐标；若不存在， 试说明理由.第 19 题20．（18 分）一只青蛙，位于数轴上的点 a k ，跳动一次后到达 a k +1 ，且 a k +1 - a k= 1（ k 为任意正整数），青蛙从 a 1 开始，经过(n - 1) 次跳动的位置依次为 a 1 ， a 2 ， a 3 ，……， a n ． （1）写出一种跳动 4 次的情况，使 a 1 = a 5 = 0 ，且 a 1 + a 2 + + a 5 > 0；（2）若 a 1 = 7 ， a 2016 = 2020 ，求 a 2000 ；（3）对于整数 n (n ≥ 2)，如果存在一种跳动(n - 1) 次的情形，能同时满足如下两个条件：① a 1 = 2 ，② a 1 + a 2 + a 3 + + a n =2． 求整数 n 被 4 除的余数．。
浙江省温州市温州中学2024届高三第一次模拟考试数学试题
一、单选题1. 设函数f (x )＝若函数g (x )＝f (x )－b 有三个零点，则实数b 的取值范围是（ ）A ．(1，＋∞)B．C ．(1，＋∞)∪{0}D ．(0，1]2. 直线经过椭圆的左焦点，交椭圆于、两点，交轴于点，若，则该椭圆的离心率是（ ）A．B．C．D．3. 已知集合，，则（ ）A．B．C．D．4. 若函数()的值域是，则实数 的取值范围是（ ）A．B．C．D．5. 雨滴在下落过程中，受到的阻力随速度增大而增大，当速度增大到一定程度时，阻力与重力达到平衡，雨滴开始匀速下落，此时雨滴的下落速度称为“末速度”．某学习小组通过实验，得到了雨滴的末速度v （单位：m/s ）与直径d （单位：mm ）的一组数据，并绘制成如图所示的散点图，则在该实验条件下，下面四个回归方程类型中最适宜作为雨滴的末速度v 与直径d 的回归方程类型的是（）．A．B．C．D．6.已知双曲线的渐近线方程为，则双曲线的离心率为A．B．C．D．7. 已知边长为2的菱形中，点为上一动点，点满足，，则的最小值为（ ）A．B．C．D．8. 下图是2013-2020年国家财政性教育经费（单位：万元）和国家财政性教育经费占总教育经费占比的统计图，下列说法正确的是（）浙江省温州市温州中学2024届高三第一次模拟考试数学试题浙江省温州市温州中学2024届高三第一次模拟考试数学试题二、多选题三、填空题A ．2019年国家财政性教育经费和国家财政性教育经费占总教育经费占比均最低B ．国家财政性教育经费逐年增加C ．国家财政性教育经费占比逐年增加D ．2020年国家财政性教育经费是2014年的两倍9. 若平面向量，，其中，，则下列说法正确的是（ ）A ．若，则B ．若，则与同向的单位向量为C ．若，且与的夹角为锐角，则实数的取值范围为D ．若，则的最小值为10. 正四棱锥中，，，过点作截面分别交棱于点，且，则下列结论正确的是（）A ．若为中点，则B．若平面，则截面的面积C ．若为所在棱的中点，则D ．若为所在棱的中点，则点到平面的距离为11. 已知圆上的三个点分别为，，，直线的方程为，则下列说法正确的是（ ）A．圆的方程为B．过作直线与线段相交，则直线的斜率的取值范围为C ．若直线被圆截得的弦长为2，则的方程为或D ．当点到直线的距离最大时，过上的点作圆的两条切线，切点分别为，，则四边形面积的最小值为12. 已知函数，，若，则下列说法正确的是（ ）A ．当时，有2个零点B．当时，恒在的上方C ．若在上单调递增，则D ．若在有2个极值点，则13. 抛物线具有以下光学性质：从焦点出发的光线经抛物线反射后平行于抛物线的对称轴．该性质在实际生产中应用非常广泛．如图所示，从抛物线的焦点F 向y 轴正方向发出的两条光线a ，b 分别经抛物线上的A ，B 两点反射，已知两条入射光线与x 轴所成锐角均为60°，且，则______．四、解答题14.已知数列的前项和，如果存在正整数，使得成立，则实数的取值范围是_____________.15. 已知函数的定义域为，，，若此函数同时满足：①当时，有；②当时，有，则称函数为函数．在下列函数中：①；②；③是函数的为__________．（填出所有符合要求的函数序号）16. 如图，在四棱锥P-ABCD中，平面平面ABCD ．是等腰三角形，且．在梯形ABCD中，，，，，．（Ⅰ）求证：平面PDC ；（Ⅱ）求二面角A-PB-C 的余弦值；（Ⅲ）在线段AP 上是否存在点H ，使得平面ADP ？请说明理由．17.某企业参加项目生产的工人为人，平均每人每年创造利润万元.根据现实的需要，从项目中调出人参与项目的售后服务工作，每人每年可以创造利润万元（），项目余下的工人每人每年创造利图需要提高（1）若要保证项目余下的工人创造的年总利润不低于原来名工人创造的年总利润，则最多调出多少人参加项目从事售后服务工作？（2）在（1）的条件下，当从项目调出的人数不能超过总人数的时，才能使得项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润，求实数的取值范围.18.已知函数(1)当时，证明:.(2)若有两个零点且求的取值范围.19. 在平面直角坐标系中， 圆为 的内切圆.其中.（1）求圆的方程及 点坐标；（2）在直线上是否存在异于的定点使得对圆上任意一点，都有为常数 )？若存在，求出点的坐标及的值；若不存在，请说明理由.20. 已知函数（是自然对数的底数）．（1）求函数的最小值；（2）若函数有且仅有两个不同的零点，求实数的取值范围．21. 已知数列的通项公式为.（1）若成等比数列，求的值；（2）是否存在使得成等差数列，若存在，求出常数的值；若不存在，请说明理由；（3）求证：数列中的任意一项总可以表示成数列中的其他两项的积.。
温州中学提前招生数学模拟卷
2017年温州中学提前招生数学模拟卷（二）时量：90分钟满分：100分题号一二三总分合分人复查人13 14 15 16 17得分一．选择题（6×4=42分）1．若α、β是方程x2﹣x﹣2006=0的两个实数根，则α+β2的值是（）A．1 B．2007 C．﹣1 D．20062．把一枚六个面编号分别为1，5，6的质地均匀的正方体骰子先后投掷2次，若两个正面朝上的编号分别为m，n，则二次函数y=x2+mx+n的图象与x轴有两个不同交点的概率是（）A．B．C．D．3．观察下列等式：=1﹣，=﹣，=﹣，…=﹣将以上等式相加得到+++…+=1﹣．用上述方法计算：+++…+其结果为（）A． B． C． D．4．如图，在Rt△ABC中，∠P是BC边上不同于B，C的一动点，过点P作PQ⊥AB，垂足为Q，连接AP．若AC=3，BC=4，则△AQP的面积的最大值是（）A． B． C． D．5．已知a3±b3=（a±b）（a2±ab+b2），如果一列数a1，a2，…满足对任意的正整数n都有，则的值为（）A．B． C． D．6．已知，实数x，y，z满足，则x4+y4+z4=（）A．4 B． C． D．以上都不对二．填空题（6×4=24分）7．点A（x1，y1），B（x2，y2），C（x3，y3），D（﹣2，4）是双曲线上的四个点，若x3＜x2＜0＜x1，则y1，y2，y3的大小关系是．8．若x、y、z满足3x+7y+z=1和4x+10y+z=2001，则分式的值为．9．如图，△ABC中，AD与B已知S△AFB=12cm2，S△BFD=9cm2，S△AFE=6cm2，那么四边形CDFE的面积为cm2．10．一枚商标示，点A1，A2，A3，A4和C1，C2，C3，C4分别是?ABCD边AB和CD的五等分点，点B1，B2和D1，D2分别是BC和DA的三等分点，已知?ABCD的面积5，则阴影四边形A4B2C4D2的面积是．11．如图，一个粒子在第一第一分钟内它从原点运动到（1，0），而后它接着按图所示在与x 轴、y轴平行的方向或在x轴、y轴上来回运动，且每分钟移动1个单位长度，那么在2071分钟后这个粒子所处位置为．12．已知一次函数f（b经过点（10，13），它在x轴上的截距是一个质数，在y轴上的截距是一个正整数，则函数的个数有个．三．解答题（共5小题，共58分）13．（10分）如图，D中，AB=3cm，BC=4cm．设P，Q分别为BD，BC上的动点，在点P自点D 沿DB方向作匀速移动的同时，点Q自点B沿BC方向向点C作匀速移动，移动的速度均为1cm/s，设P，Q移动的时间为t（0＜t≤4）．（1）当t为何值时，△PBQ为等腰三角形？（2）△PBQ能否成为等边三角形？若能，求t的值；若不能，说明理由．14．（10分）如图，△ABC是边三角形，P是AB边上的一个动点（P与B不重合），以线段CP 为边作等边△CPD（D、A在BC的同侧），连接AD．（1）判断四边形ABCD的形状，并给予证明；（2）设BP=x，△PAD的面积为y，求出y关于x的函数关系式，并求出△PAD面积的最大值及取得最大值时x的值．15．（12分）若直线l：y=x+3交x轴于点A，交y轴于点B．坐标原点O关于直线l的对称点O′在反比例函数y=的图象上．（1）求反比例函数y=的解析式；（2）将直线l绕点A逆时针旋转角θ（0°＜θ＜45°），得到直线l′，l′交y轴于点P，过点P作x轴的平行线，与上述反比例函数y=的图象交于点Q，当四边形APQO′的面积为9﹣时，求θ的值．16．（13分）已知在关于x的分式方程①和一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0②中，k、m、n均为实数，方程①的根为非负数．（1）求k的取值范围；（2）当方程②有两个整数根x1、x2，k为整数，且k=m+2，n=1时，求方程②的整数根；（3）当方程②x1、x2，满足x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），且k为负整数时，试判断|m|≤2是否成立？请说明理由．17．（13分）如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE 的中点，连接CF，DF．（1）如图①，当点D在AB上，点E在AC上时，请判断线段CF，DF有怎样的数量关系和位置关系？为什么？（2）如图②，将图①中的△ADE绕点A旋转到图②位置时，请判断（1）中的结论是否仍然成立？并证明你的判断．参考答案一．选择题（共6小题）1．【分析】定义，可知β2﹣β﹣2006=0，即β2=β+2006①，再由一元二次方程根与系数的关系，可得α+β=1②，然后把①②分别代入所求式子α+β2，即可求出其值．解：∵β是方程x2﹣x﹣2006=0的根，∴β2﹣β﹣2006=0，即β2=β+2006，又∵α、β是方程x2﹣x﹣2006=0的两个实数根，∴α+β=1．∴α+β2=α+（β+2006）=1+2006=2007．故选B．2．【分析】本题可先列出出况，因为二次图象开口向上，要使图象与x轴有两个不同的交点，则最低点要小于0，即4n﹣m2＜0，再把m、n的值一一代入检验，看是否满足．最后把满足的个数除以掷骰子可能出现的点数的总个数即可．解：掷骰子有6×6=36种情况．根据题意有：4n﹣m2＜0，因此满足的点有：n=1，m=3，4，5，6，n=2，m=3，4，5，6，n=3，m=4，5，6，n=4，m=5，6，n=5，m=5，6，n=6，m=5，6，共有17种，故概率为：17÷36=．故选C．3．【分析】本题是规律性题型，基本方法是，将一个分数分为两个分数的差，因为所求式子，每一个分母的两个因数相差2，一个分数分为两个分数时，需要乘以．解：由上式可知+++…+=（1﹣）=．故选A．4．【分析】先利用“两角法PBQ与△ABC相似，再设BP=x（0＜x＜4）．由勾股定理、相似三角形的对应边成比例以及三角形的面积公式，列出S与x的函数关系式，利用配方法求得二次函数的最值．解：设BP=x（0＜x＜4），由勾股定理得 AB=5，∵∠PQB=∠C=90°，∠B=∠B，∴△PBQ∽△ABC，∴==，即==∴PQ=x，QB=xS△APQ=PQ×AQ=+x=∴当x=时，△APQ的面积最大，最大值是．故选（C）5．【分析】令n=1、2、3…，求出a1，a2，…的值，在表示出a2﹣1，a3﹣1，…从而得出规律，再提取后利用拆项法解答．解：根据题意，当n=1时，a1=13=1，当n=2时，a1+a2=23，a2=23﹣1=7，所以a2﹣1=7﹣1=6=3×（1×2），当n=3时，a1+a2+a3=33，a3=33﹣23=19，所以a3﹣1=19﹣1=18=3×（2×3），当n=4时，a1+a2+a3+a4=43，a4=43﹣33=37，所以a4﹣1=37﹣1=36=3×（3×4），…a100=1003﹣993=（100﹣99）×（1002+100×99+992）=1002+100×（100﹣1）+（100﹣1）2=1002+1002﹣100+1002﹣200+1=3×1002﹣300+1，所以a100﹣1=3×1002﹣300+1﹣1=100×（300﹣3）=100×297=3×（99×100），++…+=+++…+=（﹣+﹣+﹣+…+﹣）=×（1﹣）=×=．故选A．6．【分析】根据已知条件先求出xy+xz+yz=，再求出xyz=，根据完全平方公式即可求解．解：∵，∴由（1）代入上式得：xy+xz+yz=（4），而x3+y3+z3﹣3xyz=（x+y+z）（x2+y2+z2﹣xy﹣xz﹣yz），把（3）（4）代入上式得：xyz=（5），由（4）平方得：；把（5）代入上式得：，∴．故选C．二．填空题（共6小题）7．【分析】先根据点D（﹣2，4）在反比例函数y=的图象上求出k的值，再判断出函数图象所在的象限，根据函数图象在每一象限内的增减性即可得出结论．解：∵D（﹣2，4）是双曲线上的点，∴k=（﹣2）×4=﹣8＜0，∴双曲线的两个分支分别位于二四象限，且在每一象限内y随x的增大而增大，∵x3＜x2＜0＜x1，∴B（x2，y2），C（x3，y3）在第二象限，A（x1，y1）在第四象限，∴y2＞y3＞0，y1＜0，∴y2＞y3＞y1．故答案为：y2＞y3＞y1．8．【分析】分式=，视x+3y与x+y+z为两个整体，对方程组进行整体改造后即可得出答案．解：由x、y、z满足3x+7y+z=1和4x+10y+z=2001，得出：，解得：，∴=，==﹣3999．故答案为：﹣3999．9．【分析】连接CF，设S△CEF=x，S△CDF=y，根据三角形的面积与三角形底边成比例，进而求出四边形CDFE的面积．解：连接CF，设S△CEF=x，S△CDF=y，则==，==，解得x=，y=，故四边形CDFE的面积=x+y=．故答案为：．10．【分析】可以设平CD的面积是S，根据等分点的定义利用平行四边形ABCD的面积减去四个角上的三角形的面积，就可表示出四边形A4B2C4D2的面积，从而得到两个四边形面积的关系，即可求解．解：设平行四边形ABCD的面积是S，设AB=5a，BC=3b．AB边上的高是3x，BC边上的高是5y．则S=5a?3x=3b?5y．即ax=by=．△AA4D2与△B2CC4全等，B2C=BC=b，B2C边上的高是?5y=4y．则△AA4D2和△B2CC4的面积是2by=．同理△D2C4D与△A4BB2的面积是．则四边形A4B2C4D2的面积是S﹣﹣=，又∵S=9，∴四边形A4B2C4D2的面积=×5=3．故答案为：3．11．【分析】要弄清粒子的运动规律，先观察横坐标和纵坐标的相同点：（0，0），粒子运动了0分钟．（1，1）就是运动了2=1×2分钟，将向左运动！（2，2）粒子运动了6=2×3分钟，将向下运动！（3，3），粒子运动了12=3×4分钟．将向左运动…（45，45）点处粒子运动了45×46=2070分钟！此时粒子会将左移动．解：要弄清粒子的运动规律，先观察横坐标和纵坐标的相同点：（0，0），粒子运动了0分钟．（1，1）就是运动了2=1×2分钟，将向左运动！（2，2）粒子运动了6=2×3分钟，将向下运动！（3，3），粒子运动了12=3×4分钟．将向左运动…于是会出现：（45，45）点处粒子运动了45×46=2070分钟，此时粒子会将左移动．从而在运动了2071分钟以后，粒子所在位置为（44，45）故答案填：（44，45）．12．【分析】设与x轴交点为（p，0），与y轴交点为（0，q），把点（10，13）代入y=ax+b，得10a+b=13；把（p，0），（0，q）也代入y=ax+b，得b=q，a=﹣．所以13p=﹣10q+pq，则q=，p是质数，q是正整数，再利用整除的性质讨论即可．解：设于x轴交点为（p，0），与y轴交点为（0，q），把点（10，13）代入y=ax+b，得10a+b=13；把（p，0），（0，q）也代入y=ax+b，得b=q，a=﹣．所以13p=﹣10q+pq，则q=，p是质数，q是正整数，当p﹣10=1时，p=11，q=143，符合题意；当p﹣10=13时，p=23，q=23，符合题意；当p﹣10=p时，无解．所以满足条件的所有一次函数的个数为2个．故答案为2．三．解答题（共5小题）13．【分析】（1）此题由3种情况，①从假设△BPQ是等腰三角形入手．求证△BMP∽△BCD，利用对应边成比例即可求得t的值．在Rt△BMP中，利用cos∠DBC=，解得t．③如图，当BQ=PQ时，自点Q向BD引垂线，垂足为N．利用Rt△BNQ∽Rt△BCD其对应边成比例即可求得t．（2）若△PBQ为等边三角形，则BQ=BP=PQ．由②，知当BQ=BP时，．由①，知当BP=PQ 时，．而BQ=BP与BP=PQ不能同时成解：（1）若△BPQ是等腰三角形．①如图，当PB=PQ时，自点P向BC引垂线，垂足为M，则有BM=MQ．方法一：由△BMP∽△BCD，得，∴．∴，解得．方法二：在Rt△BMP中，．∴，解得．②当BQ=BP时，有t=5﹣t，解得．③如图，当BQ=PQ时，自点Q向BD引垂线，垂足为N．由Rt△BNQ∽Rt△BCD，得．∴，解得．（2）不能．若△PBQ为等边三角形，则BQ=BP=PQ．由（2）②，知当BQ=BP时，．由（2）①，知当BP=PQ时，．∴BQ=BP与BP=PQ不能同时成立，∴△PBQ不可能为等边三角形．14．【分析】（1）①当点P不与点A重合时，②当点P与点A重合时，分别证明即可；（2）由（1）知∠BAD=1=BP=x，过P作DA延长线的垂线PM，M为垂足，则∠PAM=60°，∠APM=30°，表示出△PAD面积然后根据配方法即可得出答案．解：（1）四边形ABCD是梯形或菱形，证明如下：①当点P不与点A重合时，∵△ABC与△CPD都是等边三角形，∴∠ACB=∠DCP=60°，∴∠1=∠2，∴△ADC≌△BPC，∴∠DAC=∠B=∠BCA=60°，∴AD∥BC．又∵∠1=∠2＜60°，∴∠DCB＜120°，即∠B+∠DCB＜180°，∴DC与AB不平行，∴四边形ABCD是梯形；②当点P与点A重合时，PC与AC重合，此时AB=BC=CA=AD=DC，四边形ABCD是菱形，综上所述，四边形ABCD是梯形或菱形；（2）由（1）知∠BAD=120°，AD=BP=x，过P作DA延长线的垂线PM，M为垂足，则∠PAM=60°，∠APM=30°，又BP=x，AB=1，∴AP=1﹣x，∴AM=，PM=∴（0＜x＜1）．当时，y取最大值为，即当时△PAD面积取得最大面积为．15．【分析】（1）求出点A、B的坐标，然后根据坐标原点O与O′关于直线l对称求出点O′，再利用待定系数法即可求解；（2）根据题意作出草图，设点P的坐标为（0，a），先求出点Q的坐标，然后分别求出梯形O′BPQ的面积与正方形AOBO′的面积，再根据S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′﹣S△AOP，列式计算即可求出a的值为3，根据三角函数求出∠PAO=60°，∠BAO=45°，两角相减即可解：（1）当x=0时，y=0+3=3，当y=0时，x+3=0，解得x=﹣3，∴点A、B的坐标分别为A（﹣3，0），B（0，3），∵坐标原点O与O′关于直线l对称，∴O′（﹣3，3），∴3=，解得k=﹣9，∴反比例函数y=的解析式为：y=﹣；（2）设点P的坐标为（0，a），∵PQ∥x轴，∴a=﹣，解得x=﹣，∴点Q的坐标为（﹣，a）；S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′﹣S△AOP=×（+3）（a﹣3）+3×3﹣×3×a，=﹣+9，∵四边形APQO′的面积为9﹣，∴﹣+9=9﹣，解得a=3，∴tan∠PAO===，tan∠BAO===1，∴∠PAO=60°，∠BAO=45°，θ=∠PAO﹣∠BAO=60°﹣45°=15°．故答案为：15°．16．【分析】（1）先解出分式方程①的解，根据分式的意义和方程①的根为非负数得出k（2）先把k=m+2，n=1代入方程②化简，由方程②有两个整数实根得△是完全平方数，列等式得出关于m的等式，由根与系数的关系和两个整数根x1、x2得出m=1和﹣1，再根据方程有两个整数根得△＞0，得出m＞0或m＜﹣，符合题意，分别把m=1和﹣1代入方程后解出即可．（3）根据（1）中k的取数得出k=﹣1，化简已知所给的等式，并将两根和与积代入计算得出m的等式，并由根的判别式组成两式可做出判断．解：（1）∵关于x的分式方程的根为非负数，∴x≥0且x≠1，又∵x=≥0，且≠1，∴解得k≥﹣1且k≠1，又∵一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0中2﹣k≠0，∴k≠2，综上可得：k≥﹣1且k≠1且k≠2；（2）∵一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0有两个整数根x1、x2，且k=m+2，n=1时，∴把k=m+2，n=1代入原方程得：﹣mx2+3mx+（1﹣m）=0，即：mx2﹣3mx+m﹣1=0，∴△＞0，即△=（﹣3m）2﹣4m（m﹣1），且m≠0，∴△=9m2﹣4m（m﹣1）=m（5m+4）＞0，则m＞0或m＜﹣；∵x1、x2是整数，k、m都是整数，∵x1+x2=3，x1?x2==1﹣，∴1﹣为整数，∴m=1或﹣1，由（1）知k≠1，则m+2≠1，m≠﹣1∴把m=1代入方程mx2﹣3mx+m﹣1=0得：x2﹣3x+1﹣1=0，x2﹣3x=0，x（x﹣3）=0，（3）|m|≤2成立，理由是：由（1）知：k≥﹣1且k≠1且k≠2，∵k是负整数，∴k=﹣1，（2﹣k）x2+3mx+（3﹣k）n=0且方程有两个实数根x1、x2，∴x1+x2=﹣==﹣m，x1x2==n，x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），x12﹣x1k+x22﹣x2k=x1x2﹣x1k﹣x2k+k2，x12+x22═x1x2+k2，（x1+x2）2﹣2x1x2﹣x1x2=k2，（x1+x2）2﹣3x1x2=k2，（﹣m）2﹣3×n=（﹣1）2，m2﹣4n=1，n=①，△=（3m）2﹣4（2﹣k）（3﹣k）n=9m2﹣48n≥0②，把①代入②得：9m2﹣48×≥0，m2≤4，则|m|≤2，∴|m|≤2成立．17．【分析】（1）根据“边上的中线等于斜边的一半”可知DF=BF=CF，根据∠DFE=2∠DCF，∠BFE=2∠BCF，得到∠EFD+∠EFB=2∠ABC=90°，进而得出DF⊥BF；（2）延长DF至G，连接BG，CG，DC，先判定△BFG≌△EFD（SAS），得到∠FBG=∠FED，BG=ED，结合△ADE和△ACB都是等腰直角三角形，得出∠CBG=∠DAC，再判定△BCG≌△ACD（SAS），进而得到GC=DC，∠BCG=∠ACD，根据△DCG是等腰直角三角形，以及F是DG的中点，即可得到CF⊥DF且CF=DF．解：（1）CF=DF且CF⊥DF．理由如下：∴∠BDE=90°，又∵∠BCE=90°，点F是BE的中点，∴CF=DF=BE=BF，∴∠1=∠3，∠2=∠4，∴∠5=∠1+∠3=2∠1，∠6=∠2+∠4=2∠2，∴∠CFD=∠5+∠6=2（∠1+∠2）=2∠ABC，又∵△ABC是等腰直角三角形，且∠ACB=90°，∴∠ABC=45°，∴∠CFD=90°，∴CF=DF且CF⊥DF．（2）（1）中的结论仍然成立．理由如下：如图，延长DF至G使FG=DF，连接BG，CG，DC，∵F是BE的中点，∴BF=EF，又∵∠BFG=∠EFD，GF=DF，∴△BFG≌△EFD（SAS），∴∠FBG=∠FED，BG=ED，∴BG∥DE，∵△ADE和△ACB都是等腰直角三角形，∴DE=DA，∠DAE=∠DEA=45°，AC=BC，∠CAB=∠CBA=45°，又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣（180°﹣∠AEB﹣∠EAB）﹣45°=∠DEF﹣180°+∠AEB+∠EAB﹣45°=（∠DEF+∠AEB）+∠EAB﹣225°=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB，∴∠CBG=∠DAC，又∵BG=ED，DE=DA，∴BG=AD，又∵BC=AC，∴△BCG≌△ACD（SAS），∴GC=DC，∠BCG=∠ACD，∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°，∴△DCG是等腰直角三角形，又∵F是DG的中点，∴CF⊥DF且CF=DF．。
浙江省温州市温州中学2024届高三第一次模拟考试数学试题及答案
浙江省温州市温州中学2024届高三第一次模拟考试数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题A ．−iB ．iC ．0D ．12．某校高一年级18个班参加艺术节合唱比赛，通过简单随机抽样，获得了10个班的比赛得分如下：91，89，90，92，94，87，93，96，91，85，则这组数据的80%分位数为（ ） A ．93B ．93.5C ．94D ．94.53．已知直线l:y =2x +b 与圆C:(x +2)2+(y −3)2=5有公共点，则b 的取值范围为（ ） A ．[2,12] B ．(−∞,2]∪[12,+∞) C ．[−4,6]D ．(−∞,−4]∪[6,+∞)4．三棱锥P −ABC 中，PA ⊥平面ABC ，△ABC 为等边三角形，且AB =3，PA =2，则该三棱锥外接球的表面积为（ ）5．已知等比数列{a n }的首项a 1>1，公比为q ，记T n =a 1a 2⋅⋅⋅a n （n ∈N ∗），则“0<q <1”是“数列{T n }为递减数列”的（ ） A ．充要条件 B ．充分不必要条件 C ．必要不充分条件D ．既不充分也不必要条件7．在直角梯形ABCD ，AB⊥AD ，DC//AB ，AD=DC=1，AB=2，E ，F 分别为AB ，BC 的中点，点P 在以A 为圆心，AD 为半径的圆弧DEM 上变动（如图所示），若AP ⃗⃗⃗⃗⃗ =λED ⃗⃗⃗⃗⃗ +μAF ⃗⃗⃗⃗⃗ ，其中λ,μ∈R ，则2λ−μ的取值范围是（ ）8．已知a=10lg4,b=9lg5,c=8lg6，则a,b,c的大小关系为（）A．a>b>c B．a>c>b C．b>c>a D．c>b>a 二、多选题A．x<1B．log0.5x2>log0.5xC．3x2<3x D．|x(x−1)|=x(1−x)11．在三棱锥P−ABC中，AC⊥BC，AC=BC=4，D是棱AC的中点，E是棱AB上一点，PD=PE=2，AC⊥平面PDE，则（）12．设F为抛物线C:y2=4x的焦点，直线l:2x−ay+2b=0(a≠0)与C的准线l1，交于点A．已知l与C相切，切点为B，直线BF与C的一个交点为D，则（）A．点(a,b)在C上B．∠BAF<∠AFBC．以BF为直径的圆与l相离D．直线AD与C相切三、填空题15．直三棱柱ABC−A1B1C1的底面是直角三角形，AC⊥BC，AC=6，BC=8，AA1= 4．若平面α将该直三棱柱ABC−A1B1C1截成两部分，将两部分几何体组成一个平行六面体，且该平行六面体内接于球，则此外接球表面积的最大值为．16．对任意x∈(1,+∞)，函数f(x)=a x lna−aln(x−1)≥0(a>1)恒成立，则a的取值范围为．四、解答题17．在△ABC中，内角A,B,C的对边分别为a，b，c，且a2+c2−b2=ac，a=√3，cosA=√53.(1)求角B及边b的值；(2)求sin(2A−B)的值.18．已知数列{a n}的前n项和为S n，且S n=2a n−n．(1)求数列{a n}的通项公式；(2)若数列{b n}满足b n=a n+1a n a n+1，其前n项和为T n，求使得T n>20232024成立的n的最小值．19．如图，正三棱锥O−ABC的三条侧棱OA、OB、OC两两垂直，且长度均为2．E、F分别是AB、AC的中点，H是EF的中点，过EF作平面与侧棱OA、OB、OC或其延长线分别．相交于A1、B1、C1，已知OA1=32（1）求证：B1C1⊥平面OAH；（2）求二面角O−A1B1−C1的大小．20．甲、乙、丙为完全相同的三个不透明盒子，盒内均装有除颜色外完全相同的球.甲盒装有4个白球，8个黑球，乙盒装有1个白球，5个黑球，丙盒装有3个白球，3个黑球.(1)随机抽取一个盒子，再从该盒子中随机摸出1个球，求摸出的球是黑球的概率；(2)已知（1）中摸出的球是黑球，求此球属于乙箱子的概率.21．设椭圆C:x29+y2b2=1(0<b<√6)，P是C上一个动点，点A(1,0)，PA长的最小值为√102．(1)求b的值：(2)设过点A且斜率不为0的直线l交C于B,D两点，E,F分别为C的左、右顶点，直线BE和直线DF的斜率分别为k1,k2，求证：k1k2为定值．22．已知f(x)=3lnx−k(x−1).(1)若过点(2,2)作曲线y=f(x)的切线，切线的斜率为2，求k的值；(2)当x∈[1,3]时，讨论函数g(x)=f(x)−2πcosπ2x的零点个数.参考答案：1．D【分析】利用复数的除法运算，得到复数的代数形式，由此求得复数的虚部.【详解】因为1+i1−i =(1+i)2(1+i)(1−i)=2i2=i，所以虚部为1.故选：D．2．B【分析】利用百分位数的定义即可得解.【详解】将比赛得分从小到大重新排列：85，87，89，90，91，91，92，93，94，96，因为10×80%=8，所以这组数据的80%分位数第8个数与第9个数的平均值，即93+942=93.5.故选：B.3．A【分析】由圆心到直线距离小于等于半径，得到不等式，求出答案.【详解】由题意得，圆心(−2,3)到直线l:y=2x+b的距离|−4−3+b|√1+4≤√5，解得2≤b≤12，故b的取值范围是[2,12].故选：A4．B【分析】首先作图构造外接球的球心，再根据几何关系求外接球的半径，最后代入三棱锥外接球的表面积公式.【详解】如图，点H为△ABC外接圆的圆心，过点H作平面ABC的垂线，点D为PA的中点，过点D作线段PA的垂线，所作两条垂线交于点O，则点O为三棱锥外接球的球心，因为PA⊥平面ABC，且△ABC为等边三角形，PA=2,AB=3，所以四边形AHOD为矩形，AH=√33AB=√3，OH=12PA=1，所以OA=√(√3)2+12=2，即三棱锥外接球的半径R=2，.则A (0,0)，E (1,0)，D (0,1)，C (1,1则F (32,12)，AP ⃗⃗⃗⃗⃗ =(cosα,sinα)，ED ⃗⃗⃗⃗⃗ ∵AP⃗⃗⃗⃗⃗ =λED ⃗⃗⃗⃗⃗ +μAF ⃗⃗⃗⃗⃗ ，15．104π【分析】α可能是AC的中垂面，BC的中垂面，AA1的中垂面.截下的部分与剩余的部分组合成为长方体,用公式求出外接球直径进而求解.【详解】平行六面体内接于球，则平行六面体为直四棱柱，如图α有如下三种可能.截下的部分与剩余的部分组合成为长方体，则2R=√32+82+42=√89或2R=√62+42+42=√68或2R=√62+82+22=√104，所以S max=4πR2=104π．故答案为：104π16．[e1e,+∞)【分析】变形为a x−1lna x−1≥(x−1)ln(x−1)，构造F(t)=tlnt,t>0，求导得到单调性进而a x−1>1恒成立，故F(a x−1)>0，分当x−1∈(0,1]和x−1>1两种情况，结合g(u)=lnuu单调性和最值，得到a≥e 1e，得到答案.【详解】由题意得a x−1lna≥ln(x−1)，因为x∈(1,+∞)，所以(x−1)a x−1lna≥(x−1)ln(x−1)，即a x−1lna x−1≥(x−1)ln(x−1)，令F(t)=tlnt,t>0，则F(a x−1)≥F(x−1)恒成立，因为F′(t)=1+lnt，令F′(t)>0得，t>e−1，F(t)=tlnt单调递增，令F′(t)<0得，0<t<e−1，F(t)=tlnt单调递减，且当0<t≤1时，F(t)≤0恒成立，当t>1时，F(t)>0恒成立，因为a>1,x>1，所以a x−1>1恒成立，故F(a x−1)>0，当x−1∈(0,1]时，F(x−1)≤0，此时满足F(a x−1)≥F(x−1)恒成立，因为E、F分别是AB、AC的中点，所以AE=12AB,AF=12AC，因为AB=AC，所以AE=AF，因为H是EF的中点，所以AH⊥EF，所以AH⊥B1C1．因为OA⊥OB，OA⊥OC，OB∩OC=O，所以OA⊥平面OBC，因为B1C1⊂平面OBC，所以OA⊥B1C1，因为OA∩AH=A因此B1C1⊥面OAH．（2）作ON⊥A1B1于N，连C1N．因为OC1⊥OA1,OC1⊥OB1,OA1∩OB1=O，因为OC1⊥平面OA1B1，因为A1B1⊂平面OA1B1，所以OC1⊥A1B1，因为ON∩OC1=O，所以A1B1⊥平面OC1N，因为C1N⊂平面OC1N，所以C1N⊥A1B1，所以∠ONC1就是二面角O−A1B1−C1的平面角．过E作EM⊥OB1于M，则EM∥OA，则M是OB的中点，则g(x)在[1,m)内单调递增，在(m,3]内单调递减，且g(1)=0，可知g(m)>g(1)=0，可知g(x)在[1,m)内有且仅有1个零点，且g(3)=3ln3−2k，ln3≤k<4时，则g(x)在(m,3]内有且仅有1个零点；①当g(3)=3ln3−2k≤0，即32②当g(3)=3ln3−2k>0，即0<k<3ln3时，则g(x)在(m,3]内没有零点；2ln3)∪[4,+∞)时，g(x)在[1,3]内有且仅有1个零点；综上所述：若k∈(−∞,32若k∈[3ln3,4)时，g(x)在[1,3]内有且仅有2个零点.2【点睛】方法点睛：对于函数零点的个数的相关问题，利用导数和数形结合的数学思想来求解．这类问题求解的通法是：（1）构造函数，这是解决此类题的关键点和难点，并求其定义域；（2）求导数，得单调区间和极值点；（3）数形结合，挖掘隐含条件，确定函数图象与x轴的交点情况进而求解．答案第15页，共15页。
浙江省温州市温州中学2024届高三第一次模拟考试数学试题
一、单选题二、多选题1. 已知函数的部分图象如图所示，下列关于函数的表述正确的是（）A ．函数的图象关于点对称B．函数在上递减C ．函数的图象关于直线对称D．函数的图象上所有点向左平移个单位得到函数的图象2. “田忌赛马”的故事千古流传，故事大意是：在古代齐国，马匹按奔跑的速度分为上中下三等．一天，齐王找田忌赛马，两人都从上、中、下三等马中各派出一匹马，每匹马都各赛一局，采取三局两胜制．已知田忌每个等次的马，比齐王同等次的马慢，但比齐王较低等次的马快．若田忌不知道齐王三场比赛分别派哪匹马上场，则田忌获胜的概率为（ ）A．B．C．D．3. 已知函数．给出下列命题：①函数的值域为；②为函数的一条对称轴；③为奇函数；④，对恒成立．其中的真命题有（ ）A ．①②B ．③④C ．②③D ．①④4. 若集合，，则集合（ ）A．B．C．D．5. 已知命题，，则为（ ）A ．，B ．，C ．，D ．，6. 已知中，若，则的值为A ．2B ．3C ．4D ．57. 已知椭圆和双曲线的离心率之积为1，则双曲线的两条渐近线的倾斜角分别为（ ）A．，B．，C．，D．，8. 已知数列为等差数列，前项和为，则“”是“数列为单增数列”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件9.已知函数，则（ ）A ．在上单调递减，在上单调递增B ．有2个不同的零点C ．若a ，，则D ．若且，则浙江省温州市温州中学2024届高三第一次模拟考试数学试题浙江省温州市温州中学2024届高三第一次模拟考试数学试题三、填空题四、解答题10. 某商场前有一块边长为60米的正方形地皮，为了方便消费者停车，拟划出一块矩形区域用于停放电动车等，同时为了美观，建造扇形花坛，现设计两种方案如图所示，方案一：，在线段上且，方案二：在圆弧上且．若花坛区域工程造价0.2万元/平方米，停车区域工程造价为0.1万元/平方米，则下列说法正确的是（）A ．两个方案中矩形停车区域的最大面积为2400平方米B ．两个方案中矩形停车区域的最小面积为1200平方米C ．方案二中整个工程造价最低为万元D ．两个方案中整个工程造价最高为万元11. 已知直四棱柱，底面是菱形，，且，为的中点，动点满足，且，，则下列说法正确（ ）A ．当平面时，B．当时，的最小值为C ．若，则的轨迹长度为D ．当时，若点为三棱锥的外接球的球心，则的取值范围为12.已知函数，则下列结论正确的有（ ）A ．为奇函数B ．是以为周期的函数C．的图象关于直线对称D ．时，的最大值为13. 已知向量，，，若A ，B ，D 三点共线，则_________．14.已知函数则_____.15. 已知函数是奇函数，则______．16.如图，在四棱锥中，底面四边形的边长均为2，且，棱的中点为.(1)求证：平面；(2)若的面积是，求点到平面的距离.17. 已知函数.（1）讨论函数的极值；（2）记关于的方程的两根分别为，求证：.18. 已知等比数列的首项，公比为q，是公差为的等差数列，，，是与的等比中项．(1)求数列的通项公式；(2)设的前n项和为，数列满足，求数列的前n项和．19. 若.(1)当，时，讨论函数的单调性；(2)若，且有两个极值点，，证明：.20. 已知函数．(1)若，求曲线在处的切线方程；(2)当时，证明：．21. 如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD⊥CD，AD BC，PA=AD=CD=2，BC=3，E为PD的中点，点F在PC上，且.(1)求二面角F-AE-P的余弦值；(2)设点G在PB上，且.判断直线AG是否在平面AEF内，说明理由.。
2020年温州市温州中学自主招生数学模拟试卷及答案解析
第1页（共16页）2020年温州市温州中学自主招生数学模拟试卷一．选择题（共8小题，满分40分，每小题5分）1．（5分）设x =√5−32，则代数式x （x +1）（x +2）（x +3）的值为（ ） A ．0 B ．1 C ．﹣1 D ．22．（5分）方程x 2+2xy +3y 2＝34的整数解（x ，y ）的组数为（ ）A ．3B ．4C ．5D ．6 3．（5分）已知A ，B 是两个锐角，且满足sin 2A +cos 2B =54t ，cos 2A +sin 2B =34t 2，则实数t 所有可能值的和为（ ）A ．−83B ．−53C ．1D ．1134．（5分）已知整数a 1、a 2、a 3、a 4、……满足下列条件：a 1＝0，a 2＝﹣|a 1+1|，a 3＝﹣|a 2+2|，a 4＝﹣|a 3+3|，……，a n +1＝﹣|a n +n |（n 为正整数）依此类推，则a 2019的值为（ ）A ．﹣1007B ．﹣1008C ．﹣1009D ．﹣10105．（5分）方程组{xy +yz =63xz +yz =23的正整数解的组数是（ ） A ．1 B ．2 C ．3 D ．46．（5分）如图，已知在正方形ABCD 中，点O 是对角线AC 的中点，过O 点的射线OM 、ON 分别交AB 、BC 于点E 、F ，且∠EOF ＝90°，BO 、EF 交于点P ，下列结论：①图形中全等的三角形只有三对； ②△EOF 是等腰直角三角形；③正方形ABCD 的面积等于四边形OEBF 面积的4倍；④BE +BF ＝OA ；⑤AE 2+BE 2＝2OP •OB ．其中正确的个数有（ ）个．A ．4B ．3C ．2D ．17．（5分）已知实数a ，b 满足a 2+b 2＝1，则a 4+ab +b 4的最小值为（ ）A ．−18B ．0C ．1D ．98 8．（5分）已知2x 2﹣x ﹣1＝0的两根为x 1、x 2，则x 1+x 2为（ ）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
温州中学提前招生数学模拟卷精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-2017年温州中学提前招生数学模拟卷（三）题号一二三总分1－8 9－14 15 16 17 18得分评卷人复查人一、选择题（共8小题，每小题5分，满分40分）1．已知x、y、z都是实数，且x2+y2+z2=1，则m=xy+yz+zx（）A．只有最大值 B．只有最小值C．既有最大值又有最小值 D．既无最大值又无最小值2．如图，在矩形ABCD中，对角线长2，且∠1=∠2=∠3=∠4，则四边形EFGH的周长为（）A．2 B．4 C．4 D．63．设直线kx+（k+1）y且为正整数）与两坐标轴围成的三角形的面积为Sk（k=1，2，…，2011），则S1+S2+…+S2011=（）A． B． C． D．4．（x+a）（x+b）+（x+b）（x+c）+（x+c）（x+a）是完全平方式，则a，b，c的关系可以写成（）A．a＜b＜c B．（a﹣b）2+（b﹣c）2=0 C．c＜a＜b D．a=b≠c5．实数a、b、m、n满足a＜b，﹣1＜n＜m，若，，则M与N的大小关系是（）A．M＞N B．M=N C．M＜N D．无法确定的6．一个等腰直角三角形和一个正，被分割成了5个部分．①，②，③这三块的面积比依次为1：4：41，那么，④，⑤这两块的面积比是（）A．3：4 B．9：14 C．4：5 D．9：16 7．现有价格相同的5种不同商品每天分别降价10%或20%，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r，则r的最小值为（）A． B． C． D．8．书架上有a本经济类书，7本数学书，b本小说，5本电脑游戏类书．现某人随意从架子上抽取一本书，若得知取到经济类或者数学书的机会为，则a，b的关系为（）A．a=b﹣2 B．a=b+12 C．a+b=10 D．a+b=12二、填空题（共6小题，每小题5分，满分30分）9．数学小组中男孩子数大于小组总人数的40%小于50%，则这个数学小组的成员至少有人．10．若二次函+bx，存在不同实数x1，x2且x1﹣x2≠2使得f（x1﹣1）=f（x2﹣1），则f（x1+x2）=．11．已知一次函数f（x）过点（10，13），它在x轴上的截距是一个质数，在y轴上的截距是一个正整数，则函数的个数有个．12．如果函数f（x）式：f（﹣x）+f（x）=0，f（x+2）+f（x）=0，又知当0≤x≤1时，f （x）=x，则f（）=．13．如图，△ABC与△CDE均是等边三角形，若∠AEB=145°，则∠DBE的度数是．14．方程x2+（）2=45的四个实数根中，最小的一个是．三、解答题(共4题，分值依次为12分、12分、13分和13分，满分50分)15．已知a、b为整数，若一元二次方程x2﹣ax a﹣b+（2a﹣b﹣1）x+a2+a﹣b﹣4=0的根都是整数，求a、b的值．16．已知A（x1、y1），B（x2，y2）是直线y=﹣x+2与双曲线（k≠0）的两个不同交点．（1）求k的取值范围；（2）是否存在这样k的值，使得若存在，求出这样的k值；若不存在，请说明理由．17．直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．（1）如图1，已知AE∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；（2）如图2，延长BA至G，已知OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF=°；在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．18．如图，△为1的等边三角形，P是AB边上的一个动点（P与B不重合），以线段CP为边作等边△CPD（D、A在BC的同侧），连接AD．（1）判断四边形ABCD的形状，并给予证明；（2）设BP=x，△PAD的面积为y，求出y关于x的函数关系式，并求出△PAD面积的最大值及取得最大值时x的值．参考答案一．选择题（共8小题）1．【分析】先用配方法化成m=[（x+y+z）2﹣（x2+y2+z2）]=[（x+y+z）2﹣1]的形式，即可得出最小值，再根据x2+y2≥2xy，y2+z2≥2yz，x2+z2≥2xz，三式相加可得最大值．解：∵（x+y+z）2=x2+y2+z2+2xy+2yz+2xz，∴m=[（x+y+z）2﹣（x2+y2+z2）]=[（x+y+z）2﹣1]≥﹣，即m有最小值，而x2+y2≥2xy，y2+z2≥2yz，x2+z2≥2xz，三式相加得：2（x2+y2+z2）≥2（xy+yz+xz），∴m≤x2+y2+z2=1，即m有最大值1．故选C．2．【分析】由∠1=∠2=∠3=∠4可得出∠GHE=∠GFE，∠HGF=∠HEF，从而可得出∠GHE+∠HGF=180°，∠GHE+∠HEF=180°，这样即可得出HG∥EF，GF∥HE，HGFE是平行四边形，连接AC、BD，则有：=，=，从而可得+=+=1，即GF+HG=AC=2，根据平行四边形的性质可得出四边形EFGH的周长．解：∵∠1=∠2=∠3=∠4，∴∠GHE=∠GFE，∠HGF=∠HEF，在四边形GHEF中，∠GHE+∠HGF=180°，∠GHE+∠HEF=180°，故可得HG∥EF，GF∥HE，HGFE是平行四边形，∴△AHG≌△CFE，△DGF≌△BEH，△BEH∽△CEF，△DGF∽△CEF，∴==，∴EF∥BD，同理HG∥BD，∴=，=，∴+=+=1，又∵+=+，AC=BD，即GF+HG=AC=2，∴四边形EFGH的周长=2（GF+HG）=4．故选B．3．【分析】求出当x=0时，y=，当y=0时，x=，根据三角形面积公式求出S k，求出S1=×（1﹣），S2=×（﹣），以此类推S2011=×（﹣），相加后得到×（1﹣），求出即可．解：当x=0时，y=，当y=0时，x=，∴S k=××，∴S1=×1×=×（1﹣），S2=××=×（﹣），S3=（﹣），…S2011=×（﹣），∴S1+S2+S3+…+S2011=×（1﹣+﹣+﹣+…+﹣），=×（1﹣）=，故选D．4．【分析】先把原式展开，合并，由于它是完全平方式，故有3x2+2（a+b+c）x+（ab+bc+ac）=[x+（a+b+c）]2，化简有ab+bc+ac=a2+b2+c2，那么就有（a﹣b）2+（b ﹣c）2+（c﹣a）2=0，三个非负数的和等于0，则每一个非负数等于0，故可求a=b=c．故选答案B．解：原式=3x2+2（a+b+c）x+（ab+bc+ac），∵（x+a）（x+b）+（x+b）（x+c）+（x+c）（x+a）是完全平方式，∴3x2+2（a+b+c）x+（ab+bc+ac）=[x+（a+b+c）]2，∴ab+bc+ac=（a+b+c）2=（a2+b2+c2+2ab+2ac+2bc），∴ab+bc+ac=a2+b2+c2，∴2（ab+bc+ac）=2（a2+b2+c2），即（a﹣b）2+（b﹣c）2+（c﹣a）2=0，∴a﹣b=0，b﹣c=0，c﹣a=0，∴a=b=c．故选B．5．【分析】首先将M，N变形，即可得M﹣N=（b﹣a），继而求得答案．解：∵=a+b，=a+b，∴M﹣N=（﹣）a+（﹣）b=a+ b=（b﹣a），∵a＜b，﹣1＜n＜m，∴m﹣n＞0，1+m＞0，1+n＞0，b﹣a＞0，∴M﹣N＞0，∴M＞N．故选A．6．【分析】面积比，可以求出KB和HK的比值，根据②面积和③面积求出HK和BD的比值．即可求出④，⑤的面积，计算面积的比值即可．解：①和②的面积比为1：4，故边长比即KB：KH=1：2，设BK=x，则HK=2x，根据①和③的面积等于1：41，故EH==7x，故⑤的面积为7x×（7x﹣3x）=28x2，④的面积为×（7x﹣x）×（7x﹣x）=18x2，故④和⑤的面积比为18：28=9：14．故选B．7．【分析】根据题意可得n天后每种商品的价格可表示为a（1﹣10%）k（1﹣20%）n﹣k=a，由此可得出5种商品的价格，从而可得出r的最小值．解：设5种商品降价前的价格为a，过了n天．n天后每种商品的价格一定可以表示为a（1﹣10%）k（1﹣20%）n﹣k=a，其中k为自然数，且0≤k≤n．要使r的值最小，五种商品的价格应该分别为：①a，②a，③a，④a，⑤a，其中i为不超过n的自然数．所以r的最小值为=．故选B．8．【分析】由取到经济类或者数学书的机会为，可知经济类和数学书的本数占全部的，列出代数式即可求出ab的关系．解：由已知可得a+7=，解得a+2=b，即a=b﹣2．故选A．二．填空题（共6小题）9．【分析】设这个数学小组的成员共有b人，男孩为a人，根据题意列出不等式组即可求解．解：设这个数学小组的成员共有b人，男孩为a人，a，b均为自然数，且，即：2b＜5a且2a＜b，于是：2b≤5a﹣1且2a＜b﹣1，则有：，所以4b+2≤5b﹣5，解得：b≥7，∴b的最小值为7．故答案为：7．10．【分析】根据二次函数x1﹣1），（x2﹣1），（x1+x2）看成一项，然后根据f（x1﹣1）=f（x2﹣1）求出（x1+x2）的值，代入二次函数即可得出答案．解：由f（x1﹣1）=f（x2﹣1），得a（x1﹣1）2+b（x1﹣1）=a（x2﹣1）2+b（x2﹣1），即（x1﹣x2）[a（x1+x2﹣2）]+b=0，∵x1≠x2x1﹣x2≠0，∴，故．11．【分析】设与x轴交点为（p，0），与y轴交点为（0，q），把点（10，13）代入y=ax+b，得10a+b=13；把（p，0），（0，q）也代入y=ax+b，得b=q，a=﹣．所以13p=﹣10q+pq，则q=，p是质数，q是正整数，再利用整除的性质讨论即可．解：设于x轴交点为（p，0），与y轴交点为（0，q），把点（10，13）代入y=ax+b，得10a+b=13；把（p，0），（0，q）也代入y=ax+b，得b=q，a=﹣．所以13p=﹣10q+pq，则q=，p是质数，q是正整数，当p﹣10=1时，p=11，q=143，符合题意；当p﹣10=13时，p=23，q=23，符合题意；当p﹣10=p时，无解．所以满足条件的所有一次函数的个数为2个．故答案为2．12．【分析】根据f（﹣x=0，f（x+2）+f（x）=0可将f（）=变形为﹣f（），再由当0≤x ≤1时，f（x）=x可得出答案．解：∵f（x+2）=﹣f（x），以及f（﹣x）=﹣f（x），∴f（）=﹣f（）=f（）=﹣f（）=f（﹣）=﹣f（）=﹣．故答案为：﹣．13．【分析】首先根据明△ACE≌△BCD，再根据三角形全等的性质可得到∠AEC=∠BDC=60°+∠3，最后根据三角形的内角和定理，角间的关系可得∠AEB的度数．解：如右图∵等边△ABC和等边△DCE∴∠ACB=∠DCE=∠ABC=∠ECD=60°在△ACE与△BCD中∵∠ACB=∠ECD∠ACB﹣∠ECB=∠ECD﹣∠ECBAC=BC∠1=∠2 EC=DC△ACE≌△BCD∴∠AEC=∠BDC=60°+∠3∴∠AEB=360°﹣∠AEC﹣∠CED﹣∠BED则360°﹣∠AEC﹣∠CED﹣∠BED=145°，360°﹣（60°+∠3）﹣60°﹣∠BED=145°，360°﹣120°﹣（∠3+∠BED）=145°，360°﹣120°﹣（180°﹣∠EBD）=145°，解得，∠EDB=85°．14．【分析】先求出原方程的四个实数根，再取其最小的一个值即可．由于方程的左边是平方和的形式，可以添项后配成完全平方式，再将看作一个整体，运用十字相乘法求出它的值，进而得出未知数x的值．注意解此方程需要检验．解：添项，得x2﹣2x++2x=45，（x﹣）2+4?=45，所以（）2+4?﹣45=0，（+9）（﹣5）=0，+9=0或﹣5=0．当+9=0时，得x2+9x+18=0，所以x1=﹣3，x2=﹣6；﹣5=0时，得x2﹣5x﹣10=0，所以x3=，x4=．经检验，x1=﹣3，x2=﹣6，x3=，x4=都是原方程的根．∵﹣6＜﹣3＜＜，∴四个实数根中，最小的一个是﹣6．故答案为﹣6．三．解答题（共4小题）15．【分析】因为方程x2﹣（2a﹣b﹣1）x+a2+a﹣b﹣4=0为一元二次方程，且两根和a，b 均为整数，根据根与系数的关系和一元二次方程的定义分情况讨论分别求解a，b值，即可得出答案．解：根据题目分三种情况讨论：①当a﹣b=2即b=a﹣2时，原方程可化为：（1﹣a）x2+（a+1）x+（a2﹣2）=0，设方程两根为：x1，x2，则：x1+x2=，x1x2=，∵x1，x2为整数，∴x1+x2=，x1x2=均为整数，可得：或者；②当a﹣b=1即b=a﹣1时，原方程可化为：x2+a2﹣3=0，当：x1，x2，a，b为整数时，无解；③当a﹣b=0即a=b时，原方程可化为：x2+（a﹣1）x+a2﹣a﹣4=0，△=（a﹣1）2﹣4（a2﹣a﹣4）=﹣3a2+2a+17≥0，解得﹣≤a≤+，∵a、b为整数，根是整数，∴a=﹣2，b=﹣2；a=1，b=1；a=2，b=2．16．【分析】（1）直线y=﹣x+2与双曲线（k≠0）联立，用△＞0即可求出k的取值范围．（2）假设存在k，然后根据求出k，验证是否符合题意即可．解：（1）∵直线y=﹣x+2与双曲线（k≠0）的两个不同交点，﹣x+2=，即：x2﹣2x+k=0，∴△=4﹣4k＞0，解得：k＜1且k≠0；（2）假设存在k，使，∴x1x2﹣2（x1+x2）+4==，∵x1，x2是方程x2﹣2x+k=0的两根，∴x1+x2=2，x1x2=k，∴k﹣4+4=，解得：k=﹣1±，又k＜1且k≠0，∴k=﹣1﹣．故存在k=﹣1﹣使得成立．17．【分析】（1）根据直线MN与直线PQ垂直相交于O可知∠AOB=90°，再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=∠OAB，∠ABE=∠ABO，由三角形内角和定理即可得出结论；（2）由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=∠BAO，∠EOQ=∠BOQ，进而得出∠E的度数，由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°，在△AEF中，由一个角是另一个角的3倍分四种情况进行分类讨论．解：（1）∠AEB的大小不变，∵直线MN与直线PQ垂直相交于O，∴∠AOB=90°，∴∠OAB+∠OBA=90°，∵AE、BE分别是∠BAO和∠ABO角的平分线，∴∠BAE=∠OAB，∠ABE=∠ABO，∴∠BAE+∠ABE=（∠OAB+∠ABO）=×90°=45°，∴∠AEB=135°；（2）∵AE、AF分别是∠BAO和∠OAG的角平分线，∴∠EAO=∠BAO，∠FAO=∠GAO，∴∠EAF=（∠BAO+∠GAO）=×180°=90°．故答案为：90；∵∠BAO与∠BOQ的角平分线相交于E，∴∠EAO=∠BAO，∠EOQ=∠BOQ，∴∠E=∠EOQ﹣∠EAO=（∠BOQ﹣∠BAO）=∠ABO，即∠ABO=2∠E，在△AEF中，∵有一个角是另一个角的3倍，故分四种情况讨论：①∠EAF=3∠E，∠E=30°，则∠ABO=60°；②∠EAF=3∠F，∠E=60°，∠ABO=120°（舍去）；③∠F=3∠E，∠E=°，∠ABO=45°；④∠E=3∠F，∠E=°，∠ABO=135°（舍去）．∴∠ABO为60°或45°．18．【分析】（1）①当点P不与点A重合时，②当点P与点A重合时，分别证明即可；（2）由（1）知∠BADAD=BP=x，过P作DA延长线的垂线PM，M为垂足，则∠PAM=60°，∠APM=30°，表示出△PAD面积然后根据配方法即可得出答案．解：（1）四边形ABCD是梯形或菱形，证明如下：①当点P不与点A重合时，∵△ABC与△CPD都是等边三角形，∴∠ACB=∠DCP=60°，∴∠1=∠2，又∵AC=BC，DC=PC，∴△ADC≌△BPC，∴∠DAC=∠B=∠BCA=60°，∴AD∥BC．又∵∠1=∠2＜60°，∴∠DCB＜120°，即∠B+∠DCB＜180°，∴DC与AB不平行，∴四边形ABCD是梯形；②当点P与点A重合时，PC与AC重合，此时AB=BC=CA=AD=DC，四边形ABCD是菱形，综上所述，四边形ABCD是梯形或菱形；（2）由（1）知∠BAD=120°，AD=BP=x，过P作DA延长线的垂线PM，M为垂足，则∠PAM=60°，∠APM=30°，又BP=x，AB=1，∴AP=1﹣x，∴AM=，PM=∴（0＜x＜1）．当时，y取最大值为，即当时△PAD面积取得最大面积为．。