箱形梁畸变理论
c)箱形成型品的内翘曲变形.
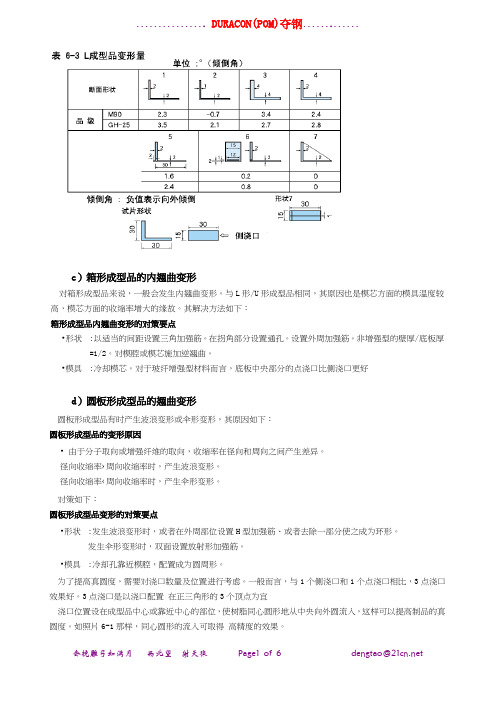
c)箱形成型品的内翘曲变形对箱形成型品来说,一般会发生内翘曲变形。
与L形/U形成型品相同,其原因也是模芯方面的模具温度较高,模芯方面的收缩率增大的缘故。
其解决方法如下:箱形成型品内翘曲变形的对策要点•形状:以适当的间距设置三角加强筋。
在拐角部分设置通孔。
设置外周加强筋。
非增强型的壁厚/底板厚=1/2。
对模腔或模芯施加逆翘曲。
•模具:冷却模芯。
对于玻纤增强型材料而言,底板中央部分的点浇口比侧浇口更好d)圆板形成型品的翘曲变形圆板形成型品有时产生波浪变形或伞形变形,其原因如下:圆板形成型品的变形原因• 由于分子取向或增强纤维的取向,收缩率在径向和周向之间产生差异。
径向收缩率›周向收缩率时,产生波浪变形。
径向收缩率‹周向收缩率时,产生伞形变形。
对策如下:圆板形成型品变形的对策要点•形状:发生波浪变形时,或者在外周部位设置H型加强筋、或者去除一部分使之成为环形。
发生伞形变形时,双面设置放射形加强筋。
•模具:冷却孔靠近模腔,配置成为圆周形。
为了提高真圆度,需要对浇口数量及位置进行考虑。
一般而言,与1个侧浇口和1个点浇口相比,3点浇口效果好。
3点浇口是以浇口配置在正三角形的3个顶点为宜浇口位置设在成型品中心或靠近中心的部位,使树脂同心圆形地从中央向外圆流入,这样可以提高制品的真圆度。
如照片6-1那样,同心圆形的流入可取得高精度的效果。
e)圆柱形成型品的变形细长的圆柱形成型品倾向于两端外径大、中间外径小的弓形。
这是由于两端固化快而中间固化慢的缘故。
但是,如果改为二重圆筒等形状使厚度变薄,则会有好的转变。
在改为二重圆筒等形状时,使连接外壁和内壁的加强筋厚度越薄,可以减少因加强筋引起的凹痕等影响。
f)细长形成型品的翘曲变形如果将浇口设置在细长形成型品的长边的一侧,则一般向浇口方面成弓形翘曲。
所以,原则上浇口要设置在短边方面。
见图6-3示例。
g)成型条件与变形作为与变形有关的成型条件必须特别注意的是注射及保压时间、冷却时间、注射速度、模具温度。
薄壁箱梁的扭转和畸变理论-文档资料

自由扭转 约束扭转增量
主广义扇性静矩
4、约束扭转扭角微分方程
根据截面上内外扭矩平衡
根据截面上纵向位移协调
翘曲系数 截面极惯矩
合并两微分方程后得到
约束扭转的弯 扭特性系数
常用边 界条件
箱梁的畸变应力
1、弹性地基梁比拟法基本原理
畸变角微分方程
弹性地基梁微分方程
弹性地基梁与受畸荷载箱梁各物理量 之间相似关系
的 主 弯扭刚度比
要 增大抗扭惯矩可以大大减小扭转变形
因
素 扇性惯矩
曲线桥
平 计算方法综述
面
–杆系结构力学+横向分布
弯
–有限元法
桥
• 梁格法
的
• 板壳单元
设
计
计
算
线桥
平 面 曲 梁 的 变 形 微 分 方 程
混凝土徐变
定义 混凝土在不变荷载长期作用下,其应
变随时间而继续增长的现象称为混凝土的 徐变。 特点
T形梁翼板有效分布宽度
T 梁 有 效 分 布 宽 度
无承托:B=δ+2λ 有承托: B=δ+2λ+承托宽度
曲线桥
漳 龙 高 速 公 路
曲线桥
弯 拱 桥
曲线桥
弯 连 续 刚 构
曲线桥
弯 立 交 桥
曲线桥
弯 立 交 桥
曲线桥
由于曲率的影响,梁截面在发生竖向弯 受 曲时,必然产生扭转,而这种扭转作用又 力 将导致梁的挠曲变形,称之为“弯—扭” 特 耦合作用 点
徐变的发展规律是先快后慢,通常在 最初六个月内可完成最终徐变量的70-80%, 第一年内可完成90%左右,其余部分在以后 几年内逐步完成,经过2-5年徐变基本结束。
薄壁箱梁的扭转和畸变理论

薄壁箱梁的设计原则和流程
总结词
薄壁箱梁的设计应遵循结构安全、经济合理、施工方 便等原则,设计流程包括初步设计、详细设计和施工 图设计等阶段。
详细描述
在薄壁箱梁的设计过程中,应充分考虑结构的安全性、 稳定性和耐久性,确保结构在承受各种载荷和气候条件 下的性能表现。同时,设计时应注重经济合理性,优化 材料用量和结构尺寸,降低制造成本。此外,设计时应 考虑施工的方便性,合理安排施工顺序和工艺方法,提 高施工效率。设计流程一般包括初步设计、详细设计和 施工图设计等阶段,每个阶段都有相应的设计内容和要 求。
通过建立有限元模型,模拟薄壁箱梁的畸 变行为,考虑了材料的弹塑性和几何非线 性等因素。
能量平衡法
几何非线性理论
基于能量守恒原理,通过分析薄壁箱梁在 不同外力作用下的能量变化,推导出畸变 的计算公式。
采用大变形理论,考虑了薄壁箱梁在受力 过程中的大位移和转动,适用于分析复杂 受力状态下的畸变问题。
05 薄壁箱梁的扭转和畸变控 制
计算结果分析
根据计算结果,可以对薄壁箱梁的扭转效应进行分析和评估。如果发现存在较大的扭转响 应,应采取相应的措施进行优化和加固,以提高桥梁的安全性和稳定性。
Hale Waihona Puke 04 薄壁箱梁的畸变理论畸变的定义和特性
畸变定义
畸变是指薄壁箱梁在受到外力作用后,其截 面形状和尺寸发生改变的现象。
畸变特性
畸变具有非线性、时变性和空间性等特点, 与箱梁的几何形状、材料属性、外力大小和 作用方式等因素密切相关。
薄壁箱梁的扭转计算方法
计算方法
薄壁箱梁的扭转计算方法主要包括有限元法和解析法。有限元法是通过将梁体离散化为有 限个单元,然后对每个单元进行受力分析,最后汇总得到整体的受力情况。解析法则是通 过数学公式推导,直接求解出梁体的扭转响应。
单箱三室箱梁在正对称荷载作用下局部畸变效应的理论研究

单箱三室箱梁在正对称荷载作用下局部畸变效应的理论研究单箱三室箱梁在正对称荷载作用下局部畸变效应的理论研究摘要:箱梁是一种常见的结构构件,具有承受大荷载的能力,而在工程实践中往往需要研究箱梁在不同荷载作用下的变形和破坏情况。
本文以单箱三室箱梁为研究对象,对其在正对称荷载作用下的局部畸变效应展开了理论研究。
通过有限元数值模拟,分析了箱梁中不同截面位置的应力和变形情况,并通过力学理论进行解释。
研究结果表明,正对称荷载作用下,单箱三室箱梁会出现局部畸变效应,即局部应力集中、变形增大,从而影响其整体性能和承载能力。
关键词:单箱三室箱梁;正对称荷载;局部畸变效应;有限元模拟;力学理论1. 引言箱梁是一种常见的结构构件,由于其在承受大荷载下具有较好的稳定性和刚度,因此在桥梁、建筑、航空航天等领域得到了广泛应用。
然而,在工程实践中,箱梁承受正对称荷载时,由于结构的不均匀性和材料特性的差异,往往会引起局部畸变效应,即局部应力集中、变形增大。
2. 研究方法本文采用有限元数值模拟的方法,对单箱三室箱梁在正对称荷载作用下的局部畸变效应进行研究。
首先,根据实际工程中常见的箱梁尺寸和材料参数,建立了单箱三室箱梁的有限元模型。
然后,通过施加正对称荷载,分析了箱梁中不同截面位置的应力和变形情况。
最后,利用力学理论对结果进行解释和分析。
3. 结果与讨论通过有限元模拟分析,得到了单箱三室箱梁在正对称荷载作用下的应力和变形结果。
研究发现,正对称荷载作用下,单箱三室箱梁中的应力主要集中在中央截面,呈现出明显的局部应力集中现象。
同时,箱梁中心位置的变形较大,而两侧的变形相对较小。
这些结果表明,单箱三室箱梁在正对称荷载下会出现局部畸变效应,即局部应力集中和变形增大。
通过力学理论分析,可以解释单箱三室箱梁在正对称荷载作用下的局部畸变效应。
在正对称荷载作用下,箱梁中的应力分布不均匀,导致局部应力集中。
同时,由于材料的非均匀性以及结构的几何形状,箱梁中心位置的变形较大。
箱梁的畸变分析

高等桥梁结构理论
误差还是比较大。 畸变是在闭口薄壁杆件受到偏心荷载的时候产生的,薄壁杆件在偏心荷载作
用的时候,受力特性比较复杂,会产生纵向弯曲(图 1-a),扭转(图 1-b),畸 变(图 1-c)以及横向挠曲(图 1-d)四种基本变形。(如图 1 所示)
图1 另外能引起畸变的荷载主要有一下几种,竖直偏心荷载(图 2-a)、水平偏心 荷载(图 2-b)和在自重作用下由于支点倾侧(所谓三条腿)(图 2-c)产生的扭 矩等荷载。
的曲线,所以此处一阶导数为 0) Q = − (由于此处研究的是a1sinθP4 = 1的
8
高等桥梁结构理论
情况,所以跨中处的剪力为− ),M =
。将初参数和 x=0 代入(3-11)和(3-12)
以及转角和剪力表达式,列出一个以 Bi 为未知数的方程组。 解得:源自1 =2 == 1
− 4 +
(3-13)
3.1 两种物理模型之间的比拟关系
弹性地基梁
常截面畸变
A.控制微分方程 EIby,,,,+Ky=q B.相似物理量
EJAγ2,,,,+ EJBγ2=a1sinθP4
Ib—弹性地基梁惯矩(m4)
JA—箱梁畸变翘曲惯矩(m6)
EIb—弹性地基梁抗弯刚度(kn·m2) EJA—箱梁畸变翘曲刚度(kn·m4)
53.72 × ( × 10 ) + 17.717 × 17.717 × ( × 10 ) − 3.605
解得:
+ 166.121 = 0 + 5.131 = 0
= 0.68 × 10
= 2.628 N ∙ m
代回式(3-14)和(3-15)
y( ) = 0.68 × 10 ∙ [
第四章 畸变

−λs x
y
P
x
P 2
y
x
当 x →∞ 时,可认为在离 无限远的点上,挠度及曲率为零,只 可认为在离P无限远的点上 挠度及曲率为零, 无限远的点上, 和,可由 有在( ) 等于零时, 有在(a)式中的系数 C2 和 C1 等于零时,于是右边这段梁的挠 度曲线方程变成: 度曲线方程变成:
y = e−λs x (C3 cosλs x + C4 sin λs x)
箱形梁的畸变角(弧度) 箱形梁的畸变角(弧度) BDω 箱形梁的畸变双力矩
I EI
k q
弹性地基梁抗弯惯矩( 弹性地基梁抗弯惯矩( m4 ) 2 弹性地基梁抗弯刚度( 弹性地基梁抗弯刚度( kN⋅ m ) 弹性地基梁地基弹性系数( 弹性地基梁地基弹性系数( kN m ) 弹性地基梁的分布荷载( 弹性地基梁的分布荷载( kN m )
ˆ EI : 箱梁畸变翘曲刚度 b : 箱梁底板宽 计算公式见 P92 4-2 表 EIR : 箱梁框架刚度 Vd : 畸变荷载
ˆ EIγ (4) + EI Rγ = Vd ⋅ b
(4 − 40)
将上式写成: 将上式写成:
A
D
d2 ˆ (EIγ ′′) + EI Rγ = Vd ⋅ b dz 2 ˆ 引进: 引进: BDω = −EIγ ′′ 畸变双力矩
根据相似关系对比
Vd ⋅ b ˆ y =γ EI = EI γ + 4λ γ = (4 − 44) k = EIR ˆ EI q =Vd ⋅ b BDω = M λs = λ q (4) 4 y + 4λs y = (4 − 45) EI 则无限长梁( 当跨中截面作用单位畸变荷载( 则无限长梁(λL ≥ 4 时,当跨中截面作用单位畸变荷载(P = 1 ) ), 4 EIR ⇒ k = λs ⋅ 4EI )得: 利用上式( 利用上式( Vd ⋅ b λ γ= [e−λx (cos λx + sin λx)]
等截面梯形箱梁畸变效应分析计算

等截面梯形箱梁畸变效应分析计算摘要:本文通过对箱梁畸变理论的学习,分析了畸变计算方法,提出了等截面梯形简支箱梁畸变效应的计算步骤,采用MATLAB实现了弹性地基梁比拟法的程序设计,并结合实例进行了计算。
关键词:箱梁畸变;MATLAB;荷载分解;1 引言随着城市现代化进一步加快,大量薄壁钢箱梁已经在城市立交以及轨道交通建设过程中被广泛采用,尤其在城市立交、跨线桥梁的建设过程中,考虑到桥梁下部道路通车需要以及桥墩布置合理性,此时抗弯刚度和抗扭刚度大,安装养护方便、轻巧美观的薄壁钢箱梁往往成为首选。
与混凝土箱梁结构类似,薄壁钢箱梁在竖向偏心荷载作用下,箱梁既产生弯曲又产生扭转,为了防止薄壁钢箱梁在偏心荷载作用下产生伴随刚性约束扭转的畸变现象,在设计过程中,往往是在薄壁钢箱梁内部设置若干道横隔板来减小箱梁的畸变效应。
2 分析计算理论根据箱梁的受力特点,当箱梁在偏心荷载作用下,将产生对称弯曲、刚性扭转、畸变、横向弯曲四种最常见的受力状态,对于每种不同的受力状态,钢箱梁将产生不同的正应力以及剪应力,尤其是当薄壁钢箱梁在偏心荷载作用下产生刚性扭转并伴随发生畸变效应时,由于箱梁矩形截面受扭变形,截面投影以无法保证为矩形截面,箱梁将产生畸变角γ、翘曲正应力σw 以及畸变剪应力τw。
由于薄壁钢箱梁在结构构件类型中属于薄壁杆件,通过大量设计研究以及工程实践,表明此类箱形薄壁杆件的畸变效应对箱梁的扭转变形的影响是无法忽略的,对于考虑畸变效应的薄壁钢梁,在对其进行分析时,目前常用的一种方法是荷载分解法,即将作用于箱梁顶面任意位置的竖向荷载分解为相对于箱梁中心线对称或者反对称的竖向荷载,如图所示。
其中畸变荷载为P1 、P2 、P3、P4。
在此基础上,做出以下几点假设条件:①忽略薄壁钢箱梁各板面的法向正应变;②忽略各板平面内的剪切应变;③板面内的翘曲正应变沿板的厚度方向分布为一常数值,并沿箱梁截面中线方向呈直线分布,由此根据最小势能原理建立畸变角γ(Z)畸变微分方程:EI11γ(2)+EIR= Vdb式中γ(Z) ——截面畸变角;EI11 ——箱梁抵畸变的翘曲刚度;EIR——箱梁抗畸变的框架刚度;Vd ——畸变荷载的垂直分量。
波纹钢腹板曲线箱梁畸变分析

波纹钢腹板曲线箱梁畸变分析波纹钢腹板曲线箱梁具有自重轻、抗震性能好、腹板无裂缝、预应力利用效率高等优点,在城市立交、匝道逐步应用和推广[1-4]。
然而,波纹钢腹板由于纵向弹性模量较小,相比混凝土腹板箱梁更容易发生纵向翘曲变形和畸变翘曲应力,而且畸变正应力相比弯曲正应力达到不可忽略的比例[5-7];其次曲线箱梁具有弯扭耦合特性,无论是在恒载还是偏载作用下,均产生畸变翘曲应力。
因此准确计算波纹钢腹板曲线箱梁在各荷载工况下的畸变正应力具有十分重要的意义。
文献[8]针对混凝土直线箱梁进行了畸变分析理论的研究,明确了畸变中心的定义,确定了畸变位移模式,剪力了考虑剪切效应的畸变分析理论,结果表明剪切变形对畸变翘曲应力和横向弯曲应力的影响较小。
文献[7]在考虑波纹钢腹板正交异性的特点的基础上,推导了波纹钢腹板直线组合箱梁畸变控制微分方程及求解方法。
文献[9]采用节点具有9个自由度的曲线箱梁单元,包括两个畸变自由度,通过有限元准确计算箱梁畸变正应力和横向弯曲正应力。
本文在薄壁曲线箱梁的基础上[10],考虑波纹钢腹板正交应力以及曲线箱梁弯扭耦合特点,忽略剪切变形的影响,推导了波纹钢腹板曲线箱梁畸变控制微分方程,并采用弹性梁法进行求解。
1波纹钢腹板曲线箱梁畸变分析1.1基本假定波纹钢腹板曲线箱梁畸变分析时采用以下几个假定:(1)组成箱梁的各板元沿自身平面内满足平截面假定,可用初等梁理论计算弯曲应力。
(2)箱壁很薄可不考虑应力沿壁厚方向的变化,即认为翘曲正应力和翘曲剪应力沿壁厚均匀分布。
(3)忽略各板元平面的法向应变及各板元平面内的剪切变形。
1.2波纹钢腹板特性波形钢腹板示意图如图1所示,虽然曲线波形钢腹板平板段与斜板段之间的夹角α是变化的,但是由于波段长度l与曲线箱梁半径R相比很小,可以近简化为直线波形钢腹板进行研究。
波形钢腹板纵向弹性模量Ex与波高h、板厚t及波形钢腹板形状系数ζ有关,其纵向弹性模量表达式为(1)式中Es是钢材的弹性模量,由于h一般是t的几十倍以上,因此波形钢腹板的轴向弹性一般很小,可不考虑波形钢腹板在结构中的抗弯性能或者抗翘曲性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P 表示几个车轮的合力,作用在横桥方向的偏心距为 e
h
b
局部分析
P v 2
P 0 v b Pv Pv b Pv Pv b Pv b [ b h] [ b h] 2 2h 2 2h 畸变荷载是由水平分力和垂直分力组成,是一组自相平衡的力系, 由于各力作用在不同的部件上而导致畸变变形,因而由畸变变形产 生的内力也是自相平衡的。
ˆ (kN m2 ) BD EI
根据相似关系对比
Vd b ˆ y EI EI 4 (4 44) k EI R ˆ EI q Vd b BD M s q ( 4) 4 y 4s y (4 45) EI 则无限长梁(L 4)时,当跨中截面作用单位畸变荷载(P 1 ), 4 EI k 利用上式( R s 4 EI )得: Vd b x [ e (cos x sin x)]
m AD (或mBC) 则: (W为箱壁板的截面模 dt W 量)
m : 框架参数,见表4-2
现在关键是未知参数畸变角的求解,有了畸变角 双力矩 BD ,进而求出畸变应力。
即可求出畸变
二、用弹性地基梁比拟法求畸变微分方程
箱梁在畸变荷载 Vd 的作用下, 由式(4-40)可得畸变微分方程: V b Pv ( 4 ) 44 d ( 4 44) Vd ˆ EI 2 Hd EI R 4 ˆ 4 EI Pv b H d 这与受竖向荷载的弹性地基梁的微分 2h 方程有相似形式,弹性地基梁的弹性 Vd 微分方程为: 其中: q y ( 4 ) 44 ( 4 45) k : 地基系数 sy EI EI : 梁的竖向抗弯刚度 k 4 q : 竖向荷载 s 4 EI q ( x) q ( x)
箱形梁的畸变
前面假定箱梁在扭转时截面周边保持不变形,扭转就如刚体转 动,根据截面几何性质和边界条件又可分为自由扭转和约束扭转。 这在箱壁较厚或横隔板较密时,这个假设是接近实际情况,在设计 中就不必考虑扭转变形(既畸变)所引起的应力状态。但高强度混 凝土在桥跨结构中的应用以及预应力技术的普及与发展,使得薄壁 箱梁结构得到推广。由于设计和施工技术上的要求,希望在桥跨上 部箱梁间少设或不设横隔梁,因此,截面就不满足周边不变形的假 设,则在反对称荷载作用下,截面不但扭转而且要发生畸变,从而 产生畸变翘曲正应力 d 和剪应力 d ,箱壁上也将引起横向弯曲 正应力 dt 。
( 4) 4
1 x [e (cos x sin x)] BD 4 BD 1 x QD 2 e cos x 根据内力与变形的互等定理知,该曲线就是荷载作用点截面(如跨 中截面)的畸变角和畸变双力矩影响线(力作用跨中在整个梁引起 的 、BD 等于力作用其他作用点时引起跨中 、BD )
本章参考文献 • [1]郭金琼.箱形梁设计理论.北京:人民交通 出版社.1991. • [2]杜国华等.桥梁结构分析.上海:同济大学 出版社,1997. • [3]C.P.汉斯.薄壁杆中的弯曲与扭转.北京 :人民交通出版社,1980. • [4]张士铎.变高度梯形单室箱梁畸变计算 .土 木工程学报,Vol.20,No.4,1987.
1. 计算截面各项几何特征和参数 2. 根据常见支座的边界条件,确定畸变微分方程的通解中的系数, 为了工程方便书中给出了常见几种梁畸变角和畸变双力矩影响线 计算公式和图表;对无限长梁( L 4)直接利用公式绘出畸变 角和畸变双力矩影响线。 3. 在影响线上布置畸变荷载; 。 4. 求相应截面的畸变角和畸变双力矩 5. 计算A点、B点畸变翘曲应力
P v b 刚性扭转 2h
P v + 2
Pv 2
P v 2
Pv b 畸变 2h
图所示的水平向偏心荷载 P ,设其与截面扭转中心的距 离为 d ,则按力学原理。扭矩 Pd 可用角点反对称荷载 d PH P h 来代替。经分解后得到刚性扭转荷载和畸变荷载为
水 平 荷 载 的 分 解
PH h Vd 2 2b PH Hd2 Vd 2 2
W
QD
I t dBD ˆ 畸变力(剪力) EI dz
(单宽t 1)
d
Iˆ
S D
QD S D d ˆ I ˆ S ˆ d S ˆ
A
D
S ˆ
ˆ dF
B
C
横向弯曲力矩为:
EI R m AD 2(1 ) m m EI R m BC 2(1 m )
x
x
存在所列相似关系,求箱梁畸变问题转化为求弹性地基梁问题
弹性地基梁 箱形梁
微分方程
EIy ( 4) ky q
相似的物理量
ˆ ( 4) EI V b EI R d
6 箱形梁抗畸变翘曲惯矩( ) m ˆ I 4 ˆ kN m 箱形梁抗畸变翘曲刚度( ) EI 2 I R 箱形梁抗畸变框架惯矩( m ) EI R 箱形梁抗畸变框架刚度( kN ) Vd b 箱形梁上分布的畸变垂直分力的力 偶( kN m m )
ˆ : 箱梁畸变翘曲刚度 b : 箱梁底板宽 EI 计算公式见 P92表4-2 EI R : 箱梁框架刚度 Vd : 畸变荷载
ˆ ( 4) EI V b EI R d
(4 40)
将上式写成:
A
D
d2 ˆ ) EI V b ( E I R d dz 2 ˆ 畸变双力矩 引进: BD EI
I EI
k q
弹性地基梁抗弯惯矩( m 4 ) 2 弹性地基梁抗弯刚度( kN m )
弹性地基梁地基弹性系数( kN m ) 弹性地基梁的分布荷载( kN m ) 弹性地基梁的挠度( 弹性地基梁的弯矩
2
y M
m)
M EIy(kN m)
BD
箱形梁的畸变角(弧度) 箱形梁的畸变双力矩
b h
(2) 斜腹板箱梁
如图所示的斜腹板箱梁上承受反对称角点荷载,经分解后也可得 到刚性扭转荷载和畸变荷载。 在假定剪应力沿板厚均匀分布下,箱梁中剪力流为
斜腹板箱梁竖向反对称载的分解
刚性扭转荷载:
畸变荷载:
h0 2. 畸变变形 横向:组成箱梁各板元产生了箱梁 v 截面内的位移 v、h 畸变横向挠曲 箱梁横向框架刚度 纵向:由于横向挠曲而产生了相应的 v h 与梁轴线平行(垂直截面)的翘曲位移 u 畸变翘曲 箱梁翘曲刚度 假定: 1. 组成箱梁的各板沿自身平面挠曲满足平截面假设,可用初等梁理 论计算; 2. 箱壁很薄可不考虑应力沿壁厚方向的变化,既认为翘曲正应力和 剪应力沿壁厚均匀分布。 如选择箱梁截面畸变角 做为变形参数,由力学中三大关系(物 理关系、几何关系、平衡关系),得到畸变微分方程(推导略) :
B
C
畸变产生的翘曲变形和约束扭转产生的翘曲变形是一样的,由此: 畸变产生的翘曲正应力,由约束扭转翘曲率求正应力公式(3-30) 类比得: ˆ B BD w d 、 ˆ I I
ˆ 畸变翘曲率,表示畸变翘曲时,截面纵向位移参数,A、B两 为 ˆ A、 ˆ B 表示, 计算公式见P92表4-2,代入得式(4-42)和 点最大用 式(4-43)。 畸变产生的翘曲剪应力,由约束扭转翘曲率求剪应力公式(3-37) 类比得: M S QD S D
计算横向弯矩 m AD , mBC ,继而计算顶 板、底板和腹板的横向弯曲应力。 畸变翘曲剪应力 d 一般很小,可以 不计。
A
D
B
C
D
Dt
D
小结
本章介绍了 (1)偏心荷载作用下薄壁箱形梁的畸变计算理论, 分别用 (2)静力平衡法推导了单箱单室直腹板等截面箱形梁的 畸变微分方程,用 (3)能量变分原理推导了斜腹板箱形梁的畸变微分方程, 为求符号统一起见。所定义的畸变角 D虽不在同一角 上。但采用了同一符号。 由结果可见,无论直、斜腹板箱形梁,其畸变微分方 程具有相似的表达形式。对微分方程的求解,虽然都可采 用弹性地基梁比拟法,但此法求解变截面梁时全遇到计算 上的困难,建议采用加权残值法求解。 另外,分析变截面梁的畸变效应还可以采用等代梁法, 这方面内容可参考有关文献
一、畸变微分方程的建立
1. 畸变荷载的分解 垂直偏载 水平偏载 任何偏心荷载可分解为对称和反对称荷载 支点侧倾(三条腿)
P e
h
b (a)
=
P
ห้องสมุดไป่ตู้
2 Pe Pv b
+
P v
(b)
纵向弯曲
(c )
一般扭转
,则可 分解为(b)、(c),为作用在肋上的集中荷载,(c)式又通过 Pv b P b 局部分析分解为下图: 2h 2h Pv Pv
2 EI R
x
对有限长梁(L 4 )时,利用边界条件,重新确定畸变微分方程 通解的四个积分常数,其结果书中以表的形式给出,根据所求截面 位置坐标参数 u l 2 和荷载作用位置坐标参数 c l,查表418~表4-22得到不同约束情况下 、 值,再根据图4-16所列公式 计算出 、BD 。 计算步骤:
