华中师大一附中2018年自主招生考试数学试题(word版附答案)

合集下载

华中师大一附中2018年高一新生入学摸底测试数学卷(无答案)

华中师大一附中2018年高一新生入学摸底测试数学试题满分：150分限时：120分钟命题人：黄松生第I 卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填在答题卡上. 1.在同一直角坐标系内，如果正比例函数y=mx 与反比例函数y=xp的图象没有交点，那么m 与p 的关系一定是A ．m<0,p >0 B.m>0,p >0 C.m p <0 D.m p >02．在半径为5cm 的圆中，弦AB ∥CD ，AB=6cm,CD=8cm ，则AB 和CD 的距离是 A ．7cm B.1cm C.5cm D.7cm 或1cm 3．若点P(-1-2a,2a-4)关于原点对称的点在第一象限内，则a 的整数解有 A ．1个 B.2个 C.3个 D.4个4．已知两圆半径分别为R 和r(R>r)，圆心距为d ，且d 2+R 2-r 2=2dR ，那么两圆位置关系为 A ．外切 B.内切 C.外离 D.外切或内切 5．已知x 为实数，化简xx x 13---的结果为 A ．x x --)1( B ．x x ---)1(C ．x x --)1(D ．x x -+)1(6．已知关于x 的方程2x 2+x+m+41=0有两个不相等的负实根，则m 的取值范围是A ．m 〈81-B.8141〈-〈-mC.81-〉mD.181〈〈-m7．若α为直角三角形的一个锐角，则2)cos sin 1(αα--等于A ．1–sin α–cos α B.1+sin α+cos α C.0 D.sin α+cos α-18．已知点（-2,y 1)、(-531,y 2)、(151,y 3）在函数y=2x 2+8x+7的图象上，则y 1、y 2、y 3的大小关系是A ．y 1>y 2>y 3 B.y 2>y 1>y 3 C.y 2>y 3>y 1D.y 3>y 2>y 19.已知sin α·cos α=81,且0°<α<45°，则cos α-sin α的值为 A ．23B.23-C.43D.43-10.在直角坐标系中，已知点A(-2,0),B(0,4),C(0,3),过点C 作直线交x 轴于点D ，使得以D 、O 、C 为顶点的三角形与△AOB 相似，这样的直线至多可以作A ．2条 B.3条 C.4条 D.6条 11.如图所示，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OB 上一点，以OA 为直径的半圆O 1和以BC 为直径的半圆O 2相切于D ，则图中阴影部分的面积为A ．6π B.10π C.12π D.20π12．已知一元二次方程ax 2+bx+c=0的两根之和为p ，两根平方和为q ，两根立方和为r ，则ar+bq+cp 的值是Ａ.-1 B.0 C.1 D.2第Ｉ卷答题卡第II 卷（非选择题，共90分）二、填空题:本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 13.如图，AB 为⊙O 的直径，CD 是⊙O 的弦， AB 、CD 的延长线交于E 点，已知AB=2DE ， ∠E=18°，则∠AOC 的度数为__________.14.如图，已知AB 是⊙O 的直径，BC 是和⊙O 相切于B 的切线，⊙O 的弦AD 平行于OC ，若OA=2且AD+OC=6，则CD=___________.15.若规定两数a,b 通过运算得4ab ，即a*b=4ab ，若x*x+2*x-2*4=0，则x=__________. 16．某县位于沙漠边缘地带，治理沙漠，绿化家乡是全县人民的共同愿望.到2015年底，全县沙漠的绿化率已达30%，此后，政府计划在近几年内，每年将当年年初未被绿化的沙漠面积的m%栽上树进行绿化，到2017年底，全县的沙漠绿化率已达到43.3%，则m 的值等于_____________.三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.17．（本小题满分12分）如图，已知AB 是⊙O 的直径，P 是AB 延长线上一点，PC 切⊙O 于C ，AD ⊥PC 于D ，CE ⊥AB 于E ，求证：（1）AD=AE（2）PC ·CE=PA ·BE18．（本小题满分12分）已知b a ,（a>b>0)是方程x 2-5x+2=0的两个实根，求2)5(5)()22(+-++-÷--+b a a bb a a b a b a b b a a 的值.19. （本小题满分12分）如图，△ABC 中，AB=5，BC=6，BD=31BC ，AD ⊥BC 于D ，E 为AB 延长线上的一点，且EC 交AD 的延长线于F.(1)设BE 为x ，DF 为y ，试用x 的式子表示y. (2)当∠ACE=90°时，求此时x 的值.20. （本小题满分12分）通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成.以前我市通过“武汉热线”上“因特网”的费用为电话费0.18元/3分钟，上网费为7.2元/小时，后根据信息产业部调整“因特网”资费的要求，自2017年3月1日起，我市上”因特网“的费用调整为电话费0.22元/3分钟.上网费为每月不超过60小时，按4元/小时计算；超过60小时部分，按8元/小时计算.(1)根据调整后的规定，将每月上“因特网”的费用y （元）表示为上网时间x （小时）的函数；（2）资费调整前，网民聪聪在其家庭经济预算中，一直有一笔每月70小时的上网费用支出.“因特网”资费调整后，聪聪要想不超过其家庭经济预算中的上网费用支出，他现在每月至多可上网多少小时？（3）从资费调整前后的角度分析，比较我市网民上网费用的支出情况.21. （本小题满分12分）在直角坐标系xoy 中，一次函数3223-=x y 的图像与x 轴、y 轴分别交于点B 和点A ，点C 的坐标是（0，1），点D 在y 轴上且满足∠BCD=∠ABD.求D 点的坐标.22. （本小题满分14分）如图，抛物线y=ax2+bx+c与x轴交于A、B两点（点A在点B 左侧），与y轴交于点C，且当x=0和x=2时，y的值相等.直线y=3x-7与这条抛物线相交于两点，其中一点的横坐标是4，另一点是这条抛物线的顶点M.（1）求这条抛物线的解析式；（2）P为线段BM上一点，过点P向x轴引垂线，垂足为Q.若点P在线段BM上运动（点P不与点B、M重合），设OQ的长为t，四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围；（3）在线段BM上是否存在点N，使△NMC是等腰三角形？若存在，请求出点N的坐标；若不存在，请说明理由.。

湖北省华中师范大学第一附属中学2018-2019学年高二上学期期末考试数学(文)试题Word版含解析

华中师大一附中2018—2019学年度上学期期末考试高二年级数学（文科）试题一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1. 用秦九韶算法求多项式当弋--1时的值，有如下说法：①要用到6次乘法；②要用到6次加法和15次乘法；③v 3= 12 :④vo= 11.其中说法正确的是A. ①③B. ①④C. ②④D. ①③④【答案】A【解析】【分析】根据秦九韶算法求多项式的规则变化其形式，把ii.c： . ?：:>' '■等到价转化为■；-；- n 十:- … ?；..<十Q-- 号十「，就能求出结果.【详解】解：■•- ../：| .:八 X : J：!：!<..::辱-I,' ■ !.< .■.：■：./ .:需做加法与乘法的次数都是6次，,Vj = v^x -i 眄=2 x （ - ］）i 3 = 3,•I = ■■■■ ■::=：■ - （- l；；:' =--,Vj = VjX + 合厂- 3x（- ［）+ 9= 12,■-的值为12;其中正确的是①④故选：A.【点睛】本题考查算法的多样性，正确理解秦九韶算法求多项式的原理是解题的关键，属于基础题.2. 把［0 , 1］内的均匀随机数x分别转化为［0 , 2］和〔”「内的均匀随机数y1, y，需实施的变换分别为（）A. ■ = - ■■-B. ：\ =•",,*=、7- -C. p.i汀，:D. ,【答案】C【解析】【分析】先看区间长度之间的关系：故可设或•,再用区间中点之间的对应关系得到，解出kJ、，问题得以解决.【详解】解：将［0,1］内的随机数x转化为［0,2］内的均匀随机数，区间长度变为原来的2倍, 因此设=2x+ （是常数），再用两个区间中点的对应值，得当•.=.时，=1,一所以' 11\ ,可得=0,因此x与的关系为：=2x;将［0,1］内的随机数x转化为［-2,1］内的均匀随机数，区间长度变为原来的2倍，因此设」；=3x+k：、（锋是常数）,再用两个区间中点的对应值，得当时，=,所以-可得，因此x与的关系为：=3x-2 ;故选C.【点睛】本题考查均匀随机数的含义与应用，属于基础题•解决本题解题的关键是理解均匀随机数的定义，以及两个均匀随机数之间的线性关系.3. 抛物线y = 的准线方程是•，贝U的值为（）I 1A. B. —C. 8 D. -88 8【答案】B【解析】乍一7 V ,'方程"=表示的是抛物线，* ，…，二抛物线"=的准线方程是a 2a］1节=....=二，解得“ “故选A.4. 执行如图所示的程序框图，若输出n的值为9，则判断框中可填入（）【答案】D 【解析】【分析】执行程序框图，根据输出，可计算的值，由此得出判断框中应填入的条件.【详解】解：执行程序框图，可得该程序运行后是计算满足条件后，输出，由此得出判断框中的横线上可以填入■ ■ ■?.故选：D.【点睛】本题主要考查了程序框图的应用问题，正确判断退出循环的条件是解题的关键，属于基础题.5•将二进制数110 101（2）转化为十进制数为（）A. 106B. 53C. 55D. 108【答案】B 【解析】由题意可得 110101（2）=1 x 25+1 x 24+0 x 23+1 x 22+0 x 21+1 X 2°=53.选 B 。

湖北省武汉市华中师范大学第一附属中学2018-2019学年高二下学期期中考试数学(理)试题附答案

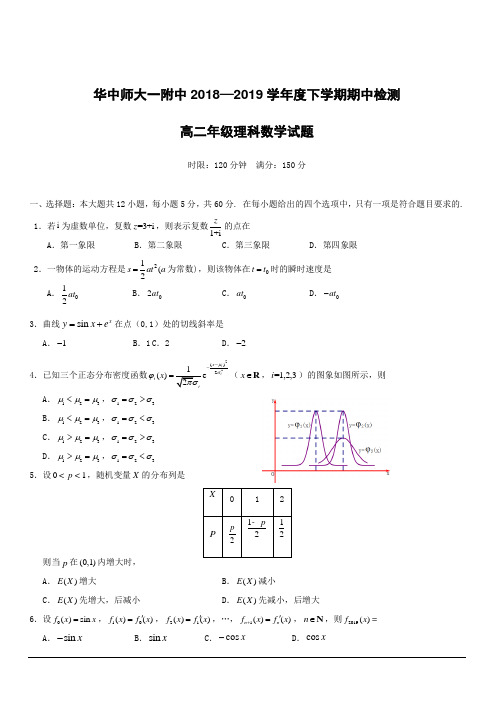
华中师大一附中2018—2019学年度下学期期中检测高二年级理科数学试题时限：120分钟满分：150分一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．若i 为虚数单位，复数=3+i z ，则表示复数1+iz的点在 A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．一物体的运动方程是21(2s at a =为常数)，则该物体在0t t =时的瞬时速度是A ．012at B ．02at C ．0at D ．0at -3．曲线sin =+xy x e 在点（0,1）处的切线斜率是 A ．1- B ．1 C ．2 D ．2-4．已知三个正态分布密度函数22()2()i i x i x μσϕ--=（x ∈R ，=1,2,3i ）的图象如图所示，则A ．123μμμ<=，123σσσ=>B ．123μμμ<=，123σσσ=<C ．123μμμ>=，123σσσ=>D ．123μμμ>=，123σσσ=< 5．设01p <<，随机变量X 的分布列是则当p 在(0,1)内增大时， A ．()E X 增大B ．()E X 减小C ．()E X 先增大，后减小D ．()E X 先减小，后增大6．设0()sin f x x =，10()()f x f x '=，21()()f x f x '=，…，1()()n n f x f x +'=，n ∈N ，则2019()f x = A ．sin x -B ．sin xC ．cos x -D ．cos x7．一次考试中，某班级数学成绩不及格的学生占20％，数学成绩和物理成绩都不及格的学生占 15％，已知该班某学生数学成绩不及格，则该生物理成绩也不及格的概率为 A ．0.15B ．0.2C ．0.3D ．0.758．设函数()f x 在定义域内可导，()y f x =的图象如图所示，则导函数()f x '的图象可能是A B C D9．分别抛掷2枚质地均匀的硬币，设“第1枚为正面”为事件A ，“第2枚为正面”为事件B ，“2枚结果相同”为事件C ，有下列三个命题： ①事件A 与事件B 相互独立； ②事件B 与事件C 相互独立； ③事件C 与事件A 相互独立．以上命题中，正确的个数是 A ．0B ．1C ．2D ．310．若130()3()d f x x f x x =+⎰，则10()d f x x =⎰A ．1-B ．13-C ．14-D ．18-11．已知函数32()31f x ax x =-+，若()f x 存在唯一的零点0x ，且00x <，则a 的取值范围是A ．(2,)+∞B ．(1,)+∞C ．(,2)-∞-D ．(,1)-∞-12．若函数()f x 满足2()2()e x xf x f x x '-=，2(2)2e f =-，则当0x >时，()f xA ．有极大值，无极小值B ．有极小值，无极大值C ．既有极大值又有极小值D ．既无极大值又无极小值二、填空题：本大题共4小题，每小题5分，共20分. 13．设复数z 满足1i 1zz+=-，则||z = . 14．如图，CDEF 是以O 为圆心，半径为1的圆的内接正方形，点H 是劣弧EF 的中点，将一颗豆子随机地扔到圆O 内，用A 表示事件“豆子落在扇形OCFH 内”，B 表示事件“豆子落在正方形CDEF 内”，则(|)P B A = .15．某一部件由四个电子元件按如图方式连接而成，元件1或元件2正常工作，且元件3或元件4正常工作，则部件正常工作.设四个电子元件的使用寿命（单位：小时）均服从正态分布)50,1000(2N ，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为 .16．传说中孙悟空的“如意金箍棒”是由“定海神针”变形得来的.定海神针在变形时永远保持为圆柱体，其底面半径原为12cm 且以每秒1cm 的等速率缩短，而长度以每秒20cm 的等速率增长.已知神针之底面半径只能从12cm 缩到4cm 为止，且知在这段变形过程中，当底面半径为10cm 时其体积最大.假设孙悟空将神针体积最小时定形成金箍棒，则此时金箍棒的底面半径为 cm .三、解答题：本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤. 17．（10分）已知1i z =+，a ，b 为实数．（1）若234z z ω=+-，求||ω；（2）若221i 1z az b z z ++=--+，求a ，b 的值．18．（12分）袋中有20个大小相同的球，其中标号为0的有10个，标号为n 的有n 个（n =1,2,3,4）.现从袋中任取一球，X 表示所取球的标号.求X 的分布列、数学期望和方差.19．（12分）已知221()(ln )x f x a x x x -=-+，a ∈R ．求()f x 的单调增区间.20．（12分）Monte-Carlo 方法在解决数学问题中有广泛的应用．下面利用Monte-Carlo 方法来估算定积分140d x x ⎰．考虑到140d x x ⎰等于由曲线4y x =，x 轴，直线1x =所围成的区域M 的面积，如图，在M 外作一个边长为1正方形OABC ．在正方形OABC 内随机投掷n 个点，若n 个点中有m 个点落入M 中，则M 的面积的估计值为mn，此即为定积分140d x x ⎰的估计值．现向正方形OABC 中随机投掷10000个点，以X 表示落入M 中的点的数目．（1）求X 的期望()E X 和方差()D X ；（2）求用以上方法估算定积分140d x x ⎰时，140d x x ⎰的估计值与实际值之差在区间（-0.01，0.01）的概率．21．（12分）已知函数2()ln(1)(0)(0)2f x x f x f x '=+--+.（1）求)(x f 的解析式；（2）若2()f x x ax b ≤++，求32b a -+的最小值． 22．（12分）已知函数2()e ln x f x ax b x =+，曲线()y f x =在(1,(1))f 处的切线方程为(3e 1)(1)e y x =--+.（e 2.71828=为21.649,e7.389≈，e0.495≈1.640，e-0.703≈0.495）（1）求a，b的值；（2）证明：11 ()10f x>.华中师大一附中2018—2019学年度下学期期中检测高二理科数学参考答案一、选择题：本大题共12小题，每小题5分，共60分.1－5.DCCBB6－10.CDADD11－12.AB二、填空题：本大题共4小题，每小题5分，共20分.13．114．2π15.91616.4三、解答题：本大题共6小题，共70分.17．(1)2(1i)3(1i)41i ω=++--=--，所以||ω=………………………………………………………5分 (2)由条件，得()(2)i1i ia b a +++=-，所以()(2)i 1i a b a +++=+所以121a b a +=⎧⎨+=⎩，解得12a b =-⎧⎨=⎩……………………………………………………………………………5分18．X 的分布列为……………………………………………………………………………………………………………………4分 ∴11131()01234 1.522010205E x =⨯+⨯+⨯+⨯+⨯=……………………………………………………4分∴2222211131()(0 1.5)(1 1.5)(2 1.5)(3 1.5)(4 1.5)22010205D x =-⨯+-⨯+-⨯+-⨯+-⨯ 2.75=……………………………………………………………………………………………………………………4分19．()f x 的定义域为(0,)+∞，223322(2)(1)'()a ax x f x a x x x x--=--+=…………………………………2分当0a ≤时，若(0,1)x ∈，则'()0f x >，()f x 单调递增…………………………………………………2分当0a >时，3(1)'()a x f x x x x ⎛-=-+ ⎝(i)当02a <<1>当(0,1)x ∈或x ⎫∈+∞⎪⎪⎭时，'()0f x >，()f x 单调递增………………………………………2分 (ii)当2a =1=，在(0,)+∞上，'()0f x ≥，()f x 单调递增……………………………………2分 (iii)当2a >时，01<<当x ⎛∈ ⎝或(1,)x ∈+∞时，'()0f x >，()f x 单调递增………………………………………2分综上所述，当0a ≤时，()f x 在(0,1)上单调递增当02a <<时，()f x 在(0,1)，⎫+∞⎪⎪⎭上单调递增当2a =时，()f x 在(0,)+∞上单调递增当2a >时，()f x在x ⎛∈ ⎝，(1,)+∞上单调递增……………………………………………………2分20．(1)依题意，每个点落入M 中的概率为1400.2p x dx ==⎰，~(100000.2)X B ，所以()100000.22000E X =⨯=，()100000.20.81600D X =⨯⨯=……………………………6分 (2)依题意，所求概率为0.010.20.0110000X P ⎛⎫-<-< ⎪⎝⎭2099100001000019010.010.20.01(19002100)0.20.810000tt t t X P P X C -=⎛⎫-<-<=<<=⨯⨯ ⎪⎝⎭∑209919001000010000100001000000.20.80.20.80.99330.00620.9871tt ttt t t t CC --===⨯⨯-⨯⨯=-=∑∑………………………………………………………………………………………………………………………12分21．(1)由已知得(0)2f =，2()ln(1)(0)22f x x f x x '=+--+从而1()2(0)21f x f x x ''=--+，(0)1f '=- 于是2()ln(1)22f x x x x =++-+由于2121()2211x f x x x x -'=+-=++，故当(1,2x ∈--时，()0f x '>；当(22x ∈-时，()0f x '<；当)2x ∈+∞时，()0f x '> 从而()f x的单调增区间为(1,2--和)2+∞单调减区间为(,22-……………………………………………………………………………………6分 (2)由已知条件得ln(1)(2)2b x a x ≥+-++设()ln(1)(2)2g x x a x =+-++，则1()(2)1g x a x '=-++ ①若20a +≤，则()0g x '>，()g x 无最大值 ②若20a +>，则当1(1,1)2x a ∈--+时，()0g x '>；当1(1,)2x a ∈-+∞+时，()0g x '< 从而()g x 在1(1,1)2a --+上单调递增，在1(1,)2a -+∞+上单调递减故()g x 有最大值1(1)3ln(2)2g a a a -=+-++所以2()f x x ax b ≤++等价于3ln(2)b a a ≥+-+ 因此3ln(2)22b a a a a --+≥++ 设ln(2)()2a a h a a -+=+，则21ln(2)()(2)a h a a ++'=+当12,2ea ⎛⎫∈-- ⎪⎝⎭时，()0h a '<；当12,e a ⎛⎫∈-+∞⎪⎝⎭时，()0h a '> 所以()h a 在12,2e⎛⎫-- ⎪⎝⎭上单调递减，在12,e ⎛⎫-+∞ ⎪⎝⎭上单调递增故()h a 有最小值1(2)1e eh -=- 从而31e 2b a -≥-+ 当且仅当12,e 3ln(2),a b a a ⎧=-⎪⎨⎪=+-+⎩即12,e 12,e a b ⎧=-⎪⎪⎨⎪=+⎪⎩时，32b a -+的最小值为1e -……………………………………………………………………………………………………12分22.(1)函数()f x 的定义域为(0,)+∞，()2(1)e x b f x ax x x'=++由题意可得(1)e=e f a =,(1)3e 3e 1f a b '=+=-故1a =，1b =-………………………………………………………………………………………………4分 (2)解法一：由(1)知，2()e ln x f x x x =-，从而11()10f x >等价于152211ln e 10xx x x+>设函数12e ()x g x x=，则321()()e 2x g x x x -'=-所以当1(0,)2x Î时，()0g x '<；当1(,)2x ∈+∞时，()0g x '>故()g x 在1(0,)2单调递减，在1(,)2+∞单调递增，从而()g x 在(0,)+∞的最小值为121()2g =设函数5211ln 10()x h x x+=，则7275()(ln )42h x x x -'=-+所以当710(0,e )x -Î时，()0h x '>；当710(e,)x -∈+∞时，()0h x '<故()h x 在710(0,e)-单调递增，在710(e ,)-+∞单调递减，从而()h x 在(0,)+∞的最大值为771042(e)e 5h -=因为5625e 4>54e17242e 5> 综上，当0x >时，()()g x h x >，即11()10f x >…………………………………………………………12分………………………………………………………………………………………………………………………１２分。

湖北省武汉市华中师大附一中2017-2018学年高一下学期期中考试数学试卷word版含答案

华中师大一附中2017—2018学年度第二学期期中检测高一年级数学试题时间：120分钟满分：150分一、选择题：(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．) 1．两个平面重合的条件是 A ．有两个公共点 B ．有能组成三角形的三个公共点 C ．有三个公共点D ．有无穷多个公共点2．记等差数列{}n a 的前n 项和为S n ，若112a =，420S =，则S 6等于 A ．16B ．24C ．36D ．483．某工厂在某年12月份的产值是这年1月份的产值的m 倍，则该厂在本年度的产值的月平均增长率为A ．11m B ．12m C ．1 D 14．如图，在正方体ABCD —A 1B 1C 1D 1中，P 为BD 1的中点，则△P AC 在该正方体各个面上的正投影(实线部分)可能是A ．①④B ．①②C ．②③D ．②④5．数列1，12，22，13，23，33，…，1n ，2n ，3n ，…，n n ，…的前25项和为 A ．20714B ．20914C ．21114D ．10676．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若6sin 4sin 3sin A B C ==，则cos B =A B ．1116C ．34D7．在各项均为正数的等比数列{}n a 中，7652a a a =+，且存在两项m a ，n a 14a =，则14m n+的最小值为 A ．53B ．32C ．94D ．438．首项为24-的等差数列从第10项起开始为正数，则公差d 的取值范围是 A ． B ．C ．D ．9．已知数列{}n a 是等比数列，数列{}n b 是等差数列，若1598a a a ⋅⋅=-，2586b b b π++=，则4637sin1b b a a +-的值是A ．12B ．12-C ．32D ．32-10．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，cos b C a =，点M 在线段AB 上，且ACM BCM ∠=∠．若66b CM ==，则cos BCM ∠=A ．104B ．34C ．74D ．6411．给出下列命题：①若0b a <<，则||||a b >；②若0b a <<，则a b ab +<；③若0b a <<，则2b a a b +>；④若0b a <<，则22a a b b <-；⑤若0b a <<，则22a b aa b b+>+；⑥若1a b +=，则2212a b +≥．其中正确的命题有A ．2个B ．3个C ．4个D ．5个12．已知a , b ∈R ，且a 是2b -与3b -的等差中项，则2||||aba b +的最大值为A ．19B ．29C ．23D ．43二、填空题：(本大题共4小题，每小题5分，共20分．) 13．若关于x 的不等式230ax x a ++≥的解集为空集，则实数a 的取值范围是____________．14．有一块多边形的花园，它的水平放置的平面图形的斜二测直观图是如图所示的直角梯形ABCD ，其中 ∠ABC =45°，AB =AD =2米，DC ⊥BC ，则这块花园的面积为____________平方米．15．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，则下列四个论断中正确论断的序号是____________．(把你认为是正确论断的序号都写上)38>d 3<d 338<≤d 338≤<d ADCB①若sin cos A B a b =，则4B π=； ②若4B π=，2b =，3a =，则满足条件的三角形共有两个；③若a ，b ，c 成等差数列，sin A ，sin B ，sin C 成等比数列，则△ABC 为正三角形； ④若5a =，2c =，△ABC 的面积S △ABC = 4，则3cos 5B =．16．已知数列{}n a 的通项公式为1221,21,2n n nn a n -⎧⎛⎫⎪ ⎪⎪⎝⎭=⎨⎪⎛⎫⎪ ⎪⎝⎭⎩为奇数为偶数，则数列{33}n a n +-的前2n 项和的最小值为____________．三、解答题：(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．) 17．（本小题满分10分）已知x , y ∈R +，且22x y x y +=+．（1）求11x y+的最小值；（2）求x y +的最大值．18．（本小题满分12分）如图，在正方体1111ABCD A B C D -中，E 、F 、G 、H 分别是棱AB 、BC 、CC 1、C 1D 1的中点．（1）判断直线EF 与GH 的位置关系，并说明理由；（2）求异面直线A 1D 与EF 所成的角的大小．19．（本小题满分12分）在锐角△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2sin 3a B b =．（1）求角A ；（2）已知2a =，求△ABC 的面积的取值范围．A 1D 1C 1B 1ABC D FEG H20．（本小题满分12分）已知单调递增的等比数列{}n a 满足23428a a a ++=，且32a +是2a 与4a 的等差中项．（1）求数列{}n a 的通项公式；（2）若12log n n n b a a =，求数列{}n b 的前n 项和S n ．21．（本小题满分12分）如图，某镇有一块空地△OAB ，其中2km OA =，23km OB =，90AOB ∠=︒．当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖△OMN ，其中M ，N 都在边AB 上，且30MON ∠=︒，挖出的泥土堆放在△OAM 地带上形成假山，剩下的△OBN 地带开设儿童游乐场．为安全起见，需在△OAN 的周围安装防护网．（1）当1km AM =时，求防护网的总长度；（2）为节省资金投入，人工湖△OMN 的面积要尽可能小，设AOM θ∠=，问：当θ多大时△OMN 的面积最小？最小面积是多少？22．（本小题满分12分）已知常数0a ≠，数列{}n a 的前n 项和为S n ，12a =，(1)nn S a a n n=+-．（1）求数列{}n a 的通项公式；（2）若3(1)n n n n b a =+-，且数列{}n b 是单调递增数列，求实数a 的取值范围；（3）若12a =，12018n n n a c a -=+，对于任意给定的正整数k ，是否都存在正整数p 、q ，使BOAMN得？若存在，试求出p 、q 的一组值(不论有多少组，只要求出一组即可)；若不存在，请说明理由．华中师大一附中2017—2018学年度下学期高一期中检测数学试题参考答案二、填空题13．3,)2（-∞- 1415．①③ 16．32三、解答题17.解：(1)∵x ，y ∈R +，x 2+y 2=x+y∴221122x y x y xyx y xy xy xy +++==≥= 取等条件为22,x y R x y x y x y +⎧∈⎪+=+⎨⎪=⎩即1==x y∴(11+x y)min =2…………………………………………………………………………………5分方法二：∵x ，y ∈R +，x 2+y 2=x+y∴22112x y x y x y x y xy xy y x +++===+≥= 取等条件为22,x y R x y x y x y y x+⎧⎪∈⎪⎪+=+⎨⎪⎪=⎪⎩即1==x y ∴(11+x y)min =2…………………………………………………………………………………5分方法三：∵x ，y ∈R +，x 2+y 2=x+y∴x+y=x 2+y 2≥2xy ，进而11x y+≥2 k p q c c c =取等条件为22,x y R x y x y x y +⎧∈⎪+=+⎨⎪=⎩即1==x y∴(11+x y)min =2…………………………………………………………………………………5分 (2)∵x 2+y 2≥2xy∴2x 2+2y 2≥x 2+2xy+y 2=(x+y)2又∵x 2+y 2=x+y∴2(x+y)≥(x+y)2即0≤x+y ≤2右边取等条件为22,x y R x y x y x y +⎧∈⎪+=+⎨⎪=⎩即1==x y∴(+x y )max =2…………………………………………………………………………………10分方法二：设x+y=t则y=t －x ，代入x 2+y 2=x+y得x 2+(t －x)2=t 即2x 2－2tx+(t 2－t)=0令Δ=(－2t)2－8(t 2－t)≥0得0≤t ≤2即0≤x+y ≤2右边取等条件为22,1x y R x y x y x +⎧∈⎪+=+⎨⎪=⎩即1==x y∴(+x y )max =2…………………………………………………………………………………10分方法三：∵x ，y ∈R +，x 2+y 2=x+y 即(x －12)2+(y －12)2=12∴可设1212x y θθ⎧=⎪⎪⎨⎪=⎪⎩，θ∈(－4π，34π)∴x+y=1+sin(θ+4π)，θ+4π∈(0，π)∴当θ=4π即x=y=1时，(+x y )max =2………………………………………………………10分18.解：(1)取CD 的中点I∵E 、F 、I 分别是正方形ABCD 中AB 、BC 、CD 的中点∴CF12EI ∴在平面ABCD 中，延长EF 与DC 必交于C 右侧一点P ，且PC=CI同理，在平面CC 1D 1D 中，延长HG 与DC 必交于C 右侧一点Q ，且QC=CI ∴P 与Q 重合进而，直线EF 与GH 相交………………………………………………………………………6分方法二：∵在正方体ABCD —A 1B 1C 1D 1中，E 、H 分别是AB 、C 1D 1的中点 ∴EB12CD HC 1 ∴EBC 1H 是平行四边形 ∴EH BC 1又∵F 、G 分别是BC 、CC 1的中点 ∴FG12BC 1 ∴EH ∥FG ，EH ≠FG∴EF 、GH 是梯形EFGH 的两腰 ∴直线EF 与GH 相交……………………………………………………………………………6分(2)解：∵在正方体ABCD —A 1B 1C 1D 1中，AA 1CC 1∴ACC 1A 1是平行四边形 ∴AC ∥A 1C 1又∵E 、F 分别是AB 、BC 的中点 ∴EF ∥AC ∴EF ∥A 1C 1∴A 1D 与EF 所成的角即为A 1D 与A 1C 1所成的角(或：A 1D 与EF 所成的角即为∠DA 1C 1及其补角中的较小角) ①………………8分又∵在正方体ABCD —A 1B 1C 1D 1中，△A 1C 1D 为等边三角形 ∴∠DA 1C 1=60°②………………10分∴由①②得直线A 1D 与EF 所成的角为60°…………………………………………………12分19.解：(1)由2sin a B =得2sin sin =A B B又∵sinB ＞0sin A ∴=又∵△ABC 是锐角三角形 ∴A=3π…………………………………………………………………………………………4分(2)由正弦定理得2R=sin a A =43∴S △ABC =12bcsinA=12(2RsinB)(2RsinC)sinA=43sinBsinC=23cos(2B －23π)+13…………………………………………………………………………………………………8分又∵△ABC 是锐角三角形，A=3π ∴022032B B πππ⎧<<⎪⎪⎨⎪<-<⎪⎩即6π＜B ＜2π…………………………………………………………10分22(,)333B πππ∴-∈- ∴21cos(2)(,1]32B π-∈233]3的取值范围为（，∆∴ABC S ………………………………………………………12分方法二：由正弦定理得2R=sin a A =43如图，过外心O 作BC 的垂线分别交BC 和外接圆于H 、A 3其中，OH=12R=13，A 3H=32R=3∴S 1A BC ∆=12·BC ·A 1H=12·BC ·2OH=233S 3A BC ∆=12·BC ·A 3H=3又∵△ABC 是锐角三角形，A=3π∴A 在弧A 1A 3A 2上(不含A 1，A 2)233]3的取值范围为（，∆∴ABC S ………………………………………………………12分20．解：(1)由题意知2311123111282(2)a q a q a q a q a q a q⎧++=⎪⎨+=+⎪⎩…………………………………………………2分解得13212a q =⎧⎪⎨=⎪⎩或122a q =⎧⎨=⎩……………………(少一组解扣２分) …………………………6分∵等比数列{a n }单调递增 ∴122a q =⎧⎨=⎩∴a n =2×2n－1=2n…………………………………………………………………………………7分(2)由(１)得b n =－n ·2n∴S n =－1×2－2×22－3×23－…－n ×2n∴2S n = －1×22－2×23－…－(n －1)×2n －n ×2n+1…………(会用错位相减法，但做错了的，也给２分)……………………………………９分∴S n =2+22+23+…+2n －n ×2n+1=2(12)12n --－n ×2n+1=(1－n)2n+1－2……………………………12分21.解：(1)∵在△OAB 中，OA=2，∴∠OAB=60°又∵在△OAM 中，OA=2，AM=1∴由余弦定理得OM 2=22+12-2×2×1×cos60°=3即=OM 即∴△OAN 为正三角形，其周长为6km∴防护网的总长度为6km ……………………………………………………………………5分(2)由题得0°＜θ＜60°在△OA Ｍ中，2sin 60sin(120)o o OM θ=-即OM=sin(120)o θ-(或sin(60)oθ+) 在△OAN 中，2sin 60sin[180(3060)]o o o o ON θ=-++即∴S △OMN ＝12·OM ·ON ·sin ∠MON=12sin30° 90AOB ∠=︒222OM AM OA ∴+=OM AN ⊥30AOM ∴∠=︒) 又∵0°＜θ＜60°即0°＜１２０°－２θ＜１２0° ∴当且仅当１２０°－２θ=90°即θ=15°时△OMN 的面积取最小值为……………………………………………………12分22.解：(1)∵ ∴na n =S n +an(n －1)∴(n －1)a n －1=S n －1+a(n －1)(n －2) 相减得na n －(n －1)a n －1=a n +2a(n －1) 即(n －1)a n －(n －1)a n －1=2a(n －1) 其中n ≥2∴a n －a n －1=2a 为定值∴是以2为首项2a 为公差的等差数列∴a n =2+(n －1)2a=2a(n －1)+2…………………………………………………………………4分方法二：∵ ∴S n －S n －1=n Sn+a(n －1)∴(1)n n S n- －S n －1=a(n －1)其中n ≥2∴n S n －11n Sn --=a 为定值 ∴{n Sn }是以2为首项a 为公差的等差数列∴n Sn =2+(n －1)a∴a n =n Sn+a(n －1)=2a(n －1)+2………………………………………………………………4分(2)由是单调递增数列得b n ＜b n+1即3n +(－1)n [2a(n －1)+2]＜3n+1+(－1)n+1(2an+2)2km ()1nn S a a n n=+-{}n a ()1nn S a a n n =+-{}n b即(－1)n a＜3(1)221n nn---……………………………………………………………………5分1°若为正奇数则－a＜3221nn+-在n为正奇数时恒成立设f(n)=32 21 nn+-则f(n)－f(n+2)=3221nn+--23223nn+++=－4[(43)32](21)(23)nnn n---+＜0∴f(1)＜f(3)＜f(5)＜…∴－a＜f(1)=5即a＞－5………………………………………………………………………6分方法二：则f(n)－f(n+1)=3221nn+-－13221nn+++=－4[(1)31](21)(21)nnn n---+它在n=1时为正，在n≥2为负∴f(1)＞f(2)＜f(3)＜f(4)＜f(5)＜…∴－a＜min{f(1)，f(3)}=min{5，295}=5即a＞－5………………………………………6分2°若n为正偶数则a＜3221nn--在n为正偶数时恒成立设g(n)=32 21 nn--则g(n+2)-g(n)=23223nn+-+-3221nn--=4[(43)32](21)(23)nnn n-+++＞0∴g(2)＜g(4)＜g(6)＜…方法二：则g(n+1)－g(n)=13221nn+-+-3221nn--=4[(1)31](21)(21)nnn n-+-+＞0∴g(1)＜g(2)＜g(3)＜g(4)＜…n∴a ＜g(2)=73 综合1°2°及a ≠0得－5＜a ＜73且a ≠0……………………………………………………8分(3)由(1)得1=+n a n2019∴=+n n c n ∴可化为201920192019=+++k p q k p q 方法一：即p=(2019)k q q k +-=1(2019)kq k q k ⨯+-=(2019)k q q k⨯+-…………………………10分令12019q k p kq k -=⎧⎨=+⎩得220201p k k q k ⎧=+⎨=+⎩ (或令2019q k k p q -=⎧⎨=+⎩得220192p k q k=+⎧⎨=⎩，或交换前两组p ，q 的值，能够确定的有四组) ∴存在满足要求的p ，q ，且有一组值为220201p k k q k ⎧=+⎨=+⎩………………………………12分方法二：即pq －kp －kq=2019k 即(p －k)(q －k)=k(k+2019)=1×(k 2+2019k)=k ×(k+2019)…………………………………………………………………………………………………10分令212019p k q k k k -=⎧⎨-=+⎩即212020p k q k k =+⎧⎨=+⎩ (或令2019p k k q k k -=⎧⎨-=+⎩即222019p k q k =⎧⎨=+⎩，或交换前两组p ，q 的值，共能确定四组)∴存在满足要求的p ，q ，且有一组值为212020p k q k k=+⎧⎨=+⎩………………………………12分k p q c c c =。

2018年___自主招生数学试卷(含答案解析)

2018年___自主招生数学试卷(含答案解析)2018年___自主招生数学试卷一、选择题（本大题共6小题，共24.0分）1.√16的平方根是()A.4B.±4C.22.若√(1−x)2=x−1成立，则x满足()A.x≥1B.x≥C.x≤1D.±23.已知x=√5−1，则x2+2x的值是()A.2B.3C.4D.54.如图所示的四条直线a、b、c、d，直线a、b与水平线平行，以其中一条为x轴，d与水平线垂直，取向右为正方向；直线c、以其中一条为y轴，取向上为正方向．某同学在此坐标平面上画了二次函数x=xx2+2xx+2(x≠0)的图象如图，则下面结论正确的是()A.a为x轴，c为y轴B.a为x轴，d为y轴C.b为x轴，c 为y轴D.b为x轴，d为y轴5.如图，已知AB为圆的直径，C为半圆上一点，D为半圆的中点，xx⊥xx，垂足为H，HM平分∠xxx，HM交AB于x.若xx=3，xx=1，则MH长为()A.1B.1.5C.0.5D.0.76.如图，△xxx中，∠x=90°，D是BC边上一点，∠xxx=3∠xxx，xx=8，xx=7.则AB的值为()A.15B.20C.2√2+7D.2√2+√7二、填空题（本大题共10小题，共40.0分）7.已知实数x、y满足x+2x=5，则x−x=3.8.分解因式：x2+4xx+4x2+x+2x−2=(x+2x+1)2−3.9.在平面直角坐标系中，点A，B的坐标分别为(x,3)，(3x−1,3)，若线段AB与直线x=2x+1相交，则m的取值范围为(0,1)。

10.若一个圆锥的侧面展开图是半径为18cm，圆心角为240°的扇形，则这个圆锥的底面半径长是9cm。

11.如图，已知在矩形ABCD中，点E在边BC上，BE=2CE，将矩形沿着过点E的直线翻折后，点C、D、N处，B在同一直线上，分别落在M、F与BE交于点G.设AB=√3，那么△xxx的周长为4+4√3.12.如图，已知点x1，x2，…，xx均在直线x=x−1上，点x1，x2，…，xx均在双曲线x=−x上，x1x1⊥x并且满足：x1x2⊥x轴，x2x2⊥x轴，…，xx−1xx⊥x轴，xxxx⊥x轴，且x1x2=x2x3=…=xx−1xx，则n的最小值为2.1.由题意可知，点B在x轴负半轴，点A在x轴正半轴，且AB垂直于x轴，因此AB的斜率为0，即AB为x轴，所以B的纵坐标为0.又因为B在x轴负半轴，所以其横坐标为负数，设为-a。

2018届武汉华中师范大学第一附属中学高三上学期期中考试理科数学试题及答案精品

华中师大一附中2018—2018学年度上学期高三期中检测数学（理）试题时限：120分钟满分：150分命题人：蔡卉付靖宜审题人：钟涛第I 卷（选择题共60分）注意事项：务必将每小题的答案填在答题卡的相应位置.答在试卷上无效.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将你认为正确的选项代号涂填在选择题的答题卡内. 1．已知集合2{|lg()}A x y x x ==-,集合2{|0(0)}B x x cx c =-<>错误！未找到引用源。

,若A B ⊆错误！未找到引用源。

,则c 的取值范围为A.(0,1]B.(0,1)C.[1,)+∞D.错误！未找到引用源。

2.复数241i z i+=-错误！未找到引用源。

(i 为虚数单位)在复平面内对应点的坐标为A.(3,3)B.(1,3)-C.(3,1)-D.(2,4)3.已知向量(1,2),(2,1)a x b =-=错误！未找到引用源。

，则“0x >”是“a 与b 错误！未找到引用源。

夹角为锐角”的A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件4.已知定义在R 上的奇函数()f x 满足(1)(1)f x f x +=-,数列错误！未找到引用源。

的前n 项和为n S 错误！未找到引用源。

,且错误！未找到引用源。

,则错误！未找到引用源。

=A. 0 B .0或1 C.1-或0D.1或1-5.已知()sin(2)(0)f x A x A α=->错误！未找到引用源。

且430()0f x dx π=⎰错误！未找到引用源。

,则()f x 的一个对称中心为A.(,0)πB.4(,0)3π C.5(,0)3πD.7(,0)6π6.函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<的图象如图所示，为的了得到()cos g x A x ω=-的图象，可以将()f x 图象A.向右平移12π个单位长度 B.向右平移512π个单位长度C.向左平移12π个单位长度 D.向左平移512π个单位长度7.已知向量a ，b 是单位向量，若0a b ⋅=，且25c a c b -+-=，则c a b +-的取值范围是A.3,55⎡⎤⎢⎥⎣⎦B. C. D.8.若对于任意的x [1,0]∈-，关于x 的不等式2320x ax b ++≤错误！未找到引用源。

湖北省华中师范大学第一附属中学2018届高三上学期期中考试数学(理)试题Word版含答案

华中师大一附中2017-2018学年度上学期高三年级期中检测数学（理）试题第I 卷一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知复数2z1i，则下列命题中正确的个数为①2=z ②i z -=1 ③z 的虚部为i ④z 在复平面上对应点在第一象限 A ．1 B ．2 C ．3 D ．4 2．下列函数为偶函数且在(0，＋∞)上为增函数的是A ．20()(cos )x f x tdt B ．223()f x x x C ．21()2f x x x D ．()()xx f x x e e3．已知集合2lg 2x A x y x ⎧-⎫==⎨⎬+⎩⎭，集合{}21B y y x ==-，则集合{x x A B 且}x A B 为A ．[]()2,12,-+∞ B ．()()2,12,-+∞C ．()[),21,2-∞-D ．(](),21,2-∞-4．下列说法正确的是 A ．“,x yR ，若0xy，则1x且1y ”是真命题B ．在同一坐标系中，函数(1)y f x =+与(1)y f x =-的图象关于y 轴对称．C ．命题“x R ，使得2230x x ”的否定是“x R ，都有2230x x ”D ．aR ，“11a”是“1a ”的充分不必要条件5．如图，在ABC 中，13AN NC ，P 是BN 上的一点，若29AP mABAC ，则实数m 的值为 A ．19 B ．13C ．1D ．3 第5题图6．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有女子善织，日益功，疾，初日织五尺，今一月织七匹三丈（1匹=40尺，一丈=10尺），问日益几何？”其意思为：“有一女子擅长织布，每天比前一天更加用功，织布的速度也越来越快，从第二天起，每天比前一天多织相同量的布，第一天织5尺，一月织了七匹三丈，问每天增加多少尺布？”若这一个月有31天，记该女子一个月中的第n 天所织布的尺数为n a ，则132931242830a a a a a a a a ++⋅⋅⋅++++⋅⋅⋅++的值为A ．2930 B ．1615 C ．13D ．15 7．若13tan ,(,)tan 242ππααα-=∈，则sin(2)4πα+的值为 A ．210±B ．25C ．210D ．25±8．某食品的保鲜时间y （单位：小时）与储存温度x （单位：C ）满足函数关系bkx ey +=（ 718.2=e 为自然对数的底数，,k b 为常数），若该食品在0C 的保鲜时间是192小时，在22C 的保鲜时间是48小时，则该食品在33C 的保鲜时间是( )小时．A ．22B ．23C ．24D ．33 9．已知函数()sin()(0,)2f x x πωϕωϕ=+><的部分图像如所示，为了得到()y f x 的图像需将cos 2yx 的图像A ．向右平移3π个单位长度 B ．向左平移3π个单位长度 C ．向右平移6π个单位长度D ．向左平移6π个单位长度 10．已知定义在R 上的偶函数)(x f ，满足)()4(x f x f =+，且]2,0[∈x 时，()sin 2sin f x x xππ=+，则方程0lg )(=-x x f 在区间[0,10]上根的个数是A ．18B ．19C ．10D ．9 11．在ABC 和AEF 中，B 是EF 的中点，1633AB EF BC CA ，，，若2AB AE AC AF ，则EF 与BC 的夹角的余弦值为第9题图A ．12 B ．23 C ．34 D ．1312．设函数()()x x f x e x ae （其中e 为自然对数的底数）恰有两个极值点12,x x 12()x x ，则下列说法中正确的是A ．103aB ．21x C ．1(0)02f -<< D ．12()()0f x f x第II 卷二、填空题（每题5分，共20分，将答案填在答题纸上） 13．函数2lg(23)y x x =--+的单调递增区间是________．14．已知向量(6,2)a =-，(1,)b m =，且a b ⊥，则2a b -= ． 15．已知数列{}n a 的通项公式为219104na n n，当123234a a a a a a 345a a a12n n n a a a 取得最大值时，n 的值为_________．16．若函数()y f x =满足b x a f x a f 2)()(=-++（其中220ab ），则称函数)(x f y =为“中心对称函数”，称点),(b a 为函数()f x 的“中心点”．现有如下命题：①函数()sin 1f x x =+是“中心对称函数”；②若“中心对称函数”()y f x =在R 上的“中心点”为()(),a f a ，则函数()()()F x f x a f a =+-是R 上的奇函数；③函数()32362f x x x x =-+-是“中心对称函数”，且它的“中心点”一定为()1,2；④函数x x x f cos 2)(-=是“中心对称函数”，且它的“中心点”一定为(,)2ππ．其中正确的命题是___ _____．（写出所有正确命题的序号）三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．（本小题满分10分）已知向量(,cos())a sinx x π=-，(2cos ,2cos )b x x ，函数()1f x a b ．（Ⅰ）求()f x 的对称中心；（Ⅱ）求函数()f x 在区间[0,]2π上的最大值和最小值，并求出相应x 的值．18．（本小题满分12分)已知函数()f x ＝4log (41)x+＋kx (k R ∈)．（Ⅰ）当12k时，若方程()f x －m ＝0有解，求实数m 的取值范围；（Ⅱ）试讨论()f x 的奇偶性．19．(本小题满分12分)已知数列{}n a ，{}n b ，n S 为数列{}n a 的前n 项和，且满足214a b =，22n n S a =-，21(1)n n nb n b n n +-+=+（*n N ∈）．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）试问{}nb n能否为等差数列，请说明理由；（III ）若数列{}n c 的通项公式为,24n n n n n a b n c a b n ⎧-⎪⎪=⎨⎪⎪⎩为奇数，为偶数，令n T 为{}n c 的前n 项的和，求2n T ．20．（本小题满分12分)已知函数()-xf x e ax =（a R ∈，e 为自然对数的底数）．（Ⅰ）讨论函数()f x 的单调性；（Ⅱ）若1a =，函数()()()2xg x x m f x e x x =--++在()2,+∞上为增函数，求实数m 的取值范围．21．(本小题满分12分)如图所示，某住宅小区一侧有一块三角形空地ABO ，其中3,OA km 33,OBkm90AOB ．物业管理拟在中间开挖一个三角形人工湖OMN ，其中,M N 都在边AB 上（,M N 不与,A B 重合，M 在,A N 之间），且30MON ．（Ⅰ）若M 在距离A 点2km 处，求点,M N 之间的距离；（Ⅱ）为节省投入资金，三角形人工湖OMN 的面积要尽可能小．试确定M 的位置，使OMN 的面积最小，并求出最小面积．22．（本小题满分12分）已知数列{}n a 满足1n na t =+(,,3,)n t N t t n t *∈≥≤，为常数．（Ⅰ）设1121111nni inS a a a a ，*n N ，证明：(1)ln(1)nS t n ；（Ⅱ）证明：1n a na e -<（e 为自然对数底数）；（Ⅲ）设1231()=()()()()nttt t t n kn k T a a a a a ==+++∑ ，*nN ，试比较与n T 与1的大小关系，并说明理由．第21题图1． C 2． D 3． D 4． B 5． A 6． B 7． C 8． C 9． A 10． B 11． B 12． C第II 卷二、填空题：每题5分，满分20分，将答案填在答题纸上． 13． (3,1]或(3,1) 14． 45 15． 9n16．①②③三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．解：（I ）因为()1f x a b =2sin cos cos(π)2cos 1x x x x +-⋅+22sin cos 2cos 1x x x =-+=sin 2cos2x x -=2sin(2)4x………4分所以()f x 的对称中心为(,0)()28k k Z ππ+∈ ……………5分（II ）由（I ）得，()f x =sin 2cos2x x -=2sin(2)4x π-， …………7分因为π0,2x ⎡⎤∈⎢⎥⎣⎦，所以π3π2,444x π⎡⎤-∈-⎢⎥⎣⎦，所以当242x ππ-=时，即8x 3π=时，()f x；当244x ππ-=-时，即0x =时，()f x 的最小值是1-． …………10分 18．（本小题满分12分)解：（Ⅰ）由m ＝()f x ＝4log (41)x+－12x ，∴m ＝441log 2x x +＝41log (2)2xx+． ∵1222xx，∴m ≥12． ……………………………………6分（Ⅱ）依题意得定义域为R ,关于原点对称∵()f x 4log (41)x +＋kx ，()f x 4log (41)x -+－kx ，令()()f x f x ，得441log 41x x-++＝2kx -，即4log 4x＝2kx -， ∴2x kx 对一切k R ∈恒成立．∴12k时()()f x f x ，此时函数()f x 是偶函数……………………9分∵0441(0)log (41)0log 22f k =+-⨯==，∴函数()f x 不是奇函数，综上，当12k时，函数()f x 是偶函数；当12k 时，函数()f x 是非奇非偶函数． …………12分 19、(本小题满分12分)解：（Ⅰ）当1n =时，111222S a a =-⇒=，当2n ≥时，由112222n n n n S a S a --=-⎧⎨=-⎩，得：122n n n a a a -=-，则12n n a a -=，综上，{}n a 是公比为2，首项为2的等比数列，2nn a =；………………3分（Ⅱ）{}nb n是等差数列，理由如下： ∵214a b =，∴11b =，∵21(1)n n nb n b n n +-+=+，∴111n nb b n n+-=+ 综上，{}n b n 是公差为1，首项为1的等差数列，且211n n bn b n n=+-⇒=；…7分（Ⅲ）令212n n n p c c -=+22122221(21)2(2)2(41)2(41)424n nn n n n n n ----⋅⋅=-+=-⋅=-⋅01212123123474114(41)443474114(45)4(41)4n n n nn T n T n n --⎧=⨯+⨯+⨯++-⨯⎪⎨=⨯+⨯+⨯++-⨯+-⨯⎪⎩ ①② ①-②，得：012121644334444444(41)43(41)414nn nnn T n n --⋅-=⋅+⋅+⋅++⋅--⋅=+--⋅- 所以27127499nn n T -=+⋅． ……………… ………12分20．（本小题满分12分)解：（Ⅰ）函数()f x 的定义域为R ，()xf x e a '=-．当0a ≤时，()0f x '>，∴()f x 在R 上为增函数；当0a >时，由()0f x '=得ln x a =，当(),ln x a ∈-∞时，()0f x '<，∴函数()f x 在(),ln a -∞上为减函数，当()ln ,x a ∈+∞时，()0f x '>，∴函数()f x 在()ln ,a +∞上为增函数……4分（Ⅱ）当1a =时，()()()2x x g x x m e x e x x =---++，∵()g x 在()2,+∞上为增函数；∴()10xxg x xe me m '=-++≥在()2,+∞上恒成立，即11x x xe m e +≤-在()2,+∞上恒成立， …………………………6分令()11xx xe h x e +=-，()2,x ∈+∞，则()()()2221x x xxe xe e h x e --'==-()()221x x xe e x e---，令()2xL x e x =--，()10xL x e '=->在()2,+∞上恒成立，即()2xL x e x =--在()2,+∞上为增函数，即()()2240L x L e >=->，∴()0h x '>，即()11x x xe h x e +=-在()2,+∞上为增函数，∴()()222121e h x h e +>=-，∴22211e m e +≤-，所以实数m 的取值范围是2221,1e e ⎛⎤+-∞ ⎥-⎝⎦． ………………12分21．(本小题满分12分)解：（Ⅰ）在ABO 中，因为33390OAOBAOB ，，，所以60OAB ，在OAM 中，由余弦定理得：2222cos 7OM AO AM AO AM A，所以7OM，所以22227cos 27OA OM AM AOM AO AM，在OAN 中，sin sin()sin(90)ONA A AON AOM 27cos 7AOM，在OMN 中，由sin 30sin MN OMONA，得7172427MN；… ………6分（Ⅱ）解法1：设,060AOM，在OAM 中，由sin sin OM OAOAB OMA ，得332sin(60)OM，在OAN 中，由sin sin ONOA OAB ONA ，得32sin(90)2cos ON θθ==+，所以11sin 22OMNSOM ONMON 2sin(60)θ⋅+12＝2716sin(60)cos θθ+6060)4θ<<+．当26090θ+=，即15θ=时，OMN S27(23)4．所以应设计15AOM ，可使△OMN 27(23)4km 2…12分解法2：设AM ＝x ，0＜x ＜3．在△OAM 中，由余弦定理得OM 2＝AO 2＋AM 2－2AO ·AM ·cos A ＝x 2－3x ＋9，所以OM ＝x 2－3x ＋9，所以cos ∠AOM ＝OA 2＋OM 2－AM 22OA ·OM ＝6－x2x 2－3x ＋9，在△OAN 中，sin ∠ONA ＝sin(∠A ＋∠AON )＝ sin(∠AOM ＋90°)＝cos ∠AOM ＝6－x2x 2－3x ＋9，由ON sin ∠OAB ＝OA sin ∠ONA，得ON ＝36－x2x 2－3x ＋9·32＝33x 2－3x ＋96－x，所以S △OMN ＝12OM ·ON ·sin ∠MON ＝12·x 2－3x ＋9·33x 2－3x ＋96－x ·12＝33(x 2－3x ＋9)4(6－x )，0＜x ＜3，令6－x ＝t ，则x ＝6－t ，3＜t ＜6，则：S △OMN ＝33(t 2－9t ＋27)4t ＝334(t －9＋27t )≥334·(2t ·27t －9)＝27(2－3) 4．当且仅当t ＝27t ，即t ＝33，x ＝6－33时等号成立，S △OMN 的最小值为27(2－3) 4，所以M 的位置为距离A 点6－3 3 km 处，可使△OMN 的面积最小，最小面积是27(2－3) 4km 2．22．（本小题满分12分）解：（Ⅰ）即证：12111ln(1)(1)(1)(1)nn t a t a t a +++>++++，即证：1111ln(1)23n n++++>+，设()ln(1)g x x x =-+，1()111xg x x x '=-=++， ∵当0x >时，()0g x '>，()g x 在(0,)+∞上单调递增，当10x -<<时，()0g x '<，()g x 在(1,0)-上单调递减， ∴()ln(1)(0)0g x x x g =-+≥=（当且仅当0x =时等号成立），即0x >时，有ln(1)x x >+， ∴1113411ln 2ln ln lnln(1)2323n n n n+++++>++++=+， ∴12111(1)ln(1)n t n a a a +++>++ ……………………………4分（用数学归纳法给分）（Ⅱ）由（Ⅰ）知：当1x >-且0x ≠时，有ln(1)x x >+，即当0x >且1x ≠时，有1ln x x ->，因为0111n n t a t t <=≤<++，所以 1ln n n a a ->，即1n a na e -<………………………………………8分（Ⅲ）1231()=()()()()1nt t t t tnk n k T a a a a a ，理由如下：解法一：由（Ⅱ）知：123()()()()t t tt n a a a a ++++3121111()()()()n a a a a t t t t e e e e 3121111()()()()n a a a a t t t t e e e e2111(1)1t tn t t t t ee e-+++-=-22211111(1)111t t t t t t t t t t ee e e e--+++++--≤=--，设 1t t eq +=，因为3142t t q ee +=≥>，21111t t t t ee-++-∴=-1111111t t q q q q q ----=<<---，所以1231()=()()()()1nttt t t n kn k T a a a a a ==++++<∑ ………………12分解法二：因为,*n t N ∈，且n t ≤，所以1231231()=()()()()()()()()nt t t t t t t t t nk n t k T a a a a a a a a a12()()()111tt t t t t t下面用数学归纳法证明：*3,t tN 时，12()()()1111tt t t t t t，即12(1)tt t t t t ，①当3t时，左边333312336(13)，即当3t 时不等式成立；②假设当(3)t k k时不等式成立，即12(1)kkkk k k ，则当1tk时，111112(1)k kkk k k 11122(1)k k k k k k k 1(1)(12)(1)k k k k k k k11(1)(1)(1)2(1)kkk kkkk，11111112111()(1)1()()1111k k k k k k k C C k kk k111121kC k，11(2)2(1)k k k k，11111112(1)2(1)(2)kkkkkk k kkk，所以当1t k时，不等式也成立；综合①②*3,t tN 时，12(1)tttt t t ，即12()()()1111tt t t tt t成立，所以1231()=()()()()1nt t t t t n kn k T a a a a a ==++++<∑．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

华中师大一附中2018年高中招生考试数学试题考试时间：70分钟卷面满分：120分说明：所有答案一律书写在答题卡上，写在试卷上作答无效．一、选择题 (本大题共5小题，每小题7分，共35分．在每小题给出的四个选项中，有且只有一项是正确的．)1．二次函数y =x 2＋2x ＋c 的图象与x 轴的两个交点为A(x 1，0)，B(x 2，0)，且x 1＜x 2，点P(m ，n )是图象上一点，那么下列判断正确的是( ) A ．当n ＞0时，m ＜x 1 B ．当n ＞0时，m ＞x 2 C ．当n ＜0时，m ＜0D ．当n ＜0时，x 1＜m ＜x 22．已知实数a 、b 、c 满足a ＜b ＜c ，并目k =1a−b ＋1b−c ＋1c−a ，则直线y =－kx ＋k 一定经过( ) A ．第一、三、四象限 B ．第一、二、四象限 C ．第一、二、三象限D ．第二、三、四象限3．下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”．执行该程序框图，若输入的a 、b 分别为16、22，则输出的a =(a ←a －b 的含义：将a －b 的结果赋给a )( ) A ．0 B ．2 C ．4D ．144．直线l ：kx －y －2k －1=0被以A(1，0)为圆心，2为半径的⊙A 所截得的最短弦长为( ) A ．√2 B ．2 C ．2√2 D ．45．如图，△ABC 中，AB=AC=8，BC=4，BF ⊥AC 于F ，D 是AB 的中点，E 为AC 上一点，且2EF=AC ，则tan ∠DEF=( ) A ．√15B ．√1515C ．√154D ．14二、填空题(本大题共5小题，每小题7分，共35分)．6．若a ＋b －2√a −1－4√b −2=3√c −1−12c −5，则(b −c )a 的值为__________．7．已知△ABC 的一边长为4，另外两边长恰是方程2x 2−12x ＋m ＋1=0的两实根，则实数m 的取值范围是__________．A CDEF8．如图，D是△ABC的边AB上的一点，且AB=3AD，P是△ABC外接圆上一点，使得=__________．∠ADP=∠ACB，则PBPD9．有十张正面分别标有数字1，2，3，4，5，6，7，8，9，10的不透明卡片，它们除数字不同外其余全部相同，将它们背面朝上，洗匀后从中任取一张，以卡片上的数字作为关于x的不等式5x−a≤5中的系数a，使得该不等式的正整数解只有1和2的概率为__________．10．若四个互不相等的正实数a，b，c，d满足(a2018−c2018)(a2018−d2018)=2018，(b2018−c2018)(b2018−d2018)=2018，则(ab)2018−(cd)2018的值为__________．三、解答题(本大题共3小题，共50分．解答应写出文字说明、证明过程和演算步骤) 11．(本小题满分16分)如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．(1)求证：CE=CF；(2)在图1中，若G在AD上，且∠GCE=45°，则GE、BE、GD有什么数量关系？说明理由；(3)运用(1)(2)解答中所积累的经验和知识，完成下题：如图2，在直角梯形ABCD中，AD∥BC(BC＞AD)，∠B=90°，AB=BC=6，E是AB上一点，且∠DCE=45°，BE=2，求DE的长．12．(本小题满分16分)如图1，在平面直角坐标系xOy内，已知点A(−1，0)，B(−1，1)，C(1，0)，D(1，1)，记线段AB为L1，线段CD为L2，点P是坐标系内一点．给出如下定义：若存在过点P的直线l与L1，L2都有公共点，则称点P是L1−L2相关点，例如，点P(0，1)是L1－L2相关点．(1)以下各点中，__________是L1－L2相关点(填出所有正确的序号)；①(−1，2)；②(−5，2)；③(4，2)．(2)直接在图1中画出所有L1－L2相关点所组成的区域，用阴影部分表示；(3)已知点M在y轴上，以M为圆心，r为半径画圆，若⊙M上有且只有一个点为L1−L2相关点．①当r=1时，求点M的纵坐标；②求r的取值范围．13．(本小题满分18分)定义：点P(x，y)为平面直角坐标系中的点，若满足x=y时，则称该点为“平衡点”，例如点(－1，－1)，(0，0)，(√3，√3)都是“平衡点”．①当－1≤x≤3时，直线y=2x＋m上存在“平衡点”，则实数m的取值范围是__________．(2)直线y=3mx＋n－1上存在“平衡点”吗？若存在，请求出“平衡点”的坐标；若不存在，请说明理由；(3)若抛物线y=ax2＋bx＋1(a＞0)上存在两个不同的“平衡点”A(x1，x1)，B(x2，x2)，且满足，试求实数t的取值范围．0＜x1＜2，∣x2−x1∣=2，令t=b2－2b＋11748华中师大一附中2018年高中招生考试数学试题参考答案考试时间：70分钟卷面满分：120分说明：所有答案一律书写在答题卡上，写在试卷上作答无效．一、选择题(本大题共5小题，每小题7分，共35分．在每小题给出的四个选项中，有且只有一项是正确的．)题号 1 2 3 4 5答案 D A B C A二、填空题(本大题共5小题，每小题7分，共35分)．10．－2018 6．36 7．9<m≤17 8．√39．１２三、解答题(本大题共3小题，共50分．解答应写出文字说明、证明过程和演算步骤．) 11．(1)证明：在正方形ABCD中，∵BC=CD，∠B=∠CDF，BE=DF，∴△ACBE≌△CDF．∴CE=CF．……………………………4分(2)GE=BE＋GD．理由如下：∵△CBE≌△CDF，∴∠BCE=∠DCF．∴∠ECD＋∠ECB=∠ECD＋∠FCD．即∠ECF=∠BCD=90°．又∠GCE=45°，∴∠GCF=∠GCE=45°．∵CE=CF，∠GCF=∠GCE，GC=GC，∴△ECG≌△FCG．∴EG=EF．∴GE=DF＋GD=BE＋GC．……………………………10分(3)过C作CG⊥AD，交AD延长线于G，在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∠CGA=90°，AB=BC，∴四边形ABCG为正方形．∴AG=BC=6．已知∠DCE=45°，根据(1)(2)可知，ED=BE＋DG，设DE=x，则DG=x－2，∴AD=AG－DG=8－x，AE=AB－BE=6－2=4．在Rt△AED中∵DE2=AD2＋AE2，即x2=(8－x)2＋42解得x=5．∴DE=5……………………………16分12．(1)②，③是L 1－L 2相关点。

(写出一个给2分)……………………………4分(2)所有L 1－L 2相关点所组成的区域为图中阴影部分(含边界)．……………………………8分(3)①∵点M 在y 轴上，⊙M 上只有一个点为L 1－L 2相关点，阴影部分关于y 轴对称， ∴⊙M 与直线AC 相切于(0，0)，或与直线BD 相切于(0，1)，如图所示．又∵⊙M 的半径r =1，∴点M 的坐标为(0，－1)或(0，2)，经检验：此时⊙M 与直线AD ，BC 无交点， ⊙M 上只有一个点为L 1－L 2相关点，符合题意． ∴点M 的坐标为(0，－1)或(0，2)． ∴点M 的纵坐标为－1或2．(求出一个给1分，不检验不扣分)……………………………10分 ②阴影部分关于直线y=１２对称，故不妨设点M 位于阴影部分下方，∵点M 在y 轴上，⊙M 上只有一个点为L 1－L 2相关点，阴影部分关于y 轴对称， ∴⊙M 与直线AC 相切于O(0，0)，且⊙M 与直线AD 相离．作ME ⊥AD 于E ，设AD 与BC 的交点为F ， ∴MO=r ，ME ＞r ，F(0，１２)．在Rt △AOF 中，∠AOF=90°，AO=1，OF=１２，∴AF=√AO 2＋OF 2=√52，sin ∠AFO=AO AF =2√55．在Rt △FEM 中，∠FEM=90°， FM=FO ＋OM=r ＋１２sin ∠EFM=sin ∠AFO=2√55， ∴ME=FM ·sin ∠EFM=√5(2r ＋1)5， ∴√5(2r ＋1)5＞r ，又∵r ＞0，∴0＜r ＜√5＋2．……………………………16分13．(1)－3≤m ≤1(2)由y =3mx ＋n －1，当y =x 时，3mx ＋n －1=x 即(3m －1)x =1－n当3m －1=0，1－n =0，即m=13，n=1时，方程有无数个解，此时直线y =x 上所有点都是“平衡点”，坐标为(x ，x )，x 为任意实数……………………6分当3m －1=0，1－n ≠0，即m=13，n ≠1时，方程无解，此时直线y =x 上不存在“平衡点”，………………………………8分当3m －1≠0，即m ≠13时，方程有唯一解x =1−n3m−1，此时直线y =x 上只有一个“平衡点”，其坐标为(1−n 3m−1，1−n3m−1)，x 为任意实数…………10分(3)联立{y =ax 2＋bx ＋1y =x，消去y 并整理得：ax 2＋(b －1)x ＋1=0∵抛物线上存在两个不同的“平衡点”A(x 1，x 1)，B(x 2，x 2) ∴x 1，x 2是方程ax 2＋(b －1)x ＋1=0两个不相等的实数根 ∴x 1＋x 2=1−b a，x 1·x 2=1a ，△=(b －1)2－4a ＞0……………………………12分∵a ＞0，∴x 1x 2=1a ＞0，∴x 1、x 2同号 ∵0＜x 1＜2，∣x 2−x 1∣=2，∴2＜x 2＜4∴0＜x 1x 2＜8，0＜1a ＜8，∴a ＞18……………………………16分 t =b 2－2b ＋11748=(b －1)2＋6948=4a 2＋4a ＋6948=4(a ＋12)2＋2148，∵当a ＞－12时，t 随a 的增大而增大，a ＞18＞－12∴t ＞4(18＋12)2＋2148=2即t ＞2……………………………18分。