第五章(优化设计)
第五章+约束优化计算方法讲解

机械优化设计
二.初始复合形的构成
机械优化设计
1. 复合形顶点数K的选择
建议: n 1 K 2n
n 小取大值, n 大取小值
* 1) 为保证迭代点能逼近极小点, 应使
间接解法是将约束优化问题转化为一系列无约束优化问题来 解的一种方法。
由于间接解法可以选用已研究比较成熟的无约束优化方 法,并且容易处理同时具有不等式约束和等式约束的问题。 因而在机械优化设计得到广泛的应用。
间接解法中具有代表性的是惩罚函数法。
直接解法的基本思想:
在由m个不等式约束条件gu(x)≤0所确定的可行域φ内,选择 一个初始点x(0),然后确定一个可行搜索方向S,且以适当的步 长沿S方向进行搜索,取得一个目标函数有所改善的可行的新点 x(1),即完成了一次迭代。以新点为起始点重复上述搜索过程, 每次均按如下的基本迭代格式进行计算:
机械优化设计
a) 可行域是凸集;b)可行域是非凸集
机械优化设计
间接解法的求解思路:
将约束函数进行特殊的加权处理后,和目标函数结合起来, 构成一个新的目标函数,即将原约束优化问题转化为一个 或一系列的无约束优化问题。
m
l
x, 1, 2 f x 1G g j x 2H hk x
hj ( x) 0 ( j 1,2, , p)
机械优化设计
上一章讨论的都是无约束条件下非线性函数的寻 优方法,但在实际工程中大部分问题的变量取值都有 一定的限制,也就是属于有约束条件的寻优问题。
与无约束问题不同,约束问题目标函数的最小值 是满足约束条件下的最小值,即是由约束条件所限定 的可行域内的最小值。只要由约束条件所决定的可行 域必是一个凸集,目标函数是凸函数,其约束最优解 就是全域最优解。否则,将由于所选择的初始点的不 同,而探索到不同的局部最优解上。在这种情况下, 探索结果经常与初始点的选择有关。为了能得到全局 最优解,在探索过程中最好能改变初始点,有时甚至 要改换几次。
优化设计八年级下册答案

优化设计八年级下册答案第五章中国的地理差异第一节四大地理区域的划分快乐预习一、1、经济 2、尺度二、2、北方地区西北地区 3、季风和非季风区夏季风的影响一二轻松尝试1.B2.D3.B4.B5.C6.C7.(画图略)智能演练1.C2.C3.C4.C5.A6.D7.C8.C9.B 10.B 11.B 12.D 13.B 14.A 15.C16.(1)北方地区南方地区西北地区青藏地区(2)a —③ b—② c—① (3) B D C C(4)青藏地区北方地区南方地区西北地区17. (1) 青藏地区 (2) 南方地区 (3) 西北地区 (4) 北方地区第二节北方和南方地区第一课时快乐预习一、1.地形气候2.大兴安岭横断平原平原黄土长江中下游平原3.(1)温带季风(2)亚热带4.小有长5.(1)温带落叶阔叶林(2)亚热带常绿阔叶林轻松尝试1.B2.B3.D4.B5.D6.D7.(1)季风多半湿润三秦岭—淮河一线(2)东北平原秦岭黄土高原淮河华北平原黄河长江珠江智能演练1.A2.D3.C4.D5.B6.B7.A8.A9.D 10.A 11.A 12.D 13.D 14.B 15.A16.(1)北方南方秦岭—淮河 0℃ 800 气候(2)季风区(3)亚热带季风温带季风雨热同期(或高温多雨与多雨期一致)(4)温带落叶阔叶林亚热带常绿阔叶林(5)东北黄土东南长江中下游(6)B A17. ①江西庐山②山东济南③河南洛阳④江苏南京第二课时快乐预习二、1.生产方式生活习惯 2.(1)旱地水田(2)两年一熟(3)花生水稻3.高亢委婉唢呐箫陆运水运轻松尝试1.A2.B3.B4.A5.B6.A7. ②①③⑤④⑥智能演练1.C2.C3.C4.C5.D6.D7.A8.C9.D 10.A 11.B 12.B 13.A 14.A 15.C16.(1)D B (2)减少 (3) ① (4)旱地亚热带常绿阔叶林一年二至三熟一年一熟或两年三熟17.(1)南方地区(2)亚热带季风气候(3)水稻油菜甘蔗(4)亚热带常绿阔叶林第三节西北地区和青藏地区第一课时轻松尝试一、1.高原盆地 3.内流河塔里木 4.荒漠草原 5.干旱塔克拉玛干雅丹轻松预习1.A2.B3.B4.A5.D6.A7.(1)新疆维吾尔内蒙古(2)塔里木 G(3)蒙古俄罗斯(4)大兴安岭宁夏天山塔里木昆仑内蒙古智能演练1.C2.A3.D4.C5.A6.B7.C8.C9.B 10.B 11.B 12.B 13.D 14.B 15.A16.(1)塔里木柴达木 (2)准噶尔黄土华北 (3)春 (4)荒漠 17.×××1.B2.C3.A4.A5.A6.A7.(1)①(2)A (3)香港(4)住房紧张,交通拥挤;环境污染加剧;治安状况变差等。
实验活动4 用化学沉淀法去除粗盐中的杂质离子

【实验目的】 1.用化学沉淀法去除粗盐中的Ca2+、Mg2+和 SO42- 。 2.熟练掌握溶解、过滤、蒸发等操作,认识化学方法在物质分离和提纯中 的重要作用。 【实验器材及试剂】 1.器材 天平、药匙、量筒、烧杯、玻璃棒、胶头滴管、漏斗、滤纸、蒸发皿、 坩埚钳、铁架台(带铁圈)、石棉网(或陶土网)、酒精灯、火柴。 2.试剂 粗盐、蒸馏水、0.1 mol·L-1 BaCl2溶液、20% NaOH溶液、饱和Na2CO3溶 液、6 mol·L-1盐酸、pH试纸。
解析 制备流程:向废液中加入双氧水,将溴离子氧化成溴单质,然后加入四
氯化碳后通过萃取、分液分离出溴的CCl4溶液,通过操作③(蒸馏)得到四 氯化碳和溴单质;无色液体Ⅰ中含有K+、Cl-、Ca2+、Mg2+、SO42- ,分别加
入BaCl2、KOH、K2CO3溶液过滤后得到无色液体Ⅱ和固体A,再调节液体 Ⅱ的pH除去 CO32- 、OH-,得到无色液体Ⅲ,最后通过蒸发结晶获得氯化钾
4.过滤 将烧杯中的物质进行过滤,除去生成的沉淀和不溶性的杂质。若滤液仍浑 浊时,要重新过滤一次。 5.调pH 向所得的滤液中滴加稀盐酸,用玻璃棒搅拌,直到没有气泡冒出,并用 pH试纸检验,使滤液呈中性或微酸性。
6.蒸发结晶
(1)将滤液倒入蒸发皿中,用酒精灯加热,同时用玻璃棒不断搅拌。当蒸发 皿中出现较多固体时,停止加热,利用蒸发皿的余热使滤液蒸干。 (2)用坩埚钳将蒸发皿夹持到石棉网(或陶土网)上冷却,即可得到除去了杂 质的精盐。
①发生反应的离子方程式为
第5章-PDC钻头水力参数优化设计方法精选全文完整版
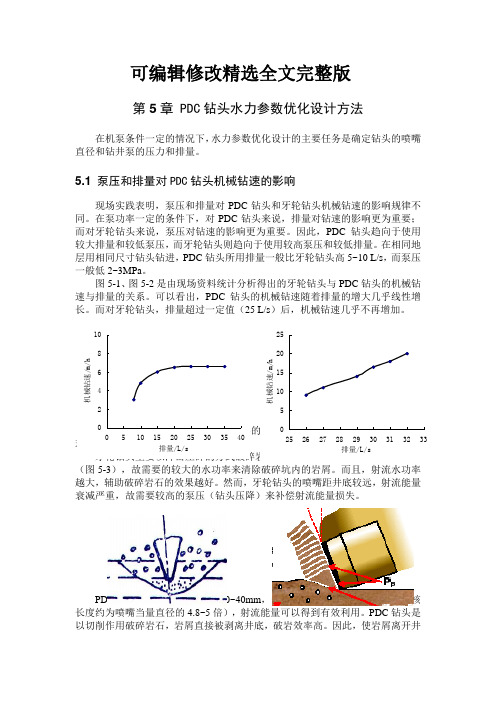
可编辑修改精选全文完整版第5章 PDC 钻头水力参数优化设计方法在机泵条件一定的情况下,水力参数优化设计的主要任务是确定钻头的喷嘴直径和钻井泵的压力和排量。
5.1 泵压和排量对PDC 钻头机械钻速的影响现场实践表明,泵压和排量对PDC 钻头和牙轮钻头机械钻速的影响规律不同。
在泵功率一定的条件下,对PDC 钻头来说,排量对钻速的影响更为重要;而对牙轮钻头来说,泵压对钻速的影响更为重要。
因此,PDC 钻头趋向于使用较大排量和较低泵压,而牙轮钻头则趋向于使用较高泵压和较低排量。
在相同地层用相同尺寸钻头钻进,PDC 钻头所用排量一般比牙轮钻头高5~10 L/s ,而泵压一般低2~3MPa 。
图5-1、图5-2是由现场资料统计分析得出的牙轮钻头与PDC 钻头的机械钻速与排量的关系。
可以看出,PDC 钻头的机械钻速随着排量的增大几乎线性增长。
而对牙轮钻头,排量超过一定值(25 L/s )后,机械钻速几乎不再增加。
图5-1 排量对牙轮钻头钻速的影响 图5-1 排量对PDC 钻头钻速的影响泵压和排量对牙轮钻头和PDC 钻头的影响不同,是因为两种钻头的破岩机理和结构不同。
牙轮钻头主要以冲击压碎的方式破碎岩石,在井底形成裂纹发育的破碎坑穴(图5-3),故需要的较大的水功率来清除破碎坑内的岩屑。
而且,射流水功率越大,辅助破碎岩石的效果越好。
然而,牙轮钻头的喷嘴距井底较远,射流能量衰减严重,故需要较高的泵压(钻头压降)来补偿射流能量损失。
图5-3 牙轮钻头破岩作用 图5-3 PDC 钻头破岩作用PDC 钻头的喷嘴距井底只有30~40mm ,一般小于射流等速核长度(等速核长度约为喷嘴当量直径的4.8~5倍),射流能量可以得到有效利用。
PDC 钻头是以切削作用破碎岩石,岩屑直接被剥离井底,破岩效率高。
因此,使岩屑离开井0510152025252627282930313233排量/L/s机械钻速/m /h02468100510152025303540排量/L/s机械钻速/m /h底原位置并不困难,关键问题是有效地将岩屑清离井底。
第五章ANSYS优化设计

第五章ANSYS 优化设计拓扑优化拓扑优化是指形状优化,也称为外形优化,其目的是寻找载荷作用下的物体最佳材料分配方案,最大刚度设计。
拓扑优化的原理是在满足结构体积缩减量的条件下使结构的柔度极小化。
极小化的结构柔度实际就是要求结构的刚度最大化。
ANSYS提供的拓扑优化技术用于确定系统的最佳几何形状,其原理是系统材料发挥最大利用率,同时确保诸如整体刚度、自振频率等在满足工程要求的条件下获得极大或极小值。
优化参数:不需要人工定义优化参数,而是自动将材料分布当作优化参数。
目标函数:是在满足给定的实际约束条件下(如体积减小等)需要极大或极小化的参数,通常采用的目标函数是结构柔量能量(the energy of structure compliance)极小化和基频最大等。
支持的单元类型:二维实体单元:PLANE2、PLANE82,用于平面应力或轴对称问题;三维实体单元:SOLID92、SOLID95;壳单元:SHELL93。
特别提醒:1、ANSYS程序只对单元类型编号等于1的单元部分进行拓扑优化,对于单元类型编号等于或大于2的单元网格不进行拓扑优化。
2、(1)拓扑优化只能基于线性结构静力分析或模态分析,其它分析类型暂时还不支持。
(2)ANSYS实际提供的拓扑优化为基于线性结构静力分析的最大静态刚度拓扑优化设计和基于模态分析的最大动态刚度优化设计,同时需要达到体积最小化目的。
(3)采用单载荷步或多载荷步的线性结构静力分析时,施加相应的载荷和边界条件。
采用模态频率分析,仅仅施加边界条件。
3、拓扑优化的结果对网格划分密度非常敏感,较细密的网格可以产生更加清晰、确定的拓扑结果,但计算会随着单元规模的增加而需要更多的收敛时间;相反,较粗的网格会生成模糊、不确定的拓扑结果。
另外,拓扑优化结果对载荷情况十分敏感,有时很小的载荷变化将导致拓扑优化结果的巨大差异。
优化设计1. 简介举例:如何在原材料消耗最少情况下,使水杯的容积最大。
2018版高中物理必修2《优化设计》第五章曲线运动第4节

第4节圆周运动一、线速度阅读教材第16~17页“线速度”部分,知道线速度的概念,了解线速度的方向,知道匀速圆周运动线速度大小特征。
1.定义:物体做圆周运动通过的弧长与通过这段弧长所用时间的比值。
2.公式:v=Δs Δt。
3.意义:描述做圆周运动的物体运动的快慢。
4.方向:线速度是矢量,方向与圆弧相切,与半径垂直。
5.匀速圆周运动:(1)定义:物体沿着圆周运动,并且线速度大小处处相等的运动。
(2)性质:线速度的方向是时刻变化的,所以圆周运动是一种变速运动。
思维拓展匀速圆周运动和匀速直线运动中的两个“匀速”的含义相同吗?有什么区别?答案不同。
前者指线速度的大小不变,后者指速度的大小和方向都不变。
二、角速度阅读教材第17~18页“角速度”和“角速度的单位”部分,了解角速度的概念,知道角速度的单位,知道转速、周期的概念。
1.定义:连接物体与圆心的半径转过的角度与转过这一角度所用时间的比值。
2.公式:ω=ΔθΔt。
3.意义:描述物体绕圆心转动的快慢。
4.单位:(1)角的单位:国际单位制中,弧长与半径的比值表示角的大小,称为弧度,符号:rad。
(2)角速度的单位:弧度每秒,符号是rad/s或rad·s-1。
思维拓展如图1所示,钟表上的秒针、分针、时针以不同的角速度做圆周运动。
图1(1)秒针、分针、时针它们转动的快慢相同吗?相同时间内,谁转动的角度大?谁转动得最快?(2)请指出秒针、分针和时针的周期。
答案(1)不相同。
根据角速度公式ω=ΔθΔt知,在相同的时间内,秒针转过的角度最大,时针转过的角度最小,所以秒针转得最快。
(2)秒针的周期为60 s,分针的周期为60 min,时针的周期为12 h。
三、线速度与角速度的关系阅读教材第18页“线速度与角速度的关系”部分,知道线速度与角速度的关系表达式。
1.在圆周运动中,线速度的大小等于角速度大小与半径的乘积。
2.关系式:v=ωr。
思维拓展月亮绕地球做圆周运动。
工程设计优化管理办法(试行)

优化设计管理办法(试行)第一章优化设计的原则第一条优化设计的原则是不降低设计标准、不影响使用功能并确保工程质量、合同工期、投资控制的目标。
第二章优化设计的内容第二条路线优化:在工程开工之前,根据设计文件和现场核查情况,对线路走向、纵坡、线位地质、工程结构物规模与数量、土石方数量、软基处理、路基填料及征地拆迁的类别与数量等项目进行统计分析、综合评估,通过线位方案比选,选定更为合理的路线方案。
第三条软土路基:通过现场挖深坑、触探等方法对照设计图进行地质核对,对设计漏探的位置进行补探、核对设计图中软基的深度、宽度、长度。
并根据核对的结果合理调整软基处理的范围及深度,或合理调整工程处理措施等方式的设计变更。
第四条路基防护:通过进一步的地质勘探与分析计算,对通过降缓路埑边坡取消挡护或更改防护类型,既能利用降坡土方填筑路基,又能起到生态防护的作用;挡护合并或增减挡护长度,高度等方式的设计变更。
第五条结构物的平面位置、标高、规模及数量的优化1.涵渠、通道位置与沟槽或既有道路是否吻合;涵渠出入口标高与路面、水渠流水面或水沟是否顺接,上游流水是否顺利兼顾;孔跨能否满足要求;有无沟渠合并或倒虹吸管改圆管涵的可能;立交与排洪或灌溉能否兼顾;有无涵渠合并或取消以及结构型式的改变的必要。
2.核对设计结构物地基承载力,并根据核对的结果,合理调整结构物基底处理方式或基础结构型式。
3.桥墩台位置是否避开道路或沟心,有无必要移位或调整交角角度;孔跨和净高能否满足要求;桩孔开挖方法是否变更;桩底标高是否合理;上部构造设计是否经济。
4.核对隧道的地质围岩级别是否与设计相符,并根据围岩级别的变化,合理调整施工临时支护措施及永久支护厚度等。
第六条采用新技术、新工艺、新设备,达到减少投资、加快速度、保证质量的目的。
第三章优化设计的提出第七条设计优化工作要贯穿工程建设的全过程,在通过实地调研、收集资料、研究论证和评审后。
总承包项目部、驻地办、总监办、设计单位、公司均可提出设计优化方案。
实验设计与数据处理第五章-现代当代的其他实验设计方法

我们取出其中一段,便可以接着使用黄金分割法了
双因素优选法
双因素优选问题,就是要迅速找到二元函数Z=f(x,y)的最大 值。 在这里x,y代表的是双因素。假定处理的是单峰问题,也 就是把x,y平面作为水平面,实验结果z看成平面上的山峰。
x,y,z
画出x,y,z的等高线,等高线的最高点就 是山峰,即最优值
爬山法效果和快慢和起点关系很大,起点选得好,可以省很多 次实验,很多时候直觉和经验可以帮助我们选一个好的起点。
使用技巧:
爬山法的步伐大小很关键,一般来说先向各个方向迈出一小步 试探,找对方向后开始阶段可稍大一些步伐,快到顶点时,减 小步伐。一般来说,越接顶点,试验指标随因素变化越缓慢。
多峰情况:
前面介绍的方法只适用于单峰情况,遇到多峰怎么办? 可以采用下述两种方法: 1)先不管单峰多峰,使用上面介绍的方法,找到一个峰后,如 果达到生产要求,就先按它生产,以后再找其他更高的峰,可 采用分区寻找的方法。 2)先做一批分布比较均匀,疏松的实验,看它是否有“多峰” 现象。如果有,则在每个可能出现的高峰范围内做实验,把这 些峰找出来,这时,第一批试验点最好按照a:b=0.618:0.382的 比例划分,如下图所示:
310分钟
150 80 30分钟
55度
A
B
C
65
67
75度
平行线法
• 两个因素中,一个例如x易于调整,另一个 例如y不容易调整,则建议用平行线法,先 将Y固定在范围(c,d)的0.618处,即取
Y=c+(d-c)X0.618
用单因素法找最大值,假定在p点取得这一值 ,再把Y固定在范围(c,d)的0.382处,即 取
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1 概述 (1)无约束优化问题
给定目标函数g ( X ), X 为设计变量X (x1 , x2 ,..., xn ), 寻找X *, 使g ( X *)值最小。 由于-g ( X *)值最小与g ( X *)最大等价,所以优化目标函数总 是假设使目标函数最小。
例:
2 min{x1 x2 3x1x2 4x14}
(3)线性规划问题 目标函数和约束函数都是线性函数的优化问题。
例:假如生产零件A消耗材料9kg , 消耗时间3小时, 消耗电能4kW , 获利润60块,生产零件B消耗材料4kg , 消耗时间10小时,消耗电能5kW , 获利润120块,现有 材料360kg,时间300个小时,电能200KW,如何布置生 产才能获得最大利润?
x1+x2+x3+x4+x5=100 X>=0 Min{0.1x2+0.2x3+0.3x4+0.4x5}
5.3.3 二次规划求解函数quadprog 数学模型:
1 T min{ X GX qT X } 2 s.t : AX b Aeq beq lb X ub 用法:
x = quadprog(G,q,A,b) x = quadprog(G,q,A,b,Aeq,beq) x = quadprog(G,q,A,b,Aeq,beq,lb,ub) x = quadprog(G,q,A,b,Aeq,beq,lb,ub,x0) x = quadprog(G,q,A,b,Aeq,beq,lb,ub,x0,options)
(2)约束优化问题
给定目标函数g ( X ), X 为设计变量X (x1 , x2 ,..., xn ), 满足: 等式约束条件:pi ( x) 0, (i 1, 2,..., l ) 不等式约束条件:q j ( x) 0, ( j 1, 2,..., m) 假设两者约束的变量空间为D,寻找X * D, 使g ( X *)值最小。
Output:保存输出状态的变量 Grad:保存梯度计算值的变量 Hessian:保存目标函数Hessian矩阵的变量
强烈建议使用格式[x y exit]=fminunc(@fun,x0,options)
计算设置: op=optimset('MaxIter',10000); op=optimset(op,'TolFun',1.e-4); op=optimset(op,'TolX',1.e-6); [x y exit]=fminunc(@f2,[1;2],op); function f=f2(X) y1=X(1)+cos(X(2)); y2=sin(X(1))+X(2)+10; f=y1*y1+y2*y2;
假设产品A生产x个,产品B生产Y个,那么: 利润: max f ( x, y ), f ( x, y ) 60 x 120 y 约束条件: 9 x 4 y 360 3 x 10 y 300 4 x 5 y 200 x 0, y 0
(4)多目标规划问题 目标函数个数大于1的约束或无约束优化问题
用法: x = linprog(c,A,b) x = linprog(c,A,b,Aeq,beq) x = linprog(c,A,b,Aeq,beq,lb,ub) x = linprog(c,A,b,Aeq,beq,lb,ub,x0)
x = linprog(c,A,b,Aeq,beq,lb,ub,x0,options) 英文Help说第2个 [x,fval] = linprog(...) 参数为Lagrange乘 [x,fval,exitflag] = linprog(...) 子参数, 是错误的, [x,fval,exitflag,output] = linprog(...) [x,fval,exitflag,output,lambda] = linprog(...) 实际上仍为目标 函数值 Set Aeq=[] and beq=[] if no equalities exist. Set A=[] and b=[] if no inequalities exist. Set lb=[] and ub=[] if no boudary exist 1:function converged to a solution x. 0:Number of iterations exceeded options.MaxIter. -2:No feasible point was found. -3:Problem is unbounded. -4:NaN value was encountered during execution of the algorithm. -5:Both primal and dual problems are infeasible. -7:Search direction became too small. No further progress could be made.
(3)确定步长a*, X k 1 X k ad k , 保证X 在允许空间内, 并求 min f ( X k ad k )对应a *. (4)如果f ( X k a * d k )满足设计要求, 或者 || f ( X k 1 ) || 很小, 或者k 大于给定计算次数,或者 || X k 1 - X k || 足够小, 那么转(5) 结束, 否则k k 1转(2). (5)结束.
例:人字架由两根钢管组成,顶点 受力2F,跨度为2 B,壁厚为T, 弹性模量为E,密度为,许应 应力为[ ],求钢管在不超过许 应应力和失稳条件下,耗材最少 的人字架的高度h很钢管外径半R.
(a)目标函数模型 g (h, R) 2 h 2 B 2 ( R 2 ( R T ) 2 )
(b)设计变量约束条件 假设F1为钢管所受压力,那么 F1 强度条件为: [ ] A 稳定性条件为:F1
2 EI
l2 其中A ( R 2 ( R T ) 2 ),l 2 h 2 B 2 4 几何条件 : R T , h 0 I
( R 4 ( R T )4 )
[x,fval] = quadprog(...) [x,fval,exitflag] = quadprog(...) [x,fval,exitflag,output] = quadprog(...) [x,fval,exitflag,output,lambda] = quadprog(...) 返回标志: 1:Function converged to a solution x. 3:Change in the objective function value was smaller than the specified tolerance. 4:Local minimizer was found. 0:Number of iterations exceeded options.MaxIter. -2:Problem is infeasible. -3:Problem is unbounded. -4:Current search direction was not a direction of descent. No further progress could be made. -7:Magnitude of search direction became too small. No further progress could be made.
例:假如生产零件A消耗材料9kg , 消耗时间3小时, 消耗电能4kW , 获利润60块,生产零件B消耗材料4kg , 消耗时间10小时,消耗电能5kW , 获利润120块,现有 材料360kg,工时300个,供电200kW,如何布置生产 才能消耗电能最少、生产时间最少、耗材最少,获取 最大利润?
假设产品A生产x个,产品B生产Y 个,那么问题转化为: min{ f ( x, y )} f ( x, y ) 60 x 120 y min{9 x 4 y}
例:某车间要100套钢架,每套钢架由2.0m, 2.1m,1.5m长的钢材 各一段组成,现有钢材每条240m,如何分配才能使尾料最少。
段数
套1
套2
套3
套4
套5
2.9
2.1 1.5 尾料
1
0 3 0
2
0 1 0.1
0
2 2 0.2
1
2 0+5.8x2+2.9x3<=240 4.2x3+4.2x4+2.1x5<=240 4.5x1+1.5x2+3x3+4.5x5<=240
求解下降方 向d不同方法 对应不同优 化算法
5.3 优化问题的matlab求解函数 5.3.1 fminunc函数:求无约束目标函数最小值
用法: x = fminunc(@fun,x0) x = fminunc(@fun,x0,options) [x,fval] = fminunc(...) [x,fval,exitflag] = fminunc(...) [x,fval,exitflag,output] = fminunc(...) [x,fval,exitflag,output,grad] = fminunc(...) [x,fval,exitflag,output,grad,hessian] = fminunc(...) X:极小点 Fval:极小值 Fun:目标函数名字 X0:初值,列 向量 Option:选项 Exitflag:=1求解成功,其他值表示不成功
例:
min{x 2xy y 4x 6 y}
4 4
(a)定义目标函数 (b)调用fminunc函数 (c)根据返回结果,如果计算不成功(可用计算点判断 它是否满足约束条件),修改计算选项,直至计算结 果满意。
