精彩编辑题11压杆稳定
材料力学答案- 压杆稳定
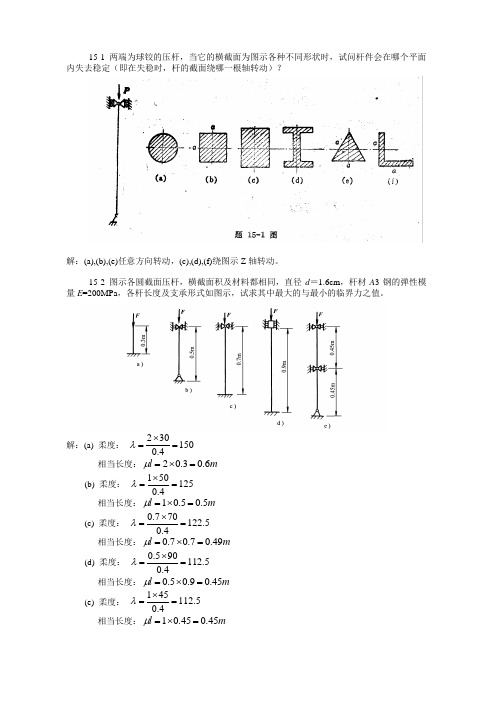
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题

角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解:1.查型钢表得
习题 11-12 图
No.16aI:Iz = 1130cm4,Wz = 141cm3 2No. 63×63×5: A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用,欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以,轴不安全。
11-11 图示正方形桁架结构,由五根圆截面钢杆组成,
连接处均为铰链,各杆直径均为 d=40 mm,a=1 m。材料 均为 Q235 钢,E=200 GPa,[n]st=1.8。试;
网
ww w
.k hd 案
μ =1
co
界力。
m
11-5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论,试判断哪一种是正确 的。 (A)FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d); (B)FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d); (C)FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c);
案
对于 A3 钢, λ P = 102,
λs = 61.6 。因此,第一杆为大柔度杆,第二杆为中柔度杆,
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
静力学11、压杆稳定

Fcr
2 EI l2
μ= 1
2 EI Fcr (0.7l)2
μ= 0.7
2 EI Fcr (0.5 l ) 2
μ= 0.5
2EI Fcr (2l )2
μ= 2
2 EI Fcr l 2
μ= 1
§11.4 欧拉公式的适用范围.经验公式
一、欧拉临界应力公式及使用范围
1.细长压杆的临界应力:临界力除以压杆横截面面积
0
Pcr d EI
k
2d
将边界条件代入统一微分方程的通解得:
式 0
如 图
k 0
1 0 k2
0 1 0
1 0 0
0 0 k
2
C1
C C
2 3
0
sinkL
coskL L 1
k 2 sinkL k 2 coskL 0 0
1 0
Cd4
有非零解的充要条件为:系数行列式值为零;
解得压杆失稳特征方程为:coskL 0
解: (1) 2 E I
Pcr ( l)2
2E d4
64
( l)2
1 16
2E I正
(2)
Pcr 正 Pcr 圆
( l)2 2E I圆
d2 2
a4 4
I正 I圆
12
d4
12
d4
3
( l)2
64
64
例5:五根直径都为 d的细长圆杆铰接构
成平面正方形杆系ABCD,如各杆材料相 同,弹性模量为E。求图 (a)、(b)所示两种 载荷作用下杆系所能承受的最大荷载。
60
2. cr=S时: 强度破坏,采用强度公式。
≤ S—粗短杆(小柔度杆);
表 1 直线公式的系数 a 和 b
压杆稳定习题

压杆稳定一、判断题1.临界力Fij只与压杆的长度及两端的支撑情况有关。
()2.对于细长压杆,临界应力σij的值不应大于比例极限σp。
()3.压杆的柔度与压杆的长度,横截面的形状和尺寸以及两端的支撑情况有关。
()4.压杆的杆端约束作用愈强,那么长度系数越小,临界压力越大。
()5.压杆的临界应力应该由欧拉公式计算。
()6.欧拉公式的适用条件是。
()7.细长压杆,若长度系数μ增大一倍,则临界力Fij增加一倍。
()图 18.两端铰支细长压杆,若在其中加一铰支座如图1所示,则欧拉临界力是原来的4倍。
()9.如果细长压杆有局部削弱,削弱部分对压杆的稳定性没有影响。
()10.在材料,长度,横截面形状和尺寸保持不变的情况下,杆端约束越强,则压杆的临界力越小。
11.压杆的临界荷载是压杆保持不稳定平衡所承受的最大轴向压力。
()二、选择题1.在压杆的材料、长度、横截面形状和尺寸保持不变的情况下,杆端约束越强,则压杆的临界力()。
A. 越大B.保持不变C.越小D.以上三种可能都有2.已知细长压杆两端球形铰支,若截面面积相等时,采用下列那种截面最稳定?()A B CD三、分析题1.在压杆稳定计算中,是一个与_______,________和______有关的参数,称为压杆的。
2.欧拉公式的适用范围是什么?3.图2两根杆件的截面形状、尺寸及材料均相同,试比较哪一根杆件稳定性好?为什么?图 24.两根细长压杆,材料相同,一根截面形状为正方形,一根截面为圆形。
假设两根杆截面面积相同,支承相同,试问:①横截面惯性矩各为多少?②哪根杆容易受压失稳?为什么?5.一压杆两端约束一定,在截面面积不变情况下,为了更有效地提高其临界力应采用()措施。
6.若两根细长压杆的回转半径()相等。
当相等时,它们的柔度()相等,若两杆的柔度相等,当_______相等时,它们的临界应力相等。
7.写出压杆稳定条件的计算公式。
8.图3所示两根直径均为d的圆截面压杆,材料相同,已知,d=20mm,试判断哪根压杆容易失稳图 3四、计算题1.二圆形截面受压杆的材料相同,尺寸如图4所示,已知二杆均为大柔度杆,试比较二杆的临界力和临界应力2.圆形截面受压杆,长L=1.5m,直径d=3cm,钢材的弹性模量,比例极限σp=200Mpa,试求压杆的临界力。
精选题11压杆稳定

压杆稳定1. 图示结构,AB 为刚性杆,其它杆均为直径10 mm d =的细长圆杆,弹性模量200 GPa E =, 屈服极限s 360 MPa σ=,试求此结构的破坏载荷F 值。
解:12.37 m, sin 26H α⎛⎫== ⎪⎝⎭,0.169()Cy Dy F F F =-=↓,N1N4N2N30.507F F F F F ==-=-=由杆1,4,N11s 0.507F F A σ==,s 155.8 kN 0.507AF σ==由杆2,3,2N2cr 2π0.673 kN EIF F l ===, cr 2 1.33 kN 0.507F F ==结构破坏载荷 1.33 kN F =2. 图示桁架由5根圆截面杆组成。
已知各杆直径均为30 mm d =, 1 m l =。
各杆的弹性模量均为200 GPa E =,p 100λ=,061λ=,直线经验公式系数304 MPa a =, 1.12 MPa b =,许用应力[]160 MPa σ=,并规定稳定安全因数st []3n =,试求此结构的许可载荷[]F 。
解:由平衡条件可知杆1,2,3,4受压,其轴力为N1N2N3N4N 2F F F F F =====杆5受拉,其轴力为N5F F = 按杆5的强度条件:N5[], []113 kN F F A Aσσ≤≤= 按杆1,2,3,4的稳定条件 p 133λλ=> 由欧拉公式 cr 78.48 kN F =crst N[]F n F ≥ 37.1 kN F ≤ , []37.1 kN F =3. 钢杆和铜杆截面、长度均相同,都是细长杆。
将两杆的两端分别用铰链并联,如图,此时两杆都不受力。
试计算当温度升高多少度时,将会导致结构失稳?已知杆长 2 m l =,横截面积220 cm A =,惯性矩440 cm z I =;钢的弹性模量s 200 GPa E =,铜的弹性模量1.2m F ACFB HD0.4m1324lF︒45l12345钢铜c 100 GPa E =,钢的线膨胀系数6s 12.510α-=⨯℃-1,铜的线膨系数6c 16.510α-=⨯℃-1。
压杆稳定习题及答案

压杆稳定习题及答案【篇一:材料力学习题册答案-第9章压杆稳定】xt>一、选择题1、一理想均匀直杆受轴向压力p=pq时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( a )。
a、弯曲变形消失,恢复直线形状;b、弯曲变形减少,不能恢复直线形状; c、微弯状态不变; d、弯曲变形继续增大。
2、一细长压杆当轴向力p=pq时发生失稳而处于微弯平衡状态,此时若解除压力p,则压杆的微弯变形( c )a、完全消失b、有所缓和c、保持不变d、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( d)来判断的。
a、长度b、横截面尺寸c、临界应力d、柔度 4、压杆的柔度集中地反映了压杆的( a)对临界应力的影响。
a、长度,约束条件,截面尺寸和形状;b、材料,长度和约束条件;c、材料,约束条件,截面尺寸和形状;d、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( c )a.60;b.66.7;c.80;d.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( d )所示截面形状,其稳定性最好。
≤?≥?- 1 -10、在材料相同的条件下,随着柔度的增大( c)a、细长杆的临界应力是减小的,中长杆不是;b、中长杆的临界应力是减小的,细长杆不是; c、细长杆和中长杆的临界应力均是减小的; d、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( a )a. 临界应力一定相等,临界压力不一定相等;b. 临界应力不一定相等,临界压力一定相等;c. 临界应力和临界压力一定相等;d. 临界应力和临界压力不一定相等;a、杆的材质b、杆的长度c、杆承受压力的大小d、杆的横截面形状和尺寸二、计算题1、有一长l=300 mm,截面宽b=6 mm、高h=10 mm的压杆。
工程力学压杆的稳定问题

稳定安全系数一般大于强度安全系数。
例题 : 1000吨双动薄板液压冲压机的顶出器杆为一
端 固 定 、 一 端 铰 支 的 压 杆 。 已 知 杆 长 l=2m , 直 径 d=65mm,材料的E=210GPa,p=288MPa,顶杆工作 时承受压力F=18.3吨,取稳定安全系数nst=3.0。试校 核该顶杆的稳定性。
①
90
②
l
解:由静力平衡条件可解得两杆的压力分别为:
N1 P cos , N 2 P sin
两杆的临界压力分别为:
2E I 2E I Pcr 1 2 , Pcr 2 2 l1 l2
要使P最大,只有 N1、 N2 都达
到临界压力,即
P
() 1 () 2
①
P cos P sin
2E cr 2 p
或写成:
2E p
令: 2 E p
p
欧拉公式的 适用范围:
p
满足该条件的杆称为细长杆或大柔度杆
如对A3钢,当取E=206GPa,σp=200MPa,则
E p p
2
2 206 109
200 106
应用欧拉公式
654 1012 2 (210 109 ) ( ) 2 EI 64 Fcr N 925.2kN 2 2 (l ) (0.7 2)
Fcr 925.2 103 5.16 n 3 18.3 10 9.8 F
该杆满足稳定性要求
> nst 3.0
x l时:v 0
sin kl 0
kl n (n 0,1, 2,)
n k l
工程力学:压杆稳定 习题与答案

一、单选题1、压杆一般分为三种类型,它们是按压杆的()。
A.惯性半径分B.杆长分C.柔度分D.杆端约束情况分正确答案:C2、细长压杆,若其长度系数增加一倍,则()。
A.Pcr增加一倍B.Pcr增加到原来的4倍C.Pcr为原来的二分之一倍D.Pcr为原来的四分之一倍正确答案:D3、下列结论中正确的是()。
①若压杆中的实际应力不大于该压杆的临界应力,则杆件不会失稳;②受压杆件的破坏均由失稳引起;③压杆临界应力的大小可以反映压杆稳定性的好坏;④若压杆中的实际应力大于scr=πE2/λ2,则压杆必定破坏。
A.①+②B.②+④C.①+③D.②+③正确答案:C4、压杆临界力的大小()。
A.与压杆所承受的轴向压力大小有关B.与压杆的柔度大小有关C.与压杆材料无关D.与压杆的柔度大小无关正确答案:B5、两端铰支的圆截面压杆,若λp=100,则压杆的长度与横截面直径之比l/d在时,才能应用欧拉公式()。
A.25B.50C.400D.200正确答案:A6、若两根细长压杆的惯性半径i相等,当()相同时,它们的柔度相等。
①杆长;②约束类型;③弹性模量;④外部载荷A.①+②B.①+②+③C.①+②+④D.①+②+③+④正确答案:A7、a、b两根都是大柔度杆,材料、杆长和横截面形状大小都相同,杆端约束不同。
其中a为两端铰支,b为一端固定,一端自由。
那么两杆临界力之比应为()。
A.4B.1/4C.2D.1/2正确答案:A8、提高水稻抗倒伏性能的可能措施包括()。
A.选用茎秆强壮品种B.选用节间较短的矮秆品种C.使用植物生长调节剂,以调控节间长度与株高等D.以上都是正确答案:D9、圆形压杆和矩形压杆在稳定性校核时有何区别()。
A.圆形压杆不需要考虑失稳方向性,而矩形压杆需要考虑B.圆形压杆需要考虑失稳方向性,而矩形压杆不需要考虑C.两者都不需要考虑D.两者都需要考虑正确答案:A10、压杆合理设计措施包括:①合理选用材料;②合理选择截面;③合理安排压杆约束与杆长()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压杆稳定1. 图示结构,AB 为刚性杆,其它杆均为直径10 mm d =的细长圆杆,弹性模量200 GPa E =, 屈服极限s 360 MPa σ=,试求此结构的破坏载荷F 值。
解:12.37 m, sin 26H α⎛⎫== ⎪⎝⎭,0.169()Cy Dy F F F =-=↓,N1N4N2N30.507F F F F F ==-=-=由杆1,4,N11s 0.507F F A σ==,s 155.8 kN 0.507AF σ==由杆2,3,2N2cr 2π0.673 kN EIF F l ===, cr 2 1.33 kN 0.507F F ==结构破坏载荷 1.33 kN F =2. 图示桁架由5根圆截面杆组成。
已知各杆直径均为30 mm d =, 1 m l =。
各杆的弹性模量均为200 GPa E =,p 100λ=,061λ=,直线经验公式系数304 MPa a =, 1.12 MPa b =,许用应力[]160 MPa σ=,并规定稳定安全因数st []3n =,试求此结构的许可载荷[]F 。
解:由平衡条件可知杆1,2,3,4受压,其轴力为N1N2N3N4N F F F F F =====杆5受拉,其轴力为N5F F = 按杆5的强度条件:N5[], []113 kN F F A Aσσ≤≤= 按杆1,2,3,4的稳定条件 p 133λλ=> 由欧拉公式 cr 78.48 kN F =crst N[]F n F ≥ 37.1 kN F ≤ , []37.1 kN F =3. 钢杆和铜杆截面、长度均相同,都是细长杆。
将两杆的两端分别用铰链并联,如图,此时两杆都不受力。
试计算当温度升高多少度时,将会导致结构失稳?已知杆长 2 m l =,横截面积220 cm A =,惯性矩440 cm z I =;钢的弹性模量s 200 GPa E =,铜的弹性模量c 100 GPa E =,钢的线膨胀系数6s 12.510α-=⨯℃-1,铜的线膨系数6c 16.510α-=⨯℃-1。
m解:铜杆受压,轴力为Nc F ,钢杆受拉,轴力为Ns F ,Nc Ns N F F F ==由协调条件 s c l l ∆=∆ 即 N N s c s c F l F ltl tl E A E Aαα∆+=∆- N c s s c 11 ()F t A E E αα⎛⎫∆=+ ⎪-⎝⎭铜杆为细长杆 2c cr 2π98.7 kN E IF l==当 Nc cr F F =时失稳, 此时 185 C t ∆=4. 图示矩形截面杆AC 与圆形截面杆CD 均用低碳钢制成,C ,D 两处均为球铰,材料的弹性模量200 GPa E =,强度极限b 400 MPa σ=,屈服极限s 240 MPa σ=,比例极限p 200 MPa σ=,直线公式系数304 MPa a =, 1.118 MPa b =。
p 100λ=,061λ=,强度安全因数[] 2.0n =,稳定安全因数st [] 3.0n =,试确定结构的最大许可载荷F 。
解:(1) 由梁AC 的强度2max maxmax 2, , []36 97.2 kNz zM F bh M W W F σσ===≤≤得 (2) 由杆CD 的稳定性crp cr N N 1200, 15.50 kN, ,3315.50 kN, []15.50 kNCD CD F F F F F F F λλ=>==≥≤=5. 图示两端固定的工字钢梁,横截面积226.1 cm A =,惯性矩41 130 cm z I =,493.1 cm y I =,长度 6 m l =,材料的弹性模量200 GPa E =,比例极限p 200 MPa σ=,屈服极限s 240 MPa σ=,直线公式的系数304 MPa a =, 1.12 MPa b =,线膨胀系数712510/l α-=⨯℃,当工字钢的温度升高10t ∆=℃时,试求其工作安全因数。
解:p 158.799.3λλ=>=由欧拉公式,可得临界应力cr 78.2 MPa σ=温度应力 25 MPa l tE σα=∆= 工作安全因数 crst 3.13n σσ==6. 图示正方形平面桁架,杆AB ,BC ,CD ,DA 均为刚性杆。
杆AC ,BD 为弹性圆杆,其直径20 mm d =,杆长550 mm l =;两杆材料也相同,比例极限p 200 MPa σ=, 屈服极限s 240 MPa σ=,弹性模量200 GPa E =,直线公式系数304 MPa a =, 1.12 MPa b =,线膨胀系数612.510/l α-=⨯℃,当只有杆AC 温度升高,其他杆温度均不变时,试求极限的温度改变量cr t ∆。
解:由平衡方程可得:N N N AC BD F F F == (压) 由变形协调方程,并注意到小变形, 有ACBD ΔΔ即 N N AC BD l F l F ltl EA EAα∆-=又由 p 11099λλ=>=, 知2cr 2πEIF l=令 N cr F F =, 得 22cr 2π130.58d t l α∆==℃7. 图示结构,已知三根细长杆的弹性模量E ,杆长l ,横截面积A 及线膨胀系数α均相同。
问:当升温t ∆为多大时,该结构将失稳。
解:由 N l F ltl EA α∆=, 可得 N l F tEA α=∆细长杆: 2cr 2π EIF l =当 N cr F F =时失稳 22πl EItEA lα∆= 得 22πl I t Al α∆=8. 图示结构ABC 为矩形截面杆,60 mm, 100 mm, 4 m b h l ===,BD 为圆截面杆,直径60 mm d =,两杆材料均为低碳钢,弹性模量200 GPa E =, 比例极限p 200 MPa σ=,屈服极限s 240 MPa σ=,直线经验公式为cr (304 1.12) MPa σλ=-,均布载荷 1 kN/m q =,稳定安全因数st []3n =。
试校核杆BD 的稳定性。
解:(1) 由协调方程,Δcos45BDB l f =得 34N cos 45(2)25(2)3844845BD F l l q l EI EI - 解得 N 7.06 kN BD F = (2) 杆BD :p 377100λλ=>= 由欧拉公式:cr 39 kN F = cr st st N 5.56[]BDFn n F ==>,安全。
BDAC9. 正方形截面杆,横截面边长a 和杆长l 成比例增加,它的长细比有4种答案: (A)成比例增加; (B)保持不变; (C)按2(/)l a 变化; (D)按2(/)a l 变化。
答:B10. 非细长杆如果误用了欧拉公式计算临界力,其结果比该杆的实际临界力 。
答:大。
11. 两根细长压杆,横截面面积相等,其中一个形状为正方形,另一个为圆形,其它条件均相同,则横截面为 的柔度大,横截面为 的临界力大。
答:圆形;正方形。
12. 在水平面ABC 上用同材料的三根杆支持F 。
A 、B 、C 、D 均为铰链节点。
铅直力F 的作用线恰好通过等边三角形ABC 的形心G 。
已知DG AB h ==。
三杆截面均为圆形,直径为d ,材料的弹性模量为E 。
适用欧拉公式的临界柔度是90。
已知20h d =,试确定最大力F 。
解:2sin 60 3BE BE h BG BD =︒=====1234N N , 3sin , N N N N F F F F F DBG F F ===∠===所以434422π92.490,64π0.03π ()d Ed EdF h h λ23==>==⨯=所以13. 图示结构,由圆杆AB 、AC 通过铰链联结而成,若二杆的长度、直径及弹性模量均分别相等,BC 间的距离保持不变,F 为给定的集中力。
试按稳定条件确定用材最省的高度h 和相应的杆直径D 。
(设给定条件已满足大柔度压杆的要求。
) 解:杆达到临界状态时,cr 22πEIF h l 2=+, 此时之F 值为:4222πEI F h l 23==+可求得:4D =(a)二杆之总体积为:V == (b)222d 0, 5, d 2V lh l h h h ==+=得所以 (c) 将(c)式代入(a)式得, 1.303D =14. 长方形截面细长压杆,/1/2b h =;如果将b 改为h 后仍为细长杆,临界力cr F 是原来的多少倍?有4种答案:(A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。
答:C15. 压杆下端固定,上端与水平弹簧相连,如图所示,则压杆长度因数μ的范围有4种答案:(A)μ<0.5; (B)0.5μ<<0.7; (C)0.5μ<<2; (D)μ<2。
答:C16. 圆截面的细长压杆,材料、杆长和杆端约束保持不变,若将压杆的直径缩小一半,则其临界力为原压杆的 ;若将压杆的横截面改变为面积相同的正方形截面,则其临界力为原压杆的 。
答:1π;163。
17. 试导出具有初始挠度0sin(π/)y a x l =的图示压杆的挠度曲线方程()y x 。
证:2220() , , sin(π/)FEIy F y y k y k y k a x l EI''''=-+=+=-令 22sin(π/)sin()cos()π/1a x l y A kx B kx k l 2''=++-由0, 0; 0, , 0; 0x y B x l y A ====== 得 22sin(π/)πal F x l y EI l F2=-x18. 某结构失稳时,挠曲线如图(a)所示,即上端可水平移动但不能转动,下端固定,试推导临界力欧拉公式及挠曲线方程。
证:222e cr cr e cr, [], M F y F k M y k y k y EI EI F -''''==+= ecrsin()cos()M y A kx B kx F =++由 ecr0, 0, 0, 0, M x y y A B F '=====-e cr 2cr [1cos()]π, , 0, sin()0, kx M EI y x l y kl F F l2-'=====[1cos(/)], 2x l x l y y δπδ-==,=。
19.的临界载荷。
解:给以微干扰,由其平衡状态求cr Fcr cr 0 22B k l klM F F δδ'∑==,=得20. 图示刚性杆,由弹簧支持,左右弹簧的刚度分别为1k 、2k ,试导出它的临界载荷。
