第十一章 压杆稳定
第11章压杆的稳定性分析与设计

d
d
2
d
2 = 0
+
令 2 =
有
d 2
这样一个二阶常系数线性微分方程,其通解为
w
= sin + cos
式中,A、B为待定常数,可以通过压杆边界条件确定
w(0) = 0, w(l) = 0
大连大学
33
11.2.1 两端铰支的压杆
将边界条件w(0) = 0和 w(l) = 0代入 = sin + cos ,可求得
FF
F
F
F
F
F
F<Fcr
Fcr
Δ
F´
临界点
F>Fcr
Δ
O
稳定
大连大学
不稳定
22
11.1 弹性平衡稳定性的基本概念——
11.1.3 三种类型的压杆的不同临界状态
大连大学
23
11.1.3 三种类型的压杆的不同临界状态
▪ 不是所有受压杆件都会发生屈曲,也不是所有发生屈曲的压杆都是弹
性的。理论分析与试验结果都表明,根据不同的失效形式,受压杆件
形,或称为临界状态(critical state)。处于临界状态的平衡构形,有
的是稳定的,有的是不稳定的,也有的是中性的。
▪ 非线性弹性稳定理论已经证明了:对于细长压杆,临界平衡构形是稳
定的。
▪ 使杆件处于临界状态的压缩载荷称为临界载荷(critical load),用Fcr
表示。
大连大学
21
11.1.2 临界状态与临界载荷
=0
sin = 0
要使 sin = 0, 或者sin 必等于零。但若等于零,且由 = 0可知此
压杆稳定

受压极限应力。这是因为当临界应力达到材料的受压极限应
力时,压杆已因为强度不足而破坏。因此,对于由塑性材料
制成的压杆,其临界应力不允许超过材料的屈服应力 s ,即:
或
cr (aa bs)/ bs
令
s (as)/b
(11-15)
得 式中,
s
s
为临界应力等于材料的屈服点应力时压杆的柔度值。
但应工大力程于超中某过有个比许数 例多值 极压限 s杆的的,压压它杆杆们稳,的定称柔问为度题中往,长往其杆小临。于界这应P类,力压对一杆于般属用于由临实P界
验所得到的经验公式来计算,常用的有直线形经验公式和抛 物线形经验公式。
1.直线形经验公式
直线形经验公式把压杆的临界应力 下列线性关系:
上一页 下一页 返回
第二节压杆的临界力与临界应力
如果将式(11-9)和式(11-13)中的临界应力与柔度之间的函数
关的系曲绘线在图形cr,称直为角临坐界标应系力内总,图将。得如到图临11界-8应所力示随,柔图度中变曲化线
ACB是按欧拉临界应力公式(11-9)制的;曲线EC是按抛物线 形经验公式(11-17)绘制的。两曲线交于C点,C点的坐标可 由式(11-9)和式(11-17)联立解得。例如对Q235钢E = 200 GPa, a = 235 MPa, b= 0. 006 68MPa,此时
cr
与压杆的柔度
表示为
crab
(11-14)
上一页 下一页 返回
第二节压杆的临界力与临界应力
式中,a和b为与材料有关的常数,其单位为MPa。一些常用 材料的a、b值可见表11-2。
图11-7表示厂直线形经验公式与欧拉曲线。应当指出,经验 公式(11-14 )也有其适用范围,它要求临界应力不超过材料的
第十一章压杆的稳定 - 工程力学

第十一章压杆的稳定承受轴向压力的杆,称为压杆。
如前所述,直杆在轴向压力的作用下,发生的是沿轴向的缩短,杆的轴线仍然保持为直线,直至压力增大到由于强度不足而发生屈服或破坏。
直杆在轴向压力的作用下,是否发生屈服或破坏,由强度条件确定,这是我们已熟知的。
然而,对于一些受轴向压力作用的细长杆,在满足强度条件的情况下,却会出现弯曲变形。
杆在轴向载荷作用下发生的弯曲,称为屈曲,构件由屈曲引起的失效,称为失稳(丧失稳定性)。
本章研究细长压杆的稳定。
§11.1 稳定的概念物体的平衡存在有稳定与不稳定的问题。
物体的平衡受到外界干扰后,将会偏离平衡状态。
若在外界的微小干扰消除后,物体能恢复原来的平衡状态,则称该平衡是稳定的;若在外界的微小干扰消除后物体仍不能恢复原来的平衡状态,则称该平衡是不稳定。
如图11.1所示,小球在凹弧面中的平衡是稳定的,因为虚箭头所示的干扰(如微小的力或位移)消除后,小球会回到其原来的平衡位置;反之,小球在凸弧面上的平衡,受到干扰后将不能回复,故其平衡是不稳定的。
(a) 稳定平衡图11.1 稳定平衡与不稳定平衡上述小球是作为未完全约束的刚体讨论的。
对于受到完全约束的变形体,平衡状态也有稳定与不稳定的问题。
如二端铰支的受压直杆,如图11.2(a)所示。
当杆受到水平方向的微小扰动(力或位移)时,杆的轴线将偏离铅垂位置而发生微小的弯曲,如图11.2(b)所示。
若轴向压力F较小,横向的微小扰动消除后,杆的轴线可恢复原来的铅垂平衡位置,即图11.2(a),平衡是稳定的;若轴向压力F足够大,即使微小扰动已消除,在力F 作用下,杆轴线的弯曲挠度也仍将越来越大,如图11.2(c)所示,直至完全丧失承载能力。
在F =F cr 的临界状态下,压杆不能恢复原来的铅垂平衡位置,扰动引起的微小弯曲也不继续增大,保持微弯状态的平衡,如图11.2(b)所示,这是不稳定的平衡。
如前所述,直杆在轴向载荷作用下发生的弯曲称为屈曲,发生了屈曲就意味着构件失去稳定(失稳)。
第11章压杆稳定
材料力学
第29页/共63页
二、折减因数法
s
F A
[s w ]
s cr
nst
scr、nst与压杆柔度有关,[sw]是的 函数。
[sw]=j [s ]
[s ]——强度许用应力 j —— 折减因数 j 1
稳定条件
与柔度有关
s FP j[s ] 工作应力不大于
A
稳定许用应力
注 不必由柔度判断压杆属何种性质的杆,简化计算。 意
强度 条件
sr
[s ]
s0
n
相当应力不大 于许用应力
极限应力
s0
s
{
s
sb
塑性材料 脆性材料
极限应力和安全因数只与材料有关,与实 际应力状态无关,即强度许用应力为常数。
材料力学
第27页/共63页
稳定 条件
s
F A
[s
w
]
s0
nst
s cr
nst
工作应力不大于稳定许用应力。
极限应力(临界应力)和稳定安全因数不仅 与材料有关,而且与实际压杆的长度、约束 条件、横截面尺寸和形状有关,即与实际压 杆的柔度有关,所以稳定许用应力不是常数。
z
ml
iz
1 940 14.43
65.1
第36页/共63页
F A
z
材料力学
l1 z
B l1
y Fx
z
h
b
F x
x-z 面内,两端固定
绕y轴发生失稳
m = 0.5
iy
b 23
20 23
5.77 mm
y
ml
iy
0.5 880 5.77
76.3
第十一章压杆的稳定_工程力学

第十一章 压杆的稳定承受轴向压力的杆,称为压杆。
如前所述,直杆在轴向压力的作用下,发生的是沿轴向的缩短,杆的轴线仍然保持为直线,直至压力增大到由于强度不足而发生屈服或破坏。
直杆在轴向压力的作用下,是否发生屈服或破坏,由强度条件确定,这是我们已熟知的。
然而,对于一些受轴向压力作用的细长杆,在满足强度条件的情况下,却会出现弯曲变形。
杆在轴向载荷作用下发生的弯曲,称为屈曲,构件由屈曲引起的失效,称为失稳(丧失稳定性)。
本章研究细长压杆的稳定。
§11.1 稳定的概念物体的平衡存在有稳定与不稳定的问题。
物体的平衡受到外界干扰后,将会偏离平衡状态。
若在外界的微小干扰消除后,物体能恢复原来的平衡状态,则称该平衡是稳定的;若在外界的微小干扰消除后物体仍不能恢复原来的平衡状态,则称该平衡是不稳定。
如图11.1所示,小球在凹弧面中的平衡是稳定的,因为虚箭头所示的干扰(如微小的力或位移)消除后,小球会回到其原来的平衡位置;反之,小球在凸弧面上的平衡,受到干扰后将不能回复,故其平衡是不稳定的。
上述小球是作为未完全约束的刚体讨论的。
对于受到完全约束的变形体,平衡状态也有稳定与不稳定的问题。
如二端铰支的受压直杆,如图11.2(a )所示。
当杆受到水平方向的微小扰动(力或位移)时,杆的轴线将偏离铅垂位置而发生微小的弯曲,如图11.2(b)所示。
若轴向压力F 较小,横向的微小扰动消除后,杆的轴线可恢复原来的铅垂平衡位置,即图11.2(a ),平衡是稳定的;若轴向压力F 足够大,即使(a ) 稳定平衡 图11.1 稳定平衡与不稳定平衡微小扰动已消除,在力F 作用下,杆轴线的弯曲挠度也仍将越来越大,如图11.2(c)所示,直至完全丧失承载能力。
在F =F cr 的临界状态下,压杆不能恢复原来的铅垂平衡位置,扰动引起的微小弯曲也不继续增大,保持微弯状态的平衡,如图11.2(b)所示,这是不稳定的平衡。
如前所述,直杆在轴向载荷作用下发生的弯曲称为屈曲,发生了屈曲就意味着构件失去稳定(失稳)。
第11章 压杆稳定性问题

相等,则此压杆的临界压力又为多少?
(压杆满足欧拉公式计算条件)
h
动脑又动笔
解: 一端固定,一端自由,长度因数 μ=2 在应用欧拉公式时,截面的惯性
矩应取较小的I 值。
Iy 1 3 1 hb 90 403 mm 4 48 104 mm 4 12 12
b
F
l
1 3 1 I z bh 40 903 mm 4 243 104 mm 4 12 12
理解长细比、临界应力和临界应力总图的概念,熟 悉各类压杆的失效形式。
§11–1 压杆稳定性的基本概念
① 强度 衡量构件承载能力的指标 ② 刚度 ③ 稳定性 工程中有些构件具有足够的强度、刚度,却不一定能安全 可靠地工作。 杆件在各种基本变形下的强度和刚度问题在前述各章节中 已作了较详细的阐述,但均未涉及到稳定性问题。事实上, 杆件只有在受到压力作用时,才可能存在稳定性的问题。
屈曲曲线是偏离原直线轴线不远的微弯状态。
F F EI L
M d2w 2 EI dx
§11–2 细长压杆的临界荷载—欧拉临界力
一、两端铰支压杆的临界力
多大的轴向压力才会使压杆失稳?
d2w EI 2 Fw 0 dx
y
M EI x w L
记
F
k2
F EI
F
F
x
d2w 2 k w0 2 dx
§11–3长细比的概念 三类不同压杆的判断
三、临界应力总图
cr
S
P
cr s
cr a b
2E cr 2
粗短杆 s
s s a
b
中长杆
P
细长杆
第11章压杆稳定

压杆截面如图所示。两端为柱形铰链约束,
若绕 y 轴失稳可视为两端固定,若绕 z 轴失稳可视为 两端铰支。已知,杆长l=1m ,材料的弹性模量
E=200GPa,sp=200MPa。求压杆的临界应力。
解:
iy 1 3 ( 0 . 03 0 . 02 ) Iy 12 0.0058m A 0.03 0.02
3.压杆失稳:
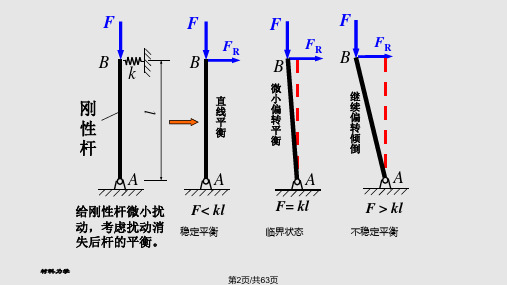
弹性杆件 稳定直线平衡
F Fcr
F Fcr
F Fcr
F Fcr
微小扰动 恢复直线平衡 不稳定直线平衡
F Fcr
弯曲 除去扰动
v
弯曲
微小扰动
新的弯曲平衡 随遇平衡
除去扰动
F Fcr 除直线平衡形式外,无穷小邻域内,可能微弯平衡
压杆从直线平衡形式到弯曲平衡形式的转变,称为失稳
一、两端铰支的细长压杆:
x
Fcr
F M(x)=Fw
l m w B m
m
x
m
B y F
x
y
Fcr
压杆任一 x 截面沿 y 方向的位移 w f ( x ) 该截面的弯矩
M ( x ) Fw
杆的挠曲线近似微分方程
EIw '' M ( x ) Fw
2
( a)
m
F 令k 得 w '' k 2 w 0 (b) EI
16
4.压杆的临界压力: 稳 定 平 衡 临界状态
过 渡
临界压力:Fcr
不 即:使压杆保持在微 稳 弯状态下平衡的最小 定 轴向力。 平 衡
F Fcr —稳定平衡状态 F Fcr —临界平衡状态 F Fcr —不稳定平衡状态
材料力学-第11章 压杆稳定new

引言
压杆稳定的利用 - 柔性电子器件
材料力学-第11章 压杆稳定
引言
基本概念
F
压杆失稳(屈曲): 受压杆件由直线平衡状态变为弯曲平衡状态 临界载荷:
使得受压杆件由直线平衡态转为弯曲平衡态的临界力
材料力学-第11章 压杆稳定 受压杆件为什么会失稳?
F
引言
杆件压力超过临界载荷时,弯曲构型具有更 小的应变能
Fcr
π 2 EI
l
2
这一表达式称为欧拉公式。其中l为不同压杆屈曲后挠曲线上正弦 半波的长度,称为有效长度(effective length);
为反映不同支承影响的系数,称为长度因数(coefficient of
1ength),可由屈曲后的正弦半波长度确定。
材料力学-第11章 压杆稳定
FPcr
π 2 EI
l
2
需要注意的是, 临界载荷公式只有在压杆的微弯 曲状态下仍然处于弹性状态时才是成立的。
材料力学-第11章 压杆稳定
§11-3 两端非铰支细长压杆的临界载荷
例题
图示四根压杆,已知杆件横截面和材料完全相同。 试:将压杆按承载能力大小排序
5m
7m
(a)
(b)
3m
(c)
§11-3 两端非铰支细长压杆的临界载荷 长度因数 由屈曲后的正弦半波长度确定
欧拉公式可写为:
2 EI
正弦半波长
2
两端铰支 =1.0
一端自由, 一端固定 =2.0
一端铰支, 一端固定 =0.7
两端固定 =0.5
材料力学-第11章 压杆稳定
§11-3 两端非铰支细长压杆的临界载荷
F
Fcr
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使Fcr最小的方向为实际弯曲方向,I为挠曲时横
截面对其中性轴的惯性矩。
如销孔类铰链,即所谓的柱状铰。约束特点为:
在垂直于轴销的平面内,轴销对杆的约束相当于铰支;
而在轴销平面内,轴销对杆的约束则接近于固定端。
第十一章 压杆稳定问题
思考:试判断下列压杆长度系数的取值范围
μ>2
0.7<μ<2
cr
2E 2
P
或
2E p
E
p
P
(10 10)
P值仅与弹性模量E及比例极限P 有关, P仅随材料
性质而异。柔度≥P的压杆称大柔度杆。
当 ≥P(大柔度压杆或细长压杆)时,才能应用欧
拉公式。
当<P时(中、小柔度压杆),不能应用欧拉公式。
第十一章 压杆稳定问题
P 的大小仅取决于压杆材料的 力学性能。例如,对于Q235 钢,E=206GPa, P=200MPa,得
0.7
0.5
欧拉临界压力公式的统一表达式:
Fcr
2EI (l)2
(10 6)
第十一章 压杆稳定问题
Fcr为维持微弯平衡状态最小的压力
各方向约束情况相同时:
Fcr
2EI (l)2
乘积l称为压杆的相当长度或有效长度。 为常数,称长度因素,代表支持方式对临界载荷的
影响。 I=Imin––– 最小形心主惯性矩
第十一章 压杆稳定问题
压杆的稳定(4学时)
教学内容:压杆稳定的概念,细长压杆的临界力和欧 拉公式,欧拉公式的适用范围,中、小柔度杆的临界 应力,压杆的稳定计算,提高压杆稳定性的措施。 教学要求: 1、了解丧失稳定、临界力的概念,中、小柔度杆的临 界应力,压杆的稳定条件,提高压杆稳定性的措施; 2、理解细长压杆的临界力和欧拉公式,临界应力、惯 性半径、柔度的概念,欧拉公式的适用范围。 重点:细长压杆的临界力和欧拉公式。 难点:细长压杆的临界力和欧拉公式。
故取
Fcr
2EI
(0.5a)2
第十一章 压杆稳定问题
练习: 求下列细长压杆的临界力。
y
y
xz
h
z
L1
解: ①绕
y
L2
轴,两端铰支:
b
=
1
.
0
,I
y
b3h 12
②绕 z 轴,左端固定,右端铰支:
,
Fcr, y
2 EI L22
y
=0.7,
I
z
bh3 12
,
Fcr , z
2EIz
(0.7 L1 )2
l22
(1) (2)
F ① 90 ②
将式(2)除以式(1)便得:
tg (l1 l2 )2 ctg2
l
由此得: arctg(ctg2 )
第十一章 压杆稳定问题
二、小绕度理论与理想压杆模型的实际意义
P322图11-6 直线AG与曲线AB的交点称为临界点,相应之载荷即为临
界载荷。临界点也称分支点,从该点开始,出现两种平衡 形态。按大挠度理论,当压杆处于临界状态时,其唯一的 平衡形态是直线,而非微弯。 在A点附近的很小一段范围内,可以近似地用水平线代替 曲衡线,。也从可力在学任上何,微当弯位F=置Fcr保时持,平压衡杆。既由可此在可直见线,位以置“保微持弯平 平衡”作为临界状态的特征,并根据挠曲轴近似微分方程 确定临界载荷的方法,是利用小变形对大挠度理论的一种 合理简化,它不仅正确,而且,由于求解简单,更为实用。 曲线AB在A点附近极为平坦,因此,当轴向压力F略高于 临界值Fcr时,挠度即急剧增长。由此可见,大挠度理论更 鲜明地说明了失稳的危险性。
(l)3 0.7 1.6a 1.12a
第十一章 压杆稳定问题
练习:已知图示压杆EI,且杆在B支承处不能转动 求:临界压力
F
解: l AB 0.5 a 0.5a
c
lBC 0.7 0.5a 0.35a
B
F AB cr
2EI
(0.5a)2
F BC cr
2EI
(0.35a)2
a\2
a
A
同,μ不同,视综合情况而定。
4、端约束越强,Fcr越大,越不易失稳。
5、为了保证不同的方向μ尽可能相同,端约束用球铰, 这样,各方向有较一致的约束。
6、Fcr非外力也非内力,是反映构件承载能力的力学量。
第十一章 压杆稳定问题
§11-4 中、小柔度杆的临界应力
一、临界应力与柔度 压杆处于临界状态时横截面上的平均应力,称为压杆
二、中心受压直杆稳定性分析
举例:一端固定,一端自由的钢板尺受轴向压力作用。
F
F<Fc干r
F>Fcr
扰
干
力
扰
直
稳 去不
力
线
定 除稳
去
平
平 ,定
除
衡
衡 恢平
,
状
复衡
继
态
直
续
线
弯
曲
第十一章 压杆稳定问题 三、稳定与失稳
1.压杆稳定性:压杆维持其原直线平衡状态的能力。
2.压杆失稳(屈曲):压杆丧失其原直线平衡状态, 不能稳定地工作。 3.临界状态:由稳定平衡向不稳定平衡过渡的状态。 4.临界载荷Fcr:使压杆直线形式的平衡开始由稳定转 变为不稳定的轴向压力值,或使压杆在微弯状态保持 平衡的最小轴向压力,称为压杆的临界载荷,用Fcr表 示。即压杆的压力逐渐上升,使压杆的平衡由稳定平衡 状态向不稳定状态的质变的转折点。
第十一章 压杆稳定问题
例: 图示各细长压杆材料和截面均相同,试问哪一 根杆能承受的压力最大, 哪一根的最小?
P P
P 因为 l 1 l 2 l 3
又
Fcr
2EI
l 2
a 1.3a
1.6a
可知 Fcr1 Fcr2 Fcr3
(1)
(2)
(l)1 2a (l)2 1.3a
(3)
杆(1)能承受的压力最小,最先失稳; 杆(3)能承受的压力最大,最稳定。
0<θ<π/2)。
F
解:由静力平衡条件可
解得两杆的压力分别为: ① 90 ②
N1 F cos ,N2 F sin
两杆的临界压力分别为 :
l
Fcr1
2E l12
I, F cr2
2EI
l22
第十一章 压杆稳定问题
要使F最大,只有
N1、N
都达到临界压力,即
2
F cos 2EI
l12
F
sin
2EI
两端铰支细长压杆的临界载荷与截面抗l弯刚度EI成正比,与杆件长度平方成反
比。在推导过程中,运用了边界条件,说明临界力与两端支座条件有关,惯性矩
I应为压杆横截面的最小惯性矩Imin。两端铰支细长压杆临界状态时的挠曲线为一 正弦曲线,最大挠度或幅值A则取决于压杆微弯的程度。由此可见,压杆在临界
状态时的平衡,是一种有条件的随遇平衡,微弯程度虽然可以任意,但挠曲轴形
实际压杆所能承受的最大压力必小于理想中心压杆 的临界力Fcr。
第十一章 压杆稳定问题
§11-2 两端铰支细长压杆的临界载荷
一、临界载荷的欧拉公式
1、分析思路:Fcr→临界状态(微弯)→弯曲变形→挠
曲线微分方程。
x
挠曲线微分方程:EIw" M (x) Fcr w
2、推导:Fcr
x
引用记号:k 2 Fcr ,得:w" k 2w 0 EI
二、两端固定的压杆
挠曲线:分成三段,两拐点与两端
相距均为l/4
中间段与两端铰支时一样,
相当长度为l/2
Fcr
2EI
(l / 2)2
2EI
(0.5l)2
第十一章 压杆稳定问题
3、一端固定,一端铰支的压杆
F
挠曲线:分成二段,拐点与一 端距离为0.7l
0.7l 较长的段与两端铰支时一样,
相当长度为0.7l
第十一章 压杆稳定问题
§11-1 引言 §11-2 两端铰支细长压杆的临界载荷 §11-3 两端非铰支细长压杆的临界载荷 §11-4 中、小柔度杆的临界应力 §11-5 压杆的稳定条件与合理设计 §11-6 提高压杆稳定的措施
第十一章 压杆稳定问题
§11-1 引言
①强度
构件的承载能力: ②刚度
③稳定性
0.3l
Fcr
2EI
(0.7l ) 2
统一表达式:Fcr
2EI (l)2
---相当长度系数,代表支持
方式对临界载荷的影响。µl称压 杆的相当长度或有效长度,即相 当的两端铰支压杆的长度,或压 杆挠曲轴拐点间的距离。
第十一章 压杆稳定问题
F
F
F
l
l
0.7l 0.3l
F
l/4 l/2 l/4
2
1
第十一章 压杆稳定问题
cr
Fcr A
2EI
l2 A
2E
l / i2
2E 2
l
i
称为压杆的柔度(细长比)。综合地 反映了压杆的长度l,支持方式 与截 面几何性质i对临界应力的影响。
cr
2E 2
Fcr
A cr
2EA 2
细长压杆的临界应力,与柔度的平方成反比, 越大,相应的 cr 越小,压杆越容易失稳。
压杆保持直线状态平衡 的最大力;使压杆失稳
第十一章 压杆稳定问题
在临界载荷作用下,压杆既可在直线状态下保持 平衡,也可在微弯状态下保持平衡。所以,当轴向压力 达到或超过压杆的临界载荷时,压杆将失稳。 5.压杆失稳原因:
①杆轴线本身不直(初曲率); ②加载偏心; ③压杆材质不均匀; ④外界干扰力。
