第10章 压杆稳定
合集下载
第10章 杆件稳定性
(F )
a
II (大 挠 度 理 论) II (小 挠 度 理 论)
Fcr
B I (稳 定)
D'
O
a)
b)
第10章
两条平衡路径Ⅰ 的交点为分支点 分支点 B 将 分支点。 两条平衡路径 Ⅰ和 Ⅱ 的交点为 分支点 。
10.1 稳定性概念
原始的平衡路径Ⅰ分为两段：前段 OB 上的点属于稳定 原始的平衡路径Ⅰ 分为两段： 平衡， 上的点属于不稳定平衡。 平衡 ， 而后段 BC 上的点属于不稳定平衡 。 具有这种特 征的失稳形式称为分支点失稳形式。 征的失稳形式称为 分支点失稳形式。 分支点失稳形式
θ
例10.2
第10章
考虑如图(a)的单自由度非完善体 考虑如图(a)的单自由度非完善体 (a)
F k
B B'
系，刚性杆AB有初倾角 ε 。 刚性杆 有初倾角
k
10.1 稳定性概念
l
l
A
A
（a） ）
（b） ）
解：在图(b)中，平衡条件(水平方向)为 在图(b)中 平衡条件(水平方向) (b)
F tan(θ + ε ) − kl[sin(θ + ε ) − sin ε ] = 0 sin ε F = kl cos(θ + ε )[1 − ] sin(θ + ε )
第10章
例10.5
10.1 稳定性概念
如图所示， 如图所示，由三根相同的刚性杆组
成的系统，一端作用外力 ,铰结处B、 都是弹性 成的系统，一端作用外力F,铰结处 、C都是弹性 系数为k的弹性支座。试用两种方法求临界载荷。 系数为 的弹性支座。试用两种方法求临界载荷。 的弹性支座
a
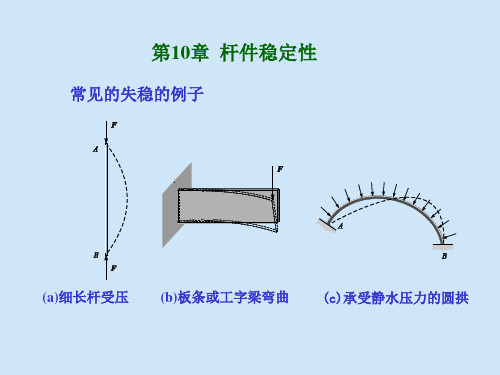
II (大 挠 度 理 论) II (小 挠 度 理 论)
Fcr
B I (稳 定)
D'
O
a)
b)
第10章
两条平衡路径Ⅰ 的交点为分支点 分支点 B 将 分支点。 两条平衡路径 Ⅰ和 Ⅱ 的交点为 分支点 。
10.1 稳定性概念
原始的平衡路径Ⅰ分为两段：前段 OB 上的点属于稳定 原始的平衡路径Ⅰ 分为两段： 平衡， 上的点属于不稳定平衡。 平衡 ， 而后段 BC 上的点属于不稳定平衡 。 具有这种特 征的失稳形式称为分支点失稳形式。 征的失稳形式称为 分支点失稳形式。 分支点失稳形式
θ
例10.2
第10章
考虑如图(a)的单自由度非完善体 考虑如图(a)的单自由度非完善体 (a)
F k
B B'
系，刚性杆AB有初倾角 ε 。 刚性杆 有初倾角
k
10.1 稳定性概念
l
l
A
A
（a） ）
（b） ）
解：在图(b)中，平衡条件(水平方向)为 在图(b)中 平衡条件(水平方向) (b)
F tan(θ + ε ) − kl[sin(θ + ε ) − sin ε ] = 0 sin ε F = kl cos(θ + ε )[1 − ] sin(θ + ε )
第10章
例10.5
10.1 稳定性概念
如图所示， 如图所示，由三根相同的刚性杆组
成的系统，一端作用外力 ,铰结处B、 都是弹性 成的系统，一端作用外力F,铰结处 、C都是弹性 系数为k的弹性支座。试用两种方法求临界载荷。 系数为 的弹性支座。试用两种方法求临界载荷。 的弹性支座
材料力学10压杆稳定_1欧拉公式
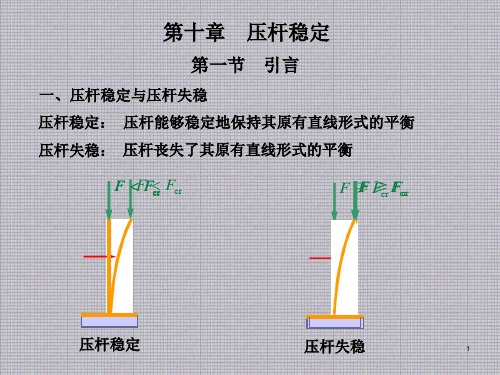
◆ 本例中，三杆截面面积基本相等，但由于其形状不同， Imin 不
同，致使临界力相差很大。最合理的截面形状为圆环形。
14
[例3] 图示各杆均为圆形截面细长压杆。已知各杆的材料及直径相 等。问哪个杆先失稳？ 解：由于各杆的材料及 截面均相同，故只需比
1.3 a F F F
较其相当长度 l 即可
a
杆A： 2 l 2a
F
F
2 1
0.7
压杆两端固定可轴向移动：
0.5
6
上述弹性压杆临界力的计算公式称为欧拉公式
Fc r
π 2 EI
l
2
说明： 1）欧拉公式的适用范围：线弹性（ ≤ p）
2）在压杆沿各个方向约束性质相同的情况下（即各个方向上 的 相等），I 应取最小值 3） l 称为压杆的相当长度
2
2000年10月25日上午10 时，南 京电视台演播中心由于脚手架 失稳使屋顶模板倒塌，导致死 6 人，伤 34 人。
3
2010年1月3日，通往昆明新机场的一座在建桥梁施工时因 支撑结构中的压杆失稳而坍塌，共导致 40 余人死伤。
4
二、压杆的临界力 使压杆由稳定向失稳转化的轴向压力的界限值称为压杆的临界力， 记作 Fcr 。即当 F ＜ Fcr ： 压杆稳定 F ≥ Fcr ： 压杆失稳 亦可将压杆的临界力 Fcr 理解为使压杆失稳的最小轴向压力
hb3 1 Iy 90 403 48 108 m 4 12 12
根据欧拉公式，此压杆的临界力
Fcr
π 2 EI y l
2
23.8 kN
11
[例2] 一端固定，一端自由的中心细长压杆。已知杆长 l = 1m , 材 料的弹性模量 E = 200 GPa。当分别采用图示三种截面时，试计算 其临界力。
(英汉双语)工程力学第十章 压杆稳定
P x L P P
P
M ( x, y ) = Py
②Approximate differential equation of the deflection curve
y
xM P P 2 2 y ′′ + y = y ′′ + k y = 0 , where : k = EI EI 19
M P y ′′= = y EI EI
EIy′′= M ( x)= Py+M
x M0 Let
k2 = P EI
y ′′ + k 2 y = k 2
M0 P P
M0
M y = c cos kx + d sin kx + ′ = d cos kx c sin kx P y
The boundary conditions are:
M P
x=0, y= y′=0;x=L, y= y′=0 27
③Solution of the differential equation： ④Determine the integral constants：
y = A sin x + B cos x
y ( 0 )= y ( L )= 0
A× 0 + B = 0 That is A sin kL + B cos kL = 0
Instable equilibrium
15
二、压杆失稳与临界压力 ： 1.理想压杆：材料绝对理想；轴线绝对直；压力绝对沿轴线作用。 2.压杆的稳定平衡与不稳定平衡：
稳 定 平 衡
不 稳 定 平 衡
16
3).loss of stability of compressed column：
第10章压杆稳定
9
这表明用低碳钢Q235制成的压杆，仅在柔度≥100时， 才能应用欧拉公式计算其临界应力或临界力，常用材料柔度
可查表。
第十章
四、中小柔度杆的临界应力
压杆稳定
10.2 临界力的确定
对于不能应用欧拉公式计算临界应力的压杆，即压杆内 的工作应力大于比例极限但小于屈服极限时，可应用在实验 基础上建立的经验公式。常见经验公式有直线公式和抛物线
公式。其中，直线公式为
cr a b a s cr a b s b a s s s p
b
抛物线公式为：
cr a1 b1
2
第十章
压杆稳定
10.3 压杆稳定的计算与校核
前面的讨论表明，对各种柔度的压杆，总可以用欧拉公
稳定安全因素
10.3 压杆稳定的计算与校核
nst
一般要大于强度安全因素。这是因
为一些难以避免的因素，如杆件的初弯曲、压力偏心、材料 不均匀和支座缺陷等，都严重影响压杆的稳定，降低了临界
压力。而同样这些因素，对杆件强度的影响不象对稳定那么
严重。关于稳定安全因素 中查到。
nst
一般可以在设计手册或规范
第十章
F Fcr ，
撤消横向干扰力后杆件能够恢复到 原来的直线平衡状态（图10–2b），
则原有的平衡状态是稳定平衡状态；
第十章
压杆稳定性的概念：
压杆稳定
10.1 压杆的稳定概念
当轴向压力增大到一定值
F Fcr
时，撤消横向干扰力后杆件不能再恢复到 原来的直线平衡状态（图10–2c），则原
有的平衡状态是不稳定平衡状态。 会进一
10.1 压杆的稳定概念
如果小球受到微小干扰而稍微偏离它原有的平衡位置， 当干扰消除以后，它不但不能回到原有的平衡位置，而且 继续离去，那么原有的平衡状态称为不稳定平衡状态， 如图c 所示。
这表明用低碳钢Q235制成的压杆，仅在柔度≥100时， 才能应用欧拉公式计算其临界应力或临界力，常用材料柔度
可查表。
第十章
四、中小柔度杆的临界应力
压杆稳定
10.2 临界力的确定
对于不能应用欧拉公式计算临界应力的压杆，即压杆内 的工作应力大于比例极限但小于屈服极限时，可应用在实验 基础上建立的经验公式。常见经验公式有直线公式和抛物线
公式。其中，直线公式为
cr a b a s cr a b s b a s s s p
b
抛物线公式为：
cr a1 b1
2
第十章
压杆稳定
10.3 压杆稳定的计算与校核
前面的讨论表明，对各种柔度的压杆，总可以用欧拉公
稳定安全因素
10.3 压杆稳定的计算与校核
nst
一般要大于强度安全因素。这是因
为一些难以避免的因素，如杆件的初弯曲、压力偏心、材料 不均匀和支座缺陷等，都严重影响压杆的稳定，降低了临界
压力。而同样这些因素，对杆件强度的影响不象对稳定那么
严重。关于稳定安全因素 中查到。
nst
一般可以在设计手册或规范
第十章
F Fcr ，
撤消横向干扰力后杆件能够恢复到 原来的直线平衡状态（图10–2b），
则原有的平衡状态是稳定平衡状态；
第十章
压杆稳定性的概念：
压杆稳定
10.1 压杆的稳定概念
当轴向压力增大到一定值
F Fcr
时，撤消横向干扰力后杆件不能再恢复到 原来的直线平衡状态（图10–2c），则原
有的平衡状态是不稳定平衡状态。 会进一
10.1 压杆的稳定概念
如果小球受到微小干扰而稍微偏离它原有的平衡位置， 当干扰消除以后，它不但不能回到原有的平衡位置，而且 继续离去，那么原有的平衡状态称为不稳定平衡状态， 如图c 所示。
第10章压杆稳定
第10章压杆稳定10.1【学习基本要求】1、理解压杆稳定的稳定平衡、不稳定平衡、临界力的概念。
2、掌握不同杆端约束下细长杆的临界力的计算公式。
3、理解长度系数的意义，掌握与常见的几种约束形式对应的长度系数。
4、掌握临界力与压杆长度、横截面形状、杆端约束的关系。
5、理解压杆的柔度的概念，掌握柔度的计算方法。
6、明确欧拉公式的适用范围和临界应力计算。
7、熟练掌握大柔度杆、中柔度杆、小柔度杆的判别方法及临界应力总图。
8、掌握压杆的稳定条件。
9、能熟练运用安全系数法对不同柔度压杆的稳定性进行分析计算。
10、掌握提高压杆稳定性的措施。
10.2【要点分析】1、压杆稳定的概念稳定性：压杆能保持稳定的平衡性能称为压杆具有稳定性。
失稳：压杆不能保持稳定的平衡叫压杆失稳。
稳定平衡：细长杆在轴向压力下保持直线平衡状态，如果给杆以微小的侧向干扰力，使杆产生微小的弯曲，在撤去干扰力后，杆能够恢复到原有的直线平衡状态而保持平衡，这种原有的直线平衡状态称为稳定平衡。
．．．不稳定平衡：撤去干扰力后，杆不会回到原来的平衡，而是保持微弯或力F继续增大，杆继续弯曲，产生显著的变形，甚至发生突然破坏，则称原有的平衡为不稳定平衡。
．．．失稳：轴向压力F由小逐渐增大的过程中，压杆由稳定的平衡转变为不稳定的平衡，这种现象称为压杆丧失稳定性或压杆失稳。
临界平衡状态：压杆在稳定平衡和不稳定平衡之间的状态称为临界平衡状态。
临界压力或临界力：压杆由直线状态的稳定平衡过渡到不稳定平衡时所对应的轴向压力，称为压杆的临界压力或临界力。
（即能使压杆保持微弯状态下的平衡的力）【注意】①临界状态也是一种不稳定平衡状态。
②临界状态下压杆即能在直线状态下也能在微弯状态下保持平衡。
③临界力使压杆保持微小弯曲平衡的最小压力。
2、理想压杆理想压杆是指不存在初弯曲、初偏心、初应力的承受轴向压力的均匀连续、各向同性的直杆。
工程中实际压杆与理想压杆有很大的区别，因为实际压杆常常带有初始缺陷，如：①初弯曲的存在使压杆截面形心轴线不是理想直线；②初偏心的存在造成压力作用线与杆件轴线不重合；③残余应力造成材料内部留有初应力；④材质不可能是完全均匀连续的。
材料力学-10-压杆的稳定问题
0 A＋1 B 0 sinkl A coskl B 0
根据线性代数知识，上述方程中，常数A、B不全为零 的条件是他们的系数行列式等于零：
0
1
sinkl coskl
0
sinkl 0
第10章 压杆的稳定问题
两端铰支压杆的临界载荷欧拉公式
sinkl 0
FP k EI
第10章 压杆的稳定问题
临界应力与临界应力总图 长细比是综合反映压杆长度、约束条件、截面尺寸和截面 形状对压杆分叉载荷影响的量，用表示，由下式确定：
＝
l
i
I A
其中，I为压杆横截面的惯性半径，由下式确定：
i
从上述二式可以看出，长细比反映了压杆长度、支承条件以 及压杆横截面几何尺寸对压杆承载能力的综合影响。
不同刚性支承条件下的压杆，由静力学平衡方法得到的平衡 微分方程和边界条件都可能各不相同，确定临界载荷的表达式亦 因此而异，但基本分析方法和分析过程却是相同的。对于细长杆， 这些公式可以写成通用形式：
FPcr
π 2 EI
l
2
这一表达式称为欧拉公式。其中l为不同压杆屈曲后挠曲线上正弦 半波的长度，称为有效长度(effective length)； 为反映不同支承 影响的系数，称为长度系数（coefficient of 1ength），可由屈曲后 的正弦半波长度与两端铰支压杆初始屈曲时的正弦半波长度的比 值确定。
第10章 压杆的稳定问题
临界应力与临界应力总图
临界应力与长细比的概念
前面已经提到欧拉公式只有在弹性范围内才是适用的。这 就要求在分叉载荷即临界载荷作用下，压杆在直线平衡构形时， 其横截面上的正应力小于或等于材料的比例极限，即
材料力学 第十章 压杆稳定问题
由杆，B处内力偶
MB Fcraq1 , q1
由梁，B处转角
MB Fcr a
q2
MBl 3EI
q1 B
MB MBl Fcra 3EI
3EI Fcr al
q2 C
l
Page21
第十章 压杆稳定问题
作业
10-2b，4，5，8
Page22
第十章 压杆稳定问题
§10-3 两端非铰支细长压杆的临界载荷
稳定平衡
b. F k l
临界(随遇)平衡
c. F k l
不稳定平衡
Fcr kl 临界载荷
F
k l
F 驱动力矩 k l 恢复力矩
Page 5
第十章 压杆稳定问题
（3）受压弹性杆受微干扰
F Fcr 稳定平衡 压杆在微弯位置不能平衡,要恢复直线
F >Fcr 不稳定平衡 压杆微弯位置不能平衡,要继续弯曲,导致失稳
(
w)
令 k2 F
EI
d 2w dx2
k
2w
k
2
l
l
FM w
x
F B
F
B F
Page24
第十章 压杆稳定问题
d 2w dx2
k2w
k 2
F
w
通解：
A
x
B
w Asinkx Bcoskx
l
考虑位移边界条件：
x 0, w 0,
B
x 0, q dw 0
Page31
第十章 压杆稳定问题
二、类比法确定临界载荷
l
压杆·稳定性
=
2 ，因为 h＞b ，则 I y
=
hb3 12
＜ bh3 12
=
Iz ，由式（10.3）得
Pcr
=
π 2 EI (μl)2
=
π2
× (200 ×103
MPa) × ( 1 × 40 mm × (20 12
(2 ×1000 mm)2
mm)3 ) ≈13200
N
= 13.2
kN
10.2.2 临界应力
当压杆受临界压力作用而维持其不稳定直线平衡时，横截面上的压应力仍然可按轴向压
10.3.2 临界应力经验公式与临界应力总图
在工程实际中，常见压杆的柔度λ 往往小于 λp ，即 λ＜λp ，这样的压杆横截面上的应力 已超过材料的比例极限，属于弹塑性稳定问题。这类压杆的临界应力可通过解析方法求得， 但通常采用经验公式进行计算。常见的经验公式有直线公式与抛物线公式等，这里仅介绍直 线公式。把临界应力 σcr 与柔度λ 表示为下列直线关系称为直线公式。
式中，λ 称为压杆的柔度或长细比，为无量纲量，它综合反映了压杆的长度、约束形式及截 面几何性质对临界应力的影响。于是，式（10.4）中的临界应力可以改写为
·219·
材料力学
σ cr
=
π2E λ2
式（10.6）是欧拉公式（10.3）的另一种表达形式，两者并无实质性差别。
（10.6）
10.3 欧拉公式的适用范围·临界应力总图·直线公式
2
≤σ
p
或
λ≥π E σp
（10.7）
令
于是条件式（10.7），可以写成
λP = π
E σp
（10.8）
λ ≥ λp
（10.9）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
(0.5l )
2
例：图示两桁架中各杆的材料和截面均相 同，设P1和P2分别为这两个桁架稳定的最大载 荷，则 (A) P1=P2 (B) P1<P2 (C) P1>P2 (D) 不能断定P1和P2的关系
第14页
解：图(a) 中，AD杆受压 2 EI N AD 2 P 1 2 2a
第38页
P cra : P crb : P crc cra A1 : crb A2 : crc A3
1: 2 : 20
第39页
例：图示圆截面压杆d=40mm，σs=235MPa。
求可以用经验公式σcr=304-1.12λ (MPa)计算 临界应力时的最小杆长。
第40页
a s 304 235 616 . 解： s 112 . b 由
2
，则 v k v 0
2 2
2
特征方程为 r k 0
有两个共轭复根 ki
第 5页
通解： v A sin kx B cos kx 边界条件：x 0时：v 0 B 0 x l 时：v 0 A sin kl 0
sin kl 0 kl n
Pc r
2 2 2
2
第26页
l
i
2
压杆的长细比 压杆的柔度
cr
E 2
计算压杆的临界 应力的欧拉公式
第27页
二、欧拉公式的适用范围 经验公式
在推导欧拉公式时,使用了挠曲线的近似微分
方程:
E I v M ( x)
在推导该方程时,应用了胡克定律。因此，欧拉 公式也只有在满足胡克定律时才能适用：
Pmax 2 Pcr
第22页
2 Ed
3
4
64a
2
例：图示结构，①、②两杆截面和材料相
同，为细长压杆。确定使载荷 P 为最大值时的
θ角（设0<θ<π /2）。
①
90
②
第23页
解：由静力平衡条件可解得两杆的压力分别为： N1 P cos ， N 2 P sin
两杆的临界压力分别为：
2
2
由此得
arc tg(ctg )
①
90
②
第25页
§10-3 压杆的临界应力及临界应力总图
一、压杆的临界应力
EI Pcr 2 (l )
2
E (i A) E EI cr 2 2 2 (l ) A A (l ) A l i 2 l E 令 则 cr 2 i
i
1 6 4 80 0.3
z y 面 内 ， y = 2.0
2 6 4 y 160 max i 0.3
第45页
L
2、求折减系数
木杆: 80时, 3000 2
160时, 3000 2 0.117
3、求许用压力
cr
Pcr 1
2E I
l1
2
，
Pcr 2
2E I
l2 2
要使P最大，只有N1、N 2 都达 到临界压力，即
P cos P sin
①
EI
2
l1 l2
2
（1） （2）
第24页
90
②
2E I
2
将式 (2) 除以式 (1), 便得
l1 tg ctg 2 l2
cr
E 2 p
2
第28页
或写成
E p
2
记
E p p
2
则 欧拉公式的适用范围：
p
满足该条件的杆称为细长杆或大柔度杆
第29页
对A3钢，当取E=206GPa，σp=200MPa,则
2 9 E 206 10 p 100 6 p 200 10
材料有关。
第43页
[ ] －许用应力； ( ) 1 －折减系数，与压杆的柔度和
二、稳定性计算分类
1、校核稳定性；
2、设计截面尺寸；
3、确定外荷载。
三、强度计算和稳定性计算的区别
强度的许用应力只与材料有关；稳定的许用 应力不仅与材料有关，还与压杆的支承、截 面尺寸、截面形状有关。
第44页
记 a s s b
a s 即 b
则 s p
经验公式的适用范围
第33页
对于 λ＜λs的杆，不存在失稳问题，应考虑强度
问题
cr s
经验公式中，抛物线公式的表达式为
cr a1 b1
第34页
2
式中 a1 、b1 也是与材料性质有关的系数，可 在有关的设计手册和规范中查到。
2
l
2
1
第 9页
Pc r
EI
2
(2 l )
2
2
第10页
Pc r
EI
2
( 0.7 l )
2
0.7
第11页
Pc r
EI
2
( 0.2页
Pc r
EI
2
l
2
EI 2 (2l )
2
第13页
EI
2
EI
2
( 0.7l )
第47页
2、折减系数法 l 1 3.4 100 145.9
i 79.94 14.73
查表——λ =140，φ=0.349； λ=150，φ=0.306。
0.349 0.306 145 .9 0.349 5.9 0.33 10
P 60 10 max 40.7( MPa ) 2 A 14.73 10 0.33 140 46.2( MPa )
例：图示压杆AB为圆松木，长 L= 6m，[ ] =11MPa，直径为d = 0.3m；xy 面两端视为铰支；xz 面一端视为固定，一端视为自 2 由；试求此杆的许用压力。 (木杆: 80时, 3000 )
x
y
解：折减系数法
1、最大柔度
xy 面内， z = 1.0
z
z
L
2
第17页
例：圆截面的细长压杆，材料、杆长和杆端
约束保持不变，若将压杆的直径缩小一半，则
其临界力为原压杆的＿＿＿＿＿；若将压杆的
横截面改变为面积相同的正方形截面，则其临 界力为原压杆的＿＿＿＿＿。
第18页
解：(1)
EI Pcr 2 ( l)
2
E
2
d
4
64 ( l) 2
1 16
第20页
解：(a ) 杆BD受压，其余杆受拉 BD杆的临界压力:
Pcr
EI
2
2a
2
EI
2
2a
2
故杆系所能承受的最大载荷
Pmax Pcr
EI
2
2a
2
Ed
3
4
128a
2
第21页
(b) 杆BD受拉，其余杆受压
四根受压杆的临界压力：
Pcr
EI
2
a
2
故杆系所能承受的最大载荷：
l
i
s
得：
0.04 i 4 l s 616 . 0.88 m 0.7
第41页
§10-4 压杆的稳定性计算
一、稳定性条件
Pmax
Pc r [ns t ]
式中 Pmax ------压杆所受最大工作载荷 Pc r ------压杆的临界压力 [nst ]------压杆的规定稳定安全系数
2E 2E 2E 2 2 2 : 2 : 2 i1 :i2 :i3 2 1 2 3
I1 I 2 I 3 : : A1 A2 A3
d
4
642 d 4
1:1: 5
2 4 2 d d d 4 d 4 2 2 64 4 64 : : 2 2 d d 2 4 4 4
3
第48页
§10-5 提高压杆稳定性的措施
2 EI 2 E Pcr 2 A 2 ( l )
l
i
i
I A
1、选择合理的截面形状：
I P cr
1.287 (MPa)
3002
4
第46页
cr
Pcr A cr
1.287 91(kN )
例：一等直压杆长 L=3.4 m，A=14.72 cm2，I=79.95 cm4， E = 210GPa，F = 60kN，材料为A3钢，两端为铰支座； [nst] = 2、[σ]=140 MPa。分别用安全系数法和折减系数 法进行稳定性校核。 解：1、安全系数法：
2 2
E I正
2
(2)
Pcr 正 Pcr 圆
( l)
2
2
E I圆
( l)
2
I正 I圆
d 4 a4 12 12 4 4 d d 64 64
3
第19页
例：五根直径都为 d的细长圆杆铰接构成 平面正方形杆系ABCD，如各杆材料相同，弹 性模量为E。求图 (a)、(b)所示两种载荷作用下 杆系所能承受的最大载荷。
1、许用临界压力法:
Pmax [ P cr ]
第42页
Pcr [ Pcr ] [nst ]