线性系统理论作业

合集下载

线性系统理论大作业

目录题目一 (2)（一）状态反馈加积分器校正的输出反馈系统设计 (2)(1)建立被控对象的状态空间模型，并判断系统性质 (2)(2)状态反馈增益矩阵和积分增益常数的设计 (4)(3)全维观测器设计 (6)(4)如何在闭环调速系统中增加限流环节 (8)（二）二次型最优全状态反馈控制和按负载扰动前馈补偿的复合控制系统设计 (8)(1)线性二次型最优全状态反馈设计 (8)(2)降维观测器设计 (13)题目二 (15)(1)判断系统是否存在最优控制律 (15)(2)非零给定点的最优控制设计和仿真分析 (16)(3)权矩阵的各权值对动态性能影响分析 (17)题目一（一）状态反馈加积分器校正的输出反馈系统设计 (1)建立被控对象的状态空间模型，并判断系统性质1)画出与题目对应的模拟结构图，如图1所示：图1原始系统结构图取状态变量为1x =n ，2x =d I ，3x =d u ，控制输入u=c u1222212333375375111T Le la la la s s s C x x T GD GD C x x x x RT T RT K xx u T T ⎧=-⎪⎪⎪=--+⎨⎪⎪=-+⎪⎩将已知参数代人并设输出y=n=1x ，得被控对象的状态空间表达式为L x Ax Bu ET y Cx=++=其中，237500039.768011=-3.696-17.85727.05600-588.235100T ela lala s C GD C A RT T RT T ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦，000=023529.41s s B K T ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦，2375-30.4880=000GD E ⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，[]100C = 2)检查被控系统的结构性质判断系统能控性、能观性、稳定性程序如下：A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41];C=[1 0 0]; Qc=ctrb(A,B); Qo=obsv(A,C); L=length(A); if rank(Qc)==Ldisp('系统是状态完全能控'); elsedisp('系统是状态不完全能控'); endif rank(Qo)==Ldisp('系统是状态完全能观'); elsedisp('系统是状态不完全能观'); enddisp(eig(A))%利用A 的特征值判断系统稳定性运行结果：系统是状态完全能控系统是状态完全能观 1.0e+02 *-0.0893 + 0.0820i -0.0893 - 0.0820i -5.8823 + 0.0000i由于矩阵A 全部特征值均具有负实部，因此系统渐近稳定。

线性系统控制理论作业精简版

X 和模态矩阵 M。
4、求
2 0 A= 0 0
0 0 0 0
1 0 0 0
0 1 0 0
的特征值λ，特征向量 X 和模态矩阵 M。
5、将二次型 Q(Z)= 2 x1 x2 2 x1 x3 6 x2 x3 化为标准型。 6、将 Q= X
T
AX X 1
X2
2 5 X 1 8 X 3 2 11 2 X 2 5 2 8 X3
= 8 X 12 11X 22 8 X 32 4 X 1 X 2 10 X 1 X 3 4 X 2 X 3 化为标准型。 7、用求矩阵秩的程序，验证题 1、2
第 5 页共 7 页
4、用叠加法对下图电路列状态方程。
第七、八章习题 1、已知状态方程的系数矩阵 A(t)＝ 2、求离散系统状态方程齐次解
t 1 （级数取三项即可），求 (t ,0) 。 1 t
X 1 ( K 1) 1 5 1 X 1 ( K ) 2 , 其中X (0) 。 1 X 2 ( K 1) 12 1 5 X 2 ( K )
第九章习题 1、一连续系统中 A= 和可观测性。 2、判断下图电路的能控性和能观性。
2 5 1 ，B= ，C= 1 4 0 1
1 ，试判断该系统的可控性
第 6 页共 7 页
第十一章习题 1、已知 X X ，用李氏第一方法和二次型法确定其稳定性。 1 1 2、用 LYAPUNOV 两种方法判断下面系统在原点的稳定性。已知系统方程为：
4.求
2 X 1 X 2 3X 3 2
X1 2X 2 X 3 1

线性系统理论第一章(习题)

若 li 是 A 的特征值，试证 [1 li li 2 li n -1 ]T 是属于 li 的特征向量。 1—2 若 li 是 A 的一个特征值，试证 f (li ) 是矩阵函数 f (A) 的一个特征值。 1—3 试求下列矩阵的特征多项式和最小多项式
é l1 1 0 0 ù ê ú ê 0 l1 1 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 1 ú ê ú ê 0 0 0 l1 ú ë û
y =
t
ò0 g(t - t )u(t )d t
若脉冲响应 g 由图 1—12(a)给定。试问，由图 1—12(b)所示的输入而激励的输出为何？ g(t) 1 1 (a) 图 1—12 脉冲响应和输入作用 1—12 试求图 1—13 所示系统的动态方程式(略)
29
u(t) 1 2 t 1 2 (b) t
n >m
试证，给定初始状态 x(m ) = x0 下，时刻 n 的状态为 x(n )=F(n, m )x(0) 。若 A 与 n 无关，则
F(n, m ) 为何？
1—27 证明 x(n + 1) = A(n )x(n ) + B(n )u(n ) 的解为
n -1
x(n ) = F(n, m )x(m ) +
1 ù ú s+3ú 5s + 1 úú s + 2 úû
的实现，并画出其模拟图。 1—25 设{ A , B , C , D }和{ A , B , C , D }是两个线性时不变系统，其维数不一定相同。证明当且仅当

清华线性系统控制理论作业一参考解答

2．(根据框图写出状态空间描述) 图2.2中描述了列车悬浮系统的工作原理，其中，1、2、3、 4为电磁装置，车辆通过电磁力的作用，悬浮于轨道上。磁悬浮控制系统的目的是通过调整电磁作用力的输入，保证列车在运行过程中的平稳。这里我们考虑车辆运行过程中产在x和y 轴两个方向的位移，给出其线形化系统框图如图2.1所示
描述，其中g 是重力加速度常数，如图3所示，h 是自行车质心距地面高度，w 是两个轮子与地面接触点的距离， b 是自行车质心投影与后轮和地面接触点的距离。试给出该线性系统的一个状态空间描述。
图3 参考文献： [3.1] Bicycles, motorcycles, and models-single-track vechicle modeling and control, IEEE Control Systems Magazine, October, 2006. 参考解答：
作业一
1．（线性化）已知倒立摆系统满足如下非线性状态方程
1 (t ) x2 (t ) x 2 (t ) ( g / l ) sin x1 (t ) u (t ) x
通过线性化给出系统在平衡解 [ x1 (), x2 ()] [0,0] ， u () 0 的邻域内的线性模型。参考解答：
图 2.2
参考解答：
注意状态变量的维数. 3．（从传递函数得到状态方程描述）图3中给出了解释自行车姿态动态平衡的原理图示。在前进速度保持为定常v 的假设下，车把转角对车身姿态角的作用在平衡点（＝0，＝0）附近范围内可用微分方程

g v2 bv h hw wh
图2.1 这里A11=[100 0；0 200] B21=[10 -3；-5 16] C22=[1 1；1 -1]。这里输入向量u是控制的作用力，也就是车辆的加速度量，输出向量y是车辆在两个轴方向的位移量，通过间隙传感器测量。试列写出系统的状态空间模型。参考文献： [2.1] H2 and H∞ control for MagLev vehicles，IEEE Control System Magazine, 1998 [2.2] Experimental comparison of linear and nonlinear controllers for a magnetic suspension, Proceedings of the 2000 IEEE International Conference on Control Applications，2000 [2.3] 广义线性磁悬浮对象的H∞控制问题，西安交通大学学报，Feb，2000

第一篇线性系统理论习题答案

⎡ s +1 ⎢s2 + s +1 ⎢ −1 = [1 0 1]⎢ 2 ⎢s + s +1 ⎢ 0 ⎢ ⎣
9－7 设有三维状态方程
⎡0 ⎤ ⎢1 ⎥ ⎢ ⎥ ⎢ ⎣1 ⎥ ⎦
1 s + s +1 s 2 s + s +1
2
0
⎤ 0 ⎥ ⎥ ⎡0 ⎤ s 2 + 2 s 1⎥ = 3 0 ⎥ ⎢ ⎢ s −1 ⎥ ⎥ 1 ⎥ ⎢ ⎣1⎥ ⎦ s − 1⎥ ⎦
⎡ R M ⎤ ⎡ R −1 ∵⎢ ⎥×⎢ ⎣0 T ⎦ ⎣ 0
− R −1 MT −1 ⎤ ⎡ R −1 ⎥=⎢ T− ⎦ ⎣ 0
⎡R M ⎤ ∴⎢ ⎥ ⎣0 T ⎦
9－10 解
−1
⎡ R −1 =⎢ ⎣ 0
− R −1 MT −1 ⎤ ⎥ T −1 ⎦
−1
对可控标准形 A 和 b ，计算 ( sI − A) b
+
v2
& 2 = x1 + y = x1 − C 2 x
写成矩阵形式为
1 1 x2 + U R2 R2
图 9－1 RLC 网络
⎡ R1 − & x ⎡ 1 ⎤ ⎢ L1 ⎢x ⎥=⎢ ⎣ &2 ⎦ ⎢ 0 ⎢ ⎣
⎤ ⎡ 1 ⎤ 0 ⎥ x ⎡ ⎤ ⎢ L ⎥ ⎥ ⎢ 1 ⎥ + ⎢ 1 ⎥U − 1 ⎥ ⎣ x2 ⎦ ⎢ − 1 ⎥ ⎢ R2 C 2 ⎥ ⎦ ⎣ R2 C 2 ⎥ ⎦
x1 ， x 2 有下列关系存在 x1 = x1 + x 2 x 2 = − x1 − 2 x 2
试求系统在 x 坐标中的状态方程。解 ①
&1 = x & = x2 x &2 = & & = −2 x1 − 3 x 2 + u x x

《线性系统理论基础》第一章作业及答案

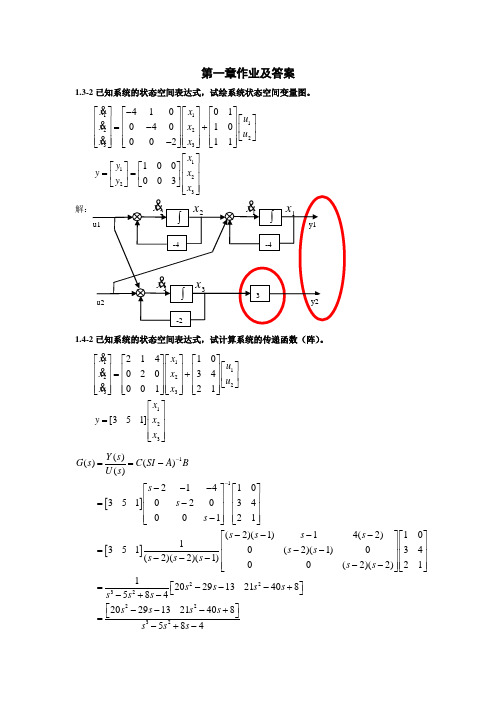
第一章作业及答案1.3-2已知系统的状态空间表达式，试绘系统状态空间变量图。

11122233112241001040100021110003xx u x x u x x x y y x y -⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦1.4-2已知系统的状态空间表达式，试计算系统的传递函数（阵）。

11122233123214100203400121[351]xx u x x u x x x y x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦[][]112232()()()()21410351020340121(2)(1)14(2)1013510(2)(1)034(2)(2)(1)00(2)(2)21120291321408584Y s G s C SI A B U s s s s s s s s s s s s s s s s s s s s s s --==----⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥---⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤=---+⎣⎦-+-223220291321408584s s s s s s s ⎡⎤---+⎣⎦=-+-注意：也可写做[][][]23220212940138584s s s s s +--+--+-1.5-1已知系统传递函数，试用传递函数求出系统的状态空间模型。

2()35()()(3)(2)Y s s G s U s s s +==++解：通过赋予研究对象不同的内部结构可将传递函数转换成不同的状态空间模型。

（1）求出上述传递函数能控标准型表示由已知条件可知该传递函数为严格真分式，且该系统为单入单出（SISO ）三阶系统。

根据公式10111()...(),(1)()...mm mn n nY s b s b s b G s n m U s s a sa --+++===++++其中，可将传递函数写为223235035()(3)(2)82118s s s G s s s s s s +++==+++++其中，123012a 8,21,18,0,3,5a a b b b ======。

《线性系统理论》作业参考答案

x 11 e t x 21 , 21 0 , x
x11 ( t 0 ) 1 x 21 ( t 0 ) 0
，
x 12 e t x 22 , 22 0 , x
x12 ( t 0 ) 0 x 22 ( t 0 ) 1
解得
x12 e t e t 0 x11 1 ， x 21 0 x 21 1 1 (t ) x 0 e
( sI A )
1
s ( s 1) 0 2 det( sI A ) s ( s 1) 0 adj ( sI A ) 1
s 1 ( s 1) 0
2
s ( s 1) 1 s ( s 1) 1 s 1 1
2
所以 e
。
可以看出， f ( i ) 是 f ( A ) 的一个特征值。
1-3 解：(1) 特征多项式为 1 ( ) ( 1 ) .
4
验证
A 1 I 0 , ( A 1 I ) 2 0 , ( A 1 I ) 3 0 , ( A 1 I ) 4 0
At
e t 1 1 L [( sI A ) ] 0 0
e 1 1 0
t
t t 1 e te t e 1 。 t e
1-5 证明：因为 D 1 存在，所以由 D R p p
A det C B IA det D 0 BD A I D C
c
k 0
k
A
k
设 x 是属于 i 的一个非零特征向量，故
A x i x
.
2 2 因此 A x A Ax A i x i Ax i i x i x .

华工自动化线性系统第一次大作业

三、求状态转移矩阵的几种方法
求的方法有时域的求解方法和频域的求解方法。方法1：根据或者的定义直接计算：
=I+++…++…= 从公式可以看出，右边是一个无穷项的和，要精确计算出
结果是很困难的，所以无论是手工计算还是利用电脑计算，都不可能取无穷项计算，通常是取有限项,得到一个近似的值，以满足不同的精度要求即可.对于不同的精度要求，n的值会不同。在工程上，只要取它的前几项就可以满足要求，本方法易于理解，适合计算机编程。方法2：利用拉氏反变换法求：
版本）正在进行着陆（速度V=16英里/小时）。描述飞机纵向运动的状态空间方程
给出如下：
控制输入是升降舵角度和向量的状态变量分别是速度的变化，迎角，俯仰速率和俯仰度。
该飞机的纵向模式称为短周期和长周期。在长周期特征值，这也是一种复杂的共轭特征值接近虚轴，造成长周期运动，在水平面缓慢地震荡。
二、状态转移矩阵的重要性与意义
线性系统理论大作业
专业：控制理论与控制工程学号与姓名：
一、飞行器原理及结构和空间坐标系
为了进行控制系统设计的目的，飞机动力学经常称为飞行姿态的一些操作状态进行线性化，它假设飞机的速度（马赫数）和姿态是不变的。控制面（The control surfaces）和发动机推力装置设置或修改，以达到这些状态，我们设计控制系统就是为了维护这些条件，例如，强制将到这些状态的扰动（偏差）变为零。
syms M s d1 t XT X0; A=[-0.0507 -3.861 0 -32.2;-0.00117 -0.5164 1 0;-0.000129 1.4168 -0.4932 0;0 0 1 0]; disp('矩阵A的行列式如下:'); d1=det(A); I=eye(4); disp('[sI-A]^(-1)为:'); B=(s*I-A); C=inv(B); digits(4) C=vpa(C) disp('状态转移阵为'); D=ilaplace(C); digits(4); M=vpa(D) X0=[0;0;0;0]; B=[0;-0.0717;-1.645;0]; XT=M*(X0+B) %求解系统的状态响应。 %画图 subplot(2,2,1) %画出x(t)d第一个分量X1(t),并把它显示在左上角。 ezplot(XT(1,1),[0,2]) subplot(2,2,2) %画出x(t)d第二个分量X2(t),并把它显示在右上角。 ezplot(XT(2,1),[0,2])

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《线性系统理论》设计报告专业：学号：姓名：教师：取状态变量为X=[U d,I d,n]T,则系统的状态空间描述为：{X=AX+Bu+ET lY=CX其中A=[−1T s0 01T la R−1T la−C eT la R0 375C TGD20]B=[K sT S]E=[−375GD2]C=[0 0 1 ]代入数据得：A=[−588.235 0 026.709 −20.833 −3.678 0 48.821 0 ]B=[23529.41]通过matlab检测系统的能控能观性并求出系统的特征值：对应的matlab程序如下：%原始系统能控能观性判断与特征值求解%A=[-588.235 0 0;26.709 -20.833 -3.678;0 48.821 0];B=[23529.41 0 0]';C=[0 0 1];D=0;disp(eig(A)); % 计算并输出特征值 %sys1=ss(A,B,C,D);Qc=ctrb(A,B); %生成能控性判别矩阵%Qo=obsv(A,C); %生成能观性判别矩阵%if length(A)==rank(Qc) %系统能控性判别%disp('系统完全可控！');elsedisp('系统不完全可控！');endif length(A)==rank(Qo) %系统能观性判别%disp('系统完全可观！');elsedisp('系统不完全可观！');end运行结果如下：1.0e+002 *-0.104165000000000 + 0.084297191975771i-0.104165000000000 - 0.084297191975771i-5.882350000000000系统完全可控！系统完全可观！系统特征值实部均为负，由此可知该系统为外部稳定的能控但不能观测系统，设负载转矩为0时，输入为阶跃信号，系统的simulink仿真如下：图1. 原始开环系统结构框图图2.原始开环系统仿真图1、状态反馈加积分器校正的输出反馈系统根据仿真结果可以看出原系统的调节时间大于1s ，不能满足不大于0.5s 的要求;又要求系统跟踪阶跃输入信号的稳态误差为零，故系统不仅要通过求解状态反馈增益矩阵改变极点配置，还需设置积分器校正的输出反馈来消除稳态误差。

因为要求被控系统∑(A,B,C )能控,又控制维数(r=1)不少于误差的维数(m=1)且rankC=1=m, 即增广系统状态完全能控，因此可采用状态反馈控制律：u =−K 1x +K 2w改善系统的动态和稳态性能，式中K 1=[K 11 K 12 K 13] 。

闭环控制系统的特征多项式为：12()det 0A BK BK p s sI C-⎡⎤=-=⎢⎥-⎣⎦s 4+(609.068+23529.41K 11)s 3+(12434.263+628447.012K 12+490188.199K 11)s 2+(30681411.558K 13+4225026.46K 11+105625.617)s +30681411.558K 2由于最大超调量%10021⨯=--ζζπeM p ，当振幅进入%2±范围内时调节时间ns t ζω4=，其中Tn 1=ω为系统自然振荡角频率。

由于系统设计要求为超调量不超过10%，调节时间不超过0.5秒，可计算得到：%10≤P M ，591.0≥ζ，取0.7ζ=，5.04≤=ns t ζω，53.13≥n ω，取14n ω=，二阶系统的特征根122,1-±-=ζωζωn n s ，可得期望特征值19.89.99S j =-+，29.8-9.99S j =-，原系统闭环非主导极点离虚轴为主导极点的5倍以上，故无需进行配置，再取另一个期望非主导极点为-50，则S 3=-588.235, S 4=-50,运用expand 函数求得期望特征多项式为：expand((s+588.35)*(s+50)*(s+9.8-9.99i)*(s+9.8+9.99i))运行结果：s^4 + (13159*s^3)/20 + (421250001*s^2)/10000 + (140319505567*s)/200000 + 23044504567/4000即(s −s 1)(s −s 2)(s −s 3)(s −s 4)=s 4+657.95s 3+42125s 2+701597.528s +5761126.14根据对应系数相等计算得到：K 11=0.00208，K 12=0.04562,K 13=0.01914,K 2=0.18777 确定了状态反馈增益矩阵1K 和积分增益常数2K ，在未考虑扰动作用时（设d=0），闭环系统对给定输入v(t)为阶跃信号的响应可通过求解下式获得，即 []1210010A BK BK x v w C w x y C xw ⎧-⎡⎤⎡⎤⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎢⎥⎢⎥-⎪⎣⎦⎣⎦⎣⎦⎣⎦⎨⎡⎤⎪==⎢⎥⎪⎣⎦⎩x && 式中, v(t)=1(t)Simulink 仿真如下：图3.状态反馈加积分器校正的输出反馈系统仿真图输出波形：图4.状态反馈加积分器校正的输出反馈系统仿真波形0秒时加阶跃的负载扰动，其仿真波形如下：图5 加负载扰动时仿真波形由图4可知，该状态反馈系统的静、动态性能如下：σ=1.0435−11×100%=4.35%，t s <0.5s,皆满足系统要求。

扰动后,曲线最终稳定在1，则系统稳态误差为0。

2、全维状态观测器的设计闭环状态观测器的状态方程ˆˆ()xA GC x Gy Bu =-++，又由观测误差 ()()000ˆ()()[()()]A GC t A GC t x x t e t e xt x t --∆=∆=-知，通过选择输出偏差反馈增益矩阵G 使A GC -的所有特征值均位于复平面的左半平面，尽管初始时刻0t 时，0()x t 与0ˆ()x t 存在差异，观测器的状态ˆ()xt 仍将以一定精度和速度渐渐逼近系统的实际状态()x t 。

而输出偏差反馈增益矩阵G 由观测器极点决定，因此，状态估计误差收敛速度是由观测器极点所决定。

通过合理选择观测器极点而配置的反馈矩阵G ，状态估计误差收敛速度足够快，就能使重构状态ˆ()xt 渐近等价于真实状态()x t ，从而达到状态反馈的效果，即改善被控系统的稳定性、稳态误差和动态品质因数，而且可实现闭环系统的解耦控制和最优控制。

由原系统完全能观可知，可构造状态观测器对其状态给出估值。

设观测器增益矩阵[]Tg g g G 21=，()0()det p s sI A GC =--=s 3+(609.068+g2)s 2+(1243.4+48.821g1+609.068g2)s +105625.617+1303.960g0+28718.221g1+12254.7g2经过状态反馈后的系统状态空间表达式中个矩阵分别为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=00-2e 1131211s 37511GD C RT C T RT T K K T K K T K K T T la la lass s s ss A ，00s s K T B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，[]100=C ，带入数据可得A =[−637.117 −1073.51 −450.31626.709 −20.833 −3.6780 48.821 0 ]B =[23529.41] []100=C 由第一问求得反馈矩阵K 11=0.00208，K 12=0.04562,K 13=0.01914 F=K=[ 0.00208 0.04562 0.01914]在MATLAB 输入程序如下： P=poly(A-B*K); roots(P) ans =-506.563 -147.896 -7.717图6 全维状态观测器结构图从工程实际出发，兼顾快速性、抗干扰性等，选择观测器的响应速度比所考虑的状态反馈闭环系统快2-5倍。

故取s 1∗=−1200,s 2∗=−500,s 3∗=−35，则期望特征多项式为：D ∗=s 3+1735s 2+659500s +21000000D(s)= s 3+(609.068+g2)s 2+(1243.4+48.821g1+609.068g2)s +105625.617+1303.960g0+28718.221g1+12254.7g2可解得g0= 17853.509, g1=-563.539, g2=1125.932带观测器的状态反馈加积分调节系统仿真结构如图6。

仿真输出与观测器输出波形图如下：图7 系统加全维观测器输出波形图图7 全维状态观测器波形图由仿真图可知，系统的稳态误差为0，动态误差满足超调量σ<10%,调节时间T s<0.5s的要求。

状态估计误差收敛速度与状态观测器极点的配置有关。

一般而言状态观测器极点在复平面的左半开平面距离虚轴距离越远，则估计误差收敛速度越快。

但是，观测器响应速度过快会产生大量噪声，影响系统的正常工作故不宜取值过大。

综合工程实际出发，一般取为比状态反馈闭环系统快2—5倍。

3、限制电动机电枢过电流方法为了解决反馈闭环调速系统的起动和堵转时电流过大的问题，系统中引入电流截止负反馈，电流截止负反馈调速系统通过一个电压比较环节，使电流负反馈环节只有在电流超过某个允许值时才起作用，电动机启动时，因为电流截止负反馈作用，从而限制启动电流。

正常工作时，电流截止负反馈作用很小。

电动机发生堵转时，由于电流截止负反馈的作用，使U d大大下降，因而使I a不致过大。

允许的堵转电流一般为电动机额定电流的2~2.5倍。

系统工作在额定值时，由于电流截止负反馈起作用，从而保证系统设备的安全。

4、二次型最优控制由前边的计算可知原始系统为完全可控的，最优控制的性能指标函数为：01()()()()2T T t J x t Qx t u t Ru t dt ∞⎡⎤=+⎣⎦⎰，其中，Q 为状态加权系数矩阵，R 为控制加权系数矩阵，设Q =[q 11 0 00 q 22 00 0 q 33],R 取1。

非零点给定的定常输出器设计中，KX r k PX B R U T-=-=-11*，P 为代数方程01=-+---Q P B PBR P A PA T T 的解。

为求得最优状态反馈矩阵K 和k1，先令q 11=1，q 22=1,q 33=100，反代入上式，利用matlab 中的lqr 函数计算线性二次型最优控制的解。

即：K=lqr （A ，B ，Q ，R ），运行得：K=[0.9867,10.081,31.4838],k1=1.702 系统在零负载转矩下的阶跃响应仿真程序如下：A=[-588.235 0 0;26.709 -20.833 -3.678;0 48.821 0]; B=[23529.41 0 0]'; C=[0 0 1]; D=0;R=1;Q= [1 0 0;0 1 0;0 0 1000]; K=lqr(A,B,Q,R);ac=A-B*K;k1=inv((-C/(A-B*K))*B); bc=B*k1; cc=C; dc=D;step(ac,bc,cc,dc);Grid运行后仿真结果如下图：图8线性二次型最优全状态反馈仿真曲线为了研究系统二次型性能指标泛函中权矩阵Q的不同选取对动态性能的影响，对q11、q22、q33取不同值时的权矩阵进行仿真试验。