线性系统理论
线性系统理论全课件
2/2,13/50
2.4 由系统输入输出描述导出状态空间描述
由输入输出描述导出状态空间描述
5/7,9/50
离散时间线性系统的状态空间描述 状态空间描述形式 离散时间线性时不变系统 X (k 1) Gx(k) Hu (k) Y (k) Cx(k) Du (k)
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
离散时间线性时变系统 X (k 1) G(k)x(k) H (k)u(k ) Y (k) C(k)x(k) D(k)u(k)
cM
J
ce La f
J
ia
1
La 0
e
0
1ia
上式可表为形如 X AX Bu Y CX Du
Ra
i f const
J,F
La
2/7,6/50
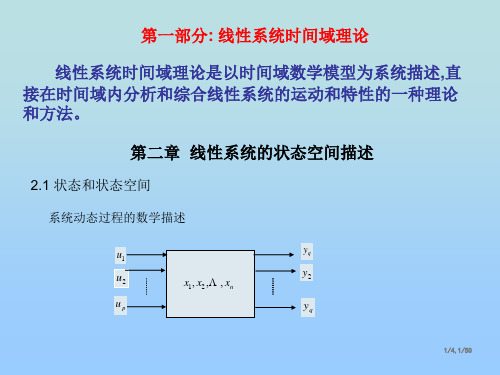
连续时间线性系统的状态空间描述 动态系统的结构
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
u1
yq
外部描述常被称作为输出—输入描述
u2
x1, x2 , , xn
y2
up
yq
例如.对SISO线性定常系统:时间域的外部描述:
y(n) an1 y(n1) a1 y(1) a0 y bn1u(n1) b1u (1) b0u
复频率域描述即传递函数描述
线性系统理论和设计

线性系统理论和设计是控制工程中的重要内容,涉及到对线性系统的建模、分析和控制设计。
以下是关于线性系统理论和设计的基本内容:
1. 线性系统模型
-线性系统描述:线性系统是指具有线性性质的动态系统,其输出与输入之间满足线性关系。
-线性系统模型:通常用微分方程、差分方程或状态空间方程描述线性系统的动态特性。
2. 线性系统分析
-系统稳定性分析:通过研究系统的零点、极点等性质来判断系统的稳定性。
-频域分析:通过频率响应、波特图等方法分析系统在频域下的性能。
-时域分析:通过阶跃响应、脉冲响应等方法研究系统在时域下的响应特性。
3. 线性系统设计
-控制器设计:设计合适的控制器来实现系统的性能要求,常见的控制器包括比例积分微分(PID)控制器、根轨迹设计等。
-系统鲁棒性设计:设计具有鲁棒性的控制器,能够抵抗参数变化和外部干扰的影响。
-最优控制设计:利用最优控制理论设计最优的控制器,使系统性能
达到最佳。
4. 线性系统应用
-自动控制系统:将线性系统理论和设计方法应用于自动控制系统,实现对各种工程系统的自动控制和调节。
-信号处理系统:利用线性系统理论设计数字滤波器、信号处理算法等,对信号进行处理和提取。
-机电系统:应用线性系统理论设计机电系统的控制器,实现机电系统的精密控制和运动规划。
线性系统理论和设计在控制工程领域具有广泛的应用,能够帮助工程师分析和设计各种复杂系统的控制策略,提高系统的性能和稳定性。
线性系统理论总结ppt

线性系统理论总结ppt
一、线性系统简介
1.线性系统定义:
线性系统是指用线性微分方程、线性积分方程和线性算子(算子运算)来表示、描述和分析的一个系统。
这种系统的输入输出之间的关系可以表
示为线性函数的形式。
2.线性系统的实例:
线性系统的例子包括信号处理、控制系统、数字图像处理、模式识别
等等。
线性系统的应用也很广泛,可以应用在机器人、汽车、航空、通信、医疗和金融等行业中。
二、线性系统的演示
1.系统模型:
线性系统通常用状态空间模型来描述,该模型由一组线性微分方程以
及输入、输出和内部状态变量组成。
该模型的工作原理是:系统的输入到
达模型的输入,系统的内部状态变量发生改变,然后将内部状态变量产生
的输出发送到系统的输出端。
2.系统特性:
线性系统具有许多特性,包括平衡点、平稳性、稳定性、反馈和动力
学建模等等。
这些特性是线性系统能够更好地实现高效操作和有效控制的
基础。
三、线性系统的分析
1.状态变量分析:
状态变量是描述系统当前状态的量,它们通过系统的状态转移方程的变化反映系统的行为。
状态变量的分析包括:求出状态变量的收敛状态,判断系统的稳。
线性系统理论

系统:系统一词来源于英文system的音译,即若干部分相互联系、相互作用,形成的具有某些功能的整体。
中国著名学者钱学森认为:系统是由相互作用相互依赖的若干组成部分结合而成的,具有特定功能的有机整体,而且这个有机整体又是它从属的更大系统的组成部分。
线性系统:线性系统是一数学模型,是指用线性运算子组成的系统。
相较于非线性系统,线性系统的特性比较简单。
线性系统需满足线性的特性,若线性系统还满足非时变性(即系统的输入信号若延迟τ秒,那么得到的输出除了这τ秒延时以外是完全相同的),则称为线性时不变系统。
线性系统理论:系统控制的理论与实践被认为是20世纪中对人类生产和社会生活活动产生重大影响的科学领域之一。
其中,线性系统理论是系统控制理论的一个最为基本的与成熟发展的分支。
概述:线性系统科学技术是一门应用性很强的学科,面对着各种各样错综错杂的系统,控制对象可能是确定性的,也可能是随机性的,控制方法可能是常规控制,也可能需要最优化控制。
控制理论和社会生产及科学技术的发展密切相关,近代得到极为迅速的发展。
线性系统理论是现代控制理论中最基础、最成熟的分支,是控制科学重要课程之一。
线性系统理论内容丰富、思想深刻、方法多样、充满美感,不仅提供了对线性控制系统进行建模、分析、综合系统完整的理论,而且其中蕴涵着许多处理复杂问题的方法,这些方法使系统的建模、分析、综合得以简化,为系统控制理论的其它分支乃至其它学科提供了可借鉴的思路,它们是解决复杂问题的一条有效途径。
主要特点:与经典线性控制理论相比,现代线性系统理论的主要特点是:研究对象一般是多变量线性系统;除输入变量和输出变量外,还着重考虑描述系统内部状态的状态变量;在分析和综合方法方面以时域方法为主,兼而采用频域方法;使用更多的数学工具,除经典理论中使用的拉普拉斯变换外,现代线性系统理论大量使用线性代数、矩阵理论和微分方程理论等。
线性系统理论全

稳定性判据与判定方法
稳定性判据
在控制工程中,常用的稳定性判据有Routh判据、Nyquist判据、 Bode判据等。这些判据通过分析系统的特征方程或频率响应来判 断系统的稳定性。
判定方法
除了使用稳定性判据外,还可以通过时域仿真、频域分析、根轨 迹法等方法来判定系统的稳定性。这些方法各有优缺点,适用于 不同类型的线性系统和不同的问题背景。
100%
线性偏差分方程
处理离散空间和时间的问题,如 数字滤波器和图像处理等。
80%
初始条件与边界条件
在差分方程中,初始条件确定系 统的起始状态。
状态空间模型
状态变量与状态方程
表示系统内部状态的变化规律 ,揭示系统动态特性。
输出方程
描述系统输出与状态变量和输 入的关系,反映系统对外部激 励的响应。
状态空间表达式的建立
复频域分析法
拉普拉斯变换
将时域信号转换为复频域信号,便于分析系统的稳定性和动态性 能。
系统函数
描述Байду номын сангаас统传递函数的复频域表示,反映系统的固有特性和对输入信 号的响应能力。
极点、零点与稳定性
通过分析系统函数的极点和零点分布,可以判断系统的稳定性以及 动态性能。
04
线性系统稳定性分析
BIBO稳定性
01
线性系统理论全
目
CONTENCT
录
• 线性系统基本概念 • 线性系统数学模型 • 线性系统分析方法 • 线性系统稳定性分析 • 线性系统能控性与能观性分析 • 线性系统优化与综合设计
01
线性系统基本概念
线性系统定义与性质
线性系统定义
满足叠加性与均匀性的系统。
线性系统性质
《线性系统理论》课程教学探讨

《线性系统理论》课程教学探讨《线性系统理论》是控制理论中的基础课程之一,主要研究线性动态系统的建模、分析与控制。
在工程领域,线性系统理论被广泛应用于自动控制、信号处理、通信系统等各个方面。
对于控制理论专业的学生来说,学习《线性系统理论》课程是非常重要的。
在教学中,如何更好地教授《线性系统理论》课程,引导学生深入理解并掌握相关知识,是每位控制理论教师都面临的一个重要问题。
本文将探讨如何进行《线性系统理论》课程的教学,包括教学内容、教学方法、教学手段等方面,以期能够为相关教师提供一些启发与帮助。
一、教学内容《线性系统理论》课程的教学内容主要包括线性系统的基本概念、线性系统的数学描述、线性系统的时域分析、线性系统的频域分析、线性系统的稳定性分析、线性系统的控制器设计等方面。
时域分析包括状态空间描述、零输入响应、零状态响应、传递函数描述等内容;频域分析包括拉普拉斯变换、傅里叶变换、频率响应等内容;稳定性分析包括系统的内稳定性、外稳定性等内容;控制器设计包括状态反馈控制、输出反馈控制、最优控制等内容。
在教学内容的安排上,可以根据教学大纲和学生的实际需求进行适当的调整和补充。
可以结合具体的工程案例,引入一些实际的控制问题,让学生通过学习《线性系统理论》课程,能够更好地理解和应用所学知识。
二、教学方法针对《线性系统理论》课程的教学方法,可以采用多种方式,包括课堂讲授、案例分析、实验教学等。
在课堂讲授方面,可以通过引入生动的实例和案例,以及讲解一些与线性系统相关的最新研究成果,激发学生的学习兴趣,增强他们的学习动力。
在案例分析方面,可以选取一些实际的控制工程问题,进行详细的分析和讨论,让学生通过具体的案例了解线性系统理论的应用。
在实验教学方面,可以通过实验平台、仿真软件等工具,进行相应的实验操作和数据分析,让学生通过实际操作来加深对线性系统理论的理解。
还可以采用小组讨论、课外阅读、学术论文撰写等方式,培养学生的团队合作能力、独立思考能力和科研创新能力。
线性系统理论(第一章).ppt

x2
0
x3 640
1 0 194
0 x1 0
1
x2
0
u
16 x3 1
x1
y 720
160
0
x2
x3
第一章
⑵当 m n时,将有理分式进行严格真化,
y
[bn
(bn1 bnan1) pn1 pn an1 pn1
(b0 bna0 ) ]u a1 p a0
x1(t)
X
(t
)
,
t t0
xn (t)
状态空间:状态向量取值的一个向量空间。
第一章
动力学系统的状态空间描述 一个动力学系统的结构示意图。
u1 u2
• ••
x1 x2
动力学部件
•
• u p
•
xn
状态变量组:x1, x2 , , xn
输入变量组:u1,u2 , ,u p 输出变量组:y1, y2 , , yq
第一章
例:给定系统的输入—输出描述为
y(3) 16 y(2) 194 y(1) 640 y 4u(3) 160u(1) 720u
则 x1 0
x2
0
x3 640
1 0 194
0 x1 0
1
x2
0
u
16 x3 1
y 1840
616
x1
64
x2
4u
x3
R1
C
uc
e(t)
L iL
R2 uR2
u 解:确定状态变量,最多2个线性无关的变量,取 c 和 iL
作为状态变量。
第一章
列出原始电路方程:由电路定律。
右回路:
线性系统理论

a<0 t
当a>0时,也只有一个吸引子。 同时,从严格意义上讲,线性系统不存在分叉或突变的情 况,除非强加外力。比如有一个恒定速度的物理模型,除 非外力作用,否则将一直沿既定轨道运动。
线性系统的划一性:
1、线性系统的轨道稳定性完全取决于控制参量或特 征值,与系统初态无关。
(如音量调节器,不论初始音量事多少,我们旋转音量按钮,则音量固定 为几分贝而不是当前初始值的多少倍。)
2、只要判明一条轨道稳定或不稳定,既可断定所 有轨道是否稳定。唯一例外的是存在鞍点的情况, 有一个特征方向上存在稳定轨道,但是其他所有 轨道并不是稳定的。
注意点: 满足叠加原理是线性系统的基本判断依据。
有了数学模型,就可以直接按模型判别; 如果没有数学模型可以采用实验手段进行判别。 但是如果未加假设的话,叠加原理只适用于有 限项之和。
叠加原理和整体涌现性的区别:
1
• 线性系统是一种数学抽象,是忽略了系统固有的非 线性因素的结果,系统的非线性效应就是整体涌现 性。 • 即使是线性系统,其整体功能也不能归结为部分功 能之和,二者一般没有可比性,部分或部分简单相 加不 具备与整体可作数量比较的功能。 • 不同系统的整体涌现性一般在质和量都有表现,线 性模型仅描述那些只有平庸的、低水平的涌现性的 系统,部分之间相互作用的相干效应在定量方面的 表现微弱,因而可以忽略。但是系统功能等定性性 质的涌现性不能忽略。
第五章 线性系统理论
数学模型是由描述系统的变量和常量 构成的数学表达式,建立数学模型后,首 先要区分系统是线性还是非线性的。
以前的科学研究主要对象是线性系统, 而今正转向非线性系统,并且未来科学的 本质上是非线性科学
线性与非线性原本就是一对数学关系,用以区 分不同变量之间的两种基本的相互关系。 常量之间并没有线性和非线性的区分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Linear Systems Theory: A Structural Decomposition Approach
线性系统理论: 结构分解法
Ben M. Chen (陈本美)
新加坡国立大学
Zongli Lin(林宗利)
美国弗吉尼亚大学
Yacov Shamash (雅科夫 司马诩)
美国纽约州立大学石溪分校
此书献给我们的家人
前两位作者谨以这中译版献给他们的母校 厦门大学
目录
绪论
1 导论和预览
1.1 背景
1.2 各章预览
1.3 符号和术语
2 数学基础
2.1 导论
2.2 矢量空间和子空间
2.3 矩阵代数和特性
2.3.1 行列式、逆和求导
2.3.2 秩、特征值和约当型
2.3.3 特殊矩阵
2.3.4 奇异值分解
2.4 范数
2.4.1 矢量范数
2.4.2矩阵范数
2.4.3 连续时间信号范数
2.4.4 离散时间信号范数
2.4.5 连续时间系统范数
2.4.6 离散时间系统范数
3 线性系统理论复习
3.1 导论
3.2 动态响应
3.3 系统稳定性
3.4 可控性和可观性
3.5 系统可逆性
3.6 常态秩、有限零点和无限零点3.7 几何子空间
3.8 状态反馈和输出馈入的特性3.9 练习
4 无驱动和/或无检测系统的分解
4.1 导论
4.2 自治系统
4.3 无驱动系统
4.4 无检测系统
4.5 练习
5. 正则系统的分解
5.1 导论
5.2 SISO系统
5.3 严格正则系统
5.4 非严格正则系统
5.5 结构化分解特性的证明
5.6 系统矩阵的Kronecker型和Smith型5.7 离散时间系统
5.8 练习
6 奇异系统的分解
6.1 导论
6.2 SISO奇异系统
6.3 MIMO描述系统
6.4 定理6.3.1的证明和性质
6.5 离散时间奇异系统
6.6 练习
7 双线性变换的结构化映射
7.1 导论
7.2 连续到离散时间系统的映射
7.3 离散时间到连续时间系统的映射7.4 定理7.2.1的证明
7.5 练习
8 系统因子分解
8.1 导论
8.2 严格正则系统
8.3 非严格正则系统
8.4 离散时间系统
8.5 练习
9 通过选择传感器/执行器实现的结构配置9.1 导论
9.2 同时有限和无限零点结构配置
9.2.1 SISO系统
9.2.2 MIMO系统
9.3 完全结构配置
9.4 练习
10 通过状态反馈实现的时间尺度和特征结构配置10.1 导论
10.2 连续时间系统
10.2.1 设计步骤和基本特性
10.2.2 控制、控制和干扰解耦
10.3 离散时间系统
10.3.1设计步骤和基本特性
10.3.2 控制、控制和干扰解耦
10.4 练习
11 通过静态输出反馈实现的干扰解耦
11.1 导论
11.2 左可逆系统
11.3 一般的多变量系统
11.4 练习
12 软件工具箱
12.1 导论
12.2 m-函数描述
12.2.1 自治系统的分解
12.2.2 无驱动和无检测系统的分解
12.2.3 正则系统的分解和特性
12.2.4 矢量空间的运算
12.2.5 奇异系统的分解和特性
12.2.6 系统分解
12.2.7 通过选择传感器/执行器实现结构配置
12.2.8 具有特征结构配置的状态反馈控制
12.2.9 通过静态输出反馈实现干扰解耦
参考文献
索引
前言
系统的结构特性对我们理解以状态空间表示的线性系统起着重要作用。
线性系统的结构化规范型表示不仅揭示了系统的结构特性,而且能使各种控制反馈策略的设计更为便利。
具体地说,结构化规范型将系统分解成各种子系统,这些子系统以及它们之间存在的相互内在联系清晰地显示了系统的结构特性。
子系统的简洁性和相互之间的显式连接使我们能够更深入的理解反馈控制对整体控制系统所产生的作用,从而能够清晰地构造满足设计目标的反馈律。
系统结构化规范型在反馈控制设计中的应用及研究已有相当长的历史。
最近以来,结构分解的优点已经很广泛和深入地应用在非线性系统控制理论中。
本书的目的是系统地给出线性系统的各种规范分解、清晰地显示系统的不同结构特性、对在系统分析和设计方面应用的最新进展情况进行综述。
我们所考虑的系统将包括自治系统,它的内在特性完全由代表其动态特性的矩阵决定;无驱动或无检测系统,它的内在特性由一对矩阵确定,一个是代表内部动态的矩阵,另一个是测量或控制矩阵;还有正则系统,它的内在特性由一个矩阵三元组或矩阵四元组来决定。
我们也将考虑线性奇异系统,它的结构特性由一个矩阵五元组决定。
所有的结果都分别以连续时间和离散时间形式给出。
同时也建立在双线性变换下连续时间系统和离散时间系统的结构特性之间的相互关系。
本书面向的读者包括研究生、从事控制的工程师、以及在系统和控制工程相关领域的研究工作者。
在本书的撰写过程中,我们力图达到自成一体。
所以在本书的开始部分全面回顾了从矩阵理论到线性系统理论的各种主题。
尽管如此,读者还是需要些线性代数、线性系统和控制理论的预备知识。
前两位作者要对已故的华盛顿州立大学教授Chin S. Hsu表达深深的谢意,作者在华盛顿州立大学求学时得到了他的热心帮助,他的线性系统理论课程生动且有趣。
第三章的一些练习题就是来自于他所布置的课后练习和测试题。
两位作者还要感谢华盛顿州立大学的Ali Saberi教授和美国新泽西州罗特格斯大学的Pedda Sannuti教授,作者在华盛顿州立大学攻读博士学位期间得到了他们的严谨指导,是他们把我们引入了线性系统特殊坐标基理论,这是本书的关键部分。
第三位作者要感谢Ali Saberi教授,是他把作者引入了这个研究方向并且有早期的合作。
第一位作者要特别感谢Pedda Sannuti教授在撰写科学专著方面所给予的无价指导。
第二位作者还要感谢北京控制工程研究所的严拱添老师,他对作者在矩阵理论和线性系统理论方面进行了严格的训练。
新加坡国立大学的刘新民先生为本书的M A TLAB工具箱的完成做出了贡献,清华大学郑大钟教授在书稿的校正方面提供了帮助。
我们还要感谢新加坡国立大学的储德林教授,彭可茂博士,程国杨博士,何英杰博士和何明华博士。
我们和新加坡国力大学的李崇兴教授,美国得克萨斯州阿灵顿得克萨斯大学的Frank L. Lewis教授,澳大利亚墨尔本大学的Iven Mareels教授,加拿大西蒙弗雷泽大学的Mehrdad Saif教授有过许多有益的学术讨论,在此表示感谢。
感谢新加坡国立大学,弗吉尼亚大学,纽约州立大学石溪分校为我们各自的基础研究工作提供了优越的环境。
系列丛书的主编William S. Levine 教授对我们完成这本书给予了热情的鼓励。
我们还要感谢Birkhauser的编辑们,特别是Thomas Grasso先生和Seth Barnes先生对我们的编辑工作所提供的宝贵帮助。
最后,我们要强调书中所包括的每个算法都已经包含在MATLAB环境下的线性系统工具箱中。
读者可以在或.sg/~bmchen/上得到工具箱的beta版本。
这个工具箱将极大的有助于理解书中各种分析和设计算法的应用。
对于那些已经有早期版本的有兴趣读者,即由Chen(1988)[17],Lin(1989)[84]和Lin等(1991)[90]所报道的特殊坐标基实现软件,我们建议更新到最新版的工具箱。
特殊坐标基是本书所包括的结构化分解技术之一,新版的工具箱是基于Chu等(2002)[36]最近发表的更加稳定的数值计算方法以及本书中所新介绍的新方法来实现的。
本著是作者采用L A T EX排版。
所有的仿真和数值计算由M A TLAB完成。
插图则由L INUX 中的X FIG和M A TLAB中的S IMULINK所生成的。
陈本美,新加坡肯特冈
林宗利,美国弗吉尼亚州夏城
雅科夫 司马诩,美国纽约州石溪
2004年6月。
