电力电缆相序阻抗计算与分析
第十一章 电力系统各元件的序阻抗和等值电路

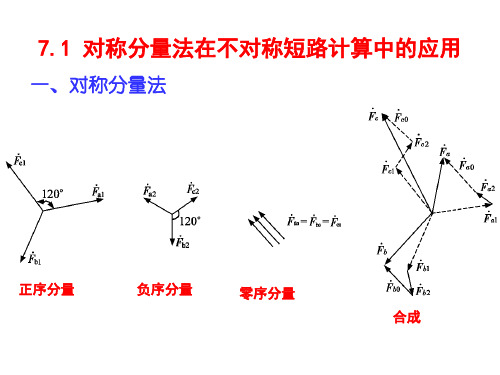
对称分量法及元件的序模型与参数Symmetrical Components Method,Sequence ModelAnd Parameters第17讲问题1、计算电力系统三相不对称故障的总体思路?2、如何将相分量分解为正序、负序、零序分量之和?3、正常电力系统如何对正序、负序、零序三序解耦?4、发电机、线路的正序、负序、零序等值参数的定义及等值电路5、中性点上的阻抗对发电机或负荷的正序、负序、零序阻抗有什么影响?6、如何根据变压器的连接组别确定其零序等值电路?如何计算不对称短路故障?1、对于三相短路(对称短路),可用一相代表三相进行计算,采用相量分析方法,非常简单。
2、对于不对称故障,无法用一相代替三相,因而计算复杂,必须寻求新的方法。
单相短路无法用一相代替三相,如何求解?1、对称分量法(Symmetrical Components)•不对称故障后电力系统的特点•对称分量法•正序、负序、零序分量(Positive, Negative and Zero Sequence Components)等值2、各序分量对对称电力系统的作用•正常电力系统元件的对称性;三相参数完全相同三相参数循环(旋转)对称由这些元件连接成的电力系统是三相对称的。
•各序分量电量作用于对称系统的性质各序分量作用于对称系统的性质稳态分析中已有的结论:1、三相对称的网络注入三相正序电流,节点上只产生三相正序电压;三相正序电压施加在三相对称的网络只产生三相正序电流。
发电机正序电压加到电力网上,只产生正序电压与正序电流推测的结论:2、三相对称的网络注入三相负序电流,节点上只产生三相负序电压;三相负序电压施加在三相对称的网络只产生三相负序电流。
3、三相对称的网络注入三相零序电流,节点上只产生三相零序电压;三相零序电压施加在三相对称的网络只产生三相零序电流。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡222222222222222222222)()()(a s n ma m s n a n m s a s a n a m a m a s a n a n a m a s cb a s n mm s n n m s c b a I a Z a Z Z I a Z a Z Z I a Z a Z Z I a Z I a Z I Z I a Z I a Z I Z I a Z I a Z I Z I I I Z Z Z Z Z Z Z Z Z U U U 如对称矩阵加负序电流,产生的电压为所以ac a b U a U U a U ==,2负序电流产生的电压为负序电压!⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000000000000)()()(a s n m a m s n a n m s a s a n a m a m a s a n a n a m a s c b a s n mm s n n m s c b a I Z Z Z I Z Z Z I Z Z Z I Z I Z I Z I Z I Z I Z I Z I Z I Z I I I Z Z Z Z Z Z Z Z Z U U U 对称矩阵加零序电流,产生的电压为所以ab c U U U ==零序电流产生的电压为零序电压!定理2正序量作用于对称系统后只产生正序量;负序量作用于对称系统后只产生负序量;零序量作用于对称系统后只产生零序量;三种分量对对称电力系统相互独立,互相解耦。
电力电缆阻抗计算

一.电力电缆正负序阻抗计算:
电缆金属护套中无感应电流,且电缆线路正三角形排列时的正负序阻抗:
Z1=Z2=Rc+j2ψ*10^(-4)*ln(s/GMRc)ohm/km(式1)
电缆金属护套中无感应电流,且电缆线路等间距直线排列时的正(负)序阻抗:
Z1=Z2=Rc+j2ψ*10^(-4)*ln[2^(1/3)*s/GMRc]ohm/km(式2)任意排列的电缆线路,设电缆A相至B相的距离为s,A相至C 相的距离为n,B相至C相的距离为m,电缆金属护套中有感应电流时,单回路电缆线路的正(负)序阻抗:
Z1=Z2=Rc+[Xm^2*Rs/(Xm^2+Rs^2)]+ j2ψ*10^(-4)*ln[(nm)^(1/3) *s/GMRc]-j*Xm^2/(Xm^2+Rs^2)ohm/km
Xm=Xs= j2ψ*10^(-4)*ln{(nm)^(1/3)*s/GMRc}
式中,Z1 为正序阻抗;Z2 为负序阻抗;Rc 为电缆导体电阻;s 为电缆相间中心距离(式1、2);GMRc 为电缆导体几何平均半径;Rs为金属护套电阻;GMRs为金属护套几何平均半径
二.电力电缆线路零序阻抗计算:
Z0=3*(Rc/3+Rg+j2ψ*10^(-4)*ln(Dd/GMRo)ohm/km
GMRo=[GMRc^3*(s*n*m)^2]^(1/9)
式中,Rg为大地电阻,Rg=0.0493Ω/km;Dd 为等效回路深度,Dd=1000米;GMR0为三相线路等效几何平均半径,其余同上。
电力电缆相序阻抗计算与分析

电力电缆相序阻抗计算与分析随着城市建设的飞速发展和城市规划的要求,城区220 kV和110 kV线路大量采用电力电缆,而电力电缆参数的准确性(主要指正序和零序阻抗)是继电保护整定计算的重要基础。
由于电缆线路X0/X1的关系与架空线路不一样,因此需要对电力电缆参数理论计算方法、测量方法和其特点规律进行分析和研究,以便于指导生产实际。
1 电缆参数计算和分析电缆线路参数与金属护套接地方式、互联和换位、回流线和回路数有关,下面分几种情况进行讨论。
1.1 电缆线路的正、负序阻抗(1)金属护套内无电流当单芯电缆线路的金属护套只有一点互联接地;或各相电缆和金属护套均换位,且三个换位小段长度相等;或金属护套连续换位得很好时,金属护套内不存在感应电流,此时电缆线路正、负序单位阻抗计算与架空线一样(见图1):图 1 以比率表示的任意排列单回线中各项电缆之间的中心距离Z1=Z2=RC+j2ω×10-4ln(S×nS×mS)13 (GMRA×GMRB×GMRC)13 (1)式中Z1为正序单位阻抗,Ω/km;Z2为负序单位阻抗,Ω/ km;Rc为三相线芯的平均交流电阻,Ω/km;ω为角频率; GMRA、GMRB,GMRC为自几何均距。
(2)金属护套内有电流如果电缆的金属护套两端直接互联,金属护套的感应电压在护套形成的闭环回路中产生和线芯电流方向相反的护套电流,并产生护套损耗,导致线芯正、负序电阻减小,正、负序感抗增加,计算公式:Z1=Z2=RC+Xm2RSXm2+RS2+j2ω×10-4 ×ln(nm)13SGMRC-jXm3Xm2+RS2 (2)式中Xm为金属护套与线芯间的单位互感抗;Rs为金属护套的直流电阻(50℃),Ω/km;GMRC为线芯的几何半径。
1.2 电缆线路的零序阻抗(1)短路电流以大地作回路电缆线路的金属护套只在一端互联接地,而邻近无其它平行的接地导线,则在电网发生单相接地故障时,短路电流以大地作回路。
第7章序阻抗
7.3、电力系统各序网络
➢等值电路的绘制原则 根据电力系统的原始资料,在故障点分别 施加各序电势,从故障点开始,查明各序 电流的流通情况,凡是某序电流能流通的 元件,必须包含在该序网络中,并用相应 的序参数及等值电路表示。
一、正序网络
特点: 1. 正序电动势就是发电机的电动势。 2. 流过正序电流的全部元件的阻抗均用正序阻抗表示。 3. 不包括中性点接地阻抗、空载线路、空载变压器。 4. 短路点处要加上短路点正序分量,短路点计为f1,零电
G
T-1
L-1 Ⅰ Ⅱ L-4 L-5
T-5
G2
xn1
ⅠⅡ
Ⅲ
f
ⅡⅠ
Ⅲ
L-2
L-3
L-6
ⅡⅠ ⅡⅠ
T-3
T-4
G3
正序
G-1
T-2
G
T-1
L-1 Ⅰ Ⅱ L-4 L-5
零电位点和00连接起来。
无源网络
零序网络:必须首先确定零序电流的流通路径。
Va 0
Va 0
jXT1
f j3Xn1 jX0(L1) 0 jX0(L2) jX1
零序网络 Va 0
jXⅡ j3Xn2 jX0(L3) jXT3 jXⅢ
O0
例7-4
补充例题
补充例题
习题:
三相四柱式
G-1
T-2
Zs
Z m
Z sc
0
0
Z Z
s
m
0 Z1 0 0
0
0
Z 2
0
0
0
Z s
2Z m
0
0 Z0
V120 Zsc I120
Va1 Va2
Z 1 Ia1 Z 2 Ia2
线缆阻抗计算公式

线缆阻抗计算公式线缆阻抗是指电缆或导线对电流流动的阻碍程度,是电缆或导线的物理特性之一。
了解线缆阻抗的计算公式对于电气工程师和电子技术人员来说非常重要。
本文将介绍线缆阻抗的计算公式及其应用。
一、什么是线缆阻抗?线缆阻抗是指电缆或导线对电流流动的阻碍程度。
它是由电缆或导线的电感、电容和电阻等因素综合决定的。
电缆或导线的阻抗越大,通过它的电流越小;阻抗越小,通过它的电流越大。
二、线缆阻抗计算公式常见的线缆阻抗计算公式如下:1. 电缆或导线的电感阻抗计算公式:ZL = jωL其中,ZL为电感阻抗,j为虚数单位,ω为角频率,L为电感。
2. 电缆或导线的电容阻抗计算公式:ZC = 1 / (jωC)其中,ZC为电容阻抗,C为电容。
3. 电缆或导线的电阻阻抗计算公式:ZR = R其中,ZR为电阻阻抗,R为电阻。
4. 电缆或导线的总阻抗计算公式:Z = √(ZL^2 + ZC^2 + ZR^2)其中,Z为总阻抗,ZL为电感阻抗,ZC为电容阻抗,ZR为电阻阻抗。
三、线缆阻抗计算公式的应用线缆阻抗计算公式在电气工程和电子技术中具有广泛的应用。
1. 电缆设计:根据电缆的使用环境和要求,计算线缆的阻抗,选择适合的电缆材料和规格。
2. 信号传输:在数据通信中,为了保证信号的传输质量,需要计算线缆的阻抗,选择匹配的信号源和负载。
3. 电气系统分析:在电气系统中,计算线缆的阻抗有助于分析电路的特性和性能,确保电流和电压的稳定传输。
4. 高频电路设计:在射频电路设计中,计算线缆的阻抗有助于匹配电路的传输线和负载,提高电路的工作效率和性能。
线缆阻抗计算公式是电气工程和电子技术中必不可少的工具。
掌握线缆阻抗的计算方法,可以帮助工程师和技术人员设计和分析电路,提高电气系统的性能和可靠性。
同时,合理选择线缆材料和规格,可以有效降低能耗和成本,提高电缆的传输效率和质量。
电缆的电抗和阻抗计算

电缆的电抗和阻抗计算
电缆是电力传输和信号传输中常用的导线,其电抗和阻抗的计算对于电力系统的设计和电路的分析非常重要。
本文将介绍电缆电抗和阻抗的计算方法及其应用。
首先,我们来了解一下电抗和阻抗的概念。
电抗是指电缆对交流电的阻碍程度,可以分为电感抗和电容抗。
电感抗是指电缆对电流变化的反应,主要由电感引起;电容抗是指电缆对电压变化的反应,主要由电容引起。
阻抗是指电缆对交流电的总体阻碍程度,包括电阻和电抗。
对于计算电缆的电感抗,我们可以使用下面的公式:
XL=2πfL
其中,XL表示电感抗,f表示频率,L表示电感。
对于计算电缆的电容抗,我们可以使用下面的公式:
XC=1/(2πfC)
其中,XC表示电容抗,f表示频率,C表示电容。
在计算电缆的总电抗时,我们需要考虑电感抗和电容抗的综合影响。
可以使用下面的公式计算电缆的总电抗:
Z=√(R^2+(XL-XC)^2)
其中,Z表示电缆的总电抗,R表示电缆的电阻,XL表示电感抗,XC表示电容抗。
通过计算电缆的电抗和阻抗,我们可以评估电缆在交流电路中的性能和稳定性。
在电力系统设计中,合理计算电缆的电抗和阻抗有助于保证电缆的传输效率和稳定性。
在电路分析中,我们可以根据电缆的电抗和阻抗来预测电路的响应和特性。
总之,电缆的电抗和阻抗计算是电力系统设计和电路分析中的重要内容。
通过合理计算电缆的电抗和阻抗,我们可以评估电缆的性能和稳定性,保证电力传输和信号传输的有效性。
这对于提高电力系统的运行效率和电路分析的准确性具有重要意义。
【国家电网 系统】7 电力系统各元件序阻抗和等值电路

•
有阻尼绕组电机负序电抗应为:
X
" q
X
2
X
" d
•
无阻尼绕组电机负序电抗应为:
X
' d
X2 Xq
7.2 元件的序阻抗
• 不同型式的短路,电机的负序电抗。
单相短路
X2
X
" d
X0 2
X
" q
X0 2
X0 2
两相短路
X2
X d"
X
" q
两相短路接地 X
" d
X
" q
X 2 X2
1 2
Va2
ZG0 ZL0 Ia0
Va0
3Zn
7.1 对称分量法
Z1 Ia1 Va1
E Z2 Ia2 Va2
Z0 Ia0 Va0
序网方程
E0IaI2aZ1Z21VVaa21
0
Ia0Z0
Va0
六个未知量,三个方程, 还需要三个方程------每种故障的故障条件
(边界条件,各种短路不 相同)
各种短路都适用
7.2 元件的序阻抗
Ia0
Zn
Va0
Va0
Va0
(f)
0 Ia0(ZG0 ZL0) (Ia0 Ia0 Ia0)Zn Va0
Ia0 Ia0 Ia0 Ia0 Ib0 Ic0 3Ia0
0 Ia0(ZG0 ZL0) 3Ia0Zn Va0
单线图表示:
ZG1 ZL1 Ia1
Va1
E a
ZG2 ZL2 Ia2
2
1.45
X
' d
• 无确切参数,电机的负序电抗一般取
电力课件第七章电力系统各元件的序参数和等值电路应用概念课件

可见,a、b、c相的正序阻抗为:
(7-8)
由式(7-8)可知,正序阻抗在三相中是相同的。由于正序电压和电流时正常对称状态下的三相电压和电流,所以正序阻抗就是电路在正常对称运行状态下的一相等值阻抗。
如在这个电路上施加负序电压,则电路中将流过负序相电流,且中性线电流为零。此时,相电压与相电流之比叫做该电路的负序阻抗。和推导上述正序阻抗的过程相似,可得各相的负序阻抗为:
(7-9)
对于无阻抗绕组凸极机,取为Xd’和Xd的几何平均值,即
(7-10)
在近似计算中,对于汽轮发电机及有阻尼绕组的水轮发电机,也可采用X2=1.22Xd’’。对于没有阻尼绕组的水轮发电机,可采用X2=1.45Xd’’。
如果对于同步发电机的参数缺乏了解,其负序电抗也可按表7-2取值。
表7-2同步电机的负序电抗X2和零序电抗X0
表7-1同步发电机的负序电抗X2
短路种类
负序电抗
两相短路
单相接地短路
两相接地短路
表7-1中X0为同步发电机的零序电抗。由表7-1可见,若Xd’’=Xq’’,则负序电抗X2=Xd’’,与同步发电机的短路种类无关。当同步发电机经外电抗X短路时,表中所有Xd’’、Xq’’、X0都应以Xd’’+X,Xq’’+X,X0+X代替。此时同步发电机转子纵横间不对称的影响将被削弱。当纵横轴向的电抗接近相等时,表中三个公式的计算结果差别很小。电力系统短路一般发生在电力线路上,所以在短路电流计算中,同步发电机本身的负序电抗,可以当做短路种类无关,并取Xd’’和Xq’’的算述平均值,即
第七章 电力系统各元件的序参数和等值电路
三相短路为对称短路,短路电流交流分量三相是对称的。在对称三相系统中,三相阻抗相同,三相电压和电流的有效值相等。因此对于对称三相系统三相短路的根系与计算,可只分析和计算其中一相。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2002 年第 4 期
供 用 电
25
2 电缆参数测试方法
211 正、负序阻抗的测量 将线路对侧三相短路并接地, 采用单相电源法测量,
接线见图 2 (以 AB 为试验相)。
图 2 正、负序阻抗测量接线图 电缆正序阻抗可按下列公式计算:
co sΥAB =
P AB U AB IAB
·
ZAB =
R AB +
GM RA、GM RB , GM RC 为自几何均距。
(2) 金属护套内有电流
如果电缆的金属护套两端直接互联, 金属护套的感应
电压在护套形成的闭环回路中产生和线芯电流方向相反
的护套电流, 并产生护套损耗, 导致线芯正、负序电阻减
小, 正、负序感抗增加, 计算公式:
Z 1=
Z 2=
R C+
X
X m 2R S m 2+ R
附表
理论计算值
实测结果
名称 天鹿线 罗鹿线 西罗线
Z 1 8 km 011818 011821 012430
Z 0 8 km 011884 011884 11710
Z 1 8 km 011825 011778 012350
Z 0 8 km 011886 011816 116970
由附表可知: (1) 金属护套仅在一端互联接地时, 电缆零序单位阻
地时, 短路电流通过大地部分可忽略不计, 可认为短路电 流全部以金属护套作回路, 回路电阻为金属护套的并联电 阻, 则单回路的零序单位阻抗为:
1
Z 0= R C + R S + j6Ξ×10- 4 ln
GM R S GM RC
3
(4)
式中 GM R s 为金属护套的几何半径。
113 正、负与零序阻抗参数的关系
图 1 以比率表示的任意排列单回线中 各项电缆之间的中心距离
Z 1= Z 2=
R C+
j2Ξ×10-
4 ln
(S
×nS
×m
S
)
1 3
(GM
RA ×GM
RB ×GM
RC)
1 3
(1)
式中 Z 1 为正序单位阻抗, 8 km ; Z 2 为负序单位阻抗, 8
km ; R c 为三相线芯的平均交流电阻, 8 km ; Ξ 为角频率;
由于 3R g 较大, 比较公式 (1) 和 (3) 可知, 金属护套一
端互联时, 电缆的零序单位阻抗 Z 0 远大于 Z 1 和 Z 2。由于
金属护套与线芯间的单位互感抗 X m 大于金属护套的直
流电阻 R S , 比较公式 (2) 和 (4) 可知, 金属护套两端互联
时, 电缆的零序单位阻抗 Z 0 一般略大于 Z 1 和 Z 2。
1 电缆参数计算和分析
电缆线路参数与金属护套接地方式、互联和换位、回 流线和回路数有关, 下面分几种情况进行讨论。 111 电缆线路的正、负序阻抗
(1) 金属护套内无电流 当单芯电缆线路的金属护套只有一点互联接地; 或各 相电缆和金属护套均换位, 且三个换位小段长度相等; 或 金属护套连续换位得很好时, 金属护套内不存在感应电 流, 此时电缆线路正、负序单位阻抗计算与架空线一样 (见 图 1):
4 结论
本文通过理论计算和实测方法, 对高压电力电缆线路 相序阻抗参数与金属护套接地互联方式等方面的关系以 及各序阻抗之间的关系进行研究分析, 从而对电缆线路参 数的规律和特点有了正确认识和理解, 有利于继电保护装 置的正确整定, 可靠运行。
收稿日期: 2001 年 12 月 20 日 毛为民 广州电力工业局 广州中山一路 32 号 510600
它平行的接地导线, 则在电网发生单相接地故障时, 短路 电流以大地作回路。 单回路的零序单位阻抗为:
Z 0=
3
RC 3
+
R
g+
j2Ξ×10-
4 ln
De
[ GM
RC3
(S
×nS
×m
S
)
2
]
1 9
(3) 式中D e 为故障电流以大地作回路时等值回路的深度; R g 为大地的漏电电阻。
(2) 短路电流全部以金属护套作回路 电缆线路的金属护套在两端直接互联或交叉互联接
第 19 卷第 4 期
24
供 用 电
2002 年 8 月
电力电缆相序阻抗计算与分析
广州电力工业局 毛为民
摘 要 在城市电网建设中, 220 kV 和 110 kV 线路愈来愈广泛采用电力电缆, 因此必须正确认识和掌握电 缆线路的相序阻抗参数特点。 本文论述了电力电缆正、负和零序阻抗的理论计算和采用单相电源法进行参数 实测的试验方法, 阐述了金属护套不同的接地互联方式下电缆相序阻抗参数特点和各序阻抗之间的关系, 有 助于电缆参数的正确测量和继电保护装置的可靠运行。 关键词 电力电缆; 相序阻抗; 金属护套 中图分类号: TM 71 文献标识码: B 文章编号: 100626357 (2002) 0420024202
抗值约为正、负序单位阻抗值的 7~ 10 倍。 (2) 金属护套在两端互联接地时, 电缆零序单位阻抗
仅略大于正、负序单位阻抗值, 而架空线路的 X 0 约为 X 1 的 3 倍。
(3) 金属护套一端直接互联接地与两端互联接地时, 电缆正、负序单位阻抗值的相差不大。
(4) 金属护套一端直接互联接地与两端互联接地的 电缆零序单位阻抗值相差近十倍。
随着城市建设的飞速发展和城市规划的要求, 城区 220 kV 和 110 kV 线路大量采用电力电缆, 而电力电缆参 数的准确性 (主要指正序和零序阻抗) 是继电保护整定计 算的重要基础。由于电缆线路 X0 X1 的关系与架空线路不 一样, 因此需要对电力电缆参数理论计算方法、测量方法 和其特点规律进行分析和研究, 以便于指导生产实际。
co sΥ0=
P0 U 0I0
·
Z 0=
R 0+
jX 0=
3U I0
0
co
sΥ0
+
j
3U I0
0
s in Υ0
R 0=
3P 0
I
2 0
X 0=
U0 I0
2
-
R
2 0
3 例证
220 kV 罗鹿线和天鹿线电缆均为单回路, 金属护套 交叉互联, 两端接地, 等间距直线排列, 没有回流线; 110 kV 西罗线电缆为金属护套一端直接互联接地, 没有回流 线。 上述三条电缆线路的正、零序阻抗的理论计算值与实 测结果见附表。
图 3 零序阻抗测量接线图
jX
AB =
U AB IAB
co
sΥAB
+
j
U AB IAB
s
in
ΥAB
R AB =
P AB IA2B
X AB =
U AB IAB
2
-
R
2 AB
式中 co sΥAB 为试验 AB 相功率因数, R AB 为试验 AB 相正序
有效电阻,
·
ZAB
为试验
A
B
相正序阻抗。
然后, 依次以 BC
相和 CA
相为试验相,
S
2
+
j2Ξ×10-
4
1
×ln
(nm ) 3 S GM RC
-
j
X
Xm m 2+
3
R
S
2
(2)
式中 X m 为金属护套与线芯间的单位互感抗; R s 为金属
护套的直流电阻 (50℃) , 8 km ; GM RC 为线芯的几何半
径。
112 电缆线路的零序阻抗 (1) 短路电流以大地作回路 电缆线路的金属护套只在一端互联接地, 而邻近无其
可测得
·
Z BC
和
·
Z CA
,
·
(ZAB +
·
ZBC +
·
Z CA ) =
R 1+
jX 1
R 1=
1 6
(R AB +
R BC +
R CA )
X 1=
Z
2 1
-
R
2 1
212 零序阻抗的测量
将线路对侧三相短路并接地, 本侧测量端三相短路,
单相电源经隔离变压器接入, 接线见图 3。
零序阻抗计算公式如下:
