垂径定理解题应用举例
垂径定理实例练习题

垂径定理实例练习题
根据垂径定理,设有一个圆,有一个直径和一个点位于该圆上,连接该点与直径的两个端点,则连接该点与圆心的线段垂直于直径。
下面是一些关于垂径定理的实例练题:
1. 问题描述:在一个圆上,有一条直径AB,并且连接圆上一
点C与直径的两个端点A和B,证明线段AC与线段BC互相垂直。
解答:因为AC连接了圆上的一点与圆心,所以根据垂径定理,线段AC与直径AB垂直。
同理,线段BC与直径AB也垂直。
因此,线段AC与线段BC互相垂直,证毕。
2. 问题描述:在圆P上,有一条直径EF,并且连接了圆上一
点D与直径的两个端点E和F。
已知EF长度为10厘米,点D离
圆心的距离为8厘米,求线段DF的长度。
解答:根据垂径定理,因为点D连接了圆上的一点与圆心,所以线段DF垂直于直径EF。
由于EF长度为10厘米,根据直角三角
形的性质,可以使用毕达哥拉斯定理计算线段DF的长度。
根据毕达哥拉斯定理,我们有:
其中,c代表斜边(即线段EF),a和b代表直角边(即线段DF和DE)。
已知EF长度为10厘米,代入公式可得:
解方程可得DF的值为6厘米,即线段DF的长度为6厘米。
以上是垂径定理的一些实例练习题的讲解。
希望能够帮助你理解和应用垂径定理。
如有任何问题,请随时向我提问。
典中点圆专训2 垂径定理的四种应用技巧
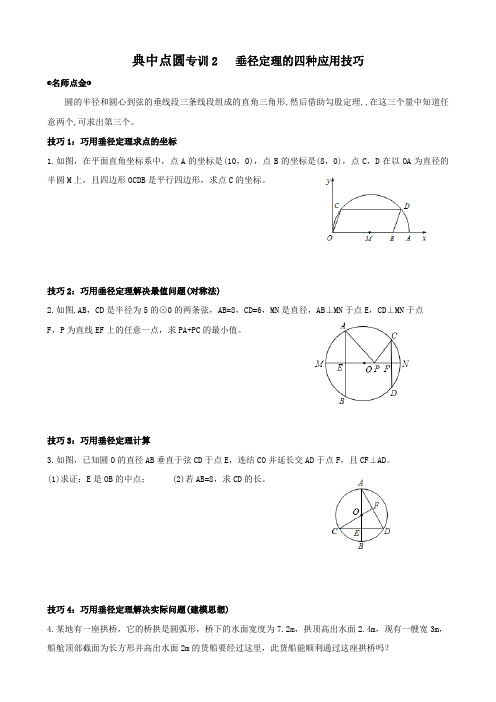
典中点圆专训2 垂径定理的四种应用技巧
◐名师点金◑
圆的半径和圆心到弦的垂线段三条线段组成的直角三角形,然后借助勾股定理,,在这三个量中知道任意两个,可求出第三个。
技巧1:巧用垂径定理求点的坐标
1.如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标是(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标。
技巧2:巧用垂径定理解决最值问题(对称法)
2.如图,AB,CD是半径为5的⊙0的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点
F,P为直线EF上的任意一点,求PA+PC的最小值。
技巧3:巧用垂径定理计算
3.如图,已知圆O的直径AB垂直于弦CD于点E,连结CO并延长交AD于点F,且CF⊥AD。
(1)求证:E是OB的中点; (2)若AB=8,求CD的长。
技巧4:巧用垂径定理解决实际问题(建模思想)
4.某地有一座拱桥,它的桥拱是圆弧形,桥下的水面宽度为7.2m,拱顶高出水面2.4m,现有一艘宽3m,船舱顶部截面为长方形并高出水面2m的货船要经过这里,此货船能顺利通过这座拱桥吗?。
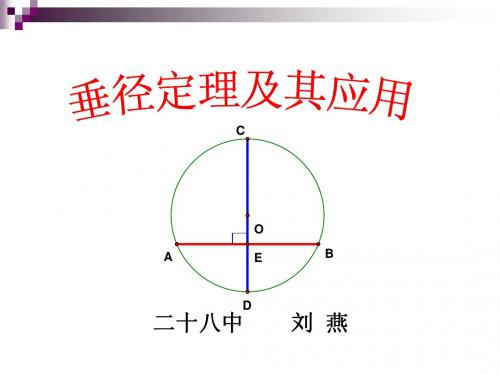
垂径定理及其应用
A C
O
D B
O
A
C
E
D
B
C
A D
O A D E B
B
A
O D C B
O
C
A
C D
B
A
O C B
O
随堂练习
挑 战自我
1、对于一个圆中的弦长a、圆心到弦的距离d、圆半 径r、弓形高h,这四个量中,只要已知其中任意两个 量,就可以求出另外两个量,如图有: ⑴d + h = r
a 2
h d o
a 2 ⑵ r d ( ) 2
E D
E
B
O 340
A
B
D
300
小结
1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧. 2.逆定理: ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 ②弦的垂直平分线经过圆心,并且平分弦所对的两条弧. ③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. 3.求圆中求有关线段的长度时,常过圆心作垂直于弦的垂线段,或连结半径等辅 助线,借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
2 2
r
2、熟练地运用垂径定理及其推论、勾股定理,并用 方程的思想来解决问题.
垂径定理的应用
1.如图,一条排水管的截面。已知排水管
的半径为13cm,水面宽AB=24cm。求水 的最大深度.
解:过O点作OD⊥AB于E点,交⊙O 于D点,连接OA。 1 由垂径定理得 AE= AB=12cm 2 A 在Rt△OAE中,
O
A
C
B
求圆中有关线段的长 度时,常借助垂径定理 转化为直角三角形,从 而利用勾股定理来解 决问题.
(文章)垂径定理解题应用举例

垂径定理解题应用举例垂径定理及其推论是《圆》一章的重要考点,定理告诉我们,对于一个圆和一条直线来说,如果具备下列五个条件中的任何两个,那么也具有其它三个:①垂直于弦,②过圆心,③平分弦,④平分弦所对的优弧,⑤平分弦所对的劣弧。
它反映了圆的重要性质,是证明线.段相等...、角相等...、垂直关系....的重要依据,同时也为圆的计算和作图提供了方法和依据,下面分类举例说明。
一、利用垂径平分弦所对的弧,来处理角的关系例1 (重庆市)如图1,⊙O 的直径CD 过弦EF 的中点G ,∠EOD =40°,则∠DCF 等于( )A.80°B. 50°C. 40°D. 20° 【析解】本题可由②③⇒①④⑤,所以可得ED DF =,从而得出∠DCF 与∠EOD 的关系。
解:∵直径CD 平分弦EF , ∴ ED DF =, ∴ ∠DCF =12∠EOD =20°。
故选(D ).二、利用垂径垂直平分弦,证相关线段相等例2 (南京市)如图2,矩形ABCD 与与圆心在AB 上的⊙O 交于点G 、B 、F 、E , GB =8cm ,AG =1cm ,DE =2cm ,则EF = cm .【分析】本题上手有点不知所措,其实利用矩形和垂径定理相关知识可以得到解决。
分别过O ,G 作OM ⊥CD ,GN ⊥DC ,即可求出EF 的长。
解:如图2,分别过O ,G 作OM ⊥CD ,GN ⊥DC ,则根据矩形的性质可得:NC =GB =8,DN =AG =1,GN ∥OM ∥BC ,∵ OM ⊥EF , ∴ EM =MF ,∵ OG =OB ,GN ∥OM ∥BC , ∴ MN =MC ,∴ CF =NE , ∵ DE =2,∴ NE =DE -DN =DE -AG =1, ∴ EF =NC -NE -CF =8-2=6.三、利用垂径定理,构造直角三角形,利用勾股定理 例 3 (长春市)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,图3是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面;(2)若这个输水管道有水部分的水面宽AB =16cm ,水面最深地方的高度为4cm ,求这个圆形截面的半径.分析:(1)要补全输水管道的圆形截面,需要画出图3所在的圆,因此首先确定所在图1O G FEDC N M OGF E D C BA图2图3圆的圆心和半径.⑴任作两条弦,⑵分别作出两弦的垂直平分线,⑶两弦的垂直平分线的交点为圆心,⑷以交点为圆心,交点到圆上任意一点为半径作圆,所作出的圆即为所求.作图过程:略.(2)本题的解题关键是作垂直于弦的半径,然后构造直角三角形,应用勾股定理列方程求解.解:(1)正确作出图形,并做答.(2)如图4,解:过O 作OC ⊥AB 于D ,交弧AB 于C , ∵OC ⊥AB , ∴BD =21AB =21×16=8cm . 由题意可知,CD =4cm .设半径为x C m ,则OD =(x -4)cm . 在Rt △BOD 中,由勾股定理得:OD 2+BD 2=OB 2, ∴( x -4)2+82=x 2.∴x =10.四、利用垂径垂直弦,构造成特殊四边形例4 (四川省)如图5,在⊙O 中,AB 、AC 是互相垂直的两条弦, AB =8cm ,AC =6cm ,那么⊙O 的半径OA 的长( )A .4 cmB .5 cmC .6 cmD .8 cm【分析】要求半径OA 的长,可通过垂径定理构造Rt △,于是过O 分别作OD ⊥AB ,OE ⊥AC ,则可得矩形ADOE 。
怎样利用垂径定理

怎样利用垂径定理垂径定理是一个被广泛应用于几何学的定理,它指出,任何一条垂线到直线的距离,都等于该直线到它的垂足的距离。
也就是说,任意一条垂线都将其垂足与它与直线相交的点连接起来,而且两个距离也将会相等。
垂径定理在几何图形中是非常有用的。
它能够帮助我们更加准确地分析各种形状。
例如,用垂径定理,我们可以得出三角形的两个棱边长度之和和斜边长度的平方和之间的关系。
通过利用垂径定理,我们可以计算出三角形的斜边长度,从而得出整个三角形的形状大小。
此外,垂径定理还可以用来求解锐角三角形中各边的长度。
根据垂线定理,设有一个锐角三角形,它的一条边长为a,另一条边长为b,两个角分别为α和β,那么a^2 + b^2 = c^2,其中c为斜边的长度。
根据此公式,我们可以得出三角形的三边长度之和以及斜边的长度。
垂径定理还可以用来求解圆的半径,即它的斜线长度。
垂线定理指出,若a为圆的圆心至圆上一点的距离,b为圆的圆心至该点的垂足的距离,那么a^2 + b^2 = r^2,其中r为所求的圆的半径。
也就是说,通过求解圆心至圆上一点的距离以及圆心至圆上一点的垂足的距离,就可以得出所求圆的半径。
另外,垂径定理也可以应用在构造正方形,正方形中若有一条边,它的其他三条边也可以通过垂径定理求出。
比如说,设有一个正方形,它的一条边长为a,它的垂足距离其相交点的距离为b,那么a^2 + b^2= c^2,该公式描述的就是垂径定理。
通过这个公式,我们就可以求出其他三条边的长度。
以上就是垂径定理的应用了。
垂径定理的优点在于,它可以用来很方便地分析各种几何图形的形状和尺寸,这一点是非常实用的。
它还可以用来求解圆或正方形等形状中各边长度之间的关系。
因此,垂径定理是几何学中一个非常有用的定理。
垂径定理在实际问题中的应用举例

- 1 -垂径定理在实际问题中的应用“数学源于生活,生活中充满着数学”,我们刚刚学过的垂经定理在生活中就有着广泛的应用,中考中也常常体现这一点,现采撷几例,以飨读者.例1小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图1所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( ) A .第①块 B .第②块 C .第③块 D .第④块析解:显然,小明带到商店去的应是一块能确定其圆心和半径的玻璃碎片,观察图中的玻璃碎片,根据垂径定理可知,由第②块可确定出圆心和半径(如图2所示),故选答案B.例2高速公路的隧道和桥梁最多.如图3是一个隧道的横截面,若它的形状是以O 为圆心的圆的一部分,路面AB =10米,净高CD =7米,则此圆的半径OA =( )A.5B.7C. 537D. 737析解:本题主要考查垂径定理与勾股定理的知识.设圆的半径为r ,有(7-r)2+52=r 2. 解之得,r=737.故选D. 例3兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图4所示,已知AB =16m ,半径 OA =10m ,高度CD 为_____m .析解:考查垂径定理及其应用,如图根据垂径定理,三角形ADO是Rt △,所以OD=221610()62-=,CD=10-6=4,填4.例4如图是“明清影视城”的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据,于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20 cm ,且AB ,CD 与水平地面都是垂直的.根OD ABC 图3DBAOC图4O MN G图5图1- 2 -据以上数据,请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少? 析解:本题解决的关键是利用垂径定理构造直角三角形,进行运用勾股定理求出圆弧形门所在圆的半径.如图5,连接AC ,作AC 的中垂线交AC 于G ,交BD 于N ,交圆的另一点为M ,由垂径定理可知:MN 为圆弧形的所在的圆与地面的切点,取MN 的中点O ,则O 为圆心,连接OA 、OC , ∵AB ⊥BD ,CD ⊥BD , ∴AB ∥CD . ∵AB=CD,∴四边形ABCD 为矩形, ∴AC=BD=200cm,GN=AB=CD=20 cm, ∴AG=GC=12AC=100 cm . 设⊙O 的圆心为R,由勾股定理得 OA 2=OG 2+AG 2,即R 2=(R -20)2+1002, 解得R=260 cm, ∴MN=2R=520 cm .答:这个圆弧形门的最高点离地面的高度是=520 cm .总评:垂径定理及其推论是圆中的重要性质,它是根据圆的对称性推导出来的,希望同学们熟练掌握其内容,并会灵活应用,同时注意它经常和勾股定理结合来解决问题。
圆的垂径定理练习题
圆的垂径定理练习题圆的垂径定理是几何学中的重要定理之一,它给出了圆上的垂径之间的关系。
在这篇文章中,我们将通过一些练习题来加深对这个定理的理解和应用。
练习题一:给定一个半径为5的圆,其中一条垂径的长度为12。
求另一条垂径的长度。
解析:根据圆的垂径定理,垂径的乘积等于半径的平方。
设另一条垂径的长度为x,则有12 * x = 5 * 5。
解这个方程可以得到x的值,进而求出另一条垂径的长度。
练习题二:在一个半径为8的圆中,一条垂径的长度为15。
求另一条垂径的长度。
解析:同样地,根据圆的垂径定理,垂径的乘积等于半径的平方。
设另一条垂径的长度为y,则有15 * y = 8 * 8。
解这个方程可以得到y的值,进而求出另一条垂径的长度。
练习题三:在一个半径为10的圆中,一条垂径的长度为24。
求另一条垂径的长度。
解析:同样地,根据圆的垂径定理,垂径的乘积等于半径的平方。
设另一条垂径的长度为z,则有24 * z = 10 * 10。
解这个方程可以得到z的值,进而求出另一条垂径的长度。
通过以上三个练习题,我们可以看到圆的垂径定理的应用。
它告诉我们,对于一个圆来说,任意两条垂径的乘积都等于半径的平方。
这个定理在解决一些几何问题中非常有用。
除了上述练习题,我们还可以通过一些实际问题来应用圆的垂径定理。
例如,假设有一个圆形花坛,我们想在花坛中心种一棵树。
为了确保树能够均匀地分布在花坛中,我们可以利用垂径定理来确定每棵树之间的最佳位置。
另一个实际应用的例子是在建筑设计中。
如果我们想在一个圆形庭院中建造一个喷泉,我们可以利用垂径定理来确定喷泉的位置,以确保水能够均匀地喷射到庭院的各个角落。
综上所述,圆的垂径定理是一个重要的几何定理,它给出了圆上的垂径之间的关系。
通过练习题和实际应用,我们可以更好地理解和应用这个定理。
无论是解决几何问题还是在实际生活中应用,垂径定理都发挥着重要的作用。
垂径定理及其应用
垂径定理解及其应用【知识整理】垂径定理的题设和结论。
题设 结论()⎧⎫⎪⇒⎬⎨⎭⎪⎩直线直径平分弦直线过圆心(直径)直线平分弦所对优弧直线垂直于弦直线平分弦所对劣弧注意:题设中的两个条件缺一不可。
垂径定理的实质可以理解为:一条直线,如果它具有两个性质:(1)经过圆心;(2)垂直于弦,那么这条直线就一定具有另外三个性质:(3)平分弦,(4)平分弦所对的劣弧,(5)平分弦所对的优弧(如图所示). 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧, 推论1的实质是:一条直线(如图)(1)若满足:i)经过圆心,ii)平分弦,则可推出:iii)垂直于弦,iv)平分弦所对的劣弧,v)平分弦所对的优弧. (2)若满足:i)垂直于弦,ii)平分弦。
则可推出:iii)经过圆心,iv)平分弦所对的劣弧,v)平分弦所对的优弧. (3)若满足;i)经过圆心,ii)平分弦所对的一条弧,则可推出:iii)垂直于弦,iv)平分弦,v)平分弦所对的另一条弧.推论2: 圆的两条平行弦所夹的弧相等. 如图中,若AB∥CD,则AC =BD注意:在圆中,解有关弦的问题时,常常需要作“垂直于弦的直径作为辅助线。
【例题选讲】一、利用垂径垂直平分弦,证有关线段相等例1.如图,AB 是⊙O 的直径,弦CD 与AB 相交,过A ,B 向CD 引垂线,垂足分别为E ,F ,求证:CE=DF 。
二、利用垂径平分弦所对的弧,处理角的关系例2.已知△ABC内接于⊙O,且AB=AC,⊙O的半径等于6cm,O点到BC的距离为2cm,求AB的长。
分析:因为不知道△ABC是锐角三角形,还是钝角三角形(由已知分析,△ABC不会是直角三角形,因为若是直角三角形,则BC为斜边,圆心O在BC上,这与O点到BC的距离为2cm矛盾),因此圆心有可能在三角形内部,也可能在三角形外部,所以需分两种情况进行讨论:三、利用垂径定理,构造勾股定理例3.已知如图:直线AB与⊙O交于C,D,且OA=OB。
2 垂径定理的四种应用技巧
双休作业(六) 2 垂径定理的四种应用技巧
1
2
3
4
技巧 1 巧用垂径定理求点的坐标
1.如图,在平面直角坐标系中,点A的坐标是(10,
0),点B的坐标是(8,0),点C,D在以OA为直径 的半圆M上, 且四边形OCDB
是平行四边形.求点C的坐标
解:如图,连接CM,作MN⊥CD于N,CH⊥OA于H.
返回
技巧 2 巧用垂径定理解决最值问题(转化思想)
2.如图,AB,CD是半径为5的⊙O的两条弦,AB=8,
CD=6,MN是直径,AB⊥MN 于点E,CD⊥MN于点F,P为直
线EF上的任意一点.求PA+PC 的最小值.
解:如图,易知点C关于直线MN的对称点为点D, 连接AD,交MN于点P,连接PC,易知此时PA+PC最小且 PA+PC=AD.过点D作DH⊥AB于点H,连接OA,OC.易知 AE=4,CF=3,由勾股定理易得OE=3,OF=4, ∴DH=EF=7,又AH=AE+EH=4+3=7. ∴AD=7 2 ,即PA+PC的最小值为7 2 .
返回
技巧 3 巧用垂径定理证明
3.不过圆心的直线l交⊙O于C、D两点,AB是⊙O的
直径,AE⊥l,垂足为E,BF⊥l,垂足为F. (1)如图①,当AB与线段CD不相
交时,求证:CE=DF.
证明:过点O作OM⊥EF于点M,则CM=DM. ∵AE⊥EF,BF⊥EF,OM⊥EF, ∴AE∥OM∥BF. 又∵OA=OB,∴EM=FM. ∴EM-CM=FM-DM,即CE=DF.
在 Rt△ OHN 中,OH= ON2-NH2= 3.92-1.52=3.6(m). 所以 FN=DH=OH-OD=3.6-(3.9-2.4)=2.1(m). 因为 2.1 m>2 m,所以此货船能顺利通过这座拱桥.返回
垂径定理的应用
垂径定理的应用15.(2023•东营)“ 圆材埋壁”是我国古代数学名著“ 九章算术》中的一个问题:“ 今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言表达就是:如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度为26寸.【答案】26.【分析】连接OA,设⊙O的半径是r寸,由垂径定理得到AE=12AB=5寸,由勾股定理得到r2=(r-1)2+52,求出r,即可得到圆的直径长.【解答】解:连接OA,设⊙O的半径是r寸,∵直径CD⊥AB,∴AE=12AB=12×10=5寸,∵CE=1寸,∴OE=(r-1)寸,∵OA2=OE2+AE2,∴r2=(r-1)2+52,∴r=13,∴直径CD的长度为2r=26寸.故答案为:26.【点评】本题考查垂径定理的应用,勾股定理的应用,关键是连接OA构造直角三角形,应用垂径定理,勾股定理列出关于圆半径的方程.垂径定理的应用40.(2023•永州)如图,⊙O是一个盛有水的容器的横截面,⊙O的半径为10cm,水的最深处到水面AB的距离为4cm,则水面AB的宽度为16cm.【答案】16.【分析】过点O作OD⊥AB于点C,交⊙O于点D,连接OA,由垂径定理可得AC=BC,然后在Rt△AOC中根据勾股定理求出AC的长,即可得出AB的长.【解答】解:如图,过点O作OD⊥AB于点C,交⊙O于点D,连接OA,∴AC=BC=12 AB,由题意知,OA=10cm,CD=4cm,∴OC=6cm,在Rt△AOC中,AC=√OA2−OC2=√102−62=8cm,∴AB=2AC=16cm,故答案为:16.【点评】本题考查了垂径定理,熟练掌握垂径定理:垂直于弦的直径平分这条弦,同时需熟练掌握勾股定理.垂径定理的应用38.(2023•广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37m,拱高约为7m,则赵州桥主桥拱半径R约为()A.20m B.28m C.35m D.40m【答案】B【分析】设主桥拱半径R,根据垂径定理得到AD=372,再利用勾股定理列方程求解,即可得到答案.【解答】解:由题意可知,AB=37m,CD=7m,设主桥拱半径为Rm ,∴OD =OC ﹣CD =(R ﹣7)m ,∵OC 是半径,OC ⊥AB ,∴AD =BD =12AB =372m , 在RtADO 中,AD 2+OD 2=OA 2,∴(372)2+(R ﹣7)2=R 2,解得R =156556≈28. 故选:B .【点评】本题主要考查垂径定理的应用,涉及勾股定理,解题的关键是用勾股定理列出关于R 的方程解决问题.39.(2023•荆州)如图,一条公路的转弯处是一段圆弧“(AC ̂),点O 是这段弧所在圆的圆心,B 为AĈ上一点,OB ⊥AC 于D .若AC =300√3m ,BD =150m ,则AĈ的长为( )A .300πmB .200πmC .150πmD .100√3πm【答案】B【分析】先根据垂径定理求出AD 的长,由题意得OD =OA ﹣BD ,在Rt △AOD 中利用勾股定理即可求出OA 的值,然后再利用三角比计算出AĈ所对的圆心角的度数,由弧长公式求出AC ̂的长即可. 【解答】解:如图所示:∵OB ⊥AC ,∴AD =12AC =150√3m ,∠AOC =2AOB ,在Rt △AOD 中,∵AD 2+OD 2=OA 2,OA =OB ,∴AD 2+(OA ﹣BD )2=OA 2,∴(150√3)2+(OA ﹣150)2²=OA 2,解得:OA =300m ,∴sin ∠AOB =AD OA =√32, ∴∠AOB =60°,∴∠AOC =120°,∴AĈ的长=120×300π180=200πm . 故选:B .【点评】本题考查的是垂径定理,勾股定理及弧长的计算公式,根据垂径定理得出AD 的长,再由勾股定理求出半径是解答此题的关键,同时要熟记圆弧长度的计算公式.垂径定理的应用43.(2023•山西)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线“(即圆弧),高铁列车在转弯时的曲线起点为A ,曲线终点为B ,过点A ,B 的两条切线相交于点C ,列车在从A 到B 行驶的过程中转角α为60°.若圆曲线的半径OA =1.5km ,则这段圆曲线AB ̂的长为( )A .π4kmB .π2kmC .3π4kmD .3π8km【答案】B【分析】由圆的切线可得∠OAC =∠OBC =90°,进而可证明A 、O 、B 、C 四点共圆,利用圆内接四边形的性质可求得∠AOB =60°,再根据弧长公式计算可求解.【解答】解:∵过点A ,B 的两条切线相交于点C ,∴∠OAC =∠OBC =90°,∴A 、O 、B 、C 四点共圆,∴∠AOB =α=60°,∴圆曲线AB̂的长为:60π⋅1.5180=12π(km ).故选:B .【点评】本题主要考查圆的切线的性质,点与圆的位置关系,圆内接四边形的性质,弧长的计算,证明A 、O 、B 、C 四点共圆求解∠AOB 的度数是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
垂径定理解题应用举例
垂径定理及其推论是《圆》一章的重要考点,定理告诉我们,对于一个圆和一条直线来说,如果具备下列五个条件中的任何两个,那么也具有其它三个:①垂直于弦,②过圆心,③平分弦,④平分弦所对的优弧,⑤平分弦所对的劣弧。
它反映了圆的重要性质,是证明线段相等....、角相等...、垂直关系....
的重要依据,同时也为圆的计算和作图提供了方法和依据,下面分类举例说明。
一、利用垂径平分弦所对的弧,来处理角的关系
例1 (重庆市)如图1,⊙O 的直径CD 过弦EF 的中点G ,
∠EOD =40°,则∠DCF 等于( )
A.80°
B. 50°
C. 40°
D. 20°
【析解】本题可由②③⇒①④⑤,所以可得ED DF =,
从而得出∠DCF 与∠EOD 的关系。
解:∵直径CD 平分弦EF , ∴ ED DF =,
∴ ∠DCF =12∠EOD =20°。
故选(D ).
二、利用垂径垂直平分弦,证相关线段相等
例2 (南京市)如图2,矩形ABCD 与与圆心在AB 上的⊙O 交于点G 、B 、F 、E , GB =8cm ,AG =1cm ,DE =2cm ,则EF = cm .
【分析】本题上手有点不知所措,其实利用矩形和垂径定理相关知识可以得到解决。
分别过O ,G 作OM ⊥CD ,GN ⊥DC ,即可求出EF 的长。
解:如图2,分别过O ,G 作OM ⊥CD ,GN ⊥DC ,则根据矩形的性质可得:NC =GB =8,DN =AG =1,GN ∥OM ∥BC ,
∵ OM ⊥EF , ∴ EM =MF ,
∵ OG =OB ,GN ∥OM ∥BC , ∴ MN =MC , ∴ CF =NE , ∵ DE =2,∴ NE =DE -DN =DE -AG
=1, ∴ EF =NC -NE -CF =8-2=6.
三、利用垂径定理,构造直角三角形,利用勾股定
理 例3 (长春市)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,图3是水平放置的破裂管道有水部分的截
面.
图1 O G F
E D C N M O G
F E D C B A 图2 图3
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB =16cm ,水面最深地方的高度为4cm ,求这个圆形截面的半径.
分析:(1)要补全输水管道的圆形截面,需要画出图3所在的圆,因此首先确定所在圆的圆心和半径.⑴任作两条弦,⑵分别作出两弦的垂直平分线,⑶两弦的垂直平分线的交点为圆心,⑷以交点为圆心,交点到圆上任意一点为半径作圆,所作出的圆即为所求.作图过程:略.
(2)本题的解题关键是作垂直于弦的半径,然后构造直角三角形,应用勾股定理列方程求解.
解:(1)正确作出图形,并做答.
(2)如图4,解:过O 作OC ⊥AB 于D ,交弧AB 于C ,
∵OC ⊥AB , ∴BD =21AB =2
1×16=8cm . 由题意可知,CD =4cm .
设半径为x C m ,则OD =(x -4)cm .
在Rt △BOD 中,由勾股定理得:
OD 2+BD 2=OB 2, ∴( x -4)2+82=x 2.
∴x =10.
四、利用垂径垂直弦,构造成特殊四边形
例4 (四川省)如图5,在⊙O 中,AB 、AC 是互相垂直的两条弦, AB =8cm ,AC =6cm ,那么⊙O 的半径OA 的长( )
A .4 cm
B .5 cm
C .6 cm
D .8 cm
【分析】要求半径OA 的长,可通过垂径定理构造Rt △,于是过O 分别作OD ⊥AB ,OE ⊥AC ,则可得矩形ADOE 。
解:如图5,过O 分别作OD ⊥AB 于D ,OE ⊥AC 于E , 则得矩形ADOE ,∴ OD =AE ,
又∵ AD =12AB =4,OD =AE =12AC =3; ∴ AO =2234 =5cm .故选(B ).
O E
D
C B A 图5 图4。
