SPSS实验报告 线性回归 曲线估计
用SPSS进行曲线回归分析实例

用SPSS进行曲线回归分析实例曲线回归分析在一元回归中,若因变量和自变量相关的趋势不是线性分布,呈现曲线关系。
这种情况可以利用SPSS提供的曲线估计过程(Curve Estimation)方便地进行线性拟合,选出最佳的回归模型来拟合出相应曲线。
下面以一个实例来介绍曲线拟合的基本步骤和使用方法。
例子台湾稻螟蚁螟侵入不同叶龄稻茎后的生存率数据(表4-1)。
拟合出适合的曲线模型,来表达不同叶龄稻茎对台湾稻螟蚁螟侵入的生存关系。
表4-1 台湾稻螟蚁螟侵入不同叶龄稻茎后的生存率数据本例子数据保存在DATA6-3.SAV。
1)准备分析数据在SPSS数据编辑窗口建立变量“生存率”和“叶龄”两个变量,把表6-13中的数据输入到对应的变量中。
或者打开已经存在的数据文件(DATA6-3.SAV)。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Curve Estimation”项,将打开如图4-1所示的线回归对话窗口。
图4-1 线回归对话窗口3) 设置分析变量设置因变量:从左侧的变量列表框中选择一个或多个因变量进入“Dependent(s)”框。
本例子选“生存率”变量为因变量。
设置自变量:选择一个变量为自变量,进入“Independent”框,也可选取“Independent”框中的“Time”项,即以时间为自变量。
本例子选“叶龄”变量为自变量。
选择标签变量: 选择一个变量进入到“Case Labels”框中,该变量为标签变量,可以利用该变量的值在图上查找观测值。
本例子没有标签变量。
4)选择曲线方程模型在“Models”框中选择一个或多个回归方程模型,这11个模型都可化为相应的线性模型。
其中各项的意义分别为:(1) Linear 线性模型(2) Quadratic 二次模型(3) Compound 复合模型(4) Growth 生长模型(5) Logarithmic 对数模型(6) S 形模型(7) Cubic 抛物线模型(8) Exponential 指数的模型(9) Inverse 倒数模型(10) Power 幂函数模型(11) Logistic 逻辑斯蒂模型在各项模型上单击鼠标右键,可以得到模型的方程类型。
SPSS实验报告_线性回归_曲线估计

《数据分析实务与案例实验报告》曲线估计学号:****************班级:2013 应用统计姓名:日期: 2 0 1 4 – 12 – 7数学与统计学学院一、实验目的1. 准确理解曲线回归分析的方法原理。
2. 了解如何将本质线性关系模型转化为线性关系模型进行回归分析。
3. 熟练掌握曲线估计的SPSS 操作。
4. 掌握建立合适曲线模型的判断依据。
5. 掌握如何利用曲线回归方程进行预测。
6. 培养运用多曲线估计解决身边实际问题的能力。
二、准备知识1. 非线性模型的基本内容变量之间的非线性关系可以划分为 本质线性关系和本质非线性关系。
所谓本质线性关系是指变量关系形式上虽然呈非线性关系,但可以通过变量转化为线性关系,并可最终进行线性回归分析,建立线性模型。
本质非线性关系是指变量之间不仅形式上呈现非线性关系,而且也无法通过变量转化为线性关系,最终无法进行线性回归分析,建立线性模型。
本实验针对本质线性模型进行。
下面介绍本次实验涉及到的可线性化的非线性模型,所用的变换既有自变量的变换,也有因变量的变换。
乘法模型:123y x x x βγδαε=其中α,β,γ,δ 都是未知参数,ε是乘积随机误差。
对上式两边取自然对数得到123ln ln ln ln ln ln y x x x αβγδε=++++上式具有一般线性回归方程的形式,因而用多元线性回归的方法来处理。
然而,必须强调指出的是,在求置信区间和做有关试验时,必须是2ln (0,)n N I εδ ,而不是2n N I εδ(0,) ,因此检验之前,要先检验ln ε 是否满足这个假设。
三、实验内容已有很多学者验证了能源消费与经济增长的因果关系,证明了能源消费是促进经济增长的原因之一。
也有众多学者利用C-D 生产函数验证了劳动和资本对经济增长的影响机理。
所有这些研究都极少将劳动、资本、和能源建立在一个模型中来研究三个因素对经济增长的作用方向和作用大小。
曲线回归估计的spss分析
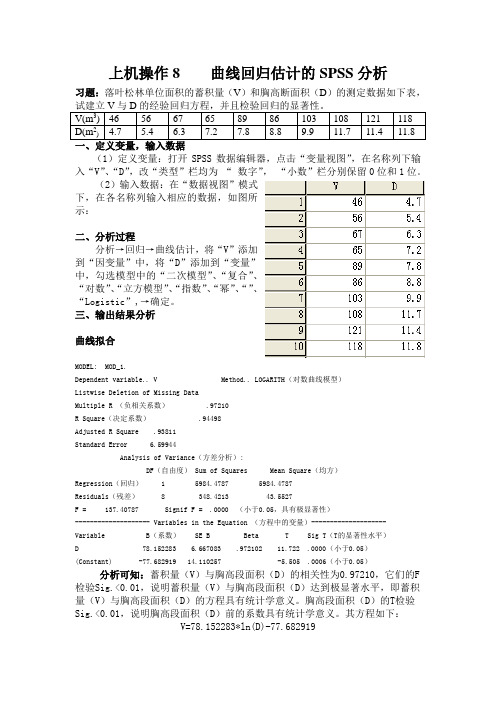
上机操作8 曲线回归估计的SPSS分析习题:落叶松林单位面积的蓄积量(V)和胸高断面积(D)的测定数据如下表,V(m3) 46 56 67 65 89 86 103 108 121 118D(m2) 4.7 5.4 6.3 7.2 7.8 8.8 9.9 11.7 11.4 11.8(1)定义变量:打开SPSS数据编辑器,点击“变量视图”,在名称列下输入“V”、“D”,改“类型”栏均为“数字”,“小数”栏分别保留0位和1位。
(2)输入数据:在“数据视图”模式下,在各名称列输入相应的数据,如图所示:二、分析过程分析→回归→曲线估计,将“V”添加到“因变量”中,将“D”添加到“变量”中,勾选模型中的“二次模型”、“复合”、“对数”、“立方模型”、“指数”、“幂”、“”、“Logistic”,→确定。
三、输出结果分析曲线拟合MODEL: MOD_1.Dependent variable.. V Method.. LOGARITH(对数曲线模型)Listwise Deletion of Missing DataMultiple R (负相关系数) .97210R Square(决定系数) .94498Adjusted R Square .93811Standard Error 6.59944Analysis of Variance(方差分析):DF(自由度) Sum of Squares Mean Square(均方)Regression(回归) 1 5984.4787 5984.4787Residuals(残差) 8 348.4213 43.5527F = 137.40787 Signif F = .0000 (小于0.05,具有极显著性)-------------------- Variables in the Equation (方程中的变量)--------------------Variable B(系数) SE B Beta T Sig T(T的显著性水平)D 78.152283 6.667083 .972102 11.722 .0000(小于0.05)(Constant) -77.682919 14.110257 -5.505 .0006(小于0.05)分析可知:蓄积量(V)与胸高段面积(D)的相关性为0.97210,它们的F 检验Sig.<0.01,说明蓄积量(V)与胸高段面积(D)达到极显著水平,即蓄积量(V)与胸高段面积(D)的方程具有统计学意义。
多元线性回归SPSS实验报告
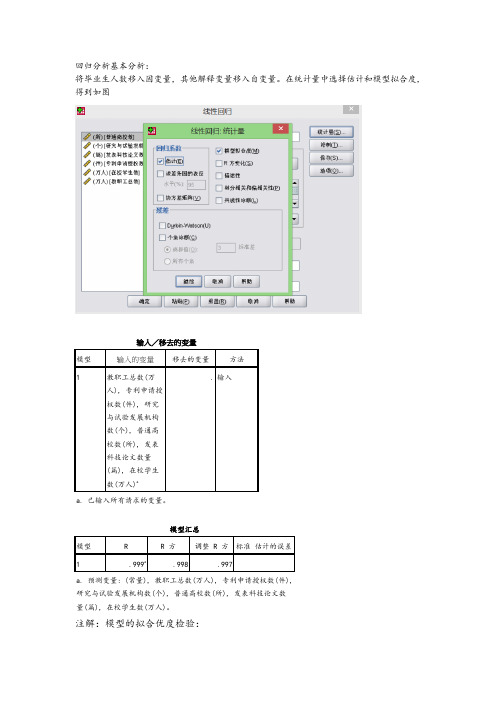
49%;可以认为:这些变量存在多重共线性。需要建立回归方程。
2.重建回归方程
模型
输入/移去的变量b
输入的变量
移去的变量
方法
1
教职工总数(万
人), 专利申请授
权数(件), 研究
b. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表 科技论文数量(篇)。 c. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 发表科技论文数量(篇)。 d. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 发表科技论文数量(篇)。 e. 预测变量: (常量), 教职工总数(万人), 发表科技论文数量(篇)。 f. 因变量: 毕业生数(万人)
. 输入
a. 已输入所有请求的变量。
模型汇总
模型
R
R 方 调整 R 方 标准 估计的误差
1
.999a
.998
.997
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表科技论文数 量(篇), 在校学生数(万人)。
注解:模型的拟合优度检验:
第五列:回归方程的估计标准误差=
Anovab
模型
平方和
df
均方
F
Sig.
1
回归
6
.000a
残差
7
总计
13
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构 数(个), 普通高校数(所), 发表科技论文数量(篇), 在校学生数(万人)。 b. 因变量: 毕业生数(万人)
【精品】SPSS统计实验报告多元线性回归分析

【精品】SPSS统计实验报告多元线性回归分析
本文旨在通过多元线性回归分析,深入研究X、Y、Z三个变量之间的关系,以探究这三个变量对结果的影响。
本实验中样本数量为100人,本文采用SPSS22.0计算软件进行多元线性回归分析,统计计算结果如下:
(一)检验变量X、Y、Z三个变量是否有关:
Sig.=.633。
结果显示,该值大于0.05,表明X、Y、Z三者之间没有显著统计关系;
(二)确定拟合模型:
以X、Y、Z三个变量回归拟合,得出模型为:y=1.746+0.660X+0.783Y+0.430Z。
(三)检验回归模型的有效性:
1. 回归系数的统计量检验
模型的R方为.668,该值表明,X、Y、Z三个自变量可以解释本回归模型的67.0%的变化量;
2.F检验
结果显示,f分数为20.670,Sig.=.000,结果显示,f分数小于阈值0.05,因此可以接受回归模型;
检验结果显示,当其他X、Y、Z三个自变量的条件不变的情况下,X、Y、Z三个自变量对Y的影响是有显著性的。
综上所述,本文使用SPSS22.0计算软件进行多元线性回归分析,探究X、Y、Z三个变量之间的关系。
结果显示,X、Y、Z三者之间没有显著统计关系;拟合模型为:
y=1.746+0.660X+0.783Y+0.430Z;最后,证实X、Y、Z三个自变量对Y的影响是有显著性的。
实验报告四.SPSS一元线性相关回归分析预测
a
均值 159.1000 .000 .781 159.2740 .00000 .000 -.038 -.17402 .007 .900 .104 .100
标准 偏差 1.79729 1.000 .308 1.95023 1.75840 .943 1.025 2.10525 1.084 1.583 .133 .176
广东金融学院实验报告
课程名称:市场调查与预测
实验编号 及实验名称 姓 名
实验四:SPSS 一元线性相关回归分析预测 马秀文 实验中心 周刺天
系 班
别 级
工商管理系 市场营销 2 班 4
学
号
111521216 2013/12/9 无
实验地点 指导教师
实验日期 同组其他成员
实验时数 成 绩
一、实验目的及要求 利用 SPSS 进行回归分析。 二、实验环境及相关情况(包含使用软件、实验设备、主要仪器及材料等) 通过实验教学中心的教学环境发布相关练习资料。 软件运行环境:操作系统 WindowsXP,办公自动化软件,SPSS 统计分析软件包。 硬件设备:实验室的个人电脑。 三、实验内容及步骤(包含简要的实验步骤流程) 为了了解某地母亲身高 x 与女儿身高 Y 的相关关系,随机测得 10 对母女的身高(见文 件“母女身高.sav”) 。利用 SPSS 软件,完成以下任务: 1.画出 x、Y 散点图,观察因变量与自变量之间关系是否有线性特点; 2.试对 x 与 Y 进行一元线性回归分析,列出一元线性回归预测模型; 3.预测当母亲身高为 161cm 时女儿的身高?
第 2 页 共 7 页
四、实验结果(包括程序或图表(截图) 、 自变量与因变量有线性特点, 即母亲身高和女儿身高有线性特点, 且大致呈正相关的关系。
SPSS回归分析实验报告

中国计量学院现代科技学院实验报告实验课程:应用统计学实验名称:回归分析班级:学号:姓名:实验日期: 2012.05.23 实验成绩:指导教师签名:一.实验目的一元线性回归简单地说是涉及一个自变量的回归分析,主要功能是处理两个变量之间的线性关系,建立线性数学模型并进行评价预测。
本实验要求掌握一元线性回归的求解和多元线性回归理论与方法。
二.实验环境中国计量学院现代科技学院机房310三.实验步骤与内容1打开应用统计学实验指导书,新建excel表地区供水管道长度(公里)全年供水总量(万平方米)北京15896 128823 天津6822 64537 河北10771.2 160132 山西5669.3 77525 内蒙古5635.5 59276 辽宁21999 280510 吉林6384.9 159570 黑龙江9065.9 153387 上海22098.8 308309 江苏36632.4 380395 浙江24126.9 235535 安徽7389.4 204128 福建6270.4 118512 江西5094.7 143240 山东26073.9 259782 河南11405.6 185092 湖北15668.6 257787 湖南9341.8 262691 广东35728.8 568949 广西6923.1 134412 海南1726.7 20241 重庆6082.7 71077 四川12251.3 165632 贵州3275.3 45198 云南5208.5 52742 西藏364.9 5363陕西4270 73580甘肃5010 62127青海893 14390宁夏1538.2 22921新疆3670.2 766852.打开SPSS,将数据导入3.打开分析,选择回归分析再选择线性因变量选全年供水总量,自变量选供水管道长度统计里回归系数选估计,再选择模型拟合按继续再按确定会出来分析的结果对以上结果进行分析:(1)回归方程为:y=28484.712+11.610X(X是自变量供水管道长度,Y是因变量全年供水总量)(2)检验1)拟合效果检验根据表2可知,R2=0.819,即拟合效果好,线性成立。
SPSS的线性回归分析实验报告

农业总产值(亿元)
农业劳动力(万人)
灌溉面积(万公顷)
化肥用量(万吨)
户均固定资产(元)
农机动力(万马力)
北京
19.61
90.1
33.84
7.5
394.3
435.3
天津
14.4
95.2
34.95
3.9
567.5
450.7
河北
149.9
1639
357.26
92.4
706.89
2712.6
山西
55.07
需求量/万台
价格/千元
家庭平均收入/千元
3.0
4.0
6.0
5.0
4.5
6.8
6.5
3.5
8.0
7.0
3.0
10.0
8.5
3.0
16.0
7.5
3.5
20
10.0
2.5
22
9.0
3.0
24
11
2.5
26
12.5
2.0
28
2、一般认为,一个地区的农业总产值与该地区的农业劳动力、灌溉面积、化肥用量、农户固定资产、农业机械化水平等因素有关。下表为某年我国北方地区12个省市的相关数据。试建立我国北方地区的农业产出线性回归模型,分析影响农业产出的主要因素,并说明理由。
第一题
实验结果:拟合优度系数接近1说明拟合好。回归方程的p值<0.05,说明显著线性。回归系数p值<0.05,说明显著线性。
线性回归方程:y=11.167+0.17x1-1.903x2
第二题
实验结果分析:拟合优度系数接近1,说明拟合度好。存在多重线性。化肥用量p值<0.05.说明线性显著。线性回归方程:y=19.501+1.526x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数据分析实务与案例实验报告》曲线估计学号: 204班级: 2013 应用统计姓名:日期: 2 0 1 4 – 12 – 7数学与统计学学院一、实验目的1. 准确理解曲线回归分析的方法原理。
2. 了解如何将本质线性关系模型转化为线性关系模型进行回归分析。
3. 熟练掌握曲线估计的SPSS 操作。
4. 掌握建立合适曲线模型的判断依据。
5. 掌握如何利用曲线回归方程进行预测。
6. 培养运用多曲线估计解决身边实际问题的能力。
二、准备知识1. 非线性模型的基本内容变量之间的非线性关系可以划分为 本质线性关系和本质非线性关系。
所谓本质线性关系是指变量关系形式上虽然呈非线性关系,但可以通过变量转化为线性关系,并可最终进行线性回归分析,建立线性模型。
本质非线性关系是指变量之间不仅形式上呈现非线性关系,而且也无法通过变量转化为线性关系,最终无法进行线性回归分析,建立线性模型。
本实验针对本质线性模型进行。
下面介绍本次实验涉及到的可线性化的非线性模型,所用的变换既有自变量的变换,也有因变量的变换。
乘法模型:123y x x x βγδαε=其中α,β,γ,δ 都是未知参数,ε是乘积随机误差。
对上式两边取自然对数得到123ln ln ln ln ln ln y x x x αβγδε=++++上式具有一般线性回归方程的形式,因而用多元线性回归的方法来处理。
然而,必须强调指出的是,在求置信区间和做有关试验时,必须是2ln (0,)n N I εδ ,而不是2n N I εδ(0,) ,因此检验之前,要先检验ln ε 是否满足这个假设。
三、实验内容已有很多学者验证了能源消费与经济增长的因果关系,证明了能源消费是促进经济增长的原因之一。
也有众多学者利用C-D 生产函数验证了劳动和资本对经济增长的影响机理。
所有这些研究都极少将劳动、资本、和能源建立在一个模型中来研究三个因素对经济增长的作用方向和作用大小。
现从我国能源消费、全社会固定资产投资和就业人员的实际出发,假定生产技术水平在短期能不会发生较大变化,经济增长、全社会固定资产投资、就业人员、能源消费可以分别采用国内生产总值、全社会固定资产投资总量、就业总人数、能源消费总量进行衡量,并假定经济增长与能源消费、资本和劳动力的关系均满足C-D 生产函数。
问题中的C-D 生产函数为:Y AK L E αβγ=式中:Y 为GDP ,衡量总产出;K 为全社会固定资产投资,衡量资本投入量;L 为就业人数,衡量劳动投入量;E 为能源消费总量,衡量能源投入量;A,α,β, γ 为未知参数。
根据C-D 函数的假定,一般情形α,β,γ均在0和1之间,但当α,β,γ中有负数时,说明这种投入量的增长,反而会引起GDP 的下降,当α,β,γ中出现大于1的值时,说明这种投入量的增加会引起GDP 成倍增加,这在经济学现象中都是存在的。
以我国1985—2004年的有关数据建立了SPSS 数据集,参见“”。
请以此数据集为基础估计生产函数中的未知参数。
四、实验步骤及结果分析1. 确定非线性回归模型的类型有上述分析过程确定要建立的回归模型为:Y AK L E αβγ=式中,Y 为自变量,K,L,E 为解释变量,A 为常数项。
2. 通过变换将非线性方程转化为线性方程将原回归模型两遍同时取对数:ln ln ln ln ln Y A K L E αβγ=+++得:123y c x x x αβγ=+++式中,123ln ,ln ,ln ,ln ,ln y Y c A x K x L x E ===== 。
选择【转换】—【计算变量】,对所有数据取对数完成数据的处理,过程及结果如下图:3. 进行初步线性回归分析(选入所有变量)用最小二乘法建立回归方程由非线性模型转化为线性模型后,即可按照建立多元线性回归模型的步骤进行操作,求得回归方程表达式。
(1) 选择【分析】→【回归】→【线性】,弹出“线性回归”对话框。
将lnY 选入“因变量”框,lnk 到lnE 选入“自变量”框。
注意,可以通过点击“上一张”与“下一张”按钮切换,选择不同的自变量构建模型,每个模型中可以对不同的自变量采用不同的方法进行回归。
“方法”下拉框中有5个选项,此处先选择“进入”,即所选变量全部强行进入回归模型。
(2) 点击“统计量”按钮,选择输出各种常用判别统计量,本案例选择“估计”、 “模型拟合度”、“描述性”、“共线性诊断”,以及残差中的“Durbin-Watson ”检验和“个案诊断”。
得到如下结果:由模型汇总表,20.991R =,20.989R =,拟合优度很强。
统计量DW=,该检验用于判断相邻残差序列的相关性,其判断标准如下: DW<d L ,认为残差序列存在正的一阶自相关;d u <DW<4-d U ,认为残差序列间不存在一阶自相关;DW>4-d L ,认为残差序列间存在负的一阶自相关;d L <DW<d U 或4-d U <DW<4-d L 时,无法确定残差序列是否存在自相关。
本例中,k=4,n=21(k 为解释变量的数目,包括常数项,n 是观察值的数目)时,5%的上下界:dL=,dU=。
有l DW d < ,认为残差序列存在一阶自相关。
由方差分析表,统计量F=,p 值小于,认为方程在95%的置信水平下是显著的。
但是,0.025(2131) 2.110t --= 变量lnK 、lnL 、常量lnA 的t 值均大于,所以这几个变量对方程的影响都很显著,而变量lnE的t值很小且p值明显大于且回归系数为零,说明该变量对方程影响不显著,回归模型是无效的。
4.消除模型中变量的共线性(逐步回归)“共线性统计量”中,容忍度Tolerance越接近于0,表示复共线性越强,越接近于1,复共线性越弱。
而方差膨胀因子VIF的值越接近于1,解释变量间的多重共线性越弱,如果VIF的值大于或等于10,说明一个解释变量与其他解释变量之间有严重的多重共线性。
本例中,变量lnK和lnE的VIF值都大于10,说明它们与其他解释变量之间有严重的多重共线性,不符合经典假设,需要修正。
通过以上结果分析,采用逐步回归的方法来消除变量之间的多重共线性。
重复以上步骤从新建立回归方程,将【进入】替换为【逐步】如下图所示:得到如下结果:从上表可以看出通过逐步回归剔除掉了变量lnE,整个模型的拟合优度上升,调整R方从上升至。
方差膨胀因子VIF值均小于10,多重共线性已消除。
T 检验的概率明显小于说明变量对模型的影响显著。
而此时DW值并未有明显改变,残差序列仍然存在一阶自相关。
此时采用数据变换的方法来消除残差的自相关。
5.消除残差的自相关对于自相关的处理方法,其基本思想是通过一些数学转化,对数据进行处理,消ρ=除数据的自相关性,在对参数进行估计。
当误差序列的自相关系数已知,且1时,采用差分法,即利用增量数据来代替原有的样本数据建立方程。
当误差序列的自相关系数未知时,先求处自相关系数,再通过反复迭代法消除来自相关。
我们知道DW与ρ之间的近似关系:≈-2(1)DWρ其中:因为DW=,代入上式很明显得出ρ 不为1,所以此处不能用差分而采用迭代的方法消除自相关性。
这里先求出lny 的一元线性回归方程:ln 4.5290.655ln 0.782ln y K L =-++ 中的残差i e ,i=1, … ,n,将残差代入如下公式:11,112,()()n in i n e e e e r --+--=∑其中11,12,11211,11n n n i n i i i e e e e n n ---====--∑∑ 残差序列代入上式求的一阶自相关系数0.60966r =再令:**11,,1,...,1i i i i i y y ry x x rx i n ++=-=-=-用EXCEL 完成数据的迭代得到新的数据,这里用Y1代表原先的lnY ,K1代表原先的lnK ,L1代表原先的lnL 。
并导入到SPSS 中,重复以上步骤对新的数据进行回归分析。
得出结果的:数据经过一次迭代以后DW 的值有明显增加,查表k=3,n=20(k 为解释变量的数目,包括常数项,n 是观察值的数目)时,5%的上下界:dL=,dU=。
有d u <DW<4-d U ,认为残差序列间不存在一阶自相关。
此时得到新的回归方程:1 2.2160.61010.9201Y K L =-++6. 残差正态性检验点击“绘制”按钮,将“ZRESID”选入Y轴,“ZPRED”选入X轴,绘制散点图,并在“标准化残差图”中选择“直方图”,输出带有正态曲线的标准化残差的直方图。
点击“保存”按钮,在对话框中保存一些统计量的值,此案例在“预测值”框中选择“未标准化”,在“残差”框中选择“未标准化”,在“预测区间”框中选择“均值”和“单值”。
其他不变,点击【继续】→【确定】。
输出结果如下图:上面操作已输出残差的直方图,还可以通过【分析】→【描述统计】→【P-P 图】和【分析】→【描述统计】→【Q-Q图】输出正态分布的P-P图、Q-Q图,若散点围绕图中所给斜线有规律的分布,则可以认为所检测变量服从正态分布。
P-P图Q-Q图从以上图形可以初步认为该模型的残差服从正态分布。
进一步进行K-S检验。
选择【分析】→【非参数检验】→【旧对话框】→【1-样本 K-S检验】,弹出“单样本Kolmogorov-Smirnov检验”窗口,将未标准化残差选入变量框,K-S检验输出结果K-S检验统计量为,检验概率p值为,大于,可以认为在95%的置信水平下,该模型的残差服从正态分布。
7.残差的其他检验(1)异方差检验:根据回归分析输出的标准化残差的散点图,初步判断是否存在异方差,但此种判断方法较主观,且不容易判断。
进一步用Spearman等级相关检验分析是否存在异方差。
首先对未标准化残差取绝对值,点击【转换】→【计算变量】,弹出“计算变量”窗口,“目标变量”输入“abs”,“数学表达式”输入“abs(RES_1)”,选择【分析】→【相关】→【双变量】,将abs、所有回归变量及未标准化预测值选入变量框中,【相关系数】栏选择“Spearman”,点击确定。
Spearman相关系数表观察系数表的“abs”行,发现未标准化预测值与残差绝对值的相关性p值为大于,说明该模型的残差不存在的异方差问题。
五、实验总结根据上述分析,采用逐步回归法得到最后确定的回归方程:1 2.2160.61010.9201Y K L =-++其中1111ln ln 1ln ln 1ln ln ,1,...,1i ii ii i Y y r y K k r k L l r l i n +++=-=-=-=-代入上式得回归方程为:111ln ln 2.2160.610(ln ln )0.920(ln ln )i i i i i i y r y k r k l l +++-=-+-+-(i=1,2, (21)将上式同时取以e 为底数进行指数变换得到非线性模型中的本质线性关系的方程:2.2161110.6100.920,1,...,20,0.6097i i i r r r i i i y k l e i r y k l -+++⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭根据所建的回归方程可以看出社会固定资产投资(K )和劳动力(L )对GDP 增长的影响较明显,而能源的消费(E)对经济的增长没有明显影响。
