spss实验报告线性回归曲线估计
用SPSS进行曲线回归分析实例

用SPSS进行曲线回归分析实例曲线回归分析在一元回归中,若因变量和自变量相关的趋势不是线性分布,呈现曲线关系。
这种情况可以利用SPSS提供的曲线估计过程(Curve Estimation)方便地进行线性拟合,选出最佳的回归模型来拟合出相应曲线。
下面以一个实例来介绍曲线拟合的基本步骤和使用方法。
例子台湾稻螟蚁螟侵入不同叶龄稻茎后的生存率数据(表4-1)。
拟合出适合的曲线模型,来表达不同叶龄稻茎对台湾稻螟蚁螟侵入的生存关系。
表4-1 台湾稻螟蚁螟侵入不同叶龄稻茎后的生存率数据本例子数据保存在DATA6-3.SAV。
1)准备分析数据在SPSS数据编辑窗口建立变量“生存率”和“叶龄”两个变量,把表6-13中的数据输入到对应的变量中。
或者打开已经存在的数据文件(DATA6-3.SAV)。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Curve Estimation”项,将打开如图4-1所示的线回归对话窗口。
图4-1 线回归对话窗口3) 设置分析变量设置因变量:从左侧的变量列表框中选择一个或多个因变量进入“Dependent(s)”框。
本例子选“生存率”变量为因变量。
设置自变量:选择一个变量为自变量,进入“Independent”框,也可选取“Independent”框中的“Time”项,即以时间为自变量。
本例子选“叶龄”变量为自变量。
选择标签变量: 选择一个变量进入到“Case Labels”框中,该变量为标签变量,可以利用该变量的值在图上查找观测值。
本例子没有标签变量。
4)选择曲线方程模型在“Models”框中选择一个或多个回归方程模型,这11个模型都可化为相应的线性模型。
其中各项的意义分别为:(1) Linear 线性模型(2) Quadratic 二次模型(3) Compound 复合模型(4) Growth 生长模型(5) Logarithmic 对数模型(6) S 形模型(7) Cubic 抛物线模型(8) Exponential 指数的模型(9) Inverse 倒数模型(10) Power 幂函数模型(11) Logistic 逻辑斯蒂模型在各项模型上单击鼠标右键,可以得到模型的方程类型。
SPSS实验报告_线性回归_曲线估计

《数据分析实务与案例实验报告》曲线估计学号:****************班级:2013 应用统计姓名:日期: 2 0 1 4 – 12 – 7数学与统计学学院一、实验目的1. 准确理解曲线回归分析的方法原理。
2. 了解如何将本质线性关系模型转化为线性关系模型进行回归分析。
3. 熟练掌握曲线估计的SPSS 操作。
4. 掌握建立合适曲线模型的判断依据。
5. 掌握如何利用曲线回归方程进行预测。
6. 培养运用多曲线估计解决身边实际问题的能力。
二、准备知识1. 非线性模型的基本内容变量之间的非线性关系可以划分为 本质线性关系和本质非线性关系。
所谓本质线性关系是指变量关系形式上虽然呈非线性关系,但可以通过变量转化为线性关系,并可最终进行线性回归分析,建立线性模型。
本质非线性关系是指变量之间不仅形式上呈现非线性关系,而且也无法通过变量转化为线性关系,最终无法进行线性回归分析,建立线性模型。
本实验针对本质线性模型进行。
下面介绍本次实验涉及到的可线性化的非线性模型,所用的变换既有自变量的变换,也有因变量的变换。
乘法模型:123y x x x βγδαε=其中α,β,γ,δ 都是未知参数,ε是乘积随机误差。
对上式两边取自然对数得到123ln ln ln ln ln ln y x x x αβγδε=++++上式具有一般线性回归方程的形式,因而用多元线性回归的方法来处理。
然而,必须强调指出的是,在求置信区间和做有关试验时,必须是2ln (0,)n N I εδ ,而不是2n N I εδ(0,) ,因此检验之前,要先检验ln ε 是否满足这个假设。
三、实验内容已有很多学者验证了能源消费与经济增长的因果关系,证明了能源消费是促进经济增长的原因之一。
也有众多学者利用C-D 生产函数验证了劳动和资本对经济增长的影响机理。
所有这些研究都极少将劳动、资本、和能源建立在一个模型中来研究三个因素对经济增长的作用方向和作用大小。
曲线回归估计的spss分析
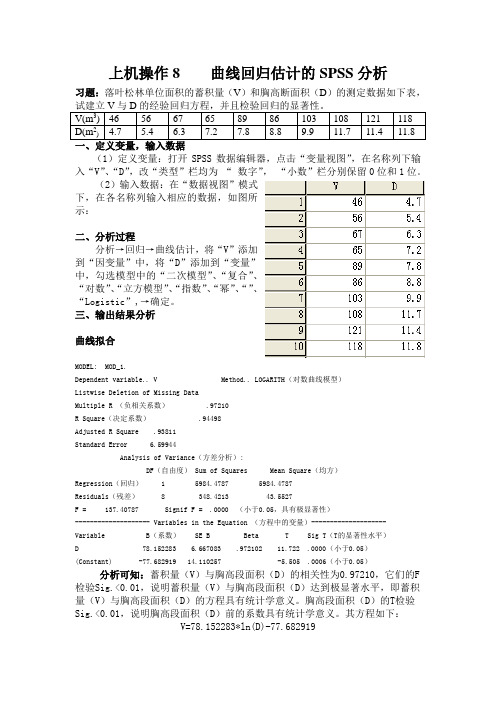
上机操作8 曲线回归估计的SPSS分析习题:落叶松林单位面积的蓄积量(V)和胸高断面积(D)的测定数据如下表,V(m3) 46 56 67 65 89 86 103 108 121 118D(m2) 4.7 5.4 6.3 7.2 7.8 8.8 9.9 11.7 11.4 11.8(1)定义变量:打开SPSS数据编辑器,点击“变量视图”,在名称列下输入“V”、“D”,改“类型”栏均为“数字”,“小数”栏分别保留0位和1位。
(2)输入数据:在“数据视图”模式下,在各名称列输入相应的数据,如图所示:二、分析过程分析→回归→曲线估计,将“V”添加到“因变量”中,将“D”添加到“变量”中,勾选模型中的“二次模型”、“复合”、“对数”、“立方模型”、“指数”、“幂”、“”、“Logistic”,→确定。
三、输出结果分析曲线拟合MODEL: MOD_1.Dependent variable.. V Method.. LOGARITH(对数曲线模型)Listwise Deletion of Missing DataMultiple R (负相关系数) .97210R Square(决定系数) .94498Adjusted R Square .93811Standard Error 6.59944Analysis of Variance(方差分析):DF(自由度) Sum of Squares Mean Square(均方)Regression(回归) 1 5984.4787 5984.4787Residuals(残差) 8 348.4213 43.5527F = 137.40787 Signif F = .0000 (小于0.05,具有极显著性)-------------------- Variables in the Equation (方程中的变量)--------------------Variable B(系数) SE B Beta T Sig T(T的显著性水平)D 78.152283 6.667083 .972102 11.722 .0000(小于0.05)(Constant) -77.682919 14.110257 -5.505 .0006(小于0.05)分析可知:蓄积量(V)与胸高段面积(D)的相关性为0.97210,它们的F 检验Sig.<0.01,说明蓄积量(V)与胸高段面积(D)达到极显著水平,即蓄积量(V)与胸高段面积(D)的方程具有统计学意义。
SPSS实验简单线性回归分析11

Partial
Part
1
(Constant)
27.396
5.210
5.258
.000
16.449
38.342
期中成绩
.713
.061
.940
11.724
.000
.585Biblioteka .840.940.940
.940
a. Dependent Variable:总成绩
注释:这个表给出了包括常数项在内所有系数的检验结果并用了t检验同时给出了标准系数和非标准系数,由相应的P值可知道这些系数都是显著的。具有统计意义。拟合的 , ,所以所拟合的简单线性回顾方程为:
Variables Entered/Removedb
Model
Variables Entered
Variables Removed
Method
1
期中成绩a
.
Enter
a. All requested variables entered.
b. Dependent Variable:总成绩
注释:从这张表可以得出所选的自变量期中成绩是符合要求能够作为我们回归方程的自变量的。
Residual
105.204
18
5.845
Total
908.550
19
a. Predictors: (Constant),期中成绩
b. Dependent Variable:总成绩
由表可见回归模型的F统计量F=137.449,相应的P值为0.000,因此我们可以用的这个模型是显著的是有统计意义的。由于这里我们只用了一个自变量,所以模型的检验等价于系数的检验。
注释:从表中可得线性回归出来的相关系数为R=0.940,方程拟合优度R方为0.884,调整后的R方为0.878,说明所做的回归方程拟合度较好。
SPSS的线性回归分析

多元线性回归方程的检验
(一)拟和优度检验:
(1)判定系数R2:
n 1 SSE 均方误差 R2 1 n k 1 SST 因变量的样本方差 – R是y和xi的复相关系数(或观察值与预测值的相关系数),测定 了因变量y与所有自变量全体之间线性相关程度 (2)调整的R2: R2 1
17
多元线性回归分析
(一)多元线性回归方程 多元回归方程: y= β0 +β1x1+β2x2+...+βkxk
– β1、β2、βk为偏回归系数。 – β1表示在其他自变量保持不变的情况下,自变量x1变动一个 单位所引起的因变量y的平均变动
(二)多元线性回归分析的主要问题
– 回归方程的检验 – 自变量筛选 – 多重共线性问题
• 于是: 因变量总变差=自变量引起的+其他因素引起的 • 即: 因变量总变差=回归方程可解释的+不可解释的 • 可证明:因变量总离差平方和=回归平方和+剩余平方和
6
一元线性回归方程的检验
(一)拟和优度检验:
(3)统计量:判定系数
R2 ˆ ( y
n
i 1 i 1 – R2=SSR/SST=1-SSE/SST. – R2体现了回归方程所能解释的因变量变差的比例;1-R2则体 现了因变量总变差中,回归方程所无法解释的比例。 – R2越接近于1,则说明回归平方和占了因变量总变差平方和 的绝大部分比例,因变量的变差主要由自变量的不同取值造 成,回归方程对样本数据点拟合得好 – 在一元回归中R2=r2; 因此,从这个意义上讲,判定系数能够 比较好地反映回归直线对样本数据的代表程度和线性相关性。
8
一元线性回归方程的检验
(三)回归系数的显著性检验:t检验 (1)目的:检验自变量对因变量的线性影响是否显著. (2)H0:β=0 即:回归系数与0无显著差异 (3)利用t检验,构造t统计量: i S ti S S i (x x )
【精品】SPSS统计实验报告多元线性回归分析

【精品】SPSS统计实验报告多元线性回归分析
本文旨在通过多元线性回归分析,深入研究X、Y、Z三个变量之间的关系,以探究这三个变量对结果的影响。
本实验中样本数量为100人,本文采用SPSS22.0计算软件进行多元线性回归分析,统计计算结果如下:
(一)检验变量X、Y、Z三个变量是否有关:
Sig.=.633。
结果显示,该值大于0.05,表明X、Y、Z三者之间没有显著统计关系;
(二)确定拟合模型:
以X、Y、Z三个变量回归拟合,得出模型为:y=1.746+0.660X+0.783Y+0.430Z。
(三)检验回归模型的有效性:
1. 回归系数的统计量检验
模型的R方为.668,该值表明,X、Y、Z三个自变量可以解释本回归模型的67.0%的变化量;
2.F检验
结果显示,f分数为20.670,Sig.=.000,结果显示,f分数小于阈值0.05,因此可以接受回归模型;
检验结果显示,当其他X、Y、Z三个自变量的条件不变的情况下,X、Y、Z三个自变量对Y的影响是有显著性的。
综上所述,本文使用SPSS22.0计算软件进行多元线性回归分析,探究X、Y、Z三个变量之间的关系。
结果显示,X、Y、Z三者之间没有显著统计关系;拟合模型为:
y=1.746+0.660X+0.783Y+0.430Z;最后,证实X、Y、Z三个自变量对Y的影响是有显著性的。
实验报告四.SPSS一元线性相关回归分析预测
a
均值 159.1000 .000 .781 159.2740 .00000 .000 -.038 -.17402 .007 .900 .104 .100
标准 偏差 1.79729 1.000 .308 1.95023 1.75840 .943 1.025 2.10525 1.084 1.583 .133 .176
广东金融学院实验报告
课程名称:市场调查与预测
实验编号 及实验名称 姓 名
实验四:SPSS 一元线性相关回归分析预测 马秀文 实验中心 周刺天
系 班
别 级
工商管理系 市场营销 2 班 4
学
号
111521216 2013/12/9 无
实验地点 指导教师
实验日期 同组其他成员
实验时数 成 绩
一、实验目的及要求 利用 SPSS 进行回归分析。 二、实验环境及相关情况(包含使用软件、实验设备、主要仪器及材料等) 通过实验教学中心的教学环境发布相关练习资料。 软件运行环境:操作系统 WindowsXP,办公自动化软件,SPSS 统计分析软件包。 硬件设备:实验室的个人电脑。 三、实验内容及步骤(包含简要的实验步骤流程) 为了了解某地母亲身高 x 与女儿身高 Y 的相关关系,随机测得 10 对母女的身高(见文 件“母女身高.sav”) 。利用 SPSS 软件,完成以下任务: 1.画出 x、Y 散点图,观察因变量与自变量之间关系是否有线性特点; 2.试对 x 与 Y 进行一元线性回归分析,列出一元线性回归预测模型; 3.预测当母亲身高为 161cm 时女儿的身高?
第 2 页 共 7 页
四、实验结果(包括程序或图表(截图) 、 自变量与因变量有线性特点, 即母亲身高和女儿身高有线性特点, 且大致呈正相关的关系。
SPSS的线性回归分析分析

SPSS的线性回归分析分析SPSS是一款广泛用于统计分析的软件,其中包括了许多功能强大的工具。
其中之一就是线性回归分析,它是一种常用的统计方法,用于研究一个或多个自变量对一个因变量的影响程度和方向。
线性回归分析是一种用于解释因变量与自变量之间关系的统计技术。
它主要基于最小二乘法来评估自变量与因变量之间的关系,并估计出最合适的回归系数。
在SPSS中,线性回归分析可以通过几个简单的步骤来完成。
首先,需要加载数据集。
可以选择已有的数据集,也可以导入新的数据。
在SPSS的数据视图中,可以看到所有变量的列表。
接下来,选择“回归”选项。
在“分析”菜单下,选择“回归”子菜单中的“线性”。
在弹出的对话框中,将因变量拖放到“因变量”框中。
然后,将自变量拖放到“独立变量”框中。
可以选择一个或多个自变量。
在“统计”选项中,可以选择输出哪些统计结果。
常见的选项包括回归系数、R方、调整R方、标准误差等。
在“图形”选项中,可以选择是否绘制残差图、分布图等。
点击“确定”后,SPSS将生成线性回归分析的结果。
线性回归结果包括多个重要指标,其中最重要的是回归系数和R方。
回归系数用于衡量自变量对因变量的影响程度和方向,其值表示每个自变量单位变化对因变量的估计影响量。
R方则反映了自变量对因变量变异的解释程度,其值介于0和1之间,越接近1表示自变量对因变量的解释程度越高。
除了回归系数和R方外,还有其他一些统计指标可以用于判断模型质量。
例如,标准误差可以用来衡量回归方程的精确度。
调整R方可以解决R方对自变量数量的偏向问题。
此外,SPSS还提供了多种工具来检验回归方程的显著性。
例如,可以通过F检验来判断整个回归方程是否显著。
此外,还可以使用t检验来判断每个自变量的回归系数是否显著。
在进行线性回归分析时,还需要注意一些统计前提条件。
例如,线性回归要求因变量与自变量之间的关系是线性的。
此外,还需要注意是否存在多重共线性,即自变量之间存在高度相关性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数据分析实务与案例实验报告》曲线估计学号: 204班级: 2013 应用统计姓名:日期: 2 0 1 4 – 12 – 7数学与统计学学院一、实验目的1. 准确理解曲线回归分析的方法原理。
2. 了解如何将本质线性关系模型转化为线性关系模型进行回归分析。
3. 熟练掌握曲线估计的SPSS 操作。
4. 掌握建立合适曲线模型的判断依据。
5. 掌握如何利用曲线回归方程进行预测。
6. 培养运用多曲线估计解决身边实际问题的能力。
二、准备知识1. 非线性模型的基本内容变量之间的非线性关系可以划分为 本质线性关系和本质非线性关系。
所谓本质线性关系是指变量关系形式上虽然呈非线性关系,但可以通过变量转化为线性关系,并可最终进行线性回归分析,建立线性模型。
本质非线性关系是指变量之间不仅形式上呈现非线性关系,而且也无法通过变量转化为线性关系,最终无法进行线性回归分析,建立线性模型。
本实验针对本质线性模型进行。
下面介绍本次实验涉及到的可线性化的非线性模型,所用的变换既有自变量的变换,也有因变量的变换。
乘法模型:123y x x x βγδαε=其中α,β,γ,δ 都是未知参数,ε是乘积随机误差。
对上式两边取自然对数得到123ln ln ln ln ln ln y x x x αβγδε=++++上式具有一般线性回归方程的形式,因而用多元线性回归的方法来处理。
然而,必须强调指出的是,在求置信区间和做有关试验时,必须是2ln (0,)n N I εδ: ,而不是2n N I εδ:(0,) ,因此检验之前,要先检验ln ε 是否满足这个假设。
三、实验内容已有很多学者验证了能源消费与经济增长的因果关系,证明了能源消费是促进经济增长的原因之一。
也有众多学者利用C-D 生产函数验证了劳动和资本对经济增长的影响机理。
所有这些研究都极少将劳动、资本、和能源建立在一个模型中来研究三个因素对经济增长的作用方向和作用大小。
现从我国能源消费、全社会固定资产投资和就业人员的实际出发,假定生产技术水平在短期能不会发生较大变化,经济增长、全社会固定资产投资、就业人员、能源消费可以分别采用国内生产总值、全社会固定资产投资总量、就业总人数、能源消费总量进行衡量,并假定经济增长与能源消费、资本和劳动力的关系均满足C-D 生产函数。
问题中的C-D 生产函数为:Y AK L E αβγ=式中:Y 为GDP ,衡量总产出;K 为全社会固定资产投资,衡量资本投入量;L 为就业人数,衡量劳动投入量;E 为能源消费总量,衡量能源投入量;A,α,β, γ 为未知参数。
根据C-D 函数的假定,一般情形α,β,γ均在0和1之间,但当α,β,γ中有负数时,说明这种投入量的增长,反而会引起GDP 的下降,当α,β,γ中出现大于1的值时,说明这种投入量的增加会引起GDP 成倍增加,这在经济学现象中都是存在的。
以我国1985—2004年的有关数据建立了SPSS 数据集,参见“”。
请以此数据集为基础估计生产函数中的未知参数。
四、实验步骤及结果分析1. 确定非线性回归模型的类型有上述分析过程确定要建立的回归模型为:Y AK L E αβγ=式中,Y 为自变量,K,L,E 为解释变量,A 为常数项。
2. 通过变换将非线性方程转化为线性方程将原回归模型两遍同时取对数:ln ln ln ln ln Y A K L E αβγ=+++得:123y c x x x αβγ=+++式中,123ln ,ln ,ln ,ln ,ln y Y c A x K x L x E ===== 。
选择【转换】—【计算变量】,对所有数据取对数完成数据的处理,过程及结果如下图:3. 进行初步线性回归分析(选入所有变量)用最小二乘法建立回归方程由非线性模型转化为线性模型后,即可按照建立多元线性回归模型的步骤进行操作,求得回归方程表达式。
(1) 选择【分析】→【回归】→【线性】,弹出“线性回归”对话框。
将lnY 选入“因变量”框,lnk 到lnE 选入“自变量”框。
注意,可以通过点击“上一张”与“下一张”按钮切换,选择不同的自变量构建模型,每个模型中可以对不同的自变量采用不同的方法进行回归。
“方法”下拉框中有5个选项,此处先选择“进入”,即所选变量全部强行进入回归模型。
(2) 点击“统计量”按钮,选择输出各种常用判别统计量,本案例选择“估计”、 “模型拟合度”、“描述性”、“共线性诊断”,以及残差中的“Durbin-Watson ”检验和“个案诊断”。
得到如下结果:由模型汇总表,20.991R =,20.989R =,拟合优度很强。
统计量DW=,该检验用于判断相邻残差序列的相关性,其判断标准如下: DW<d L ,认为残差序列存在正的一阶自相关;d u <DW<4-d U ,认为残差序列间不存在一阶自相关;DW>4-d L ,认为残差序列间存在负的一阶自相关;d L <DW<d U 或4-d U <DW<4-d L 时,无法确定残差序列是否存在自相关。
本例中,k=4,n=21(k 为解释变量的数目,包括常数项,n 是观察值的数目)时,5%的上下界:dL=,dU=。
有l DW d < ,认为残差序列存在一阶自相关。
由方差分析表,统计量F=,p 值小于,认为方程在95%的置信水平下是显着的。
但是,0.025(2131) 2.110t --= 变量lnK 、lnL 、常量lnA 的t 值均大于,所以这几个变量对方程的影响都很显着,而变量lnE的t值很小且p值明显大于且回归系数为零,说明该变量对方程影响不显着,回归模型是无效的。
4.消除模型中变量的共线性(逐步回归)“共线性统计量”中,容忍度Tolerance越接近于0,表示复共线性越强,越接近于1,复共线性越弱。
而方差膨胀因子VIF的值越接近于1,解释变量间的多重共线性越弱,如果VIF的值大于或等于10,说明一个解释变量与其他解释变量之间有严重的多重共线性。
本例中,变量lnK和lnE的VIF值都大于10,说明它们与其他解释变量之间有严重的多重共线性,不符合经典假设,需要修正。
通过以上结果分析,采用逐步回归的方法来消除变量之间的多重共线性。
重复以上步骤从新建立回归方程,将【进入】替换为【逐步】如下图所示:得到如下结果:从上表可以看出通过逐步回归剔除掉了变量lnE,整个模型的拟合优度上升,调整R方从上升至。
方差膨胀因子VIF值均小于10,多重共线性已消除。
T 检验的概率明显小于说明变量对模型的影响显着。
而此时DW值并未有明显改变,残差序列仍然存在一阶自相关。
此时采用数据变换的方法来消除残差的自相关。
5.消除残差的自相关对于自相关的处理方法,其基本思想是通过一些数学转化,对数据进行处理,消ρ=除数据的自相关性,在对参数进行估计。
当误差序列的自相关系数已知,且1时,采用差分法,即利用增量数据来代替原有的样本数据建立方程。
当误差序列的自相关系数未知时,先求处自相关系数,再通过反复迭代法消除来自相关。
我们知道DW与ρ之间的近似关系:µ≈-2(1)DWρ其中:因为DW=,代入上式很明显得出ρ 不为1,所以此处不能用差分而采用迭代的方法消除自相关性。
这里先求出lny 的一元线性回归方程:ln 4.5290.655ln 0.782ln y K L =-++ 中的残差i e ,i=1, … ,n,将残差代入如下公式:11,112,()()n in i n e e e e r --+--=∑其中11,12,11211,11n n n i n i i i e e e e n n ---====--∑∑ 残差序列代入上式求的一阶自相关系数0.60966r =再令:**11,,1,...,1i i i i i y y ry x x rx i n ++=-=-=-用EXCEL 完成数据的迭代得到新的数据,这里用Y1代表原先的lnY ,K1代表原先的lnK ,L1代表原先的lnL 。
并导入到SPSS 中,重复以上步骤对新的数据进行回归分析。
得出结果的:数据经过一次迭代以后DW 的值有明显增加,查表k=3,n=20(k 为解释变量的数目,包括常数项,n 是观察值的数目)时,5%的上下界:dL=,dU=。
有d u <DW<4-d U ,认为残差序列间不存在一阶自相关。
此时得到新的回归方程:1 2.2160.61010.9201Y K L =-++6. 残差正态性检验点击“绘制”按钮,将“ZRESID”选入Y轴,“ZPRED”选入X轴,绘制散点图,并在“标准化残差图”中选择“直方图”,输出带有正态曲线的标准化残差的直方图。
点击“保存”按钮,在对话框中保存一些统计量的值,此案例在“预测值”框中选择“未标准化”,在“残差”框中选择“未标准化”,在“预测区间”框中选择“均值”和“单值”。
其他不变,点击【继续】→【确定】。
输出结果如下图:上面操作已输出残差的直方图,还可以通过【分析】→【描述统计】→【P-P 图】和【分析】→【描述统计】→【Q-Q图】输出正态分布的P-P图、Q-Q图,若散点围绕图中所给斜线有规律的分布,则可以认为所检测变量服从正态分布。
P-P图Q-Q图从以上图形可以初步认为该模型的残差服从正态分布。
进一步进行K-S检验。
选择【分析】→【非参数检验】→【旧对话框】→【1-样本 K-S检验】,弹出“单样本Kolmogorov-Smirnov检验”窗口,将未标准化残差选入变量框,K-S检验输出结果K-S检验统计量为,检验概率p值为,大于,可以认为在95%的置信水平下,该模型的残差服从正态分布。
7.残差的其他检验(1)异方差检验:根据回归分析输出的标准化残差的散点图,初步判断是否存在异方差,但此种判断方法较主观,且不容易判断。
进一步用Spearman等级相关检验分析是否存在异方差。
首先对未标准化残差取绝对值,点击【转换】→【计算变量】,弹出“计算变量”窗口,“目标变量”输入“abs”,“数学表达式”输入“abs(RES_1)”,选择【分析】→【相关】→【双变量】,将abs、所有回归变量及未标准化预测值选入变量框中,【相关系数】栏选择“Spearman”,点击确定。
Spearman相关系数表观察系数表的“abs”行,发现未标准化预测值与残差绝对值的相关性p值为大于,说明该模型的残差不存在的异方差问题。
五、实验总结根据上述分析,采用逐步回归法得到最后确定的回归方程:1 2.2160.61010.9201Y K L =-++其中1111ln ln 1ln ln 1ln ln ,1,...,1i ii ii i Y y r y K k r k L l r l i n +++=-=-=-=-代入上式得回归方程为:111ln ln 2.2160.610(ln ln )0.920(ln ln )i i i i i i y r y k r k l l +++-=-+-+-(i=1,2, (21)将上式同时取以e 为底数进行指数变换得到非线性模型中的本质线性关系的方程:2.2161110.6100.920,1,...,20,0.6097i i i r r r i i i y k l e i r y k l -+++⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭根据所建的回归方程可以看出社会固定资产投资(K )和劳动力(L )对GDP 增长的影响较明显,而能源的消费(E)对经济的增长没有明显影响。
