地震计算
地震系数法

地震系数法是我国目前工程设计中通用的方法,等效静荷载包括:结构本身的水平惯性力1F 、结构本身竖向惯性力F 2、结构上方土柱的垂直惯性力F 3、结构上方土柱水平惯性力F 4、主动侧压力增量四部分。
1、结构本身水平惯性力1F 可以表示为:
1c h F K mg η=
其中:g 为重力加速度;m 为构件或结构的质量;K h 为与地震加速度有关的地震系数,沈阳七度设防烈度取K h =0.1;ηc=0.25。
注意,使用软件计算时,只需加上水平惯性力就可模拟结构自重产生的水平惯性力,水平惯性力大小即为K h *ηc=0.025,施加方法同重力加速度。
2、结构上方土柱的水平惯性力F 3可以表示为:
F 3=ηcK h P
其中P 为上方土柱重量,施加时按照均布荷载施加,其余符号同上。
3、结构本身竖向惯性力F 2可以表示为:
F 2=ηcK v mg
其中:g 为重力加速度;m 为构件或结构的质量;K v =1/2*K h ;ηc=0.25。
注意,使用软件计算时,重力加速度+K v *ηc 即可。
4、结构本身惯性力F 4=ηcKv*mg 可以表示为:
F 4=ηcKv *P
5、主动土压力增量
主动土压力增量为梯形荷载
q e a a i )(=λλ'-∆ )2/45(tan 2ϕλ-= a ;)2/)(45(tan 2θϕλ--=' a。
关于地震等级与建筑物抗震设防烈度的计算

地震是一种自然灾害,能够给人类社会带来严重的破坏。
在地震来临之际,建筑物的抗震设防烈度显得尤为重要。
本文将从地震等级与建筑物抗震设防烈度的计算两个方面展开阐述。
一、地震等级的计算1. 地震等级的概念地震等级是指地震的强度,常用烈度表示。
烈度是根据地震对人、建筑物和地壳的影响进行的评价,通常采用罗氏烈度标准。
2. 地震等级的计算方法地震等级的计算是通过地震记录的地震波的振幅与地震距离的关系,来确定地震的强度。
目前,地震等级的计算常采用矩震级或震级两种方法。
3. 地震等级的参考标准地震等级的参考标准主要有世界地震等级有ISO、GB、USGS等标准,这些标准都对地震等级的计算方法有详细的规定。
二、建筑物抗震设防烈度的计算1. 抗震设防烈度的概念建筑物抗震设防烈度是指建筑物在地震作用下不受破坏的程度,这是由建筑物所承受地震力与建筑物自身抗震能力之间的关系确定的。
2. 抗震设防烈度的计算方法建筑物抗震设防烈度的计算方法主要有经验值法、响应谱法和有限元法等。
这些方法各有侧重,可根据具体情况选择适用的方法。
3. 抗震设防烈度的参考标准建筑物抗震设防烈度的参考标准主要有国家标准GBxxx《建筑抗震设计规范》以及国际上的一些相关标准,如美国的ASCE、欧洲的EUROCODE等。
三、地震等级与建筑物抗震设防烈度的关系1. 地震等级与建筑物抗震设防烈度的关系地震等级与建筑物抗震设防烈度之间存在着直接的通联,地震等级的高低将影响到建筑物所承受的地震力,从而影响到建筑物的抗震设防烈度。
2. 如何根据地震等级确定建筑物抗震设防烈度根据地震等级确定建筑物抗震设防烈度的计算是一个复杂的过程,需要考虑到建筑物的性质、材料、结构形式以及地震烈度等因素,再根据抗震设计规范进行综合评估。
3. 工程实践中的地震等级与抗震设防烈度的应用在工程实践中,地震等级与建筑物抗震设防烈度的计算是抗震设计的重要环节,通过合理的计算和确定,可以保证建筑物在地震发生时具有足够强的抗震能力。
地震计算公式

地震震级的计算公式为:M=lg(A/T)max+1.66lgΔ+3.5。
其中,A代表地震面波最大地动位移,取两个水平分向地动位移的矢量和,单位为微米(μm);T代表相应周期,单位为秒(s);Δ代表震中距,单位为度(°)。
在实际的地震观测工作中,地震震级M应根据多个台站测定结果的平均值确定。
该标准还规定,各级地震部门提供地震信息,新闻机构报道我国地震新闻,各级政府发布地震预报,各级地震部门制定监测预报方案、防震减灾措施时以及在各种社会应用中,均应使用该标准规定的M来表示地震震级。
如需更多关于“地震计算公式”的信息,建议咨询地震专家或查阅相关研究文献。
水平地震作用计算方法

水平地震作用计算方法
水平地震作用是指地震破裂在水平方向上对地壳和岩石产生的应力。
以下是常用的水平地震作用计算方法:
1. 直接计算法:利用地震学公式直接计算水平地震作用。
该方法需要知道地震破裂的物理条件和地震参数,然后利用地震学公式和岩石力学理论进行计算。
2. 破裂模拟法:通过模拟地震破裂的物理过程,计算出水平地震作用。
该方法需要建立地震破裂模型,模拟地震破裂时地壳和岩石发生的变形和应力过程,然后根据岩石力学理论计算出水平地震作用。
3. 专业模型法:利用专业模型对地震破裂进行模拟,并计算出水平地震作用。
该方法适用于研究复杂地质条件下的地震破裂,如断层带等。
常用的水平地震作用计算方法有 direct method、破裂模拟法和专业模型法等。
这些方法都需要具体的地震破裂数据和研究模型,因此在研究地震破裂时需要选择合适的方法进行计算。
抗震计算
G1
k1
F 1kN
V1 400 300 700 kN V2 300kN
(2)计算各楼层处的水平位移
x2
x1
u1 V1 / k1 700/ 14280 0.049 m
u2 V1 / k1 V2 / k2 0.049 300/ 10720 0.077m
dw=6m
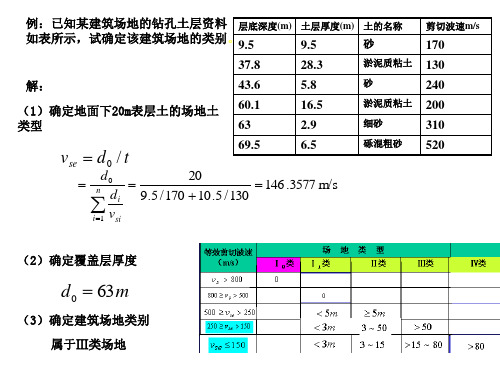
例2 图示为某场地地基剖面图 上覆非液化土层厚度du=5.5m 其下为沙土,地下水位深度 为dw=6m.基础埋深db=2.5m, 该场地为8度区。确定是否考 虑液化影响。
2) 细判
采用标准贯入试验判别 钻孔至试验土层上15cm处,用63.5公斤穿心锤,落 距为76cm,打击土层,打入30cm所用的锤击数记作 N63.5,称为标贯击数。用N63.5与规范规定的临界值 Ncr比较来确定是否会液化。
G1
k1
V1 400 300 700 kN V2 300kN
(2)计算各楼层处的水平位移
u1 V1 / k1 700/ 14280 0.049 m
u2 V1 / k1 V2 / k2 0.049 300/ 10720 0.077m
(3)计算基本周期
T1 2
1---穿心锤 2---锤垫 3---触探杆 4---贯入器头 5---出水孔 6---贯入器身 7---贯入器靴
例:单层单跨框架。屋盖刚度为无穷大,质量集中于屋 盖处。已知设防烈度为8度,设计地震分组为二组,Ⅰ类 场地;屋盖处的重力荷载代表值G=700kN,框架柱线刚 度 ic EIc / h 2.6 104 kN m ,阻尼比为0.05。试求该结构多 遇地震时的水平地震作用。
地震属性计算公式

1.层序类层属性1) 大于门槛值的百分比(Percent Greater than Threshold)该类属性用于分析储层内的同相轴,如由很高的值集中于数据引起的振幅异常。
计算公式为:该属性主要用于分析地层的延伸,海进和海退垂直序列层序会在高振幅砂岩面和低振幅页岩面之间产生。
通过该属性,可以确定这些垂直变化和绘出横向变化的范围图。
同样,它可以帮助区分出整合基底(高振幅)、丘状起伏基底(较低振幅)和杂乱反射基底(低振幅)之间的不同。
2) 小于门槛值的百分比(Percent Less than Threshold)该类属性用于分析储层内的同相轴,如由很低的值集中于数据引起的振幅异常。
计算公式为:该属性主要用于地层走向方面的研究。
在特定的第三纪盆地内,三角洲层序是从富含砂,高均方根振幅,到富含页岩前三角洲或深海平原里面的低振幅来划分的。
这些油页岩比率的变化通过看图中的小于门槛值的百分比就可以很容易确定。
同样,它可以帮助区分出整合基底(高振幅)、丘状起伏基底(较低振幅)和杂乱反射基底(低振幅)之间的不同。
3) 吸收系数(Absorption Coefficient)吸收系数α是用来表示地震波振幅A 沿传播距离的衰减系数,即:0x A A e α-=其中,x 为波的传播距离,0A 为起始振幅。
吸收系数与地震波速度之间存在明显的对比关系,高速的岩石,吸收系数低;低速的岩石,吸收系数高。
吸收系数如同速度一样,频数异常现象较弱。
2.地震纹理属性(1)地震数据灰度化设三维地震数据中的一个地震体素点为X(x,y,z,a),其中x ,y ,z 代表了线号、道号和时间;a 代表振幅值。
设定某个灰度阶数G ,用100%PGT =⨯大于门槛值的样点数总的样点数100%PLT =⨯小于门槛值的样点数总的样点数min max mina A g G A A -=⨯- 将地震数据a 转化为灰度数据g ,式中A min 和A max 所有地震数据中的最小值和最大值;灰度阶数G 决定了地震数据的粗化程度。
地震作用标准值计算

地震作用标准值计算(1)各层总重力荷载代表值计算1.屋面层总重力荷载代表值女儿墙重量:(1.95+0.51+0.875)×[(11.4+0.2)×2+(25+0.2)×2-(2.5+0.4×10+0.5×4)]=217.11kN屋面板重量:6.4×(4-0.2-0.15)×(11.4-0.2-0.3-0.2)×2=499.90kN7.7×(6-0.15×2)×(11.4-0.2-0.3-0.2)×2=939.25kN5.9×[(6-0.2-0.15)×(2.5-0.3)×2+(2.5-0.3)×(3.6-0.3)]+6.4×(1.8-0.25)×(2.5-0.3)=211.33kN499.90+939.25+211.33=1650.48kN电梯机房重量:0.91+2.366+1.333+3.465+1.43+3.887+25×0.3×0.3×1.5×2+25×0.2×0.2×(1.8×2+2.5×2)+5.9×1.6×2.3=50.453kN楼梯间重量:(7.275+15.132+3.958)×2+(1.275+1.716+0.449+1.62)+(2.61+5.148+1.346+0.486)=67.38kN4.5×[(2.5-0.4)+(2.5-0.25-0.2)+(5.4-0.3-0.25)+(5.4-0.3-0.2)]=62.55kN3.89+4.031+0.432+0.571=8.924kN25×3×(0.4×0.4×3+0.5×0.5)=54.75kN5.9×(5.4-0.35)×(2.5-0.3)=65.55kN67.38+62.55+8.924+54.75+65.55=259.15kN楼梯板重量:25×(0.3×0.15/2×1.1×9+3×1.1×0.12+0.2×0.3×2.5)+3×1.1×2.3+17×0.02×[1.1×2.3+2.3×(0.2+0.2+0.2)+1.1×3]+2.12=31.38kN8层柱重量:25×1.5×(0.4×0.4×9+0.5×0.5×5)=100.88kN17×0.02×1.5×(0.4×4×9+0.5×4×5-0.2×2×14)=9.59kN100.88+9.59=110.47kN梁重量:4.5×[(11.4+0.2)×7-0.4×12-0.5×8-0.3)]=324.45kN4.5×[(25+0.2)×3-0.4×12-0.5×8]=300.6kN1.5×(2.5-0.3)=3.3kN2.122×2+4.243×2+3.89+4.031+3.89+4.972+1.428×2+2.418×2+0.432+0.714×2+1.18×2+0.571+0.443=42.44kN324.45+300.6+3.3+42.44=670.79kN7层墙、门、窗重量:54.253×2+28.925×2+42.844+41.342+40.291+14.463×2+15.826×2+18.378+11.172×2+8.629+14.463×2+23.598×2+5.573+8.374+8.439×2+15.06×2+10.184+8.706×2+26.611+5.597×2=603.23kN7层柱重量:25×3×(0.4×0.4×12+0.5×0.5×8)=294kN17×0.02×3×(0.4×4+0.7×4+1.7×2+1×2+0.6×3+1.4×2+0.9×2+1)=17.544kN294+17.544=311.544kN因屋面可变载不计入重力荷载代表值,故屋面层的重力荷载代表值为:G=217.11+1650.48+50.453+259.15+31.38+110.47+670.79+603.23/2+311.544/2 7=3447.22kN2-6层重力荷载代表值楼面板重量:3.5×(4-0.35)×(11.4-0.2-2.25-0.2)×2=223.563kN3.0×[(2-0.25)×(2.5-0.3)+(4-0.25)×(2.5-0.3)+(6-0.3)×(2.9-0.25)+(2.5-0.3)×(6-0.55)+(2-0.25)×(4-0.55)]×2+3.0×(3.6-0.3)×(2.5-0.3)=296.325kN4.8×(6-0.3)×(6-0.35)×2=309.168kN3.5×(1.5-0.2)×(6-0.3)×2=51.87kN223.563+296.325+309.168+51.87=880.93kN柱重量:25×3×(0.4×0.4×12+0.5×0.5×8)=294kN17×0.02×3×(0.4×4+0.7×4+1.7×2+1×2+0.6×3+1.4×2+0.9×2+1)=17.544kN294+17.544=311.544kN楼梯板重量:31.38×2=62.76kN梁重量:[1.5×(2.5-0.3)+3×(6-0.3)+1.5×(4-0.35)+3×(6-0.3)+1×(2-0.25)]×2+1×(5-0.6)=93.85kN4.5×1.5×4=27kN0.431×2+2.267×2+0.422+0.305+0.384+2.648×2+0.22×2+0.676×4=14.947kN670.79+93.85+27+14.947=806.59kN墙、门、窗、栏杆重量:603.23+1.06×4+4.239×2=615.948kN楼面可变荷载:2.0×[(25-0.1)×(11.4-0.1)-1.8×2.5]+2.5×6×1.5×2=598.74kN因楼面可变荷载按等效均布荷载计算,要乘以组合值系数0.5,故2-6层的总重力荷载G=880.93+311.544+62.76+806.59+615.948+0.5×598.74=2977.14kN代表值为:621层重力荷载代表值楼面板重量:3.5×(4-0.35)×(11.4-0.2-2.25-0.2)×2=223.563kN3.0×[(2-0.25)×(2.5-0.3)+(4-0.25)×(2.5-0.3)+(6-0.3)×(2.9-0.25)+(2.5-0.3)×(6-0.55)+(2-0.25)×(4-0.55)]×2+3.0×(3.6-0.3)×(2.5-0.3)=296.325kN4.8×(6-0.3)×(6-0.35)×2=309.168kN3.5×(1.5-0.2)×(6-0.3)×2=51.87kN223.563+296.325+309.168+51.87=880.93kN柱重量:25×3.8×(0.4×0.4×12+0.5×0.5×8)=372.4kN372.4+17.544=389.944kN楼梯板重量:31.38×2=62.76kN梁重量:[1.5×(2.5-0.3)+3×(6-0.3)+1.5×(4-0.35)+3×(6-0.3)+1×(2-0.25)]×2+1×(5-0.6)=93.85kN4.5×1.5×4=27kN0.431×2+2.267×2+0.422+0.305+0.384+2.648×2+0.22×2+0.676×4=14.947kN670.79+93.85+27+14.947=806.59kN墙、门、窗、栏杆重量:因1层平面布置与标准层大致相同,此项荷载相差不大,故大小取同标准层此项荷载,为615.948kN楼面可变荷载:2.0×[(25-0.1)×(11.4-0.1)-1.8×2.5]+2.5×6×1.5×2=598.74kN因楼面可变荷载按等效均布荷载计算,要乘以组合值系数0.5,故1层的总重力荷载代表值为:G=880.93+(389.944+311.544)/2+62.76+806.59+615.948+0.5×598.74=3016.34kN 1(2)全楼横向水平地震作用计算 1.结构基本自振周期计算采用顶点位移法计算,此方法计算周期必须先求出结构在重力荷载代表值水平作用于各质点产生的顶点位移,计算过程见表3-2-15。
地震作用计算——地震反应分析 PPT

基本思路:实际应用时根据结构体系的自振周期找到对 应的加速度反应峰值,在结合结构上的质量(或重力荷载) 求出结构所受地震作用力和结构变形。计算出的结构体系的 最大反应随自振周期的变化曲线就是反应谱。
fR cx (t) C —阻尼系数
*惯性力 fI
——质量与绝对加速度的乘积
fIm [ x g(t) x (t)]
§4.2 结构动力学方法——弹性解答
4.2.2 振动微分方程及解答
一、单自由度体系
Famk tc x x tm x txt a xt xt 质点m的绝对加速度:
g ( ) ( )
xg (t) x(t)
fR
fI
fS
假定地基 完全刚性
xg (t) x(t)
——地面水平位移,可由地震
时地面运动实测记录求得。
——质点对于地面的相对弹性 位移或相对位移反应。
作用在质点上的三种力:
*弹性恢复力 fs
——使质点从振动位置回到平衡位置的力
fs kx(t)k —刚度系数
*阻尼力 fR
——使结构振动衰减的力,由外部介质阻力、 构件和支座部分连接处的摩擦和材料的非弹性 变形以及通过地基散失能量(地基振动引起) 等原因引起
例:若为两个自由度,令n=2,则有
将求出的w1、w2分别代回方程,可求出X1 、X2的相对值。
对应于w1为第一振型:
X11 X12
k12
k1112m2
对应于w2为第二振型:
X21 k12
X22 k11 22m1
§4.2 结构动力学方法——弹性解答
4.2.2 振动微分方程及解答
