材料力学组合变形习题
组合变形(例题)

A
P 450
A
0.12
103
6.37MPa
T Wn
16700.1030
35
.7MPa
3
24 2
故,安全。
6.372435.72
71.7MPa
p.8
例题
习题6.
例题
图示皮带轮传动轴传递功率N=7kW,转速n=200r/min。皮带轮重量Q=1.8kN。左端齿轮
上的啮合力Pn与齿轮节圆切线的夹角(压力角)为20o。轴的材料为45钢, [] =80MPa。
例题
b
P
25 e
a
P
5
解:(1)将外力向轴线简化,如图所示;
b
其中:M=Pe,这属于拉弯组合变形;
P
a
P
(2)求出a、b点的应力;
a
P A
Pe W
,
b
P A
Pe W
(3)二点均属单向应力状态,求出二点的轴向应变;
a
a E
P 1 e EA W
b
b E
P E
1 A
e W
(4)解方程组得 P EAa b 18.4kN
力是水平方向,B轮上胶带的张力是垂直方向,大小如图示;圆轴的许用应力[σ]=80MPa;试按
第三强度理论求轴所需的直径。
5kN
(3)求可能危险截面C和B上的合成弯矩:
AC
B
D
2kN
MC
M
2 yC
M zC 2
1.52 2.12 2.58kNm
2kN
5kN
300
500
500
MB
M
2 yB
M zB2
xz平面的弯矩图为 代入第三强度理论的强度条件得
材料力学组合变形习题

材料力学组合变形习题L1AL101ADB (3)偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案:(A ) e=d; (B ) e>d;(C ) e越小,d越大; (D ) e越大,d越小。
正确答案是______。
答案(C )1BL102ADB (3)三种受压杆件如图。
设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,现有下列四种答案:(A )max1σ=max 2σ=max3σ; (B )max1σ>max 2σ=max3σ;(C )max 2σ>max1σ=max3σ; (D )max 2σ<max1σ=max3σ。
正确答案是______。
答案(C )1BL103ADD (1)在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案:(A )A点; (B )B点; (C )C点; (D )D点。
正确答案是______。
答案(C )1AL104ADC (2)一空心立柱,横截面外边界为正方形, 内边界为等边三角形(二图形形心重 合)。
当立柱受沿图示a-a线的压力时,此立柱变形形态有四种答案:(A )斜弯曲与中心压缩组合; (B )平面弯曲与中心压缩组合;(C )斜弯曲; (D )平面弯曲。
正确答案是______。
答案(B )1BL105ADC (2)铸铁构件受力如图所示,其危险点的位置有四种答案:(A )①点; (B )②点; (C )③点; (D )④点。
正确答案是______。
答案(D )1BL106ADC (2)图示矩形截面拉杆中间开一深度为h/2的缺口,与不开口的拉杆相比,开口处的最大应力的增大倍数有四种答案:(A )2倍; (B )4倍; (C )8倍; (D )16倍。
正确答案是______。
答案(C )1BL107ADB (3)三种受压杆件如图,设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,它们之间的关系有四种答案:(A )max1σ<max 2σ<max3σ; (B )max1σ<max 2σ=max3σ;(C )max1σ<max3σ<max 2σ; (D )max1σ=max3σ<max 2σ。
材料力学习题组合变形#(精选.)

组合变形基 本 概 念 题一、选择题1. 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到 形心的距离e 和中性轴到形心距离d 之间的关系是( )。
A .e = dB .e >dC .e 越小,d 越大D .e 越大,d 越小2.三种受压杆件如图所示,设杆1、杆2和杆3中的最大压应力(绝对值)分别用1max σ、2max σ、3max σ表示,则( )。
A .1max σ=2max σ=3max σB .1max σ>2max σ=3max σC .2max σ>1max σ=3max σD .2max σ<1max σ=3max σ 题2图3.在图示杆件中,最大压应力发生在截面上的( )。
A .A 点B .B 点C .C 点D .D 点题3图 题4图4. 铸铁杆件受力如图4所示,危险点的位置是( )。
A .①点B .②点C .⑧点D .④点5. 图示正方形截面直柱,受纵向力P 的压缩作用。
则当P 力作用点由A 点移至B 点时柱内最大压应力的比值()max A σ﹕()max B σ为( )。
A .1﹕2B .2﹕5C .4﹕7D .5﹕26. 图示矩形截面偏心受压杆件发生的变形为( )。
A .轴向压缩和平面弯曲组合B .轴向压缩,平面弯曲和扭转组合C .轴向压缩,斜弯曲和扭转组合D .轴向压缩和斜弯曲组合-41-题5图 题6图 7. 图所示悬臂梁的横截面为等边角钢,外力P 垂直于梁轴,其作用线与形心轴y 垂直,那么该梁所发生的变形是( )。
A .平面弯曲B .扭转和斜弯曲C .斜弯曲D .两个相互垂直平面(xoy 平面和xoz 平面)内的平面弯曲题7图 8. 图示正方形截面杆受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案,正确的是( )。
A .截面形心B .竖边中点A 点C .横边中点B 点D .横截面的角点D 点题8图 题9图9. 图示正方形截面钢杆,受弯扭组合作用,若已知危险截面上弯矩为M ,扭矩为T ,截面上A 点具有最大弯曲正应力σ和最大剪应力τ,其抗弯截面模量为W 。
组合变形习题及参考答案

组合变形一、判断题1.斜弯曲区别与平面弯曲的基本特征是斜弯曲问题中荷载是沿斜向作用的。
( )2.斜弯曲时,横截面的中性轴是通过截面形心的一条直线。
( )3.梁发生斜弯曲变形时,挠曲线不在外力作用面内。
( )4.正方形杆受力如图1所示,A点的正应力为拉应力。
( )图 15. 上图中,梁的最大拉应力发生在B点。
( )6. 图2所示简支斜梁,在C处承受铅垂力F的作用,该梁的AC段发生压弯组合变形,CB段发生弯曲变形。
( )图 27.拉(压)与弯曲组合变形中,若不计横截面上的剪力则各点的应力状态为单轴应力。
( )8.工字形截面梁在图3所示荷载作用下,截面m--m上的正应力如图3(C)所示。
( )图 39. 矩形截面的截面核心形状是矩形。
( )10.截面核心与截面的形状与尺寸及外力的大小有关。
( )11.杆件受偏心压缩时,外力作用点离横截面的形心越近,其中性轴离横截面的形心越远。
( )12.计算组合变形的基本原理是叠加原理。
()二、选择题1.截面核心的形状与()有关。
A、外力的大小B、构件的受力情况C、构件的截面形状D、截面的形心2.圆截面梁受力如图4所示,此梁发生弯曲是()图 4A、斜弯曲B、纯弯曲C、弯扭组合D、平面弯曲三、计算题1.矩形截面悬臂梁受力F1=F,F2=2F,截面宽为b,高h=2b,试计算梁内的最大拉应力,并在图中指明它的位置。
图 52.图6所示简支梁AB上受力F=20KN,跨度L=2.5m,横截面为矩形,其高h=100mm,宽b=60mm,若已知α=30°,材料的许用应力[σ]=80Mpa,试校核梁的强度。
3.如图7所示挡土墙,承受土压力F=30KN,墙高H=3m,厚0.75m,许用压应力[σ]ˉ=1 Mpa,许用拉应力[σ]﹢=0.1 Mpa,墙的单位体积重量为,试校核挡土墙的强度。
图 6 图 74.一圆直杆受偏心压力作用,其偏心矩e=20mm,杆的直径d=70mm,许用应力[σ]=120Mpa,试求此杆容许承受的偏心压力F之值。
吉林大学考研材料力学题型四:组合变形

(2000)四、钢制平面直角曲拐ABC,受力如图。
q=2.5πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P x=qL,试设计AB段的直径d。
(15分)(2001)三、已知直径为d的钢制圆轴受力如图。
(1)试确定可能危险点的位置,并用单元体表示其应力状态;(2)若此圆轴单向拉伸时的许用应力为[σ],试列出校核此轴强度的强度条件。
(10分)(2001)九、试指出下面各截面梁在P的作用下,将产生什么变形?(6分)(2002)二、图示矩形截面杆,上、下表面的轴向线应变分别为:εa=1×10-3,εb=0.4×10-3,E=210Gpa1)试求拉力P和偏心距e;2)并画出横截面上的正应力分布图。
(10分)(2002)五、直径为d的钢制圆轴受力如图。
已知:P1=20KN,P2=10KN,m=20KN·m,q=5KN/m,[σ]=160Mpa,试设计AB 轴的直径。
(10分)(2003)三、钢制实心圆截面轴AC,[σ]=140Mpa,L=100cm,a=15cm,皮带轮直径D=80cm,重Q=2KN,皮带水平拉力F1=8KN,F2=2KN,试设计AC轴的直径d。
(15分)m=qL2,P=qL,试用第三强度理论设计该圆周的直径d。
(15分)L、P、M=4PL,试用第三强度理论设计该轴的直径D。
(15分)(2005)十一、图示为一等直杆受偏心拉伸,试确定其任意X截面上的中性轴方程。
若设Y P=H/6,Z P=B/6,求其中性轴在Y轴和Z轴上的截距(A Y=?、A Z=?)各为多少?(8分)(2006)六、直径为D的钢制平面曲拐圆轴受力如图所示,已知材料的许用应力为[Σ]=160MP A,Q=20KN/M,F1=10KN,F2=20KN,L=1M,试设计AB轴的直径D。
(2006)九、已知矩形截面铝合金杆A点处的纵向线应变ΕX=5×10-4,E=70GP A,H=18CM,B=12CM,试求荷载F。
材料力学_陈振中_习题第九章组合变形
第九章组合变形9.1 试求图示各构件在指定截面上的内力分量。
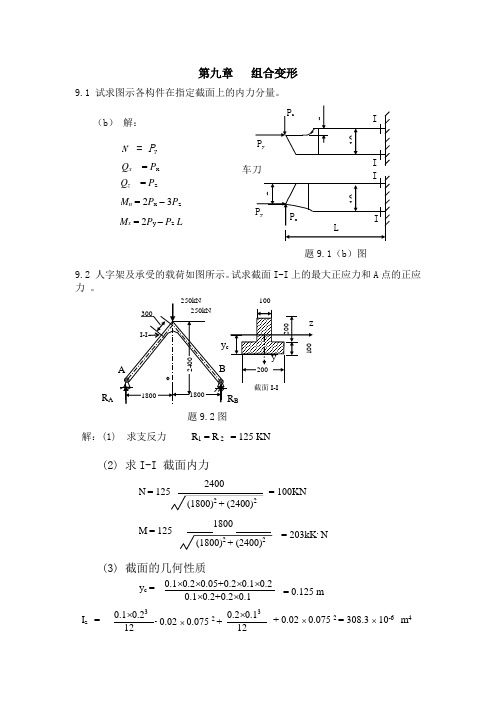
9.2 人字架及承受的载荷如图所示。
试求截面I-I上的最大正应力和A点的正应力9.3 图示起重架的最大起吊重量(包括行走小车等)为P = 40kN ,横梁AC 由两根No.18槽钢组成,材料为A3钢,许用应力[σ] = 120 MPa 。
试校核横梁的强度。
9.7 图示短柱受载荷P 和H 的作用,试求固定端截面上角点A 、B 、C 及D 的正应力,并确定其中性轴的位置。
9.14 图为操纵装置水平杆,截面为空心圆形,内径d = 24 mm,外径D = 30 mm。
材料为A3钢,[σ] = 100 MPa。
控制片受力P1= 600 N。
试用第三强度理论校核杆的强度。
9.17图示皮带轮传动轴,传递功率N = 7kW,转速n =200r/min。
皮带轮重量Q = 1.8kN。
左端齿轮上啮合力Pn与齿轮节圆切线的夹角(压力角)为200。
轴的材料为A5钢,其许用应力[σ] = 80 MPa。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
9.19 飞机起落架的折轴为管状截面,内径d =70 mm ,外径D = 80 mm 。
材料的许用应力[σ] = 100 MPa ,试按第三强度理论校核折轴的强度。
若P = 1 kN ,Q = 4 kN 。
9.24 端截面密封的曲管的外径为100mm ,壁厚t = 5mm ,内压p = 8MPa 。
集中力P = 3kN 。
A 、B 两点在管的外表面上,一为截面垂直直径的端点,一为水平直径的端点。
试确定两点的应力状态。
解:在内压p 作用下,B 点应力状态分别如图9.24a ,b 所示。
σp1 = pD/(2t) = 8⨯100/(2⨯5) = 80 MPa, σp2 = pD/(4t) = 40 MPa 在集中力P 作用下,曲管受弯扭组合变形,A 点和B 点应力状态分别如图9.24c ,d 所示。
中南大学材料力学--组合变形答案
组合变形答案一、概念题1.A ;2.A ;3.D ;4.C ;5.B ;6.A ;7.C ;8.D ;9.C ;10.C11.略12. 13σσσ=-=二、计算题1截面形心和惯性矩计算:126459.5240.484.8810z z mmz mm I mm ===⨯1-1 截面上的内力:28857.6.12N M Py N mF P kN ====2max 1max 26.8[]32.3[]t Nt Zc Nc ZF Mz MPa A I F Mz MPa A I σσσσ=+=<=-+=< 安全2设切口深度为x ,则偏心距为:x /23112100.005(0.04)P t F A x σ⨯==-322121020.005(0.04)6t xMx W σ⨯⨯==⨯-61210010t t σσσ=+≤⨯ 得 212864000.00521x x x m -+== 3 2642()()P A hP F M PP A W bh bh bh σ⨯=-+=-+=-A 点的应力状态为单向压缩应力状态 454522AP bh σσσ-===-4545451122()()P P E E bh bh εσυσυ-=-=+2(1)Ebh P αευ=-4 过O 点横截面上的应力232324202()()P hP F M P P A W d d d σπππ⨯=+=+= 28T P M P W d τπ== O 点的应力状态为二向应力状态:0x y y σσσττ===220xa P E d E σεπ== 2452452454518cos 90sin 90222cos90sin 902214()x yx y xy x y x yxy b P d Pd P E d Eσσσσστπσσσσστπεσυσπ--+-=+---=+-=+-==-=- 5a 点的应力状态为二向应力状态:32412.710P P P F F F A d σπ===⨯ 3216 5.1010e T P P M M F W dτπ===⨯33031203593030120cos 60sin 6013.91022cos 240sin 240 1.24102211()(13.90.3 1.24)1014.331020010x y x y xy P x y x yxy P P F F F E σσσσστσσσσστεσυσ-+-=+-=⨯+-=+-=-⨯=-=+⨯⨯=⨯⨯2107 2.107.P e F N M N m ==采用第三强度理论校核强度31334.33[]r MPa σσσσ=-==< 安全 61) 计算954920.46.163.68491.1408.9293.75252.3488.66Pz Py Ay By Az Bz P m N m nF N F NF NF NF N F N =====-===-2) 作计算简图3) 作内力图4) 危险截面为A 截面: max max max 20.46.28.08.21.28.T z y M N mM N m M N m===-5)危险点于A 截面的边缘a 点,a 点的应力状态为二向应力状态:2.87MPa σ==2160.83eTP M M MPa W dτπ===max 3.1min 0.2212313max 23.100.22 1.662x yMPaMPaMPaMPaMPaMPaσσσσσσσστ-+=±====--== 6)采用第三强度理论校核强度313 3.32[]r MPa σσσσ=-==< 安全。
材料力学习题组合变形
组合变形基 本 概 念 题一、选择题1. 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心距离d 之间的关系是( )。
A .e = dB .e >dC .e 越小,d 越大D .e 越大,d 越小2.三种受压杆件如图所示,设杆1、杆2和杆3中的最大压应力(绝对值)分别用1max σ、2max σ、3max σ表示,则( )。
A .1max σ=2max σ=3max σB .1max σ>2max σ=3max σC .2max σ>1max σ=3max σD .2max σ<1max σ=3max σ 题2图3.在图示杆件中,最大压应力发生在截面上的( )。
A .A 点B .B 点C .C 点D .D 点题3图 题4图4. 铸铁杆件受力如图4所示,危险点的位置是( )。
A .①点B .②点C .⑧点D .④点5. 图示正方形截面直柱,受纵向力P 的压缩作用。
则当P 力作用点由A 点移至B 点时柱内最大压应力的比值()max A σ﹕()max B σ为( )。
A .1﹕2B .2﹕5C .4﹕7D .5﹕26. 图示矩形截面偏心受压杆件发生的变形为( )。
A .轴向压缩和平面弯曲组合B .轴向压缩,平面弯曲和扭转组合C.轴向压缩,斜弯曲和扭转组合D.轴向压缩和斜弯曲组合-41-题5图题6图7.图所示悬臂梁的横截面为等边角钢,外力P垂直于梁轴,其作用线与形心轴y垂直,那么该梁所发生的变形是()。
A.平面弯曲B.扭转和斜弯曲C.斜弯曲D.两个相互垂直平面(xoy平面和xoz平面)内的平面弯曲题7图8.图示正方形截面杆受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案,正确的是( )。
A.截面形心B.竖边中点A点C.横边中点B点D.横截面的角点D 点题8图题9图9.图示正方形截面钢杆,受弯扭组合作用,若已知危险截面上弯矩为M,扭矩为T,截面上A点具有最大弯曲正应力σ和最大剪应力τ,其抗弯截面模量为W。
(材料力学课件)第8章组合变形作业
D4.17m, 取: D4.17 m
8-11 解: (a) (1) 截面几何性质
z
①
④
A 82 0 10 6 0 52 4 10 6 0 0 .4m 1 2 1
4
第 Iy Iz 8 0 8 1 3 0 0 1 2 0 10 24 54 4 1 0 10 2 0 .0m 4 3800
合 变 形
C 1 D C2 D (22 .4 3 )2 8 1.2 8 2 6 2.7 1 M 1 C P1 a A C 3 A maxCD 121.71MP
作
业 题
1 O 1 A C 1 A O C 2.7 1 1 (22 .4 3 ) 8 3.4 3 M 5 Pa
2 0
3 O 3 O A C C 3 A 1.7 1 4 2.7 1 1 9 .9M 7 Pa
23
1O 4
y
8 章
iy2iz2IA y 00..401310.07m 32
组
③
②
合 (2) 中性轴的截距(m) ay 0.4,az 0
800
变
形 作 业
y
iy2 ay
0.18,3z
0
确定点1
同理求出点2,3,4
题
当中性轴绕棱角点旋转时,外力作用点移动轨迹为直线。
故点1和2间亦为直线。
8-12 解:
题 90.91MPa[bs]
Fs
Fs
Fs
3F/4
Fs
F
1F
(3) 板拉伸强度计算
上板轴力图
F/4
(+)
2 孔 F 面 A N 4 ( b 3 F 2 d d ) 4 ( 8 1 0 3 2 8 0 2 1 0 3 1 2 ) 0 1 0 6 0 1.7 6 M 6 [P ] a
材料力学习题册答案-第8章 组合变形
第 八 章 组 合 变 形一、选择题1、偏心拉伸(压缩)实质上是(B )的组合变形。
A .两个平面弯曲B .轴向拉伸(压缩)与平面弯曲C .轴向拉伸(压缩)与剪切D .平面弯曲与扭转 2、图示平面曲杆,其中AB ⊥BC 。
则AB 部分的 变形为( B )。
A . 拉压扭转组合B .弯曲扭转组合C .拉压弯曲组合D .只有弯曲二、计算题1、如图所示的悬臂梁,在全梁纵向对称平面内承受均布荷载 q=5kN/m ,在自由端的水平对称平面内受集中力P=2kN 的作用。
已知截面为25a 工字钢,材料的弹性模量E=2×105MPa ,求: (1)梁的最大拉、压应力(2)若[σ]=160MPa ,校核梁的强度是否安全。
解:(1)固定端截面为危险截面。
22max 115210kN m 22z M ql ==⨯⨯=⋅max 224kN m y M Pl ==⨯=⋅查表得:3348.283cm ,401.883cm y z W W ==由于截面对称,最大拉、压应力相等。
33max max max max661010410()Pa 108MPa 401.8831048.28310y z t c z y M M W W σσ--⨯⨯==+=+=⨯⨯(2)校核梁的强度[]max 108MPa 160MPaσσ=<=可见,梁的强度是足够的。
2、矩形截面木檩条,尺寸及受载情况如图所示。
已知q=2.1kN/m,木材许用拉应力[σt ]=11MPa ,许用挠度[w]= l /200,弹性模量E=10GPa 。
校核其强度和刚度。
ABCq解:(1)受力分析,计算内力。
根据梁的受力特点可知梁将产生斜弯曲。
因此,将载荷q 沿两对称轴分解为cos y q q ϕ= , sin z q q ϕ=在q 作用下,梁跨中截面的弯矩最大,为危险截面。
由q z 、q y 引起的最大弯矩M ymax 、M zmax 为202max 202max112.1sin 2634'4 1.88kN m 88112.1cos 2634'43.76kN m 88y z z y M q l M q l ==⨯⨯⨯=⋅==⨯⨯⨯=⋅(2)确定危险点位置,计算危险点应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学组合变形习题L1AL101ADB (3)偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案:(A ) e=d; (B ) e>d;(C ) e越小,d越大; (D ) e越大,d越小。
正确答案是______。
答案(C )1BL102ADB (3)三种受压杆件如图。
设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,现有下列四种答案:(A )max1σ=max 2σ=max3σ; (B )max1σ>max 2σ=max3σ;(C )max 2σ>max1σ=max3σ; (D )max 2σ<max1σ=max3σ。
正确答案是______。
答案(C )1BL103ADD (1)在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案:(A )A点; (B )B点; (C )C点; (D )D点。
正确答案是______。
答案(C )(A )max1σ<max 2σ<max3σ; (B )max1σ<max 2σ=max3σ;(C )max1σ<max3σ<max 2σ; (D )max1σ=max3σ<max 2σ。
正确答案是______。
答案(C )1AL108ADB (3)图示正方形截面直柱,受纵向力F的压缩作用。
则当F力作用点由A点移至B点时柱内最大压应力的比值()max A σ/()max B σ有四种答案:(A )1:2; (B )2:5; (C )4:7; (D )5:2。
正确答案是______。
答案(C )1AL109ADC (2)一空间折杆受力如图所示,则AB杆的变形有四种答案:(A )偏心拉伸; (B )纵横弯曲;(C )弯扭组合; (D )拉、弯、扭组合。
正确答案是______。
答案(A )1AL110ADD (1)图示矩形截面偏心受压杆发生的变形有下列四种答案:(A )轴向压缩和平面弯曲组合;(B )轴向压缩,平面弯曲和扭转组合;(C )轴向压缩和斜弯曲组合;(D )轴向压缩,斜弯曲和扭转组合。
正确答案是______。
答案(C )1BL111BDC (2)图示受压柱横截面上最大压应力的位置在____点处。
答案 切口段各横截面的b,e 各点1BL112BDD (1)图示杆中的最大压应力的数值是____。
答案 最大压应力数值()max 2/F bh σ=1AL113BDD (1)图示立柱AB,其危险截面上的内力分量(不计剪力)是________; _________;___________。
答案 轴力N F F =(拉);弯矩3y M Fe =-;z M Fl =-。
1BL114BDD (1)偏心压缩实际上就是____和____的组合变形问题。
答案 轴向压缩 弯曲1AL115CCA短柱受力如图,试导出柱的底面上中性轴的方程。
答案 3()/12z I ab = 3()/12y I ba =固定端截面上的内力N F F = (/2)z M F b =g y M Fh =任一点(y,z )处的应力[]/()/(/2)/y z F A Fhz I F b y I σ=---g令max /6e b =0σ=得中性轴方程为226120a y bhz a b ++=3AL116CCA证明:在矩形截面杆的两个端面上,当偏心拉力F作用在图示三分点上如1 点,或2点,···时,截面上max σ=2F/(bh),min σ=0。
答案 在h/3两边的点N F F = /6M Fh = max //2/()F A M W F bh σ=+= min 0σ=同理可证在b/3两边的点max 2/()F bh σ= min 0σ=1AL117CCC证明当图示柱中去掉其中一个力F时,最大压应力值不变。
答案 两力作用时2/()F bh σ=-去掉一个F 后[]/()(/6)/2/()F bh F h W F bh σ=-+=-g两者相等1BL118DBC具有切槽的正方形木杆,受力如图。
求(1)m -m 截面上的max t σ和max c σ;(2)此max t σ是截面削弱前的t σ值的几倍?答案 (1)2max ()//8/t F A M W F a σ=+=2max ()//4/c M W F A F a σ=-=(2)max ()/8t t σσ=1BL119DBB结构如图,折杆AB与直杆BC的横截面面积为A=422cm ,y z W W ==4203cm [σ]=100Mpa 。
求此结构的许可载荷[P ]。
答案 竖杆横截面上的内力2/3N F F = 24/3B M F F ==[]max ()//t N F A M W σσ=+≤30F KN ≤ []30F KN =1BL120DBC矩形截面杆受轴向力F的作用,若在杆上开了个图示槽口,已知F=60KN , a=60mm 。
作出Ⅰ-Ⅰ,Ⅱ-Ⅱ截面上的应力分布图。
答案Ⅰ-Ⅰ截面11/16.7N F A Mpa σ==Ⅱ-Ⅱ截面max 222()//66.7t N F A M W MPa σ=+=max 222()//33.3c N F A M W MPa σ=-=-1BL121DBB矩形截面木接头受力如图, 已知顺纹许用挤压应力[]10bs MPa σ=, [τ]=1MPa ,[]t σ=6MPa ,[]c σ=10MPa 。
求接头尺寸a和c。
答案 []3(5010)/(250)l ττ=⨯≤ 200l mm ≥[]3(5010)/(250)bs bs a σσ=⨯≤ 20a mm ≥[]332max ()(5010)/(250)5010()/2/(250/6)t t c a c c σσ⎡⎤=⨯+⨯+≤⎣⎦147c mm ≥取200l mm =,a=20mm,c=147mm1BL122DBD图示偏心受压杆。
试求该杆中不出现拉应力时的最大偏心距。
答案 //0t y Fe W F A σ=-=即2max /1/(6)/0t F e hb F bh σ⎡⎤=⨯-=⎣⎦由此得max /6e b =1AL123DBC矩形截面杆受力如图,求固定端截面上A、B、C、D各点的正应力。
答案 []max 2222()//294.9c N c F A M W KPa σσ=+=</ 2.5N N F A MPa σ==(拉) / 2.5MZ Z Z M W MPa σ== (B.C 拉,A.D 压)/6My y y M W MPa σ== (C.D 拉,A.B 压)2.5 2.561B MPa σ=+-=-2.5 2.566A MPa σ=--=-2.5 2.5611C MPa σ=++=2.5 2.566D MPa σ=-+=1BL124DBC已知一矩形截面梁,高度h=100mm ,跨度l=1m 。
梁中点受集中力F, 两端受拉力S=30KN 。
此拉力作用在横截面的对称轴y上,距上表面a= 40mm 。
若横截面内最大正应力与最小正应力之比为5/3。
试求F值。
答案 偏心距/210p y h a mm =-= 最大弯矩在跨中央截面内max /4p M Fl Sy =-轴力N F S =22max min //()6(/4)/()//()6(/4)/()5/3N p N p F bh Fl Sy bh F bh Fl Sy bh σσ⎡⎤⎡⎤=+---=⎣⎦⎣⎦F=1.7KN1BL125DBA偏心拉伸杆,弹性模量为E,尺寸、受力如图所示。
试求:⑴最大拉应力和最大压应力的位置和数值;⑵AB长度的改变量。
答案 (1)最大拉应力在AB 线上,最大压应力在CD 线上。
22max (/2)/(/6)(/2)/(/6)/()7/()t Fb hb Fh h b F bh F bh σ=++=max 3/()3/()/()5/()c F bh F bh F bh F bh σ=--+=-(2)/7/()AB l l E Fl bhE εσ∆===1AL126DCA图示矩形截面梁。
已知b、h、l、E和F。
试求AB纤维的伸长量∆l。
答案 //(2)F A Fh W σ=+()//()/(2)l dx dx E Fl EA Fhl WE εσ∆===+⎰⎰1CL127DBA矩形截面杆,尺寸如图所示,杆右侧表面受均布载荷作用,载荷集度(单位长 度所受的力)为q,材料的弹性模量为E,试求最大拉应力及左侧表面a.b 总 长度的改变量。
答案 2max (/2)/(/6)/()4/()qlh bh ql bh ql bh σ=+=2x (/2)/(/6)/()2/()qxh bh qx bh ql bh σ=-+=-/x x E εσ=120/()AB x dx ql bhE ε∆==-⎰3CL128DAAb为250mm 、h为400mm 的矩形截面柱、受偏心轴向力F作用,在柱 的某横截面处沿杆轴测得a 、b 、c 、d 四点处的线应变值a ε=-55με, b ε=10με,c ε=25με,d ε=-40με, 材料的E=200GPa 。
⑴求F值及作用位置;⑵求截面上四个角点1、2、3、4处的应力值;⑶确定截面上的中性轴位置,示于图上。
答案 (1)2/()6/()a p a F bh Fy hb E σε=-=2/()6/()b p b F bh FZ hb E σε=+=2/()6/()c p c F bh Fy hb E σε=+=2/()6/()d p d F bh FZ hb E σε=-=得()/2300a c F E bh KN εε=+=-(偏心压力)0.111p y m =- 0.111p Z m =-(2)135816MPa σ=---=- 23586MPa σ=-+-=-335810MPa σ=-++= 40σ=(3)2()/46.9y z p a j y mm =-=2()/120z y p a j z mm =-=1BL129DCC图示矩形截面钢杆,用应变片测得杆件上、下表面的轴向正应变分别为a ε= 1×310-、b ε=0.4×310-,材料的弹性模量E=210GPa 。
⑴试绘制横截面上的正应力分布图;⑵求拉力F及其偏心距δ的数值。
答案 F=18.38KN 1.785mm δ=1AL130DBB图示梁已知F=75KN ,q=6KN /m ,l=2m ,b=100mm , h=150mm ,求梁内最大拉应力及跨中截面的中性轴位置。
答案 22max ()(/8)/(/6)8q ql bh MPa σ==/()5p F bh MPa σ==max max ()13q p MPa σσσ=+=222/(3)46.9y Fh ql mm ==3AL131DBA图示预应力简支梁。
