最优化方法习题一
重庆大学最优化方法习题答案

s.t.x1 + 2x2 ≤ 5 x1, x2 ≥ 0
解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在 A 点取得最优值, 最优值 z=5
(2) min z = x1 − 6x2 2x1 + x2 ≤ 1
s.t.− x1 + x2 ≤ 7 x1, x2 ≥ 0
解:图中阴影部分表示可行域,由图可知原问题在点 A 处取得最优值,最优值 z=-6.
(3) max z = 3x1 + 2x2
− x1 + x2 ≤ 1 s.t.x1 − 2x2 ≥ −4
x1, x2 ≥ 0
解:如图 所示,可行域为图 中阴影部 分,易得 原线性规 划问题 为无界 解。
所以 x(2) , x(4) , x(6) 是原问题的基可行解, x(6) 是最优解,最优值是 z = −3 。
(2) max z = x1 + x2 − 2x3 + x 4 − x5
x1 + x2 + x3 + x4 = 1 s.t.− x1 + 2x2 + x5 = 4
xi ≥ 0,i = 1,2,3,4,5
解:易知
x1
的系数列向
量
p1
= 1− 1
,
x2
的系数列向
量
p2
=
1
2
,
x3
的系
数列向量
1
1
0
p3
=
0
,
x4
的系数列向量
p4
=
0
,
x5
的系数列向量
运筹学与最优化方法习题集

一.单纯性法一.单纯性法1.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 122121212max 25156224..5,0z x x x x x s t x x x x =+£ìï+£ïí+£ïï³î 2.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 12121212max 2322..2210,0z x x x x s t x x x x =+-³-ìï+£íï³î 3.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 1234123412341234max 24564282..2341,,,z x x x x x x x x s t x x x x x x x x =-+-+-+£ìï-+++£íï³î4.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 123123123123123max 2360210..20,,0z x x x x x x x x x s t x x x x x x =-+++£ìï-+£ïí+-£ïï³î 5.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 12312312123max 224..26,,0z x x x x x x s t x x x x x =-++++£ìï+£íï³î6.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 15 分)分) 12121212max 105349..528,0z x x x x s t x x x x =++£ìï+£íï³î7.用单纯形法求解下列线性规划问题(共用单纯形法求解下列线性规划问题(共 16 分)分) 12121212max 254212..3218,0z x x x x s t x x x x =+£ìï£ïí+£ïï³î二.对偶单纯性法二.对偶单纯性法1.灵活运用单纯形法和对偶单纯形法解下列问题(共灵活运用单纯形法和对偶单纯形法解下列问题(共 15 分)分)12121212max 62..33,0z x x x x s t x x x x =++³ìï+£íï³î 2.灵活利用单纯形法和对偶单纯形法求解下列线性规划问题(共灵活利用单纯形法和对偶单纯形法求解下列线性规划问题(共 15 分)分) 121212212max 3510501..4,0z x x x x x x s t x x x =++£ìï+³ïí£ïï³î 3.用对偶单纯形法求解下列线性规划问题(共用对偶单纯形法求解下列线性规划问题(共 15 分)分) 1212121212min 232330210..050z x x x x x x s t x x x x =++£ìï+³ïï-³íï³ïï³î4.灵活运用单纯形法和对偶单纯形法求解下列线性规划问题(共灵活运用单纯形法和对偶单纯形法求解下列线性规划问题(共 15 分)分) 124123412341234min 262335,,,0z x x x x x x x s t x x x x x x x x =+-+++£ìï-+-³íï³î5.运用对偶单纯形法解下列问题(共运用对偶单纯形法解下列问题(共 16 分)分) 12121212max 24..77,0z x x x x s t x x x x =++³ìï+³íï³î6.灵活运用单纯形法和对偶单纯形法解下列问题(共灵活运用单纯形法和对偶单纯形法解下列问题(共 15 分)分) 12121212max 62..33,0z x x x x s t x x x x =++³ìï+£íï³î三.0-1整数规划整数规划1.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 12345123451234512345123345max 567893223220..32,,,,,01z x x x x x x x x x x x x x x x s t x x x x x x x x x x x or =++++-++-³ìï+--+³ïí--+++³ï=î 2.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共 10 分) 12312312323123min 4322534433..1,,01z x x x x x x x x x s t x x x x x or =++-+£ì++³ïí+³ïï=î 3.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共 10 分) 1234512345123451234512345max 20402015305437825794625..81021025,,,,01z x x x x x x x x x x x x x x x s t x x x x x x x x x x =++++++++£ìï++++£ïí++++£ïï=î或 4.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 12345123451234512345max 2534327546..2420,,,,01z x x x x x x x x x x s t x x x x x x x x x x =-+-+-+-+£ìï-+-+£íï=î或 5.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 12341234123412341234min 25344024244..1,,,01z x x x x x x x x x x x x s t x x x x x x x x =+++-+++³ì-+++³ïí+-+³ïï=î或6.7.用隐枚举法解下列0-1型整数规划问题(共型整数规划问题(共10 分) 123451234513451245max 325232473438..116333z x x x x x x x x x x x x x x s t x x x x =+--+++++£ìï+-+£ïí-+-³ï 1231231231223max 3252244..346z x x x x x x x x x s t x x x x =-++-£ìï++£ïï+£íï+£ïï=四.K-T 条件条件1.利用库恩-塔克(K-T )条件求解以下问题(共)条件求解以下问题(共 15 分)分)22121122121212max ()104446..418,0f X x x x x x x x x s t x x x x =+-+-+£ìï+£íï³î2.利用库恩-塔克(K-T )条件求解以下非线性规划问题。
最优化问题

最优化问题最优化问题(一)例1:一只平底锅上只能剪两只饼。
用它剪1只饼需要2分钟(正面、反面各1分钟)。
问剪3只饼需要几分钟?怎样剪?例2:6个人各拿一只水桶到水龙头接水。
水龙头注满6个人的水桶所需时间分别是5分钟、4分钟、3分钟、10分钟、7分钟、6分钟。
现在只有这一个水龙头可用,问怎样安排这6个人的打水次序,可使他们总的等候最短?这个最短时间是多少?例3:小红放学回家,想让爸爸、妈妈下班后就能吃上晚饭。
她准备做大米饭和炒鸡蛋。
小红家有两个炉灶。
估计一下,洗锅要用1分钟,淘米要用5分钟,做大米饭要用30分钟,打蛋要用1分钟,洗炒勺要用1分钟,烧油要1分钟,炒鸡蛋要3分钟。
你认为最合理的安排要几分钟能做好饭菜?例4:在公路上,每隔100千米有一个仓库,共有5个仓库。
1号仓库里有10吨货物,2号仓库里有20吨货物,5号仓库里有40吨货物,其余两个仓库都是空的。
现在想把所有的货物集中存放在一个仓库里,若每吨货物运输一千米要0.5元运输费,那么至少要花费多少元运费才行?例5:沿铁路有5个工厂,A,B,C,D,E(如图),各厂每天都有10吨货物要外运。
现在想建一座车站,使这5个工厂的货物运到车站的行程总和越小越好。
车站应建在何处?如果在E的右侧增加一个工厂,车站建在何处总行程最小呢?例6:在公路干线的附近,有5个工厂A,B,C,D,E(如图),各厂每天都有10吨货物要存库。
现在想在公路干线上建一座库房,使这5个工厂的货物运到库房的行程总和越小越好,库房应建在何处?例7:工地上有手推车20辆,其中10辆从A1到B1运垃圾,要60车次运完。
另外10辆从A2到B2运砖头,要40车次运完。
工地上的可行道路及路程如图(单位:米)所示。
有人说上面的安排不合理,因为跑空车的路程还可以更少些。
那么,怎样安排才算合理呢?【练习题】1、有7个满杯水、7个半杯水和7个空杯。
不许倒水,你能把这些东西平均分给3个人,使得每人有7只杯子和3杯半水吗?2、有8个人在交通事故中受伤,救援人员1人可以救护2人,而1辆救护车只可以坐4个人。
最优化练习题一

最优化练习题1.设A 为m n ⨯阶矩阵,nb R ∈,试证集合{|,,0}n S x x R Ax b x =∈=≥为凸集。
2.试证平面上椭圆22221x y a b+=所包围的区域为凸集。
3.判断下列函数为凸函数或凹函数或严格凸函数或严格凹函数:(1)221212(,)23f x x x x =+;(2)2221231231231(,,)22712f x x x x x x x x x x =+++--+4.设()f x 为定义在凸集D 上的凸函数,试证()f x 的任何局部极小点同时也必为全局极小点。
5.设n 阶矩阵0T Q Q =>,非零向量12,,,()n n p p p R m n ∈≤为Q 共轭的,证明:(1)12,,,n p p p 线性无关;(2)若n 维向量x 和12,,,n p p p 为Q 共轭的,则x=0。
6.设()TTf x x Ax b x =-,2112A ⎡⎤=⎢⎥⎣⎦,(3,3)T b =,取1(0,0)Tx =,1(1,0)T p =,2(1,2)T p =-,试证由共轭方向法产生的3x 为()f x 的最优解。
7.设1()2TT f x x Qx b x c =++,0T Q Q =>,试证由精确线搜索的共轭梯度法中,有 T k k k T k kg dd Qd λ=-8.取初始点0(0,0)T x =,并且设定净度误差0.01ε=,试利用最速下降法求解下面的优化问题:222112212min 243x Rx x x x x x ∈-++-9.考虑极小化问题1min ()2nTT x Rf x x Ax b x ∈=+,其中0T A A =>,n b R ∈。
记函数()()g x f x Ax b =∇=+。
设从k x 点出发,利用精确搜索的最速下降法求出改进点1k x +,证明:(1)最速下降法的迭代公式形如1T k k k k k T k k g gx x g g Ag +=-,其中()k k g g x =;(2)一步迭代中引起目标函数的下降量为21()()()2T k k k k Tk kg g f x f x g Ag +-=。
最优化设计 课后习题答案

最优化方法-习题解答张彦斌计算机学院2014年10月20日Contents1第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、412第二章线搜索算法-P27习题2、4、643第三章最速下降法和牛顿法P41习题1,2,374第四章共轭梯度法P51习题1,3,6(1)105第五章拟牛顿法P73-2126第六章信赖域方法P86-8147第七章非线性最小二乘问题P98-1,2,6188第八章最优性条件P112-1,2,5,6239第九章罚函数法P132,1-(1)、2-(1)、3-(3),62610第十一章二次规划习题11P178-1(1),5291第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、4 1.验证下列各集合是凸集:(1)S={(x1,x2)|2x1+x2≥1,x1−2x2≥1};需要验证:根据凸集的定义,对任意的x(x1,x2),y(y1,y2)∈S及任意的实数λ∈[0,1],都有λx+(1−λ)y∈S.即,(λx1+(1−λ)y1,λx2+(1−λ)y2)∈S证:由x(x1,x2),y(y1,y2)∈S得到,{2x1+x2≥1,x1−2x2≥12y1+y2≥1,y1−2y2≥1(1)1把(1)中的两个式子对应的左右两部分分别乘以λ和1−λ,然后再相加,即得λ(2x1+x2)+(1−λ)(2y1+y2)≥1,λ(x1−2x2)+(1−λ)(y1−2y2)≥1(2)合并同类项,2(λx1+(1−λ)y1)+(λx2+(1−λ)y2)≥1,(λx1+(1−λ)y1)−2(λx2+(1−λ)y2)≥1(3)证毕.2.判断下列函数为凸(凹)函数或严格凸(凹)函数:(3)f(x)=x21−2x1x2+x22+2x1+3x2首先二阶导数连续可微,根据定理1.5,f在凸集上是(I)凸函数的充分必要条件是∇2f(x)对一切x为半正定;(II)严格凸函数的充分条件是∇2f(x)对一切x为正定。
最优化方法习题答案
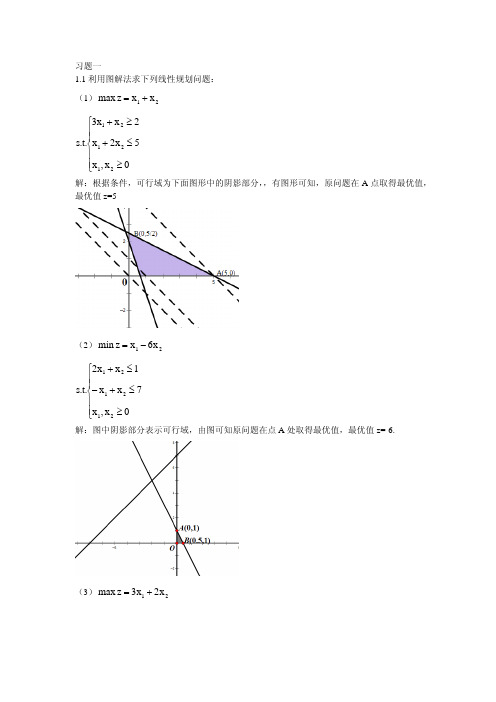
月份 4 5 6
买进单价/(元/件) 17 16.5 17
售出单价/(元/件) 18 18 19
解:设 xi 表示每个月进货量, yi 表示相应月份售货量,其中 i 1,2,3 ,则有数学模型:
max z 18y1 18y2 19y3 17x1 16.5x2 17x3
x1 600 200
x1 y1 x2 600 200
x1
x2
x3
x4
x5 x6
x7
10+2M
15+M
12+M
0
0 -M 0
z
x4
5
3
1
1
00
09
x5
-5
6
15
0
10
0 15
x7
2
1
1
0
0 -1
15
以 x1 为换入变量, x 4 为换出变量
x1
x2
x3
x4
x5 x6
x7
0
z
x1 1
9 M 5
0.6
x5 0
9
x7 0
-0.2
10 3M 5
0.2
2 2M 5
(3) min z 2x1 3x2 x3 x1 4x2 2x3 8
s.t.3x1 2x2 6 x1, x2 , x3 0
解:引入剩余变量 x 4 , x5 和人工变量 x6 , x7 ,利用两阶段法得到辅助线性规划 max w x6 x7 max z' 2x1 3x2 x3
x1
x2
x3
x4
x5
x6
x7
z'
5
0
1
最优化方法习题答案
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
第一讲最优化问题
第一讲:最优化问题例题:用一只平底锅煎鸡蛋,每次只能放两个,煎一个需要2分钟(规定正反面各需要1分钟)。
问煎三个至少需要多少分钟?【思路导航】先将两个鸡蛋同时放入锅中一起煎,1分钟后两个都熟了一面,这时可将一个取出,另一个翻过去。
再放入第三个,又煎了1分钟,将两面都煎好的那个取出,把第三个翻过去。
再将第一个放入,再煎1分钟就全部都好了。
所以,煎三个至少需要3分钟。
【练习题:】1、用一只平底锅做煎饼,每次能同时放两块饼,如果煎一块饼需要4分钟(正反两面各需2分钟),问煎2004块饼至少需要几分钟?2、家里来了客人,妈妈要给客人沏茶,洗水壶要一分钟,烧开水要10分钟,洗茶杯要2分钟,取茶叶要1分钟,泡茶要2分钟。
为了让客人早点喝到茶,你来设计,如何安排所需时间最少?3、老师分别要和甲、乙、丙三个人谈话,和甲谈要8分钟,和乙要谈5分钟,和丙要谈6分钟。
甲、乙、丙三位同学同时到办公室,老师应该如何安排和他们谈话的次序,使他们三人所花的总时间最少?总时间是多少分钟?4、用34厘米的钢丝围成一个长方形,长和宽的长度都是整厘米数,围成的长方形的面积最大是多,j hbtyy 6少?第二讲:巧妙求和【知识讲解】若干个数排成一列,称为数列。
数列中的每一个数称为一项,其中第一项称为首项,最后一项称为末项。
数列中的个数称为项数。
从第二项开始,后项与其相邻的前项之差都相等的数列称为等差数列,后项与前项的差称为公差。
我们需要记住三个公式:通项公式:第N项=首项+(项数—1)×公差项数公式:项数=(末项—首项)÷公差+1求和公式:总和=(首项+末项)×项数÷2【练习题】1、有一个数列4、10、16、……52,这个数列共有多少项呢?(提示:项数公式:项数=(末项—首项)÷公差+1)2、有一个等差数列3,7,11,15,……,这个等差数列的第100项是多少?提示:第N项=首项+(项数—1)×公差3、有这样的一个数列1,2,3,4,……,99,100,请你求出这数列各项相加的和。
天津大学《最优化方法》复习题含答案
天津大学《最优化方法》复习题(含答案)天津大学《最优化方法》复习题(含答案)第一章 概述(包括凸规划)一、 判断与填空题1 )].([arg )(arg m in m axx f x f nnRx Rx -=∈∈ √2 {}{}.:)(min :)(max nnR D x x f R D x x f ⊆∈-=⊆∈ ⨯3 设.:R R D f n →⊆ 若nR x∈*,对于一切nR x ∈恒有)()(x f x f ≤*,则称*x 为最优化问题)(minx f Dx ∈的全局最优解. ⨯4 设.:R RD f n→⊆ 若Dx∈*,存在*x 的某邻域)(*x N ε,使得对一切)(*∈x N x ε恒有)()(x f x f <*,则称*x 为最优化问题)(minx f Dx ∈的严格局部最优解. ⨯5 给定一个最优化问题,那么它的最优值是一个定值. √6 非空集合nR D ⊆为凸集当且仅当D 中任意两点连线段上任一点属于D . √7 非空集合nR D ⊆为凸集当且仅当D 中任意有限个点的凸组合仍属于D . √8 任意两个凸集的并集为凸集. ⨯ 9 函数RR D f n→⊆:为凸集D 上的凸函数当且仅当f -为D 上的凹函数. √10 设RRD f n→⊆:为凸集D 上的可微凸函数,Dx ∈*.则对D x ∈∀,有).()()()(***-∇≤-x x x f x f x f T⨯ 11 若)(x c 是凹函数,则}0)( {≥∈=x c R x D n是凸集。
√12 设{}kx 为由求解)(minx f Dx ∈的算法A 产生的迭代序列,假设算法A 为下降算法,则对{},2,1,0∈∀k ,恒有)()(1kk x f x f ≤+ .13 算法迭代时的终止准则(写出三种):_____________________________________。
14 凸规划的全体极小点组成的集合是凸集。
√15 函数RR D f n→⊆:在点kx 沿着迭代方向}0{\n kR d∈进行精确一维线搜索的步长kα,则其搜索公式为 .16 函数RRD f n →⊆:在点kx 沿着迭代方向}0{\n kR d∈进行精确一维线搜索的步长kα,则=+∇k T k k k d d x f )(α 0 .17 设}0{\n kR d∈为点nkR D x⊆∈处关于区域D 的一个下降方向,则对于0>∀α,),0(αα∈∃使得.D d x k k∈+α⨯二、 简述题1 写出Wolfe-Powell 非精确一维线性搜索的公式。
最优化方法习题1答案
《最优化方法》(研究生)期末考试练习题答案二.简答题1.;0, ,843 ,2 2-,3 34 s.t. ,95- min 2121212121≤=--≥+≥++y y y y y y y y y y 2.,065 6143≥+x x (以1x 为源行生成的割平面方程) 注意:在1x 为整数的情况下,因为3x ,04≥x ,该方程自然满足,这是割平面的退化情形,2141 41 43≥+x x (以2x 为源行生成的割平面方程)3.6648.31854.1*2)854.1()(2131.01146.1*2)146.1()(854.13*618.00)(618.0146.13*382.00)(382.03,031311111111111=+-==+-==+=-+==+=-+===μϕλϕμλa b a a b a b a 0.927.21.8540]1.8540[854.1,0)()(,*2211=+===≤x b a 近似的最优解:。
,初始的保留区间为即:。
所以,不经计算也可以看出事实上μϕλϕ4.令1.01.0)(4.04.0)(11)(7.27.2)(222222221)2(*111)1(*111)0(*121)1(*11-=-=-=-=-=-=-=-=-------x x x x x x x e x e x x f ex ex x f x e x x f e x e x x f拟合问题等价于求解下列最小二乘问题:∑=412))((mini ix f三.计算题1.分别用最速下降方法和修正的牛顿法求解无约束问题 22214)(min x x x f +=。
取初始点()()Tx 2,21=,.1.0=ε()().1641642,2821121⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫⎝⎛=∇=⎪⎪⎭⎫⎝⎛=∇d f x x x f T方向为:从而最速下降法的搜索,在初始点,解:()()()()直至满足精度。
继续迭代方向为:从而最速下降法的搜索,,在从而求解得到:其中满足最优步长,.48/6565/19248/65-65/19265/6,65/96)65/6,65/96((-4,-16)*130/172,2 130,/17.)162(4)42()162,42()()(min )(122221)1(1)1(1*)1(*⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=∇-=-=+==-+-=--=++=+d f x x f d x f d x f d x f TTT Tλλλλλλλλλλ()()2-2- 1648/1002/1 8/1002/1,8002 2,21111⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∇-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==--f G d G G x T索方向为:从而修正的牛顿法的搜,在初始点()()()()即为所求的极小点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题一一、考虑二次函数f(x)=x x x x x x 2122212132+-++1) 写出它的矩阵—向量形式: f(x)=x Qx b x TT +21 2) 矩阵Q 是不是奇异的?3) 证明: f(x)是正定的 4) f(x)是凸的吗? 5) 写出f(x)在点x =)1,2(T处的支撑超平面(即切平面)方程解:1) f(x)=x x x x x x 2122212132+-++=⎪⎪⎭⎫ ⎝⎛x x 2121⎪⎪⎭⎫ ⎝⎛6222⎪⎪⎭⎫ ⎝⎛x x 21+⎪⎪⎭⎫ ⎝⎛-11T⎪⎪⎭⎫⎝⎛x x 21 其中x=⎪⎪⎭⎫ ⎝⎛x x 21 ,Q=⎪⎪⎭⎫ ⎝⎛6222 , b=⎪⎪⎭⎫⎝⎛-11 2) 因为Q=⎪⎪⎭⎫⎝⎛6222 ,所以 |Q|=6222=8>0 即可知Q 是非奇异的 3) 因为|2|>0,6222=8>0 ,所以Q 是正定的,故f(x)是正定的 4) 因为)(2x f ∇=⎪⎪⎭⎫ ⎝⎛6222,所以|)(2x f ∇|=8>0,故推出)(2x f ∇是正定的,即)(2x f ∇是凸的5) 因为)(x f ∇ =1)x 6x 1,2-x 2x (22121+++T,所以)(x f ∇=(5,11)所以 f(x)在点x 处的切线方程为5(21-x )+11(12-x)=0二、 求下列函数的梯度问题和Hesse 矩阵 1) f(x)=2x 12+x x x xx 23923121+++x x x 2322+2) f(x)=ln(x 12+x x x 2221+)解: 1) )(x f ∇= (,94321x x x ++ 26321+++x x x , x x 219+))(2x f ∇=⎪⎪⎪⎭⎫ ⎝⎛0191619142) )(x f ∇=(x x x x x x 112221221+++ ,x x x x xx 112221221+++))(2x f ∇=⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----------++++++++)()()()(2221212222212142221214222121222222121222212122221212212122x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 三、设f(x)=x x x x x x x 323223322122--+++,取点)1,1,1()1(Tx =.验证d )1(=(1,0,-1)是f(x)在点x)1(处的一个下降方向,并计算min >t f(x )1(+t d )1() 证明: )(x f ∇=)124,123,x 2(233221-+-+x x x x T)5,4,2()(1Tx f =∇d )(1x f ∇=(1,0,-1)⎪⎪⎪⎭⎫ ⎝⎛542= -3<0所以d)1(是f(x)在x)1(处的一个下降方向f(x)1(+td)1()=f((1+t,1,1-t)) =433)1(1)1(221(222)1()1+-=----+++-+t t t t t t∇f(x )1(+t d )1()=6t-3=0 所以t=0.5>0所以min >t f(x )1(+t d )1()=3*0.25-3*0.5+4=3.25 四、设aj,b ,cj(j=1,2,….,n )考虑问题Min f(x)=∑=nj jj xc 1s.t. b nj jjxa =∑=10≥xj(j=1,2,….,n)1) 写出其Kuhn Tuker 条件2) 证明问题最优值是])([12112∑=n j j j b c a 解:1)因),....,1(n j x j = 为目标函数的分母故0>xj所以λ*j(j=1,…,n )都为0所以Kuhn Tuker 条件为 0)()(=∇+∇x h x f μ即 ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---x c x c x c n n 2222211 +⎪⎪⎪⎪⎪⎭⎫ ⎝⎛a a a n 21μ=0 2)将ac x jj j μ=代入 h(x)=0 只有一点得∑=∑==⇒=nj jjn j j j b n c a bca 122)(1μ故有acc a x jj nj jjjb ∑==1所以最优解是])([12112∑=nj j j b c a 五、使用Kuhn Tuker 条件,求问题min f(x)=)2()1(2122--+x xs.t. 0,021212112≥≥=+=-x x x x x x的Kuhn Tuker 点,并验证此点为问题的最优解解:x=(1/2,3/2) 0≠ 故λ*1,λ*2=0则 0)()()(2211=+∇+∇x x x f h h μμ即0111142222121=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛--μμx x ⇒1,021-==μμ而⎪⎪⎭⎫ ⎝⎛=∇2002)(2x f 故08)(2>=∇x x f x T 即其为最优解六、在习题五的条件下证明 L(μλ,,x *)),,(),,(μλμλ*****≤≤x L L x其中 L (x,μλ,)=f(x)+)2()1(2112-++--xx x x μλ证明:L(μλ,,x*)=f(x *)+)2()1(2112-++--****x x x x μλ= f(x *) = f(x *)+λ*)1(12--**x x +μ*-+**x x 21(2)= ),,(μλ***x L= f(x *))2()1()()(2112-++--+=≤**x x x x x f x f μλ= μλ**,,(x L )习题二一、设f(x)为定义在区间[a,b]上的实值函数,x*是问题min{f(x)|a b x ≤≤}的最优解。
证明:f(x)是[a,b]上的单谷函数的充要条件是对任意x x x x b a 2121],,[,≠∈满足f(x x 21)1(λλ-+)<max{f(x 1),f(x 2)},)1,0(∈λ证明:不妨设x 1<x 2,则x 1<xx x 221)1(<-+λλ“必要性” 若x x x *<-+21)1(λλ则由单谷函数定义知)())1((121x x x f f <-+λλ故有)}(),(max{))1((2121x x x x f f f <-+λλ“充分性” 由x1,x 2的任意性取x 1=x *时,f(x 2)>f(x 1)则x2>x x 21)1(λλ-+>x 1=x *且f(x x 21)1(λλ-+)<f(x 2)若取 x 2=x *时, f(x 1)>f(x 2)x *=x 1<x x 21)1(λλ-+<x 2且 f(x x 21)1(λλ-+)<f(x 1)满足单谷函数的定义二、设x 1<x 2,0)(,0)(21>'<'x x f f1)证明:满足条件 )()(),()(),()(221111x x x x x x f f f '=''='=ϕϕϕ的二次函数)(x ϕ是(严格)凸函数2)证明:由二次插值所得f(x)的近似极小值点(即)(x ϕ的驻点)是)()()()(122122x x x x x x f f f x '-''--=或者)()()()(121121x x x x x x f f f x '-''--=证明:1)设)(x ϕ=c bx ax++2(0≠a )则 b ax x +='2)(ϕ由)(2)()(2)(222111x x x x x x f b a f b a '=+=''=+='ϕϕ得)())()(()(,0)(2)()(1212111212x x x x x x x x x x f f f b f f a -'-'-'=>-'-'=或 )())()(()(121222x x x x x x f f f b -'-'-'=故1)得证2))(x ϕ的驻点为)()()()(2121121x x x x x x f f f abx '-''--=-=或-=xx 2)()()()(12212x x x x x f f f '-''-三、设f(x)=0,21>=++Q c x Qx Q b x T TT 试证:共轭梯度法的线性搜索中)()()()()()(0min d t x d x k k k k k t f t f +=+≥,有dd dg t k Tk Tk k Q k )()()()(-=,其中)()(x gk kf ∇=证明:由已知 ,得b Qx x f +=∇)( 令=)(t ϕ)()()(d xk k t f +为t 的凸二次函数。
要使t k 是)(t ϕ的极小点即为驻点,故满足0)(='tk ϕ而∇=')(t k ϕ)()()(dxk k t f +dk )( = db d t x Q k T k k )(])([)()(++=d d tQ b x Q k Tk k )(][)()(++=d d dg k Tk T kQ k t )())((+)(故有0)(()()=+dd t dg k Tk k T kQ k )(得 dd dg t k Tk T kkQ k )()()()(-=四、用共轭梯度法求解: min f(x)=x x x x x 121222122123--+ , x R 2∈ 取初始点)4,2()1(-=Tx解:易知⎪⎪⎭⎫ ⎝⎛--=1113A ⎪⎪⎭⎫⎝⎛-=02b 第一次迭代: ),23(1221)(x x x x Tx f ---=∇)6,12()(11-=∇=Tx gf)6,12()()1()1(-=-∇=Tx df线性搜索得步长1756121113)6,12(612)6,12()1()1()1(11)(=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛---=-=dd d g A TTα 从而d xx)1(1)1()2(α+==⎪⎪⎭⎫ ⎝⎛3826171 第二次迭代:)1712,176()()2(Txf =∇ =g 2)1712,176(T=β12981)1()1()1(2)(=-d d d g A A TT⎪⎪⎪⎪⎭⎫⎝⎛--=+-=28921028990)1(12)2(d g d β 线性搜索得步长:7.12=α⎪⎪⎭⎫ ⎝⎛=+=11)2(2)2()3(dxxα)0,0()()3(3Tx gf =∇=所以 最优解为)1,1(*Tx=五、用拟Newton 法求解:min R x x x x x x x f 21212221,422)(∈--+=取初始点)1,1()1(Tx=解:1)DFC 法取初始对称矩阵 ⎪⎪⎭⎫ ⎝⎛=10011H 第一次迭代: 计算得)2,4(1-=Tg,)2,4(111-=-=Tg H d经一维线性搜索得:α1=0.25)25.0,2(1112Td x x =+=α)5.0,1(1-=Tδ)4,3(1-=Ty)2,1(2--=Tg2.011111==yH y yT T r δ置⎪⎪⎭⎫⎝⎛==2.0002.011H H r⎪⎪⎭⎫⎝⎛--=-+=472.0704.0204.0728.01111111111112yH y Hy y H y y H H TTT Tδδ 第二次迭代 )24.0,32.0(222Tg H d =-=经一维线性搜索得:α1=6.25)2,4(2223Td x x =+=α)0,0(3Tg=故最优解为:)2,4(3*Tx x ==2)BFGS 法取定初始对称矩阵⎪⎪⎭⎫⎝⎛=10011H第一次迭代: 计算得)2,4(1-=Tg,)2,4(111-=-=Tg H d经一维线性搜索得:α1=0.25)25.0,2(1112Td x x =+=α同DFP 法,初始修正矩阵⎪⎪⎭⎫⎝⎛=2.0002.01H⎪⎪⎭⎫ ⎝⎛=--++=14.002.002.036.0)1(11111111111111112yHyy H yyH y H HT TT T Tδδδδδδ 第二次迭代:)3.0,4.0(222Tg H d =-=经一维线性搜索得:52=α)2,4(2223Td x x =+=α)0,0(3Tg=故最优解为:)2,4(3*Tx x==习题三1、 给定问题min x x x x x x x f 212221211462)(--++=s.t. 0,0,032232121321≥≥≥≤+-=++x x x x x x x x取初始点)0,1,1()1(Tx =,用简约梯度法求其最优解解:约束条件为 0,0,032232121321≥≥≥≤+-=++x x x x x x x x则)0,1,1()1(T x=,⎪⎪⎭⎫⎝⎛-=10210111A)0014462(2121)(-+-+=∇x x x x Tx f()00931--=Tg{}211=I ⎪⎪⎭⎫ ⎝⎛-=2111B ⎪⎪⎭⎫⎝⎛=1001N)(1)()(x f x f BTN NN B g∇∇--==⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛25933131313200 ⎪⎪⎭⎫ ⎝⎛-=40dN⎪⎭⎫⎝⎛-=-=-34341TNB d B d N)403434()1(--=Td ()d d x d x T f f )1()1()1()()1()1()(αααϕ+∇=+'='=0324964=-α 得89=α21}42min{max =--=α 得 21},min{max 1==ααα )003531()1(1)1()2(Td x x =+=α⎪⎭⎫⎝⎛--=0073112Tg}2,1{2=I ⎪⎪⎭⎫ ⎝⎛-=2111B ⎪⎪⎭⎫ ⎝⎛=1001N⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=91094373113131313200gN⎪⎪⎭⎫ ⎝⎛=00d N⎪⎪⎭⎫ ⎝⎛=-=-001d B d NB N0)2(=d故)003531()2(Tx =为问题的K-T 点2、 用梯度投影法求解问题min )3()2(21)(22-++=x x x fs.t. 40003322121≤≤≥=--x x x x取初始点()13)1(Tx =解: )62,42(21)(-+=∇x x Tx f迭代(1) )4,10(1-=Tg}1{1=I⎪⎪⎭⎫ ⎝⎛-=321AT投影矩阵⎪⎪⎪⎪⎭⎫ ⎝⎛=-=-13413613613911111)(A A A A T I P T )1344,1366(1)1(--=-=Tg d P)313441()213663(22)1()1()()(--+-+=+=ααααϕd xf0413881013132)(=--+-='αααϕ 11039=α4413}4413,6639min{max ==α 故4413},min{max 1==ααα)0,23()1(1)1()2(Tdxx=+=α)6,7(2-=Tg}3,1{2=I故⎪⎪⎭⎫ ⎝⎛-=13022AT 投影矩阵⎪⎪⎭⎫ ⎝⎛=-=-000022212)(A A A A T I P T)0,0(2)2(Tg dP =-=令)29,27()(221)2(22Tg A A A uT ==-故)0,23()2(Tx=为其 K-T 点3、用可行方向法求解问题min )1()2(21)(22--+=x x x fs.t. 0,022742212121≥≥≤-≤+x x x x x x取初始点 )0,0()1(Tx =解:)22,42(21)(--=∇x x Tx f迭代一:)2,4()()1(--=∇Txf有效约束}4,3{1=I确定下降方向min -4d d212-s.t. 1121≤≥≥≤-dd d ii=1,2解得121==dd 且其最优值为-6,即x)1(处的搜索方向)1,1()1(Td=线性搜索 562)()(2)1()1(+-=+=αααϕαd xf064)(=-='ααϕ 23=⇒α 而67}2,67min{max==α 67}67,23min{1==α)67,67()1(1)1()2(Td x x =+=α迭代2:)31,35()()2(-=∇Tx f 有效约束}1{1=I 确定下降方向min -35d d 2131+s.t.142121≤≥+≤-dd d ii=1,2得)1,1()2(-=Td且其最优值为-2线性搜索 181322)()(2)2()2(+-=+=αααϕαd xf 024)(=-='ααϕ 21=⇒α 而185}67,185min{max==α 185}185,21min{1==α)98,913()2(2)2()3(Tdxx =+=α迭代3:)92,910()()3(--=∇Tx f有效约束}2{1=I 确定下降方向min -910d d 2192-s.t.12121≤≥-≤-d d d ii=1,2得)1,21()3(Td = ,其最优值为-97线性搜索 81269745)()(2)3()3(+-=+=αααϕαd x f 09725)(=-='ααϕ 1445=⇒α 而 67}2,67min{max ==α91}91min{3==α)1,23()3(2)3()4(Tdxx =+=α迭代 4:)0,1()()4(-=∇Tx f有效约束}2,1{1=I确定下降方向min -d 1s.t. 10204212121≤≤-≤+≤-d d d d d ii=1,2得)0,0()4(Td = ,其最优值为0=x *)1,23()4(Tx=为K-T 点。
