北航最优化方法大作业参考
北航最优化方法大作业参考
1 流量工程问题1.1 问题重述定义一个有向网络G=(N,E)，其中N是节点集，E是弧集。
令A是网络G的点弧关联矩阵，即N×E阶矩阵，且第l列与弧里(I,j)对应，仅第i行元素为1，第j行元素为-1，其余元素为0。
再令b m=(b m1,…,b mN)T，f m=(f m1,…,f mE)T，则可将等式约束表示成：Af m=b m本算例为一经典TE算例。
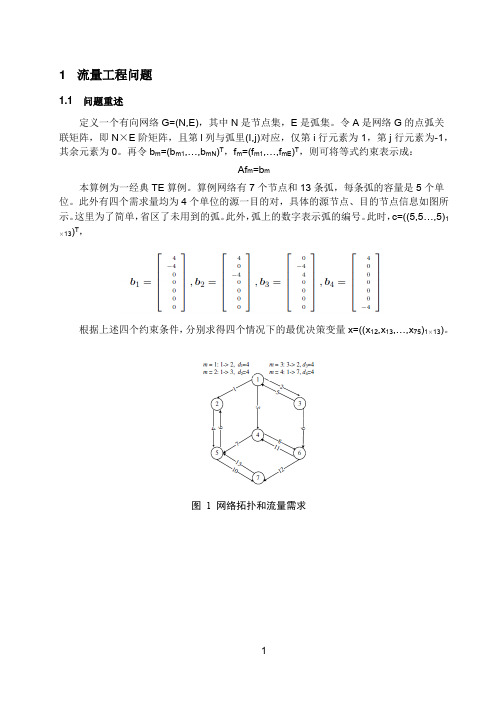
算例网络有7个节点和13条弧，每条弧的容量是5个单位。
此外有四个需求量均为4个单位的源一目的对，具体的源节点、目的节点信息如图所示。
这里为了简单，省区了未用到的弧。
此外，弧上的数字表示弧的编号。
此时，c=((5,5…,5)1 )T，×13)。
根据上述四个约束条件，分别求得四个情况下的最优决策变量x=((x12,x13,…,x75)1×13图 1 网络拓扑和流量需求1.2 7节点算例求解1.2.1 算例1（b1=[4;-4;0;0;0;0;0]T）转化为线性规划问题：Minimize c T x1Subject to Ax1=b1x1>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x1*=[4 0 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x1=201.2.2 算例2（b2=[4;0;-4;0;0;0;0]T）Minimize c T x2Subject to Ax2=b2X2>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x2*=[0 4 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x2=201.2.3 算例3（b3=[0;-4;4;0;0;0;0]T）Minimize c T x3Subject to Ax3=b3X3>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x3*=[4 0 0 0 4 0 0 0 0 0 0 0 0]T对应的最优值c T x3=401.2.4 算例4（b4=[4;0;0;0;0;0;-4]T）Minimize c T x4Subject to Ax4=b4X4>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x4*=[4 0 0 4 0 0 0 0 0 4 0 0 0]T对应的最优值c T x4=601.3 计算结果及结果说明1.3.1 算例1（b1=[4;-4;0;0;0;0;0]T）算例1中，由b1可知，节点2为需求节点，节点1为供给节点，由节点1将信息传输至节点2的最短路径为弧1。
北航最优化大作业
北航最优化大作业1.引言旅行商问题（Traveling Salesman Problem，TSP）是一种经典的组合优化问题，目标是找到一条路径，使得旅行商从起点出发，途经所有城市一次后返回起点，并且总路径长度最短。
TSP问题具有NP-hard的特性，寻找最优解是一个非常具有挑战性的任务。
本文将基于禁忌算法，探讨TSP问题的求解方法。
2.禁忌算法简介禁忌算法是一种基于局部的元启发式算法，通过在过程中禁止一定的动作来跳出局部最优解，以期望获得更好的全局最优解。
算法通过引入禁忌表和禁忌长度等机制，避免过程中陷入局部最优解。
3.TSP问题的数学建模假设有n个城市，城市之间的距离可以表示为一个n×n的距离矩阵D。
TSP问题的目标可以定义为：min ∑_(i=1)^n ∑_(j=1)^(n) D_ij*x_ijs.t. ∑_(i=1)^n x_ij=1,∑_(j=1)^n x_ij=1,∀i ≠ jx_ij∈{0,1}, 1≤i,j≤n其中x_ij表示城市i与城市j之间的路径是否存在，1表示存在，0表示不存在。
4.禁忌算法在TSP问题中的应用（1）初始化选取一个起始解x，计算其路径长度f(x)。
将x设为当前解x_best，将f(x)设为当前解的最优值f_best。
（2）选择邻域解选择当前解的一个邻域解x'，使得x'与x只有一个位置上的交换。
通过随机选择两个位置，进行交换操作。
（3）禁忌判断如果邻域解x'的路径长度f(x')小于当前解的最优值f_best，则更新f_best为f(x')，并将x'设为新的当前解。
否则，比较x'与当前解的禁忌情况。
（4）禁忌更新如果x'未在禁忌表中，或者禁忌表中对应的禁忌周期已过，则将x'设为新的当前解。
否则，选择一个路径长度较短的邻域解x''，即使其路径长度f(x'')大于f_best。
北航最优化大作业
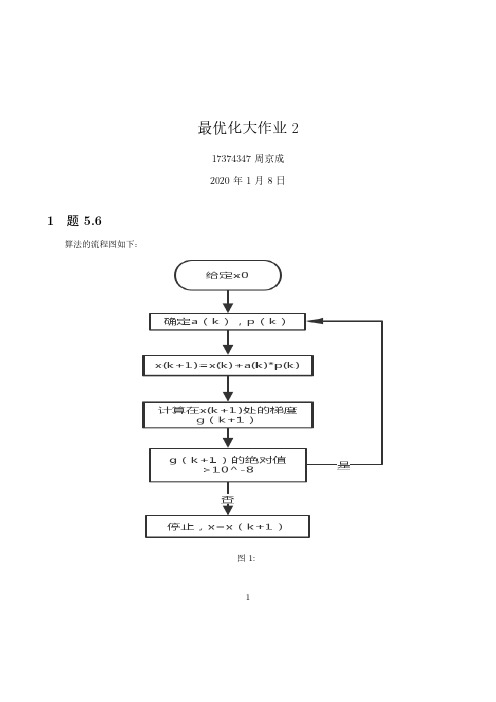
图 18: 前两行为迭代点 xk, 后面一行为梯度的 2 范数，显然，前两行行都趋于无穷大，发散，梯度的 2 范数 趋于 13.4536（从 matlab 变量表格中得到）。 4: 初始点 x(0) = (10, 20)T 前两行为迭代点 xk, 后面一行为梯度的 2 范数，显然，前两行行都趋于无穷大，发散，梯度的 2 范数 趋于 13.4536（从 matlab 变量表格中得到）。
33
图 57: 7、9、11、13 迭代停止测试。
当 n=50 时，解 x*=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1] 判断矩阵：
图 58: 可以发现，没有发现负曲率的情况，第 1 和第 2 次的迭代到了边界，第 4、6、8、10、12、14、16 次 迭代到了边界。
▽f (x) = g = −400x1(x2 − x21) + 2x1 − 2
200(x2 − x21)
[
]
▽2f (x) = G = 1200x21 − 400x2 + 2 −400x1
−400x1
200
14
4.1 最速下降法
代码和流程图：
图 33:
图 34: 15
4.1.1 初始点为 (1.2,1.2)
++
)
x1 + x12 − 100
x11
x1
−
50 1
−
x2
−10 − µ(
++
)
x1 + x2 − 100 x2 −x1 + 50 + x2
北航最优化方法作业答案co_lcp
第 8 章 约束优化：线性约束规划
数学规划基础
LHY-SMSS-BUAA
线性等式约束规划
f (x) 是 n 元函数；ai 是 n 维常向量； bi 是常数 有解时 凸规划 ⊙ f(x) 是凸函数 KKT点即为全局极小点 f(x) 严格凸 ：有唯一的极小点 ⊙ f(x) 是非凸函数 可能存在不是全局解的局部解 找全局解是NP-难问题 引入矩阵 ，使得 且 非奇异 解的情况： 无可行解、无界、有解
约束优化：线性约束规划
Constrained Optimization: Linearly Constrained Programming
第 8 章 约束优化：线性约束规划
数学规划基础
LHY-SMSS-BUAA
二次规划(quadratic programming)
G 是 n 阶对称方阵 d，ai 是 n 维常向量 解的情况：无可行解、无界、有解 有解时： ⊙ G半正定 KKT点即为全局极小点 凸规划 G 正 定 ：有唯一的极小点 ⊙ G不定 可能存在不是全局解的局部解 找全局解是NP-难问题
第 8 章 约束优化：线性约束规划
数学规划基础
LHY-SMSS-BUAA
等式约束二次规划－广义消元法(续)
第 8 章 约束优化：线性约束规划
数学规划基础
LHY-SMSS-BUAA
第 8 章 约束优化：线性约束规划
数学规划基础
LHY-SMSS-BUAA
实用二次规划算法概述
⊙ 经典的积极集法(active-set methods)
有价证券的组合优化(续)
Markowitz引入风险容许参数(risk tolerance parameter)
找出“最优的”证券投资组合！ ⊙ 参数 ，设定值依赖于投资者的个人偏好
最优化方法与应用大作业(一)最速下降法
最优化方法与应用大作业（一）
---最速下降法部分：
1.问题描述:
用梯度下降法求解以下优化问题
min f(x)=(x1+10*x2)^2+5(x3-x4)^2+(x2-2*x3)^4+10*(x1-x4)^4
2.编程感想：
该算法需要计算Hesse矩阵，C语言在向量运算时没有Matlab方便，所以手工完成了理论计算，再输入，破坏了程序的移植性。
同时，实验表明当初始值离理想点较远且精度要求较高时，最速下降法的收敛速率极慢，迭代几乎不可能完成，这对初值的选取提出了一定限制。
3.结果分析：
编译界面（Mac os X，Xcode环境）
输入参数（设定为(0.1,0.2,0.3,0.4)）：
结果（此处列出每次迭代结果）。
明显的看到，最速下降法的收敛较慢，最终结果接近理论值（F（0，0，0，0）=0）所以该结果可以满意。
4.算法代码见下页
西安电子科技大学电子工程学院020951
李骏昊02095005。
最优化大作业2
最优化大作业2⚫姓名：cxf⚫班级学号：****20****⚫学院：******学院⚫选择方式：方式4——撰写课程小论文⚫题目来源：附录二备选问题（计算机通信网）中文献[9]——F. Kelly. The Mathematics of Traffic in Network. Princeton University Press, 2005.⚫工作方式：独立完成⚫完成时间：2020年12月15日交通网络中的数学优化问题研究cxf（北京航空航天大学 ******学院， 北京 100191）摘要 由于交通网络流中分散控制的程度差异，人们往往需要寻求一种解决方案对系统进行继续扩展和优化。
车流量控制问题一直是交通网络所面临的重要挑战，也是研究者研究的重点。
本论文用微积分来描述拥堵如何依赖于车流量，以Wardrop 均衡和Braess’s 悖论等理论为基础，建立车流分配控制问题的数学模型，并利用Lingo 优化软件对原始问题进行求解。
最后，由优化模型的结果可知，当网络达到均衡状态时不一定是最优的车流分配方案，且达到最优解状态时能够使通信网络中的分散控制能够表现的更好。
但是，这最优方案需强制执行，否则自私车辆又会选择最短的路径，即形成新的均衡状态。
关键词 交通网络，车流分配， Wardrop 均衡， 优化模型.1.问题背景许多网络中都普遍存在着拥堵现象，其拥堵的发生方式和原因不尽相同。
然而，流量通过网络的流动方式是不同用户之间微妙而复杂交互的结果。
例如，在交通网络中，每位驾驶员都会尝试选择最方便的路径，以便节省时间和开销，而这一选择将取决于驾驶员期望在不同道路上遇到的延迟，且这些延迟反过来取决于其他人对路径的选择。
这种相互依赖关系，使得人们很难预测系统变化的影响，例如建造新的道路或在某地方实行收费等。
在电话网、互联网和交通网等大型网络系统中，主要的实际问题就是控制权的分散程度不同。
发展至今，这种分散式节点之间的流量控制方法已经显示出紧张的迹象，如果网络作为一个整体要继续扩展和进化，则需要进一步优化网络流量控制。
最优化方法大作业模板
命题人：审核人：大作业学期：至学年度第学期课程：最优化方法课程代号：签到序号：使用班级：姓名：学号：题号一二三四五六七八九十总分得分一、（目标1）请从以下6种算法中任选一种，说明算法的来源、定义、基本思想和优缺点，并给出算法步骤（包含算法流程图）和例子（包含程序与运算结果）。
①禁忌搜索算法；②模拟退火算法；③遗传算法；④神经网络算法；⑤粒子群算法；⑥蚁群算法。
二、（目标1）某工厂生产甲、乙两种产品，已知生产这两种产品需要消耗三种材料A 、B 和C ，其中生产过程中材料的单位产品消耗量和总量，以及单位产品的利润如下表所示。
该如何配置安排生产计划，使得工厂所获得的利润最大？材料甲乙资源总量材料A （Kg ）3265材料B （Kg ）2140材料C （Kg ）0375单位利润（元/件）15002500-（1）要保证工厂利润的最大化，写出相应的生产计划数学模型；（2）根据对偶理论，直接写出该线性规划的对偶问题；（3）采用单纯形表法对该该线性规划问题进行求解，写出详细的计算过程；（4）采用Matlab 软件对该线性规划问题进行求解，写出完整的源程序，并给出程序运行结果；（5）讨论当材料B 的资源总量发生变化时，该线性规划问题的最优解会如何变化？课程目标目标1……题号一、二、三、四、五……分值20、25、20、20、15……得分得分三、（目标1）求解下列无约束非线性规划问题（1）采用黄金分割法求解：min 4()24f x x x =++。
初始区间为[-1.0]，精度为ε=10-4。
（要求：采用黄金分割法进行Matlab 编程求解，写出源程序，并给出运行结果，列出迭代过程的数据表格）（2）采用阻尼牛顿法求解：222121212min (,)4f x x x x x x =+-。
分别取两个初始点：x A =(1,1)T ，x B =(3,4)T 。
（要求：采用阻尼牛顿法进行Matlab 编程求解，并给出运行结果，列出迭代过程的数据表格）四、（目标1）求解下列约束非线性规划问题：22112212121212min ()23532..00f x x x x x x x x x x x s t x x =-+--+≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩（1）采用罚函数法进行求解，需写出具体计算过程；（2）采用二次规划方法进行求解，需写出具体计算过程，并进行MATLAB 编程，写出源程序和运算结果；五、（目标1）（1）某商店在未来的4个月里，准备利用它的一个仓库来专门经营某种商品，仓库的最大容量为1000单位，而且该商店每月只能出卖仓库现有的货。
北航机械优化大作业
现代机械优化设计授课老师：王春洁2014-12-17目录第一部分一、一维优化方法 (2)1. 进退法 (2)2. 格点法 (2)3. 牛顿法 (2)4. 二次插值 (3)应用原则： (4)二、多维无约束优化 (4)1. 梯度法 (4)2. 二阶牛顿法与阻尼牛顿法 (5)3. DFP变尺度法 (6)4. 单纯形法 (6)三、多维约束优化 (6)1. 随机方向搜索法 (8)2. 可行方向法 (8)3. 惩罚函数法 (8)第二部分一、采用有约束多维优化方法解决箱梁模板的设计问题 (10)问题的描述 (11)多维约束优化 (14)总结与致谢 (18)参考文献 (19)第一部分本部分为简述学过的优化算法（一维，多维无约束，多维有约束）的选择方法及应用原则。
一、 一维优化方法1. 进退法由单峰函数的性质可知，在极小点m x 左边函数值应严格下降，而在极小值右边函数值应严格上升。
因此，可从某一个给定的初始点0x 出发，以初始步长0h 沿着函数值的下降方向，逐步前进（或后退），直至找到相继的3个试点的函数值按“高---低---高”变化为止。
2. 格点法格点法是一种计算极其方便的方法，其迭代步骤可简要概括为把搜索区间等分成n 个点12,,n x x x …,，计算各个点对应的数值，取出函数值最小的点的横坐标m x ，之后，在m x 两侧取临点11,m m x x -+，作为新的区间并判断11m m x x eps +--<是否成立，倘若成立，则m x 就是最优解，对应的函数值m y 即为最优值；若不成立则以11[]m m x x -+为新区间重复以上过程直到满足条件为止。
3. 牛顿法牛顿法是用切线代替弧，逐渐逼近函数根值的方法。
当目标函数()f x 有一阶连续导数并且二阶导数大于零时，在曲线'()y f x =上作一系列切线，使之与x 轴的脚垫(0)(1)(2)(3),,,......x x x x 逐渐趋于'()0f x =的根*x 。
《最优化方法》参考答案及评分标准
《最优化方法》参考答案及评分标准1. 某文教用品厂用原材料白坯纸生产原稿纸、日记本和练习本三种产品。
该厂现有工人100人，每月白坯纸供应量为30 000 kg.已知工人的劳动生产率为：每人每月可生产原稿纸30捆，或生产日记本30打，或练习本30箱。
已知原材料消耗为：每捆原稿纸用白坯纸133kg,每打日记本用白坯纸1133kg,每箱练习本用白坯纸2263kg.又知每生产一捆原稿纸可获利2元，生产一打日记本获利3元，生产一箱练习本获利1元。
试确定：(a)现有生产条件下获利最大的方案；(b)如白坯纸的供应数量不变，当工人数不足时可招收临时工，临时工工资支出为每人每月40元，则该厂要不要招收临时工，招多少临时工最合适？ 解：（a ）分别用123,,x x x 代表原稿纸、日记本和练习本的每月生产量。
(2分) 建立线性规划模型(4分)⎪⎪⎩⎪⎪⎨⎧≥≤++≤++++0,3000038034031010030/30/30/32max 32,1321321321x x x x x x x x x x x x （b ）临时工影子价格高于市场价格，故应招收。
用参数规划计算确定招200人为最适宜。
（5分）2. 求解下列产销平衡的运输问题，表中列出的为产地到销地之间的运价。
(1)用左上角法、最小元素法、沃格尔法求初始基本可行解。
(2)由上面所得的初始方案出发，应用表上作业法求最优方案，并比较初始方案需要的迭代次解：3. 用动态规划求解下面的问题解：（1）建立动态规划模型：①阶段变量k=1,2,3。
(1分) ②状态变量s k 表示第k 阶段初各决策变量之积，则s 3=27。
(1分) ③决策变量x k 分别表示第k 阶段的x 的值 (1分) ④状态转移方程s k+1=s k /x k 。
(1分) ⑤指标函数v k (s k ,x k )表示第k 阶段的总成本，即x 1+x 2+…+x k (1分)由已知可得k k k k x x s v =),((1分)⑥基本方程为⎪⎩⎪⎨⎧=+=++≤≤0)()}(),({max )(441160s f s f x s v s f k k k k k x k k k (2分) （2）用动态规划的正向或反向推理算法求解可得：（12分）()()9)(min 333321==x f x x x评分标准：以上的推理过程，每一阶段的计算正确得3分（共3个阶段），其中，列写出s 或x 的范围得1分，列写出决策表得1分，列写出最优决策表得1分，每出现一处错误，扣0.5分，至扣完本项分值为止。
北航最优化方法大作业参考
北航最优化方法大作业参考旅行商问题是一个经典的组合优化问题，目标是找到一条最短路径，使得旅行商能够在访问所有城市后回到起始城市。
在实际应用中，旅行商问题有着广泛的应用，例如物流配送、城市规划等领域。
为了解决旅行商问题，我们可以采用启发式算法，其中一个常用的方法是遗传算法。
遗传算法是一种模拟自然进化过程的优化算法，通过模拟生物遗传的选择、交叉和变异等操作，逐步优化问题的解。
首先，我们需要对问题进行建模。
假设有N个城市，我们可以通过一个N*N的距离矩阵来表示各个城市之间的距离。
同时，我们需要定义一个染色体表示一条路径，其中每个基因表示一个城市的编号。
接下来，我们可以采用遗传算法来求解最优解。
遗传算法一般包括以下几个步骤：1.初始化种群：随机生成初始的染色体种群，每个染色体都表示一条路径。
2.适应度评价：根据染色体的路径长度来评估每个染色体的适应度，路径越短适应度越高。
3.选择操作：选择适应度较高的染色体作为父代，采用轮盘赌选择算法确定父代。
4.交叉操作：采用部分映射交叉算子对父代进行交叉操作，生成新的子代。
5.变异操作：对子代进行变异操作，以增加种群的多样性。
6.环境选择：根据适应度选择下一代种群，同时保留精英个体，避免解的丢失。
7.终止条件：当达到预设的迭代次数或者达到最优解时，终止算法。
通过以上步骤的迭代，我们可以逐步优化路径的长度，最终得到一条最短路径。
除了遗传算法，我们还可以尝试其他的优化算法，例如模拟退火算法、蚁群算法等。
这些算法在求解旅行商问题时都有一定的优势和适用性。
总结起来，旅行商问题是一个经典的组合优化问题，在北航最优化方法大作业中可以选择使用启发式算法来解决。
我们可以尝试使用遗传算法来求解最优路径，并根据实际情况选择合适的算法参数和终止条件。
通过不断地迭代和优化，我们可以得到一条最短路径，满足旅行商的需求。
以上是关于北航最优化方法大作业的参考内容，希望对你的写作有所帮助。
如果有其他疑问，欢迎继续提问。
最优化方法习题答案
x3
-M
0
0
0
5
-1
1
2
x4
x5
1+ 2 M
0
3
ห้องสมุดไป่ตู้
x2
1 3
1
x5
2 3
0
以 x1 为换入基， x5 作为换出基有
-1- M 3
1 3 1
3
-M
0
0
0
5
3
-1
1
1
3
x1
x2
x3
x4
x5
0
x2
0
x1
1
0
1
2
1
1
2
0
1
2
3
3 M
-5.5
2
2
1
1
1.5
2
2
3 3
0.5
22
以 x 4 换入， x 2 换出有
⑤因为 p2 , p4 线性相关， x 2 , x 4 不能构成基变量；
⑥因为 p3, p4 线性无关，可得基解 x(6) (0,0,1,1) ， z6 3 ；
所以 x(2) , x(4) , x(6) 是原问题的基可行解， x(6) 是最优解，最优值是 z 3 。
（2） max z x1 x2 2x3 x4 x5
x1 2x2 3x3 4x4 7 s.t.2x1 x2 x3 2x4 3
x1, x2 , x3, x4 0
解：易知
x1 的系数列向量
p1
1
2
，x 2
的系数列向量
p2
2
1
最优化方法课后习题答案
最优化方法课后习题答案最优化方法课后习题答案最优化方法是一门重要的数学学科，它旨在寻找给定问题的最佳解决方案。
在这门课程中，学生将学习各种最优化算法和技术，以解决不同类型的优化问题。
课后习题是巩固所学知识的重要方式，下面将为大家提供一些最优化方法课后习题的答案。
1. 线性规划问题的单纯形法是如何工作的？单纯形法是一种用于解决线性规划问题的常用方法。
其基本思想是通过不断迭代改进当前解决方案，直到找到最优解。
具体步骤如下：1) 初始解：选择一个可行解作为初始解，通常是通过求解一个相应的松弛问题得到。
2) 进入变量：选择一个进入变量，即使目标函数值增加最快的变量。
3) 离开变量：选择一个离开变量，即使约束条件仍然保持满足的变量。
4) 改进解：通过改变进入变量和离开变量的值，得到一个更好的解。
5) 终止条件：当无法找到更好的解时，算法终止。
2. 什么是凸优化问题？如何判断一个问题是否是凸优化问题？凸优化问题是指目标函数和约束条件都是凸函数的优化问题。
凸函数具有以下性质：1) 对于任意两个点x和y以及0≤λ≤1，有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)。
2) 对于任意两个点x和y以及0≤λ≤1，有g(λx+(1-λ)y)≤λg(x)+(1-λ)g(y)，其中g(x)表示约束函数。
要判断一个问题是否是凸优化问题，可以通过以下步骤：1) 检查目标函数和约束条件是否都是凸函数。
2) 检查约束条件是否满足凸集的定义，即对于任意两个点x和y以及0≤λ≤1，有λx+(1-λ)y满足所有约束条件。
如果以上两个条件都满足，则问题是凸优化问题。
3. 最小二乘法是如何解决无约束优化问题的？最小二乘法是一种常用的解决无约束优化问题的方法。
其基本思想是通过最小化目标函数和实际观测值之间的差距来找到最优解。
最小二乘法的步骤如下：1) 建立目标函数：根据实际观测值和模型假设，建立一个与待优化参数相关的目标函数。
2) 求解最优解：通过对目标函数求导，并令导数等于零，求解出最优解。
结构优化设计大作业(北航)
《结构优化设计》大作业报告实验名称: 拓扑优化计算与分析1、引言大型的复杂结构诸如飞机、汽车中的复杂部件及桥梁等大型工程的设计问题，依靠传统的经验和模拟实验的优化设计方法已难以胜任，拓扑优化方法成为解决该问题的关键手段。
近年来拓扑优化的研究的热点集中在其工程应用上，如: 用拓扑优化方法进行微型柔性机构的设计，车门设计，飞机加强框设计，机翼前缘肋设计，卫星结构设计等。
在其具体的操作实现上有两种方法，一是采用计算机语言编程计算，该方法的优点是能最大限度的控制优化过程，改善优化过程中出现的诸如棋盘格现象等数值不稳定现象，得到较理想的优化结果，其缺点是计算规模过于庞大，计算效率太低;二是借助于商用有限元软件平台。
本文基于matlab 软件编程研究了不同边界条件平面薄板结构的在各种受力情况下拓扑优化，给出了几种典型结构的算例，并探讨了在实际优化中优化效果随各参数的变化，有助于初学者初涉拓扑优化的读者对拓扑优化有个基础的认识。
2、拓扑优化研究现状结构拓扑优化是近20年来从结构优化研究中派生出来的新分支，它在计算结构力学中已经被认为是最富挑战性的一类研究工作。
目前有关结构拓扑优化的工程应用研究还很不成熟，在国外处在发展的初期，尤其在国内尚属于起步阶段。
1904 年Michell在桁架理论中首次提出了拓扑优化的概念。
自1964 年Dorn等人提出基结构法，将数值方法引入拓扑优化领域，拓扑优化研究开始活跃。
20 世纪80 年代初，程耿东和N. Olhoff在弹性板的最优厚度分布研究中首次将最优拓扑问题转化为尺寸优化问题，他们开创性的工作引起了众多学者的研究兴趣。
1988年Bendsoe和Kikuchi发表的基于均匀化理论的结构拓扑优化设计，开创了连续体结构拓扑优化设计研究的新局面。
1993年Xie.Y.M和Steven.G.P 提出了渐进结构优化法。
1999年Bendsoe和Sigmund证实了变密度法物理意义的存在性。
北航最优化方法作业答案co_theory
原始问题
min-max问题是研究对偶问题的基础！各种对偶的区别： 的定义方式不同！ 原始问题(primal problem)
◎ 前提: 两人采取理性行为 不管对方采取何种策略，该行为都能保证自己的最大获益 该行为都能保证自己的最大获益 －不管对方采取何种策略 Peter: 选 最多要支付 Harriet： 选 最少收到 需要解决的问题： max-min问题←→对偶问题
第 7 章 约束优化：理论 数学规划基础 LHY‐SMSS‐BUAA 第 7 章 约束优化：理论 数学规划基础 LHY‐SMSS‐BUAA
4
线性规划的对偶理论
线性规划的对偶理论： 原始问题←→对偶问题 • 原始问题－minimize，对偶问题－maximize • 原始问题最优解所对应的单纯形乘子是对偶问题的解 • 弱对偶性 • 强对偶性(之一有解，则另一个必有解，且最优值相等)
其中 是凸函数. 定理. 凸规划的任一KKT点是全局极小点. 注1. 凸规划的所有局部解也是全局解. 注2. 线性规划是凸规划；二次规划中目标函数的Hessian阵 半正定时，也是凸规划.
第 7 章 约束优化：理论 数学规划基础 LHY‐SMSS‐BUAA
则 . 从而 Lagrange乘子的解释：最优值关于约束的灵敏度，即 约束函数变化时，对应的最优值的变化率！
原始问题(primal problem) 例1.
Lagrange对偶－例
其中 的其它约束. 对任意的
, 是凸函数，X是凸集，是希望分别处理 ，定义对偶函数 定义对偶函数(dual (d l function) f ti )
对偶函数
对偶问题： 对偶问题(dual problem)：
注：如果要求 ci(x) = 0，则对偶问题中与之对应的变量没 有符号限制.
结构优化设计大作业（北航）
结构优化设计大作业（北航）《结构优化设计》大作业报告实验名称: 拓扑优化计算与分析1、引言大型的复杂结构诸如飞机、汽车中的复杂部件及桥梁等大型工程的设计问题，依靠传统的经验和模拟实验的优化设计方法已难以胜任，拓扑优化方法成为解决该问题的关键手段。
近年来拓扑优化的研究的热点集中在其工程应用上，如: 用拓扑优化方法进行微型柔性机构的设计，车门设计，飞机加强框设计，机翼前缘肋设计，卫星结构设计等。
在其具体的操作实现上有两种方法，一是采用计算机语言编程计算，该方法的优点是能最大限度的控制优化过程，改善优化过程中出现的诸如棋盘格现象等数值不稳定现象，得到较理想的优化结果，其缺点是计算规模过于庞大，计算效率太低;二是借助于商用有限元软件平台。
本文基于matlab软件编程研究了不同边界条件平面薄板结构的在各种受力情况下拓扑优化，给出了几种典型结构的算例，并探讨了在实际优化中优化效果随各参数的变化，有助于初学者初涉拓扑优化的读者对拓扑优化有个基础的认识。
2、拓扑优化研究现状结构拓扑优化是近20年来从结构优化研究中派生出来的新分支，它在计算结构力学中已经被认为是最富挑战性的一类研究工作。
目前有关结构拓扑优化的工程应用研究还很不成熟，在国外处在发展的初期，尤其在国内尚属于起步阶段。
1904 年Michell在桁架理论中首次提出了拓扑优化的概念。
自1964 年Dorn等人提出基结构法，将数值方法引入拓扑优化领域，拓扑优化研究开始活跃。
20 世纪80 年代初，程耿东和N. Olhoff在弹性板的最优厚度分布研究中首次将最优拓扑问题转化为尺寸优化问题，他们开创性的工作引起了众多学者的研究兴趣。
1988年Bendsoe和Kikuchi发表的基于均匀化理论的结构拓扑优化设计，开创了连续体结构拓扑优化设计研究的新局面。
1993年Xie.Y.M和Steven.G.P提出了渐进结构优化法。
1999年Bendsoe和Sigmund证实了变密度法物理意义的存在性。
最优化方法练习题答案
练习题一1、建立优化模型应考虑哪些要素“答：决策变量、目标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停顿准则。
答：针对一般优化模型，讨论解的可行域，假设存在一()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===L L D 点，对于均有则称为优化模型最优解，最优解存在；*X D ∈X D ∀∈*()()f X f X ≤*X 迭代算法的收敛性是指迭代所得到的序列，满足，(1)(2)(),,,K X X X L L (1)()()()K K f X f X +≤则迭代法收敛；收敛的停顿准则有，，(1)()k k x x ε+-<(1)()()k k k x x xε+-<，，等等。
()()(1)()k k f x f x ε+-<()()()(1)()()k k k f x f x f x ε+-<()()k f x ε∇<练习题二1、*公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3，欲出价收购〔可能用于生产附加值更高的产品〕。
如果你是该公司的决策者，对这3种资源的收购报价是多少？〔该问题称为例2.1的对偶问题〕。
解：确定决策变量对3种资源报价作为本问题的决策变量。
123,,y y y 确定目标函数问题的目标很清楚——“收购价最小〞。
确定约束条件资源的报价至少应该高于原生产产品的利润，这样原厂家才可能卖。
因此有如下线性规划问题：123min 170100150w y y y =++*2、研究线性规划的对偶理论和方法〔包括对偶规划模型形式、对偶理论和对偶单纯形法〕。
答：略。
3、用单纯形法求解以下线性规划问题：〔1〕⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ；〔2〕⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min 53243232132 i x x x x x x x x x x t s x x z i 解：〔1〕引入松弛变量*4，*5，*6c j →1-11C B基b*1*2*3*4*5*60*421[1]-21000*532110100*64-101001c j -z j1-11因检验数σ2<0，故确定*2为换入非基变量，以*2的系数列的正分量对应去除常数列，最小比值所在行对应的基变量*4作为换出的基变量。
北航最优化方法习题2015版(下)
易见最优解 件为：
y∗
=0， 于是得原问题的解
x∗
=
1, y ∗
=0.
(b) 该问题的 Lagrange 函数 L(x, y, λ) = x2 + y 2 + λ((x − 1)3 − y 2 ) . KKT条 2x + 3λ(x − 1)2 = 0 2y − 2λy = 0 (x − 1)3 − y 2 = 0.
9 T ∗ 首先，因为 x∗ = ( 3 2 , 4 ) 满足约束条件，且有 I (x ) = {1} , 所以由互补条件有 ∗ ∗ λ∗ 2 = λ3 = λ4 = 0 . 再将
3 1 g ∗ = (− , )T , 2 2
T a∗ 1 = (3, −1) .
代入上边的梯度条件，即KKT条件的前两个方程，解得 λ∗ 1 = 足KKT条件.
由两个等式约束得 x1 = 2x2 , x3 =
750 , x2 2
从而原问题可既约为
16x2 2+
33000 x2
minimize √
subject to x2 > 0.
3 求稳定点， 得 x∗ 2 = 10
33 32 .
将 x∗ 代入 KKT 条件中的梯度条件(第一个和第三个方程)，解得 Lagrange
7.6 考虑找曲线 (x − 1)3 = y 2 上哪个点离原点最近(在Euclidean范数意义下)的问题.
可以将该问题表述为
minimize
x,y
f (x, y ) = x2 + y 2
subject to (x − 1)3 = y 2 . (a) 用图解法求解该问题. 消去 y 求解问题, 所得到的函数有极小点吗？给出结 果不一致的可能原因. 消去 x 求解问题, 得到怎样的结果? (b) 对于该问题, 找到所有的KKT点. LICQ 成立吗?请给出结果可能的解释.
最优化方法大作业
学号《最优化方法》课程实践完成时间：2015年5月30日星期六选择题目：题目一使用优化软件，编写重要算法的程序1.第一大题：（1）学习最优流量工程问题，nonsmooth_MCFP.pdf（2）问题重述：Figure 1一个简单的网络拓扑和流量需求如Figure 1所示，网络有7 个节点，13 条弧，每条弧的容量是5 个单位. 此外有四个需求量均为4个单位的源－目的对（M=4)，具体的源节点、目的节点信息如图所示. 这里为了简单，省去了未用到的弧，此外弧上的数字表示弧的编号。
（3）极小化MAU设定变量x，为531⨯的向量，其中(53)x即为变量z。
使用linprog 函数求解极小化问题得到x。
之前确定三个约束条件。
1、Ax b⨯的矩阵，b为131⨯的向量。
≤，其中A为13532、eq eq x b A =，其中eq A 为2853⨯的矩阵，eq b 为281⨯的向量。
3、x lb ≥，其中lb 为153⨯的向量 编程计算后得到结果如下：（4） 极小化FT 成本函数设定变量x ，为651⨯的向量，其中(53:65)x 即为变量l z 。
使用linprog 函数求解极小化问题得到x 。
之前确定三个约束条件。
1、Ax b ≤，其中A 为7865⨯的矩阵，b 为781⨯的向量。
2、eq eq x b A =，其中eq A 为2865⨯的矩阵，eq b 为281⨯的向量。
3、x lb ≥，其中lb 为165⨯的向量 编程计算后得到结果如下：2. 第二大题： 2.1. 习题5.6 2.1.1. 问题分析问题2112212()(101810)/241513q x x x x x x x =-++-+ 通过matlab 画出其等高线为：2.1.2. 最速下降法最速下降法中，取值：k k p g =-==()()k k k kk T k k T k g p g g p Gp g Ggα- x1x 2等高线-224681012(1)()k x k x k p α+=+2.1.3. 算法流程图如下图所示：2.1.4. 初始值（0,0）编程运行结构为：收敛过程曲线为：2.1.5. 初始值（-0.4,0）编程运行结构为：收敛过程曲线为：x1x 2等高线-2246810122.1.6. 初始值（10,0）编程运行结构为：收敛过程曲线为：x1x 2-2246810122.1.7. 初始值（11,0）编程运行结构为：收敛过程曲线为：x1x 2-2246810122.2. 习题5.7 2.2.1. 问题分析问题()94ln(7)f x x x =--497g x =-- 24(7)G x =- Matlab 画出在区间(7 10)的函数、一阶导数、二阶导数的变化曲线为x1x 2-22468101277.588.599.510707274767880828486xf函数变化曲线77.588.599.510-35-30-25-20-15-10-50510xg一阶导数g 变化曲线2.2.2. 牛顿法牛顿法中，取值：k k k G s g =- 1k k k s xx +=+其中，如果G 不是半正定，则采用修正牛顿法(+)k k k G I s g λ=-77.588.599.51050100150200250300350400xg二阶导数G 变化曲线2.2.3.算法流程图如下图所示：2.2.4.初始值7.40编程运行结构为：收敛过程曲线为：2.2.5. 初始值7.20编程运行结构为：收敛过程曲线为：7.397.47.417.427.437.447.457.4670.24570.2570.25570.2670.265xf2.2.6. 初始值7.01编程运行结构为：收敛过程曲线为：7.17.27.37.47.57.67.770.270.470.670.87171.271.471.6xf2.2.7. 初始值7.80编程运行结构为：收敛过程曲线为：6.856.9 6.9577.057.17.157.27.257.37.35727476788082xf2.2.8. 初始值7.88编程运行结构为：收敛过程曲线为：7.17.27.37.47.57.67.77.87.97070.57171.572xf2.2.9. 分析函数在区间（7，7.8888）内是凸函数，G 恒大于零，所以单纯牛顿法保证收敛。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北航最优化方法大作业参考1 流量工程问题1.1 问题重述定义一个有向网络G=(N,E)，其中N是节点集，E是弧集。
令A是网络G的点弧关联矩阵，即N×E阶矩阵，且第l列与弧里(I,j)对应，仅第i行元素为1，第j行元素为-1，其余元素为0。
再令b m=(b m1,…,b mN)T，f m=(f m1,…,f mE)T，则可将等式约束表示成：Af m=b m本算例为一经典TE算例。
算例网络有7个节点和13条弧，每条弧的容量是5个单位。
此外有四个需求量均为4个单位的源一目的对，具体的源节点、目的节点信息如图所示。
这里为了简单，省区了未用到的弧。
此外，弧上的数字表示弧的编号。
此时，c=((5,5…,5)1 )T，×13根据上述四个约束条件，分别求得四个情况下的最优决策变量x=((x12,x13,…,x75)1×)。
13图 1 网络拓扑和流量需求1.2 7节点算例求解1.2.1 算例1（b1=[4;-4;0;0;0;0;0]T）转化为线性规划问题：Minimize c T x1Subject to Ax1=b1x1>=0 利用Matlab编写对偶单纯形法程序，可求得:最优解为x1*=[4 0 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x1=201.2.2 算例2（b2=[4;0;-4;0;0;0;0]T）Minimize c T x2Subject to Ax2=b2X2>=0 利用Matlab编写对偶单纯形法程序，可求得:最优解为x2*=[0 4 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x2=201.2.3 算例3（b3=[0;-4;4;0;0;0;0]T）Minimize c T x3Subject to Ax3=b3X3>=0 利用Matlab编写对偶单纯形法程序，可求得:最优解为x3*=[4 0 0 0 4 0 0 0 0 0 0 0 0]T对应的最优值c T x3=401.2.4 算例4（b4=[4;0;0;0;0;0;-4]T）Minimize c T x4Subject to Ax4=b4X4>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x4*=[4 0 0 4 0 0 0 0 0 4 0 0 0]T对应的最优值c T x4=601.3 计算结果及结果说明1.3.1 算例1（b1=[4;-4;0;0;0;0;0]T）算例1中，由b1可知，节点2为需求节点，节点1为供给节点，由节点1将信息传输至节点2的最短路径为弧1。
图 2 算例1最优传输示意图求得的最优解为x1*=[4 0 0 0 0 0 0 0 0 0 0 0 0]T，即只经过弧1运输4个单位流量，其余弧无流量。
又因为，每条弧的费用均为5，所以最小费用为20。
经分析，计算结果合理可信。
1.3.2 算例2（b2=[4;0;-4;0;0;0;0]T）算例2中，由b2可知，节点3为需求节点，节点1为供给节点，由节点1将信息传输至节点2的最短路径为弧2。
图 3 算例2最优传输示意图求得的最优解为x2*=[0 4 0 0 0 0 0 0 0 0 0 0 0]T，即只经过弧2运输4个单位流量，其余弧无流量。
又因为，每条弧的费用均为5，所以最小费用为20。
经分析，计算结果合理可信。
1.3.3 算例3（b3=[0;-4;4;0;0;0;0]T）算例3中，由b3可知，节点2为需求节点，节点3为供给节点，由节点3将信息传输至节点2的最短路径为弧5->弧1。
图 4 算例3最优传输示意图求得的最优解为x3*=[4 0 0 0 4 0 0 0 0 0 0 0 0]T，即经过弧5运输4个单位流量至节点1，再经弧1运输4个单位流量至节点2，其余弧无流量。
又因为，每条弧的费用均为5，所以最小费用为40。
经分析，计算结果合理可信。
1.3.4 算例4（b4=[4;0;0;0;0;0;-4]T）算例4中，由b4可知，节点7为需求节点，节点1为供给节点，由节点1将信息传输至节点7的最短路径为弧1->弧4->弧10。
图 5 算例3最优传输示意图求得的最优解为x4*=[4 0 0 4 0 0 0 0 0 4 0 0 0]T，即经过弧1运输4个单位流量至节点2，再经弧4运输4个单位流量至节点5，最后经弧5运输4个单位流量至节点7，其余弧无流量。
又因为，每条弧的费用均为5，所以最小费用为60。
经分析，计算结果合理可信。
2 重要算法编写与观察2.1 习题5.6（a）初值为（0,0）时本算法令g的2范数在<10-4时，停止迭代，经过86次迭代收敛。
收敛因子（f(k+1)-f*）/（f(k)-f*）=0.7623图 6 收敛因子截图（b）初值为（-0.4,0）时本算法令g的2范数在<10-4时，停止迭代，经过112次迭代收敛。
收敛因子（f(k+1)-f*）/（f(k)-f*）=0.81图7 收敛因子截图（c）初值为（10,0）时本算法令g的2范数在<10-4时，停止迭代，经过5次迭代收敛。
收敛因子（f(k+1)-f*）/（f(k)-f*）=3.9022e-4图8 收敛因子截图（d）初值为（11,0）时本算法令g的2范数在<10-4时，停止迭代，经过2次迭代收敛。
收敛因子（f(k+1)-f*）/（f(k)-f*）= 0图9 收敛因子截图图10 自变量（x1,x2）截图总结：最速降线法的收敛因子随着初值的不同而变化，对于个别初值（如本习题初值取（11,0）时），算法可迅速收敛。
因此，初值的选取对于最速降线法的收敛速度有较大影响。
2.2 习题5.7（a ） 由()94ln(7)f x x x =--可得：4'()97f x x =-- 24"()(7)f x x =- 故，牛顿迭代法的确切公式为：24974(7)x s x --=-- （b ）从以下五个初值开始迭代 （1）x(0)=7.40（2）x(0)=7.20（3）x(0)=7.01（4）x(0)=7.80（5）x(0)=7.88（c）本问题的最优值为7.4444444。
由上述五个初值点的前五步迭代可以看出：当初值点在区间（7.4444444，7.8888）内时，第二次迭代点将落在（7，7.4444444）之间，随后逐渐增加，直至逼近最优值。
当初值点在区间（7，7.4444444）内时，则迭代点逐渐增加，逼近最优值。
当取初值不在（7,7.8888）内时，牛顿法不收敛。
2.3 习题5.8（a）没有线搜索的牛顿法μ=0.1时，μ=1时，（b）具有线搜索的牛顿法μ=0.1时，μ=1时，（未完成）2.4 习题5.9（a）初值选（1.2,1.2）时，◆最速降线法：本算法令g的2范数在<10-2时，停止迭代，经过3262次迭代得到以下结果。
图11 最速降线法初值为（1.2,1.2）的等值线图及迭代轨迹◆牛顿法：本算法令s的4范数在<10-6时，停止迭代，经过4次迭代得到以下结果。
图12 牛顿法初值为（1.2,1.2）的等值线图及迭代轨迹（b）初值选（-1.2,1）时，最速降线法：本算法令g的4范数在<10-2时，停止迭代，经过6835次迭代得到以下结果。
图13 最速降线法初值为（-1.2,1）的等值线图及迭代轨迹牛顿法：本算法令s的4范数在<10-6时，停止迭代，经过6次迭代得到以下结果。
图14 牛顿法初值为（-1.2,1）的等值线图及迭代轨迹2.5 习题5.19N=5迭代6次后，满足收敛条件。
N=8迭代19次后，满足收敛条件。
N=14迭代49次后，满足收敛条件。
（表略）N=40迭代74次后，满足收敛条件。
（表略）2.6 习题5.27调用MATLAB自带的lsqnonlin.m函数，计算可得对应的x(1)、x(2)和标准差如下表所示。
由上可知，标准差值较为恒定，随初值变化不十分显著；x1和x2值随初值选取的不同而不同。
2.7 习题6.4（未完成）3 附录3.1 对偶单纯形法函数MATLAB程序function [sol,val,kk]=duioudanchun(A,N)B=A;[mA,nA]=size(A);kk=0;flag=1;while flagkk=kk+1;if A(:,nA)>=0flag=0;sol=zeros(1,nA);for i=1:mA-1sol(N(i))=A(i,nA);endval=sol*(B(mA,:))';elsefor i=1:mA-1if A(i,nA)<0&A(i,1:nA-1)>=0disp('have infinite solution!');flag=0;break;endendif flagtemp=0;for i=1:mA-1if A(i,nA)<temptemp=A(i,nA);outb=i;endendsita=zeros(1,nA-1);for i=1:nA-1if A(outb,i)<0sita(i)=A(mA,i)/A(outb,i);endendtemp=-inf;for i=1:nA-1if sita(i)<0&sita(i)>temptemp=sita(i);inb=i;endendfor i=1:mA-1if i==outbN(i)=inb;endendA(outb,:)=A(outb,:)/A(outb,inb);for i=1:mAif i~=outbA(i,:)=A(i,:)-A(outb,:)*A(i,inb);A(mA,nA)=0;endendendendend3.2 最速降线法求Rosenbrock函数最小值matlab程序如下：function rb = rbfun(x,y)rb=100*(y-x^2)^2+(1-x)^2endclearclcsyms x y g Gg=gradient(rb(x,y),[x y]) %定义梯度向量G=hessian(rb(x,y),[x y]) %定义海森阵X(1,:)=[-1.4 1]; %定义初始点x=X(1,1);y=X(1,4);A(1,:)=subs(g) %给梯度赋初值i=1while(norm(A(i,:),4)>10^(-4)) %收敛条件f(i)=rb(x,y) %记录函数值P(i,:)=-A(i,:) %得到迭代方向fz(i)=-A(i,:)*P(i,:)' %-gT*p %精确搜索法步长的分子fm(i)=P(i,:)*subs(G)*P(i,:)' %精确搜索法步长的分母a(i)=fz(i)/fm(i) %精确搜索法步长X(i+1,:) = X(i,:)+a(i)*P(i,:) %产生新的点x=X(i+1,1);y=X(i+1,4)A(i+1,:)=subs(g) %产生新的梯度i=i+1end3.3 牛顿法求Rosenbrock函数最小值matlab程序如下：function rb = rbfun(x,y)rb=100*(y-x^2)^2+(1-x)^2endclearclcsyms x y g Gg=gradient(rb(x,y),[x y]) %定义梯度向量G=hessian(rb(x,y),[x y]) %定义海森阵X(1,:)=[-1.4 1]; %定义初值x=X(1,1);y=X(1,4);A(1,:)=subs(g) %给梯度赋初值H=subs(inv(G)) %得到海森阵初值S(1,:)=-A(1,:)*H %得到s初值i=1while (norm(S(i,:),4)>10^(-6)) %收敛条件f(i)=rb(x,y) %定义函数值X(i+1,:) = X(i,:)+S(i,:) %得到下一迭代点x=X(i+1,1);y=X(i+1,4) %给x,y分别赋值A(i+1,:)=subs(g) %得到新的梯度值H=subs(inv(G)) %得到新的海森阵S(i+1,:)=-A(i+1,:)*H %得到新的增量s i=i+1end3.4 共轭梯度法求解习题5.19程序如下：clearclcK=40G=zeros(K,K)for m = 1: Kfor n = 1: KG(m,n)=1/(m+n-1)endendX(1,:)=zeros(1,K)b=ones(1,K)A(1,:)=X(1,:)*G-bP(1,:)=-A(1,:)i=1while (norm(A(i,:),4)>10^(-6)) %收敛条件d=P(i,:)*Gfz(i)=A(i,:)*A(i,:)' %精确搜索法步长的分子fm(i)=P(i,:)*d' %精确搜索法步长的分母a(i)=fz(i)/fm(i) %精确搜索法步长X(i+1,:) = X(i,:)+a(i)*P(i,:) %产生新的点A(i+1,:)=A(i,:)+a(i)*dbeta(i+1)=(A(i+1,:)*A(i+1,:)')/(A(i,:)*A(i,:)')P(i+1,:)=-A(i+1,:)+beta(i+1)*P(i,:)i=i+1end。