伺服电机选型计算实例
伺服电机选型计算实例
4
1.2 加速力矩的计算 计算加速力矩:步骤 1
·直线加/减速
伺服电机计算选择应用实例
如果负载惯量比 3 倍的电机惯量大的多,则控制特性将大大下降。 此时,电机的特性需要特殊调整。使用中应避免这样大的惯量。若 机械设计出现这种情况,请与 FANUC 联系。
按下步骤计算加速力矩: 假定电机由 NC 控制加/减速,计算其加速度。将加速度乘 以总的转动惯量(电机的惯量 + 负载惯量),乘积就是加速力矩。 计算式如下。
= 100.1(kgf.cm.) = 9.81(Nm)
5
伺服电机计算选择应用实例
由α2/3000 的速度-转矩特性可以看到,9.81(Nm)的加速 力矩处于断续工作区的外面(见上面的特性曲线和电机的数据单)。 (α2/3000 的力矩是不够的。) 如果轴的运行特性(如,加速时间)不变,就必须选择大电机。比 如,选择α3/3000(Jm 为 0.02 kgf.cm.s2),重新计算加速力矩如下:
Ta=12.1 Nm,;Tm=To=0.9 Nm;t1= 0.1 s;t2=1.8s;t3=7.0s。
(12.1+0.9)2×0.1+0.92×1.8+(12.1-0.9)2×0.1+0.92×7
Trms =
t0
= 20.2 Nm < Ts×0.9=2.9×0.9=2.61 Nm 因此,用α3/3000 电机可以满足上述运行条件。(条件 3)
计算力矩时,要注意以下几点: 。考虑由镶条锁紧力(fg)引起的摩擦力矩
根据运动部件的重量和摩擦系数计算的力矩通常相当小。镶条 锁紧力和滑动表面的质量对力矩有很大影响。 。滚珠丝杠的轴承和螺母的预加负荷,丝杠的预应力及其它一些因 素有可能使得滚动接触的 Fc 相当大。小型和轻型机床其摩擦力矩 会大大影响电机的承受的力矩。 。考虑由切削力引起的滑动表面摩擦力(Fcf)的增加。切削力和驱 动力通常并不作用在一个公共点上如下图所示。当切削力很大时, 造成的力矩会增加滑动表面的负载。 当计算切削时的力矩时要考虑由负载引起的摩擦力矩。
伺服电机计算选择应用实例

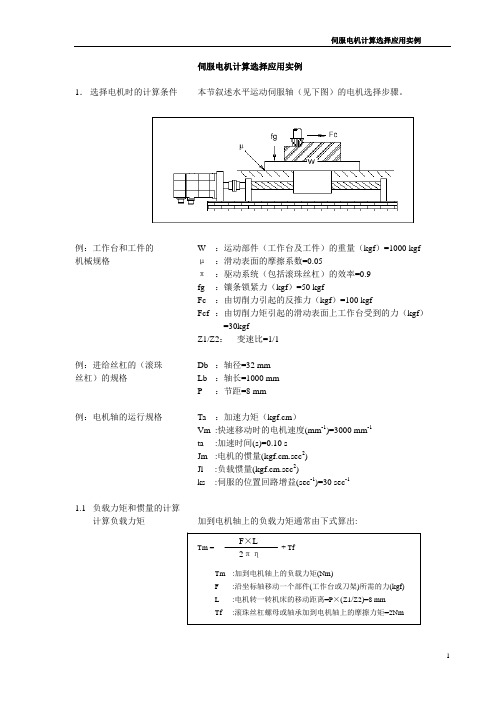
伺服电机计算选择应用实例1. 选择电机时的计算条件 本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的 W :运动部件(工作台及工件)的重量(kgf )=1000 kgf 机械规格 μ :滑动表面的摩擦系数=0.05π :驱动系统(包括滚珠丝杠)的效率=0.9 fg :镶条锁紧力(kgf )=50 kgfFc :由切削力引起的反推力(kgf )=100 kgfFcf :由切削力矩引起的滑动表面上工作台受到的力(kgf )=30kgfZ1/Z2: 变速比=1/1 例:进给丝杠的(滚珠 Db :轴径=32 mm 丝杠)的规格 Lb :轴长=1000 mm P :节距=8 mm例:电机轴的运行规格 Ta :加速力矩(kgf.cm )Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -1 1.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + TfTm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2Nm无论是否在切削,是垂直轴还是水平轴,F 值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F 值还与平衡锤有关。
对于水平工作台,F 值可按下列公式计算: 不切削时: F = μ(W+fg ) 例如: F=0.05×(1000+50)=52.5 (kgf) Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf) 例如: F=100+0.05×(1000+50+30)=154(kgf) Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm ),最高转速应高于3000(min -1)。
伺服电机计算选择应用实例

伺服电机计算选择应用实例1. 选择电机时的计算条件 本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的 W :运动部件(工作台及工件)的重量(kgf )=1000 kgf 机械规格 μ :滑动表面的摩擦系数=0.05π :驱动系统(包括滚珠丝杠)的效率=0.9 fg :镶条锁紧力(kgf )=50 kgfFc :由切削力引起的反推力(kgf )=100 kgfFcf :由切削力矩引起的滑动表面上工作台受到的力(kgf )=30kgfZ1/Z2: 变速比=1/1例:进给丝杠的(滚珠 Db :轴径=32 mm 丝杠)的规格 Lb :轴长=1000 mm P :节距=8 mm例:电机轴的运行规格 Ta :加速力矩(kgf.cm )Vm :快速移动时的电机速度(mm -1)=3000 mm -1ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2)Jl :负载惯量(kgf.cm.sec 2)ks:伺服的位置回路增益(sec -1)=30 sec-11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L:电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf :滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L 2πη无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。
伺服电机计算选择应用实例

伺服电机计算选择应用实例1.选择电机时的计算条件本节叙述水平运动伺服轴(见下图)的电机选择步骤。
例:工作台和工件的W :运动部件(工作台及工件)的重量(kgf)=1000 kgf 机械规格μ:滑动表面的摩擦系数=0.05π:驱动系统(包括滚珠丝杠)的效率=0.9fg :镶条锁紧力(kgf)=50 kgfFc :由切削力引起的反推力(kgf)=100 kgfFcf :由切削力矩引起的滑动表面上工作台受到的力(kgf)=30kgfZ1/Z2:变速比=1/1例:进给丝杠的(滚珠Db :轴径=32 mm丝杠)的规格Lb :轴长=1000 mmP :节距=8 mm例:电机轴的运行规格Ta :加速力矩(kgf.cm)Vm :快速移动时的电机速度(mm-1)=3000 mm-1ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec2)Jl :负载惯量(kgf.cm.sec2)ks :伺服的位置回路增益(sec-1)=30 sec-11.1 负载力矩和惯量的计算计算负载力矩加到电机轴上的负载力矩通常由下式算出:Tm = + TfTm :加到电机轴上的负载力矩(Nm)F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf)L :电机转一转机床的移动距离=P×(Z1/Z2)=8 mmTf :滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF×L2πη无论是否在切削,是垂直轴还是水平轴,F值取决于工作台的重量,摩擦系数。
若坐标轴是垂直轴,F值还与平衡锤有关。
对于水平工作台,F值可按下列公式计算:不切削时:F = μ(W+fg)例如:F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1,应根据数据单选择电机,其负载力矩在不切削时应大于0.9(Nm),最高转速应高于3000(min-1)。
伺服传动的应用计算

伺服传动的选型计算案例1:丝杠直线传动已知条件(负载质量m=5KG,丝杠传动导程p=10mm,工位移载行程s=1000mm,移载所需时间2.2s)据上述要求旋转一款合适的伺服电机。
解析:1. 首先一般伺服电机的额定转速为n=3000转,运动过程可视为恒扭矩传动x0.01=0.5 m/s∴ 丝杠传动的最快直线速度 ν=300060V (m/s)0.5 m/s0 t1 t2 t3 t ( s)加减速过程的速度变化图为了方便计算,可设定减速与减速时间相等均为t,最终匀速为0.5m/s∴s=1at2x2+0.5(2.2−2t)=1m2∴可得:1.1−0.5t= 1 得t=0.2s,则a=2.5 m/s22.根据需要的加速度可推算所需要的丝杠的轴向推力,从而推算出所需的扭矩已知负载质量:M=5kg,且经上推算的加速度a=4 m/s2(暂定)根据 F=m.a=5x2.5=12.5N (F为丝杠轴向推力)还可以根据丝杠传动电机扭矩与轴向力之间转换关系:T∗2∗π∗η=F∗p (T为电机扭矩,η为效率可取0.9)T =FP2πη=12.5x0.015.652= 0.0221 Nm3.根据需要出的扭矩再反推出所需电机的功率: ∴ 根据功率扭矩之间的转换公式: T =9550∗p n反推得出P =T∗n 9550=0.0221x30009550=0.00695 kw = 6.95w从扭矩的角度100W 以下的伺服电机都能满足要求4.伺服电机是精确定位的马达,不能只满足驱动扭矩,还需从惯量上去校核够不够, (丝杠φ15,长度1100): 丝杠传动系的惯量:J=J 1负载+J 2丝杠(可得其惯量0.426 x10−4 kgm 2) J 1=m ∗r 2=5x(p 2π)2=5x(0.159)210−4 kgm 2=0.1267x10−4 kgm 2∴ J=(0.426+0.1267)x10−4 kgm 2=0.5527 x10−4 kgm 2所以可得总负载的惯量为0.5527 x10−4 kgm 25.电机所需承受的总惯量已得知,则需要查询所选电机的惯量参数,这里以三菱电机为例由三菱电机属性的惯量匹配比为15~25,则可得:J 电机=0.552720=0.0276 ∴ 可得100W 的电机惯量太小,尽管扭矩够了,但是不能很精准地控制负载的定位所以应该选用HF-MP23G1(K9020)案例2:同步带直线传动已知条件(负载质量m=5KG,同步带轮直径d=50mm,工位移载行程s=1000mm,移载所需时间2s)据上述要求旋转一款合适的伺服电机。
伺服电机选型计算实例

1
·注
伺服电机计算选择应用实例
无论是否在切削,是垂直轴还是水平轴,F 值取决于工作台的重量, 摩擦系数。若坐标轴是垂直轴,F 值还与平衡锤有关。对于水平工 作台,F 值可按下列公式计算:
不切削时: F = μ(W+fg) 例如: F=0.05×(1000+50)=52.5 (kgf) Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm) = 0.9(Nm)
Ta =
Vm × 2π× 1
60
ta
×Jm×(1-e-ks。ta)+
+ Vm × 2π× 1
60
ta
×JL×(1-e-ks。ta)÷η
1 Vr = Vm×{1- Ta·ks
(1- e-ks。ta )}
Ta :加速力矩(kgf·cm) Vm :电机快速移动速度(min-1) ta :加速时间(sec) Jm :电机的惯量(kgf.cm.s2) JL :负载的惯量(kgf.cm.s2) Vr :加速力矩开始下降的速度(与 Vm 不同) (min-1) Ks :位置回路的增益(sec-1) η :机床的效率
切削时: F = Fc+μ(W+fg+Fcf) 例如: F=100+0.05×(1000+50+30)=154(kgf) Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm) =2.1(Nm)
为了满足条件 1,应根据数据单选择电机,其负载力矩在不切削时 应大于 0.9(Nm),最高转速应高于 3000(min-1)。考虑到加/减速, 可选择α2/3000(其静止时的额定转矩为 2.0 Nm)。
伺服电机选型案例

伺服电机选型案例伺服电机功率计算选型例子伺服电机功率计算选型例子(新手必看,经典案例分析)伺服电机选型也有相应的规律和公式可循的。
最常见的机械传动结构有同步带,齿轮齿条,丝杆等。
以同步带为例,需要计算的参数有电机转速,电机力矩,转动惯量。
第一,电机额定转速N=(v/2πr)*i,启动瞬间需要的拉力F=(M+m1-m2)a+δ(M+m1-m2)g(水平),F=(M+m1-m2)a+δ(M+m1-m2)g+(M+m1-m2)g(垂直),T扭矩=F*R。
T电机=T扭矩/机械减速比n,电机功率=N*T 电机/10,启动惯量J=1/2mR2,电机惯量J电机=J/减速比的平方n2/惯量比i。
第二,同步带轮直径D=100mm、提升机载货台总重M=30kg、货物总重m1=10kg,配重m2=25kg,提升滚动摩擦系数取δ=0.03、加速度a=2m/S2、提升速度v=3m/s。
减速机减速比i=5,电机额定转速n=(v/2πr)*i=3/(2*3.14*0.05)*5*60=2866r/min,启动瞬间需要的拉力F=(M+m1-m2)a+&delta,(M+m1-m2)g+(M+m1-m2)g=(30+10-25)*2+0.03(30+10-25)*10+(30+10-25)*10=184.5N。
T扭矩=F*R=184.5*0.05=9.225Nm,折算电机需要扭矩T1=9.225Nm/5=1.85Nm,折算电机功率P1=2866*1.85/10=0.5KW。
启动惯量J=1/2mR2=0.5*(10+30+25)*0.0025=0.08125kgm2,折算电机需要惯量J1=0.08125/25=0.00325kgm2,根据经验值取惯量比=10,则实际J电=J1/10=0.000325kgm2。
经计算电机至少满足以下条件下面看下1.2千瓦3000RPM,4牛米的电机的惯量是2.98*10-4kgm2。
所以可以选择80ST-M04030的电机。
伺服电机功率计算选型案例

如果选择500W电机,JM = 8.17kg.cm2,则15625 / R2 < 3*8.17,R2 > 637,R > 25
输出转速=2000/25=80 rpm,满足要求。
这种传动方式阻力很小,忽略扭矩计算。
14
实用文档
举例计算1
这种传动方式与前一种传动方式相同, 选型时主要考虑负载惯量的计算,计 算公式也与前面相同。
作用,根據切線方向的牛頓第二運動定
律 Ft m at
rFt r m at
m r 2
4
实用文档
Ft F
rm 轉軸
將剛體看成是由許多質點所構成,則每一質點都滿足類似 的方程式
i miri2 i 1,2,3, ,n 對每一質點作加總即得到
i ( miri2)
i
i
m F
mF
左邊的合力矩只需考慮外力所產生的力矩,由內力所產生
总结:转动型负载主要考虑惯量计算。
15
实用文档
举例计算2
M
1:R2
D
1:R1
已知:负载重量M=50kg,同步带轮直径 D=120mm,减速比R1=10,R2=2,负载与 机台摩擦系数µ=0.6,负载最高运动速 度30m/min,负载从静止加速到最高速 度时间200ms,忽略各传送带轮重量, 驱动这样的负载最少需要多大功率电机?
匀速扭矩Tb = Tf = 1.387 N.m
减速扭矩Tc = TA – Tf = 11.285 N.m
实效扭矩Trms = sqrt[(Ta2*t1 + Tb2*t2 + Tc2*t3) / (t1+t2+t3)]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伺服电机选型计算实例
伺服电机是一种控制器控制的电机,具有高精度和高速度的特点,广泛应用于机械设备中。
在选型伺服电机时,需要考虑多个参数来满足具体的应用要求。
下面以一个选型计算实例来详细介绍伺服电机的选型过程。
假设我们需要选型一台伺服电机用于驱动一个线传动机构,具体要求如下:
1.最大负载力为2000N,工作速度范围为0-10m/s。
2. 线传动机构的负载惯量为500kg·m²。
3. 需要保证驱动精度在±0.2mm范围内。
4.工作环境温度范围为0-40℃。
首先,我们需要计算所需的转矩。
根据公式:转矩=负载力×工作半径,其中工作半径等于线传动机构的负载惯量÷2、由于我们没有具体的线传动机构参数,假设负载惯量为500kg·m²,即工作半径为0.25m。
则最大转矩=2000N×0.25m=500N·m。
考虑到一般情况下,峰值转矩为最大转矩的2倍,即1000N·m。
接下来,我们需要计算伺服电机的速度要求。
根据给定的工作速度范围0-10m/s,我们可以选择合适的额定转速。
假设我们选择的额定转速为2000rpm,则转速范围为0-2000rpm。
考虑到加速度和减速度的要求,一般额定转速的选择会略高于平均线速度,假设为2200rpm。
接下来,我们需要选择合适的伺服电机型号。
在选型之前,我们还需要考虑工作环境的温度范围。
根据给定的工作环境温度范围为0-40℃,
我们需要选择具备合适温度范围的伺服电机。
一般伺服电机的温度范围为0-50℃,因此我们可以选择标准型号的伺服电机。
在选择伺服电机型号时,我们需要参考厂家提供的电机性能参数。
主要包括额定转矩、额定转速、额定电压、额定电流、额定功率等。
根据我们的要求,我们可以对比不同型号的伺服电机并选择合适的型号。
最后,我们需要根据具体应用需求考虑伺服电机的控制方式、接口类型以及其他附件等。
综上所述,选型伺服电机时,需要考虑负载力、工作速度、转矩、功率、工作环境等多个参数,以满足具体应用要求。
在具体选型过程中,需要参考厂家提供的性能参数,综合比较不同型号的伺服电机,并考虑控制方式、接口类型等因素。
选型伺服电机需要充分了解应用需求,尽量选择能够满足工作要求的型号,以提高机械设备的性能和稳定性。
