有理数的减法(1)
有理数的减法(1)

有理数的减法(1)一、选择题1、差是-7.2,被减数是0.8,减数是( ) A 、-8 B 、8 C 、6.4 D 、-6.42、下列结论中正确的是 ( )A 、两个有理数的和一定大于其中任何一个加数B 、两个有理数的差一定小于被减数C 、两个负数相减,差为负数D 、负数减去正数,差为负数 3、下列说法,其中正确的有 ( )①减去一个负数等于加上这个数的相反数;②正数减负数,差为正数;③零减去一个数,仍得这个数;④两数相减,差一定小于被减数;⑤两个数相减,差不一定小于被减数;⑥互为相反数两数相减得零. A 、2个 B 、3个 C 、4个 D 、5个4、若0a >,且a b >,则a b -是 ( ) A 、正数 B 、正数或负数 C 、负数 D 、05、算式-4-5不能读作( ) A 、-4与5的差 B 、-4与-5的和 C 、-4与-5的差 D 、-4减去5的差6、-3,-14,7的和比它们的绝对值的和小 ( ) A 、-34 B 、-10 C 、10 D 、347、计算2-(-3)的结果是( ) A .-5 B .5 C .-1 D .18、某市某日的气温是-2℃~6℃,则该日的温差是( ) A .8℃ B .6℃ C .4℃ D .-2℃ 9、计算1-|-2|结果正确的是 ( ) A .3 B .1 C .-1 D .-310、某市2005年的最高气温为39℃,最低气温为零下7℃,则计算2005年温差列式正确的是( ) A .(+39)-(-7) B .(+39)+(+7) C .(+39)+(-7) D .(+39)-(+7) 11、计算12--的结果是( ) A 、3- B 、2- C 、1- D 、312、a ,b 在数轴上的对应点的位置如图,则( )A 、a +b =0 B 、a +b >0 C 、a -b <0 D 、a -b >0二、填空题1、温度6℃比-6℃高________;从海拔350米处下降到海拔-100米,下降了_____米。
1.3.2 有理数的减法(1)

=(-2.5)+(-5.9) =1.9+(+0.6)
=5
=-8.4
=2.5
2 计算
(1)比2℃低8℃的温度
(2)比-3℃低6℃的温度
解: 2-8=-6
比2℃低8℃的温度是-6 ℃
解 -3-6=-9
比-3℃低6℃的温度是-9 ℃
探索:输入-1,按图所示的程序运算,并写出
输出的结果。
解:当输入为-1时
5
1 ) 4
8
3 4
例6、 全班学生分为五个组进行游 戏,每组的基本分为100分,答对 一题加50分,答错一题扣50分,游 戏结束时,各组的分数如下:
第一组 第二组 第三组 第四组 第五组
100 150 -400 350 -100
(1) 第一名超出第二名多少分?
(2) 第二名超出第五名多少分?
解: 由上表可以看出,第一名得了 350分,第二名得了150分,第五名 得了- 400分
4-(-3)=7 ①
另一方面,我们知道 4+(+3)=7 ②
由①②有
4-(-3)=4+(+3) ③
4
7
0
-3
探究 减一个负数等于加上这个数的相反数
4-(-3)=4+(+3)③
从③式能看出减-3相当于加哪个数吗? 减-3相当于加-3的相反数
把4换成0,-1,-5,用上面的方法考虑
0-(-3) =3 0+3 =3 (-1)-(-3) =2 -1+3 =2
果加上20分的加分,她的成绩应该是 692。”吴老师说,何旋考出好成绩的秘 诀是心态好。“她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区
有理数的减法教学设计(1)

人教版七年级数学上有理数的减法(1)
河南省济源市轵城镇实验中学 赵玉荣 教材分析
本节是在学习了正负数、相反数、有理数加法运算之后,以初中代数第一 册 的有理数减法法则及有理数减法运算的例 1、例 2 为课堂教学内容。有理数的减 法运算是一种基本的有理数运算,对今后正确熟练地进行有理数的混合运算,并 对解决实际问题都有十分重要的作用。
学生口述解题过 程,教师板书做示 范,从中培养学生 严谨的学风和良 好的学习习惯.例 1(2)题是 0 减去一 个数,学生在开始 学时很容易出错, 这里作为例题是 为引起学生的重 视.(3)(4)两 题是简单的变式 题目,意在说明有 理数减法法则不 但适用于整数,也 适用于分数、小 数,即有理数.
组织学生自己编题, 学 教师与学生以平 等身份参与教学, 生回答. (小组交流合 放手让学生自己 作) 编拟有理数减法 的题目,其目的是 让学生巩固已学 知识.这样做,一 方面可以活跃学 生的思维,培养学 生的表达能力.另 一方面通过出题, 相互解答,互相纠 正,能增强学生学 习的主动性和参 与意识.同时,教 师可以获取学生 掌握知识的反馈 信息,对于存在的 问题及时回授.
3、
作为初一新生,学生的学习惯还尚未培养,虽然学习积极性较高,探索欲 望也较强,但交流合作意识不强,自主探索的效率也较低,自我管理能力 也很差。 教学目标
1、经历探索有理数减法法则的过程。
2、理解探索有理数减法法则,渗透化归思想。 3、能较为熟练地进行两个有理数减法的运算。 4、能解决简单的实际问题,体会数学与现实生活的联系。
先请同桌两位同学互 相交流,然后请 2—3 个同学发言 学生思考后回答: 减- 2 等于加+2
.允许学生从不同 角度观察得出温 差,采用温度计从 5 数到零下 2 度, 只要学生的方法 合理,都应鼓励。 此处先让学生回 顾加法与减法互 为逆运算关系,有 助于学生理解 5-(-2)=7 教师发挥主导作 用,注重学生的参 与意识,充分发展 学生的思维能力, 让学生通过尝试, 自己认识减法可 以转化为加法计 算。 由于学生刚刚接 触有理数减法运 算难度较大,为面 向全体,通过变换 题给予学生进一 步观察比较的机 会,学生自己总 结、归纳、思考, 此时学生的思维 活跃,易于充分发 挥学生的学习主 动性,同时也培养 了学生分析问题 的能力,达到能力 培养的目标
教案(有理数减法(1) 教学设计)

四、课堂小测
有理数减法基础练习1
五、课堂小结
1、有理数的减法法则:a-b=a+(-b)
2、注意两变
六、布置作业
1、完成课本20面练习题;
2、完成新课程《第3课时 有理数的减法》;
3、完成洋葱数学《有理数的减法 基础练习1》
重点
有理数减法法则及运用
难点
有理数减法法则的推导
教法
启发引导、讲授和讨论结合等
学法
归纳、合作、识记、练习
教学手段
多媒体、微课
课时安排
1课时
教学过程
设计意图
一、复习引入
有理数加法法则:
1、同号两数相加,取相同的符号,并把绝对值相加;
2、绝对值不相等的异号两数相加,取绝对值较大的加数的的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
3、一个数同0相加,仍得这个数。
二、讲解错题
1、洋葱数)》第5、8、9、10题;《有理数加法(2)》6、7、8、9题。
三、讲授新课
探究点:有理数的减法法则
1、有理数减法法则的直接运用
例1:计算:(1)7.2-(-4.8);(2)-3 -5 .
解析:判断a,b差的符号,可能不好理解,不妨把它转化为加法a-b=a+(-b),利用加法法则进行判定.
解:因为b<0,所以-b>0.又因为a<0,a-b=a+(-b),所以a与-b是异号两数相加,那么它们和的符号由绝对值较大的加数的符号决定,因为|a|>|b|,即|a|>|-b|,所以取a的符号,而a<0,因此a-b的符号为负号.
有理数减法(1)

口算:
(1)3 – 5 ; (3)( – 3) – 5; (2)3 – ( – 5);
(4)( – 3) – ( –5);
(5)–6 –( –6); (6) – 7 – 0; (7)0 – ( –7) ;(8 )( – 6) – 6 (9)9 – ( –11)
习题、计算: (1)0-8
1 5 (4) 5 8 7 7
当a-b=0时,比较a,b的大小。 当a-b<0时,比较a,b的大小。 4、若a<b,b<0且|a|>|b|,那么a-b是 ( A、正数 B、负数 C、0
)
D、以上都有可能
5、(1)10-(______)=15 (3)(____)-(+8)=-4
(2)-7-(_____)=+5 (4)(____)-(-1.2)=-2.4
1.3.2 有理数减法(1)
-6 1、( 5 ) ( 1) ___
-4 2、( 8 ) ( 4 ) ______
0 3、( 205 ) 205 ____ 4、0 1999
-1999
___
35 5、 1 . 5 36 . 5 ________
1、-2的相反数是_________,+0.3的相反数是_________。
2、相反数是它的本身的数是_______,________的相反数 大于0。 3、绝对值是它本身的数是_______. 4、计算: 2 (1)10-8=____ 8 (3) 21-13=___ 2 (2) 10+(-8)=_____ 8 (4) 21+(-13)=_____
课堂小结
1、本课学习了有理数的减法运算,在进行 有理数减法运算时,我们先把减法运算转 化为加法,然后再根据加法运算的法则进 行。 2、在进行有理数减法运算时,要注意两变一不 变,“两变”即减号变成加号,减数的符号要改 变;“不变”是指被减数不变。
有理数的减法(1)
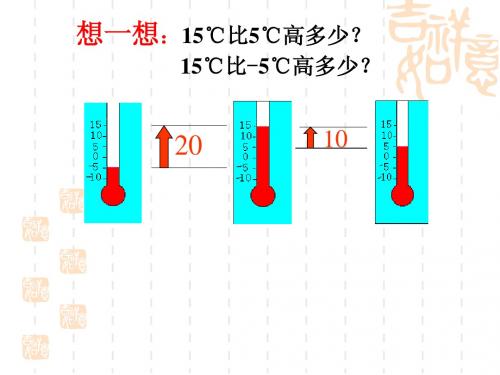
想一想:15℃比5℃高多少?
15℃比-5℃高多少? 解: 15 – 5 = 10 15 –(–5)= 20 答:15º C比5º C高10º C,15º C比–5º C高20º C.
你发现了什么?
(2)减数变为它 的相反数
5 (-3)-(-5)=(-3)+___
有有理数减法法则理数的减法法 则:
减去一个数练习:
⒈计算:
⑴(-11)-(-13) ⑵(-3.4)-(-2.7) ⑶(+5)-(-11) ⑷ (-13)-(+25)
想一想:15℃比5℃高多少?
15℃比-5℃高多少?
20
10
数
学
七年级 (上)
1.3.2 有理数的减法
学习目标:
会将有理数的减法转换成 有理数的加法进行运算.
自学指导:
认真看P.21-22. ⑴换几个数完成探究
⑵理解有理数减法的法则;
⑶看例题时思考每一步的依据.
试一试:
(-5) (-3)-5=(-3)+___ (1)减号变为加 5 3-(-5)=3+___ 号 (-5) 3-5=3+___
小结与回顾
请你计算以下各城市的日温差
北京
0~8℃
天津
-2~9℃
沈阳
长春
哈尔滨
-7~2℃ -10~1℃ -14~ -5℃
课堂作业
.必做题 : P.25 3 , 4 选做题: 1.一架直升飞机在海 平面上方80米处记作+80米,一
2.2有理数的减法(1)——黄有宇

这一天内 杭州的温差 是多少呢?
4
4 3 2 1 0 -1 -2 -3 -4
-
(-3)
4 3 2 1 0 -1 -2 -3 -4
= 7 ?
4 3 2 1 0 -1 -2 -3 -4
4
-
=
3
4 +3= 7
观察
这两个式子有什么相同
和不同的地方?
4 -(-3)=7
4 + (+3)=7
计算下列各题:
30 50 20 _____,
一个数与它的相反数的差是什么 数?你能举例加以说明吗?
在数轴上,点A、B、C、D表示的有理 数分别是+1,+5,-2,-3,请问以下 两点间的距离是多少:
(1)A、B两点;
(2)C、D两点; (3)A、D两点;
两点所表示的 有理数的差与 两点间的距离 有什么关系吗?
已知有理数 a, b在数轴上对应点的位置 如图所示。 化简: b a b b a a
本分为100分,答对一题加50分,答错一题扣50
分,游戏结束时,各组的分数如下:
第一组 第二组
第三组 第四组 第五组 -400 350 -100
100
150
(1) 第一名超出第二名多少分? (2) 第二名超出第五名多少分?
受台风“莫拉克”的影响,8月8号, 钱塘江水位超过警戒线10厘米,8月9号 由于暴雨,江水继续上涨20厘米,截至 11号,水位开始下降,比警戒线低了16 厘米,求最高水位比最低水位高多少?
30-(-16)=30+16=46
1. 填空:
(1)温度3℃比-8℃高 11 ℃ ;
(2)温度-9℃比-1℃低 8℃ ;
160m (3) 海 拔 高 度 -20m 比 -180m 高 ; 72m
2.2 有理数的减法(1)

有理数减法法则 减去一个数,等于加上这 个数的相反数
a-b=a+(-b)
范例
(1)0-(-3) (2)(-5)-3 (3)13-(-13)
例1
计算: (1) 5 - (-5);
(2) 0 - 7 - 5 ;
(3) (-1.3)- (-2.1);
1 1 (4) 1 2 ; 3 2
小结:
1.有理数的减法一般是将其先转化 为加法,再来计算的。 2.转化的法则是:减去一个数,等 于加上这个数的相反数。(被减数 永远不变)
下表列出了外国几个城市与北京的时间差。 (带正号的数表示同一时刻比北京时间早的数值, 带负号的数表示同一时刻比北京时间晚的数值。 单位:小时)
城市 时差 东京 纽约 巴黎 芝加哥
+1
-13
-7
-14
(1)如果现在的北京时间是7:00,那么现在的 纽约时间是多少? (2)远在巴黎的姑妈,在当地时间是7:00时 想给芝加哥的舅妈打电话,你认为合适吗?
解:-392-(-155)=-392+155=-237(米) 答:两者相比,死海的湖面更低, 比吐鲁番盆地最低点低237米。
1、口算:
8 -2 (1)3-5=___;( 2)3-(-5)=___; 2 -8 ;(4)(-3)-(-5)=____ (3)(-3)-5=______ ; 0 -7 (5)-6-(-6)=____ __;(6)-7-0=___; -12 ; (7)0-(-7)=______;(8)(-6)- 6=_____ 20 (9) 9 -(-11)=___; 7
2、下列说法中正确的是( B ) A、两个数的差一定小于被减数 B、若两个数的差为0,则这两数必 相等 C、零减去一个数一定得负数 D、一个负数减去一个负数结果仍 是负数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姜卫红课堂实录
2.2 有理数的减法(1)
师:前面两节课我们已经学习了有理数的加法,下面先请同学几个同学口答,并说明理由。
(1)(-15)+0= (2)(-2) + (-5)= (3)-6 + (+2)= (4)+ 6 + (-2)= (5)(-2)+2= 生1:-15,理由:一个数同0相加,仍得这个数。
生2:-7,理由:同号两数相加,取与加数相同的符号,并把绝对值相加。
生3:-4 ,理由:异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
生4:4,理由:异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
生5:0,理由:互为相反数的两个数相加得0.
师:很好,下面再看一个题
根据昨晚中央电视台的天气预报,今天宁波的最低温度为+13℃,而北国哈尔滨的最低气温为—5℃,那么今天宁波比哈尔滨的最低气温高多少?
列式13—(—5)=□
这就是今天我们要学习有理数的减法,我们知道减法是加法的逆运算,下面请一些同学来口答:
(1)∵(-7)+16= ∴ -(-7)=16 ;
9+(+7)=
(2)∵50+(-10)= ∴–50 = -10 ;
40+(-50)=
(3)50 –0 = 50 + 0 = ;
(4)50 –(-20)= 50+(+20)= ;
想一想:你能得出什么结论?
生1:(1)∵(-7)+16= 9∴ 9 -(-7)=16 ;
9+(+7)= 16
生2:(2)∵50+(-10)= :40 ∴40 –50 = -10 ;
40+(-50)=-10
生3:(3)50 –0 = 50 50 + 0 = 50
生4:(4)50 –(-20)= 70 50+(+20)= 70 ;
生5:减去一个数,等于加上这个数的相反数
师:这就是减法法则
教师板书
有理数的减法法则:减去一个数,等于加上这个数的相反数
师:注意在减号变加号时,减数一定要变成相反数。
例1:计算
(1) 5 – (-5)
(2) 0-7- 5
(3) (-1.3) – (-2.1)
(4) (-51) + (-2.2) – (-10.8)
板书
解:(1)5 – (-5)=5+5=10
(2) 0-7- 5 =0+(-7)+(-5)=(-7)+(-5)= -12
(3) (-1.3) – (-2.1) =(-1.3)+2.1=2.1-1.3=0.8
(4) (-51) + (-2.2) – (-10.8) = -53.2+10.8= -42.4
师:注意,在计算时将减法先改成加法,再利用加法法则和加法运算律进行计算,减号改加号时,减数要变相反数,但是加号后面的加数不要也变成相反数。
练一练
1. 下列括号内各应填什么数?
(1)(-2)-(-3)=(-2)+();
(2)0 - (-4)= 0 +();
(3)(-6)- 3 =(-6)+();
(4)1-(+39)= 1 +()
学生口答
2. 计算:
(1)(+3)-(-2);(2)(-1.3)-(+2.1);
(3)0 -3;(4)23- 27;
(5)(-23.6)-(-12.4);(6)(-2/3)- ( - 5/6)
请六位学生到黑板上板演
生1:(1)原式=3+2=5 生2:原式= -1.3+2.1=0.8
生3:原式= 3 生4:原式=23+(-27)= -4
生5:原式= (-23.6)+12.4=11.2 生6:原式=(-2/3)+(+ 5/6)=1/6
师:大家检查一下上面同学是否有错,有错,请指出错误原因
生7:第2题错,减数没有变相反数,答案应该是-3.4
生8:第3题错,减数没有变相反数,答案应该是-3
师:我们可以从第3题得出一个结论,零减去一个数等于这个数的相反数。
生9:第5题错,加法算错,漏掉负号。
师:很好,在做计算题时,我们一定要小心,负号不要忘记,减号改加号时,减数要变相反数。
下面再看一个题目
例2、我国吐鲁番盆地最低点的海拔是-154米,死海湖面的海拔是-392米,哪里的海拔更低?低多少?
这个题目上次我们碰到过,是比较高低,现在要算低多少,用减法,哪个作为被减数,哪个作减数?
生1:解-392 - (-154)= -392+154= -238(米)答:死海的湖面海拔更低,低238米。
生2:解-154> -392-154- (-392)= -154+392=238(米)答:死海的湖面海拔更低,低238米.
师:这两种方法都对,第一种方法中负号表示低。
下面我们再来做练习
3. 填空:
(1)温度3℃比-8 ℃高;
(2)温度-9 ℃比-1 ℃低;
(3)海拔-20m比-30m高;
(4)从海拔22m到-10m,下降了
请一组同学口答
生1:11℃,
生2:8℃,
生3:10米,
生4:32米,
师:很好,全对,再看下一题
4:全班学生分成两个组进行游戏,答对一题加50分,答错一题扣50分,游戏结束时,各组分数如下:
(1)第一名超过第二名多少分?
(2)第一名超过第5名多少分?
生1: 解350-150=200(分)350-(-400)=750(分)答:第一名超过第二名200分,第一名超过第5名750分.
师:这个题应先比较各数的大小,再计算。
5.某地连续五天内每天的最高气温与最低气温记录如下表所示,哪一天的温差(最高气温与最低气温的差)最大,哪一天的温差最小?
生2:解:-1-(-7)=6;5-(-3)=8;6-(-4)=10;8-(-1)=9;11-2=9
答:第三天的温差最大,第一天的温差最小。
6.数轴上-4和4.5所对应的两点之间的距离是多少?数轴上-9和-5所对应的两点之间的距离是多少?数轴上7和4.5所对应的两点之间的距离是多少?数轴上m和n所对应的两点之间的距离是多少?
生:4.5-(-4)=8.5;-5-(-9)=4;7-4.5=2.5;m-n;
师:我们知道数轴上右边的点表示的数总比左边的大,所以只要右边的数减去左边的数,但是m,n这两个数没有告诉我们大小,而距离是正的,所以为了保证是正的,我们只要加个绝对值,即︱m-n︱.
通过本节课的探讨学习,你获得哪些新知识?
生1:减法法则:减去一个数,等于加上这个数的相反数
生2:会减法运算
生3:知道两点间距离的求法
师:大家在做减法运算时一定要注意减号改加号时,减数要变相反数。
作业:作业本和作业优化中2.2(1)。
