第七八章 稳恒磁场 电磁感应例题作业
稳恒磁场练习题答案
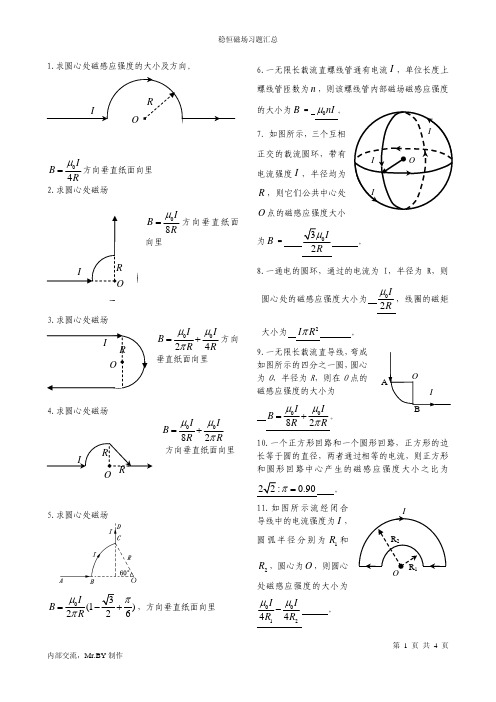
1.求圆心处磁感应强度的大小及方向。
04B R=方向垂直纸面向里2.求圆心处磁场08IB Rμ=方向垂直纸面向里3.求圆心处磁场024I IB R Rμμπ=+方向垂直纸面向里4.求圆心处磁场0082IIB RRμμπ=+方向垂直纸面向里5.求圆心处磁场(1226I B R μππ=−+,方向垂直纸面向里 6.一无限长载流直螺线管通有电流I ,单位长度上螺线管匝数为n ,则该螺线管内部磁场磁感应强度的大小为B = 0nI μ。
7.如图所示,三个互相正交的载流圆环,带有电流强度I ,半径均为R ,则它们公共中心处O 点的磁感应强度大小为B =02IR。
8.一通电的圆环,通过的电流为I,半径为R,则圆心处的磁感应强度大小为02IRμ,线圈的磁矩大小为 2I R π 。
9.一无限长载流直导线,弯成如图所示的四分之一圆,圆心为O ,半径为R ,则在O 点的磁感应强度的大小为 0082IIB RRμμπ=+。
10.一个正方形回路和一个圆形回路,正方形的边长等于圆的直径,两者通过相等的电流,则正方形和圆形回路中心产生的磁感应强度大小之比为11.如图所示流经闭合导线中的电流强度为I ,圆弧半径分别为1R 和2R ,圆心为O ,则圆心001244IIR R μμ−。
12.一载有电流强度为I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管,两螺线管单位长度上的匝数相等。
设2R r =,则两螺线管内部的磁感应强度的大小比值为:RrB B =1:1 。
13. 在同一平面上有三根等距离放置的长通电导线,如图所示,导线1、2、3分别载有1A 、2A 、3A 的电流,它们所受的安培力分别为1F 、2F 、3F ,则12F F = 7/8 ;13F F = 7/15 ;23F F = 8/15 。
(0174F d μπ=,0284F d μπ=,03154F dμπ=;故1278F F =,13715F F =,23815F F =) 14. 如图所示,长直导线中通有稳恒电流1I ,在其旁边有一导线段ab ,长为L ,距长直导线距离为d ,当它通有稳恒电流2I 时,该导线ab 所受磁力大小为012ln 2I I d Ld μπ+ 。
第7章 稳恒磁场习题解答

40 第7章 稳恒磁场7-1 如图,一个处在真空中的弓形平面载流线圈acba ,acb 为半径cm 2=R 的圆弧,ab 为圆弧对应的弦,圆心角090aob ∠=, A 40=I ,试求圆心O 点的磁感应强度的大小和方向。
解 由例7-1 线段ba 的磁感应强度 o o 40140(cos45-cos135) =410T4π0.02cos45B μ-=⨯⨯︒方向垂直纸面向外。
由例7-2 圆弧 acb的磁感应强度 4002π1402 3.1410T 2π2420.02I μB R μ-==⨯=⨯方向垂直纸面向内。
4120.8610TB B B -=-=⨯方向垂直纸面向外。
7-2 将载流长直导线弯成如图所示的形状,求圆心O 点处磁感应强度。
解 如图,将导线分成1(左侧导线)、2(半圆导线)、3(右侧导线)三部分,设各部分在O 点处产生的磁感应强度分别为1B 、2B 、3B。
根据叠加原理可知,O 点处磁感应强度321B B B B ++=。
01=B024I B Rμ=,方向垂直于纸面向里034πI B Rμ=,方向垂直于纸面向里O 点处磁感应强度大小为0O 23(1π)4πIB B B Rμ=+=+ ,方向垂直于纸面向里。
7-3 一圆形载流导线圆心处的磁感应强度为1B ,若保持导线中的电流强度不变,而将导线变成正方形,此时回路中心处的磁感应强度为2B ,试求21:B B解 设导线长度为l ,为圆环时, 2πl R = 001π2I I B R l μμ==为正方形时,边长为4l,由例7-100024(cos 45cos135)4π8IBlμ=⨯-=⨯习题7-1图41212 :πB B =7-4 如图所示,一宽为a 的薄长金属板,均匀地分布电流I ,试求在薄板所在平面、距板的一边为a 的点P 处的磁感应强度。
解 取解用图示电流元,其宽度为d r ,距板下边缘距离为r ,其在P 点处激发的磁感应强度大小为00d d d 2π22π(2)II r B (a r)a r aμμ==--,方向垂直于纸面向外。
稳恒磁场习题

稳恒磁场
1.已知一均匀磁场,其磁感应强度2m wb 0.2-⋅=B ,方向沿x 轴方向,如图所示,试求:(1)通过图中a b o c 面的磁通量;(2)通过图中b e d o 面的磁通量;(3)通过图中a c d e 面的磁通量;
2.电流均匀地流过无限大平面导体薄板,面电流密度为j ,设板的厚度可以忽略不计,
试用毕奥一萨伐尔定律求板外的任意一点的磁感应强度。
3二条长直载流导线与一长方形线圈共面,如图所示.已知a = b = c = 10cm ,l = 10m ,I 1 = I 2 = 100A ,求通过线圈的磁通量.
4载有电流I 1 的无限长直导线旁有一正三角形线圈,边长为a ,载有电流I 2,一边与直导线平等且与直导线相距为b ,直导线与线圈共面,如图所示,求I 1 作用在这三角形线圈上的力.
5 无限长同轴电缆的横截面如图所示,内导线半径为a ,载正向电流I ,圆筒形外导线的内外半径分别为b 和c ,载反向电流I ,求磁感应强度的分布.
j cm
30x z B O a b e d c y cm 30cm 50cm 40。
大学物理稳恒磁场习题及答案

衡水学院 理工科专业 《大学物理B 》 稳恒磁场 习题解答一、填空题(每空1分)1、电流密度矢量的定义式为:dIj n dS ⊥=,单位是:安培每平方米(A/m 2) 。
2、真空中有一载有稳恒电流I 的细线圈,则通过包围该线圈的封闭曲面S 的磁通量? = 0 .若通过S 面上某面元d S 的元磁通为d ?,而线圈中的电流增加为2I 时,通过同一面元的元磁通为d ?',则d ?∶d ?'= 1:2 。
3、一弯曲的载流导线在同一平面内,形状如图1(O 点是半径为R 1和R 2的两个半圆弧的共同圆心,电流自无穷远来到无穷远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=。
4小为πR 2c Wb。
5、如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情况下,等于:对环路a :dB l ⋅⎰=____μ0I __; 对环路b :d B l ⋅⎰=___0____; 对环路c :d B l ⋅⎰ =__2μ0I __。
6、两个带电粒子,以相同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,运动轨迹半径之比是_____1∶2_____。
二、单项选择题(每小题2分)( B )1、均匀磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为A. 2?r 2BB.??r 2BC. 0D. 无法确定的量( C )2、有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B 1 / B 2为A. 0.90B. 1.00C. 1.11D. 1.22( D )3、如图3所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度A. 方向垂直环形分路所在平面且指向纸内B. 方向垂直环形分路所在平面且指向纸外C .方向在环形分路所在平面内,且指向aD .为零( D )( C )??绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B 1;此正方形同样以角速度??绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感强度的大小为B 2,则B 1与B 2间的关系为A. B 1 = B 2B. B 1 = 2B 2 C .B 1 =21B 2 D .B 1 = B 2 /4 ( B )6、有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的 (A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4. (D) 2倍和1/2. 三、判断题(每小题1分,请在括号里打上√或×)( × )1、电源的电动势是将负电荷从电源的负极通过电源内部移到电源正极时,非静电力作的功。
(完整版)稳恒磁场作业习题及参考答案.doc

赵近芳编大学物理学 ch9. 稳恒磁场 作业习题及参考答案9-6 已知磁感应强度B 2.0 Wb ·m -2 的均匀磁场,方向沿x 轴正方向,如题 9-6 图所示.试求:(1) 通过图中 abcd 面的磁通量; (2) 通过图中 befc 面的磁通量; (3)通过图中 aefd 面的磁通量.解: 如题 9-6 图所示(1) 通过 abcd 面积 S 1 的磁通是 : 1B S 1 2.0i (0.3 0.4)i 0.24 ( Wb )(2) 通过 befc 面积 S 2 的磁通量 :2B S 22.0i (0.3 0.3)k(3) 设 aefd 面积 S 3 的法线正方向如图,则通过aefd 面积 S 3 的磁通量:3 B S 32 (0.30.5)cos20.15 4 0.24 ( Wb )题 9-6 图59-7 如题 9-7图所示, AB 、 CD 为长直导线, BC 为圆心在 O 点的一段圆弧形导线,其半径为R .若通以电流 I ,求 O 点的磁感应强度.解:如题9-7 图所示, O 点磁场由 AB 、 BC 、 CD 三部分电流产生.其中AB 段产生: B 1BC 段产生:B 2 0I60I(即垂直纸面向里)2R 360,方向题 9-7 图12 RCD 段产生: B 3I (sin 90 sin 60 ) 0I (13) ,方向4 R2 R 22【或: B 3I(cos120cos180 )I(13) ,方向 】4 R2 R22∴B 0B 1B 2B 30 I(13 ) , 方向 .2 R2 69-8 在真空中,有两根互相平行的无限长直导线L 1 和 L 2 ,相距 0.1m ,通有方向相反的电流, I 1 =20A,I 2 =10A ,如题 9-8图所示. A , B 两点与导线在同一平面内.这两点与导线L 2 的距离均为 5.0cm .试求 A , B 两点处的磁感应强度,以及磁感应强度为零的点的位置.解:如题 9-8 图所示, B A 方向垂直纸面向里,大小为:B A0 I120 I21.2 10 4 T2 (0.1 0.05)0.05B B 方向垂直纸面向外,大小为:0 I10 I21.33 10 5 T题 9-8 图B B22 (0.1 0.05) 0.05设 B0在 L 2 外侧距离 L 2 为 r 处,则II 20 , 解得: r 0.1 m9-12 两平行长直导线相距d =40cm ,每根导线载有电流 I 1 = I 2 =20A ,如题 9-12图所示.求:(1) 两导线所在平面内与该两导线等距的一点A 处的磁感应强度;(2) 通过图中斜线所示面积的磁通量. ( r 1 = r 3 =10cm, l =25cm) .解: (1) B A0 I10 I24 105 (T) 方向纸面向外2 ( d) 2 ( d)22题 9-12 图(2)dS ldr ,则: dB dS Bldr取面元d r 1 r 2 0 I 1 0 I 2]ldr0 I 1lln 30 I 2 lln1I 1lln 3 2.2 106( Wb )r 1 [S2 r2 (d r )2239-13 一根很长的铜导线载有电流 10A ,设电流均匀分布。
8稳恒磁场与电磁感应综合练习

稳恒磁场与电磁感应(综合练习)一. 1.BCD 2.D 3.B 4.A 5.CF解 1. 无旋场在任一个闭合回路上的积分为0,我们学过的场中只有静电场;其他三种场都是涡旋场(有旋场) 3. 由于金属框的磁通量m φ始终为0,旋转时未变, 所以0i ε=. 而组成金属框的三段线中,ab 上的 感应电动势为0,因此bc 和ac 上的感应电动势 大小相等,相互抵消。
我们先计算bc 上的感应电动势bc ε,在距b 端为任意l 处取dl 如图,dl上的感应电动势()d d i d v B l lB l εω=⨯⋅=bc 上 201d 2l bc i d lB l B l εεωω===⎰⎰,向右,如图ac 上的感应电动势要和bc 抵消,则大小相同,方向如图。
因此c 点电势比a点高,212a c U U B l ω-=-4. 由安培环路定理0LB dl I μ⋅=⎰内,可得内部r R <处磁场有2022r B r I R ππμπ⋅=, 即022Ir B R μπ=。
如图,单位长度取r r dr →+,磁能222320024402d 1d 284I r I r B dW dV r r r R R μμπμππ==⋅⋅= 则单位长度磁能2320040d 416RI r I W dW r R μμππ===⎰⎰5. 螺线管电流随时间均匀变化,因此螺线管内有均匀变化....的磁场,该磁场在螺线管内外均产生涡旋电场,而且电场不随时间变化(见笔记例题),因此A 错误;螺线管内磁场变化,因此B 错误; 由于磁场和涡旋电场场线闭合,因此通过任一闭合曲面的通量都为0,C 正确 ;螺线管无磁场,但有磁场激发产生的涡旋电场(见笔记例题),因此电子受力运动,D 错误; 由于0d 0d m i Ld B d IE d l S nS t d t d tφμ⋅=-=-=->⎰ ,(或由楞次定律)可得i E 与磁场成右手关系,因此i E方向为顺时针,电子带负电,因此受力为逆时针方向,作逆时针运动,因此F 正确,E 错误。
磁学和电磁感应(第七章和第八章)作业讲评

0i
2a0
0e
2 2
1 m e 0 a 0
8a0
其方向垂直纸面向外
第七章 恒定电流和磁场(二)
1 长直电流I2与圆形电流I1共面,并与其一直径相重合如图(但两者 间绝缘),设长直电流不动,则圆形电流将 dF (A) 绕I2旋转. (C) 向右运动. (E) 不动. 分析:圆形电流上所有电流元所受的长直电流的磁场力都在屏 幕平面上,右边的力沿径向向外,而左边的沿径向向内,所以 合力向右 它们所受的最大磁力矩之比M1/M2等于 (A)1 (C) 4 分析: M IS e n B p m B (B)2 (D) 1/4 (B) 向左运动. (D) 向上运动.
5.如图所示,在宽度为d的导体薄片上有电流I沿此导体长度方向流 过,电流在导体宽度方向均匀分布.导体外在导体中线附近处P点 的磁感强度B 的大小为 0 I /( 2 d ) . 俯 I 分析:考虑导体中线附近处P点的磁感强度时,可认 视 图 为电流分布具有面对称性,此时板外磁场方向平行 d d 于板面并与电流方向垂直,建立关于板面对称的矩 I 形回路,利用安培环路定理求解。 P
q C 0 .2 C
1 C
t
idt
0
t
(1 e
) (SI)
(2) 由全电流的连续性,得
I d i 0 . 2 e t (SI)
5.均匀带电刚性细杆AB,电荷线密度为λ,绕垂直于直线的轴O 以角速度ω匀速转动(O点在细杆AB延长线上).求:(1)O点的 磁感应强度 ;(2)磁矩 P;(3)若a>>b,求 B 和 Pm O B m O dq 解:(1) r~r+dr段电荷 dr a dI dq = dr旋转形成圆电 2 2 A 流 0 d I 0 d r b 它在O点的磁感强度 d B 0
稳恒磁场习题(包含答案)

练习八磁感应强度毕奥—萨伐尔定律(黄色阴影表示答案) 一、选择题如图所示,边长为l的正方形线圈中通有电流I,则此线圈在: AlIπμ220.(C)lIπμ2(D) 以上均不对.电流I由长直导线1沿对角线AC方向经A点流入一电阻均匀分布的正方形导线框,再由D点沿对角线BD方向流出,经长直导线2返回电源, 如图所示. 若载流直导线1、2和正方形框在导线框中心O点产生的磁感强度分别用B1、B2和B3表示,则O点磁感强度的大小为:A(A) B = 0. 因为B1 = B2 = B3 = 0 .(B) B = 0. 因为虽然B1 0, B2 0, B1+B2 = 0, B3=0(C) B 0. 因为虽然B3 = 0, 但B1+B2 0(D) B0. 因为虽然B1+B2 = 0, 但B3 03. 如图所示,三条平行的无限长直导线,垂直通过边长为a 的正三角形顶点,每条导线中的电流都是I,这三条导线在正三角形中心O点产生的磁感强度为:B(D) B=30I/(3a) . .如图所示,无限长直导线在P处弯成半径为R的圆,当通以电流I时,则在圆心O 点的磁感强度大小等于:C(A)RIπμ20.(B)Iμ.(D) )11(4πμ+RI.二、填空题如图所示,在真空中,电流由长直导线1沿切向经a点流入一电阻均匀分布的圆环,再由b点沿切向流出,经长直导线2返回电源.已知直导线上的电流强度为I,圆环半径为R,aob=180.则圆心O点处的磁感强度的大小B = .0图图图图图I练习九毕奥—萨伐尔定律(续)一、选择题1. 在磁感强度为B的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量n与B的夹角为,如图所示. 则通过半球面S的磁通量为:(A) r2B.(B) 2r2B.(C) r2B sin.(D) r2B cos.如图,载流圆线圈(半径为R)与正方形线圈(边长为a)通有相同电流I ,若两线圈中心O1与O2处的磁感应强度大小相同,R: a为(A) 1:1.(B) π2:1.三、计算题1.在无限长直载流导线的右侧有面积为S1和S2的两个矩形回路,回路旋转方向如图所示, 两个回路与长直载流导线在同一平面内, 且矩形回路的一边与长直载流导线平行. 求通过两矩形回路的磁通量及通过S1回路的磁通量与通过S2回路的磁通量之比.(此题作为悬赏题)练习十安培环路定理一、选择题2. 无限长直圆柱体,半径为R,沿轴向均匀流有电流. 设圆柱体内(r< R)的磁感强度为B1,圆柱体外(r >R)的磁感强度为B2,则有:(A) B1、B2均与r成正比.(B) B1、B2均与r成反比.(C) B1与r成正比, B2与r成反比.(D) B1与r成反比, B2与r成正比.在图(a)和(b)中各有一半径相同的圆形回路L1和L2,圆周内有电流I2和I2,其分布相同,且均在真空中,但在图(b)中,L2回路外有电流I3,P1、P2为两圆形回路上的对应点,则:(A) ⎰⋅1dLlB=⎰⋅2dLlB,21PPBB=.(B) ⎰⋅dLlB⎰⋅dLlB,21PPBB=.图图图图P1L(a)3P2(b)图(D)⎰⋅1d L l B ⎰⋅2d L l B , 21P P B B≠.如图所示,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,恒定电流I 从a 端流入而从d 端流 出,则磁感强度B 沿图中闭合路径的积分⎰⋅Ll B d 等于:(A) 0I . (B) 0I /3. (C) 0I /4. (D) 20I /3 . 如图,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理(B) 0 d =⋅⎰L l B ,且环路上任意点B =0. (C) 0 d ≠⋅⎰Ll B ,且环路上任意点B 0. (D) 0 d ≠⋅⎰Ll B,且环路上任意点B =0.二、填空题两根长直导线通有电流I ,图所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰bL l B d ;对于环路c ,=⋅⎰cL l B d . 0I , 0, 20I .练习十一安培力 洛仑兹力一、选择题如图所示. 匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是:B(A) ab 边转入纸内,cd 边转出纸外. (B) ab 边转出纸外,cd 边转入纸内. (C) ad 边转入纸内,bc 边转出纸外. (D) ad 边转出纸外,cd 边转入纸内.5. 一电子以速度v 垂直地进入磁感强度为B 的均匀磁场中,此电子在磁场中运动的轨道所围的面积内的磁通量是(A) 正比于B ,反比于v 2. (B) 反比于B,正比于v 2.图图图(C) 正比于B ,反比于v. (D) 反比于B ,反比于v练习十三 静磁场习题课一、选择题1. 一质量为m 、电量为q 的粒子,以与均匀磁场B 垂直的速度v 射入磁场中,则粒子运动轨道所包围范围内的磁通量m 与磁场磁感强度B 的大小的关系曲线是图中的哪一条 D边长为l 的正方形线圈,分别用图所示两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为:(A) B 1 = 0 . B 2 = 0.(B) B 1 = 0 . lIB πμ0222=lπ01l Iπμ0222.如图, 质量均匀分布的导线框abcd 置于均匀磁场中(B 的方向竖直向上),线框可绕AA 轴转动,导线通电转过 角后达到稳定平衡.如果导线改用密度为原来1/2的材料做,欲保持原来的稳定平衡位置(即 角不变),可以采用哪一种办法(A) 将磁场B 减为原来的1/2或线框中电流减为原来的1/2. (B) 将导线的bc 部分长度减小为原来的1/2. (C) 将导线ab 和cd 部分长度减小为原来的1/2. (D)将磁场B 减少1/4,线框中电流强度减少1/4.图图l (1)d图(A)(D) (C)(B) (E)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题
例1 真空中 载流长直导线的磁感应强度。
dB 方向均沿 x 轴的负方向
z
D
2
解 dB
0 Idz sin
4π r
2
dz
I
z
1
r
r0
*P
dB
y
0 Idz sin B dB 4π CD r 2
z r0cot , r r0 / sin
C
B
A
dF2
F2 x 0 F2 F2 y j
F2 dF2 y dF2 sin
I
0
r
o F 1
Idl
0
x
F2 dF2 y dF2 sin BIdl sin
因
dl rd
F2 BI (2r cos 0 ) j BI AB j 由于 F1 BI AB j dF2 故 F F1 F2 0
由
(v B) dl vBl
将数据带入上式,得飞机飞行时机翼两端的电势差为
U A U B Blv
代入数据得
。
U A U B 0.2V
2 8-7 有一面积为 0.5 m 的平面线圈,把它放入匀强磁场中,
dB 2 2 10 T s 时,线圈中感 线圈平面与磁感应线垂直。当 d t
d
例 5 如图一通有电流 I 的闭合回路放在磁感应强度为 B 的均 匀磁场中,回路平面与磁感强度 B 垂直 .回路由直导线 AB 和半 径为 r的圆弧导线 BCA 组成 ,电流为顺时针方向,求磁场作用于 闭合导线的力.
解 F 1 I ABBj
根据对称性分析
dF2
B
y
Idl
dz r0d / sin
2
x
o
C
B
0 I
4π r0
2
1
sin d
B
0 I
4π r0
2
1
0 I (cos1 cos 2) sin d 4π r0
P点:
B 的方向沿 x 轴的负方向.
I B
I
X
B
无限长载流长直导线的磁场.
B
(cos1 cos 2) 4π r0
0 Idl
4π R 2
Idl
R
6 + 4
2、4、6、8 点 :
dB
0 Idl
4π R
2
sin 45
0
5
2 求磁感应强度沿闭合路径的环流 对闭合回路 C1
C2
B dl 0 ( I 2 I1)
C1
I1 I
I2
3
C1
对闭合回路 C2
C B
2
dl 0 (I 2 I 4 I1 I3 )
应电动势的大小是多少? 解:
dm d( BS ) dB S 0.5 (2 10-2) =-1.0 10-2 V dt dt dt
解: B = B1 B2
B1 =
r
0 Idl
4R
2
=
0 I
4R
2
R
0
dl
0 I
4R
方向垂直纸面向里
B2 =
0 I
4r
方向垂直纸面向外
B = B2 B1 =
0 I
4 Rr
(R r)
方向垂直纸面向外
*7-3一正六边形载流导线,通有电流 I,顺时针流动,导线边长 为a ,求载流导线中心处磁感应强度大小及方向。
第八章 电磁感应 电磁场理论
例题
L 例1 一长为 的铜棒在磁感强度为B 的均匀磁场中, 以角速度在
与磁场方向垂直的平面上绕棒的一端转动,求铜棒两端的感应电 动势.
解
d i (v B) dl
i (v B) dl
i vBdl
注意:可以证明,在均匀磁 场中,任意形状的载流导线 闭合回路的平面与磁感强度 垂直,此闭合回路不受磁场 力的作用.
F2 BIr
π 0
0
sin d
y
Idl
B
C
Idl
B 0
I
d
o F 1
r
0
A
x
练习
1 判断下列各点磁感应强度的方向和大小.
1
8
7
+
2
+3
1、5 点 : dB 0 3、7点 : dB
IR
00IR 2
若线圈有N 匝
2 N 0 IR B 2 2 3
2 2 x R) (
大小:
B
0 IR 2
2( R x )
2 2 32
I
O
R
B
X
方向: 右手螺旋法则
圆心 讨 论
x0
B
(1) 载流圆环
B
0 I
2R
I
(2) 载流圆弧
0 I B 2 R 2 4R
90 , sin 1
dF12 B12 I 2dl2
0 I1I 2 dl2
2πd
d
dF12 0 I1I 2 dl2 2πd
1
I1dl1 B21
I2
I 2dl2 B12 dF21dF 12
dF21 dF12 0 I1I 2 dl1 dl2 2πd
I4 I5
3 均匀磁场中放置一半径为R的半圆形导线,电 流强度为I,导线两端连线与磁感强度方向夹角 = 30°,求此段圆弧电流受的磁力大小。
I l
B
F IRB
作业
P155 *7-1 半径分别为R , r 的同心半圆,相邻两端点由直导线连 接组成回路。现在回路中通以稳恒电流 ,在大半圆上为顺时针, I 求圆心处的磁感应强度。
0 I
B
I
例 4 设在真空中有两根相距为d 的无限长平行直导线, 分别通 以电流I1 和 I,且电流的流向相同,试求单位长度上的导线所受 2 的安培力为多少?
解: B12
0 I1
2πd
I1
I1dl1 B21
I2
I 2dl2 B12 dF21dF 12
dF12 B12 I 2dl2 sin
(× )
2 均匀磁场中,平行放有一个铜环A、一个木环B,如图所示, 比较环中的感应电动势的大小。 相等
作业
1 ,以200m s 的航速水平地飞行。 8-4 飞机金属机翼的两端相距20m
4 如果地磁场的磁感强度的铅直分量为0.5 10 T , 求机翼两端
的电势差。
解:由题意知,
l
vlB
三者互相垂直,
解:正六边形六边产生的磁感应强度大小相等,方向相同, 与电流方向符合右手螺旋定则,每一边产生的磁感应强度为
30 I B a
故正六边形在中心处产生的磁感应强度为
30 I B a
方向垂直纸面向里
7-6 两平行放置的长直载流导线相距为 d,分别通有同向的电流
I 和 2 I , 求与两导线距离相等一点的磁感应强度的大小。
解:磁感应强度B 是由两根载流导线各自产生的磁感应强
度的叠加,其大小为
B
0 2I
d 2
0 I
d 2
0 I
d
7-10 求均匀磁场中半球面的磁通量。
解:通过圆心做个大圆和半球面构成一闭合曲面,由磁场 的高斯定理可知通过这一闭合曲面的磁通量为零。故通过
半球面的磁通量为
Φm BR2
Idl
r
o
R
I
解 根据对称性分析 B dB 0
dB
dB
p *
x
0 Id l
4π r 2
0 IR 2 B dB 2||R 2R 3 33 3 方向:右手螺旋法则 2 2 2 2 2 2 2 2 22 x ) 42 ((R R x x )) 2( R x ) 2
B
0 I
D
z
2
B
r0
1 0 2 π
0 I
2π r0
I
o
x
C
1
P
y
半无限长载流长直导线的磁场
π 1 0或 2 π 2 或 π 2
BP
0 I
4 π r0
I
o
r0
* P
例2 圆形载流导线的磁场. 真空中 , 半径为R 的载流导线 , 通有电流I , 求其轴线上一点 p 的磁感强度的方向和大小.
lBdl 0 1 2 i B L 2
0 L L
+ + + + + + + +
+ + +
+ + dl + +
+ + +
P
+ + + +
B
+ + +
o v + + +
P
+ + + + + + +
i 方向
O
练习
1.矩形闭合导体回路在稳恒磁场中作匀速运动,将会产生感应电 流
