重庆一中高2022级高二上期10月月考【附答案】
2022年重庆一中高2023届10月月考语文试题参考答案

2023届10月月考语文参考答案1.B A“儒家的重要经典《春秋》”错,还有其他儒家经典,如《诗经》《尚书》等。
C“马融、郑玄、张斐、杜预等”错,张斐、杜预是晋人。
D“用儒家思想修改法律条文”错,在汉代,修改法律条文的情况是零星的情况。
2.C A“全面融入了”错。
原文“想将儒家的精华成为国家制度”。
B“当时以法家思想为基础的法律条文还有很多”错,对“可以概见其余”理解错误。
D 还根据了《诗经》3.A B“儒家的‘礼’随之开始渗入法典中”错。
在汉代儒生作法律章句时就已经渗入。
C “《春秋》在儒家经典中的重要地位”错,原文无据。
D “更重要”错。
4. “春秋决狱”是产生于汉代的一种独特的司法审判方式,它是法官援引《春秋》等儒家经典中的“经义”作为判案的依据,以“原心定罪”为核心思想,从而推动了法律儒家化的进程。
5. 材料一强调“春秋决狱”这一现象的普遍性和影响,借此论证法律儒家化的方式;材料二偏重“春秋决狱”的个案分析,通过判词揭示春秋决狱的依据;材料三重在春秋决狱的核心思想。
6.C 放在特殊的时代环境中,可知,山大师生的爱国品质受时代背景影响,而非自然因素。
7.C A、B均过度解读;D“山东精神”本质上就是民族的坚贞气节。
8.①语言幽默,“众人摩登我独古”化用古文,加入“摩登”音译的外来词语,古文句式搭配外来词,诙谐有趣。
作者借诙谐之语表现山大师生着装朴素却自得其乐。
②借“众人”和“我”的对比,突显山大师生的朴素、严肃的特点。
9.协调;①这三季的描写体现了青岛的自然环境的温暖、美好,对比突出青岛冬季环境的“严肃”。
②这三季的表现青岛社会生活怡人、闲适,后文写山大师生在悠闲的青岛仍能保持严肃的态度,保持静肃,更见山大师生心怀大义。
③突出表现了青岛自然环境之美和青岛的娱乐生活丰富,美丽动人的青岛却被外国侵略,山河破碎,令人痛心,展现了严肃的爱国主题。
或:写夏季“中外有钱有闲的人们的娱乐场所”与冬季“他们与她们都另寻出路”的差异,告知读者青岛被侵占的时代背景,使结尾的严肃的爱国情怀的表达更自然、不突兀。
重庆市第一中学2022-2023学年高三上学期10月月考地理试题含答案

★启用前【考试时间:10月7日11:00-12:15】2022年重庆一中高2023届10月月考地理试题卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号码填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将答题卡交回。
一、选择题:本题共15小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
乌裕尔河原为我国东北地区嫩江的支流。
受嫩江西移、泥沙沉积等影响,乌裕尔河下游排水受阻,成为内流河。
河水泛滥,最终形成面积相对稳定的扎龙湿地(如下图所示)。
据此完成1-2题。
1.扎龙湿地()A.总体地势较高B.降水量季节变化大C.降水量远大于蒸发量D.近年来盐度下降快2.有利于扎龙湿地生态保护的措施是()A.疏浚河道,重新沟通乌裕尔河与嫩江B.开垦湿地,发展水稻种植业C.顺其自然发展,减少人类活动D.开发湿地,发展水产养殖业人类命运共同体是“一带一路”倡议的理想愿景。
构建中国主导的“双环流全球价值链”(如下图)是构建人类命运共同体的重要途径,中国处于该价值链的中间节点位置,发挥着中心枢纽作用,据此完成3-4题。
3.不同国家和地区在“双环流全球价值链”中所处位置不同,其决定性因素是()A.产业结构B.经济总量C.科技水平D.开放程度4.图中d环节输出的最可能是()A.生产技术B.初级产品C.高端产品D.中间产品预制菜是一种运用标准化作业,对菜品原料进行简化制作,经过包装、加热或蒸炒等方式,就能直接食用的便捷菜品。
其具有即食、即热、即烹、即配等特点。
追溯历史,美国预制菜行业起源于1940年,日本则起源于1950年。
经过数十年发展美日均成长出在全球极具影响力的大型预制菜企业。
近年来我国预制菜市场发展迅速,逐渐形成了一批分散型的中小企业。
下图示意预制菜及上下游行业结构图。
据此完成5-7题。
5.下列因素中对预制菜行业影响较小的是()A.原料B.市场C.运输D.技术6.对餐饮企业来说,使用预制菜节省的主要成本是()A.包装B.人工C.物流D.燃料7.与美、日等国相比,我国预制菜企业集中度低、规模较小的原因主要是()A.饮食文化多样B.冷链流通地域性明显C.市场相对分散D.原料供应本地化为主锋前增温是指冷空气来临之前,气温反常变暖的现象,有时让人产生季节转换的错觉。
重庆一中高2022届高二上期10月月考数学试题卷

A. 相交
B. 相离
C. 相切
D. 不能确定
6. 抛物线 y2 4x 的焦点为 F ,准线为 l ,点 P 为抛物线上一点,PA l ,垂足为 A ,若直线 AF 的斜率为
3 ,则 | PF | 等于( )
A. 4
B. 4 3
C. 8
D. 2 3
Hale Waihona Puke 7. 已知过双曲线 x2 y2 1(a 0,b 0) 的右焦点为 F ,且与双曲线的渐近线平行的直线 l 交双曲线于点 A , a2 b2
重庆一中高 2022 届高二上期 10 月月考
数学试题卷
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项符 合题目要求的.
1. 已知圆 C 的标准方程为 (x 2)2 y2 1,则它的圆心坐标是( )
A. (2,0)
B. (0, 2)
C. (0, 2)
则 |MG| 的取值范围为( ) |GP|
A. (0, 2 1)
B. (0, 2 1]
C. (0, 2 1) 7
D. (0, 2 1] 7
二、多项选择题:本大题共 4 小题,每小题 5 分,共 20 分.在每小题给出的四个选项中有多项符合题 目要求,全部选对的得 5 分,部分选对的得 3 分,有选错的得 0 分.
D. PF1F2 的面积为1
10. 点 P 是直线 x y 3 0 上的动点,由点 P 向圆 O : x2 y2 4 作切线,则切线长可能为( )
A. 2 2
B. 1 2
C. 1 3
D. 3 2
11. 泰戈尔说过一句话:世界上最远的距离,不是树枝无法相依,而是相互了望的星星,却没有交会的轨
重庆市第一中学2020-2021学年高二上学期10月月考试题 化学试题 Word版含答案

秘密★启用前【考试时间:2020年10月16日9:00-12:00】重庆一中高2022级高二上期10月月考化学试题卷化学试题共6页,满分100分,时间90分钟。
注意事项:1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2. 答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3. 答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上答题无效。
本卷出题人根哥告诉你,可能用到的相对原子质量:H 1 C 12 O 16 Fe 56 Cu 64 Zn 65 Ag 108一、选择题:本题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.观察右图装置,下列说法正确的是A.若a、b接电流表,则该装置一定为原电池B.若a、b接直流电源,则该装置一定为电解池C.若a、b接直流电源,铁可能不易被腐蚀D.若a、b接电流表或接直流电源,铁都可能是负极2.将两根铁钉分别缠绕铜丝和铝条,放入滴有混合溶液的容器中,如图所示,下列叙述错误的是A.a中铁钉附近产生蓝色沉淀B.b中铁钉附近呈现红色C.a中铜丝附近有气泡产生D.b中发生吸氧腐蚀3.重庆一中化学组姜林老师,热衷于电解,在办公室组装了如下四套装置。
电极均为惰性电极,溶质、溶剂均足量,通电时间和电流强度均相同,相同条件下,产生气体总体积最大的是4.下列事实中,不能用勒夏特列原理解释的是A.使用催化剂可加快SO2转化为SO3的速率B.可用浓氨水和氢氧化钠固体快速制氨C.夏天,打开啤酒瓶时会从瓶口逸出泡沫D.光照新制的氯水时,溶液的pH 逐渐减小5 . 爱动脑筋的重庆一中化学组张郭根老师幻想着,假如存在A-F六种物质在一定条件下能按右图所示能量循环图进行相互转换,则下列说法中错误的是A. ΔH1+ΔH2+ΔH3+ΔH4+ΔH5+ΔH6=0B. ΔH7=ΔH1+ΔH2+ΔH3C. ΔH5=ΔH7-ΔH4-ΔH6D. │ΔH1+ΔH2+ΔH3│=│ΔH4+ΔH5+ΔH6│6 . 重庆一中化学组郑淇文老师,笑着拍着你的肩膀说:“这道题要是做错了,要被打板子”。
精品解析:重庆市第一中学2020-2021学年高二10月月考化学试题(解析版)

重庆一中高2022级高二上期10月月考化学试题卷注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
本卷出题人根哥告诉你,可能用到的相对原子质量:H-1 C-12 O-16 Fe-56 Cu-64 Zn-65 Ag-108一、选择题:本题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 观察如图装置,下列说法正确的是A. a、b接电流表,该装置为原电池B. a、b接直流电源,该装置为电解池C. a、b接直流电源,铁可能不易被腐蚀D. a、b接电流表或接直流电源,铁都可能是负极【答案】C【解析】【详解】A、如果液体c为乙醇等非电解质,则不符合构成原电池的条件,故A错误;B、如果液体c为乙醇等非电解质,该电路为断路,不能构成电解池,故B错误;C、连接直流电源,如果让铁作阴极,按照电解原理,铁不被腐蚀,故C正确;D、如果接电流表,构成原电池,铁作负极,如果接直流电源,构成电解池,两极的名称为阴阳极,故D错误。
2. 将两根铁钉分别缠绕铜丝和铝条,放入滴有混合溶液的容器中,如图所示,下列叙述错误的是()A. a中铁钉附近产生蓝色沉淀B. b中铁钉附近呈现红色C. a中铜丝附近有气泡产生D. b中发生吸氧腐蚀【答案】B【解析】【详解】A.a中Fe电极发生反应Fe-2e-=Fe2+,亚铁离子和铁氰酸钾反应生成蓝色沉淀,所以a中铁钉附近出现蓝色沉淀,A正确;B.b中Fe作正极被保护,Fe不参加反应,没有铁离子生成,所以铁钉附近不呈现红色,B错误;C.a中Fe为负极,Cu为正极,在强酸性条件下的腐蚀为析氢腐蚀,在Cu电极上H+得到电子变为H2逸出,因此铜丝附近有气泡产生,C正确;D.b中Fe为正极,Al作负极,电解质溶液显中性,发生吸氧腐蚀,D正确;故合理选项是B。
重庆市第一中学2022-2023学年高三上学期10月月考语文试题含答案

秘密★启用前【考试时间:2022年10月7日8:00-10:30】2022年重庆一中高2023届10月月考语文试题卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号码填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将答题卡交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一:法律之儒家化汉代已开其端。
汉律虽为法家系统,为儒家所不喜,自汉武标榜儒术以后,法家逐渐失势,而儒家抬头,此辈于是重整旗鼓,想将儒家的精华成为国家制度,使儒家主张借政治、法律的力量永垂不朽。
汉律虽已颁布,不能一旦改弦更张,但儒家确有许多机会可以左右当时的法律。
据《史记•贾生列传》,贾谊上疏不满于当时王侯大臣与众庶同黥、劓、髡、刖、笞、弃市之法而反复申论古时刑不上大夫的道理以劝文帝一事,可以概见其余。
又《晋书·刑法志》云:“马融、郑玄诸儒章句十有余家,家数十万言。
”法律在儒家注释之下,恐已非本来面目,他们可以利用解释法律的机会,左右法律。
同一法律条文因注释不同而改变其内容在历史上常有其例。
王植奏称:“臣寻晋律文简辞约,旨通大纲……张斐、杜预同注一章,而生杀永殊。
”以此例彼,可以推知诸儒章句对汉律的影响。
除了法典内容已为礼所掺入,已为儒家的伦理思想所支配外,审判决狱受儒家思想的影响也是可注意的事实,儒者为官既有司法的责任,或参加讨论司法的机会,于是常于法律条文之外,更取决于儒家的伦理学说。
我国古代法律原无律无正文不为罪的规定,可以比附,伸缩性极大。
这样,儒家思想在法律上一跃而为最高原则,与法理无异。
“胶东相董仲舒老病致仕,朝廷每有大议,数遣廷尉张汤亲至陋巷,问其得失,于是作《春秋决狱》二百三十二事。
动以经对,言之详矣。
”东汉应劭亦撰《春秋断狱》,其他以《春秋》决狱者甚众,散见“史汉”列传中。
从遗留的狱辞中来看,可以说无不以《春秋》、《尚书》为重要司法原则。
重庆市第一中学2021-2022高二数学上学期10月考试试题(含解析)
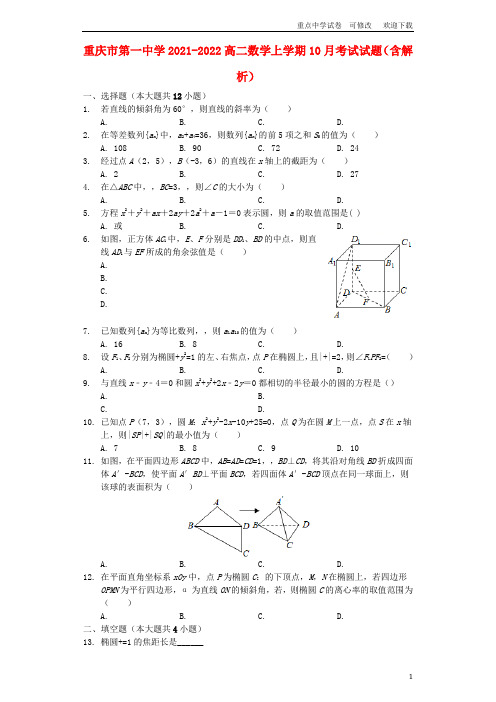
重庆市第一中学2021-2022高二数学上学期10月考试试题(含解析)一、选择题(本大题共12小题)1.若直线的倾斜角为60°,则直线的斜率为()A. B. C. D.2.在等差数列{a n}中,a2+a4=36,则数列{a n}的前5项之和S5的值为()A. 108B. 90C. 72D. 243.经过点A(2,5),B(-3,6)的直线在x轴上的截距为()A. 2B.C.D. 274.在△ABC中,,BC=3,,则∠C的大小为()A. B. C. D.5.方程x2+y2+ax+2ay+2a2+a-1=0表示圆,则a的取值范围是( )A. 或B.C.D.6.如图,正方体AC1中,E、F分别是DD1、BD的中点,则直线AD1与EF所成的角余弦值是()A.B.C.D.7.已知数列{a n}为等比数列,,则a1a10的值为()A. 16B. 8C.D.8.设F1、F2分别为椭圆+y2=1的左、右焦点,点P在椭圆上,且|+|=2,则∠F1PF2=()A. B. C. D.9.与直线x﹣y﹣4=0和圆x2+y2+2x﹣2y=0都相切的半径最小的圆的方程是()A. B.C. D.10.已知点P(7,3),圆M:x2+y2-2x-10y+25=0,点Q为在圆M上一点,点S在x轴上,则|SP|+|SQ|的最小值为()A. 7B. 8C. 9D. 1011.如图,在平面四边形ABCD中,AB=AD=CD=1,,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一球面上,则该球的表面积为()A. B. C. D.12.在平面直角坐标系xOy中,点P为椭圆C:的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,若,则椭圆C的离心率的取值范围为()A. B. C. D.二、填空题(本大题共4小题)13.椭圆+=1的焦距长是______14.已知圆C:x2+y2+8x-m+1=0与直线相交于A,B两点.若|AB|=2,则实数m的值为______.15.已知△ABC的角A,B,C对边分别为a,b,c,若a2=b2+c2-bc,且△ABC的面积为,则a的最小值为______.16.设S n为数列{a n}的前n项和,,则S1+S2+…+S100=______.三、解答题(本大题共6小题)17.已知直线l1:ax+3y+1=0,l2:x+(a-2)y+a=0.(1)若l1⊥l2,求实数a的值;(2)当l1∥l2时,求直线l1与l2之间的距离.18.已知椭圆C的焦点在x轴上,两个焦点与上顶点组成一个正三角形,且右焦点到右顶点的距离为1.(1)求椭圆C的方程;(2)过点M(3,0)作斜率为的直线l与椭圆相交于A,B两点,求|AB|.19.如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C,D用强光柱进行辅助照明,其中A,B,C,D在同一平面内,现测得CD长为100m,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.(1)求△BCD的面积;(2)求船AB的长.20.在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=,EF=1,BC=,且M是BD的中点.(1)求证:EM∥平面ADF;(2)求多面体ABCDEF的体积V.21.已知圆C的圆心C在直线x-2y=0上.(1)若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为4,求圆C的标准方程;(2)已知点N(0,-3),圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使|MN|=2|MO|(O为坐标原点),求圆心C的纵坐标的取值范围.22.已知椭圆C的两个焦点坐标分别是F1(-,0)、F2(,0),并且经过点P(,-).(1)求椭圆C的方程;(2)若直线l与圆O:x2+y2=1相切,并与椭圆C交于不同的两点A、B.当•=λ,且满足≤λ≤时,求△AOB面积S的取值范围.答案和解析1.【答案】A【解析】解:因为直线的斜率k和倾斜角θ的关系是:k=tanθ∴倾斜角为60°时,对应的斜率k=tan60°=故选:A.直接根据倾斜角和斜率之间的关系即可得到结论.本题主要考查直线的倾斜角和斜率之间的关系以及计算能力,属于基础题目.做这一类型题目的关键是熟悉公式.2.【答案】B【解析】解:在等差数列{a n}中,a2+a4=36,∴数列{a n}的前5项之和:S5====90.故选:B.利用等差数列的前n项和公式、通项公式直接求解.本题考查等差数列的前5项和的求法,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.3.【答案】D【解析】解:经过点A(2,5),B(-3,6)的直线方程为=,即+=1,故直线在x轴上的截距为27,故选:D.由题意利用直线方程的两点式求出直线的方程,再化为截距式,可得结论.本题主要考查直线方程的两点式、截距式,属于基础题.4.【答案】B【解析】【分析】由已知利用正弦定理sin C=,利用大边对大角可求∠C为锐角,即可利用特殊角的三角函数值得解.本题主要考查了正弦定理,大边对大角,特殊角的三角函数值在解三角形中的综合应用,考查了转化思想,属于基础题.【解答】解:在△ABC中,∵,BC=3,,∴由正弦定理,可得:sin C===,∵AB<BC,可得:∠A>∠C,∠C为锐角,∴∠C=.故选:B.5.【答案】D【解析】解:方程x2+y2+ax+2ay+2a2+a-1=0表示圆∴a2+4a2-4(2a2+a-1)>0∴3a2+4a-4<0,∴(a+2)(3a-2)<0,∴故选D.根据圆的方程的一般式能够表示圆的充要条件,得到关于a的一元二次不等式,整理成最简单的形式,解一元二次不等式得到a的范围,得到结果.本题考查二元二次方程表示圆的条件,考查一元二次不等式的解法,是一个比较简单的题目,这种题目可以单独作为一个选择或填空出现.6.【答案】C【解析】【分析】本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.先通过平移将两条异面直线平移到同一个起点E,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.【解答】解:如图,取AD的中点G,连接EG,GF,∠GEF为直线AD1与EF所成的角设棱长为2,则EG=,GF=1,EF=,易知是直角三角形,cos∠GEF=,故选:C.7.【答案】C【解析】解:∵,∴20=-2a4a7,解得a4a7=-8,∴a1a10=a4a7=-8,故选:C.由,可得20=-2a4a7,可得a1a10=a4a7.本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.8.【答案】D【解析】解:如图,由椭圆+y2=1,得a=2,b=1,c=,,则,即=12,由|+|=2,得,∴,即,∴∠F1PF2=.故选:D.由题意方程求得焦距,利用平面向量的减法运算得到,与已知|+|=2同时两边平方后可得,由此可得答案.本题考查了椭圆的简单性质,考查了平面向量的数量积运算,是中档题.9.【答案】C【解析】【分析】由题意先确定圆心的位置,再结合选项进行排除,并得到圆心坐标,再求出所求圆的半径.本题主要考查了由题意求圆的标准方程,作为选择题可结合选项做题,这样可提高做题的速度.【解答】解:由题意圆x2+y2+2x-2y=0的圆心为(-1,1),半径为,∴过圆心(-1,1)与直线x-y-4=0垂直的直线方程为x+y=0,所求的圆的圆心在此直线上,排除A、B,∴圆心(-1,1)到直线x-y-4=0的距离为=3,则所求的圆的半径为,故选:C.10.【答案】C【解析】解:由题意知,圆的方程化为:(x-1)2+(y-5)2=1;所以,圆心M(1,5),半径为1;如图所示,作点P(7,3)关于x轴的对称点P'(7,-3);连接MP',交圆与点Q,交x轴与点S,则|SP|+|SQ|的值最小;否则,在x轴上另取一点S',连接S'P,S'P',S'Q,由于P与P'关于x轴对称,所以|SP|=|SP',|S'P|=|S'P'|;所以,|SP|+|SQ|=|SP’|+|SQ|=|P'Q|<|S'P'|+|S'Q|=|S'P|+|S'Q|;(三角形中两边之和大于第三边).故|SP|+|SQ|的最小值为|P'M|-1=-1=9;故选:C.根据条件,转化为在x轴上找一点S,使得S到点P和点M距离之和最小问题,只需作P关于x轴的对称点P',连接P'M,则P'M与x轴交点即为点S.|P'M|-半径即为|SP|+|SQ|本题考查了点关于直线的对称问题,属于作图题,数形结合有利于解决问题,属于基础题.11.【答案】B【解析】解:由题意,四面体A-BCD顶点在同一个球面上,△BCD和△ABC都是直角三角形,所以BC的中点就是球心,所以BC=,球的半径为:,所以球的表面积为:=3π.故选:B.由题意,BC的中点就是球心,求出球的半径,即可得到球的表面积.本题是基础题,考查四面体的外接球的表面积的求法,找出外接球的球心,是解题的关键,考查计算能力,空间想象能力.12.【答案】D【解析】解:联立,解得y N=,联立,解得y M=.可得y N-y M==a,化为:a=,可得e==,同理:把直线方程y=x,y=x-a与椭圆方程分别联立可得:a=3b.即可得出离心率e=.∴椭圆C的离心率的取值范围为[,]..故选:D.联立,解得y N,联立,解得y M.利用y N-y M=a,化为:a=,利用e=即可得出.同理:把直线方程y=x,y=x-a与椭圆方程分别联立可得:a=3b.即可得出离心率.本题考查了直线与椭圆相交问题、离心率计算公式、平行四边形的性质、相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.13.【答案】【解析】解:椭圆+=1,可得a=3,b=2,则c=.椭圆+=1的焦距长是:2.故答案为:2.利用椭圆方程,转化求解即可.本题考查椭圆的简单性质的应用,考查计算能力.14.【答案】-11【解析】解:圆C:x2+y2+8x-m+1=0化为标准方程是(x+4)2+y2=15+m;则圆心C(-4,0),半径为r=(其中m>-15);所以圆心C到直线的距离为d==,化简得=,解得m=-11.故答案为:-11.化圆C的方程为标准方程,利用圆心到直线的距离d与弦长和半径的关系列方程求出m 的值.本题考查了直线与圆的位置关系应用问题,也考查了点到直线的距离应用问题,是中档题.【解析】解:根据题意,△ABC中,若a2=b2+c2-bc,则bc=b2+c2-a2,则cos A==,则sin A==,又由△ABC的面积为,则有S=bc sin A=,bc=3,a2=b2+c2-2bc cos A=b2+c2-bc≥2bc-bc=3,则a的最小值为;故答案为:.根据题意,将a2=b2+c2-bc变形可得bc=b2+c2-a2,由余弦定理可得cos A==,计算可得sin A 的值,由三角形面积公式可得S=bc sin A=,即bc=3,进而由余弦定理可得a2=b2+c2-2bc cos A=b2+c2-bc,结合基本不等式分析可得a2≥2bc-bc=bc,变形即可得答案.本题考查余弦定理的应用,关键是求出cos A的值.16.【答案】2101-102【解析】解:设S n为数列{a n}的前n项和,,①当n=1时,解得a1=1,当n≥2时,S n-1=2a n-1-1②①-②得a n=2a n-2a n-1,即(常数),所以数列{a n}是以1为首项,2为公比的等比数列.则(首项符合通项).故=2n-1,所以S1+S2+…+S100=(21+22+…+2100)-100=.故答案为:2101-102.首先利用数列的递推关系式的应用求出数列的通项公式,进一步利用前n项和公式求出结果.本题考查的知识要点:数列的递推关系式的应用,等比数列的前n项和的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.17.【答案】解:(1)由l1⊥l2可得:a+3(a-2)=0,…4分解得;…6分(2)当l1∥l2时,有,…8分解得a=3,…9分此时,l1,l2的方程分别为:3x+3y+1=0,x+y+3=0即3x+3y+9=0,故它们之间的距离为.…12分.【解析】(1)由垂直可得a+3(a-2)=0,解之即可;(2)由平行可得a=3,进而可得直线方程,代入距离公式可得答案.本题考查直线的一般式方程的平行和垂直关系,涉及平行线间的距离公式,属基础题.18.【答案】解:(1)椭圆C的焦点在x轴上,两个焦点与上顶点组成一个正三角形,且右焦点到右顶点的距离为1.可得:⇒.故椭圆的方程为;(2)过点M(3,0)作斜率为的直线l,可得直线方程为:y=(x-3),联立⇒4x2-6x-3=0,过点M(3,0)作斜率为的直线l与椭圆相交于A,B两点,所以,=.【解析】(1)利用已知条件列出方程组,求出a,b,得到椭圆方程.(2)求出直线方程与椭圆联立,利用韦达定理,弦长公式转化求解即可.本题考查椭圆的简单性质、椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及设而不求思想方法的应用,是中档题.19.【答案】解:(1)由题,∠BDM=30°,∠ACN=45°,∠BCM=60°,得∠CBD=30°,所以BC=BD=100,所以=平方米.(2)由题,∠ADC=75°,∠ACD=45°,∠BDA=45°,在△ACD中,,即,所以,在△BCD中,,在△ABD中,==,即船长为米.【解析】(1)根据题意求得∠CBD,进而求得BC,BD,进而根据三角形面积公式求得答案.(2)利用正弦定理求得AD,进而利用余弦定理分别求得BD,AB.本题主要考查了正弦定理和余弦定理的运用.解题的重要步骤就是建立数学模型.20.【答案】(1)证明:取AD的中点N,连接MN,NF.在△DAB中,∵M是BD的中点,N是AD的中点,∴MN∥AB,MN=,又∵EF∥AB,EF=,∴MN∥EF,且MN=EF.∴四边形MNEF为平行四边形,则EM∥FN,又∵FN⊂平面ADF,EM⊄平面ADF,故EM∥平面ADF;(2)解:∵∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=,EF=1,BC=,∴多面体ABCDEF的体积V=V F-ABD+V F-BED+V E-BDC==.【解析】本题考查线面平行的判定,考查了空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.(1)取AD的中点N,连接MN,NF.利用三角形中位线定理可得MN∥AB,MN=,又EF∥AB,EF=,可得四边形MNEF为平行四边形,则EM∥FN,再由线面平行的判定得EM∥平面ADF;(2)由多面体ABCDEF的体积V=V F-ABD+V F-BED+V E-BDC,结合已知及棱锥的体积公式求解.21.【答案】解:(1)因为圆C的圆心在直线x-2y=0上,所以可设圆心为(2a,a)因为圆C与y轴的负半轴相切,所以a<0,半径r=-2a,又因为该圆截学轴所得弦的弦长为 4,所以a2+(2)2=(-2a)2,解得a=-2,因此,圆心为(-4,-2),半径r=4所以圆C的标准方程为(x+4)2+(y+2)2=16(2)圆C的半径为3,设圆C的圆心为(2a,a),由题意,a>0则圆C的方程为(x-2a)2+(y-a)2=9又因为|MN|=2|MO|,N(0,-3),设M(x,y)则=2,整理得x2+(y-1)2=4,它表示以(0,1)为圆心,2为半径的圆,记为圆D,由题意可知:点M既在圆C上又在圆D上,即圆C和圆D有公共点.所以|3-2|≤≤5,且a>0所以,即,解得,解得≤a所以圆心C的纵坐标的取值范围时[,]【解析】(1)根据圆心在直线x-2y=0上,可设圆心(2a,a),再根据圆C与y轴负半轴相切得r=-2a,弦长为4列方程可解得a=-2,从而可得圆C的标准方程;(2)根据|MN|=2|MO|可得点M的轨迹为圆x2+(y-1)2=4,记为圆D,再根据圆C和圆D有公共点列式可解得.本题考查了直线与圆的位置关系,属中档题.22.【答案】解:(1)设椭圆方程为:+=1(a>b>0),由题意可得:c=,+=1,a2=b2+c2,联立解得:a=2,b=1.∴椭圆C的方程为:+y2=1.(2)由题意可知:直线l的斜率不为零,设直线l方程:x-my-n=0与圆O:x2+y2=1相切,∴=1,解得n2=m2+1.设A(x1,y1),B(x2,y2),联立,消去x整理得:(m2+4)y2+2mny+n2-4=0,∴y1+y2=-,y1y2=.又∵|AB|=|y1-y2|,∴=,λ=•=x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2==,∵≤λ≤,令t=m2+1,则λ=,可得t∈[3,6],∴S△AOB=2=,∵∈,∴(+6)∈,∴∈,∴S△AOB∈.【解析】(1)设椭圆方程为:+=1(a>b>0),由题意可得:c=,+=1,a2=b2+c2,联立解出即可得出.(2)由题意可知:直线l的斜率不为零,设直线l方程:x-my-n=0与圆O:x2+y2=1相重点中学试卷可修改欢迎下载切,可得=1.设A(x1,y1),B(x2,y2),直线方程与椭圆方程联立可得:(m2+4)y2+2mny+n2-4=0,可得:|AB|=|y1-y2|,S△AOB=d|AB|,λ=•=x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn (y1+y2)+n2,由≤λ≤,令t=m2+1,则λ=,可得t∈[3,6],利用基本不等式的性质即可得出.本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量数量积运算性质、三角形面积计算公式、基本不等式的性质、弦长公式,考查了推理能力与计算能力,属于难题.11。
重庆一中2024年高二10月月考数学试题(解析版)

重庆一中高2026届高二上期月考数学试题卷注意事项1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时、必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.4.所有题目必须在答题卡上作答,在试题卷上答题无效.一、单选题(本大题共8个小题,每题只有一个选项正确,每小题5分,共40分)1. 已知点()()1,0,1,0A B −,动点(),P x y 满足1PA PB −=,则动点P 的轨迹是( )A. 射线B. 线段C. 双曲线的一支D. 双曲线【答案】C 【解析】【分析】根据题意,计算A ,B 之间的距离,比较可得,0AB PA PB PA PB >−−>,由双曲线的定义分析可得答案.【详解】根据题意,点())1,0,1,0A B −,则2AB =,若动点P 满足1PA PB −=,且,0AB PA PB PA PB >−−>, 则P 的轨迹是以A ,B 为焦点双曲线的右支, 故选:C.2. 已知两直线1:20l x y −=和2:310l x my ++=,若12l l ∥,则m =( ) A. 6− B. 6 C.12D. 2【答案】A 【解析】【分析】利用两直线平行的充要条件,列出关于m 的方程,即可得到答案. 【详解】因为12l l //,所以()123m ×=−×,且1130×≠×, 解得6m =−.故选:A.3. 椭圆E 的一条弦AB 经过左焦点1F ,右焦点记为2F .若2ABF △的周长为8,且弦长AB 的最小值为3,则椭圆E 的焦距=( )A. 2B. 1C. D.【答案】A 【解析】【分析】借助椭圆的定义及通径概念列出等式即可求解.【详解】由2ABF △的周长为8,可得121248AF AF BF BF a +++==,即2a =, 由弦长|AAAA |的最小值为3,通径长为3,即223b a=,所以23b =,所以2221c a b =−=,即1c =, 所以椭圆E 的焦距为2. 故选:A.4. ABC 的内角,,A B C 对应的边分别为,,a b c ,若45a b B ,则c =( )A. B.C.+ D. 无解【答案】C 【解析】【分析】根据给定条件利用余弦定理列出方程求解即得.【详解】在ABC 中,因45ab B ,于是由余弦定理2222cos b a c ac B =+−得:2812c =+−,即240c −+=,解得c =故选:C5. 阿基米德在其著作《关于圆锥体和球体》中给出了一个计算椭圆面积的方法:椭圆半长轴的长度、半短轴的长度和圆周率三者的乘积为该椭圆的面积.已知椭圆()2222:10x y C a b a b+=>>的面积为10π,两焦点为1F 和2F ,直线y kx =与椭圆C 交于,A B 两点.若1110AF BF +=,则椭圆C 的半短轴的长度=( ) A. 5 B. 4 C. 6 D. 2【答案】D 【解析】【分析】根据给定条件,可得10ab =,由椭圆对称性结合已知可得210a =,求解可得椭圆的短半轴长. 【详解】因为椭圆CC :xx 2aa 2+yy 2bb 2=1(aa >bb >0)面积为10π,所以π10πab =,所以10ab =,因为y kx =过原点,结合椭圆对称性,可得线段AB ,12F F 被原点互相平分,所以四边形12AF BF 为平行四边形,所以12||||BF AF =,又1110AF BF +=,所以1210AF AF +=, 所以由椭圆的定义得210a =,解得5a =,所以510b =,解得2b =, 所以椭圆的短半轴长为2. 故选:D.6. 过定点()1,0−的直线l 与抛物线24y x =交于,A B 两点,OA OB ⋅的值为( ) A32B. 5C. 3+D. 4【答案】B 【解析】【分析】设出直线l 的方程并与抛物线方程联立,化简写出根与系数,从而求得OA OB ⋅的值.的.【详解】依题意可知直线l 与x 轴不重合、与y 轴不平行, 设直线l 的方程为()1,0y k x k =+≠,由()214y k x y x=+= ,消去x 并化简得()2222240k x k x k +−+=, ()()()2242Δ244161616110k k k k k =−−=−=+−>,解得()()1,00,1k ∈−∪,设AA (xx 1,yy 1),AA (xx 2,yy 2),则21212222442,1k x x x x k k−+=−=−+=, ()()()()22212121212121112y y k x x k x x x x k x x =++=+++=++ 224224k k =−++=,所以1212145OA OB x x y y ⋅=+=+=.故选:B7. 焦点在y 轴上的双曲线E 与双曲线()2222:10,0x yC a b a b−=>>有相同的渐近线,过点()5,0P −的直线与双曲线C 交于,A B 两点,若线段AB 的中点是()3,8M ,则双曲线E 的离心率为( )A.B.83C.D.【答案】D 【解析】【分析】设AA (xx 1,yy 1),AA (xx 2,yy 2),根据题意利差法可得b a =,设双曲线E 的方程为()2211221110,0y x a b a b −>>,结合渐近线可得11b a =.【详解】设AA (xx 1,yy 1),AA (xx 2,yy 2),则1212616x x y y +=+= ,且()121280135ABy y k x x −−===−−−, 因为22112222222211x y a b x y a b −= −= ,两式相减可得22221212220x x y y a b −−−=, 整理可得222121212222121212y y y y y y b x x x x x x a −−+=⋅=−−+,即221616b a ×=,可得b a =, 即双曲线C的渐近线方程为y x =, 设双曲线E 的方程为()2211221110,0y x a b a b −>>,则11b a = 所以双曲线E的离心率为e 故选:D.8. 已知12,F F 是椭圆与双曲线的公共焦点,P 是它们的一个公共点,且12PF PF >,线段1PF 的中垂线经过2F .记椭圆的离心率为1e ,双曲线的离心率为2e ,则2114e e +的取值范围是( )A. ()6,+∞B. ()7,+∞C. ()6,7D. ()5,+∞【答案】B 【解析】【分析】由题意可得2122PF F F c ==,结合椭圆和双曲线的定义得到12,e e 的关系式,根据2e 取值范围分析函数单调性得到结果.【详解】设椭圆的长轴长为12a ,双曲线的实轴长为22a ,它们的公共焦距为2c ,不妨设点P在第一象限.∵2F 在1PF 的中垂线上, ∴2122PF F F c ==,由椭圆、双曲线的定义得:1211222,2PF PF a PF PF a +=−=, ∴1212222a c a c PF =-=+,整理得122a a c −=, ∴122a a c c-=,即12112e e −=, ∴12112e e =+, ∴221211442e e e e +=++, 令1()42f x x x=++,由定义法可证()f x 在(1,)+∞为增函数,且(1)1427f =++=, ∵21e >,∴21147e e +>. 故选:B.二、多选题(本大题共3个小题,每小题6分,共18分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)9. 已知,m n 是空间内两条不同直线,,αβ是空间内两个不同的平面,则下列命题为假命题的是( ) A. 若,m m αβ⊥⊥,则α∥β B. 若m ∥,n α∥α,则m ∥n的C. 若,m n αα⊥⊥,则m ∥nD. 若,αγβγ⊥⊥,则α∥β 【答案】BD 【解析】【分析】根据空间线线,线面,面面的位置关系判断.【详解】对于A ,因为,αβ是两个不同的平面,,m n 是两个不同的直线,,m m αβ⊥⊥,则//αβ,故A 为真命题;对于B ,若//,//m n αα,则m 与n 可能平行,相交,异面,故B 为假命题; 对于C ,若,m n αα⊥⊥,则//m n ,故C 为真命题;对于D ,若,αγβγ⊥⊥,则α与β可能平行,相交,故D 为假命题. 故选:BD.10. 设双曲线()2222:10,0x y E a b a b−=>>的左焦点为1F ,右焦点为2F ,点P 在E 的右支上,且不与E的顶点重合,则下列命题中正确的是( )A. 若3a =且2b =,则双曲线E 的两条渐近线的方程是32y x =± B. 若12PF PF ⊥,则12F PF 的面积等于2bC. 若点P的坐标为(2,,则双曲线E 的离心率大于3 D. 以2PF 为直径的圆与以E 的实轴为直径的圆外切 【答案】BCD 【解析】【分析】将3a =且2b =,带入方程求解渐近线方程即可判断A ;12PF PF ⊥,结合双曲线的定义求解即可判断B ;把P 点坐标代入E 的方程,然后计算离心率的取值范围即可判断C ;画图,两圆的圆心距IO是12F PF 的中位线,1222222PF PF a PF IOa +===+=两圆的半径之和,故两圆外切,即可判断D. 【详解】当3a =且2b =时,E 的渐近线斜率为23b y x x a=±=±,选项A 错误; ()1212222212Δ12222122124424F PF PF PF a PF PF c a b S PF PF b PF PF c −= ⇒⋅=−=⇒=⋅= +=,故选项B 正把P 点坐标代入E 的方程得:2222222222243218199344b bc b b e e a b a a a −=⇒=+⇒==+=+>⇒>,选项C 正确;如图, 两圆的圆心距IO 是12F PF 的中位线,1222222PF PF a PF IO a +∴===+=两圆的半径之和,故两圆外切,选项D 正确. 故选:BCD11. 两个圆锥的母线长度均为l ,它们的侧面展开图恰好拼成一个圆,分别用111,,r S V 和222,,r S V 表示两个圆锥的底面圆半径、表面积、体积,则正确的有( )A. 12r r l +=B. 12S S +的最小值为23π2lC. 12V V +为定值D. 若12:1:4r r =,则12:24V V =【答案】ABD 【解析】【分析】由“它们的侧面展开图恰好拼成一个圆”为解题关键点,A 选项利用侧面展开图的圆心角和为2π得到结论;B 选项由面积公式以及A 选项结论得到结论;C 选项由体积公式得出代数式,由特殊值结论不同得到不为定值;D 选项将条件代入C 选项中体积公式即可得到比值. 【详解】A :由122π2π2πr r l l+=得12r r l +=,故A 对. B :()()()21222221212123πππππ22r r S S r r r r l l l ++=+++≥+=,故B 对.C :121211ππ33V V r r +=,如122l r r ==,与122,33l l r r ==时值不同,故不为定值,D:112121111115,:π:π:1633lr V V r r r r =,故D 对. 故选:ABD.三、填空题(本大题共3个小题,每小题5分,共15分)12. 设m 为正实数,若直线x y m −=被圆223x y +=所截得的弦长为2m ,则m =__________.【解析】【分析】借助圆心到直线距离、半径及弦长的关系计算即可得. 【详解】223x y +=的圆心为()0,0圆心到x y m −=所以m=0m >,解得m =13. 已知椭圆2212:136x y C b+=的焦点分别为1F ,2F ,且2F 是抛物线()22:20C y px p =>焦点,若P 是1C 与2C 的交点,且17PF =,则12cos PF F ∠的值为___________.【答案】57【解析】【分析】利用椭圆定义求出2PF ,再借助抛物线的定义结合几何图形计算作答.【详解】依题意,由椭圆定义得1212PF PF +=,而17PF =,则25PF =, 因点2F 是抛物线()22:20C ypx p =>的焦点,则该抛物线的准线l 过点1F ,如图, 的过点P 作PQ l ⊥于点Q ,由抛物线定义知2||||5PQ PF ==,而12//F F PQ ,则121PF F F PQ ∠=∠, 所以1211||5cos cos ||7PQ PF F F PQ PF ∠=∠==. 故答案为:5714. 已知点P 在圆22:1O x y +=上,动圆C 与圆O 内切并与直线:4l y =相切,圆心为C ,则|PPCC |的最小值为______. 【答案】12##0.5 【解析】C 的轨迹,计算即可. 【详解】如图,设圆C 的半径为R ,则1CO R =−; 又C 到:4l y =的距离为R ,则C 到3y =的距离为1R −.所以C 的轨迹是以O 为焦点,以3y =为准线的抛物线,顶点为30,2C ′, 则111.2PC CO C O ′≥−≥−=四、解答题(本大题共5个小题,共77分,解答应写出文字说明,正明过程或演算步骤)15. 已知ABC 的内角,,A B C 所对的边分别为,,a b c ,且224,(2)12b a c ==++.(1)求内角A ;(2)若ABC S M = 为BC 边上的中点,求线段AM 的长.【答案】(1)2π3(2 【解析】【分析】(1)结合已知利用余弦定理求解A 即可;(2)结合三角形面积公式求得c ,然后由()12AM AB AC =+平方,利用数量积的运算求解. 【小问1详解】由已知条件222224,(2)12416b a c c c c bc b ==++=++=++,即222c b a bc +−=−,由余弦定理可得2221cos 222c b a bc A bc bc +−−===−,因为()0,πA ∈,从而2π3A =.【小问2详解】因为2π4,3b A ==,由1sin 22ABC S bc A c === 6c =, 因为M 为BC 边上的中点,所以()12AM AB AC =+ ,平方得:)22221()2cos 74AM AB AC AB AC AB AC A =+=++⋅⋅=∣,所以AM =. 16. 如图,在直三棱柱111ABC A B C −中,11,2,AA AC AB AC AB ===⊥,D 为11A B 上一点,E 为1AA 中点,F 为CD 中点,且EF CD ⊥.(1)求证:EF ∥平面ABC ;(2)求直线DF 与平面BEF 所成角的正弦值. 【答案】(1)证明见解析;(2. 【解析】【分析】(1)结合题目条件建立空间直角坐标系,写出各点坐标,根据直线的方向向量与平面法向量垂直证明线面平行.(2)求直线的方向向量和平面的法向量,利用公式求线面所成角的正弦值. 【小问1详解】以A 为原点,建立如图所示空间直角坐标系,则()()12,0,0,0,0,1,0,,02B C E,设1,01A D t t =≤≤,得()11,1,0,,,222t D t F, ∴()1,0,,,1,122t EFCD t ==−.由EF CD ⊥,得21022t EF CD ⋅=−= ,故1t =∵面ABC 的一个法向量()0,1,0m =,且0EF m ⋅= ,EF ⊄平面ABC , ∴EF ∥面ABC . 【小问2详解】由(1)知()1112,,0,,0,,1,1,1222EB EF CD =−==−设面BEF 的法向量为nn�⃗=(xx ,yy ,zz ),.由120211022x y x z −= += , 令1x =得()1,4,1n =−,设直线DF 与平面BEF 所成角为θ,则sin cos ,CD θ= ∴直线DF 与平面BEF.17. 在平面直角坐标系中,抛物线()2:20E x py p =>的焦点为F ,准线为l .过抛物线E 上一点P 作PQ l ⊥,垂足为Q 点.已知PQF △是边长为4的等边三角形.(1)求拋物线E 的方程; (2)如图,抛物线E 上有两点,A B 位于y 轴同侧,且直线FA 和直线FB 的倾斜角互补.求证:直线AB 恒过定点C ,并求出点C 的坐标. 【答案】(1)24x y = (2)证明见解析,()0,1C − 【解析】【分析】(1)记准线与y 轴交于H 点,在Rt QFH △中,求出焦准距,即可求解抛物线方程.(2)设()()1122:,,,,AB y kx b A x y B x y =+,联立抛物线方程,韦达定理,根据倾斜角互补即斜率之和为0,化简求得1b =−,即可得解. 【小问1详解】如图,记准线与y 轴交于H 点,在Rt QFH △中,4,30QF FQH ∠== ,所以2p FH ==.故抛物线2:4E x y =. 【小问2详解】因为垂直于x 轴的直线与抛物线仅有一个公共点,所以AB 必有斜率,设()()1122:,,,,AB y kx b A x y B x y =+, 由2122440,44y kx b x kx b x x b x y=+ ⇒−−=∴=−= 且124x x k +=, 因为,A B 位于y 轴同侧,所以120x x >,则0b <, 由Δ0>得20k b +>,所以0k ≠,又点FF (0,1),直线FA 和FB 的倾斜角互补,所以1212110y y x x −−+=,=,所以()()1212210kx x b x x +−+=, 即()410k b −+=,解得1b =−, 所以直线AB 恒过定点()0,1C −.18. 已知双曲线22:13y E x −=,点()0,4A,坐标原点O .(1)直线l 经过点A ,与E 的两条渐近线分别交于点M N 、.若OMNl 的方程; (2)如图,直线y kx m =+交双曲线E 的右支于不同两点,B C .若AB AC =,求实数m 的取值范围. 【答案】(1)34y x =±+ (2)1m <− 【解析】【分析】(1)根据题意求渐近线方程,进而求点,M N 的坐标,可得,OM ON ,结合面积公式运算求解; (2)分析可知线段BC 的中垂线经过A 点,设设BC 的中点为()00,D x y ,利用点差法可得(),3D k ,结合点与双曲线的位置关系运算求解即可. 【小问1详解】对于双曲线22:13y E x −=,可知1,a b==x 轴上,则双曲线E的渐近线为y =,且直线y =2π3,设(:4l ykx k =+≠,联立方程4y kx y =+ =,解得x y==,即M , 可得OM =同理可得OM则12OMNS = 解得3k =±,所以直线l 的方程为34y x =±+. 【小问2详解】由(1)可知:k >k <,因为AB AC =,则线段BC 的中垂线经过A 点,设BC 的中点为()()()001122,,,,,D x y B x y C x y , 则12012022x x x y y y +=+=,且1212y y k x x −=−,004AD y k x −=,因为221122221313y x y x −=−=,两式作差得()2222121203y y x x −−−=, 整理可得()()121212123y y x x y y x x −+=+−,即0062x y k =⋅,可得003x y k =⋅, 又因为AD BC ⊥,则0041ADy k k k x −⋅=⋅=−, 联立方程0000341x y k y k x=⋅− ⋅=− ,解得003x k y = = ,即(),3D k , 因为点(2,3)在双曲线右支上,且(),3D k 在右支的内部,则22313k −>,所以24k >.且D 在BC 上,则00y kx m =+,可得20013m y kx k −=−<−=, 所以实数m 的取值范围为(),1∞−−. 19. 已知椭圆CC :xx 2aa 2+yy 2bb 2=1(aa >bb >0)的左、1F 和2F ,焦距为2.动点()00,M x y 在椭圆C上,当线段2MF 的中垂线经过1F 时,有21cos MF F ∠=(1)求椭圆C 的标准方程;(2)如图,过原点O 作()()22002:3M x x y y −+−= 的两条切线,分别与椭圆C 交于点P 和点Q ,直线OP OQ 、的斜率分别记为12k k 、.当点M 在椭圆上运动时,①证明:12k k ⋅恒为定值,并求出这个值; ②求四边形OPMQ 面积的最大值.【答案】(1)2212x y +=(2)①证明见解析,12−;②1 【解析】【分析】(1)根据已知条件以及椭圆的定义求得,,a b c ,从而求得椭圆方程. (2)①由直线和圆相切列方程,利用根与系数求得12k k ⋅恒为定值12−. ②先求得四边形OPMQ 面积的表达式,然后利用基本不等式求得面积的最大值. 【小问1详解】取2MF 的中点记为N ,连结1NF .在12Rt F NF中,12212,cos F F NF F =∠,所以21NF =−,则1212222a MF MF F F NF =+=+=即1,1a c b ==∴= ,所以椭圆方程为2212x y +=【小问2详解】①直线1:OP y x k =与M()2222201001020r x r k x y k y r ⇔−−+−=;直线2:OQ y k x =与M 相切,同理有()2222202002020x r kx y k y r −−+−=; 则12k k 、是关于x 的方程()22222000020x rxx y x y r −−+−=的两根,由韦达定理知22002201222220002111232322233x x y r k k x r x x −−−+−====−−−−(注:上式中,先由220012x y +=消去的0y ,再代入223r =)②由①问知2112k k =−,如图,设()()1122,,,P x y Q x y ,由1112212211122112y k x x OP x k y = ⇒=⇒===++=,同理可得OQ =,()12OPMQ OPM OQMS S S r OP OQ =+=+.()222212621k +≤+=+,≤∴1k =±()max1OPMQ S=.【点睛】本题通过椭圆的标准方程、切线性质和四边形面积的求解,综合考查了椭圆的几何性质、韦达定理及不等式求解的能力.在解题过程中,椭圆参数的确定、切线斜率的关系及面积最大值的求解环环相扣,体现了代数与几何的紧密结合.在求四边形面积的最大值时,利用了基本不等式,确保最大值的合理性,并找出条件下的最优值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020-2021学年重庆一中高2022级高二上期10月月考历史(2020.10.16)一、选择题:本大题共24小题,每小题2分,共计48分。
在每小题列出的四个选项中,只有一项是最符合题目要求的。
1.商代的甲骨文卜辞对商人的农业活动有大量的记载,几乎包括了与农业相关的各个方面,后世所谓的“五谷”、“六畜”在卜辞中都有反映。
这说明当时A.小农经济开始形成B.农业成为社会生产的重要部门C.农业生产依赖占卜D.神权与王权结合促进农业发展2.周礼规定:“礼不下庶人,刑不上大夫”。
孔子却提出:“道之以政,齐之以刑,民免而无耻;道之以德,齐之以礼,有耻且格。
”这表明孔子主张A.以德为主礼法并用B.礼制下移教化百姓C.确立儒家正统地位D.恢复西周礼乐制度3.《左传·定公》记载,周初曾经俘虏了一批以职业为姓氏的工商业者。
见下表,这说明当时姓氏A.姓氏与职业具备了必然联系B.手工业和商业出现合一趋势C.手工业生产已出现专业分工D.职业和身份已形成世代相传4.《诗经》由王室乐官制作的乐歌、公卿列士进献的诗歌及经收集、筛选的民歌构成,由周天子颁诸各国,成为通用统一的标准诗乐,从此通过各种方式流传蔓延。
《诗经》的流传A.有利于构建文化的认同B.以书面记载为主要方式C.维持了天下共主的地位D.推动了平民教育的发展5.战国时期,法家主张“剪除私门势力,选拔法术之士”,“因任而授官,循名而责实”;墨家则提出“虽在农与工肆之人,有能则举之”。
他们的主张相同之处在于A.建立集权制度B.完善人才选拔体制C.实现富国强兵D.打破原有政治秩序6.下图是南昌西汉海昏侯刘贺墓出土的简牍(局部)拓片,上有“再拜上书太后陛下”等文字。
下列从中得出的结论最合理的是A.当时可能还未普通使用书写用纸B.简牍中的文字是秦朝的标准字体C.海昏侯在书法艺术上有很高成就D.西汉已经形成了外戚专权的局面7.读东汉时期我国西南地区铁器分布表。
由此可以推知A.西南地区农业已实现精耕细作B.铁器成为西南主要生产工具C.铁器在逐步向西南地区推广D.西南冶铁技术水平大大提高8.魏晋南北朝时期,许多政治家儒玄双修,以儒学治国,以玄学自修;道教称“求仙者,要当以忠孝和顺仁信为本”,而不少高僧又有高深的玄学造诣。
这反映了当时A.儒家思想主导地位动摇B.玄学逐渐成为统治思想C.佛道思想社会影响扩大D.思想文化领域碰撞交融9.南朝时期,政府推行“土断”制度,即清查出大量依附在“私门”、“大户”的人口,把他们编入国家户籍。
这一制度A.标志着国家户籍制度的成熟B.有利于进一步推广均田制C.阻碍了北方人口南迁的趋势D.有利于增加政府财政收入10.“新建阿房壁未干,沛公兵已入长安。
帝王苦竭生灵力,大业沙崩固不难!”(唐·胡曾《阿房宫》)与这首咏史诗主旨相通的治国主张是A.“仁政”B.“无为”C.“法治”D.“非攻”11.下图为唐代长安城商业分布示意图,阴影部分为“市”以外的商业区域。
与“安史之乱”前相比,“安史之乱”后的长安城内A.市以外经营行业的种类大大增加B.商业活动日趋突破坊市功能的界限C.官府对交易场所的限制更加严格D.官府设市数量增加,坊的数量减少12.在北宋初期,造船场多在江西、湖南等地,所造船只多为“纲船”(遭运船)、座船(官员乘坐船)、战船等;北宋后期,造船场多分布在闽、浙等地,大多生产抗风浪能力较强、吃水较深的尖底船。
这一变化反映了当时A.南北经贸发展B.海外贸易兴盛C.经济重心南移D.海防建设加强13.王安石在关于风俗的论议中谈到:“……兼并之家多。
富者财产满布州域,贫者困穷不免于沟壑”。
造成当时这种现象出现的原因最可能是A.中央集权遭到削弱B.城市经济的发展C.政府经济政策调整D.贫富差距的扩大14.杂剧在元代极为隆盛,有姓名可考的杂剧作家有200人,他们多为社会地位低下的文人、演员等,观众更是遍及各个社会阶层。
据此可知,元杂剧的兴盛A.说明文学进一步走向了民间B.宣告戏剧成为中国文学主流C.得益于广大下层人民的倡导D.推动了元代社会文化的发展15.王阳明提出一套以“致良知”为核心的理论。
他认为“良知”就是隐藏在每个人心中的“天理”,往往被私欲遮蔽,需要重新发现、扩充、实行,这样就可以达到圣贤境界。
据此可知,这一理论A.坚决反对研习儒学经典B.主张格物致知寻求天理C.受到西方人文精神影响D.隐含着平等自由的倾向16.明末清初书画家陈洪缓说:“今有人焉,聚徒讲学,禁民为非,人无不笑且话也。
伶人献伴,喜叹悲啼,使人之性情顿易,善者无不劝,而不善者无不怒。
”其意在强调A.理学正统地位的动摇B.戏曲艺术的批判现实性C.戏曲艺术的教化作用D.世俗文化源于大众生活17.清初思想家唐甄称:“立国之道无他,惟在于富。
……夫富在编户,不在府库。
若编户空虚,虽府库之财积如丘山,实为贫国,不可以为国矣。
”这反映出他主张A.国富寓于民富B.加强户籍管理C.保护小农经济D.减免民众赋税18.古代有学者认为,周孔与宋儒的根本区别在于:宋儒“只教人明理”,而“孔子则教习事”;他还认为只有“能斡旋乾坤,利济苍生,方是圣贤”。
据此可知,该学者A.主张重建儒家伦理规范B.倡导经世致用的思想C.力图冲破周孔儒学束缚D.推崇重利轻义价值观19.“扬州八怪”之一的郑板桥善画竹,为了迎合顾主的喜好,他画竹常常在不同情境下寓意有别,或表长寿吉祥寓意,用于祝寿;或代表鱼竿,表向往隐居生活。
这一现象出现的背景是A.文人画逐渐走向衰落B.社会矛盾日益尖锐C.传统绘画开始商品化D.商品经济发展繁荣20.隆庆元年(1567年),明朝政府开放海禁,在漳州府的月港设督饷馆,私人海上贸易逐渐合法化。
老百姓“富家以财,贫人以驱,输中华之产,驰异域之邦,易其方物,利可十倍”。
而月港“所贸金钱,岁无虑数十万……其殆天子之南库也”。
据此可知A.明朝始终奉行鼓励对外贸易的政策B.对外贸易有利于改善国计民生状况C.福建地区是明清对外贸易主要通道D.私人海上贸易造成了贫富分化加剧21.我国第一部药学专书《神农本草经》大约成书于汉代,《唐本草》是世界上第一部由国家制定的药典,宋代颁行了多部官修本草,明代李时珍撰成药物学集大成之作《本草纲目》,由朝廷颁行。
这些史实说明,我国古代药学的发展A.源于大一统的政治体制B.得益于国家力量的支持C.是商品经济繁荣的结果D.受到了宋明理学的推动22.昆曲在明朝万历年间被视为“官腔”,到清代被誉为“雅乐”“盛世元音”,宫廷重要活动常有昆曲演出,江南地区“郡邑大夫宴款不敢不用”,甚至“演戏必请昆班,以示府城中庙会之高雅”。
这些史实表明,昆曲在明清时期的流行是因为A.陆王心学广泛传播B.吸收了京剧的戏曲元素C.社会等级观念弱化D.符合士大夫的文化品味23.有学者指出,明清时期农具较少改进。
有所创新的多是适应个体农户小规模经营的细小农具,元代王被《农书》早有记载的一些大型高效农具却十分罕见。
对出现上述现象的合理解释是明清时期A.工商业发展的冲击B.精耕细作不被重视C.农业生产技术倒退D.依靠劳动力的投入24.中国古代科技著作有以“经”为名、采用注经式编写体例的传统,例如《黄帝内经》、《周髀算经》、《神农本草经》等,这反映出古代科技A.是儒家经典的组成部分B.注重形成完整的理论体系C.受到儒家学术方法影响D.切合生产生活的实用特征二、非选择题:共4题,第25题20分,第26题12分,第27题10分,第28题10分,共52 分25.阅读材料,回答问题。
(20分)材料一材料二原本中国古代的城市以城为主,纯粹体现工商贸易功能的市镇,要到唐宋之际才出现,到明清时,唐宋以来被称做“草市”的新型市镇得到充分发展。
据统计,宋代江浙地区在行政中心之外,出现了71个市镇,明代达316个,清代增至479个,市镇之间的直线距离不过数十里。
这些市镇收纳周边个体民户产品,进行深加工……大批市镇是大中城市与广大农村联系的纽带。
这些市镇中的居民已经从农业人口中分离出来,大多从事纺织业……明中期以后,还出现了专业市镇比如景德镇居民以制瓷为业,盛泽镇居民以蚕桑为业。
到清代前期广东佛山镇在内的“天下四大镇在专业性市镇的基础上发展成为新兴的城市。
——摘编自赵冈《中国城市发展史文集》等(1)根据材料一,比较图1、图2,提取两项支代城市发展变迁的信息,并结合所学予以简要说明。
(8分)(2)根据材料二并结合所学知识,概括指出明清市镇的特点及其经济意义。
(12分)26.阅读材料,回答问题。
(12分)(原创)材料下面是张岱年、方克立主编《中国文化概论》一书的目录摘编。
第四章中国传统文化的发展历程第一节上古:中华文化的发生3.偏、玄、道、佛相与激荡第二节殷商西周:从神本走向人本第六节隋唐:隆盛时代1.般商神本文第七节两宋:内省、精致趋向与市井文化勃兴2.周人文化维新第八节江夏金元:游牧文化与农耕文明的冲突与第三节春秋战国:中国文化的“轴心时代”融合第四节秦汉:一统帝国与文化一统1.游牧文化与农耕文化冲突的双重效应第五节魏晋南北朝:乱世中的文化多元走向2.元杂刷及其文化意义1.玄学崛兴3.规模盛大的中外文化交流2.道教的创制与佛教的传入第九节明清:沉幕与开新——据《中国文化概论》整理(1)根据材料并结合所学,简要阐述作者以“一统帝国与文化一统”作为“第四节秦汉”子目标题的理由。
(6分)(2)在目录“两宋、明清”中任选一节,根据材料并结合所学完成其子目的编写并简要阐述你的编写理由。
(6分)27.阅读材料,回答问题。
(10分)(原创)材料两汉之际佛教经中亚传入中国。
汉魏之际,佛教的因果报应、轮回转世理论对生死问题提供了一种解答,颇能满足士大夫的心理需求,加上其与玄学有相通之处,故佛学传播渐广。
中国人在消化佛教哲学的同时,也把中国传统哲学思想融入佛教,使佛学本土化。
南北朝时期,佛教更盛,寺院经济发达,拥有大量的土地和依附人口,由此引发了统治者的灭佛行动,但并没有改变佛教流行并在中国扎根的趋势。
到了隋唐,佛教进入鼎盛,隋唐的佛教学说最大的特点,是把儒家的心性佛教化。
佛教文化的输入促成中国文化内容与形式重大变化的同时,其自身也变成了中国化的佛教文化。
唐宋之后的诗、书、画的发展,常常与佛教的发展变化息息相关。
——摘编自张帆《中国古代简史》等(1)根据材料并结合所学,简析魏晋南北朝时期佛教迅速发展的原因。
(6分)(2)根据材料并结合所学,简要说明汉代以降佛教发展对中国传统文化的影响。
(4分)28.阅读材料,回答问题。
(10分)材料王艮(1483-1541),江苏泰州人,人称心斋先生,泰州学派创始人。
三十七岁时拜王守仁为师,入学王门之后,他“时时不满其师说”,指出“圣人之道”就是“百姓日用”,如果不能保障百姓的物质生活需要,使他们丧失生存权利那就不是“圣人之学”。
