5-3 电偶极辐射解析
电偶极子的辐射场.
赫兹1888年用振荡电路证实了电磁波的存在.
理想的LC电路的电磁振荡如下图:
I 0
I0
I 0
I0
A q0 E H B q0
A B
A q0 E H B q0
A B
其周期和频率可表示为
T0 2 LC f 0 1 2 LC
要实现电偶极子的辐射,就要经过下面的演化:
从LC振荡电路到振荡电偶极子
在无限大均匀绝缘介质(或真空)中,平面 电磁波的性质概括如下:
1. 电磁波是横波, E , H , v 构成正交右旋关系. 电磁波是偏振波, E , H 都在各自的平面内 振动,且 E , H 是同位相的. E
v H
平面电磁波 示意图
2. 在同一点的E、H值满足下式:
E H
S沿表面的负法 向,即指向轴心
I 2R n S EH 2al
对于长 l 的导体,单位时间内通过表面积 Ａ=2al 输入的电磁能量为
I 2R 2 AS dA 2al 2al I R
四、振荡电路 赫兹实验
麦克斯韦1865年预言了电磁波的存在.
E H
坡印廷矢量
S v 同方向
对于振荡电偶极子辐射波,可导出(自证推导) 平均辐射强度:
p0 sin S 2 2 24 r v
4 2
上式表明: 1) 辐射具有方向性 2) S与4成正比
例
圆柱形导体,长为l,半径为a,电阻为R,通 有电流I,证明: Z 1)在导体表面上,坡印廷 矢量S处处垂直导体表 面并指向导体内部. 2)沿导体表面的坡印廷 矢量的面积分等于导体 内产生的焦耳热功率 I2R.
赫兹用下面的实验证实了电偶极子 产生的电磁波
电动力学课件 5.3 电偶极辐射
e ikR 0 e ikR 0 B x, t A x, t p t pt 4 R R 4 0 e ikR ike R p t 4 R p t p t i p t 由于 k 0 0 t 1 c p t i p t 2 p t 0 0 e ikR e ikR 1 B x, t p t eR p t sin e 3 3 4 0 c R 4 0c R
§5.3 电偶极辐射
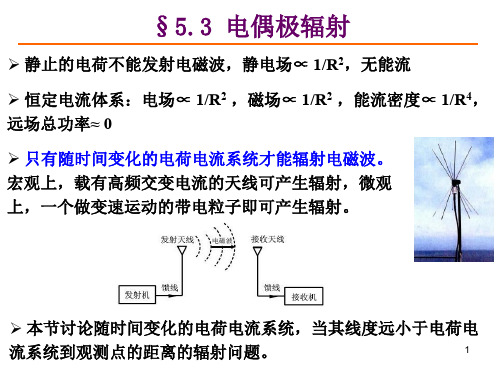
静止的电荷不能发射电磁波，静电场∝ 1/R2，无能流 恒定电流体系：电场∝ 1/R2 ，磁场∝ 1/R2 ，能流密度∝ 1/R4， 远场总功率≈ 0 只有随时间变化的电荷电流系统才能辐射电磁波。 宏观上，载有高频交变电流的天线可产生辐射，微观 上，一个做变速运动的带电粒子即可产生辐射。
电磁场能流密度正比于1/R2，沿径向辐射
e ikR B x, t p t sin e 4 0c 3 R
1
b) 辐射功率 单位时间内通过半径为 R 的球面向外辐射的平均能量，称为 辐射功率。把能流密度 S 对球面积分即得总辐射功率，即
P
S
S ds
dV
任何小区域电荷电流分布在远处某点产生的矢势可表示为位 于原点的各级电磁多极辐射的叠加 3、电偶极辐射
1 1）展开式的第一项 A x 与电偶极矩 p t 的关系
7
ikR e 由于 A1 x 0 J x dV 4 R V ikR ikR e e 1 A x , t 0 J x e i t dV 0 J x , t dV 4 R V 4 R V
电偶极辐射电场的分析及演示
１３４
进一步化简，
上式中 Ｃ’为积分常量， Ｃ’取不同数值时， 即得时刻辐射 场中不同的电场线方程， 与文献［１］得到的电 场线方程是 一致的。由于问题具有轴对称性， 故只需作出 Ｏｘｚ 平面 上的电场线， 下面对上式做进一步处理。将
代入（ １２） 式， 整理得：
（ １３）
作下列替换：
（ １２）
得
Ｔｈｅ Ａｎａｌｙｓｅ ａｎｄ Ｄｅｍｏｎｓｔｒ ａｔｉｏｎ ｏｆ ｔｈｅ Ｅｌｅｃｔｒ ｉｃ Ｆｉｅｌｄ Ｌｉｎｅ ｏｆ Ｏｓｃｉｌｌａｔｉｎｇ Ｅｌｅｃｔｒ ｉｃ Ｄｉｐｏｌｅ ＷＵ Ｎｅｎｇ－ ｚｈｉ， ＣＨＥＮ Ｙｉ－ ｃｈｅｎｇ， ＹＡＮＧ Ｗｅｉ
（Ｃｏｌｌｅｇｅ ｏｆ Ｐｈｙｓｉｃａｌ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ， Ｈｕａｚｈｏｎｇ Ｎｏｒｍａｌ Ｕｎｉｖｅｒｓｉｔｙ， Ｗｕｈａｎ ４３００７９， Ｃｈｉｎａ） Ａｂｓｔｒ ａｃｔ： Ｗｉｔｈ ｔｈｅ ｍａｔｈ－ ｓｏｆｔｗａｒｅ Ｍａｐｌｅ， ｔｈｅ ｅｑｕａｔｉｏｎ ｆｏｒ ｅｌｅｃｔｒｉｃ ｆｉｅｌｄ ｌｉｎｅ ｏｆ ｏｓｃｉｌｌａｔｉｎｇ ｅｌｅｃｔｒｉｃ ｄｉｐｏｌｅ ｉｓ ａｃｑｕｉｒｅｄ ｂｙ ａ ｇｅｎｅｒａｌ ｗａｙ， ａｎｄ ｔｈｅ ｅｌｅｃｔｒｉｃ ｆｉｅｌｄ ｉｓ ｄｅｍｏｎｓｔｒａｔｅｄ ａｎｄ ａｎａｌｙｚｅｄ ｄｉｖｉｓｉｏｎａｌｌｙ ａｎｄ ｔｉｍｅ ｓｈａｒｉｎｇ． Ｔｈｅ ｄｙｎａｍｉｃ ｄｅｍｏｎｓｔｒａｔｉｏｎ ｉｓ ｅｘｐｏｒｔｅｄ ｉｎ ｔｈｅ ＧＩＦ ｆｏｒｍａｔ ａｓ ａ ｒｅｓｕｌｔ． Ｋｅｙ Ｗｏｒ ｄｓ： ｏｓｃｉｌｌａｔｉｎｇ ｅｌｅｃｔｒｉｃ ｄｉｐｏｌｅ；ｅｑｕａｔｉｏｎ ｆｏｒ ｅｌｅｃｔｒｉｃ ｌｉｎｅ；ａｎｉｍａｔｅｄ ｄｅｍｏｎｓｔｒａｔｉｏｎ；Ｍａｐｌｅ
电偶极辐射电场线分布的分析
3
co sθ e
- i ( k 0 r-ω t)
( 19 ) ( 20 )
( ω 1 i 1 θe- i k0 r- t) sin 3 3 + 2 2 π ε 4 k0 r k0 r k0 r 0
将分量式写成实数形式 : 3 2 P0 k0 θ[ 31 3 co s ( k0 r - ω t) - 21 2 sin ( k0 r - ω t) ] Er = co s π ε 4 0 k0 r k0 r
_ _
2
( 15 )
_
er
_
eθ
eφ ( 16 )
_
E =
ic k0
θ r θ r sin r sin _ 1 × B = 9 9 ω iε 0 0μ 0 θ 9r 9 0 0 r sin θ Bφ
_
=
I△ l
er r
2
ω ε i4 π 0
I△ l
ik0 +
e θ ik0 1 2 co s 1 θθ k2 sin - 2 0 r r r r
E θ = E φ P0 k0
3
( 21 ) ( 22 ) ( 23 )
π ε 4 0 =0
θ[ ( sin
1
k0 r
3 3
-
1
k0 r
) co s ( k0 r - ω t) +
1
k0 r
2 2
sin ( k0 r - ω t) ]
4 电偶极辐射的电场线方程
电偶极辐射的电场线满足方程 Er θ 1 E = θ dr r d ( 22 ) 、 ( 23 ) 带入式 ( 24 ) , 整理后得 将式 ( 21 ) 、 1 1 ( 2 2 - 1 ) co s ( k0 r - ω t) + sin ( k0 r - ω t) k0 r k0 r θ 2 co s θ= d dr sin θ 1 1 sin ( k0 r - ω t) 2 2 co s ( k0 r - ω t) k0 r k0 r
电偶极子的辐射场.
z θ φ
v
H
r E y
p x
电 偶 极 子 的 辐 射 场
p0 sin r E (r , t ) cos t 2 4v r v 2 p0 sin r H (r , t ) cos t 4vr v
2
偶极子周围的电磁场
在无限大均匀绝缘介质(或真空)中,平面 电磁波的性质概括如下:
1. 电磁波是横波, E , H , v 构成正交右旋关系. 电磁波是偏振波, E , H 都在各自的平面内 振动,且 E , H 是同位相的. E
v H
平面电磁波 示意图
2. 在同一点的E、H值满足下式:
E H
无线电射频 电力传输
10 0 1m 10 3 1km 10 5
3
z E S a . . a H E x H p H
b . S . E y b
二、平面电磁波
在距离偶极子足够远处(r« l,变化很小), 电磁场的波动方程为:
r E E0 cos t v r H H 0 cos t v
平面电磁波方程
赫兹用下面的实验证实了电偶极子 产生的电磁波
A
振子
C
谐振器
B
发射
接收
D
频率
10 22
电磁波谱
γ 射线
X 射线
波长 10 13 1A 10 9 1nm 10
10
6
0
10
1T HZ 10
15
紫外线 可见光 红外线 微 波
1μ m
1cm
12
2
1G HZ 10
1M HZ 10 1K HZ 10
5-3 电偶极辐射
2 it
从而得到： |2 p 2 4 | p 0
P 1 4
0
p0
2
4
3c
3
五、短天线的辐射 辐射电阻 当天线的长度远小于辐 射波长时，它的辐射就 是电偶极辐射。 馈电点处电流有最大值 I0，在天线两段电流为 零。若天线长度l<<，
2
3
பைடு நூலகம்
sin d
S
2 | | p
32 0 c
2 2 | | p 2
3
2
0
d sin d
3 0
32 0 c
3
2
4 3
1 40
2 | | p
3c
3
如果偶极子作简谐振动，角频率为ω ，且有 it p( x, t ) p0 ( x )e 则 ip ip0 ( x )e it p
2n x 一般是不能忽略的，因此
x 要保留，
所以，
A( x )
0
4
V
)eik ( R n x ) J(x R
dV
把相因子对 kn x 展开，得
e
ikn x
1 ikn x
1 2!
) 2 (ikn x
从而得到矢势A的展开式为：
2 x 2n x r R 1 2 R R 1 2
2
z
r
l o x
x
P y
x
, J
由二项式展开得到（略去 x 2 / R 2 等高次项）： r R n x 由此得到
电偶极子的场及辐射
收稿日期：2003-06-14作者简介：吕宽州（1963-），男，河南扶沟人，郑州经济管理干部学院讲师。
文章编号：1004-3918（2003）05-0512-03电偶极子的场及辐射吕宽州1，姜俊2（1.郑州经济管理干部学院，河南郑州450053；2.河南省科学院，河南郑州450002）摘要：采用了镜像法等方法对电偶极子及其产生的静电场、电磁场及辐射等做了较系统和深入的分析、研究，使分析方便、简化，推出的结论有一定实际指导意义。
关键词：电偶极子；电场；磁场；辐射中图分类号：0442文献标识码：A在很多文献上，缺乏对电偶极子及其产生的静电场、电磁场及辐射等较系统和深入的分析、研究。
本文参考有关文献给出或分析、推出了重要结论，部分内容采用了镜像法，使分析更方便。
!电偶极子及其产生的静电场电偶极子由一对正、负点电荷组成，电量为l ，相距为l ，如图1所示。
其电偶极矩p =l l ，l 的方向由~l 指向+l ，在T 处产生的电场的电势为：#（r ）=l 4L e 0T +_l4L e 0T _当T !l 时，#（r ）=l l cOs 64L e 0T 2=p ·e r 4L e 0T2（1）电场强度为：E =_"@=e r P cOs 62L e 0T 3+e !P si n 64L e 0T3（2）以上结果表明，电偶极子的电势及电场强度的大小分别与距离的平方、三次方成反比，既存在于近区，且与方位角有关，这些特点都与点电荷的电场显著不同。
图2绘出了电偶极子的电力线与等位面。
图1电偶极子F i g .1E lectric d i p O le图2电偶极子的电力线与等位线F i g .2E lectric p Ow er li ne and e C ui p Otential p laneOf e lectric d i p O le第21卷第5期2003年10月河南科学HENAN SC I ENCEV O l.21N O.50ct .2003!电偶极子产生的电磁场及辐射当P =P 0e -j G t 时，为谐振电偶极子，P 0为常矢，则在近区，即l H T 时，主要地一方面将感应如上所述的静电场，另一方面，相当于I =j G C 、长为l 的电流元还将产生一稳恒磁场，其规律可用毕萨定律描述，且电场与磁场的相位相差为90 ，即电场能量与磁场能量相互转换，而平均波印亭矢量为零，故不产生辐射。
电偶极辐射
机动 目录 上页 下页 返回 结束
三．偶极辐射
1．用 p表示偶极辐射矢势
ikR 0 e A( x , t ) p 4 R
4 r
上式表示一种时谐波，这是计算辐射场矢势的一 般公式。与稳恒电流磁场相比这里 A 附加了一 个因子 e ikr ，称为推迟相因子。
机动 目录 上页 下页 返回 结束
ikr ( x)e it ( x, t ) [ dV ]e 4 0 r
同样可以得到：
it ( x , t ) ( x )e
r R n x 乘以k相对于 2 不一定是小量。 原因：
利用 e 1 x x ...
得到：
机动 目录 上页 下页 返回 结束
it J ( x, t ) J ( x)e 条件下辐射场的近似公式 it ( x , t ) ( x)e
J ( x )dV 偶极辐射公式
机动
目录
上页
下页
返回
结束
在满足 l R ， l 的前提下，按 R 与 的关系还可分为三种情况：
3．
R与 的关系
（1）R （近区） R 2 ikR R , e 1 传播时间 t T c k 这一区域内变化电磁场与静场性质类似。
eikR E ( x, t ) ( p n) n 2 4 0c R
1
ikR ikR e ike 所以有： n R R
J ( x, t )dV p
微波与天线电偶极子的辐射
磁场由：
H R H 0
得: 电场由：
Ile jkR 1 H j k sin 4R R
E H = t
E 1 j H
Ile jkR ER j 2 R 2
得:
1 j k cos R Ile jkR 2 jk 1 E j k sin 2 4 R R R E 0
微波与天线-电偶极子的辐射
天线辐射与接收的理论基础
辐射的基本概念 滞后位 电偶极子的辐射 磁偶极子的辐射
辐射的基本概念
1. 什么是辐射？ 辐射：随时间变化的电磁场离开波源向空 间传播的现象。 产生辐射的源称为天线。
2. 辐射产生的必要条件 （1）时变源存在。 （2）源电路是开放的。 3. 影响辐射强弱的原因 （1）源电路尺寸与辐射波的波长相比拟时 辐射较为明显。 （2）源电路越开放，辐射就越强。
J 其解为: A 4π V R dV
1 4 π
R
V
dV
2. 在时变场情况下，动态矢量位和动态标量位满足的方程 麦克斯韦方程：
1 E H ( A) 已知： B A H JC t B A E E ( A) ( E ) 0 t t t
V
D H JC t B E t
D V
B 0
V JC t
微分形式的麦克斯韦方程组给出了空间某点场量之间 及场量与场源之间的关系。 注意：麦克斯韦方程的微分形式只适用于媒体的物理性质 不发生突变的区域。
滞后位
1. 在静态场情况下，矢量位和标量位方程为 2 2 A J
电动力学第五章—
19
电动力学
三．辐射问题的本质也是边值问题
变化电荷、电流分布激发电磁场，电磁场又 反过来影响电荷、电流分布。空间电磁场的分布 就是在这一对矛盾相互制约下形成的。变化的电 荷电流分布一般具有边界，因此在求解时要考虑 它们的边界条件和边值关系。但是，一般情况下 这种的边界很复杂，使得电荷、电流分布无法确 定，因此使得求解问题无法进行。在本章我们仅 讨论电荷、电流分布为已知的辐射问题。
尔方程化为：
1 2 1 2 Q(t ) (r ) (r ) 2 2 2 r 0 r r c t
＊
1 2 1 2 当 r 0 时， 2 (r ) 2 0 2 r r r c t 2 2 u 1 u u (r , t ) 2 2 0 令 (r , t ) 2 r c t r
2、达朗贝尔方程及推迟势的物理意义； 3、矢势的展开和偶极辐射； 4、电磁场的动量守恒。
• 本章难点： 1、矢势的展开和偶极辐射公式的导出； 2、电磁场动量密度张量的引入和意义。
第五章 电磁波的辐射
17
电动力学
引言
一. 电磁辐射
不稳定的电荷、电流激发的电磁场随时间 变化。有一部分电磁场以波的形式脱离场源 向外运动，这被称为电磁波的辐射。
A E A t t 引入标量势函数 A E t
第五章 电磁波的辐射
A (E ) 0 t A E t
22
电动力学
5- 1
电磁场的矢势和标势
二．规范变换和规范不变性
第五章 电磁波的辐射
24
A A A E ( ) t t t t t
§3电偶极辐射
§3 电偶极辐射2、矢势的展开式dq2）远区电磁场矢势的展开对于远场区域的辐射场，可以采用近似方法求解4.时变电偶极矩在远场区激发的电磁场辐射——能流、辐射功率、角分布θ∙∙pθ∙∙p 在电偶极矩的轴线方向上没有辐射；例题：假设两个很小的金属球，之间用细导线相连，两个球上的电量分别是q(t)和-q(t)。
假设：()tqtqωcos)(=θr+-z计算平均能流密度和总辐射功率。
5、短天线的辐射辐射电阻1）短天线辐射的偶极辐射近似电偶极辐射近似：电荷体系的分布尺寸远小于辐射电磁波的波长θ∙∙p90120DefinitionAntenna (radio)：An antenna (or aerial) is atransducer that transmits or receiveselectromagnetic waves.WikipediaYagi‐Uda Antenna(八木宇田天线)Wikipedia“Rabbit ears” dipole antenna for television receptionWikipediaCell phone base stationParabolic antennaantennas天线阵列(Antenna array)相控阵天线❑天线阵是将若干个天线按一定规律排列组成的天线系统。
❑❑利用天线阵可以获得所期望的辐射特性，诸如更高的增益、需要的方向性图等。
❑组成天线阵的独立单元称为阵元，排列的方式有直线阵、平面阵等。
❑天线阵的辐射特性取决于阵元的型式、数目、排列方式、间距，以及各阵元上的电流振幅和相位等。
+Q Q-l ∆在观察轴排列的对称天线构成的二元阵，均匀直线式天线阵均匀直线阵是指天线阵的各阵元结构相同，并以相同的取向和相等的间距排列成直线，各个阵元的激励电流振幅相等、相位则沿阵的轴线以相同的比例递增或递减的天线阵。
N 个阵元沿x 轴排列，两相邻阵元的间距为d ，激励电流相位差为，则相邻两阵元辐射场的相位差为ξsin kd ψξφ=-一维天线阵列计算例子•N =7•d = λ0/2•求第一个无效角天线阵列的辐射方向0null null 2sin 16.67Nd λϕϕ±±≈±︒＝＝，sin sin 02Nkd φ⎛⎫= ⎪⎝⎭2sin 2sin Factor Array ψψN ＝扇形波束和笔形波束•N 值越大，波束夹角越小•上面的例子在θ=90o的平面上作图，但是在φ为定值的平面上，波束的夹角仍然较大,这种波束犹如薄扇,所以称为扇形波束•取7个一模一样的上例一维阵列排列成7×7的方阵，可预期波束在方向和方向的夹角都都差不多只有16°,这种波束，称为笔形波束,定向性极佳44天线电流的相位与指向性•|sin(N ψ/2)/sin(ψ/2)|之最大仍在ψ=0，亦即•波束指向转到角度φm•例如N =7，，求天线的指向方向sin m kdξφ＝sin 0kd ψξφ=-=2,/2d ξπλ==sin 1/2m kd ξφ=＝30,150m φ︒︒=The definition of Optical AntennaIEEE standard definitions of terms for antennas:a means for radiating or receiving radio wavesIn analogyOptical Antenna:A device designed to efficiently convert free-propagating optical radiation to localized energy, and vice versaMotivations of radio and optical antenna •Radio antennas: developed as solutions to a communication problem •Optical antennas: motivated by microscopyWhy?Enable us to concentrate externalradiation to dimensions smaller thandiffraction limitSome earlier IR optical antennasFabricated by Boreman etc. since late 1990s/2.7Field confinement ~ Advances in Optics and Photonics 1, 438–483 (2009)However, its size ~cmThe spectrum we interested in is optical wavelength which means we must shrink the element’s sizeBut at optical frequencies, metals are no longer perfect conductors while at microwave frequencies metals act like a mirrorLocalized electronic oscillations‐Surface Plasmon。
5-3电偶极辐射
2．求解 A(x) 的公式
因为 R >> x′ ≥ n ⋅ x′ ，所以分母中的 n ⋅ x′可以舍 但是要注意， 不能轻易舍去。 去。但是要注意，相因子中的 n ⋅ x′不能轻易舍去。 2π n ⋅ x′ 原因： 不一定是小量。 原因： 相对 2π 不一定是小量。 λ 利用 e x = 1+ x + x2 + ... 得到： 得到：
1-8
三．偶极辐射
1．用 p表示偶极辐射矢势
p = x′ρ(x′, t)dV ′
∫
ɺ p = ∫ J (x, t)dV′
µ0eikR A(x) = ∫ J (x′)dV′ 4π R 0 2．偶极辐射的电场强度和磁感应强度 . µ0 µ0 eikR . eikR eikR . B =∇× A = ∇×( p) = ∇( ) × p+ ∇× p 4π R 4π R R
1-5
R2 1 n ⋅ x′ r≈ = R( ) ≈ R(1− ) = R − n ⋅ x′ R + n ⋅ x′ 1+ n ⋅ x′ / R R
µ0 J (x′)eik(R−n⋅ x′) A(x) = dV ′ 4π ∫ R − n ⋅ x′
µ0 J (x′)eikr A(x) = ∫ dV′ 4π r
5.3 电偶极辐射
1-1
电磁波是从变化的电荷、 电磁波是从变化的电荷 、 电流系统辐射 出来的。 宏观上， 出来的 。 宏观上 ， 主要是利用载有高频交 变电流的天线产生辐射， 微观上， 变电流的天线产生辐射 ， 微观上 ， 一个做 变速运动的带电粒子即可产生辐射。 变速运动的带电粒子即可产生辐射。
1
eikR ikeikR 所以有： 所以有：∇ n ≈ R R
偶极子辐射 和 自发辐射
偶极子辐射和自发辐射偶极子辐射和自发辐射1. 介绍偶极子辐射和自发辐射的概念偶极子辐射和自发辐射是物理学中重要的概念，涉及到原子和分子的能级结构和电磁辐射的产生。
偶极子辐射是指在外加电场的作用下，原子或分子中的电子在能级之间跃迁时所辐射出的电磁波。
而自发辐射则是指在没有外加电场的情况下，原子或分子内部的电子由于量子涨落而发生能级跃迁产生的辐射。
2. 偶极子辐射的原理在外加电场的作用下，原子或分子的电子会发生能级跃迁。
根据量子力学的原理，这些能级跃迁发生时会伴随着电子的波函数的变化。
当电子由高能级跃迁到低能级时，其波函数的变化将导致辐射电磁波。
这个辐射过程类似于一个振荡的电子偶极子在空间中产生电磁波，因此被称为偶极子辐射。
3. 自发辐射的特点和机制自发辐射是由于原子或分子内部的电子发生能级跃迁而产生的辐射。
与偶极子辐射不同，自发辐射并不需要外加电场的作用。
自发辐射的机制是由于量子涨落导致的电子能级的随机跃迁。
原子或分子内部的电子在不受外界干扰的情况下，由于量子涨落而发生能级跃迁，并伴随着辐射电磁波。
4. 偶极子辐射和自发辐射的应用及意义偶极子辐射和自发辐射在光谱学、激光技术以及原子与分子物理等领域有着广泛的应用。
通过研究偶极子辐射和自发辐射过程，可以深入了解原子与分子的能级结构和电磁辐射的机制。
这对于实现一些重要的科学技术和应用有着重要的意义。
5. 个人观点和理解在我看来，偶极子辐射和自发辐射是探索微观世界的窗口。
通过研究它们可以了解原子和分子的内部结构以及它们与电磁辐射的相互作用。
这对于我们理解物质的基本特性和发展相关的技术具有重要意义。
偶极子辐射和自发辐射也为光学、光谱学等领域提供了重要的实验现象和理论基础，推动了相关领域的发展与创新。
总结回顾：通过本文的探讨，我们了解了偶极子辐射和自发辐射的概念、原理、特点和应用。
偶极子辐射是在外加电场作用下，原子或分子中的电子由高能级跃迁到低能级时产生的辐射电磁波。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
从而得到矢势A的展开式为：
0 eikR 1 2 A( x ) J ( x ) 1 ik n x ( ik n x ) 4 R V 2!
展开式的各项对应于各级电磁多极辐射。
三、电偶极辐射
展开式的第一项
ikR e A(1) ( x ) 0 4 R
在近区内， kr <<1 ，推迟因子 eikr~1 ，因而场保持
稳恒场的主要特点，即电场具有静电场的纵向形式，
磁场也和稳恒场相似。 b) 远区（辐射区）r>>λ，而且也保证r>>l。
1 1 在此区域中场强E和B均可略去 的高次项， R | x |
该区域内的场主要是横向电磁场。
c) 感应区（过渡区），r ~ λ，但满足r>>l。 这个区域是一个过渡区域。它介于似稳区和辐射区
根据小区域的意义
l ~| x | ,
l ~| x | r.
因此，在计算辐射场时只须保留1/R的最低次项。 而 R r , r | x |，所以分母中可以去掉 n x 项。但分子不能去掉 n x 项，这是因为这项贡献 一个相因子： ikn x i 2n x /
若电流 J ( x, t ) 是一定频率ω的交变电流，有
J ( x, t ) J ( x)e
因此
it
式中 k c 为波数
0 J ( x)ei ( k r t ) Α( x, t ) dV 4 r
如果令 A( x, t ) A( x )e it
( x, t )
40 r
c dV
由此可见，由矢势公式就可以完全确定电磁场。 磁场
ic 电场（在电荷分布区域外面） Ε Β k 二、矢势A的展开式
1. 小区域内的电流所产生的辐射的特点： 对于矢势
Β Α
0 J ( x)eikr A( x ) dV 4 V r
ikR e (1) J d V p p 由于 ，所以 A ( x ) 0 4 R V
V
J ( x)dV
可见A(1)表示振荡电偶极矩产生的辐射，简称为电 偶极辐射。 由于讨论远区场时，只保留1/R的最低次项，因而 算符▽不需作用到分母上，而仅需作用到相因子 ikR e 上即可达到要求。
2 2
1
x
r
x
P y
x 2 2 n x 2 x r R 1 R 2 R 由二项式展开得到（略去 x 2 / R 2 等高次项）：
, J
r R n x
由此得到
0 J ( x)eik ( R n x) A( x ) dV 4 V R n x
则有
0
式中因子eikr是推迟作用因子，它表示电磁波传到场 点时有相位滞后kr。 由电荷守恒定律，在一定频率的交变电流情形中有
i J
可见，只要电流密度给定，则电荷密度也自然确定， 标势也随之确定。 r
( x, t )
注意到其中三个线度问题：
第一，电荷分布区域的线度l ，它决定积分区域 内| x’ |的大小；
2 第二，波长 的线度； k
第三，电荷到场点的距离r。 我们研究分布于一个小区域内的电流所产生的辐 射。所谓小区域是指：l 对于r 和λ的关系，可分为三种情况：
l r
a) 近区（似稳区） r , 但仍满足 r l
结论：
1 ikR | sin( )e ˆ E e | p 2 40 c R
磁力线是围绕极轴的圆周，B总是横向的;电场线是经面上 的闭合曲线，由于在空间中 E 0 ，E线必须闭合。因此E不 可能完全横向，只有当略去1/E的高次项后，才近似为横向。
§5.3 电偶极辐射
电磁波是交变运动的电荷系统辐射 出来的，在宏观情形电磁波由载有交变 电流的天线辐射出来；在微观情形，变 速运动的带电粒子导致电磁波的辐射。 本节研究宏观电荷系统在其线度远 小于波长情形下的辐射问题。
一、计算辐射场的一般公式 当电流分布 J ( x, t ) 给定时，计算辐射场的基础是 推迟势： A( x, t ) 0 J ( x, t )dV r 4 V
的过渡区域中。
2. 辐射场的矢势展开式（远区） 选坐标原点在电流分布区域内，则 x 与l 同数 量级， R x ,
z
r x x 。
r
l o
x
, J
P
x
y
x
由图可知：
r | x x | | x | x 2 x x
2 2 2
2
z
l o
R x 2 Rn x
ic ic E B ikn B cB n k k 1 ikR n) n e ( p 2 40 c R
如果取球坐标，原点在电荷电流分布
区域内，并以 p 方向为极轴，则由上
式可知： B沿纬线上振荡，E沿经线上振荡。
z
1 ikR | sin( )e ˆ B e | p 3 40 c R
作用结果相当于代换： ikn , i t 由此得到，辐射场为 i0 k ikR B A ikn A e n p 4R
1 1 ikR ikR n e i n p e p 3 3 40 c R 40 c R
e
e
所以涉及的是小参数 x 而不是 x R ，相位差
2n x 一般是不能忽略的，因此 x
要保留，
ik ( R n x ) 所以， A( x ) 0 J ( x )e dV 4 V R
把相因子对 kn x 展开，得
e
ikn x
1 2 1 ikn x (ikn x ) 2!