用解析法作牛头刨床的运动分析.doc
牛头刨床工作原理

牛头刨床的组成
原动部分:电动机; 传动部分:带轮机构,齿轮机构,曲轴连杆机构, 棘轮机构,螺旋机构; 执行部分:滑枕 ,工作台; 控制部分:离合手柄,变速控制手柄。
滑枕运动路线图
电动机→变速机构→摇杆机构→滑枕往复运动
牛头刨床摆动导杆机构运动简图及 自由度计算。
F 3n 2PL PH
档位 1 2 3 4 5 6
大斜 15.13 85.27 齿轮 转速 (r/mi n)
61.1
42.63 30.01 17.15
斜齿轮转速数据
快进电机参数:型号:Y801L2-4B5。功率: 0.55KW,转速:1390r/min。蜗杆头数: Z1=2,右旋。蜗轮齿数Z2=35,右旋。模 数m=2.5mm。
牛头刨床V带传动运动简图
工作台横向进给运动路线图
电动机→变速机构→棘轮进给机构→ 工作台横向进给运动。
V带传动特点分析
当量摩擦因数较大,V带传动产生的最大摩擦力 大约是平带的3倍,允许包角小,传动比较大,中 心距较小,预紧力较小;传动效率85%~95%, 带速范围20 ~ 30m/s,传递功率可达700KW, 只适合开口传动。
牛头刨床解析牛头刨床工作时装有刀架的滑枕3由床身内部的摆杆带动沿床身顶部的导轨作直线往复运动使刀具实现切削过程的主运动通过调整变速手柄5可以改变滑枕的运动速度行程长度则可通过滑枕行程调节柄6调节
牛头刨床机械系统及工 作原理PPT汇总
装备1011第6组: 王平
牛头刨床外形图及基本参数
牛头刨床主要由床身、滑枕、 刀架、工作台、横梁等组成, 如图所示。因其滑枕和刀架形 似牛头而得名。
圆锥齿轮数据
编号 14 15 16 17 18
齿数
牛头刨床运动分析

连杆机构运动分析机构运动分析的解析法有多种,其中比较常用的有矢量方程解析法、矩阵法和复数矢量法等。
用解析法作机构运动分析时,首先建立机构的位置方程,然后将其对时间求一次、二次导数,可以得到机构的速度方程和加速度方程,完成运动分析。
例3-1 图示为一牛头刨床的结构简图。
设已知各构件的尺寸为:,,,,。
并知原动件1 的方位角和等角速度。
求导杆3 的方位角,角速度及角加速度3ε和刨头5上点E 的位移,速度和加速度。
解:该牛头刨床为一个六杆机构。
先建立一直角坐标系如图,并标出各杆矢及各杆矢的方位角。
其中共有四个未知量、、、。
为求解需建立两个封闭矢量方程,为此需利用两个封闭图ABCA 及CDEGC 。
(1)求导杆3 的角位移,角速度和角加速度,由封闭形ABCA 可得写成复数形式为313126θθπi i ie s e l e l =+ (a )展开得解上述两式可得因式中分子分母均为正,故知在第一象限。
式(a )对时间t 求导,注意为变量,有33133311θθθωωi i i e dtds ie s ie l += (b ) 展开后可得m/srad/s (逆时针方向)再将式(b )对时间t 求导,则有 3333133232233332112θθθθθωωεωi i i i i ie dt dse dts d es ies e l ++-=- (c )展开后可求得1471.0/]2)s i n ([333132113=--=s dtds l ωθθωε rad/s 2 (逆时针方向)m/s 2其方向与相反。
(2)求刨头上点E 的位移,速度和加速度。
由封闭形CDEGC 可得写成复数形式为 E ii i s el el e l +=+2'64343πθθ (d )展开得解之得由机构简图知在第二象限,故=175.3266º,而m式(d )对时间t 求导可得dtds ie l ie l Ei i =+434433θθωω (e ) 解之得rad/s (逆时针方向)m/s其方向与相反。
【精品毕设】牛头刨床的运动分析

《机械原理》
课程设计计算说明书题目:牛头刨床主传动机构的设计与分析
系别工程与应用科学系
专业班级 08级机械工程及自动化2班
学生姓名高峰
学号 12008247801
指导教师李辉
2010年7月
目录
一、概述
§1.1、课程设计的任务和目的————————————— 1 §1.2、课程设计的要求———————————————— 1 §1.3、课程设计的数据———————————————— 1
二、牛头刨床主传动机构的结构设计与分析
§2.1、机构选型、方案分析及方案的确定———————— 2 §2.2、主传动机构尺寸的综合与确定—————————— 2 §2.3、杆组拆分——————————————————— 3 §2.4、绘制机构运动简图——————————————— 3 §2.5、绘制刀头位移曲线图—————————————— 3
三、牛头刨床主传动机构的运动分析及程序
§3.1、解析法进行运动分析—————————————— 3 §3.2、程序编写过程(计算机C语言程序)——————— 5 §3.3、计算数据结果————————————————— 6 §3.4、位移、速度和加速度运动曲线图与分析—————— 7
四、小结
心得体会—————————————————————— 8
五、参考文献
参考文献—————————————————————— 8。
牛头刨床机构方案分析
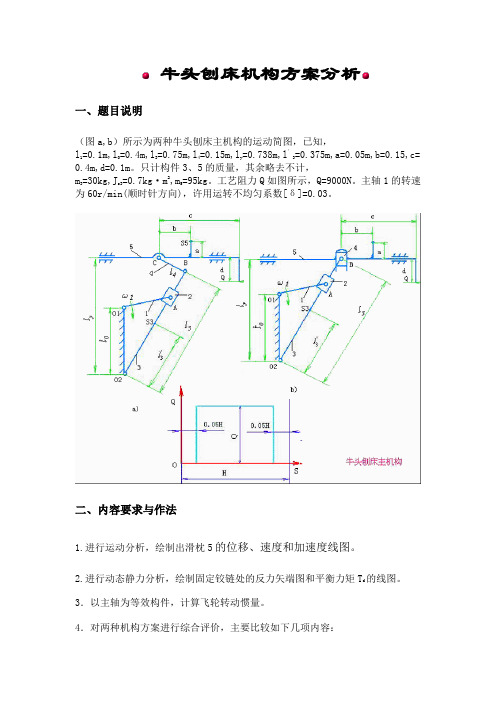
牛头刨床机构方案分析一、题目说明(图a,b)所示为两种牛头刨床主机构的运动简图,已知,l1=0.1m,l0=0.4m,l3=0.75m,l4=0.15m,l y=0.738m,l′3=0.375m,a=0.05m,b=0.15,c= 0.4m,d=0.1m。
只计构件3、5的质量,其余略去不计,m3=30kg,J s3=0.7kg·m2,m5=95kg。
工艺阻力Q如图所示,Q=9000N。
主轴1的转速为60r/min(顺时针方向),许用运转不均匀系数[δ]=0.03。
二、内容要求与作法1.进行运动分析,绘制出滑枕5的位移、速度和加速度线图。
2.进行动态静力分析,绘制固定铰链处的反力矢端图和平衡力矩T d的线图。
3.以主轴为等效构件,计算飞轮转动惯量。
4.对两种机构方案进行综合评价,主要比较如下几项内容:工作行程中滑枕 5 的速度均匀程度。
固定铰链处的反力大小及方向变化。
平衡力矩平均值及波动情况。
飞轮转动惯量大小。
上机前认真读懂所用子程序,自编主程序,初始位置取滑枕 5 的左极限位置。
主程序中打开一数据文件“DGRAPS”,写入需要显示图形的数据。
三、课程设计说明书内容上机结束后,每位学生整理出课程设计说明书一份,其内容应包括:1.机构简图和已知条件。
2.滑枕初始位置及行程H的确定方法。
3.杆组的拆分方法及所调用的杆组子程序中虚参与实参对照表。
4.飞轮转动惯量的计算方法。
5.自编程序中主要标识符说明。
6.自编程序及计算结果清单。
7.各种线图:①滑枕的位移、速度和加速度线图,②平衡力矩线图③固定铰链处反力矢端图④等效转动惯量,等效阻力矩,等效构件角速度线图。
8.对两种方案的比较,评价。
9.以一个位置为例,用图解法做机构的运动分析,与解析法计算结果比较误差。
10.主要收获与建议。
指导教师参考上述内容提出具体要求,学生按照指导教师的要求书写并制订成册。
牛头刨床机械原理课程设计8’运动分析

牛头刨床机械原理课程设计8’运动分析本文旨在讨论牛头刨床机械原理课程设计8’运动分析。
牛头刨床机械原理是一门重要的工程课程。
本课程旨在帮助学习者了解牛头刨床机械原理,包括设计和分析运动系统机构的基本概念,分析复杂机械系统的工作原理,建立有效的算法来预测机械系统的运动特性,以及研究驱动和控制机械系统的方法。
在牛头刨床机械原理课程中,学习者需要经过大量学习和实践,才能掌握有关牛头刨床机械原理的知识,为此,教师应利用一些适当的实验,帮助学生加强对有关运动分析的理解,以及更好地掌握牛头刨床机械原理的知识。
本文首先介绍了牛头刨床机械原理的基本概念,并详细说明了牛头刨床机械原理课程设计8’运动分析的内容。
其次,对8’运动分析进行了具体阐述,详细说明了运动分析时所涉及到的四个阶段,即:运动分析的前提条件、机械原理分析、系统仿真分析和系统评估。
具体而言,运动分析的前提条件包括牛头刨床的数据、结构与参数。
机械原理分析包括牛头刨床的功能分析和运动学分析;系统仿真分析包括系统建模和仿真;最后,系统评估旨在通过数据和模拟结果来评估系统功能和性能。
接下来,本文提出了实施牛头刨床机械原理课程设计8’运动分析的一些建议。
首先,教师应重点介绍牛头刨床机械原理课程设计8’运动分析的基本概念,以便学生能够更好地理解牛头刨床机械原理的基本原理。
其次,应利用实验来加强学生对牛头刨床机械原理课程设计8’运动分析的理解,帮助学生更好地掌握牛头刨床机械原理的基本知识。
最后,教师应该尽可能地结合实践与理论,让学生在实践中重新领悟牛头刨床机械原理,并熟练应用其在实际工程中的应用。
本文通过分析牛头刨床机械原理课程设计8’运动分析,结合实践和理论,提出了一些有关实施牛头刨床机械原理课程设计8’运动分析的建议,以帮助学生更好地理解牛头刨床机械原理课程设计的基本概念,并能够熟练应用牛头刨床机械原理的知识在实际工程中。
牛头刨床的连杆机构运动分析

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
(整理)牛头刨床的连杆机构运动分析.

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
牛头刨床导杆机构运动分析方案四

牛头刨床导杆机构运动分析一、设计任务及要求:(1)已知:牛头刨床的导杆机构的曲柄每分钟转速n2,各构件尺寸及重心位置,且报头导路x-x位于导杆端点B所作圆弧的平分线上。
数据如下表所示:1、用c语言编写计算程序,对机构进行动态分析和动态显示。
2、上机调试程序并打印结果。
3、画出导杆4的角位移,角速度,角加速度的曲线。
4、编写设计计算说明书。
二、数学模型的建立如图三个向量组成封闭图形,于是有0321=+-Z Z Z按复数式可以写成a (cos α+isin α)-b(cos β+isin β)+d(cos θ3+isin θ3)=0 (1)由于θ3=90º,上式可化简为a (cos α+isin α)-b(cos β+isin β)+id=0 (2)根据(2)式中实部、虚部分别相等得acos α-bcos β=0 (3)asin α-bsin β+d=0 (4)(3)(4)联立解得 β=arctanacosaasinad + (5)b= 2adsina d a 22++ (6) 将(2)对时间求一阶导数得 ω2=β’=baω1cos(α-β) (7) υc =b ’=-a ω1sin(α-β) (8)将(2)对时间求二阶导数得 ε3=β’=b1[a ε1cos(α-β)- a ω21sin(α-β)-2υc ω2] (9) a c =b ”=-a ε1sin(α-β)-a ω21cos(α-β)+b ω22 (10)a c 即滑块沿杆方向的加速度,通常曲柄可近似看作均角速转动,则ε1=0。
三、程序框图四、程序清单及运行结果:#include<graphics.h>#include<math.h>#include<conio.h>#include<stdio.h>#define PI 3.1415926#define M PI/180#define C 2*PI*70/60#define l1 95#define l2 400#define l4 800#define l5 (0.32*l4)#define l7 l4-Ys6void dtmn();void pist(float x0,float y0,float l,float h, float theta);void slide(float x0,float y0,float x1,float h);void pirot(float x0,float y0,float l);void sgd();void cur();/****************************主函数****************************/ main(){int Q2,i=0,j=0,Q_2[72];float Q4,Q41,Q411,w3,a3,Q5,Q51;float Q511,sA,sA1,sA11,Se,w4,Ve,Se1,a4,Se11;float S_e[72],S_e1[72],S_e11[72],Q_511[72];FILE *fl;","w"))==NULL){printf("mydata.txt cannot open!\n");exit(0);}/*int gd=DETECT,gm;initgraph(&gd,&gm,"c:\\turboc2");cleardevice();*/clrscr();printf(" zhuanjiao weiyi sudu jiaojiasudu jiasudu \n");for(Q2=0;Q2<=360;Q2+=5){i++;if(i%12==0){getch();printf(" zhuanjiao weiyi sudu jiaojiasudu jiasudu \n");}if(Q2>=0&&Q2<90||Q2>270&&Q2<=360){Q4=atan((l2+l1*sin(Q2*M))/(l1*cos(Q2*M)));Q4/=M;}else if(Q2==90||Q2==270){Q4=90;}else if(Q2>90&&Q2<180){Q4=PI-atan((l2+l1*sin(Q2*M))/(-l1*cos(Q2*M)));Q4/=M;}else if(Q2>=180&&Q2<270){Q4=PI-atan((l2+l1*sin(Q2*M))/(-l1*cos(Q2*M)));Q4/=M;}if(Q4==90) sA=l2+l1;else if(Q4==270) sA=l2-l1;elsesA=l1*cos(Q2*M)/cos(Q4*M);sA1=-l1*C*sin((Q2-Q4)*M);Q41=-l1*C*cos((Q2-Q4)*M)/sA;w3=Q41;Q411=(C*C*l1*sin((Q4-Q2)*M)-w3*sA1)/sA;a3=Q411;if(((l7-l4*sin(Q4*M))/l5)>=0&&((l7-l4*sin(Q4*M))/l5)<=1)Q5=180-asin(l7-(l4*sin(Q4*M))/l5)/M;else if(((l7-l4*sin(Q4*M))/l5)>=-1&&((l7-l4*sin(Q4*M))/l5)<=0)Q5=180+asin((l7-l4*sin(Q4*M))/l5)/M;Se=l4*cos(Q4*M)+l5*cos(Q5*M);Q51=-w3*l4*cos(Q4*M)/(l5*cos(Q5*M));w4=Q51;Se1=-w3*l4*sin((Q4-Q5)*M)/cos(Q5*M);Q511=(Q41*Q41*l4*sin(Q4*M)+Q51*Q51*l5*sin(Q5*M)-Q411*l4*cos(Q4* M))/(l5*cos(Q5*M));Se11=-(a3*l4*sin((Q4-Q5)*M)+w3*w3*l4*cos((Q4-Q5)*M)-w4*w4*l5)/cos( Q5*M);S_e[j]=Se;S_e1[j]=Se1;Q_511[j]=Q511;S_e11[j]=Se11;Q_2[j]=Q2;printf("%7d % % % %\n",Q_2[j],S_e[j],S_e1[j],Q_511[j],S_e11[j]);fprintf(fl,"%7d % % % %\n",Q_2[j],S_e[j],S_e1[j],Q_511[j],S_e11[j]);}j++;fclose(fl);cur();dtmn();sgd();}/**********************sudu,jiasudu,weiyi,quxiantuhanshu*************************/void cur(){/*float w1=2*PI,L1=110,L4=135,L61=490,L3=540,L6=380; */float Q4,Q2,sA,w3,sA1,sA11,Se,Se1,Se11,a3,a4,Q411,Q5,Q51,w4;int gd=DETECT, gmode,i;initgraph(&gd,&gmode,"c:\\turboc2");clrscr();for(Q2=0;Q2<=2*PI;Q2+=1.0*PI/1000){if(Q2>=0&&Q2<PI/2||Q2>PI*1.5&&Q2<=2*PI)Q4=atan((l2+l1*sin(Q2))/(l1*cos(Q2)));else if(Q2==PI/2.0||Q2==1.5*PI)Q4=PI/2;else if(Q2>PI/2&&Q2<PI)Q4=PI-atan((l2+l1*sin(Q2))/(-l1*cos(Q2)));elseQ4=PI-atan((l2+l1*sin(Q2))/(-l1*cos(Q2)));if(Q2!=PI/2&&Q2!=1.5*PI)sA=l1*cos(Q2)/cos(Q4);else if(Q2==PI/2)sA=l1+l2;elsesA=l2-l1;/* sA1=-l1*w1*sin(Q2-Q4); */w3=l1*C*cos(Q2-Q4)/sA;Q411=(C*C*l1*sin(Q4-Q2)-2*w3*sA)/sA;a3=Q411;if(((l7-l4*sin(Q4))/l5)>=0&&((l7-l4*sin(Q4))/l5)<=1)Q5=PI-asin((l7-l4*sin(Q4))/l5);else if(((l7-l4*sin(Q4))/l5)>=-1&&((l7-l4*sin(Q4))/l5)<0)Q5=PI+asin((l7-l4*sin(Q4))/l5);Se=l4*cos(Q4)+l5*cos(Q5);Q51=-w3*l4*cos(Q4)/(l5*cos(Q5));w4=Q51;Se1=-w3*l4*sin(Q4-Q5)/cos(Q5);/*Q511=(Q41*Q41*l4*sin(Q4)+Q51*Q51*l5*sin(Q5)-Q411*Q411*l4*cos(Q4 ))/(l5*cos(Q5));*/Se11=-(a3*l4*sin(Q4-Q5)+w3*w3*l4*cos(Q4-Q5)-w4*w4*l5)/cos(Q5);line(100,200,500,200);setcolor(5);line(492,201,500,200);line(492,199,500,200);line(100,10,100,350);setcolor(5);line(99,18,100,10);line(101,18,100,10);putpixel(100+Q2*180/PI,200-Se/5,1); /*绘制位移曲线*/putpixel(100+Q2*180/PI,200-Se1/100,2); /*绘制速度曲线*/putpixel(100+Q2*180/PI,200-Se11/100,4);} /*绘制加速度曲线*/ setcolor(10);settextjustify(CENTER_TEXT,0);outtextxy(300,300,"RED___JIASUDU");outtextxy(300,330,"GREEN___SUDU");outtextxy(300,360,"BLUE___WEIYI");/* outtextxy(300,50,"SUDU JIASUDU WEIYI GUAN XI QU XIAN TU");*/outtextxy(300,50,"SUDU JIASUDU WEIYI GUAN XI QU XIAN TU");getch();closegraph();}/***************************运动模拟图函数*******************/void dtmn(){int gd=DETECT,gmode,n;initgraph(&gd,&gmode,"c:\\turboc2");cleardevice();do{setbkcolor(0);sgd();}while(!kbhit());getch();}/****************************导轨函数*********************/ void slide(float x0,float y0,float x1,float h){float xr;int i,n;xr=x0+x1;line(x0,y0,xr,y0);n=x1/h;for(i=0;i<=n;i++){moveto(x0+i*h,y0+h);lineto(x0+(i+1)*h,y0);}}/************************摇块函数*************************/ void pist(float x0,float y0,float l,float h,float theta){float x,y;x=x0-cos(theta)*l/2+h/2*sin(theta);y=y0+l/2*sin(theta)+h/2*cos(theta);moveto(x,y);linerel(l*cos(theta),-l*sin(theta)); /***绘制轮廓线******/linerel(-h*sin(theta),-h*cos(theta));linerel(-l*cos(theta),l*sin(theta));lineto(x,y);}/*************************支点函数*********************/void pirot(float x0,float y0,float l){/*float PI=3.1415926;*/float x,y;int i,n;int h=4;setcolor(4);circle(x0,y0,3);setcolor(9);x=x0-l/2;y=y0+sin(PI/3)*l;moveto(x0,y0);lineto(x,y);linerel(18,0);lineto(x0,y0);n=l/4;for(i=0;i<=n;i++){moveto(x+i*h,y+h);lineto(x+(i+1)*h,y);}}/************************连杆,摇块,导轨函数***************/ void sgd(){int i;int x04,y04,x02,y02;int l02a=l1/2;int l04b=l4/2;float xa,ya,xb,yb,xc,yc,l;float lbc=l5/2;float ss,theta;for(i=0;i<64;i++) /*****动态模拟******/;/*坐标计算*/x04=400; x02=400;y04=400; y02=225;xa=x02+l02a*cos(ss);ya=y02+l02a*sin(ss);l=sqrt((xa-x04)*(xa-x04)+(ya-y04)*(ya-y04));xb=x04+(xa-x04)*l04b/l;yb=y04+(ya-y04)*l04b/l;yc=135;xc=xb-sqrt(lbc*lbc-(yb-yc)*(yb-yc));theta=-atan((ya-y04)/(xa-x04));setcolor(4);cleardevice();circle(xb,yb,3);circle(xa,ya,3);circle(xc,yc,3);setcolor(8);line(50,135,500,135);rectangle(xc+7,yc+6,xc-7,yc-6); /*绘制滑块C*/line(x02,y02,xa,ya);line(xc,yc,xb,yb);line(xb,yb,x04,y04);setcolor(7);pirot(x02,y02,16); /*绘制支点X04,X02*/ pirot(x04,y04,16);pist(xa,ya,20,10,theta); /*绘制滑块A*/slide(60,135,100,10);slide(500,135,570,10);setcolor(8);settextstyle(3,0,2);outtextxy(200,30,"DAOGAN YUNDONG MONI");outtextxy(200,440,"PRESS ANY KEY TO RETURN");outtextxy(200,420,"PRESS BREAK TO STOP");delay(2000);}}运行结果:zhuanjiao weiyi sudu jiaojiasudu jiasudu90 -256.000 1125.473 -6.185 0.004270 -256.000 -1125.473 -6.185 0.005曲线图象及导杆图形五、课程设计总结:通过一周的课程设计,我更加了解了机械原理课程设计的各方面内容;进一步掌握了机构分析的基本知识,熟悉了机械设计的一般方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理报告
——牛头刨床机构分析
题目:
图3-12所示为一牛头刨床的机构运动简图。
设已知各构件的尺寸为:L1=125mm,L3=600mm,L4=150mm,原动件1的方位角Θ1=0°~360°和等角速度
w1=1 rad/s。
试用矩阵法求该机构中各从动件的方位角、角速度和角加速度以及E点的位移、速度和加速度的运动图线。
用解析法作牛头刨床的运动分析—Matlab程序
一、题意分析:
如图先建立坐标系,并标出各构建的尺寸为:=125mm, =600mm,=150mm,
原动件1的方位角==-?和等角速度=1 rad/s。
试用矩阵法求该机构中各从动的方位角、角速度、和角加速度以及E点的位移、速度和加速度的运动曲线图。
解:如图所示,先建立一直角坐标系,并标出各矢量及其方位角。
其中共有四个未知量及。
为求解需要建立两个封闭矢量方程,为此需要利用两个封闭图形ABCA及CDEGC,由此可得
?+ = ??????+ ?= ?+
并写成投影方程为
cos=cos
sin=+sin
cos+cos-=0
sin+sin=
由以上各式即可求得、、、四个运动变量,而滑块2的方位角=
然后,分别将上列各式对时间取一次二次导数,并写成矩阵形式,即得一下速度和加速度方程:
=
=
+
二、程序流程图
定义程序变量
↓
列出S3,Theta3,Se的表达式
↓
对S3,Theta3,Se分别求一次、
二次导数
↓
将上面导数写成矩阵形式
↓
将位移、速度、加速度的运动线
分别存放在同一图中
三、源程序:
clear all;clc;
w1=1;l1=0.125;l3=0.6;l6=0.275;l61=0.575;l4=0.15;
for m=1:3601
o1(m)=pi*(m-1)/1800;o31(m)=atan((l6+l1*sin(o1(m)))/(l1*cos(o1(m))));
if o31(m)>=0
o3(m)=o31(m);
else o3(m)=pi+o31(m);
end;
s3(m)=(l1*cos(o1(m)))/cos(o3(m));o4(m)=pi-asin((l61-l3*sin(o3(m)))/l4);
se(m)=l3*cos(o3(m))+l4*cos(o4(m));
if o1(m)==pi/2
o3(m)=pi/2; s3(m)=l1+l6;
end
if o1(m)==3*pi/2
o3(m)=pi/2; s3(m)=l6-l1;
end
A1=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3 (m)),-l4*sin(o4(m)),-1;0,l3*cos(o3(m)),l4*cos(o4(m)),0];
B1=w1*[-l1*sin(o1(m));l1*cos(o1(m));0;0];D1=A1\B1;E1(:,m)=D1;ds(m)=D1(1);w3 (m)=D1(2);w4(m)=D1(3);ve(m)=D1(4);
A2=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3 (m)),-l4*sin(o4(m)),-1;0,l3*cos(o3(m)),l4*cos(o4(m)),0];
B2=-[-w3(m)*sin(o3(m)),(-ds(m)*sin(o3(m))-s3(m)*w3(m)*cos(o3(m))),0,0;w3(m)* cos(o3(m)),(ds(m)*cos(o3(m))-s3(m)*w3(m)*sin(o3(m))),0,0;0,-l3*w3(m)*cos(o3(m )),-l4*w4(m)*cos(o4(m)),0;0,-l3*w3(m)*sin(o3(m)),-l4*w4(m)*sin(o4(m)),0]*[ds(m) ;w3(m);w4(m);ve(m)];
C2=w1*[-l1*w1*cos(o1(m));-l1*w1*sin(o1(m));0;0];B=B2+C2;D2=A2\B;E2(:,m)= D2;dds(m)=D2(1);a3(m)=D2(2);a4(m)=D2(3);ae(m)=D2(4);
end;
o11=o1*180/pi;y=[o3*180/pi;o4*180/pi];w=[w3;w4];a=[a3;a4];figure(1);
plotyy(o11,y,o11, se); axis equal;
title('位置线图');xlabel('\it\theta1');ylabel('\it\theta3,\theta4,Se');
grid on;
figure(2);
h2=plotyy(o11,w,o11,ve);
title('速度线图');
xlabel('\it\theta1');ylabel('\it\omega3,\omega4,Ve');
grid on;
figure(3);
h3=plotyy(o11,a,o11,ae);
title('加速度线图');
xlabel('\it\theta1');ylabel('\it\alpha3,\alpha4,\alphaE');
grid on;
F=[o11;o3./pi*180;o4./pi*180;se;w3;w4;ve;a3;a4;ae]';G=F(1:100:3601,:) 四、程序运行结果:
G =。
