线段中点以及角平分线解题规律总结
八年级数学角平分线的性质知识点总结

角平分线的性质是八年级数学中的重要内容之一,它是指从一个角的顶点出发,将这个角分成两个相等角的线段。
下面是关于角平分线的性质的总结,包括定义、性质和应用:一、定义:角平分线是指从一个角的顶点出发,将这个角分成两个相等角的线段。
角平分线是角的重要构造之一二、性质:1.角平分线将角分成两个相等的角。
即如果一条线段是一个角的平分线,则它将这个角分成两个度数相等的角。
2.角平分线与角的两边相交于一个点。
即角平分线与角的两边交于角的顶点。
3.角平分线与角的两边垂直相交于角平分线的中点。
即角平分线与角的两边垂直相交于角平分线上的一个点,该点同时也是角平分线的中点。
4.角平分线上的点到角的两边的距离相等。
即角平分线上的任意一点到角的两边的距离相等。
5.两条平行线与角的顶点与顶边所在的线段构成的两个相似三角形,它们的角平分线平行。
即如果一条线段是一个角的平分线,另一条与之平行的线段也是这个角的平分线。
三、应用:1.判断角平分线。
当我们需要判断一个线段是否为一个角的平分线时,可以使用角平分线的定义和性质进行判断,即判断这个线段能否将角分成两个相等的角。
2.利用角平分线的性质解决问题。
当我们遇到需要将角分成两个相等的角的问题时,可以使用角平分线的性质进行解决。
例如,在解决相似三角形的问题中,可以利用角平分线的性质进行角的划分。
3.构造角平分线。
当我们需要构造角的平分线时,可以利用直尺和圆规进行构造。
常见的构造方法有尺规作图法和五线谱法等。
四、例题:1.已知角ABC,其中角平分线AD交角的两边于E、F两点,证明:AE=AF。
证明:根据角平分线的性质4,角平分线上的点到角的两边的距离相等,即DE=DF,又因为AD为角ABC的平分线,所以∠DAE=∠DAF。
再根据等腰三角形的性质,得知AE=AF。
2.已知直角三角形ABC中,角A=90°,角B的平分线BD与AC相交于点D,求证:∠ADB=45°。
证明:由直角三角形的性质,角B=90°-角A=90°-90°=0°,即角B为零角。
类比线段中点与角平分线计算中的思想方法

类比线段中点与角平分线计算中的思想方法线段中点和角平分线计算方法虽然在数学中属于不同的概念,但它们的思想方法却有很多相似之处。
线段中点与角平分线都是在几何学中常见的概念,它们分别用来描述线段和角的特定性质和位置关系。
计算线段中点和角平分线的问题,需要运用一定的思维方法和数学原理,通过一系列推导和计算得出最终的结果。
本文将探讨线段中点与角平分线计算中的思想方法,并比较两者之间的异同点,以期能够更好地理解和运用这两种计算方法。
让我们来看看线段中点的计算方法。
线段中点是指一个线段的中间点,即将一个线段等分为两段的点。
在计算线段中点时,我们首先需要找到线段的两个端点坐标,并利用中点的定义来求解中点的坐标。
假设线段的两个端点分别为A(x1, y1)和B(x2, y2),那么线段AB的中点M的坐标可以通过以下公式来计算:M((x1+x2)/2,(y1+y2)/2)这是线段中点计算的基本思路和方法,通过利用坐标平面上点的中点定义,我们可以很容易地求出线段AB的中点坐标。
这种方法主要依托于几何学中的基本概念和坐标运算,是一种简单而直接的计算思想方法。
接下来,让我们来看看角平分线的计算方法。
角平分线是指将一个角等分为两个相等的角的直线,通常是通过角的顶点进行的平分。
在计算角平分线时,我们需要运用角的性质和角平分线的定义来进行推导和计算。
对于一个角AOC,我们要找出它的平分线BD,那么可以通过如下步骤和计算方法来求解:1. 我们需要找出角AOC的顶点O和两个边OA、OC的坐标。
2. 然后,利用角的平分线定义和角的性质,我们可以得出平分线BD和角AOC之间的关系。
3. 通过一系列的推导和计算,我们可以求出平分线BD的具体坐标和方程。
通过上述方法,我们就可以计算出角AOC的平分线BD的位置和性质。
虽然与线段中点计算有所不同,但角平分线的计算方法同样也是基于几何学的基本原理和角度运算的思想方法。
线段中点和角平分线的计算方法也有它们各自的特点和应用范围。
角平分线四大模型总结+习题+解析(最全版)
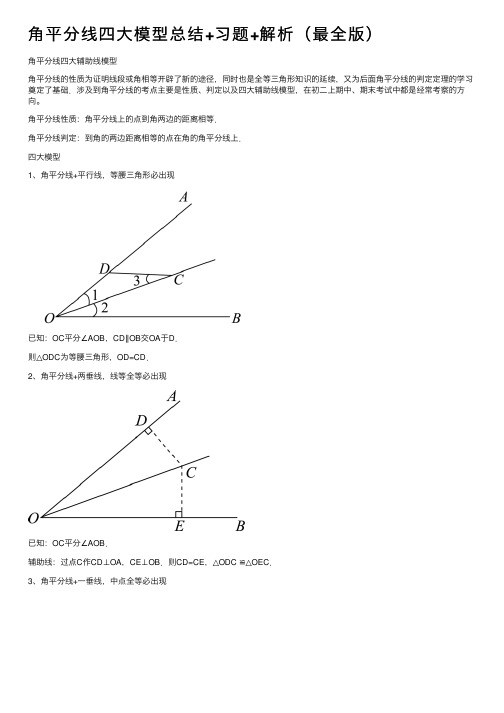
⾓平分线四⼤模型总结+习题+解析(最全版)⾓平分线四⼤辅助线模型⾓平分线的性质为证明线段或⾓相等开辟了新的途径,同时也是全等三⾓形知识的延续,⼜为后⾯⾓平分线的判定定理的学习奠定了基础.涉及到⾓平分线的考点主要是性质、判定以及四⼤辅助线模型,在初⼆上期中、期末考试中都是经常考察的⽅向。
⾓平分线性质:⾓平分线上的点到⾓两边的距离相等.⾓平分线判定:到⾓的两边距离相等的点在⾓的⾓平分线上.四⼤模型1、⾓平分线+平⾏线,等腰三⾓形必出现已知:OC平分∠AOB,CD∥OB交OA于D.则△ODC为等腰三⾓形,OD=CD.2、⾓平分线+两垂线,线等全等必出现已知:OC平分∠AOB.辅助线:过点C作CD⊥OA,CE⊥OB.则CD=CE,△ODC ≌△OEC.3、⾓平分线+⼀垂线,中点全等必出现已知:OC平分∠AOB,DC垂直OC于点C.辅助线:延长DC交OB于点E.则C是DE的中点,△ODC ≌△OEC.4、⾓平分线+截长补短线,对称全等必出现已知:OC平分∠AOB,截取OE=OD,连接CD、CE.则△ODC和△OCE关于OC对称,即△ODC ≌△OEC.【核⼼考点⼀】⾓平分线的性质与判定1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:163.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB ,另⼀把直尺压住射线OA 并且与第⼀把直尺交于点P ,⼩明说:“射线OP 就是BOA ∠的⾓平分线.”他这样做的依据是( )A .⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B .⾓平分线上的点到这个⾓两边的距离相等C .三⾓形三条⾓平分线的交点到三条边的距离相等D .以上均不正确6.(2019秋?梁平区期末)如图,若BD AE ⊥于B ,DC AF ⊥于C ,且DB DC =,40BAC ∠=?,130ADG ∠=?,则DGF ∠=.7.(2018春?开江县期末)如图,在Rt ABC ?中,90C ∠=?,以顶点A 为圆⼼,适当长为半径画弧,分别交AB 、AC 于点M 、N ,再分别以点M 、N 为圆⼼,⼤于12MN 的长为半径画弧,两弧交于点P ,射线AP 交边BC 于点D .下列说法错误的是( ) A .CAD BAD ∠=∠B .若2CD =,则点D 到AB 的距离为2C .若30B ∠=?,则CDA CAB ∠=∠D .2ABD ACD S S ??=8.(2014秋?西城区校级期中)如图,点E 是AOB ∠的平分线上⼀点,EC OA ⊥,ED OB ⊥,垂⾜分别是C ,D .下列结论中正确的有( )(1)ED EC =;(2)OD OC =;(3)ECD EDC ∠=∠;(4)EO 平分DEC ∠;(5)OE CD ⊥;(6)直线OE 是线段CD 的垂直平分线.A .3个B .4个C .5个D .6个9.(2019春?杜尔伯特县期末)如图:在ABC ?中,90C ∠=?,AD 是BAC ∠的平分线,DE AB ⊥于E ,F 在AC 上,BD DF =,证明:(1)CF EB =.(2)2AB AF EB =+.10.(2019秋?垦利区期中)如图,ABC⊥⊥且平分BC,DE AB中,AD平分BAC∠,DG BC于E,DF AC⊥于F.(1)判断BE与CF的数量关系,并说明理由;(2)如果8AB=,6AC=,求AE、BE的长.11.(2017秋?遂宁期末)某地区要在区域S内(即COD∠内部)建⼀个超市M,如图所⽰,按照要求,超市M到两个新建的居民⼩区A,B的距离相等,到两条公路OC,OD的距离也相等.这个超市应该建在何处?(要求:尺规作图,不写作法,保留作图痕迹)【核⼼考点⼆】⾓平分线+⾓两边垂线12.(2019秋?肥城市期末)如图,//AB CD ,BP 和CP 分别平分ABC ∠和DCB ∠,AD 过点P ,且与AB 垂直,垂⾜为A ,交CD 于D ,若8AD =,则点P 到BC 的距离是.13.(2015?湖州)如图,已知在ABC ?中,CD 是AB 边上的⾼线,BE 平分ABC ∠,交CD 于点E ,5BC =,2DE =,则BCE ?的⾯积等于( )A .10B .7C .5D .414.(2010秋?涵江区期末)如图所⽰,在Rt ABC ?中,90C ∠=?,BC AC =,AD 平分BAC ∠交BC 于D ,求证:AB AC CD =+.15.(2012秋?蓬江区校级期末)如图,已知90∠=∠=?,M是BC的中点,DM平分B C∠.求证:ADC(1)AM平分DAB∠;(2)DM AM⊥.16.(2016秋?西城区校级期中)已知:如图,12∠=∠,P为BN上的⼀点,PF BC⊥于F,=,PA PC(1)求证:180∠+∠=?;PCB BAP(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.【核⼼考点三】⾓平分线+垂线17.(2017秋?和平区校级⽉考)如图.在ABC ?中,BE 是⾓平分线,AD BE ⊥,垂⾜为D ,求证:21C ∠=∠+∠.18.(2013秋?昌平区期末)已知:如图,在ABC ?中,AD 平分BAC ∠,CD AD ⊥于点D ,DCB B ∠=∠,若10AC =,6AD=,求AB 的长.19.如图所⽰,ABC ?中,ACB ABC ∠>∠,AE 平分BAC ∠,CD AE ⊥于D ,求证:ACD B ∠>∠.20.已知:如图,在ABC ?中,3ABC C ∠=∠,12∠=∠,BE AE ⊥.求证:2AC AB BE -=.21.(2019秋?下陆区期中)如图,BD 是ABC ∠的⾓平分线,AD BD ⊥,垂⾜为D ,20DAC ∠=?,38C ∠=?,则BAD ∠=.22.(2019秋?曲⾩市校级⽉考)如图,在ABC ?中,AB AC =,90BAC ∠=?,BD 平分ABC ∠交AC 于D ,过C 作CE BD ⊥交BD 延长线于E .求证:12CE BD =.23.(2019?沂源县⼀模)(1)如图(a)所⽰,BD、CE分别是ABC的外⾓平分线,过点A作AD BD⊥,AE CE⊥,垂⾜分别为D、E,连接DE,求证:1() 2DE AB BC AC=++;(2)如图(b)所⽰,BD、CE分别是ABC的内⾓平分线,其他条件不变,DE与ABC三边有怎样的数量关系?并证明这个数量关系;(3)如图(c)所⽰,BD为ABC的内⾓平分线,CE为ABC的外⾓平分线,其他条件不变,DE与ABC三边⼜有怎样的数量关系?并证明这个数量关系.24.(2017秋?夏⾢县期中)如图,在ABC ?中,ABC ∠、ACB ∠的平分线相交于F ,过F 作//DE BC ,交AB 于D ,交AC 于E ,那么下列结论:①BDF ?、CEF ?都是等腰三⾓形;②DE DB CE =+;③AD DE AE AB AC ++=+;④BF CF =.正确的有.25.(2019秋?垦利区期末)如图,平⾏四边形ABCD 中,3AB cm =,5BC cm =;,BE 平分ABC ∠,交AD 于点E ,交CD 延长线于点F ,则DE DF +的长度为.26.(2010秋?海淀区期末)如图,BD 是ABC ?的⾓平分线,//DE BC ,DE 交AB 于E ,若AB BC =,则下列结论中错误的是( )A .BD AC ⊥B .A EDA ∠=∠C .2AD BC =D .BE ED =27.如图,若BD 、CD 分别平分ABC ∠和ACB ∠,过D 作//DE AB 交BC 于E ,作//DF AC 交BC 于F ,求证:BC 的长等于DEF ?的周长.28.(2018秋?邳州市期中)如图,在四边形ABCD中,对⾓线AC平分BAD >,∠,AB AD 下列结论正确的是()A.AB AD CB CD->-B.AB AD CB CD-=-C.AB AD CB CD-<-D.AB AD-与CB CD-的⼤⼩关系不确定29.(2012?⿇城市校级模拟)在ABC∠的外⾓平分线,P是AD上的任意中,AD是BAC⼀点,试⽐较PB PC+与AB AC+的⼤⼩,并说明理由.30.(2018秋?万州区期中)已知:如图,在四边形ABCD中,AC平分BAD ∠,CE AB⊥于=+.E,且180B D∠+∠=?,求证:AE AD BE31.(2017秋?海淀区期中)如图,已知AD是BAC∠=?,C=+,31的⾓平分线,AC AB BD 求B∠的度数.32.(2019秋?平⼭县期中)如图,90∠=?,OM平分AOB∠,将直⾓三⾓板的顶点PAOB在射线OM上移动,两直⾓边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.33.(2016秋?丰宁县期中)如图,在ABC ?中,100A ∠=?,40ABC ∠=?,BD 是ABC ∠的平分线,延长BD ⾄E ,使DE AD =.求证:BC AB CE =+.34.(2018秋?丰城市期中)在ABC ?中,2ACB B ∠=∠,(1)如图1,当90C ∠=?,AD 为BAC ∠的⾓平分线时,在AB 上截取AE AC =,连接DE ,求证:AB AC CD =+;(2)如图2,当90C ∠≠?,AD 为BAC ∠的⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请直接写出你的结论,不需要证明;(3)如图3,当AD 为ABC ?的外⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请写出你的猜想,并说明理由.35.(2019春?利津县期末)如图,在ABC∠平分线,AD的垂直平分线分中,AD是BAC别交AB、BC延长线于F、E.求证:(1)EAD EDA∠=∠;(2)//DF AC;(3)EAC B∠=∠.36.(2014?西城区⼆模)在ABC>,AD平分BAC∠交BC于点∠为锐⾓,AB AC,BACD.(1)如图1,若ABC是等腰直⾓三⾓形,直接写出线段AC,CD,AB之间的数量关系;(2)BC的垂直平分线交AD延长线于点E,交BC于点F.①如图2,若60∠=?,判断AC,CE,AB之间有怎样的数量关系并加以证明;ABE②如图3,若AC AB+,求BAC∠的度数.⾓平分线四⼤辅助线模型--解析⼀.⾓平分线的性质与判定(共11⼩题)1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .【分析】⾸先过点P 作PB OM ⊥于B ,由OP 平分MON ∠,PA ON ⊥,3PA =,根据⾓平分线的性质,即可求得PB 的值,⼜由垂线段最短,可求得PQ 的最⼩值.【解答】解:过点P 作PB OM ⊥于B , OP 平分MON ∠,PA ON ⊥,3PA =,3PB PA ∴==,PQ ∴的最⼩值为3.故选:C .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:16【分析】利⽤⾓平分线的性质,可得出ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼相等,估计三⾓形的⾯积公式,即可得出ABD ?与ACD ?的⾯积之⽐等于对应边之⽐.【解答】解:AD 是ABC ?的⾓平分线,∴设ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼分别为1h ,2h ,12h h ∴=,ABD ∴?与ACD ?的⾯积之⽐:8:64:3AB AC ===,故选:B .3.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm【分析】根据⾓平分线的性质得到ED EC =,计算即可.【解答】解:BE 平分ABC ∠,DE AB ⊥,90ACB ∠=?, ED EC ∴=,3AE DE AE EC AC cm ∴+=+==,故选:B .4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn【分析】过点D 作DE AB ⊥于E ,根据⾓平分线上的点到⾓的两边距离相等可得DE CD =,然后根据三⾓形的⾯积公式即可得到结论.【解答】解:如图,过点D 作DE AB ⊥于E ,BD 是ABC ∠的平分线,90C ∠=?,DE CD m ∴==,ABD ∴?的⾯积122n m mn =??=,故选:A.5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB,另⼀把直尺压住射线OA并且与第⼀把直尺交于点P,⼩明说:“射线OP就是BOA∠的⾓平分线.”他这样做的依据是()A.⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B.⾓平分线上的点到这个⾓两边的距离相等C.三⾓形三条⾓平分线的交点到三条边的距离相等D.以上均不正确【分析】过两把直尺的交点C作CE AO=,再根据⾓⊥,CF BO⊥,根据题意可得CE CF的内部到⾓的两边的距离相等的点在这个⾓的平分线上可得OP平分AOB∠;【解答】解:(1)如图所⽰:过两把直尺的交点P作PE AO⊥,⊥,PF BO两把完全相同的长⽅形直尺,PE PF∴=,∠(⾓的内部到⾓的两边的距离相等的点在这个⾓的平分线上),OP∴平分AOB故选:A.。
初中数学知识归纳三角形的中线角平分线高线

初中数学知识归纳三角形的中线角平分线高线初中数学知识归纳:三角形的中线、角平分线、高线三角形是初中数学学习中最基础的几何图形之一,它具有丰富的性质和特点。
本文将归纳总结三角形的中线、角平分线和高线的相关性质,帮助读者更好地理解和掌握这些概念。
一、三角形的中线中线是连接三角形的两个顶点和中点的线段。
三角形的中线有以下特点:1. 任意三角形的三条中线交于一点,这一点称为三角形的重心。
重心所在的位置离三角形的三个顶点距离相等,且重心将中线分成2:1的比例。
2. 三角形的重心到顶点的距离是中线对应中点到顶点距离的2倍,也就是说,如果连接重心和顶点,那么重心到顶点的距离是连接中点和顶点的线段的2倍。
3. 在等边三角形中,三条中线重合,即三条中线交于一点,同时这个点也是三角形的重心。
二、三角形的角平分线角平分线是指从一个角的顶点出发,将该角分成两个相等的角的线段。
三角形的角平分线有以下特点:1. 三角形的三条角平分线交于一点,称为三角形的内心。
内心所在的位置距离三角形的三条边的距离相等,且内心到三边的距离之和等于三角形的周长。
2. 在等腰三角形中,三条角平分线重合,即三条角平分线交于一点,同时这个点也是三角形的内心。
3. 角平分线和对边、邻边有如下关系:角平分线等分对边和邻边上的对应角;对边和邻边上的线段与角平分线比例相等。
三、三角形的高线高线是从一个顶点出发,与对边垂直相交的线段。
三角形的高线有以下特点:1. 任意三角形都有三条高线,它们分别从三个顶点出发,并与对边垂直相交。
2. 等腰三角形的高线同时也是角平分线和中线。
3. 在直角三角形中,高线就是斜边上的中线。
总结:三角形的中线、角平分线和高线都有各自的特点和性质。
通过了解和掌握这些性质,我们可以更好地理解和解决与三角形相关的问题。
在实际应用中,这些概念和性质也有着广泛的应用,例如在建筑、制图、几何证明等方面都可以看到它们的身影。
通过本文的归纳和总结,我们希望读者能够对三角形的中线、角平分线和高线有更全面的了解,并在实际问题中能够运用到这些知识,提高数学解题的能力。
例谈含有中点和角平分线条件问题的解题思路

图 1 1
如 图 6 P平 分 AO ,O B,c ∥o P A,
则 1= / _2= 3 .所 以 O : C , 即 C P
解法 5 :如图 9 ,过点 c C #A 作 G D
交 B 的 延 长 线 于 点 G,延 长 MF交 A A G 于点 日.由模 型 ,得 A G=A C,A = H AF
所 以
G= AG
中国 数学教育 [ 1年第4 2 20 0 期] 7
又 因 为 删 G=
所 以 F AC= G
G,
即 +1 :
0 c
一1 . 一2 .
解法 7 :如 图 1,过 点 肘 作 G 1 H∥
AB,交 AC 于 点 ,交 A 的延 长 线 于 D 点 G .
解法 1 :过 点 D 分 别 作 D B、 H LA
D AC GJ ,点 H、G为 垂 足 , -
所 以 G 是 AB C的 中位线. M H
所 以 G = 删 =2 M/A . ,C / H
二
一= BD= 眦 。 手 H
B C的 中点这 一 条 件 , 即这 三 条 路 行 不 通 ,
图 3
B D M C
中点.
而 M 是 B 的 中点 , C
图2
分析 :我 们要 作 AD的垂 线 ,可以有
五 条 途 径 , 即分 别过 、D、 、 C 、,五
点 作 AD 的 垂 线 , 经 尝 试 过 D、M、 F三 点 作 AD 的 垂 线 ,不 能 合 理 地 利 用 是
解 法 2:如图 4 ,过点 曰作 A D的垂 线B H,点 G为垂足 ,交 AC于点 麒
A
的平 分 线 ,且 M fA ,则 F 的长 为 F D C
中考必会几何模型:线段(双中点)、角(双角平分线)模型

线段(双中点)、角(双角平分线)模型线段(双中点)模型讲解【口诀】字母去重,线段留半 【结论1】已知点B 在线段AC 上,AB=8cm ,AC=18cm.(1)P 、Q 分别是AB 、BC 的中点,则PQ 为_________cm. (2) P 、Q 分别是AC 、BC 的中点,则PQ 为_________cm. (3) P 、Q 分别是AB 、AC 的中点,则PQ 为_________cm. 已知点B 在直线AC 上,AB=8cm ,AC=18cm.(1)P 、Q 分别是AB 、BC 的中点,则PQ 为_________cm. (2) P 、Q 分别是AC 、BC 的中点,则PQ 为_________cm. (3) P 、Q 分别是AB 、AC 的中点,则PQ 为_________cm. 【答案】9;4;5;9;4;5或13【结论2】已知点C 在线段AB 上,点M ,N 分别是AC ,BC 的中点,则MN= 12AB.【证明】∵M ,N 分别是AC ,BC 的中点, ∴CM= 12AC ,CN= 12BC,∴MN=CM+CN= 12AC+ 12BC= 12(AC+BC)= 12AB.【结论3】已知点C 是线段AB 延长线上一点,点M ,N 分别是AC ,BC 的中点,则MN= 12AB.【证明】∵M.N 分别是AC ,BC 的中点, ∴MC= 12AC ,NC= 12BC ,∴MN=MC-NC= 12AC- 12BC= 12(AC-BC)= 12AB.拓展已知点C 是线段BA 延长线上一点,点M ,N 分别是AC.BC 的中点,则MN= 12AB.无论线段之间的和差关系怎样变,MN 的长度只与AB 有美,即MN= 12AB.典型例题典例1如图,点C 是线段AB 上一点,AC <CB ,M ,N 分别是AB 和CB 的中点,AC=8,NB=5,则线段MN=___________.典例2如图,已知点A ,B ,C 在同一直线上,M ,N 分别是AC ,BC 的中点.(1)若AB=20,BC=8.求MN的长;(2)若AB= a,BC=8.求MN的长;(3)若AB= a,BC= b.求MN的长;(4)从(1) (2) (3)的结果中能得到什么结论?典例3如图,线段AB=10cm,BC=3cm,点D,E分别为AC和AB的中点,则DE的长是_________.初露锋芒1.已知线段AB=10cm,点C是直线AB上一点,BC=4 cm,若M是AC 的中点,N是BC的中点,则线段MN的长度是( ).A.7 cmB.3 cmC.5 cmD.7 cm或3 cm2.如图,已知A,B.C三点在同一直线上,AB=24.BC= 3AB,E是AC8的中点,D是AB的中点,则DE的长度是___________.3. 如果A、B、C三点在同一直线上,且线段AB=6cm,BC=4cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( ).A.5cmB.1cmC.5或1cmD.无法确定4. 已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC 的中点,N是BC的中点,则线段MN的长度是( )A.7cmB.3cmC.7cm或3cmD.5cm感受中考1.(2018贵州铜仁中考模拟)C为线段AB上任意一点,D、E分别是AC,CB的中点,若AB=10cm.则DE的长是( ).A.2 cmB.3 cmC.4 cmD.5 cm2.(2018湖南邵阳中考模拟)已知点C为线段AB上任一点,AC=8 cm,CB=6cm,M,N分别是AC,BC的中点.(1)求线段MN的长;(2)点C为线段AB上任一点,满足AC+CB= a cm,点M,N分别是AC,BC的中点,你能猜想MN的长度吗?并说明理由.(3)点C在线段AB的延长线上,满足AC-BC=b cm,M,N分别是AC,BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.(4)你能用一句简洁的话,描述你发现的结论吗?3.如图,已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为-5,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)BP=________,点P表示的数________ (分别用含t的代数式表示);(2)点P运动多少秒时,PB=2PA.(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.参考答案典例1 【答案】4【解析】∵M ,N 分别是AB 和CB 的中点, ∴根据线段(双中点)的结论,有MN= 12AC.则MN=4. 典例2【答案】从(1)(2)(3)的结果中能得到:线段MN 始终等于线段AB 的一半,与C 点的位置无关. 【解析】(1)∵AB=20,BC=8. ∴AC=AB+BC=28.∵点A ,B ,C 在同一直线上,M ,N 分别是AC ,BC 的中点. ∴MC= 12AC.NC= 12BC.∴MN=MC-NC= 12(AC-BC)= 12AB=10.(2)根据(1)得MN= 12 (AC-BC)= 12AB= 12a .(3)根据(1)得MN= 12(AC-BC)= 12AB= 12a .(4)从(1)(2)(3)的结果中能得到:线段MN 始终等于线段 AB 的一半,与C 点的位置无关.典例3 【答案】1.5【解析】∵AB=10cm ,BC=3cm ,(已知) ∴AC=AB-BC=7cm.∵点D 为AC 中点,点E 为AB 的中点,(已知) ∴AD= 12AC,AE= 12AB.(线段中点定义)∴AD=3.5cm,AE=5cm. ∴DE=AE-AD=1.5cm. 故答案为:1.5.初露锋芒1.【答案】C.【解析】当点C 在线段AB 上时,如图.∵M ,N 分别是AC ,BC 的中点,∴根据线段(双中点)的结论,可知MN= 12AB=5 cm.当点C 在线段AB 的延长线上时,如图.∵M ,N 分别是AC ,BC 的中点,∴根据线段(双中点)的结论,可知MN= 12AB=5 cm.综上所述,MN 的长为5cm. 故选C.2. 【答案】92.【解析】∵AB=24,BC= 38AB ,∴BC=9.∵E 是AC 的中点,D 是AB 的中点,∴根据线段(双中点)的结论,可知DE= 12BC= 92.3. 【答案】C【解析】如图1,当点B 在线段AC 上时,∵AB=6cm ,BC=4cm ,M ,N 分别为AB ,BC 的中点, ∴MB= 12AB = 3cm,BN = 12BC = 2cm,∴MN=MB+NB=5cm,如图2,当点C 在线段AB 上时,∵AB=6cm ,BC=4cm ,M ,N 分别为AB ,BC 的中点, ∴MB= 12AB = 3cm ,BN= 12BC=2cm,∴MN=MB-NB=1cm 。
数学初中中点总结

数学初中中点总结一、中点的定义和性质在数学中,中点是指一条线段的中间点,即将一条线段平均划分为两个相等的部分。
以下是关于中点的定义和性质的总结:1.定义:若线段AB的中点为M,则AM = MB。
2.定理1:如果一个线段的两个端点对换,则线段的中点也对换。
3.定理2:两个线段的中点连线平行于这两个线段。
4.定理3:一个线段的中点将线段平分为两个相等部分。
5.定理4:如果三个点A、B、C在同一条线段上,且B是AC的中点,则AB = BC。
二、中点的求解方法在求解一个线段的中点时,我们可以使用以下方法:1. 使用坐标求解假设线段的两个端点分别是A(x₁, y₁)和B(x₂, y₂),则线段AB的中点M的坐标可以通过以下公式求解:M = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)我们可以将上述公式应用于平面直角坐标系、极坐标系和三维空间中的线段。
2. 使用向量求解我们可以使用向量的加法运算来确定线段的中点。
假设线段的两个端点分别是A和B,则线段AB的中点M可以通过以下公式求解:M = (A + B) / 2其中,A和B是线段的位置向量。
3. 使用尺规作图法求解尺规作图是一种用尺子和圆规来进行几何作图的方法。
我们可以使用尺规作图来求解线段的中点。
方法如下:•步骤1:画出线段AB;•步骤2:以点A为圆心,以线段AB的长度为半径画一个圆;•步骤3:以点B为圆心,以线段BA的长度为半径画一个圆;•步骤4:两个圆的交点即为线段AB的中点M。
三、数学应用中点的概念在数学中有广泛的应用,以下是一些常见的应用场景:1. 几何图形的性质证明在几何证明中,我们常常需要证明线段的性质。
通过使用中点的性质和定理,我们可以更方便地证明某些几何图形的性质。
例如,在证明平行四边形的性质时,我们可以使用中点将对角线平分的性质来简化证明过程。
2. 向量运算在向量运算中,我们经常需要计算两个向量的中点。
通过求解两个向量的位置向量的中点,我们可以方便地计算向量的和、平均值等。
初中数学线段题型总结归纳

初中数学线段题型总结归纳线段是初中数学教学中的一个重要知识点,也是解决几何问题和实际进一步计算的基础。
本文旨在总结和归纳初中数学中涉及线段的常见题型,帮助学生更好地理解和应用相关知识。
一、线段的基本概念线段是由两个不同点A和B确定的,用记号AB表示。
其中,点A称为线段的起点,点B称为线段的终点。
线段的长度可以用起点和终点表示为|AB|,也可以用坐标表示为AB。
二、线段的比较1. 线段的比较大小常见于求线段长度的比较问题。
当两个线段的长度不等时,可以直接通过比较线段的长度得出结果;当两个线段的长度相等时,需要通过其他方式进行判断(如利用直角三角形的性质)。
2. 在比较线段大小时,可以利用线段的长度、坐标等信息进行比较,也可以通过等式、不等式等表示进行推导。
三、线段的运算1. 线段的加法与减法:线段的加法是指将两条线段首尾相接,组成一条新的线段。
线段的减法是指从一条线段中截取另一条线段,得到剩余部分。
2. 线段的加法减法可通过线段的长度进行求解,也可以通过坐标运算进行推导。
3. 线段的乘法与除法:乘法运算通常涉及到线段的比例关系,用来解决直角三角形的题型;除法运算则是对线段进行分割,求出给定比例的分割点坐标。
四、线段的平分点线段的平分点是指将一条线段分为两等分的点,可以通过计算线段的中点坐标来求解。
利用线段的平分点,可以进一步进行垂直平分线、角平分线等问题的解析。
五、线段的延长线与中点连线线段的延长线是指将线段向两侧延长形成直线的情况,中点连线是指连接线段的中点与其他点生成新的线段。
利用线段的延长线和中点连线,可以解决等分线段、共线点等题目。
六、线段的角关系1. 垂直线段:当两条线段的交角为直角时,称其为垂直线段。
直角线段的特点是相互垂直,即两条直角线段的斜率的乘积为-1。
2. 平行线段:当两条线段的交角为零度时,称其为平行线段。
平行线段的特点是两条线段的斜率相等。
3. 倾斜线段:当两条线段既不是垂直线段,也不是平行线段时,称其为倾斜线段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 角平分线的判定
∵∠1=∠2(或∠1= 1 ∠AOB或∠AOB= 2∠1)
2
∴射线OC平分∠AOB A
9
例2、如图,∠AOB=80°,OM是 ∠AOB内任意一条射线,若OC平分 ∠AOM,OD平分∠BOM,求∠COD 的度数.
A
10
如图,∠AOB=80°,OM是∠AOB外任 意一条射线,若OC平分∠AOM,OD平 分∠BOM,求∠COD的度数.
A
14
已知:如图1,点A、O、B依次在直线MN 上,现将射线OA绕点O沿顺时针方向以每秒2°的速度 旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速 度旋转,如图2,设旋转时间为t(0秒≤t≤90秒). (1)用含t的代数式表示∠MOA的度数. (2)在运动过程中,当∠AOB第二次达到60°时,求t 的值. (3)在旋转过程中是否存在这样的t,使得射线OB是 由射线OM、射线OA、射线ON中的其中两条组成的角 (指大于0°而不超过180°的角)的平分线?如果存在, 请直接写出t的值;如果不存在,请说明理由.
线段中点以及角平分线解题规律总结
A
1
线段中点的意义
∵P是线段AB的中点
∴AP=BP,
A
P
B
1 AP=
AB,BP= 1 AB
线段中点的性质
2
2
反之, 若P在线段AB上,且
1
BAAPP==BAPB
,
2
则P是AB中点
线段中点的判定
A
2
例1、如图,点C为线段AB上一点,AC=8cm, CB=6cm,点M、N分别是AC、BC的 中点. (1)求线段MN的长; (2)若AC+BC=acm,其他条件不变, 求线段MN的长.
A
M
C
N
B
A
3
1、如图,点C为线段AB延长线上一点, AC=8cm,CB=6cm,点M、N分别是AC、 BC的中点. (1)求线段MN的长; (2)若AC-BC=acm,其他条件不变, 求线段MN的长.
A MB
N
C
A
4
2、已知线段AC=8cm,直线AB上有一点 C,且BC=6cm,点M、N分别是AC、BC 的中点.求MN的长
A
15
通过线段中点和角平分线 的类比学习,我们发现知识之 间是相通的,只有会思考的人 才可以得到更多!
A
16
A
12
当两个角的顶点及边重合时,
两个角的平分线所组成的角,就
应该等于不重合的两边所构成角
的一半.紧扣题目中提供的角平
分线条件,从公共边出发,根据
角平分线的性质有条理的写出过
程.
A
13
2、已知:如图,ON平分∠AOC,OM平分∠BOC, ∠AOB=90° (1)若∠AOC=40°,求∠AOM和∠MON的大小; (2)当锐角∠AOC的度数发生改变时,∠MON的大小 是否发生改变?如不会改变,请写出∠MON的大小,并 写出推理过程;如会改变,也请说明理由
A
B
D
C
E
A
7
2、在一直线上有A、B、C三个点,M为 AB的中点,N为BC的中点,若AB=a, BC=b(a≠b).试用a、b的代数式表示 MN的长度
A
8
一条射线把一个角分成两个相等的角,则
这条射线叫这个角的角平分线.
符号语言
B
C
பைடு நூலகம்角平分线的性质
2
∵射线OC平分∠AOB
O1
A
∴∠1=∠2(或∠1= 1 ∠AOB或∠AOB= 2∠1)
没有图的要画图
通过以上问题的解决你有什么发现
A
5
在同一条直线上,有公共端
点两条线段中点之间的距离就
等于,不重合的那两端点距离
的一半.紧扣题目中提供的中点
条件,从公共端点出发,根据
线段中点的性质有条理的写出
过程.
A
6
1、已知:线段AB=20cm,C是线直段线AB上 一点,E是BC的中点,D是AC的中点, 求线段DE的长.
A
O
C
B MD
通过以上问题的解 决你有什么发现
A
11
1、如图,OC是∠AOB内的一条射线,OD、 OE分别平分∠AOC和∠BOC. (1)若∠AOC=40°,∠BOC=80°,求 ∠DOE的度数; (2)若∠AOB=150°,求∠DOE的度数; (3)若∠AOB=α(0≤α≤180°),请直接写 出∠DOE的度数.
