分层法和反弯点法例题
《分层法》例题详解
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的线刚度值(EIil)。
图1解:1、图1所示的二层框架,可简化为两个如图2、图3所示的,只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时,假定上、下柱的远端为固定,则与实际情况有出入。
因此,除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12,其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数,均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时,梁、柱的线刚度值均采用修正后的结果进行计算,如:G节点处:7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处:7.630.3537.63 3.7910.21HG HGHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理,可计算其余各节点的力矩分配系数,计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层:①计算各梁杆端弯矩。
先在G、H、I节点上加上约束,详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方,见图9:213.13kN m 12F GHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HI ql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处,各梁杆端弯矩总与为:13.13kN m FG GH M M ==-⋅在节点H 处,各梁杆端弯矩总与为:13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处,各梁杆端弯矩总与为:7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配,各两次,详见图9 第一次弯矩分配过程:放松节点G,即节点G 处施加力矩13.13kN m ⋅,乘以相应分配系数0、668与0、332,得到梁端+8.76kN m ⋅与柱端+4.37kN m ⋅,+8.76kN m ⋅按12传到GH 梁H 端;放松节点I,即在节点I 处施加力矩7.32kN m -⋅,乘以相应分配系数0、935与0、065,得到梁端 6.32kN m -⋅与柱端+1.00kN m ⋅, 6.32kN m -⋅按12传到IH 梁H 端;放松节点H,相应的在节点H 处新加一个外力偶矩,其中包括GH 梁右端弯矩、IH 梁左端弯矩、GH 梁与IH 梁传来的弯矩。
多层框架结构习题
多层框架结构习题一、填空题1、框架结构是由和连接而成的结构。
2、框架结构伸缩缝与沉缝的宽度一般不小于。
3、框架结构在计算纵向框架和横向框架的内力时，分别按进行计算。
4、框架结构在计算梁的惯性矩时，通常假定截面惯性矩I 沿轴线不变，对装配式楼盖，取I = I 0 ，I 0 为矩形截面梁的截面惯性矩；对现浇楼盖，中框架I = ，边框架I= 。
5、框架柱的反弯点位置取决于该柱上下端的比值。
6、框架柱的反弯点高度一般与、、、等因素有关。
7、框架梁端负弯矩的调幅系数，对于现浇框架可取。
8、用分层法计算框架结构在竖向荷载下的内力时，除底层柱外，其余层柱线刚度乘以，相应传递系数为。
9、框架柱的抗侧移刚度与、、等因素有关。
10、框架在水平荷载下内力的近似计算方法—反弯点法，在确定柱的抗侧移刚度时，假定柱的上下端转角。
11、框架结构在水平荷载下的侧移变形是由和两部分组成的。
12、框架结构在水平荷载下柱子的抗侧移刚度D= ，在一般情况下它比用反弯点法求得的柱抗侧移刚度。
13、多层框架结构总高度受限制的主要原因是。
14、框架结构中框架柱的主要内力为；框架梁的主要内力为。
15、框架结构中“柱抗侧移刚度”定义为。
16、框架结构按施工方法的不同可分为、和。
17、框架结构承重框架的布置方案有、和等三种。
18、框架结构的变形缝有、和三种。
19、伸缩缝的设置，主要与有关。
20、沉降缝的设置，主要与有关。
21、防震缝的设置，注要与有关。
22、框架结构设置伸缩缝的作用是。
23、框架结构设置沉降缝的作用是。
24、框架结构设置防震缝的作用是。
25、在水平荷载的作用下，框架柱的反弯点位置取决于。
26、作用于框架结构上的荷载，可分为和两类。
27、框架结构在竖向荷载作用下的内力常用近似计算方、和等。
28、框架结构在水平荷载作用下的内力与侧移常用近似计算方法有、、等。
29、框架结构D值法中柱的侧移刚度D= ，是考虑对柱侧移刚度的修正系数。
30、框架结构D值法中柱的标准反弯点高度与、、、有关。
第四章 框架结构内力计算
4、计算和确定梁、柱弯矩分配系数。 按修正后的刚度计算各结点周围杆件的杆 端分配系数。 5、按力矩分配法计算单层梁、柱弯矩。 6、将每个单层框架的计算结果按相应部分迭 加起来便得到原框架的计算结果，即柱的弯矩 取相邻两个单元中同一柱对应弯矩之和，而梁 的弯矩直接采用。
四、计算例题
作业2
3.2 水平荷载下内力的近似计算—反弯点法
d
i 1
m
V pj
ij
4、柱端弯矩的确定 M j V jY j 柱下端弯矩 柱上端弯矩 M j V j (h j Yj )
5、梁端弯矩的确定 M ml (M mt M m1b ) 对于边柱 ibl 对于中柱
M ml ( M mt M m1b ) M mr ibl ibr ibr ( M mt M m1b ) ibl ibr
第3章 框架结构的内力和位移计算
3.1 竖向荷载下内力的近似计算—分层法 3.2 水平荷载下内力的近似计算—反弯点法 3.3 水平荷载下内力的近似计算—D值法 3.4 水平荷载作用下侧移的近似计算
3.1 竖向荷载下内力近似计算—分层法
一、竖向荷载 自重、活荷、雪荷载及施工检修荷载等。 二、分层法的基本假设 1、忽略侧移的影响； 2、忽略每层梁的竖向荷载对其它各层梁 的影响。 三、分层法计算要点 1、将N层框架划分成N个单层框架，柱 端假定为固端， 用力矩分配法计算。
三、柱的侧移刚度D 12ic D 2 h
—为柱侧移刚度修正系数，表示梁柱刚 度比对柱侧移刚度的影响。
四、剪力计算 有了D值后，与反弯点法类似，计算各柱分 配的剪力 Dij Vij V pj Dij 五、确定柱反弯点高度比 影响柱反弯点高度的主要因素是柱上下端的 约束条件。
【精选】《分层法》例题详解
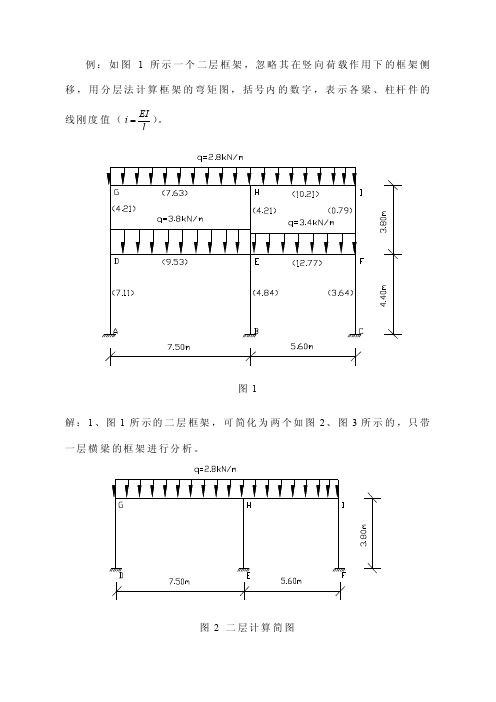
例：如图1所示一个二层框架，忽略其在竖向荷载作用下的框架侧移，用分层法计算框架的弯矩图，括号内的数字，表示各梁、柱杆件的线刚度值（EIil ）。
图1解：1、图1所示的二层框架，可简化为两个如图2、图3所示的，只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时，假定上、下柱的远端为固定，则与实际情况有出入。
因此，除底层外，其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12，其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数，均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时，梁、柱的线刚度值均采用修正后的结果进行计算，如：G节点处：7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处：7.630.3537.63 3.7910.21H G H GHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理，可计算其余各节点的力矩分配系数，计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩（1）第二层：①计算各梁杆端弯矩。
先在G、H、I节点上加上约束，详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩（顺时针转向为正号），写在各梁杆端下方，见图9：213.13kN m 12FGHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HIql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处，各梁杆端弯矩总和为：13.13kN m FG GH M M ==-⋅在节点H 处，各梁杆端弯矩总和为：13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处，各梁杆端弯矩总和为：7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配，各两次，详见图9 第一次弯矩分配过程：放松节点G ，即节点G 处施加力矩13.13kN m ⋅，乘以相应分配系数0.668和0.332，得到梁端+8.76k N m ⋅和柱端+4.37kN m ⋅，+8.76kN m ⋅按12传到GH 梁H 端；放松节点I ，即在节点I 处施加力矩7.32kN m -⋅，乘以相应分配系数0.935和0.065，得到梁端 6.32kN m -⋅和柱端+1.00kN m ⋅， 6.32kN m -⋅按12传到IH 梁H 端；放松节点H ，相应的在节点H 处新加一个外力偶矩，其中包括GH 梁右端弯矩、IH 梁左端弯矩、GH 梁和IH 梁传来的弯矩。
C二十七讲 多层多跨分层法、反弯点法
第一层
G H
多层多跨刚架的近似计算 2)固端弯矩： M 固端弯矩： 固端弯矩
F BA
例2 分层法
= −M
F AB
3× 42 = = 4(kN⋅ m) 12
3）力矩分配、传递及杆端弯矩见表。 ）力矩分配、传递及杆端弯矩见表。 （3）最后杆端弯矩及叠加两种情况的结果得最后杆端弯 ） 单位kNm）。 矩（单位 ）。
多层多跨刚架的近似计算
例2 分层法
SDA 0.9×1 µDA = = 0.23 = SDA = 4iDA = 4×(0.9×1) SDA + SDE + SDG 0.9×1+ 2 +1 SDE 2 SDE = 4iDE = 4×2 → µ = = = 0.51 DE S = 4i = 4×1 SDA + SDE + SDG 0.9×1+ 2 +1 DG DG SDG 1 µG = = = 0.26 SDA + SDE + SDG 0.9×1+ 2 +1 SEB = 4iEB = 4×(1×0.9)
-16.77
24.09
-4.11 10.93
-1.65
多层多跨刚架的近似计算
结点 杆端 分配系数 传递系数 固端弯矩 13.86 C CA AC 0.231 1/3 A AB 0.769 1/2 -60 46.14 -21.1 分配与传 递 4.87 16.23 -2.06 0.48 弯矩值 6.40 19.21 1.58 -19.21 44.86 -13.95 BA 0.508 1/2 60 23.07 -42.2 -8.12 -4.13 -1.24 -12.71 B BD 0.153 1/3
反弯点法
一、简化分析模型
1.各杆件的弯
矩图均为直线， 一般情况下每 根杆件都有一 个弯矩为零的 点，称为反弯 点； 2.所有杆件的 最大弯矩均在 杆件两端。
二、计算方法（框架结构共n层，m-1跨）
1 求柱剪力
Fn Fj
u j1
u jk
u jm
将框架在某一层的 反弯点切开。 根据平衡条件，有
i j
jk
i jk
i
k 1
m
VFj jkVFj
jk
jk为j层k柱的剪力分配系数；VFj
i j
Fi
n
为水平荷载在j层 产生的层间剪力。
求柱端弯矩 逐层取脱离体，利用上式求得各柱剪力后，根据各层反弯 点位置，可以求出柱上、下端的弯矩 底层柱：
M ct1k V1k M cb1k h1 3 2h1 V1k 3
剪力分配
柱反弯点 处的剪力
柱端 弯矩
利用节点力 矩平衡条件
梁端 弯矩
l r Mb Mb Vb l
梁端 剪力
节点竖向力 平衡条件
柱 轴力
四、课堂巩固
例题：用反弯点 法计算右图所示 框架的弯矩，并 绘出弯矩图。图 中圆括号内的数 字为杆件的相对 线刚度。
五、小结
应用范围
基本假定
反弯点法
计算步骤
VAB M AB M BA 12i 2 u AB h h
D 抗侧刚度 D 为：
12ic h2
对于j层第k柱，其侧移为 u jk ，相应的剪力可表示为
V jk D jk u jk
（物理条件）
根据平衡条件、几何条件和物理条件，可求得
V jk
毕业设计指导书(框架结构设计)-内力计算及组合
计算杆件固端弯矩时应带符号，杆端弯矩一律以顺时针方向为正，如图3-6。
图 3-6 杆端及节点弯矩正方向
1）横梁固端弯矩：
（1）顶层横梁
自重作用：
板传来的恒载作用：
（2）二～四层横梁
自重作用：
板传来的恒载作用：
2）纵梁引起柱端附加弯矩：（本例中边框架纵梁偏向外侧，中框架纵梁偏向内侧）
顶层外纵梁
相交于同一点的多个杆件中的某一杆件，其在该节点的弯矩分配系数的计算过程为：
（1）确定各杆件在该节点的转动刚度
杆件的转动刚度与杆件远端的约束形式有关，如图3-1：
（a）杆件在节点A处的转动刚度
（b）某节点各杆件弯矩分配系数
图 3-1 A节点弯矩分配系数（图中 ）
（2）计算弯矩分配系数μ
（3）相交于一点杆件间的弯矩分配
（3）求某柱柱顶左侧及柱底右侧受拉最大弯矩——该柱右侧跨的上、下邻层横梁布置活荷载，然后隔跨布置，其它层按同跨隔层布置（图3-4c）；
当活荷载作用相对较小时，常先按满布活荷载计算内力，然后对计算内力进行调整的近似简化法，调整系数：跨中弯矩1.1～1.2，支座弯矩1.0。
（a）（b） （c）
图 3-4 竖向活荷载最不利布置
∑Mik/l
V1/A=gl/2+u-∑Mik/l
M=gl/2*l/4+u*1.05-MAB-V1/A*l/2
4
21.9
4.08
2.25
6
12.24
41.06
-30.54
2.55
50.75
-60.24
3
16.61
4.08
2.25
6
12.24
31.14
分层法题目解答
分层法例：某教学楼为四层现浇钢筋混凝土框架结构。
梁的截面尺寸：250mm×600mm，混凝土采用C20；柱的截面尺寸：450mm×450mm，混凝土采用C30。
试按分层法计算钢筋混凝土框架的弯矩，并绘出弯矩图。
屋面和楼面荷载标准值见下表。
解：（1）计算梁、柱线刚度1）梁的线刚度边跨梁：k b=E b I b/l=[25.5×106×（1/12）×0.25×0.63×1.5]/5.7=24.16×103kN·m（框架梁截面惯性矩增大系数均采用1.5）中跨梁：k b=E b I b/l=[25.5×106×（1/12）×0.25×0.63×2.0]/3.00=45.90×103kN·m2）柱的线刚度底层柱：k c=E c I c/h=[30×106×（1/12）×0.45×0.453]/4.55=22.53×103kN·m 其他层柱：k c=E c I c/h=[30×106×（1/12）×0.45×0.453]/3.60=28.48×103kN·m（2）计算分配系数除底层外，各层柱的线刚度应乘以0.9。
（3）荷载分析1）屋面梁上线荷载设计值恒载：1.2[（2.93+1.00+2.60）×4.5+0.25×0.60×25×1.2]=40.67kN/m 活载： 1.4×0.7×4.5=4.41kN/m （系数1.2为考虑梁挑檐及抹灰重的系数）q1=45.08kN/m 2）楼面梁上线荷载设计值教室恒载：1.2[（1.10+1.00+2.60）×4.5+0.25×0.60×25×1.2]=30.78kN/m活载： 1.4×2.00×4.5×0.9=11.34kN/m （系数0.9为屋面及楼面活荷载折减系数）q2=42.12kN/m 走道恒载：30.78kN/m 活载： 1.4×2.50×4.5×0.9=14.18kN/mq3=44.96kN/m（4）梁端固端弯矩M F顶层边跨梁（教室）：M F=q1l12/12=45.08×5.72/12=122.05kN·m中跨梁（走道）：M F=q1l22/3=45.08×（3/2）2/3=33.81kN·m其他层边跨梁（教室）：M F=q2l12/12=41.12×5.72/12=114.04kN·m中跨梁（走道）：M F=q3l22/3=44.96×（3/2）2/3=33.72kN·m（5）弯矩分配与传递（用弯矩分配法计算）1）屋面层列表计算，如表1。
1《分层法》例题详细讲解
例：如图1所示一个二层框架，忽略其在竖向荷载作用下的框架侧移，用分层法计算框架的弯矩图，括号的数字，表示各梁、柱杆件的线。
图1解：1、简化为两个图：图2、图3所示图2 第二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数除底层外，其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为1/2，其余各层柱的弯矩传递系数为1/3。
各层梁的弯矩传递系数，均为1/2.图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数 如：G 节点处：7.630.6687.63 3.79GHGH GH GH GD GjGi i i i iμ====++∑ GD 3.790.3327.63 3.79GDGD GH GD GjGi i i i iμ====++∑H 节点处：7.630.3537.63 3.7910.21HGHG HG HG HE HI HjHi i i i i iμ====++++∑3.790.1757.63 3.7910.21HIHI HI HG HE HI HjHi i i i i iμ====++++∑10.210.4727.63 3.7910.21HEHE HE HG HE HI HjHi i i i i iμ====++++∑其余各节点的力矩分配系数见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩（1）第二层： ①计算各梁杆端弯矩。
将各杆变成单跨梁，刚节点看成是固定端。
图8 二层计算简图计算由荷载产生的、各梁的固端弯矩（顺时针转向为正号左负右正），213.13kN m 12F GHql M=-=-⋅ 213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HIql M=-=-⋅ 27.32kN m12F IH ql M ==⋅ ②各梁端节点进行负弯矩分配和传递，各两次，第一次负弯矩分配与传递后再进行第二次负弯矩分配与传递：③计算各柱的杆端弯矩。
4框架结构设计计算
（7）绘制总弯矩图
图4－6 例题1 框架总弯矩图
用分层法计算下面框架的M图
3 水平荷载下内力近似计算—反弯点法
框架所受的水平荷载主要是 风和地震作用，这些均布都 可以化成作用在框架楼层结 点上的水平集中力，如图所 示。 这时框架侧移是主要的变形 因素。对于层数不多的框架， 柱子轴力较小，截面也较小， 当梁的线刚度ib比柱的线刚 度ic大的多时，采用反弯点 法计算其内力，误差比较小。
解：（1）将三层框架按图（b）、(c)、(d)的形式分解成单层框架，并将除 底层之外的柱线刚度乘以0.9的修正系数； （2）求梁柱相对线刚度。将各梁柱线刚度除以梁的线刚度，使梁的相对线 刚度为1；柱的相对线刚度分别为： 底层ic’=1.1、其余各层ic’=1.3； （3）求节点弯矩分配系数。 以第三层A柱节点为例，求弯矩分配系数μ3i：
构件 分配系数
一层框架弯矩叠加
构件
分配系数 叠加弯矩 分配不平衡弯矩 弯矩小计
柱A12
0.32 2.688＋0.952＝3.64 －0.952×032＝－ 0.305 3.335
柱A10
0.38 3.192 －0.952×038＝ －0.362 2.83
梁1ab
0.3 －5.88 －0.952×03＝－ 0.285 －6.165
反弯点法
多层多跨框架在水平荷载作用下的弯矩图通常如图 所示。它的特点是，各杆件的弯矩图均为直线，每 杆均有一零弯矩点，称为反弯点.
如果在反弯点处将柱子切开，切断点处的内力将只有剪力和轴 力。如果知道反弯点的位置和柱子的抗侧移刚度，即可求得各柱 的剪力，从而求得框架各杆件的内力，反弯点法即由此而来。 由此可见，反弯点法的关键是反弯点的位置确定和柱子侧向刚 度的确定。
分层法与反弯点法
4.21 0.9
3.789
14.782 -1.525
0.535 -0.535
DA
E点：
1.59 -0.508 -0.178
EH
ED
D
E
16.712 14.782
F
4.22 0.9 3.798 0.123 4.22 0.9 9.53 4.84 12.77 30.938 9.53 9.53 0.308 4.22 0.9 9.53 4.84 12.77 30.938 4.84 4.84 0.156 4.22 0.9 9.53 4.84 12.77 30.938 12.77 12.77 0.413 4.22 0.9 9.53 4.84 12.77 30.938 1.79 0.9 1.611
80 2 =160kN?m
300 5 100kN 15 =
d =6 y =4
V=
300 6 120kN 15 =
V=
300 4 80kN 15 =
M 下 = 100
4 =400kN?m
M 下 = 120
4 =480kN?m
M下 =
80 4 =320kN?m
73.2 73.2 60.1
97.6
48.8
1 3.5 7.52 16.406kN m 12 1 F M ED 3.5 7.52 16.406kN m 12 1 F M EF 3.5 5.62 9.147kN m 12 1 F M FE 3.5 5.62 9.147kN m 12
12.903 16.712
与弯矩分配法对比： 14.73
6.058
1《分层法》例题详解
例：如图1所示一个二层框架，忽略其在竖向荷载作用下的框架侧移，用分层法计算框架的弯矩图，括号内的数字，表示各
1/3。
各层梁的弯矩传递系数，均为1/2.
图4 修正后的梁柱线刚度
图5 各梁柱弯矩传递系数
3、计算各节点处的力矩分配系数 如：G 节点处：
7.630.6687.63 3.79GH
GH GH GH GD Gj
G
i i i i i
μ=
===++∑
将各杆变成单跨梁，刚节点看成是固定端。
图8 二层计算简图
计算由荷载产生的、各梁的固端弯矩（顺时针转向为正号左负右正），
②各梁端节点进行负弯矩分配和传递，各两次，
图9 二层弯矩分配传递过程（2）第一层：
①计算各梁杆端弯矩。
图10 底层计算简图
计算由荷载产生的、各梁的固端弯矩（顺时针转向为正号），写在各梁杆端下
递，
13
89
图11 底层弯矩分配传递过程
5、将二层与底层各梁、柱杆端弯矩的计算结果叠加，就得到各梁、柱的最后
弯矩图，详见图12。
图12 弯矩图（单位：kN m ）
6、力矩再分配
由以上各梁、柱的杆端弯矩图可知，。
【绝对精品】土木工程本科：分层法例题
7.11
0.466
D
(9.53) E
(7.11) (4.84)
F (12.77)
(3.64)
DA
7.11 0.9 4.21 9.53
7.11
0.348
A
B
C
CSD
节点 E：
ED
9.53 9.53 0.9 4.2112.77 4.84
0.308
G
H
(0.9×4.21)
EH
9.53
0.9 4.21 0.9 4.2112.77
4.84
0.123
(0.9×4.21)
D
(9.53) E
EF
12.77 9.53 0.9 4.2112.77
4.84
0.413
(7.11)
(4.84)
I
(0.9×1.79)
F (12.77)
(3.64)
EB
9.53
4.84 0.9 4.2112.77
4.84
0.156 A
B
C
CSD
节点 F：
G
底层计算简图
G (0.9×4.21) H
(0.9×4.21)
3.8 kN/m
I
(0.9×1.79)
3.4 kN/m
D
E
FD
(9.53) E (12.77) F
顶层计算简图
(7.11) (4.84)
(3.64)
A
B
C
CSD
计算节点弯矩分配系数
G
(7.63) H
I (10.21)
节点 G：
GH
7.63 7.63 0.9 4.21
本章中，杆端弯矩以顺时针为正，剪力以使隔 离体产生顺时针转动趋势为正，轴力以受压为正； 杆端转角以顺时针为正，侧移或相对侧移以向右为 正。
分层法例题详解
例:如图1所示一个二层框架，忽略其在竖向荷载作用下的框架侧 移，用分层法计算框架的弯矩图，括号内的数字，表示各梁、柱杆件的 线刚度值(i =旦）.l解 : 1、图1所示的二层框架，可简化为两个如图2、图3所示的,只带 一层横梁的框架进行分析。
图2二层计算简图7<50rq=P<BkN∕n■■■ ■■■■E■■■■ ■ ,*,-∙、：CI二■P,J/11心H∖-’.i。
A kM/r[ •JJnJl III F r"77⅛Γ,^77?S t-VΛ5Dr 5.60r图3底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时，假定上、下柱的远端为固定，则与实际情况有出入.因此，除底层外，其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为1，其余各层柱的弯矩传递系数为—。
各层梁的弯2 3矩传递系数，均为1。
27.5On图4修正后的梁柱线刚度FC J iCIΓriGlz≡H1/21/3。
/31/3D1 Jr nE—P1/2。
JFr ，777/Z7。
50rZ_____Z7图5各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时,梁、柱的线刚度值均采用修正后 的结果进行计算，如:H 节点处：亘=—血7630。
353T。
i HG+i HEf 7.63 + 3.79+10.21 I HjH同理，可计算其余各节点的力矩分配系数,计算结果见图6、图7G 节点处：J G ^-I-I0. 6 6 8 、•・I GH ■ ∣GD 7. 633. 7 9iGjGGD—iGj Gi GD■ 1 ■i GH i GD3.79 7.63 3.79-0.332i HII HI■ +・ +・ i HG i HE iHI3.79 7.63 3.7910.2= 0.175HE∣HE∣HEViHj Hi HG i HE i HI10.21 7.63 3.79 10.21=0.472i GD图6二层节点处力矩分配系数图7底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩 1）第二层:① 计算各梁杆端弯矩。
《分层法》例题详解
例：如图1所示一个二层框架，忽略其在竖向荷载作用下的框架侧移，用分层法计算框架的弯矩图，括号内的数字，表示各梁、柱杆件的线刚度值（EIil ）。
图1解：1、图1所示的二层框架，可简化为两个如图2、图3所示的，只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时，假定上、下柱的远端为固定，则与实际情况有出入。
因此，除底层外，其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12，其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数，均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时，梁、柱的线刚度值均采用修正后的结果进行计算，如：G节点处：7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处：7.630.3537.63 3.7910.21HG HGHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理，可计算其余各节点的力矩分配系数，计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩（1）第二层：①计算各梁杆端弯矩。
先在G、H、I节点上加上约束，详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩（顺时针转向为正号），写在各梁杆端下方，见图9：213.13kN m 12FGHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HIql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处，各梁杆端弯矩总和为：13.13kN m FG GH M M ==-⋅在节点H 处，各梁杆端弯矩总和为：13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处，各梁杆端弯矩总和为：7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配，各两次，详见图9 第一次弯矩分配过程：放松节点G ，即节点G 处施加力矩13.13kN m ⋅，乘以相应分配系数0.668和0.332，得到梁端+8.76kN m ⋅和柱端+4.37kN m ⋅，+8.76kN m ⋅按12传到GH 梁H 端；放松节点I，即在节点I处施加力矩7.32kN m-⋅，乘以相应分配系数0.935和0.065，得到梁端 6.32kN m-⋅和柱端+1.00kN m⋅， 6.32kN m-⋅按12传到IH梁H端；放松节点H，相应的在节点H处新加一个外力偶矩，其中包括GH梁右端弯矩、IH梁左端弯矩、GH梁和IH梁传来的弯矩。
反弯点法例题详解
例：用反弯点法计算图1所示刚架，并画出弯矩图。
括号内数字为杆件线刚度的相对值。
图1解：顶层柱反弯点位于柱中点22h ，底层柱的反弯点位于柱高123h 处，在反弯点处将柱切开，脱离体如图2、图3所示。
F QIFQHE QGD图2 顶层脱离体F QAD F QBE F QCFGIFED817图3 底层隔离体（1）求各柱剪力分配系数kk ik k μ=∑ 顶层：20.286223GD IF μμ===⨯+30.428223HE μ==⨯+底层：30.3324DA FC μμ===⨯+40.4324EB μ==⨯+（2）计算各柱剪力：0.2868kN 2.29kN QGD QIF F F ==⨯= 0.4288kN 3.42kN QHE F =⨯= 0.325kN 7.5kN QAD QCF F F ==⨯= 0.425kN 10kN QBE F =⨯=（3）计算杆端弯矩，以节点E 为例说明杆端弯矩的计算 杆端弯矩：2 3.33.42kN 5.64kN m 22EH QHE h M F m =-⨯=-⨯=-⋅（反弯点位于22h 处）1 3.610kN 12kN m 33EB QBE h M F m =-⨯=-⨯=-⋅（反弯点位于柱123h 处） 计算梁端弯矩时，先求出节点柱端弯矩之和为：17.64kN m EH EB M M M =+=-⋅按梁刚度分配：1217.647.84kN m 27ED M =⨯=⋅ 1517.649.8kN m 27EFM =⨯=⋅ 图3是刚架弯矩图。
8173.782.51 5.643.783.133.783.783.78912.785.649.87.841212.783.781824189图3 弯矩图（单位kN m ⋅）。
电大房屋建筑混凝土结构设计形考问题详解
电大土木工程本科房屋建筑混凝土结构设计形考答案形考任务一一、选择题（共5小题，每小题10分，共50分）1.（梁板结构体系）主要承担楼（屋）面上的使用荷载，并将荷载传至竖向承重结构，再由竖向承重结构传至基础和地基。
2.（框架结构体系）由梁和柱连接而成，其中梁柱连接处一般为刚性连接，柱支座一般为固定支座。
3.（框架结构体系）的优点是建筑平面布置灵活、使用空间较大，缺点是结构抗侧刚度较小、易产生较大侧移，主要应用于10层以下多层建筑。
4.（框架-剪力墙结构体系）是将框架结构中的部分跨间布置剪力墙或把剪力墙结构的部分剪力墙抽掉改为框架承重。
5.（结构选型）的主要目的是为建筑物选择安全经济的受力体系，主要包括结构体系的选择及结构材料的确定等。
二、判断题（共10小题，每小题5分，共50分）6.混凝土结构是由基础、柱(墙)、梁(板、壳）等混凝土基本构件组成的一个空间骨架受力系统。
（√）7.混凝土结构设计，就是根据建筑功能或生产要求，依据一定的力学原理，选用合理的结构形式，并确定各组成构件的尺寸、材料和构造方法的过程。
（√）8.梁板结构体系是混凝土结构中最常用的竖向结构体系，被广泛用于建筑中的楼、屋盖结构、基础底板结构等。
（×）9.框架结构属高次超静定结构，既承受竖向荷载，又承受侧向水平力。
（√）10.在剪力墙的墙体内，侧向荷载主要产生向下的压力，竖向荷载产生水平剪力和弯矩。
（×）11.框架-剪力墙结构体系既保留了框架结构建筑布置灵活、使用方便的优点，又具有剪力墙抗侧刚度大、抗震性能好的优点，同时还可充分发挥材料的强度作用，具有很好的技术经济指标。
（√）12.先设计、后勘察、再施工，是工程建设必须遵守的程序。
（×）13.结构设计的具体内容包括基础结构设计、上部结构设计和构造细部设计。
（√）14.结构设计一般可分三个阶段：方案阶段、结构分析与计算阶段、施工图设计阶段。
（√）15.工程地质勘察报告不作为结构设计的主要依据。
2016新编《分层法》例题详解
例：如图1所示一个二层框架，忽略其在竖向荷载作用下的框架侧移，用分层法计算框架的弯矩图，括号内的数字，表示各梁、柱杆件的线刚度值（EIil ）。
图1解：1、图1所示的二层框架，可简化为两个如图2、图3所示的，只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时，假定上、下柱的远端为固定，则与实际情况有出入。
因此，除底层外，其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12，其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数，均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时，梁、柱的线刚度值均采用修正后的结果进行计算，如：G节点处：7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处：7.630.3537.63 3.7910.21H G H GHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理，可计算其余各节点的力矩分配系数，计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩（1）第二层：①计算各梁杆端弯矩。
先在G、H、I节点上加上约束，详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩（顺时针转向为正号），写在各梁杆端下方，见图9：213.13kN m 12FGHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HIql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处，各梁杆端弯矩总和为：13.13kN m FG GH M M ==-⋅在节点H 处，各梁杆端弯矩总和为：13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处，各梁杆端弯矩总和为：7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配，各两次，详见图9 第一次弯矩分配过程：放松节点G ，即节点G 处施加力矩13.13kN m ⋅，乘以相应分配系数0.668和0.332，得到梁端+8.76k N m ⋅和柱端+4.37kN m ⋅，+8.76kN m ⋅按12传到GH 梁H 端；放松节点I ，即在节点I 处施加力矩7.32kN m -⋅，乘以相应分配系数0.935和0.065，得到梁端 6.32kN m -⋅和柱端+1.00kN m ⋅， 6.32kN m -⋅按12传到IH 梁H 端；放松节点H ，相应的在节点H 处新加一个外力偶矩，其中包括GH 梁右端弯矩、IH 梁左端弯矩、GH 梁和IH 梁传来的弯矩。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第2层：
∑P=10+19=29kN
VDG=9.67kN VEH=12.89kN VFI=6.44kN 第1层： ∑P=10+19+22=51kN VGJ=17kN VHK=20.4kN
VIL=13.6kN
(2) 计算柱端弯矩
第3层
MAD=MDA=6.66kN· m MBE=MEB=8.9kN· m MCF=MFC=4.44kN· m 第2层 MDG=MGD=24.18kN· m MEH=MHE=32.23kN· m MFI=MIF=16.1kN· m
MGH=58.18kN· m
MHG=28.09kN· m
MHI=44.94 kN· m
MIH=MIF+MIL=16.1+27.2=43.3kN· m 上结果，画出M图如图12.19所示。 根据以
图12.17 节点杆端弯矩
图12.18
图12.19 M图（单位： kN· m)
【例12.1】图12.11所示一个两层两跨框架，用分层法作框 架的弯矩图，括号内数字表示每根杆线刚度的相对值。 【解】将第二层各柱线刚度遍乘0.9，分为两层计算，各层 计算单元如图12.12和图12.13所示。
用弯矩分配法计算各杆端的弯矩，其计算过程见图 12.14。
最后将图12.14中的各杆端弯矩叠加并绘弯矩图如图 12.15
图12.11 例12.1计算简图
ቤተ መጻሕፍቲ ባይዱ
图12.12 例12.1二层计算单元
图12.13 例12.1底层计算单元
图12.14
注意事项：
分层法计算的各梁弯矩为最终弯矩，各柱的最终弯矩为 与各柱相连两层计算弯矩的叠加； 图12.15 M图（单位： kN· m)
【例12.2】用反弯点法求图12.18所示框架的弯矩图。图 中括号内数字为各杆的相对线刚度。 【解】（1） 计算柱的剪力 当同层各柱h相等时，各柱剪力可直接按其线刚度分 配。 第3层： ∑P=10kN VAD=3.33kN VBE=4.45kN VCF=2.22kN
第1
MGJ=34kN· m
MJG=68kN· m MHK=40.8kN· m MKH=81.6kN· m MIL= 27.2kN· m MLI=54.4kN· m (3) 根据节点平衡条件算出梁端弯矩 第3
MAB=MAD=6.66kN· m
MBA=3.42kN· m
MBC=5.48kN· m
MCB=MCF=4.44kN· m 第2层 MDE= 30.84kN· m MED=15.82kN· m MEF=25.31kN· m MFE=20.54kN· m 第1