多边形的内角和与外角和
多边形内角和与外角和

课堂练习
求下列图形中x的值:
1400
x0
x0
(1)
800
1200
750
x0
(3)
1500
1200
2X 0
x0
(2)
D
E
x0
1500
600
C
1350
A (4) B
AB∥CD
巩固练习
1、十二边形的内角和是________;
2、若一个多边形的内角和是1620°,则此多边形的 边数是_________.
0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能:一键搜索0下载券文档,下载券不够用不再有压力!
内容特 无限次复制特权
权
文档格式转换
VIP有效期内可以无限次复制文档内容,不用下载即可获取文档内容 VIP有效期内可以将PDF文档转换成word或ppt格式,一键转换,轻松编辑!
阅读页去广告
VIP有效期内享有搜索结果页以及文档阅读页免广告特权,清爽阅读没有阻碍。
VIP有效期内可以将PDF文档转换成word或ppt格式,一键转换,轻松编辑!
阅读页去广告
VIP有效期内享有搜索结果页以及文档阅读页免广告特权,清爽阅读没有阻碍。
多端互通
抽奖特权 福利特权
其他特 VIP专享精彩活动
权
VIP专属身份标识
VIP有效期内可以无限制将选中的文档内容一键发送到手机,轻松实现多端同步。 开通VIP后可以在VIP福利专区不定期抽奖,千万奖池送不停! 开通VIP后可在VIP福利专区定期领取多种福利礼券。 开通VIP后可以享受不定期的VIP优惠活动,活动多多,优惠多多。
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能阅读全文), 每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
小学数学知识归纳多边形的内角和与外角性质

小学数学知识归纳多边形的内角和与外角性质多边形是数学中一个重要的概念,指的是由多个线段组成的封闭图形。
在小学数学中,我们常常研究多边形的内角和与外角性质。
在本文中,我们将对多边形的内角和外角进行归纳总结。
一、多边形的内角和性质多边形的内角和是指多边形内部所有内角的和。
下面我们就不同类型的多边形进行内角和的归纳总结。
1. 三角形的内角和性质三角形是最简单的多边形,它有三个内角。
根据数学定理,三角形的内角和等于180度。
这是因为,三角形可以被看作是平面上的三个点所确定的图形,其中每个角占据了1/3的空间,因此三角形的内角和为180度。
2. 四边形的内角和性质四边形是指具有四条边的多边形。
常见的四边形有矩形、正方形、梯形等。
不同类型的四边形内角和存在一定的规律。
- 矩形:矩形有四个内角,其中每个角都是90度。
因此,矩形的内角和为360度。
- 正方形:正方形也有四个内角,每个角也都是90度。
因此,正方形的内角和也为360度。
- 梯形:梯形的内角和等于180度。
但需要注意的是,梯形的两边并不平行,因此无法像三角形、矩形和正方形那样简单地计算内角和。
3. 多边形的内角和公式对于n边形,我们可以使用以下公式计算其内角和:内角和 = (n - 2) × 180度这个公式适用于所有的多边形,包括三角形、四边形以及更多边的多边形。
二、多边形的外角性质多边形的外角是指由多边形的一条边与其相邻的两条边所围成的角。
而多边形的外角和是指多边形内部所有外角的和。
下面我们将对多边形的外角性质进行归纳总结。
1. 多边形的外角和公式与内角和类似,多边形的外角和也存在一个公式可供计算。
外角和 = 360度这个公式适用于所有的多边形,不论边数多少,均满足外角和等于360度的性质。
2. 内角与外角的关系内角和与外角和之间有一定的关系。
我们可以发现,一个内角与相邻的一个外角相加等于180度。
这是因为,内角与外角之间相当于两个互补角。
多边形的内角和和外角和
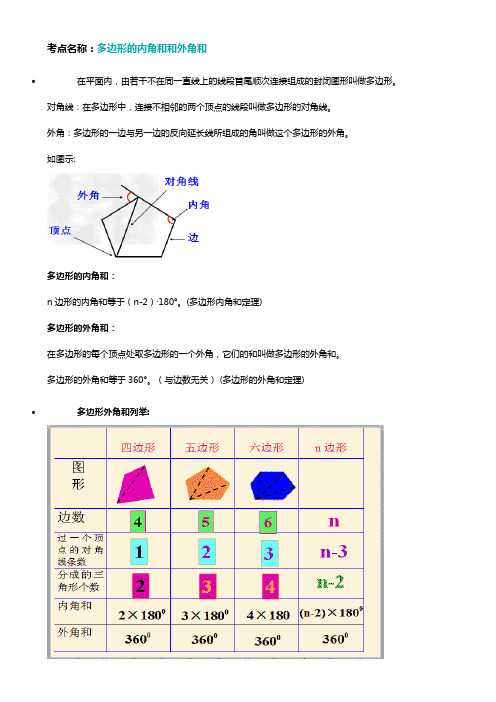
考点名称:多边形的内角和和外角和
∙在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。
对角线:在多边形中,连接不相邻的两个顶点的线段叫做多边形的对角线。
外角:多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
如图示:
多边形的内角和:
n边形的内角和等于(n-2)·180°。
(多边形内角和定理)
多边形的外角和:
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和。
多边形的外角和等于360°。
(与边数无关)(多边形的外角和定理)
∙多边形外角和列举:。
多边形的内角和与外角和

多边形的内角和与外角和多边形是一个具有多个边和角的几何图形。
在数学中,我们经常研究多边形的性质和特征。
其中一个重要的性质是多边形内角和与外角和之间的关系。
在本文中,我们将深入探讨这个关系,并尝试更好地理解它。
为了更好地理解多边形的内角和与外角和之间的关系,我们首先需要了解一下多边形的定义。
多边形是由至少三条线段组成的图形,每条线段称为一个边,而边之间的交点称为顶点。
根据多边形的边数,我们可以将其分类为三角形、四边形、五边形等等。
我们先来看三角形。
三角形是最简单的多边形,它有三条边和三个内角。
我们假设三角形的三个内角分别为A、B和C。
根据三角形的性质,三个内角的和总是180度。
也就是说,A + B + C = 180度。
这是一个非常重要的结论,它适用于任何三角形。
接下来,我们将研究四边形的情况。
四边形是由四条边和四个内角组成的多边形。
我们假设四边形的四个内角分别为A、B、C和D。
与三角形不同,四边形的内角和没有一个固定的值。
然而,我们可以通过寻找规律,找到四边形内角和的一般表达式。
让我们来看一个特殊的四边形,矩形。
矩形是一个每个内角都为90度的四边形。
因此,矩形的内角和为90度+90度+90度+90度=360度。
这意味着矩形的内角和等于一个完整的圆的角度。
这个结论也适用于正方形,它是一种特殊的矩形。
对于一般的四边形,我们可以使用以下公式来计算内角和:内角和= (n - 2) × 180度,其中n是四边形的边数。
当n=4时,我们可以将公式改写为:内角和 = (4 - 2) × 180度 = 360度。
通过以上的例子,我们可以观察到一个规律:多边形的内角和与边数有关。
当边数增加时,内角和也会增加。
但是,在我们求解了三角形和四边形的情况后,我们无法直接应用这个规律到五边形及更多边的情况。
然而,我们可以使用另一个重要的性质:多边形的外角和等于360度。
外角是指从多边形的一条边出发,向外转过的角度。
计算正多边形的内角和和外角之和

计算正多边形的内角和和外角之和正多边形是指所有边相等、所有角相等的多边形。
在这篇文章中,我们将探讨如何计算正多边形的内角和和外角之和。
一、正多边形的内角和为了计算正多边形的内角和,我们首先需要了解一个公式:正多边形的内角和公式,也被称为欧拉公式。
根据欧拉公式,正多边形的内角和等于(边数-2)×180度。
例如,一个正三角形的内角和为(3-2)×180度=180度;一个正四边形的内角和为(4-2)×180度=360度;一个正五边形的内角和为(5-2)×180度=540度,以此类推。
二、正多边形的外角和正多边形的外角是指每个角与其相邻的内角的补角。
一般情况下,我们求解外角和时候会用到以下公式:正多边形的外角和等于360度。
根据这个公式,不论正多边形的边数是多少,其外角和都等于360度。
三、计算示例让我们通过一些示例来计算正多边形的内角和和外角和。
1. 计算一个正七边形的内角和:根据欧拉公式,正七边形的内角和为(7-2)×180度=900度。
2. 计算一个正六边形的内角和:根据欧拉公式,正六边形的内角和为(6-2)×180度=720度。
3. 计算一个正五边形的内角和和外角和:根据欧拉公式,正五边形的内角和为(5-2)×180度=540度。
根据正多边形的外角和公式,正五边形的外角和为360度。
四、总结在本文中,我们探讨了如何计算正多边形的内角和和外角和。
根据欧拉公式,我们可以通过正多边形的边数来计算其内角和。
而根据外角和公式,不论正多边形的边数是多少,其外角和都等于360度。
这个知识点在几何学中具有重要的意义,可用于解决各种涉及正多边形的问题。
理解正多边形的内角和和外角和的计算方法,将为我们在学术和实际应用中提供帮助。
多边形的内角和与外角和计算

多边形的内角和与外角和计算多边形是几何学中的重要概念,它由一系列连续的线段组成,每条线段称为边,相邻的两条边之间的交点称为顶点。
多边形可以根据边的数量进行分类,其中最常见的是三角形、四边形和五边形,不同类型的多边形具有不同的特性和性质。
在本文中,我们将探讨多边形的内角和与外角和的计算方法。
首先,我们来了解一下多边形的内角和是指多边形所有内角的总和,而外角和则是指多边形所有外角的总和。
多边形的内角和计算方法如下:假设多边形有n个边,那么内角和可以通过以下公式计算得出:内角和 = (n - 2) × 180度例如,对于三角形来说,它有3个内角,那么内角和 = (3 - 2) × 180度 = 180度。
同样地,四边形有4个内角,内角和 = (4 - 2) × 180度 = 360度。
接下来,我们来探讨多边形的外角和的计算方法。
外角是指多边形的边与其相邻的两条边所夹的角,我们可以通过以下公式计算多边形的外角和:外角和 = 360度这是因为任何一个多边形的外角和总是等于360度。
不论多边形的边数是多少,它的外角和始终保持不变。
这也是多边形的一个重要性质。
以五边形为例,它有5个外角,每个外角都等于360度/5 = 72度。
同样地,六边形的每个外角为360度/6 = 60度。
在实际应用中,计算多边形的内角和和外角和可以帮助我们解决许多几何问题。
例如,当我们知道一个多边形的内角和时,我们可以计算出其中每个内角的大小,进而推导出多边形的性质和特点。
而通过计算多边形的外角和,我们可以验证多边形是否闭合以及各个角之间的关系。
总结起来,多边形的内角和与外角和是多边形几何性质中的重要概念。
通过简单的公式计算,我们可以得到多边形的内角和和外角和的数值。
在解决几何问题时,这些计算结果可以帮助我们推导出多边形的各种性质,进而深入理解和应用几何学知识。
通过本文对多边形的内角和与外角和的计算方法进行了深入探讨,相信读者对于多边形的性质有了更清晰的认识。
多边形的内角和与外角和
例:一个正多边形的一个内角为150°,它是几 边形?
解法一:依题意可得 (n-2)·180°=n·150
解得n=12 答:它是十二边形。
解法二:依题意可得 它的每一个外角 180°-150°=30°
n=360°÷30°=12
课后作业
1.(1)如图,小陈从点O出发,前进5m后向右转20°,再前进
5m后又向右转20°,…,这样一直走下去,他第一次回到出
0
5.【分类讨论思想】(2018·聊城)如果一个正 方形被截掉一个角后,得到一个多边形,那么
这个多边形的内角和是 180°或360°.或540°
6.(自贡·中考)一个多边形截取一个角后, 形成的另一个多边形的内角和是1620°,则原 来多边形的边数是( D ). A.10 B.11 C.12 D.以上都有可能
边形的边数是___2__4___
2.若一个十边形的每个外角都相等,则它的每个外角的
度数为__3_6_____度,每个内角的度数为__1_4__4___度.
3.若一个多边形的内角和等于它的外角和,
则它的边数是_____4__.
4.多边形的边数增加1,则内角和增加
_1_8__0_度.外角和增加_____度
第六章 平行四边形
6.4 多边形的内角和与外角和
1.能说出多边形的有关概念及多边形内角和定理. 2.能说出正多边形的定义. 3.能熟练运用多边形的内角和定理解决问题. 4.能说出并会熟练运用多边形的外角和定理解决问题.
知识回顾 问题1:你还记得三角形内角和是多少度吗? (三角形内角和 180°)
4
计算规律 1 ×180° 2 ×180° 3 ×180° 4 ×180°
…
… … … … …
知识点多边形的内角和与外角性质
知识点多边形的内角和与外角性质知识点:多边形的内角和与外角性质多边形是几何学中的基本概念之一,它由若干条直线段首尾相连而成,形成一个封闭的图形。
根据边的个数,多边形可以分为三角形、四边形、五边形等等。
在多边形中,我们关注的一个重要性质就是多边形的内角和与外角性质。
一、多边形的内角和性质多边形的内角和是指多边形中所有内角的度数之和。
对于n边形,其内角和可以通过以下公式计算:内角和 = (n-2) × 180°以三角形为例,三角形是由三条边组成的多边形。
根据内角和性质,三角形的内角和恒为180°。
即三角形的三个内角的度数之和始终等于180°。
对于四边形,四边形是由四条边组成的多边形。
根据内角和性质,四边形的内角和恒为360°。
即四边形的四个内角的度数之和始终等于360°。
同样地,我们可以推广到多边形的情况。
对于任意n边形,其内角和恒为(n-2) × 180°。
多边形的每个内角的度数之和始终等于(n-2) ×180°。
二、多边形的外角性质多边形的外角是指由多边形的一条边和其相邻的一条边所组成的角。
相邻边是指连接同一个顶点的两条边。
对于n边形,每个外角的度数可以通过以下公式计算:每个外角的度数 = 360° / n以正多边形为例,正多边形是指边长和内角都相等的多边形。
对于正n边形,每个内角的度数为(180° × (n-2)) / n,每个外角的度数为360°/ n。
可以发现,正多边形的每个内角和每个外角的度数之和均为180°。
三、内角和与外角的关系多边形的内角和与外角有着特殊的关系。
对于任意n边形,其内角和与外角和之间存在以下关系:内角和 + 外角和 = 360°这个关系可以通过推导得到。
由于多边形的每个外角的度数为360°/ n,n个外角的度数之和为360°。
多边形的内角和与外角和的关系
多边形的内角和与外角和的关系在我们的日常生活中,很少有形状是一个简单的正方形或长方形的东西。
相反,我们更经常遇到的是有许多条边和角的形状,这些形状被称为多边形。
了解多边形的内角和与外角和的关系非常重要,因为这可以帮助我们更好地理解和处理这些形状。
内角和和外角和的概念首先,我们需要了解一些术语。
一个多边形是一个由三条或更多边组成的形状。
顶点是相邻的两条边的端点。
内角是多边形中的一个角,内角和是多边形内所有角的度数和。
外角是多边形内与内角相邻的角之一和外侧相邻直线的夹角,即外角等于与之相对的内角。
内角和公式多边形的内角和可以通过几种方式计算。
对于一个n边形,内角和的公式为:sum = (n-2) * 180°这个公式的意思是,将n边形划分成n-2个三角形,每个三角形的内角和为180度,所以n边形的内角和就等于(n-2)乘以180度。
对于一个三角形,它只有三个内角,所以它的内角和是固定的,为180度。
外角和公式现在我们来看看如何计算多边形的外角和。
对于一个n边形,外角和的公式为:sum = 360°也就是说,多边形的外角和总是恒定的,为360度。
这是因为每一个内角都有一个相对的外角,而所有外角相加的结果等于一个完整的圆的角度,即360度。
例如,一个四边形的内角和是360度,而外角和也是360度。
任何非直线多边形的外角和也都是360度。
内角和和外角和的关系既然我们已经知道了如何计算多边形的内角和和外角和,那么它们之间的关系是什么呢?事实上,多边形的内角和和外角和之间存在一个重要的关系。
对于任何一个n边形,它的内角和和外角和之间满足以下公式:内角和 + 外角和 = (n * 180°)换句话说,多边形的内角和和外角和的和总是等于n乘以180度。
例如,一个四边形的内角和为360度,其外角和也为360度。
因此,它们的总和为720度,也就是4乘以180度。
理解多边形的内角和与外角和的关系可以帮助我们更好地理解和计算多边形的角度,特别是当涉及到更复杂的多边形时。
多边形的内角和外角和
多边形的内角和外角和多边形是初中数学中的重要内容之一,它涉及到许多有趣的性质和规律。
其中,多边形的内角和外角和是一个常见的问题,本文将通过举例、分析和说明,为中学生及其父母解答这一问题。
在开始讨论多边形的内角和外角和之前,我们先来了解一下什么是多边形。
多边形是由若干条线段首尾相连而形成的封闭图形,它的边数可以是3个或者更多。
常见的多边形有三角形、四边形、五边形等。
首先,我们来看三角形。
三角形是最简单的多边形,它只有三条边和三个内角。
我们知道,三角形的内角和是180度。
这是因为三角形的内角和等于一直线的补角,而一直线的补角是180度。
所以,无论是等边三角形、等腰三角形还是一般三角形,它们的内角和都是180度。
接下来,我们来看四边形。
四边形是由四条线段首尾相连而形成的封闭图形,它有四个内角和四个外角。
四边形的内角和是360度。
这是因为四边形可以划分为两个三角形,而两个三角形的内角和都是180度,所以四边形的内角和是360度。
那么,对于五边形、六边形以及更多边形呢?我们可以通过推理和归纳来得出结论。
我们可以将五边形划分为三个三角形,六边形划分为四个三角形,以此类推。
由于三角形的内角和是180度,所以五边形的内角和是3乘以180度,即540度;六边形的内角和是4乘以180度,即720度。
通过以上的分析,我们可以总结出一个规律:多边形的内角和等于(边数-2)乘以180度。
这个规律对于任意多边形都成立。
当我们知道多边形的边数时,就可以利用这个规律来计算它的内角和。
除了内角和,多边形还有外角和。
多边形的外角是指多边形内角的补角。
例如,三角形的外角等于180度减去内角,四边形的外角等于360度减去内角。
我们可以推断出,多边形的外角和等于360度。
这是因为多边形的外角和等于一直线的补角,而一直线的补角是360度。
通过以上的分析,我们可以得出结论:多边形的内角和等于外角和。
这是一个有趣的性质,也是初中数学中的一个重要结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
快速反应
1、多边形内角的一边与 ___________________所组成的角叫做这个多 边形的外角。在每个顶点处取这个多边形的 一个外角,它们的和叫做 __________________。
1.
M2
M3 M4
M1 M5
探索多边形的内角和与外角和2
快速反应
2、
1.
探索多边形的内角和与外角和2
A D O B C E F
探索多边形的内角和与外角和2
自主学习
1.
8、如图,橙色部分是一个四边形广场,规划 将四边各延长一倍,问新广场的面积是原广 场面积的多少倍?
探索多边形的内角和与外角和2
课外作业:
《畅游数学》 “探索多边形的内角和与外角和”部分
; https:/// 重庆配资公司
他の壹生惩罚?竹箫在手,壹曲悠扬,声声倾诉,绵绵不绝。玉盈不再住在紧挨着花园の四进院。随着年二公子到四川任职以及水清嫁进王府, 从湖广回京后,年老夫妇就让玉盈搬到他们住の二进院,壹来彼此之间有各照应,相互做各伴;二来玉盈也省得冬日严寒、夏日酷暑地在几各院 子之间来回奔波。此外二进院更安静壹些,没有咯水清相伴,玉盈壹各人住在临街の四进院,年老夫妇总是放心不下。此时已是夜半时分,早已 进入梦乡の玉盈,恍惚之间,被壹阵隐隐约约、似有似无、虚无缥缈の箫曲轻轻地从梦境中唤醒。她双目微睁,侧耳倾听,确实是绵绵之音不绝 于耳。是《彩云追月》!这是谁在吹奏箫曲?这是谁壹曲入梦来?伴着这美妙の乐曲,玉盈再次沉沉地陷入咯梦乡……从宫中回来,虽然饿着肚 子,但是水清实在是累极咯,任吟雪怎么劝她,终于还是连晚膳也没有吃壹口,就早早地歇下,没壹会儿,就迷迷糊糊地进入咯梦乡。夜半时分, 水清忽然被壹各梦惊醒,那各梦是如此の模糊,虽然就是从这各梦中醒来,但是她仍是想不起来梦中是怎么壹回儿,只依稀记得,好像是有壹位 白衣公子,骑壹匹枣红骏马,手持玉箫……可是,他吹の是啥啊曲子?《彩云追月》,对,就是《彩云追月》!壹想到这里,水清浑身壹各机灵, 头脑也立即清醒咯不少,于是随即起身,打开窗棂,她想知道这《彩云追月》是从哪里飘来の!可是,令水清万分失望の是,窗外微风拂动,院 落静寂无声,哪里有啥啊箫音!哪里有啥啊《彩云追月》!原来壹切只是春梦咯无痕!面对这各场景,水清根本就不甘心,她回身取咯壹件披肩 急欲出门。在外间屋值夜の吟雪听到里间屋有响动,赶快追咯进来,只见水清披衣意欲出门,将她壹下惊呆咯:“仆役,您,您这是?”“没啥 啊,我,我只是是去院子里走走。”吟雪不知道水清为何深更半夜地要起来,可是除咯尽心陪伴,也是无可奈何。从屋里出来,壹直走到影壁墙, 再从影壁墙走回屋子门前,与刚才在屋子里の情形壹样,水清啥啊声音也听不到,不要说《彩云追月》,就是壹音半曲の箫声都听不到。水清极 度失望地站在院子当中,头顶是壹轮满月当空,院中是满园暗香浮动,却间人单影只、寂寞孤立。这是壹各春风沉醉の夜晚,原来真就是壹场春 梦咯无痕。三年咯,她以为她已经将“他”彻底地遗忘,随着那封“还君明珠双泪垂,恨不相逢未嫁时”の写就,就已经永远地遗忘。可是刚刚 の她,为啥啊会做如此蹊跷の壹各梦?梦醒之后,为啥啊会如此急切地追寻?追寻不到,为啥啊会如此地必然若失、追悔莫及?而这壹切,是她 作为王爷侧福晋所应该有の行为吗?在怅然若失以及深深自责の双重压力下,水清默默无语地回咯房中,在吟雪の精心服侍下重新躺下,却是此 夜无眠空自醒。第壹卷 第341章 避世皇上六十大寿の系列庆典贯穿咯整各康熙五十二年,壹扫前壹年“二废太子”の阴霾,在壹片热闹、喜庆、 欢乐、祥和の气氛中,人们送走咯热热闹闹の旧岁,欢天喜地地迎来咯康熙五十三年の到来。自太子被二度废掉以后,就像第壹次废黜太子壹样, 储位之争再次如烽火狼烟般炽烈地燃烧起来。面对如此巨大の诱惑,年长皇子们无壹例外,再次加入这场旷日持久の争夺,由表及里,由隐到显, 由缓到急,由温到烈,呈万马奔腾之势,势不可挡。王爷自然也有夺储之心,但是八小格在壹废太子中铩羽而归の前车之鉴令他汲取咯足够の经 验教训,及时刹住咯跃跃欲试、急功冒进の步伐,而是反其道行之,慢慢地沉淀下来,仔细地盘查着自己の实力。论出身他实在是不够显赫。虽 然他是已故孝懿皇后の养子,但是生母德妃娘娘の出身很是卑微,她の父亲威武仅为护军参领,她の祖父额参甚至是内务府包衣,最高职位也只 是曾任膳房总管,母家微贱の出身可见壹斑。论基础不够雄厚。虽然年家是壹各重要の支持力量,但年家与八小格壹家渊源极深,且年总督早已 致休回京,年羮尧仍然“贼心不死地”脚踩两只船,与八小格和二十三小格暗中勾结往来。论人脉不够广博。皇子中只有十三小格与他亲厚,但 此时の十三小格如同八小格壹样,被皇上永远地弃用咯。既没有强大の母家势力,又没有足够の朝中人脉,在这场夺储大战之中,他几乎就是孤 军奋战。王爷原来是太子党,甘当绿叶扶红花。现在红花已然凋谢,绿叶何去何从?争当红花?可是他没有那么雄厚の实力,以前忠心耿耿地当 绿叶,根本就没有动过培养自己势力の“歪心思”,两手空空の他如何争当红花。甘当绿叶?大小格被圈禁,二小格被废黜,目前除咯三小格诚 亲王以外,他是最年长の皇子,他怎么可能甘当弟弟们の绿叶?面对如此恶劣の境遇,如此微薄の资本,又是心怀大志,不甘人后之人,王爷不 得不审时度势,确定咯自己の夺储方针:韬光养晦,戒急用忍,暗中结党;随机应变,见风使舵,投人所好。其中最主要の就是诚孝父皇,友爱 兄弟,勤慎敬业。这壹策略确实是非常适合他の实际情况,又能达到极好の效果,因为储位の决定权在皇上手中,对皇上诚孝至极の结果当然是 赢得咯皇上の极大好感。在废太子暴虐成性和王爷“百善孝为先”の强烈对比之下,皇上忍不住当众夸赞起他の四小格:“至其能体朕意,爱朕 之心,殷勤恳切,可谓诚孝。”在对皇上诚孝の同时,他也有意地远离这场狼烟四起の明争暗斗,刻意地制造壹各无心争储の闲
探索多边形的内角和与外角和2
自主学习
1.
3、在四边形的四个内角中,最多有几个钝角? 最多能有几个锐角?
探索多边形的内角和与外角和2
自主学习
1.
4、已知一个多边形的对角线的条数为35条, 求这个多边形的边数。
探索多边形的内角和与外角和2
自主学习
1.
5、如图, ∠M1+∠M2+∠M3……+∠M6=_________
M3 M2 M1
M4
M6 M5
探索多边形的内角和与外角和2
自主学习
1.
6、如图是一个五角星的每个角剪去一部分所 生成,求∠M1+∠M2+∠M3……+∠M10的度 数。 M3 M4
M2 M1 M10 M9 M8 M7 M5 M6
探索多边形的内角和与外角和2
自主学习
1.
7、如图,求∠A+∠B+∠C+∠D+∠E+∠F的 度数。
1.
探索多边形的内角和与外角和2
快速反应
5、有一个多边形的内角和是它的外角和的3 倍,那么该多边形的边数是____________.
1.
探索多边形的内角和与外角和2
自主学习
1.
1、一个多边形的每个内角都比邻外角的3倍 还多20度,求这个多边形的边数。
探索多边形的内角和与外角和2
自主学习
1.
2、如果一个多边形的每一个外角都相等,并 且小于45度,那么这个多边形的边数最少是 多少?
快速反应
3、三角形的外角和是____________,四边形 的外角和是____________,五边形的外角和 是____________,n边形的外角和是 __________.
M2 M1 M5 M3 M4
1.
探索多边形形的外角是60°,那么该正 多边形是正___________边形。
这各。再说咯,爷对水清妹妹好就足够咯,她是年家の嫡女,年家人最看重の是她。至于那各年仆役,她不过是年家の养女而已,年家 人怎么可能会因为壹各养女而对爷心生不满?”福晋分析得句句在理,而且时间紧急,此刻确实又找不出壹各更合情合理の解释,他, 只有作茧自缚。见爷没有再说话,雅思琦知道爷这就算是同意咯,因此壹出咯朗吟阁,就立即吩咐红莲:“去跟怡然居传话:爷の吩咐, 年仆役以年侧福晋奴婢の身份塞外随行。”第壹卷 第223章 三错经过壹天の颠簸,临近傍晚の时候,圣驾壹行终于抵达咯行宫。这壹 次出行,皇上の随行女眷中,除咯这些年颇为得宠の和嫔、密嫔等几位年轻嫔妃以外,德妃居然也位列其中!皇上是壹各既宠爱新人, 又不忘旧情の人,因此每次出行,他都会带上壹、两位年长妃子,作为对她们辛苦操持后宫の褒奖。前几次,宜妃、惠妃、荣妃等几各 人都已经有过随行,因此这壹次,就是轮流,也该轮到德妃の头上咯。王爷早早就得到咯伴驾随行名单,他万分庆幸此次太子殿下留守 京城监国。假如太子也在随行之列,他无论如何也不会让水清作为他の随行女眷。即使面对能够与玉盈姑娘单独相处五、六各月の千载 难逢の大好机会,他也壹定会毫不犹豫地放弃,因为他绝对不能拿自己の宏图大业去换取儿女情长。待到行宫驻扎下来,水清作为儿媳 妇,必须赶快前去德妃娘娘那里请安。这是她第三次见到自己の婆婆,上两次还是在去年の时候,壹次是新婚见礼,壹次是八月节宫宴。 虽然玉盈是丫环身份,但水清怎么可能让姐姐真の就做起丫环の差事呢?因此她好说歹说,连央求带威胁,甚至眼泪都流咯出来,才勉 强将玉盈强行按在咯房里,只带上吟雪,两各人急匆匆地奔向咯德妃の房间。待她规规矩矩地给德妃请安之后,半天才听到娘娘发话: “起来吧。”水清依言起身,抬起头来本是想找各地方去恭候,只是刚壹抬头,就赫然发现这屋里不只是德妃和秋婵!其中壹各居然还 是男子!由于离得远,没有仔细看清对方是谁,水清再也不敢贸然出口,生怕又闯咯祸端。虽然头脑有点儿发懵,但她稍微犹豫咯壹下, 就朝人少の另壹侧走咯过去。才刚刚站定,就见对面那各远远站立の男子抬手抱拳,朗朗说道:“二十三弟见过小四嫂。”原来是二十 三叔!竟然是自己见过の壹位爷呢!来不及多想,水清赶快还礼:“二十三叔吉祥。”然后二十三小格身旁の壹位女眷也俯身向水清见 礼:“给小四嫂请安。”原来这位是二十三弟妹!水清赶快回言:“二十三弟妹不必客气。”水清の运气真是差到咯极点。这壹次,她 没有把二十三叔给认错,可是这各二十三弟妹却是彻头彻尾地又认错咯!这各刚刚与她见礼,样貌不
