Mathematica 根本运算
mathematica教程

(2)把有理分式拆成简单分式(部分分式)之和 命令形式:Apart[多项式]
1 x 例3 将有理分式 2 3 拆成简单分式之和. 9 21x 16 x 4 x
2
In[3]:=y=(1-x^2)/(9+21*x+16*x^2+4*x^3)
Apart[y] 5 1 Out[3]= 2 2(3 2 x) 2(3 2 x)
命令形式3: NSolve[方程,变量] 功能:求多项式方程的所有根的近似形式。 命令形式4:NSolve[{方程1,方程2,…,方程n},{变量1, 变量2,…,变量n}] 功能:求多项式方程组所有根的近似形式。 注意:所有命令中第一字母必须大写;方程中等号用 双等号(==)。 例3 求方程组x+3y=0,x2+y2=1的所有近似根。 In[10]:=NSolve[{x+3*y==0,x^2+y^2==1},{x,y}] Out[10]={{x→-0.948683 ,y→0.316228}, {x→0.948683 ,y→-0.316228}}
(3)解方程(组) 命令形式1: Solve[方程,变量] 功能:求多项式方程的所有根,当多项式方程的次 数n4时,给出所有根的准确形式;当n>4时,不一 定能求出所有的根. 例1 求方程 x2-1=0 的根. In[1]:=Solve[x^2-1==0,x] Out[1]={{x→-1},{x→1}} 命令形式2:Solve[{方程1,方程2,…,方程n},{变量 1,变量2,…,变量n}] 功能:求多项式方程的所有根. 例2 解方程组2x+y=4,x+y=3. In[2]:=Solve[{2*x+y==4,x+y==3},{x,y}] Out[2]={{x→1},{y→2}}
mathematic使用指南
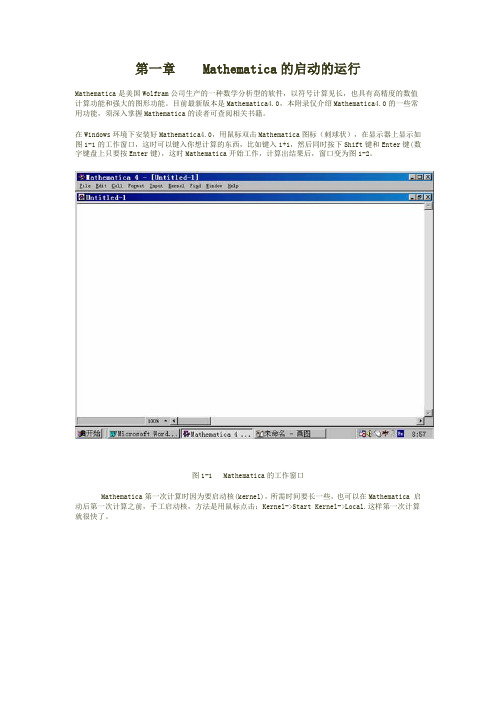
第一章Mathematica的启动的运行Mathematica是美国Wolfram公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
目前最新版本是Mathematica4.0,本附录仅介绍Mathematica4.0的一些常用功能,须深入掌握Mathematica的读者可查阅相关书籍。
在Windows环境下安装好Mathematica4.0,用鼠标双击Mathematica图标(刺球状),在显示器上显示如图1-1的工作窗口,这时可以键入你想计算的东西,比如键入1+1,然后同时按下Shift键和Enter键(数字键盘上只要按Enter键),这时Mathematica开始工作,计算出结果后,窗口变为图1-2。
图1-1 Mathematica的工作窗口Mathematica第一次计算时因为要启动核(kernel),所需时间要长一些,也可以在Mathematica 启动后第一次计算之前,手工启动核,方法是用鼠标点击:Kernel->Start Kernel->Local.这样第一次计算就很快了。
图1-2 完成运算后的Mathematica的窗口图1-2中的“In[1]:=”表示第一个输入;“Out[1]=”表示第一个输出结果。
接下来可键入第二个输入,按这样的方式可利用Mathematica进行“会话式”计算。
要注意的是:“In[1]:= ”和“Out[1]=”是系统自动添加的,不需用户键入。
Mathematica还提供“批处理”运行方式,即可以将Mathematica作为一种算法语言,编写程序,让计算机执行,这在第七章将会作简要介绍。
第二章 Mathematica的基本运算功能2.1 算术运算Mathematica最基本的功能是进行算术运算,包括加(+),减(-),乘(*),除(/),乘方(^),阶乘(!)等。
注意:1 在Mathematica中,也可用空格代表乘号;数字和字母相乘,乘号可以省去,例如:3*2可写成3 2,2*x可写成2x,但字母和字母相乘,乘号不能省去。
mathematica命令大全

mathematica命令大全mathematica命令大全Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x] 以e为底数对数函数Log[x] 自然对数,即以e为底数的对数Log[a,x] 以a为底数的x的对数开方函数Sqrt[x] 表示x的算术平方根绝对值函数Abs[x] 表示x的绝对值三角函数(自变量的单位为弧度)Sin[x] 正弦函数Cos[x] 余弦函数Tan[x] 正切函数Cot[x] 余切函数Sec[x] 正割函数Csc[x] 余割函数反三角函数ArcSin[x] 反正弦函数ArcCos[x] 反余弦函数ArcT an[x] 反正切函数ArcCot[x] 反余切函数ArcSec[x] 反正割函数ArcCsc[x] 反余割函数双曲函数Sinh[x] 双曲正弦函数Cosh[x] 双曲余弦函数Tanh[x] 双曲正切函数Coth[x] 双曲余切函数Sech[x] 双曲正割函数Csch[x] 双曲余割函数反双曲函数ArcSinh[x] 反双曲正弦函数ArcCosh[x] 反双曲余弦函数ArcTanh[x] 反双曲正切函数ArcCoth[x] 反双曲余切函数ArcSech[x] 反双曲正割函数ArcCsch[x] 反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...] 最大公约数函数LCM[a,b,c,...] 最小公倍数函数Mod[m,n] 求余函数(表示m 除以n的余数)Quotient[m,n] 求商函数(表示m除以n的商)Divisors[n] 求所有可以整除n的整数FactorInteger[n] 因数分解,即把整数分解成质数的乘积Prime[n] 求第n个质数PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为FalseRandom[Integer,{m,n}] 随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z] 实部函数Im[z] 虚部函数Arg(z) 辐角函数Abs[z] 求复数的模Conjugate[z] 求复数的共轭复数Exp[z] 复数指数函数求整函数与截尾函数Ceiling[x] 表示大于或等于实数x的最小整数Floor[x] 表示小于或等于实数x的最大整数Round[x] 表示最接近x的整数IntegerPart[x] 表示实数x的整数部分FractionalPart[x] 表示实数x的小数部分分数与浮点数运算函数N[num]或num//N 把精确数num化成浮点数(默认16位有效数字)N[num,n] 把精确数num化成具有n个有效数字的浮点数NumberForm[num,n] 以n个有效数字表示num Rationalize[float] 将浮点数float转换成与其相等的分数Rationalize[float,dx] 将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...] 求最大数Min[a,b,c,...] 求最小数符号函数Sign[x]Mathematica中的数学运算符a+b加法a-b 减法a*b (可用空格键代替*) 乘法a/b (输入方法为:“ Ctrl ” + “ / ” )除法a^b (输入方法为:“ Ctrl ” + “ ^” )乘方-a 负号Mathematica的关系运算符==等于< 小于> 大于<= 小于或等于>= 大于或等于!= 不等于注:上面的关系运算符也可从基本输入工具栏输入。
mathmatic 基本用法

mathmatic 基本用法Mathematica是一种强大的数学软件,它具有广泛的数学计算和可视化功能。
基本用法包括使用Mathematica进行数学运算、求解方程、绘制图表等。
1.数学运算:Mathematica可以进行基本的数学运算,如加减乘除、幂运算、三角函数、对数函数等。
例如,可以输入"2+3"得到结果"5",输入"Sin[π/2]"得到结果"1"。
2.方程求解:Mathematica可以求解各种类型的方程。
例如,可以输入"Solve[x^2 - 3x + 2 == 0, x]"来求解这个二次方程,得到结果"x == 1 || x == 2"。
3.符号计算:Mathematica可以进行符号计算,包括展开、化简、因式分解等。
例如,可以输入"Simplify[(x^2 + x - 6)/(x + 3)]"来化简这个表达式,得到结果"x - 2"。
4.绘图功能:Mathematica可以生成各种类型的图表,包括二维曲线图、三维曲面图、柱状图、散点图等。
例如,可以输入"Plot[Sin[x], {x, 0, 2π}]"来绘制正弦函数的曲线图。
除了基本用法外,Mathematica还有许多其他功能,如矩阵计算、微积分、概率统计、符号推导、动态演示等。
它还提供了大量的内置函数和算法,可以用于求解复杂的数学问题。
使用Mathematica还可以进行科学计算、工程计算、数据分析等各种应用领域。
总之,Mathematica是一款功能强大的数学软件,可以帮助用户进行各种数学计算和可视化操作。
Mathematica使用教程
Mathematica使⽤教程第⼆章 Mathematica 简介Mathematica 是⼀个符号计算与数值计算的通⽤数学软件包,是由美国的物理学家Stephen Wolfram 所领导的⼀个⼩组开发成功并推向市场的。
Mathematica 由最初的1.0、1.2、2.0、2.2、2.4、3.0版,到现在的4.0版,⽬前国内常⽤的版本是Windows 下的3.0及4.0版。
与Mathcad 和MATLAB 相⽐,Mathematica 才称得上是⼀个真正的数学符号计算软件包,因为只有它的内核是以符号计算为基础的,⽐如你可以定义⼀些数学规则,让它为你进⾏符号推导演算⼯作。
在Mathematica 中,你可以像Mathcad 那样进⾏草稿式的数学计算,你也可以像MATLAB ⼀样进⾏命令式的数学计算。
本章以4.0版为基础,介绍Mathematica 的使⽤⽅法。
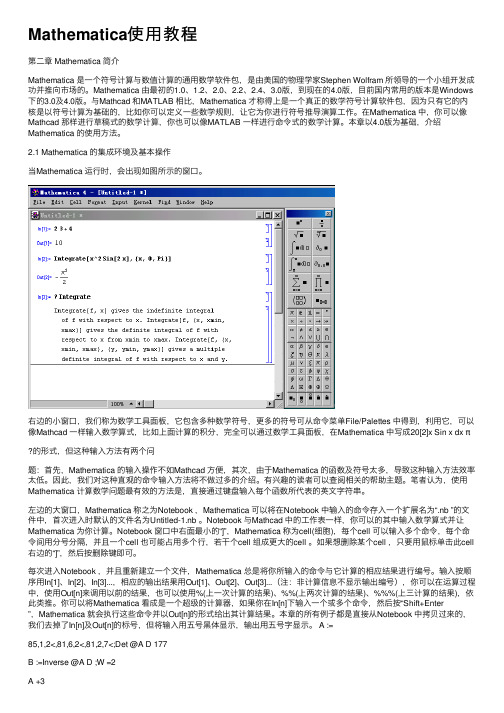
2.1 Mathematica 的集成环境及基本操作当Mathematica 运⾏时,会出现如图所⽰的窗⼝。
右边的⼩窗⼝,我们称为数学⼯具⾯板,它包含多种数学符号,更多的符号可从命令菜单File/Palettes 中得到,利⽤它,可以像Mathcad ⼀样输⼊数学算式,⽐如上⾯计算的积分,完全可以通过数学⼯具⾯板,在Mathematica 中写成20[2]x Sin x dx π的形式,但这种输⼊⽅法有两个问题:⾸先,Mathematica 的输⼊操作不如Mathcad ⽅便,其次,由于Mathematica 的函数及符号太多,导致这种输⼊⽅法效率太低。
因此,我们对这种直观的命令输⼊⽅法将不做过多的介绍。
有兴趣的读者可以查阅相关的帮助主题。
笔者认为,使⽤Mathematica 计算数学问题最有效的⽅法是,直接通过键盘输⼊每个函数所代表的英⽂字符串。
左边的⼤窗⼝,Mathematica 称之为Notebook ,Mathematica 可以将在Notebook 中输⼊的命令存⼊⼀个扩展名为“.nb ”的⽂件中,⾸次进⼊时默认的⽂件名为Untitled-1.nb 。
Mathematica 基本运算

Mathematica 基本运算a+mathematica数学实验(第2版)b+c 加a-b 减a b c 或a*b*c 乘a/b 除-a 负号a^b 次方Mathematica 数字的形式256 整数2.56 实数11/35 分数2+6I 复数常用的数学常数Pi 圆周率,π=3.141592654…E 尤拉常数,e=2.71828182…Degree 角度转换弧度的常数,Pi/180I 虚数,其值为√-1Infinity 无限大指定之前计算结果的方法% 前一个运算结果%% 前二个运算结果%%…%(n个%) 前n个运算结果%n 或Out[n] 前n个运算结果复数的运算指令a+bI 复数Conjugate[a+bI] 共轭复数Re[z], Im[z] 复数z的实数/虚数部分Abs[z] 复数z的大小或模数(Modulus)Arg[z] 复数z的幅角(Argument)Mathematica 输出的控制指令expr1; expr2; expr3 做数个运算,但只印出最后一个运算的结果expr1; expr2; expr3; 做数个运算,但都不印出结果expr; 做运算,但不印出结果常用数学函数Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数,其引数的单位为弧度Sinh[x],Cosh[x],Tanh[x],… 双曲函数ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数ArcCot[x],ArcSec[x],ArcCsc[x]ArcS inh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数Sqrt[x] 根号Exp[x] 指数Log[x] 自然对数Log[a,x] 以a为底的对数Abs[x] 绝对值Round[x] 最接近x的整数Floor[x] 小于或等于x的最大整数Ceiling[x] 大于或等于x的最小整数Mod[a,b] a/b所得的馀数n! 阶乘Random[] 0至1之间的随机数(最新版本已经不用这个函数,改为使用RandomReal[])Max[a,b,c,...],Min[a,b,c,…] a,b,c,…的极大/极小值数值设定x=a 将变数x的值设为ax=y=b 将变数x和y的值均设为bx=. 或Clear[x] 除去变数x所存的值变数使用的一些法则xy 中间没有空格,视为变数xyx y x乘上y3x 3乘上xx3 变数x3x^2y 为x^2 y次方运算子比乘法的运算子有较高的处理顺序四个处理代数指令Expand[expr] 将expr展开Factor[expr] 将expr因式分解Simplify[expr] 将expr化简成精简的式子FullSimplify[expr] Mathematica 会尝试更多的化简公式,将expr化成更精简的式子多项式/分式转换函数ExpandAll[expr] 把算式全部展开Together[expr] 将expr各项通分在并成一项Apart[expr] 把分式拆开成数项分式的和Apart[expr,var] 视var以外的变数为常数,将expr拆成数项的和Cancel[expr] 把分子和分母共同的因子消去分母/分子的运算Denominator[expr] 取出expr的分母Numerator[expr] 取出expr的分子ExpandDenominator[expr] 展开expr的分母ExpandNumerator[expr] 展开expr的分子多项式二种转换函数Collect[expr,x] 将expr表示成x的多项式,如Collect[expr,{x,y,…}] 将expr分别表示成x,y,…的多项式FactorTerms[expr] 将expr的数值因子提出,如4x+2=2(2x+1)FactorTerms[expr,x] 将expr中把所有不包含x项的因子提出FactorTerms[expr,{x,y,…}] 将expr中把所有不包含{x,y,...}项的因子提出函数和指数运算TrigExpand[expr] 将三角函数展开TrigFactor[expr] 将三角函数所组成的数学式因式分解TrigReduce[expr] 将相乘或次方的三角函数化成一次方的基本三角函数之组合ExpToTrig[expr] 将指数函数化成三角函数或双曲函数TrigToExp[expr] 将三角函数或双曲函数化成指数函数复数、次方乘积之展开ComplexExpand[expr] 假设所有的变数都是实数来对expr展开ComplexExpand[expr,{x,y,…}] 假设x,y,..等变数均为复数来对expr展开PowerExpand[expr] 将项次、系数与最高次方Coefficient[expr,form] 于expr中form的系数Exponent[expr,form] 于expr中form的最高次方Part[expr,n] 或expr[[n]] 在expr项中第n个项代换运算子expr/.x->value 将expr里所有的x均代换成valueexpr/.{x->value1,y->value2,…} 执行数个不同变数的代换expr/.{{x->value1},{x->value2},…} 将expr代入不同的x值expr//.{x->value1,y->value2,…} 重复代换到expr不再改变为止求解方程式的根Solve[lhs==rhs,x] 解方程式lhs==rhs,求xNsolve[lhs==rhs,x] 解方程式lhs==rhs的数值解Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式,求x,y,…NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式的数值解FindRoot[lhs==rhs,{x,x0}] 由初始点x0求lhs==rhs的根四种括号(term) 圆括号,括号内的term先计算f[x] 方括号,内放函数的引数{x,y,z} 大括号或串列括号,内放串列的元素p[[i ]] 或Part[p,i] 双方括号,p的第i项元素p[[i,j]] 或Part[p,i,j] p的第i项第j个元素缩短输出指令expr//Short 显示一行的计算结果Short[expr,n] 显示n行的计算结果Command; 执行command,但不列出结果查询物件?Command 查询Command的语法及说明??Command 查询Command的语法和属性及选择项?Aaaa* 查询所有开头为Aaaa的物件函数定义、查询与清除f[x_]= expr 立即定义函数f[x]f[x_]:= expr 延迟定义函数f[x]f[x_,y_,…] 函数f有两个以上的引数?f 查询函数f的定义Clear[f] 或f=. 清除f的定义Remove[f] 将f自系统中清除掉含有预设值的Patterna_+b_. b的预设值为0,即若b从缺,则b以0代替x_ y_ y的预设值为1x_^y_ y的预设值为1条件式的自订函数lhs:=rhs/;condition 当condition成立时,lhs才会定义成rhsIf指令If[test,then,else] 若test为真,则回应then,否则回应elseIf[test,then,else,unknow] 同上,若test无法判定真或假时,则回应unknow 极限Limit[expr,x->c] 当x趋近c时,求expr的极限Limit[expr,x->c,Direction->1]Limit[expr,x->c,Direction->-1]微分D[f,x] 函数f对x作微分D[f,x1,x2,…] 函数f对x1,x2,…作微分D[f,{x,n}] 函数f对x微分n次D[f,x,NonConstants->{y,z,…}] 函数f对x作微分,将y,z,…视为x的函数全微分Dt[f] 全微分dfDt[f,x] 全微分Dt[f,x1,x2,…] 全微分Dt[f,x,Constants->{c1,c2,…}] 全微分,视c1,c2,…为常数不定积分Integrate[f,x] 不定积分∫f dx定积分Integrate[f,{x,xmin,xmax}] 定积分Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] 定积分数列之和与积Sum[f,{i,imin,imax}] 求和Sum[f,{i,imin,imax,di}] 求数列和,引数i以di递增Sum[f,{i,imin,imax},{j,jmin,jmax}]Product[f,{i,imin,imax}] 求积Product[f,{i,imin,imax,di}] 求数列之积,引数i以di递增Product[f,{i,imin,imax},{j,jmin,jmax}]函数之泰勒展开式Series[expr,{x,x0,n}] 对expr于x0点作泰勒级数展开至(x-x0)n项Series[expr,{x,x0,m},{y,y0,n}] 对x0和y0展开关系运算子a==b 等于a>b 大于a>=b 大于等于a<b 小于a<=b 小于等于a!=b 不等于逻辑运算子!p notp||q||… orp&&q&&… andXor[p,q,…] exclusive orLogicalExpand[expr] 将逻辑表示式展开基本二维绘图指令Plot[f,{x,xmin,xmax}]画出f在xmin到xmax之间的图形Plot[{f1,f2,…},{x,xmin,xmax}]同时画出数个函数图形Plot[f,{x,xmin,xmax},option->value]指定特殊的绘图选项,画出函数f的图形Plot几种指令选项预设值说明AspectRatio 1/GoldenRatio 图形高和宽之比例,高/宽Axes True 是否把坐标轴画出AxesLabel Automatic 为坐标轴贴上标记,若设定为AxesLabel->{?ylabel?},则为y轴之标记。
数学软件Mathematica详解教程
生成 n 元列表 {expr,expr,...,expr}
{expr|i 在列表 list 中变化}
Table[expr,{i,a,b,h}] {expr|i 在 Range[a,b,h]中变化}
Table 中的 expr 一般给的是通项公式
RandomInteger[range,n] 生成 n 个伪随机整数,range 表示取值范围
ToExpression[str]
ToString[expr]
转化为表达式
将表达式转化为字符串
更多字符串相关函数参见 “参考资料中心”
26
列表
列表
是 Mathematica 的基本对象,可用来表示集合,数组等 分为标准列表和稀疏列表
标准列表: 用大括号括起来的有限个元素,元素之间用逗号分隔
求最大值
求最小值
19
常用初等函数
Re[x], Im[x]
Conjugate[x] Arg[x]
提取实部和虚部
取共轭 辐角
Mod[m,n]
Quotient[m,n] Sin[x], Cos[x], ... ArcSin[x], ArcCos[x], ... Sinh, Cosh, ...,
m 除以 n 的余数
In[1]:= Clear[x,y]; In[2]:= f=2*x+y; In[3]:= f./{x->2,y->3} (* f(2,3) 的值 *)
In[3]:= f./{2->5}
(*把 2 替换成 5*)
15
数的基本运算
Mathematica 中的实数分精确数和双精度数
N[x,n] N[x] IntegerPart[x] FractionalPart[x] Floor[x] Round[x] Ceil[x] Precision[expr] x 的带 n 位有效数字的近似值 x 的双精度近似值 整数部分 小数部分 取整:不大于 x 的最大整数 取整:四舍五入 取整:不小于 x 的最小整数 显示计算精度
9_基于Mathematica的数值计算
9_基于Mathematica的数值计算Mathematica是一种强大的数学软件,可以进行各种数值计算。
它提供了丰富的内置函数和算法,可以帮助用户解决各种数学问题。
本文将介绍Mathematica的一些常用数值计算功能,并结合实例说明其用法。
首先,Mathematica可以进行基本的数值计算,例如加减乘除等。
用户可以直接输入表达式,然后使用Mathematica进行计算。
例如,要计算1加2,可以输入表达式"1+2",然后按下回车键,Mathematica将返回结果3、Mathematica还支持复杂的数学函数,例如三角函数、指数函数、对数函数等。
用户可以使用这些函数进行各种复杂的数值计算。
除了基本的数学计算,Mathematica还提供了一些高级的数值计算功能。
例如,它可以进行数值积分和数值微分。
用户可以使用内置的积分函数和微分函数,将待积分或待微分的函数作为参数传递给这些函数。
Mathematica将根据给定的函数和积分或微分的区间,计算出准确的结果。
例如,要计算函数f(x)=x^2在区间[0,1]上的积分,可以使用内置函数NIntegrate[f[x],{x,0,1}],Mathematica将返回准确的积分结果。
此外,Mathematica还可以进行数值求解方程的计算。
用户可以使用内置的求解函数,将方程和待求解的变量作为参数传递给这些函数。
Mathematica将根据给定的方程和初始猜测,计算出方程的解。
例如,要求解方程x^2-2x+1=0,可以使用内置函数NSolve[x^2-2x+1==0,x],Mathematica将返回方程的解{x->1}。
除了上述功能,Mathematica还可以进行矩阵计算、数值优化、概率统计等。
用户可以使用内置的函数和算法,进行各种高级的数值计算。
例如,用户可以使用内置函数MatrixForm,对矩阵进行漂亮的格式化输出。
用户还可以使用内置函数FindMinimum,对函数进行最小化。
mathematica的使用
微积分基本运算(1)
四、数学常数:
Pi E e=2.71828… Infinity I False True
即π 欧拉常数, 无穷大∞ 虚数单位 假 真
微积分基本运算(1)
五、关系、逻辑运算:
表达式 a==b > 意义 等于 大于 表达式 !p或Not[p] p||q或Or[p,q] 意义 非运算 或运算
表达式的Mathematica内部表示 Font:
设置当前选定内容的字体
Format菜单:执行与各种格式设定相关的操作
Face: 设置当前选定内容字体是否粗体(斜体) Size: 设置当前选定内容的字体大小 TextColor: 设置当前选定内容的文本颜色 Background Color: 设置当前选定内容的背景颜色等。 Show Ruler: 是否显示标尺栏? Show ToolBar: 是否显示工具栏? Magnification: 设定当前屏幕显示的比例, 通常设置为150%较好。
微积分基本运算(1)
算术运算及N,%运算 常见数学函数,数学常量 关系、逻辑运算 求极限,求导,微分,积分: Limit,D,Dt, Integrate, 解方程,方程组 Solve 解微分方程: NSolve,DSolve
微积分基本运算(1)
一、基本算术运算及N,%运算:
(235*456+78)-54 34^45 Pi^23 N[%] 读取上一次的运算结果 N[%15] 取第15次运算结果的数值
Kernel菜单:与Mathematica软件内核运行相关的操作
Interrupt Evaluation与Abort Evaluation: 中断当前命令的运行,当程序陷入死循环 时,或程序运行很久没有反应时,通常采用此 命令,快捷键 Alt+. Show In/Out Names: 是否显示In[2]:=, Out[2]:=等 Delete All Output: 删除当前所有输出
Mathematica表达式及其运算规则
Plus Times , 2, 上面的{1,2,3,4}称为表(List),表是 , 4 FullForm 1a, b 3,c List 1, x Head Sin2, 3, 4 Sin
Mathematica中非常有用的结构。首先, 表可以理解成数学意义下的集合,例如 对集合{1,{2,3},4,{5,6,7},8,9},它是含有6 个元素的子集合,其中{2,3}及{5,6,7}此集 合的子集合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mathematica 基本运算 a+mathematica数学实验(第2版)b+c 加 a-b 减 a b c 或a*b*c 乘 a/b 除 -a 负号 a^b 次方 Mathematica 数字的形式 256 整数 2.56 实数 11/35 分数 2+6I 复数 常用的数学常数 Pi 圆周率,π=3.141592654… E 尤拉常数,e=2.71828182… Degree 角度转换弧度的常数,Pi/180 I 虚数,其值为√-1 Infinity 无限大 指定之前计算结果的方法 % 前一个运算结果 %% 前二个运算结果 %%…%(n个%) 前n个运算结果 %n 或Out[n] 前n个运算结果 复数的运算指令 a+bI 复数 Conjugate[a+bI] 共轭复数 Re[z], Im[z] 复数z的实数/虚数部分 Abs[z] 复数z的大小或模数(Modulus) Arg[z] 复数z的幅角(Argument) Mathematica 输出的控制指令 expr1; expr2; expr3 做数个运算,但只印出最后一个运算的结果 expr1; expr2; expr3; 做数个运算,但都不印出结果 expr; 做运算,但不印出结果常用数学函数 Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数,其引数的单位为弧度 Sinh[x],Cosh[x],Tanh[x],… 双曲函数 ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数 ArcCot[x],ArcSec[x],ArcCsc[x] ArcSinh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数 Sqrt[x] 根号 Exp[x] 指数 Log[x] 自然对数 Log[a,x] 以a为底的对数 Abs[x] 绝对值 Round[x] 最接近x的整数 Floor[x] 小于或等于x的最大整数 Ceiling[x] 大于或等于x的最小整数 Mod[a,b] a/b所得的馀数 n! 阶乘 Random[] 0至1之间的随机数(最新版本已经不用这个函数,改为使用RandomReal[]) Max[a,b,c,...],Min[a,b,c,…] a,b,c,…的极大/极小值数值设定 x=a 将变数x的值设为a x=y=b 将变数x和y的值均设为b x=. 或Clear[x] 除去变数x所存的值 变数使用的一些法则 xy 中间没有空格,视为变数xy x y x乘上y 3x 3乘上x x3 变数x3 x^2y 为x^2 y次方运算子比乘法的运算子有较高的处理顺序四个处理代数指令 Expand[expr] 将expr展开 Factor[expr] 将expr因式分解 Simplify[expr] 将expr化简成精简的式子 FullSimplify[expr] Mathematica 会尝试更多的化简公式,将expr化成更精简的式子多项式/分式转换函数 ExpandAll[expr] 把算式全部展开 Together[expr] 将expr各项通分在并成一项 Apart[expr] 把分式拆开成数项分式的和 Apart[expr,var] 视var以外的变数为常数,将expr拆成数项的和 Cancel[expr] 把分子和分母共同的因子消去分母/分子的运算 Denominator[expr] 取出expr的分母 Numerator[expr] 取出expr的分子 ExpandDenominator[expr] 展开expr的分母 ExpandNumerator[expr] 展开expr的分子多项式二种转换函数 Collect[expr,x] 将expr表示成x的多项式, 如 Collect[expr,{x,y,…}] 将expr分别表示成x,y,…的多项式 FactorTerms[expr] 将expr的数值因子提出, 如4x+2=2(2x+1) FactorTerms[expr,x] 将expr中把所有不包含x项的因子提出 FactorTerms[expr,{x,y,…}] 将expr中把所有不包含{x,y,...}项的因子提出函数和指数运算 TrigExpand[expr] 将三角函数展开 TrigFactor[expr] 将三角函数所组成的数学式因式分解 TrigReduce[expr] 将相乘或次方的三角函数化成一次方的基本三角函数之组合 ExpToTrig[expr] 将指数函数化成三角函数或双曲函数 TrigToExp[expr] 将三角函数或双曲函数化成指数函数复数、次方乘积之展开 ComplexExpand[expr] 假设所有的变数都是实数来对expr展开 ComplexExpand[expr,{x,y,…}] 假设x,y,..等变数均为复数来对expr展开 PowerExpand[expr] 将项次、系数与最高次方 Coefficient[expr,form] 于expr中form的系数 Exponent[expr,form] 于expr中form的最高次方 Part[expr,n] 或expr[[n]] 在expr项中第n个项代换运算子 expr/.x->value 将expr里所有的x均代换成value expr/.{x->value1,y->value2,…} 执行数个不同变数的代换 expr/.{{x->value1},{x->value2},…} 将expr代入不同的x值 expr//.{x->value1,y->value2,…} 重复代换到expr不再改变为止 求解方程式的根 Solve[lhs==rhs,x] 解方程式lhs==rhs,求x Nsolve[lhs==rhs,x] 解方程式lhs==rhs的数值解 Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式,求x,y,… NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式的数值解 FindRoot[lhs==rhs,{x,x0}] 由初始点x0求lhs==rhs的根四种括号 (term) 圆括号,括号内的term先计算 f[x] 方括号,内放函数的引数 {x,y,z} 大括号或串列括号,内放串列的元素 p[[i ]] 或Part[p,i] 双方括号,p的第i项元素 p[[i,j]] 或Part[p,i,j] p的第i项第j个元素缩短输出指令 expr//Short 显示一行的计算结果 Short[expr,n] 显示n行的计算结果 Command; 执行command,但不列出结果查询物件 ?Command 查询Command的语法及说明 ??Command 查询Command的语法和属性及选择项 ?Aaaa* 查询所有开头为Aaaa的物件函数定义、查询与清除 f[x_]= expr 立即定义函数f[x] f[x_]:= expr 延迟定义函数f[x] f[x_,y_,…] 函数f有两个以上的引数 ?f 查询函数f的定义 Clear[f] 或f=. 清除f的定义 Remove[f] 将f自系统中清除掉 含有预设值的Pattern a_+b_. b的预设值为0,即若b从缺,则b以0代替 x_ y_ y的预设值为1 x_^y_ y的预设值为1 条件式的自订函数 lhs:=rhs/;condition 当condition成立时,lhs才会定义成rhsIf指令 If[test,then,else] 若test为真,则回应then,否则回应else If[test,then,else,unknow] 同上,若test无法判定真或假时,则回应unknow 极限 Limit[expr,x->c] 当x趋近c时,求expr的极限 Limit[expr,x->c,Direction->1] Limit[expr,x->c,Direction->-1]微分 D[f,x] 函数f对x作微分 D[f,x1,x2,…] 函数f对x1,x2,…作微分 D[f,{x,n}] 函数f对x微分n次 D[f,x,NonConstants->{y,z,…}] 函数f对x作微分,将y,z,…视为x的函数全微分 Dt[f] 全微分df Dt[f,x] 全微分 Dt[f,x1,x2,…] 全微分 Dt[f,x,Constants->{c1,c2,…}] 全微分,视c1,c2,…为常数不定积分 Integrate[f,x] 不定积分∫f dx定积分 Integrate[f,{x,xmin,xmax}] 定积分 Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] 定积分 数列之和与积 Sum[f,{i,imin,imax}] 求和 Sum[f,{i,imin,imax,di}] 求数列和,引数i以di递增 Sum[f,{i,imin,imax},{j,jmin,jmax}] Product[f,{i,imin,imax}] 求积 Product[f,{i,imin,imax,di}] 求数列之积,引数i以di递增 Product[f,{i,imin,imax},{j,jmin,jmax}]函数之泰勒展开式 Series[expr,{x,x0,n}] 对expr于x0点作泰勒级数展开至(x-x0)n项 Series[expr,{x,x0,m},{y,y0,n}] 对x0和y0展开 关系运算子 a==b 等于 a>b 大于 a>=b 大于等于 a<b 小于 a<=b 小于等于 a!=b 不等于逻辑运算子 !p not p||q||… or p&&q&&… and Xor[p,q,…] exclusive or LogicalExpand[expr] 将逻辑表示式展开基本二维绘图指令 Plot[f,{x,xmin,xmax}] 画出f在xmin到xmax之间的图形 Plot[{f1,f2,…},{x,xmin,xmax}] 同时画出数个函数图形 Plot[f,{x,xmin,xmax},option->value] 指定特殊的绘图选项,画出函数f的图形Plot几种指令 选项预设值说明 AspectRatio 1/GoldenRatio 图形高和宽之比例,高/宽 Axes True 是否把坐标轴画出 AxesLabel Automatic 为坐标轴贴上标记,若设定为 AxesLabel->{?ylabel?},则为y轴之标记。
