描述两相湍流的二阶动量模型
第2章 气液两相流的模型

多相管流理论与计算
讨论
对于水平管流
dp 0, 0 dZ 重位
x表示流向坐标
2
dp dv v v dx dx d 2
对于垂直管流
90
sin 1
以h表示高度
dp dv v2 g v dh dh d 2
多相管流理论与计算
而对于不可逆过程来讲:
以 dlw 表示摩擦消耗的功,则:
dqr dlw
dqr —摩擦产生的热量
dU dq pdV dlw
代入 dU 并整理得
dlw—摩擦消耗的功
dU mvdv mgsin dZ d ( pV ) dq 0
Vdp mvdv mgsin dZ dlw 0
连续性方程
质量守恒
动量方程 能量方程
动量守恒 能量守恒
多相管流理论与计算
一、均流模型的基本方程式
1.连续方程式
根据质量守恒定律
G vA 常数
2.动量方程式
取一维流段来研究,根据动量
定理,可得动量方程式:
稳定的一维均相流动
Adp dF gAdzsin Gdv
2-2
多相管流理论与计算
分气相流动
dFsg dpsg A f sg
f f sg
l v
2
2 sg
Ddz
v 2
2
dF dp 2 g dFsg dpsg
Ddz Ddz
2 g vsg
fv 2 2 f sg g vsg
2
2 dp g dpsg
分气相折算 系数
多相管流理论与计算
由于 f 0 、 f sl 和 f sg ,都是单相流动的范宁系数,很 容易求得。所以引入折算系数的实质是将求解两相流动 的范宁系数
4 湍流气固两相流动模型

k
(nkd
3 k
/
6)
p
(58)
式中 m— 混合物密度;
— 流体(气体)的表观密度;
p , k — 颗粒的表观密度; p — 颗粒材料密度。
颗粒相及气相的体积分数定义为:
p p / p
1 p
(59)
对于稀疏气固两相流动有
3 单颗粒动力学模型 气固两相流的最简化的模型
模型假设: 忽略颗粒存在对流体流动的影响 已知流体中互不相关的无脉动的单颗粒的运动,包括颗粒平 均运动或对流运动的轨道,以及颗粒速度及温度沿轨道的变 化
mp
dv pi dt p
Fdi
Fvmi Fpi
FBi
FM i
Fsi
m k nkvi nkvim k
vki nk m k
nk vkim k
m nk vki
nk vkim k
/ mk
t
(nk vki )
(79)
流体能量分方程
t
(
h)
xj
(
v jh)
xj
(
k ckTk
)
xj
(
v jcpT
k
k vkjckTk )
(73)
xj
(
T xj
)
wsQs
qr
nkQh
nkQrk
流体(气)相组分方程
t
( Ys )
xj
(
v jYs )
xj
(D
两相流动的基本方程

= =
G (1 − x ) Gx x( ) + (1 − x ) ρ gα ρ l (1 − α )
2 3 3 x x (1 − ) 2 G 2 2 + 2 2 α ρ g (1 − α ) ρ l
2 d ρ iϕ i dV = ∑ ∫ nk ⋅ [(u k − u i ) ρ k ϕ k + Tk ]da − ∫ dt Vi k =1 a k
ζ i −δ 2
∫∫
δ1
N ⋅ [(u − u i ) ρ iϕ i + T ]d δ d ζ + ∫ ρ iφi dV
Vi
2.1二流体模型 式中 ϕ 与 φ 为流场特性参数和流场体积源。界面特性
均相模型属于经验模型范畴。
1.2分相模型
分相模型是把两相分成两种单相流动(气相 和液相)。介质参数分别取各自的介质参 数,分相模型也是一种经验模型。 1.连续方程 液相入流面: M l 液相出流面: dM
Ml +
l
dz
dz
气相转化为液相的量:
dW l C i
1.2分相模型
则液相连续方程为: dMl Ml − (Ml + dz)+dWC l i =0 dz
则:
dp τ 0C0 x (1− x) 2 d − = + g ρcm cosθ + G ( + ) dz A dz ρl (1 − α ) ρgα
2 2
X-质量气流率
1.2分相模型
摩擦压降: 加速压降: 重力压降:
dpF τ 0C0 τ 0 2π R 2τ 0 − = = = 2 dz A πR R
湍流模型介绍

湍流模型介绍因为湍流现象是高度复杂的,所以至今还没有一种方法能够全面、准确地对所有流动问题中的湍流现象进行模拟。
在涉及湍流的计算中,都要对湍流模型的模拟能力以及计算所需系统资源进行综合考虑后,再选择合适的湍流模型进行模拟。
FLUENT 中采用的湍流模拟方法包括Spalart-Allmaras模型、standard(标准)k −ε模型、RNG(重整化群)k −ε模型、Realizable(现实)k −ε模型、v2 −f 模型、RSM(Reynolds Stress Model,雷诺应力模型)模型和LES(Large Eddy Simulation,大涡模拟)方法。
7.2.1 雷诺平均与大涡模拟的对比因为直接求解NS 方程非常困难,所以通常用两种办法对湍流进行模拟,即对NS 方程进行雷诺平均和滤波处理。
这两种方法都会增加新的未知量,因此需要相应增加控制方程的数量,以便保证未知数的数量与方程数量相同,达到封闭方程组的目的。
雷诺平均NS 方程是流场平均变量的控制方程,其相关的模拟理论被称为湍流模式理论。
湍流模式理论假定湍流中的流场变量由一个时均量和一个脉动量组成,以此观点处理NS 方程可以得出雷诺平均NS 方程(简称RNS 方程)。
在引入Boussinesq 假设,即认为湍流雷诺应力与应变成正比之后,湍流计算就归结为对雷诺应力与应变之间的比例系数(即湍流粘性系数)的计算。
根据计算中使用的变量数目和方程数目的不同,湍流模式理论中所包含的湍流模型又被分为二方程模型、一方程模型和零方程模型(代数模型)等大类。
FLUENT 中使用的三种k −ε模型、Spalart-Allmaras 模型、k −ω模型及雷诺应力模型RSM)等都属于湍流模式理论。
大涡模拟(LES)方法是通过滤波处理计算湍流的,其主要思想是大涡结构(又称拟序结构)受流场影响较大,小涡则可以认为是各向同性的,因而可以将大涡计算与小涡计算分开处理,并用统一的模型计算小涡。
湍流气固两相流动模型41页PPT

11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
13、遵守纪律的风气的培养,只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致,是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机会是不守纪律的。——雨果
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
第三章-湍流模型
第三章,湍流模型第一节, 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
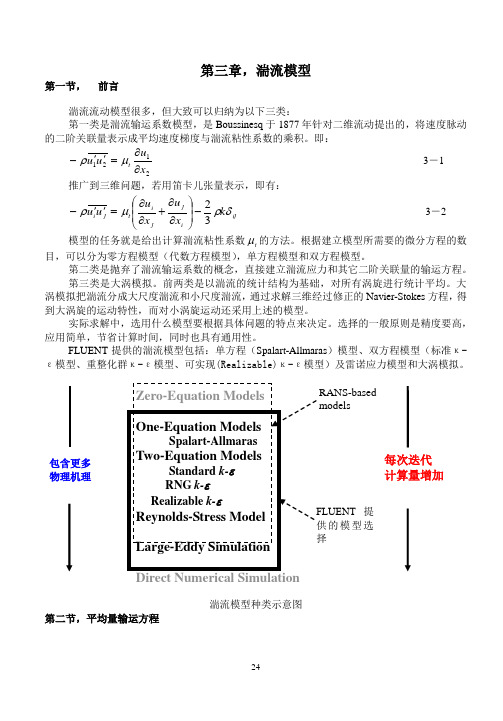
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图第二节,平均量输运方程包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。
化工装置中两相流模型的建立
化工装置中的两相流模型的建立摘要:通过文献调研,本文重点分析了大涡模型在离心泵两相流中的应用。
较为详细的概述了模型的建立以及边界条件的确定和求解方法。
关键词:文献调研、大涡模型、边界条件前言两相流动是流体力学中一门重要的分支学科,它在很多现代工程技术甚至医学中得到广泛的应用。
可以认为,绝大多数的流动都是多相流动,纯粹的单相流动只是个别情况。
降雾,下雨、下冰雹、云层流动、流沙、尘暴等是自然界中两相流动的一些例子。
各种发动机和窖炉中的喷雾燃烧、核反应堆的冷却、宇航飞行器的两相绕流、含铝推进剂固体火箭发动机中的燃气流动、石油和天然气的开采和输运、热力设备与制冷系统的工作过程、化学工艺中的流态化、吸收、蒸发、凝结和化学反应过程、采矿和冶金过程中的旋流分离和输运、气力和液力输送、煤的气化和液化、煤粉和煤浆燃烧、空气和水的污染、环保、粉尘爆炸、血液的循环与凝固、水利工程中的泥沙运动和高速渗气流等工程实际问题无不与两相流动有关。
离心泵是化工生产中最常见的装置之一,泵内流体的运动以及流体对泵的的磨蚀尤为突出,而两相流动的研究就是为设计泵以及如何防止这些机械磨蚀产生的基础和关键性的内容。
近几年,两相流动己发展到与可压缩流体力学及边界层理论有同等重要的地位。
因此固液两相流动及多相流动的研究不仅对流体力学的发展,而且对解决工程中的实际问题具有重大的理论价值和实际意义。
下面就离心泵叶轮内高浓度液-固两相湍流的大涡模拟为例阐述化工装置中两相流数学模型的建立、边界条件的确定以及求解方法的选择。
湍流大涡数值模拟(LES)是有别于直接数值模拟和雷诺平均模拟的一种数值模拟手段。
利用次网格尺度模型模拟小尺度湍流运动对大尺度湍流运动的影响即直接数值模拟大尺度湍流运动,将N-S方程在一个小空间域内进行平均(或称之为滤波),以使从流场中去掉小尺度涡,导出大涡所满足的方程。
1 大涡模拟1.1 大涡模拟的基本思想湍流运动是由许多尺度不同的旋涡组成的。
湍流的数学模型
湍流的数学模型第五讲流体仿真与应用◆湍流认识19世纪,一般都认为湍流是一种完全不规则的随机运动,Reynolds最初将这种流动现象称之为摇摆流(sinuous motion),其后Kelvin将其改名为湍流(turbulence),这个名字一直沿用至今。
◆湍流物理特征湍流由各种不同尺度的涡旋叠加而成,其中最大涡尺度与流动环境密切相关,最小涡尺度由粘性确定;流体在运动过程中,涡旋不断破碎、合并,流体质点轨迹不断变化;在某些情况下,流场做完全随机的运动,在另一些情况下,流场随机运动和拟序运动并存。
“随机”和“脉动”是湍流流场的重要的物理特征。
▼不可压缩时均运动控制方程组之所以出现方程组出现不封闭(需求解的未知函数较方程数多),在于方程中出现了湍流脉动值的雷诺应力项。
要使方程组封闭,必须对雷诺应力做出某些假定,即建立应力的表达式(或者引入新的湍流方程),通过这此表达式把湍流的脉动值与时均值等联系起来。
基于某些假定所得出的湍流控制方程,称为湍流模型。
湍流模型雷诺应力模型雷诺应力方程模型代数应力方程模型两一零方程模型方程模型方程模型湍动粘度类模型◆雷诺应力类模型这个模型的特点是直接构建表示雷诺应力的补充方程,然后联立求解湍流时均运动控制方程组。
▼雷诺应力方程是微分形式的,称为雷诺应力方程模型。
▼若将雷诺应力方程的微分形式简化为代数方程的形式,则称为代数应力方程模型。
▼一方程模型一方程模型考虑到湍流的对流输运和扩散输运,因此比零方程模型更为合理。
但是,一方程模型中如何定长度比尺仍是不容易决定的问题,因此在实际工程计算很少应用。
两方程模型是指补充2个微分方程使湍流时均控制方程组封闭的一类处理方法。
▼二方程模型两方程模型中标准模型及各种改进模型在工程中获得了最广泛的应用。
εκ−▼标准两方程模型εκ−○标准两方程模型常数取值εκ−▼标准模型的控制方程εκ−▼标准模型的适应性εκ−①模型中的相关系数,主要根据一些特定条件下的试验结果而确定的。
第三章第三次课两相流动模型(飘)
第三章第三次课两相流动模型(飘)
• Thom方法
• Thom根据流动体积份额的计算公式
xgvx1gvxvl 1x1x
• 提出空泡份额的计算式为
1x1x
第三章第三次课两相流动模型(飘)
• Lockhart-Martinelli方法 • Lockhart与Martinelli是最早提出水平管中气液两相流
动压降与空泡份额计算关系的学者。他们的两相压 降研究方法至今仍在广泛应用,这将在下一章中详 细论述。这里简要介绍一下Lockhart-Martinelli空泡 份额的计算方法。
C0
1
b
11
• 其中
0.1
b
v l
第三章第三次课两相流动模型(飘)
空泡份额的其它计算方法
• 经过多年的研究,各国学者提出了大量的空泡份额 计算模型。因此气液两相流动,特别是与反应堆等 背景相适应的饱和沸腾下的空泡份额计算方法相当 多,我们无法逐一介绍。除了前面各节提到的方法 外,这里择要介绍一下其它一些计算空泡份额的方 法。
❖ 可见,忽略壁面剪切力,F ❖ 漂移速度
只是空泡率、物性及相对 运动的函数。考虑到
jgl ug j
j g lu g ju g j 1 V g V l
F uj g us
Vg
Vl
1
g三次课两相流动模型(飘)
• 因此,漂移流通量jgl与滑移速度us仅是空泡率 和物
取决于流道直径与对比态压力 (p为系统压力,
pcr为临界压力)
p
• 关于C0的具体计算公式可以看教材表3-2 p cr
第三章(第二次课) 两相流动模型(均、分)
三、分相流模型
分相流模型是欧美国家的科学提出推崇的研究两相 流动的方法,它更接近于两相流动的真实情况,一 般适用范围比均相流模型大。 自1944年Martinelli与Lockhart发表气液两相流动推 导结果以来,分相流模型不断发展,出现了许多不 同的表达形式。常用的一些分相流模型彼此差异很 大,复杂程度也不相同。
总地来说,均相流模型的基本思想是用一等效的可 压缩流体代替两相流体。若一相均匀地弥散于另一 相中,两相间动量传递和能量传递足够快,两相的 当场平均速度和温度便基本相等。这时,若各参数 沿流道变化率不大,热力不平衡影响便可一忽略, 这样均相流模型就比较适用。比如,对于泡状流 型,均相模型比较适用;而对于分层流型,特别是 两相相向流动,均相流模型就不再适用了。
把两相流动按前述的各种基本流型区分开来再根据流型特征分析其流动特性并将基本方程组应用于这种经理想化的有代表性的流型从而求得方在气液两相流动研究中最普遍采用的简化假设是将三维流动简化为一维流动
第二课 两相流常用模型
上海交通大学 核工系
一、概述
两相流动建模的思想是:把两相流动按前述 的各种基本流型区分开来,再根据流型特征 分析其流动特性,并将基本方程组应用于这 种经理想化的有代表性的流型,从而求得方 程组的解。
均相流模型中采用的基本假设为: ① 认为两相混合得很好,气液两相具有相同 的流动线速度(ul=uv); ② 两相间处于热力平衡,对于汽液两相流 动,两相间热力平衡即蒸汽与液体具有相同 的温度且均处于饱和状态; ③ 使用合理确定的单相摩擦系数。
均相流模型适用的流型
在前面关于流型的叙述中我们知道,气液两 相的流速其实并不相等,只有在高含气率 (大量气体中含有少数液滴)或者很小含气 率(大量液体中仅含有少量气泡)时两相流 速才近似相等。因此,这一模型实际上只适 用于泡状流与雾状流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Zhou L X
Sci China Phys Mech Astron
June (2011) Vol. 54 No. 6
1099
this theory the only motive force of particle fluctuation is particle following the local gas fluctuation; particle fluctuation should be always weaker than gas fluctuation and it should decrease with the increase of particle size. In the framework of two-fluid models, this algebraic model of particle fluctuation was used by many investigators, Rizk et al. [6] for example, by combining the gas k- turbulence model with algebraic particle fluctuation models like Hinze-Tchen’s model (we call it a k--Ap model). In fact, similar approaches have been taken by Melville and Bray [7], Chen and Wood [8], Mostafa and Mongia [9]. However, our experiments and the experiments done by other investigators show that in many cases the particle fluctuation is stronger than the gas fluctuation and larger particles diffuse faster than smaller particles. Hence the concept of “particle turbulence” was proposed, by which the particle fluctuation has the nature of gas turbulence, and it obeys its own conservation law, i.e. it has its own convection, diffusion, shear production and dissipation to gas turbulence and is determined not only by local gas turbulence. Based on this consideration a transport equation of particle turbulent kinetic energy (kp equation) is derived and closed by the present author and afterwards a k--kp two-phase turbulence model was proposed. The superiority of the k--kp model over the k--Ap model (Ap denotes the Hinze-Tchen’s algebraic model) is just like that of the k-equation model over the mixing length model for single-phase flows. Subsequently, it is found that most of two-phase turbulence is anisotropic and the anisotropy of particle turbulence is much stronger than that of the gas. Hence a two-phase Reynolds stress equation model was proposed and then improved to become a unified second-order moment (USM) two-phase turbulence model with a more elaborated closure model of the two-phase velocity correlation. The k--kp model is found to be a reduced form of the USM model. Simultaneously, the k- and Reynolds stress equation models of gas turbulence were combined with a PDF transport equation model of particle turbulence to form k--PDF and DSM-PDF models. In order to simplify the USM model and retain its anisotropic features, a non-linear k--kp model was proposed. All of these models were applied to simulate gas-particle jets, sudden-expansion and swirling gas-particle flows. Subsequently, a second-order moment bubble-liquid two-phase turbulence model was proposed. In the following text a detailed description of derivation and closure of these models and their validation and application will be stated.
ZHOU LiXing
Department of Engineering Mechanics, Tsinghua University, Beijing 10008mber 23, 2010; accepted March 10, 2011; published online March 30, 2011
Turbulent dispersed multiphase flows, including gas-particle, gas-droplet and bubble-liquid flows, are widely encountered in various engineering facilities. Modeling of two-phase turbulence, in particular the dispersed phase turbulence, is the key problem in the Eulerian-Eulerian simulation of practical dispersed multiphase flows. Although different models were developed and used, the experimental validation shows that they cannot always give satisfactory prediction results. In this paper the present author give a detailed review of the unified second-order moment (USM), k--kp and nonlinear k--kp two-phase turbulence models, proposed by him. The derivation and closure of these models are described in detail and the experimental validation and application of these models are extensively discussed. dispersed multiphase flows, second-order moment model, two-phase turbulence PACS: 47.27.E-, 47.27.ep, 47.55.Ca, 47.55.Kf
1
Introduction
Turbulent dispersed multiphase reacting flows, such as turbulent gas-solid (particle), gas-droplet and bubble-liquid flows, are widely encountered in various engineering facilities, such as boiler and industrial furnaces, internal combustion engines, gas turbine combustors, ram-jet and rocket engine combustors, and chemical and nuclear reactors. The turbulence of gas itself is already a complex phenomenon. Turbulent multiphase reacting flows with dispersed phase (particles, droplets, bubbles) and continuous phase (gas, liquid) and homogeneous or heterogeneous chemical reactions are much more complex. Although in recent years there are remarkable strides in the basic studies on physics of turbulence, such as the results using the direct numerical simulation, theory of coherent structures, theory of chaos and detailed PIV measurements, these results cannot directly solve practical engineering problems. It is well known that about 60 years ago Chou [1] first proposed the
