专题3 空间垂直问题的证明方法-2019年高考数学考点讲解与真题分析
高中数学常见题型解法归纳 空间直线、平面垂直位置关系的证明
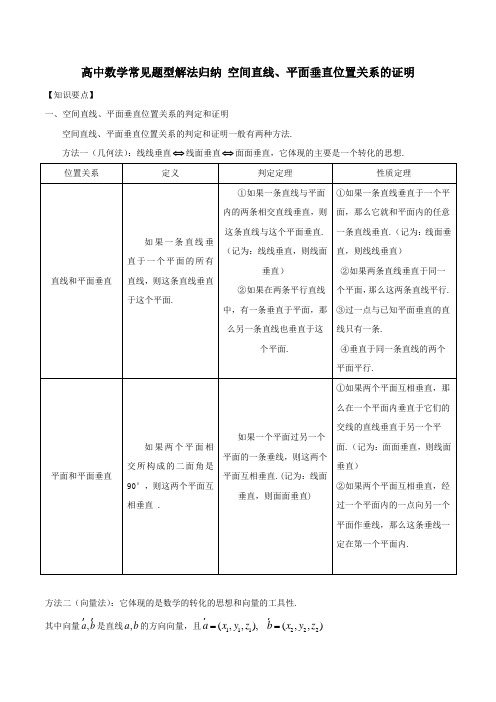
高中数学常见题型解法归纳 空间直线、平面垂直位置关系的证明【知识要点】一、空间直线、平面垂直位置关系的判定和证明空间直线、平面垂直位置关系的判定和证明一般有两种方法.方法一(几何法):线线垂直⇔线面垂直⇔面面垂直,它体现的主要是一个转化的思想.方法二(向量法):它体现的是数学的转化的思想和向量的工具性. 其中向量,a b 是直线,a b 的方向向量,且111222(,,),(,,)a x y z b x y z ==向量,m n 是平面,αβ的法向量,且333444(,,),(,,)m x y z n x y z ==1200(,1212z z a b a b a b x x y y a b a b +⊥⇔⊥⇔=⇔+=直线直线其中分别为直线,的方向向量),,31313(1x y y z z a a m x a a m λλλαα===⊥⇔⇔直线平面其中为直线的方向向量,为平面的法向量)3400(3434z z m n m n x x y y m αβαβ+⊥⇔⊥⇔=⇔+=平面平面其中,n 分别为平面,的法向量) 二、空间的几何元素的位置关系从低到高有三个层次:线线关系、线面关系和面面关系.三、空间垂直位置关系的证明,总是把要证明的垂直关系首先转化成最靠近它的位置关系去证明.如果要证明线线垂直,只能首先转化成证明线面垂直;如果要证明线面垂直,可以首先转化成证明线线垂直或者面面垂直;如果要证明面面垂直,只能首先转化成证明线面垂直. 【方法讲评】【例1】【2017北京,文18】如图,在三棱锥P –ABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,D 为线段AC 的中点,E 为线段PC 上一点.(Ⅰ)求证:PA ⊥BD ;(Ⅱ)求证:平面BDE ⊥平面PAC ; (Ⅲ)当PA ∥平面BD E 时,求三棱锥E –BCD 的体积.(III )因为PA ∥平面BDE ,平面PAC平面BDE DE =,所以PA DE ∥.因为D 为AC 的中点,所以112DE PA ==,BD DC ==由(I )知,PA ⊥平面ABC ,所以DE ⊥平面PAC .所以三棱锥E BCD -的体积1163V BD DC DE =⋅⋅=. 【点评】(1)本题的第1问证明PA ⊥BD ,转化成证明PA ⊥平面ABC ,第2问证明平面BDE ⊥平面PAC 转化成证明BD ⊥平面PAC .(2)空间垂直位置关系的证明,总是把要证明的垂直关系首先转化成最靠近它的位置关系去证明.转化成哪一条线垂直哪一条线,哪一条线垂直哪一个平面,哪一个平面垂直哪一个平面,这取决于你的观察和分析,主要关注已知条件中的有垂直关系的线和面.【例2】如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB ADAC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.(Ⅰ)证明CD AE ⊥; (Ⅱ)证明PD ⊥平面ABE ;(Ⅲ)求二面角A PD C --的大小.(Ⅲ)ABCDPEABCDPEM⊥的关键是证明CD垂直AE所在的平面PCD.(2)证明PD⊥平面ABE的【点评】(1)证明CD AEPC CD关键是证明PD垂直平面ABE内的两条相交直线,.【反馈检测1】【2017课标3,理19】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C 的余弦值.【例3】如图,已知正方体1AC 棱长为2,E 、F 、G 分别是1CC 、BC 和CD 的中点. (1)证明:1A G ⊥面EFD ;(2)求二面角E DF C --的余弦值.(2)由(1)知1(2,1,2)AG =--为面EFD 的法向量 ∵CE ⊥面CFD ,(0,0,1)CE =为面CFD 的法向量 设1AG 与CE 夹角为θ,则11cos A G CE A G CEθ⋅==⋅231-⋅23=- 由图可知二面角E DF C --的平面角为πθ- ∴二面角E DF C --的余弦值为23. 【点评】本题由于是正方体,所以方便建立空间直角坐标系,所以选择向量的方法比较直接. 当然,也可以选择几何法.【反馈检测2】如图,已知多面体ABCDEF 中,ABCD 为菱形,60ABC ∠=︒,AE ⊥平面ABCD ,,1,AE CF AB AE AF BE ==⊥.(1)求证:AF ⊥平面BDE ;(2)求二面角F BE D --的余弦值.高中数学常见题型解法归纳及反馈检测第60讲: 空间直线、平面垂直位置关系的证明参考答案【反馈检测1答案】(1)证明略;.(2)由题设及(1)知,,,OA OB OD 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA 为单位长,建立如图所示的空间直角坐标系O xyz -.则()()()()1,0,0,,1,0,0,0,0,1A B C D -.由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得12E ⎛⎫ ⎪ ⎪⎝⎭.故()()11,0,1,2,0,0,2AD AC AE ⎛⎫=-=-=- ⎪⎪⎝⎭.【反馈检测2答案】(1)见解析;(2)所求二面角得余弦值为5. 【反馈检测2详细解析】(1)设AC BD O ⋂=以O 为空间直角坐标系原点,以OB 为x +轴,以OC 为y +轴,以过O 点平行于AE 的射线为z +轴建立空间直角坐标系xOy ∵1AB AE ==,且菱形ABCD 中60ABC ∠=︒∴1110,,0,,0,,0,,0,,122222A B C D E ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ∵AECF 且()0,0,1AE =,∴设()()0,0,0CF λλ=> ∴10,,2F λ⎛⎫ ⎪⎝⎭又∵AF BE ⊥∴102AF BE λ⋅=-+=,∴12λ=,∴110,,22F ⎛⎫ ⎪⎝⎭又∵()10,1,02AF BD ⎛⎫⋅=⋅= ⎪⎝⎭∴AF BD ⊥,又AF BE ⊥且BD BE B = ∴AF ⊥平面BDE(2)设⊥m 平面BEF ,(),,x y z =m∴()11,,,1022BE x y z x y z ⎛⎫⋅=⋅-=-+= ⎪ ⎪⎝⎭m设所求二面角为θ,则有cosθ=.。
高考指南立体几何垂直证明的六大绝招秒懂

高考指南立体几何垂直证明的六大绝招秒懂!类型一AD⊥SC,求证:AD⊥面SBC证明:∵SA⊥面ABC ∴SA⊥BC又∠ACB=90°∴AC⊥BC又AC,SA⊆面SAC ∴BC ⊥面SAC∴BC⊥AD又AD⊥SC且BC,SC⊆面SBC∴AD⊥面SBC变式:如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,求证:AD⊥AC类型二利用等腰三角形中线证垂直例题:在三棱锥P-ABC中,AC=BC,AP=BP,求证PC⊥AB证明:取AB的中点M,连接PM,CM∵AC=BC,M是AB的中点,∴AB⊥CM∵AP=BP,M是AB的中点,∴AB⊥PM∴AB⊥面PCM∴AB⊥PC变式:四棱锥P-ABCD,底面ABCD是正方形,PA=AD,求证面PAD⊥面PCD类型三利用勾股定理逆定理证垂直例题:如图,四棱锥P-ABCD的底面是边成为3的正方形,PA⊥CD,PA=4,PD=5,求证:PA⊥面ABCD证明:∵PA=4,AB=3,PD=5∴PA2+AB2=PD2,∴三角形PAD是直角三角形,∴PA⊥AD又PA ⊥CD,∴PA⊥面ABCD变式:如果,在三棱台ABC-DEF中,平面BDEF⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,求证:BF⊥面ACFD类型四利用三角形全等证垂直例题:如图,三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°,求证:AB⊥PC证明:取AB的中点M,连接CM,∵△PAB是等边三角形,∴PB=PA又PC=PC,∠PAC=∠PBC=90°∴△PBC≌△PAC,∴BC=AC∴△ACB是等腰三角形,M是AB的中点,∴CM⊥AB又在等边△PAB中,M是AB的中点,∴PM⊥AB∴AB⊥面PMC∴AB⊥PC变式:如图,在以A、B、C、D、E、F为顶点的五面体中,平面CDEF⊥平面ABCD,FC=FB,四边形ABCD为平行四边形,且∠BCD=45°,求证:CD⊥BF类型五利用平行关系证明垂直例题:如图四棱锥P-ABCD,底面是正方形,PA⊥底面ABCD,∠PDA=45°,E是棱AB的中点,求证:面PCE⊥面PCD证明:分别做PC,PD的中点M,N两点,连接EM,MN,NA∵MN为△PCD的中位线,∴MN∥CD且MN=1/2CD又∵E是AB的中点,∴AE∥CD且AE=1/2CD ∴四边形AEMN是平行四边形,则EM∥AN,∵PA⊥面ABCD,∴PA⊥AD,且∠PDA=45°,∴△PAD 是等腰直角三角形又N是PD中点,∴AN⊥PD∵四边ABCD是正方形,∴CD⊥AD,又PA⊥CD,∴CD⊥面PAD,∴CD⊥AN,又上面已求PD⊥AN,∴AN⊥面PCD又∵EM∥AN,∴EM⊥面PCD∵EM ⊂面PEC,∴面PEC⊥面PCD变式:如图1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,证明CD⊥面A1OC.类型六梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD,证明:PA⊥BD。
高考数学 专题32 空间中直线、平面垂直位置关系的证明方法黄金解题模板

专题32 空间中直线、平面垂直位置关系的证明方法【高考地位】立体几何是高考的重点内容之一,每年高考大题必有立体几何题,尤其是第一问主要考查证明线面垂直、平行,面面垂直等问题,解决这类问题的方法主要有:几何法和空间向量法. 在高考中其难度属中档题. 【方法点评】方法一 几何法使用情景:转化的直线或平面比较容易找到解题模板:第一步 按照线线垂直得到线面垂直,进而得出面面垂直的思路分析解答;第二步 找到关键的直线或平面; 第三步 得出结论.例1、【2018广西桂林市第十八中模拟】如图,在三棱锥P ABC -中, ,44CBA AB π∠===,,D E 分别为线段,AB BC 的中点, ,PD AC PE BC ⊥⊥.(1)求证: CD ⊥平面PAB ;(2)若F 为PA 上的点,且2,3C PEF PF FA V -==P 平面ABC 的距离.又∵,PD AC BC AC C ⊥⋂=,∴PD ⊥面ABC , ∵CD ⊂面ABC ∴PD CD ⊥在ABC ∆中D 是AB 的中点, AC BC =,∴CD AB ⊥ ∵PD AB D ⋂=, ,PD AB ⊂面PAB ,∴CD ⊥平面PAB (2)由(1)知P 到面ABC 的距离为PD 由等体积知: 2233C PEF F PEC A PEC P AEC V V V V ----===∵3C PEF V -=2P AEC V -=∴123AEC PD S ∆⨯⨯⨯=∵122AEC S AC AE ∆=⨯⨯=, 1223PD ⨯⨯⨯=, ∴98PD =. 例2、如图所示,在四棱锥P ABCD -中,底面四边形ABCD 为等腰梯形,E 为PD 中点,PA ⊥平面ABCD ,//,,24AD BC AC BD AD BC ⊥==.证明:平面EBD ⊥平面PAC ; 【答案】详见解析线线垂直PA BD ⊥.试题解析:因为PA ⊥平面,ABCD BD ⊂平面ABCD ,所以PA BD ⊥,又因为,AC BD PA AC A ⊥=,所以BD ⊥平面PAC ,而BD ⊂平面EBD ,所以平面EBD ⊥平面PAC . 考点:面面垂直判定定理【思路点睛】利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.【变式演练1】如图, 已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面, 平面ABCD平面ABPE AB =,且2,1,AB BP AD AE AE AB ====⊥,且AE BP . 设点M 为棱PD 中点, 在面ABCD 内是否存在点N ,使得MN ⊥平面ABCD ?若存在, 请证明, 若不存在, 说明理由。
2019年高考数学 专题32 空间中直线、平面垂直位置关系的证明方法黄金解题模板

2019年高考数学 专题32 空间中直线、平面垂直位置关系的证明方法黄金解题模板【高考地位】立体几何是高考的重点内容之一,每年高考大题必有立体几何题,尤其是第一问主要考查证明线面垂直、平行,面面垂直等问题,解决这类问题的方法主要有:几何法和空间向量法. 在高考中其难度属中档题.【方法点评】方法一 几何法使用情景:转化的直线或平面比较容易找到解题模板:第一步 按照线线垂直得到线面垂直,进而得出面面垂直的思路分析解答;第二步 找到关键的直线或平面;第三步 得出结论.例1、【2018广西桂林市第十八中模拟】如图,在三棱锥P ABC -中, ,44CBA AB π∠===,,D E 分别为线段,AB BC 的中点, ,PD AC PE BC ⊥⊥.(1)求证: CD ⊥平面PAB ;(2)若F 为PA 上的点,且2,3C PEF PF FA V -==P 平面ABC 的距离.又∵,PD AC BC AC C ⊥⋂=,∴PD ⊥面ABC ,∵CD ⊂面ABC ∴PD CD ⊥在ABC ∆中D 是AB 的中点, AC BC =,∴CD AB ⊥∵PD AB D ⋂=, ,PD AB ⊂面PAB ,∴CD ⊥平面PAB(2)由(1)知P 到面ABC 的距离为PD由等体积知: 2233C PEF F PEC A PEC P AEC V V V V ----===∵3C PEF V -=2P AEC V -=∴123AEC PD S ∆⨯⨯⨯=∵122AEC S AC AE ∆=⨯⨯=, 1223PD ⨯⨯⨯=, ∴98PD =. 例2、如图所示,在四棱锥P ABCD -中,底面四边形ABCD 为等腰梯形,E 为PD 中点,PA ⊥平面ABCD ,//,,24AD BC AC BD AD BC ⊥==.证明:平面EBD ⊥平面PAC ;【答案】详见解析线线垂直PA BD ⊥.试题解析:因为PA ⊥平面,ABCD BD ⊂平面ABCD ,所以PA BD ⊥,又因为,AC BD PA AC A ⊥=,所以BD ⊥平面PAC ,而BD ⊂平面EBD ,所以平面EBD ⊥平面PAC .考点:面面垂直判定定理【思路点睛】利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.【变式演练1】如图, 已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面, 平面ABCD 平面ABPE AB =,且2,1,AB BP AD AE AE AB ====⊥,且AE BP . 设点M 为棱PD 中点, 在面ABCD 内是否存在点N ,使得MN ⊥平面ABCD ?若存在, 请证明, 若不存在, 说明理由。
空间几何中的垂线定理与推论

空间几何中的垂线定理与推论在空间几何中,垂线定理与推论是重要的基础概念。
它们帮助我们理解不同几何形体之间的关系,探索空间中的垂直性质。
本文将详细介绍垂线定理与推论的概念、证明方法以及应用场景。
1. 垂线定理的定义与证明垂线定理是指:如果两条直线垂直于同一平面上的第三条直线,并且它们互相垂直,则这两条直线平行。
该定理在解决空间中直线和平面相互垂直的问题时起到了关键作用。
假设在空间中有三条直线,分别为AB、CD和EF。
已知CD⊥EF,且AB⊥CD,我们需要证明AB∥EF。
证明过程:首先,在CD上找一点O,使得AO⊥CD。
根据垂线定义,我们知道AO与CD垂直。
然后,连接BO并假设BO与EF相交于点N。
根据角的性质,我们得到∠NOB=90°。
此外,由于AB⊥CD,所以∠BAO=90°。
根据传递性质,我们可以得出∠BAO=∠NOB。
因此,可得到AO∥BO。
接下来,我们需要证明EF⊥BO。
由于FO⊥CD,所以FO⊥BO。
此外,根据垂线定理的定义,我们知道AO∥BO,因此,可得到EF⊥BO。
根据垂线定理,我们可以得出AB∥EF。
2. 垂线推论的应用垂线定理还引申出许多有用的推论,这些推论广泛应用于几何学的各个领域。
下面列举了几个常见的垂线推论及其应用。
推论1:如果两条直线垂直于同一平面上的某条直线,它们互相垂直。
应用:在解决平面几何问题时,可以利用该推论判断两条直线是否垂直。
推论2:如果两条直线分别与同一直线垂直,并且它们不相交,则它们平行。
应用:在平面几何中,该推论帮助我们判定两条直线是否平行。
推论3:如果两个平面互相垂直,则它们的交线是一条直线。
应用:该推论在解决空间几何问题时非常有用,可以帮助我们找到两个垂直平面的交线。
推论4:如果两条直线分别与同一平面垂直,并且它们不在同一直线上,则它们平行于平面。
应用:该推论在解决空间几何问题中帮助我们判断直线与平面之间的关系。
3. 垂线定理与推论的应用举例垂线定理与推论不仅具有理论意义,还广泛应用于实际问题中。
空间几何垂直的判定定理公式

空间几何垂直的判定定理公式在我们学习数学的漫漫征途中,空间几何垂直这一板块就像是一座神秘的城堡,而垂直的判定定理公式则是打开城堡大门的神奇钥匙。
咱们先来说说线面垂直的判定定理。
如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线就与这个平面垂直。
这就好比在操场上,有一根旗杆直直地立在地面上。
假设地面是一个平面,而在地面上有两条相交的跑道线,这根旗杆和这两条跑道线都相互垂直,那这旗杆肯定就和整个地面垂直啦!再看看面面垂直的判定定理,如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直。
这就好像是两块相邻的木板,一块木板垂直地靠在另一块木板上,那这两块木板所在的平面自然就是垂直的关系。
还记得我之前教过的一个学生小明,他一开始对这些判定定理那叫一个头疼,总是搞混。
有一次做作业,碰到一个证明线面垂直的题目,他想都不想就乱写一通,结果当然是错得一塌糊涂。
我就问他:“小明啊,你想想那个操场上的旗杆,是不是得和两条相交的跑道线都垂直才能立稳呀?”小明眨眨眼,好像突然开窍了。
从那以后,他每次遇到这类问题,都会在脑海里想象那个画面,做题的准确率也越来越高。
其实啊,这些判定定理并不是什么高深莫测的东西。
咱们只要多联系实际,多做几道题,就能把它们掌握得牢牢的。
比如说,家里的墙角,是不是就是三条线两两垂直,从而形成了三个相互垂直的面?还有,建筑工地上的塔吊,那长长的吊臂和塔身是不是也存在着垂直的关系?在解决空间几何垂直问题的时候,咱们要善于从生活中寻找例子,把抽象的定理具体化。
这样一来,不仅能让我们更好地理解和记忆这些定理,还能提高我们解决问题的能力。
对于线线垂直的判定,也有一些小窍门。
如果一条直线垂直于一个平面,那么这条直线垂直于平面内的任意一条直线。
这就好比你手里拿着一根垂直于桌面的铅笔,那这根铅笔是不是和桌面上的所有直线都垂直呀?还有一种情况,如果两条平行线中的一条垂直于一条直线,那么另一条也垂直于这条直线。
2019年高考数学(理)热点题型和提分秘籍专题32直线、平面垂直的判定与性质(教学案)含解析

1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线、面垂直的有关性质与判定定理。
2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题。
热点题型一证明直线与平面垂直例1、已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点。
(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC。
证明:(1)如图,取AB中点E,连接SE、DE,∴BD ⊥平面SAC 。
方法二,若AB =BC ,则BD ⊥AC 。
由(1)知SD ⊥平面ABC ,又SD ⊂平面SAC , ∴平面ABC ⊥平面SAC ,又平面ABC∩平面SAC =AC 。
∴BD ⊥平面SAC 。
【提分秘籍】证明线面垂直的常用方法 (1)利用线面垂直的判定定理。
(2)利用“两平行线中的一条与平面垂直,则另一条也与这个平面垂直”。
(3)利用“一条直线垂直于两个平行平面中的一个,则与另一个也垂直”。
(4)利用面面垂直的性质定理。
【举一反三】如图所示,已知AB 为圆O 的直径,点D 为线段AB 上一点,且AD =13DB ,点C 为圆O 上一点,且BC =3AC ,PD ⊥平面ABC ,PD =DB 。
求证:PA⊥CD。
解析:因为AB为圆O的直径,所以AC⊥CB,在Rt△ABC中,由3AC=BC得,∠ABC=30°,热点题型二证明平面与平面垂直例2、(2018年江苏卷)在平行六面体中,.求证:(1);(2).【答案】答案见解析【解析】所以AB1⊥平面A1BC.因为AB1平面ABB1A1,所以平面ABB1A1⊥平面A1BC.【变式探究】如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC 的同侧,M为EA的中点,CE=2BD,求证:(1)平面BDM⊥平面ECA;(2)平面DEA⊥平面ECA。
∴平面BDM⊥平面ECA。
(2)∵MD⊥平面ECA,MD⊂平面DEA,∴平面DEA⊥平面ECA。
2019年高考数学(文)热点题型和提分秘籍专题32直线、平面垂直的判定与性质(题型专练)含解析

2019年高考数学(文)热点题型和提分秘籍1.在空间中,l,m,n,a,b表示直线,α表示平面,则下列命题正确的是()A.若l∥α,m⊥l,则m⊥αB.若l⊥m,m⊥n,则m∥nC.若a⊥α,a⊥b,则b∥αD.若l⊥α,l∥a,则a⊥α【答案】D2.已知平面α与平面β相交,直线m⊥α,则()A.β内必存在直线与m平行,且存在直线与m垂直B.β内不一定存在直线与m平行,不一定存在直线与m垂直C.β内不一定存在直线与m平行,但必存在直线与m垂直D.β内必存在直线与m平行,不一定存在直线与m垂直【解析】如图,在平面β内的直线若与α,β的交线a平行,则有m与之垂直.但却不一定在β内有与m平行的直线,只有当α⊥β时才存在。
9.设a,b是夹角为30°的异面直线,则满足条件“a⊂α,b⊂β,且α⊥β”的平面α,β()A.不存在B.有且只有一对C.有且只有两对 D.有无数对【答案】D10.如图7-5-10,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF 把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有()图7-5-10A.AG⊥平面EFH B.AH⊥平面EFHC.HF⊥平面AEF D.HG⊥平面AEF【答案】B【解析】根据折叠前、后AH⊥HE,AH⊥HF不变,∴AH⊥平面EFH,B正确;∵过A只有一条直线与平面EFH垂直,∴A不正确;∵AG⊥EF,EF⊥GH,AG∩GH=G,∴EF⊥平面HAG,又EF⊂平面AEF,∴平面HAG⊥AEF,过H作直线垂直于平面AEF,一定在平面HAG内,∴C不正确;由条件证不出HG⊥平面AEF,∴D不正确.故选B.11.如图7-5-11,∠BAC=90°,PC⊥平面ABC,则在△ABC,△P A C的边所在的直线中,与PC垂直的直线是________;与AP垂直的直线是________.图7-5-11【答案】AB,BC,AC;AB12.如图7-5-12所示,在四棱锥P-ABCD中,P A⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)图7-5-12【答案】DM⊥PC(或BM⊥PC)【解析】连接AC,BD,则AC⊥BD,∵P A⊥底面ABCD,∴P A⊥BD.又P A∩AC=A,∴BD⊥平面P AC,∴BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD.而PC⊂平面PCD,∴平面MBD⊥平面PCD.13.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号)【答案】②③④14.如图7-5-16,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=________时,CF⊥平面B1DF.图7-5-16【答案】a或2a【解析】∵B1D⊥平面A1ACC1,∴CF⊥B1D.为了使CF⊥平面B1DF,只要使CF⊥DF(或CF⊥B1F).设AF=x,则CD2=DF2+FC2,∴x2-3ax+2a2=0,∴x=a或x=2a.【答案】216.在△ABC中,∠ACB=90°,AB=8,∠ABC=60°,PC⊥平面ABC,P C=4,M是AB上一个动点,则PM的最小值为__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题3 空间垂直问题的证明方法垂直是直线与直线、直线与平面、平面与平面位置关系中的纽带,常常起到承上启下的作用,垂直问题更是高考考查的热点问题,不少问题常常是以垂直为解题的突破口,下面具体剖析垂直关系的复习。
一.垂直的判定与性质1.直线和平面垂直的判定方法判定定理中,“相交”两字不能少,否则命题不成立.判定一直线垂直于一平面的方法是设法在平面中找出两条相交直线,然后证明一直线垂直于两相交直线即可.所以线面垂直的判定往往归为线线垂直的判定.2.直线与平面垂直的性质3.面面垂直的判定与性质特别提示:(1)面面垂直线面垂直(线是其中一个平面内垂直于它们交线的一条直线);(2),要过内一点引平面的垂线,只需过这一点作交线的垂线。
(3)证明两个平面垂直的方法是:证明一个平面经过另一个平面的垂线。
二、温馨提示:1.在证明两平面垂直时,一般先从现有直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决,而作辅助线则应有理论根据,并有利于证明,不能随意添加。
如有平面垂直时,一般要用性质定理,在一个面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直。
在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的高(中线或角平分线)三线合一、矩形的内角、直径所对的圆周角、菱形的对角线垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.2. 证明垂直主要方法是转化:图示表示为:三.典例剖析1、线线垂直证明例1(2018•丰台区二模)如图,在三棱柱ABC﹣A1B1C1中,D是AC的中点,A1D⊥平面ABC,AB=BC,平面BB1D与棱A1C1交于点E.(Ⅰ)求证:AC⊥A1B;(Ⅱ)求证:平面BB1D⊥平面AA1C1C;【分析】(Ⅰ)推导出A1D⊥AC,BD⊥AC,从而AC⊥平面A1BD,由此能证明AC⊥A1B.(Ⅱ)推导出A1D⊥BD,BD⊥AC,从而BD⊥平面A1ACC1,由此能证明平面BB1D⊥平面AA1C1C.证明:(Ⅰ)因为A1D⊥平面ABC,所以A1D⊥AC.因为△ABC中,AB=BC,D是AC的中点,所以BD⊥AC.因为A1D∩BD=D,所以AC⊥平面A1BD.所以AC⊥A1B.(Ⅱ)因为A1D⊥平面ABC,因为BD⊂平面ABC,所以A1D⊥BD.由(Ⅰ)知BD ⊥AC.因为AC∩A1D=D,所以BD⊥平面A1ACC1.因为BD⊂平面BB1D,所以平面BB1D⊥平面AA1C1C.【点评】本题考查线线垂直、面面垂直的证明,证明线线垂直一般通过证明线面垂直求得,证明面面垂直转化为线面垂直完成。
2、线面垂直证明例2(2018•铜山区一模)如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.求证:AB⊥平面EDC;【分析】推导出CD⊥AC,从而CD⊥平面ABC,进而CD⊥AB,再求出CE⊥AB,CE⊥AB,由此能证明AB⊥平面EDC.证明:∵平面ABC⊥平面ACD,∠ACD=90°,∴CD⊥AC,∵平面ABC∩平面ACD=AC,CD⊂平面ACD,∴CD⊥平面ABC,又AB⊂平面ABC,∴CD⊥AB,∵AC=BC,E为AB的中点,∴CE⊥AB,又CE∩CD=C,CD⊂平面EDC,CE⊂平面EDC,∴AB⊥平面EDC.【点评】本题考查线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力。
本题出现面面垂直所以想到面面垂直的性质定理,再利用线面垂直的判定定理证明问题。
3.面面垂直证明例3(2018•海淀区二模)如图,已知菱形AECD的对角线AC,DE交于点F,点E为的AB 中点.将三角形ADE沿线段DE折起到PDE的位置,如图2所示.(Ⅰ)求证:DE⊥平面PCF;(Ⅱ)证明:平面PBC⊥平面PCF;【分析】(Ⅰ)折叠前,AC⊥DE;,从而折叠后,DE⊥PF,DE⊥CF,由此能证明DE⊥平面PCF.(Ⅱ)推导出DC∥AE,DC=AE.从而DC∥EB,DC=EB.进而四边形DEBC为平行四边形.从而CB∥DE.由此能证明平面PBC⊥平面PCF.证明:(Ⅰ)折叠前,因为四边形AECD为菱形,所以AC⊥DE;所以折叠后,DE⊥PF,DE⊥CF,又PF∩CF=F,PF,CF⊂平面PCF,所以DE⊥平面PCF(Ⅱ)因为四边形AECD为菱形,所以DC∥AE,DC=AE.又点E为AB的中点,所以DC∥EB,DC=EB.所以四边形DEBC为平行四边形.所以CB ∥DE.又由(Ⅰ)得,DE⊥平面PCF,所以CB⊥平面PCF.因为CB⊂平面PBC,所以平面PBC⊥平面PCF.点评:本题考查线面垂直、面面垂直的证明,处理折叠问题,要先画好平面图形,并且注意平面图形与立体图形的对照使用,这样有利于分析元素间的位置关系和数量关系.要注意分析折叠前后位置关系及数量关系的变化.一般位于折线一边的点、线间的位置关系和数量关系不变,位于折成两边的点、线间的位置关系,数量关系要发生变化.不变的关系,要注意在平面图形中处理;变化的关系,一般在立体图形中处理.四、达标测试题1.(2018•青州市三模)如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是()A.MN⊥CC1B.MN⊥平面ACC1A1C.MN∥AB D.MN∥平面ABCDA(2,0,0),=(﹣2,2,0),=2﹣2+0=0,∴AC⊥MN,又MN⊥CC1,AC∩CC1=C,∴MN⊥平面ACC1A1,故B成立;∵=(0,2,0),=(﹣1,﹣1,0),∴MN和AB不平行,故C错误;平面ABCD的法向量=(0,0,1),=0,又MN⊄平面ABCD,∴MN∥平面ABCD,故D正确.故选:C.2.(2018春•宁波期末)在棱长为1的正方体ABCD﹣A1B1C1D1中,M,N分别是BB1,A1B1的中点.点P在该正方体的表面上运动,则总能使MP与BN垂直的点P所构成的轨迹的周长等于()A.4 B.C.D.∴NB⊥平面ADGM,∴使NB与MP垂直的点P所构成的轨迹为矩形ADGM,∵正方体的棱长为1∴故由勾股定理可得,使B1C与MP垂直的点P所构成的轨迹的周长等于2+.故选:D.3(2018•泉州模拟)如图,正三棱柱ABC﹣A1B1C1中,AA1=AB,D为BB1的中点.(1)求证:A1C⊥AD;(2)若点P为四边形ABB1A1内部及其边界上的点,且三棱锥P﹣ABC的体积为三棱柱ABC ﹣A1B1C1体积的,试在图中画出,P点的轨迹.并说明理由.3【解答】(1)证明:取AB的中点F,连接CF,A1F,∵A1A⊥平面ABC,CF⊂平面ABC,∴所以A1A⊥CF.∵△ABC为正三角形,F为AB的中点,∴BA⊥CF,又∵AA1,AB⊂平面AA1B1B,AA1∩AB=A,∴CF⊥平面AA1B1B,又∵AD⊂平面AA1B1B,所以CF⊥AD,正方形AA1B1B中,∵Rt△A1AF≌Rt△ABD,∴∠DAB=∠FA1A,又∵∠AFA1+∠FA1A=90°,∴∵∠AFA1+∠DAB=90°,,故AD⊥A1F,又∵CF∩A1F=F,CF,A1F⊂平面A1FC,∴AD⊥平面A1FC,又∵A1C⊂平面A1FC,∴A1C⊥AD.4.(2018•赤峰一模)如图,四棱锥P﹣ABCD的底面ABCD是边长为2的菱形∠BAD=60°.已知PB=PD=2,PA=.(Ⅰ)证明:PC⊥BD;(Ⅱ)若E为PA上一点,记三棱锥P﹣BCE的体积和四棱锥P﹣ABCD的体积分别为V1和V2,当V1:V2=1:8时,求的值.4证明:(Ⅰ)连接BD、AC交于O点,∵PB=PD,∴PO⊥BD,又∵ABCD是菱形,∴BD⊥AC,而AC∩PO=O,∴BD⊥平面PAC,且PC⊂平面PAC,∴BD⊥PC.5.(2018•江门一模)如图,直角梯形ABEF中,∠ABE=∠BAF=90°,C、D分别是BE、AF上的点,且DA=AB=BC=a,DF=2CE=2a.沿CD将四边形CDFE翻折至CDPQ,连接AP、BP、BQ,得到多面体ABCDPQ,且AP=a.(Ⅰ)求多面体ABCDPQ的体积;(Ⅱ)求证:平面PBQ⊥平面PBD.(Ⅱ)取BP的中点G,连接GQ、DG、DQ,在△ABP中,BP==2a,∴BG=BP=a,在△BCQ中,BQ==a,PQ==a,∴PQ=BQ,∴GQ⊥BP.∴QG==a,又BD==2a=DP,∴DG⊥BP,∴DG==a,又DQ==a,∴DQ2=QG2+DG2,即QG⊥DG.又BP∩DG=G,∴QG⊥平面PBD,又QG⊂平面PBQ,∴平面PBQ⊥平面PBD.6.(2018•东莞市模拟)如图1,△ABC是边长为3的等边三角形,D在边AC上,E在边AB上,且AD=BE=2AE.将△ADE沿直线DE折起,得四棱锥A'﹣BCDE,如图2(1)求证:DE⊥A'B;(2)若平面AD'E⊥底面BCDE,求三棱锥D﹣A'CE的体积.6解:(1)证明:在图1中,由题意知AE=1,AD=BE=2,在△ADE中,由余弦定理知:DE2=AE2+AD2﹣AE×AD=12+22﹣1×2=3,所以:AE2+DE2=AD2,所以:DE⊥AE,DE⊥BE,在△ADE沿直线DE折起的过程中,DE与AE,BE的垂直关系不变,故在图2中有DE⊥A'E,DE⊥BE,又A'E∩BE=E,所以DE⊥平面A'EB,所以DE⊥A'B.7(2018•开封一模)如图1,在矩形ABCD中,AD=2AB=4,E是AD的中点.将△ABE沿BE折起使A到点P的位置,平面PEB⊥平面BCDE,如图2.(Ⅰ)求证:PB⊥平面PEC;(Ⅱ)求三棱锥D﹣PEC的高.(Ⅱ)以OB所在直线为x轴,以平行于EC所在直线为y轴,以OP所在直线为z轴建立空间直角坐标系,∵PB=PE=2,则B(,0,0),E(﹣,0,0),P(0,0,),D(﹣2,,0),C(﹣,2,0),∴=(﹣,0,﹣),=(﹣,2,﹣),∴cos∠EPC===,可得:sin∠EPC==,可得:S△EPC=||•||•sin∠EPC=2×2×=2,∵V P﹣ECD=V D﹣EPC,设三棱锥D﹣PEC的高为h,则可得:S△ECD•OP=S△EPC•h,可得:=2×h,∴解得:三棱锥D﹣PEC的高h=1.8(2018•江门一模)如图1,ABCD是一个直角梯形,∠ABC=∠BAD=90,E为BC边上一点,AE、BD相交于O,AD=EC=3,BE=1,AB=.将△ABE沿AE折起,使平面ABE ⊥平面ADE,连接BC、BD,得到如图2所示的四棱锥B﹣AECD.(Ⅰ)求证:CD⊥平面BOD;(Ⅱ)求直线AB与面BCD所成角的余弦值.(Ⅱ)由(Ⅰ)可知,四边形AECD的面积S=CD•OD=3……(7分)连接AC,则△ACD的面积S1=,三棱锥B=ACD的体积V=……(9分)△BCD的面积S2=……(10分)设A到平面BCD的距离为h,则h=,h=……(11分)直线AB与面BCD所成角的正弦值为,余弦值为……(12分)9(2018•永州三模)如图所示,在多面体ABC﹣A1B1C1中,D,E,F分别是AC,AB,CC1的中点,AC=BC=4,,CC1=2,四边形BB1C1C为矩形,平面ABC⊥平面BB1C1C,AA1∥CC1(1)求证:平面DEF⊥平面AA1C1C;(2)求直线EF与平面ABC所成的角的正切值.10(2018•桃城区校级模拟)如图,在三棱柱ABC﹣A1B1C1中,BC⊥平面AA1B1B,AB=AA1=2,∠A1AB=60°.(Ⅰ)证明:平面AB1C⊥平面A1BC;(Ⅱ)若四棱锥A﹣BB1C1C的体积为,求该三棱柱的侧面积.10证明:(1)在侧面A1ABB1中,∵A1A=AB,∴四边形A1ABB1是菱形,∴AB1⊥A1B∵CB⊥平面A1ABB1.AB1⊂平面A1ABB1,∴AB1⊥CB,∵A1B∩CB=B,∴AB1⊥平面A1CB.又∵AB1⊂平面AB1C;∴平面AB1C⊥平面A1BC;(2)由(1)及∠A1AB=60°得△A1BB1是等边三角形,取BB1的中点M,则A1M⊥BB1,又∵BC⊥平面AA1B1B,∴A1M⊥面CBB1C1,且A1M=∵四棱锥A﹣BB1C1C的体积为,∴V==∴BC=1,∴S=BB1×,S=1×2=2,在△CA1C1中,A1C1=A1C=,CC1=2,∴△A1CC1边CC1上的高为2,∴S=2×2=4.∴该三棱柱的侧面积为S=2+2+4=6+2.11.(2018•河南一模)如图所示,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,DC=DA=2AB=2,点E为AD的中点,BD∩CE=H,PH⊥平面ABCD,且PH=4.(1)求证:PC⊥BD(2)线段PC上是否存在一点F,使三棱锥P﹣BFD的体积为5?若存在,请找出点F 的位置;若不存在,请说明理由.(2)解:假设线段PC上存在一点F,使三棱锥P﹣BFD的体积为5,12(2018•商丘三模)如图,D是AC的中点,四边形BDEF是菱形,平面BDEF⊥平面ABC,∠FBD=60°,AB⊥BC,AB=BC=.(1)若点M是线段BF的中点,证明:BF⊥平面AMC;(2)求六面体ABCEF的体积.12证明:(1)连接MD,FD.∵四边形BDEF为菱形,且∠FBD=60°,∴△DBF为等边三角形.∵M为BF的中点,∴DM⊥BF.∵AB⊥BC,,又D是AC的中点,∴BD⊥AC.∵平面BDEF∩平面ABC=BD,平面ABC⊥平面BDEF,AC⊂平面ABC,∴AC⊥平面BDEF.又BF⊂平面BDEF,∴AC⊥BF.由DM⊥BF,AC⊥BF,DM∩AC=D,∴BF⊥平面AMC.13.(2018•内江三模)如图,四棱锥中P﹣ABCD,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,PA=PD,AD=2BC.(Ⅰ)证明:平面PAD⊥平面PCD;(Ⅱ)若△PAB是面积为的等边三角形,求四棱锥P﹣ABCD的体积.∴平面PAD⊥平面PCD.(Ⅱ)解:设AD的中点为E,连接PE,BE,∵PA=PD,∴PE⊥AD,∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,∴PE⊥底面ABCD.∵△PAB是面积为的等边三角形,∴PA=AB=PB=2,∵E是AD的中点,AD∥BC,∠ADC=90°,AD=2BC,∴四边形BCDE为矩形,∠AEB=90°,∴△AEB≌△PEB,故PE=AE,∴△PAE是等腰直角三角形,故AE=PE=PA=,∴在直角三角形AEB中有BE==,∴BC=BE=,AD=2,BC=,∴直角梯形ABCD的面积为(AD+BC)•CD=3,∴V P﹣ABCD=•S ABCD•PE=.14(2018•齐齐哈尔一模)如图,在直三棱柱ABC﹣A1B1C1中,BC=BB1,∠BAC=∠BCA=∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.(1)求证:BD⊥A1C;(2)求证:AB1⊥平面A1BC.(2)由(1)知AB=BC,AB⊥BC,…(7分)∵BB1=BC,∴四边形ABB1A1是菱形,∴AB1⊥A1B,…(8分)∵BB1⊥平面ABC,BC⊂平面ABC.∴BC⊥BB1…(9分)∵AB∩BB1=B,AB,BB1⊂平面ABB1A1.∴BC⊥平面ABB1A…(10分)∵AB1⊂平面ABB1A1,∴BC⊥AB1,…(11分)∵BC∩A1B=B,BC,A1B⊂平面A1BC,∴AB1⊥平面A1BC.…(12分)15(2018•孝义市一模)如图,三棱柱ABC﹣A1B1C1中,∠BCA=90°,AC1⊥平面A1BC.(1)证明:平面ABC⊥平面ACC1A1;(2)若BC=AC=2,A1A=A1C,求点B1到平面A1BC的距离.(2)解:取AC的中点D,连接A1D.∵A1A=A1C,∴A1D⊥AC.又平面ABC⊥平面ACC1A1,且交线为AC,则A1D⊥平面ABC.∵AC1⊥平面A1BC,∴AC1⊥A1C,∴四边形ACC1A1为菱形,∴AA1=AC.又A1A=A1C,∴△A1AC是边长为2正三角形,∴.∴.设点B1到平面A1BC的距离为h.则.又,∴.所以点B1到平面A1BC的距离为.。
