立体几何最值
高中数学立体几何中的最值问题专题辅导

高中数学立体几何中的最值问题 海红楼 立体几何主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、体积等最值问题常常在试题中出现。
下面举例说明解决这类问题的常用方法。
一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2,底面边长为2,点P 、Q 分别在线段BD 、SC 上移动,则P 、Q 两点的最短距离为( )A. 55B. 552C. 2D. 1解析:如图1,由于点P 、Q 分别在线段BD 、SC 上移动,先让点P 在BD 上固定,Q 在SC 上移动,当OQ 最小时,PQ 最小。
过O 作OQ ⊥SC ,在Rt △SOC 中,552=OQ 中。
又P 在BD 上运动,且当P 运动到点O 时,PQ 最小,等于OQ 的长为552,也就是异面直线BD 和SC 的公垂线段的长。
故选B 。
图1二、定性分析法求最值例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。
AB ⊥CD ,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为______。
解析:如图2,过点B 作平面α的垂线,垂足为O ,连结AO ,则∠BAO=30°。
过B 作BE//CD 交平面α于E ,则BE=CD 。
连结AE ,因为AB ⊥CD ,故AB ⊥BE 。
则在Rt △ABE 中,BE=AB ·tan ∠BAE ≥AB ·tan ∠BAO=3·tan30°=3。
故3≥CD 。
图2三、展成平面求最值例3. 如图3-1,四面体A-BCD 的各面都是锐角三角形,且AB=CD=a ,AC=BD=b ,AD=BC=c 。
平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ,则四边形PQRS 的周长的最小值是( )A. 2aB. 2bC. 2cD. a+b+c图3-1解析:如图3-2,将四面体的侧面展开成平面图形。
【高考数学大题精做】专题05 立体几何中最值问题(第三篇)(解析版)

【高考数学大题精做】第三篇 立体几何专题05 立体几何中最值问题【典例1】【河南省非凡吉创联盟2020届调研】如图,AB 是圆柱的直径,PA 是圆柱的母线,3AB =,PA =,点C 是圆柱底面圆周上的点.(1)求三棱锥P ABC -体积的最大值;(2)若1AC =,D 是线段PB 上靠近点P 的三等分点,点E 是线段PA 上的动点,求CE ED +的最小值. 【思路引导】(1)三棱锥的高为定值,要根据三棱锥体积公式13V Sh =可知,要使得体积最大,就要底面积最大,又因为边AB 为定值,故当C 到AB 的距离取得最大值时,底面积最大,故此时棱锥的体积最大;(2)反向延长AB 至C ',使得,,C D E '三点共线,三点共线时,距离最短,则C D '为CE ED +最小值. 【详解】(1)三棱锥P ABC -高h =,3AB =,点C 到AB 的最大值为底面圆的半径32,则三棱锥P ABC -体积的最大值等于1133322⨯⨯⨯=. (2)将PAC ∆绕着PA 旋转到PAC '使其共面,且C '在AB 的反向延长线上,连接C D ',C D '与PA 的交点为E ,此时CE ED +最小,为C D ';由3AB =,PA =且易知PA AB ⊥,由勾股定理知6PB =,因为12AB PB =,所以30APB ∠=o ,则60DBC ∠='o ,243BD PB ==; 134C B C A AB '+=+'==,则BDC '∆是边长为4的等边三角形,故4C D '=,所以CE ED +的最小值等于4.【典例2】【江西省新余市第四中学2020届月考】 已知梯形ABCD 中,AD ∥BC ,∠ABC =∠BAD =2π,AB=BC=2AD=4,E 、F 分别是AB 、CD 上的点,EF ∥BC ,AE =x ,G 是BC 的中点.沿EF 将梯形ABCD 翻折,使平面AEFD ⊥平面EBCF .(1)若以F 、B 、C 、D 为顶点的三棱锥的体积记为()f x ,求()f x 的最大值; (2)当 ()f x 取得最大值时,求二面角D -BF -C 的余弦值. 【思路引导】(1)由AEFD ⊥平面EBCF ,////EF BC AD ,可得AE EF ⊥,进而由面面垂直的性质定理得到AE ⊥平面EBCF ,进而建立空间坐标系E xyz -,可得()D BCF A BFC f x V V --==的解析式,根据二次函数的性质,易求出()f x 有最大值;(2)根据(1)的结论平面BCF 的一个法向量为()20,0,1n =u u v ,利用向量垂直数量积为零列方程组求出平面BDF 的法向量,代入向量夹角公式即可得到二面角D BF C --的余弦值.解:(1)∵平面AEFD ⊥平面EBCF ,AE ⊥EF,∴AE ⊥面平面EBCF ,AE ⊥EF,AE ⊥BE,又BE ⊥EF,故可如图建立空间坐标系E -xy z .则A (0,0,2),B (2,0,0),G (2,2,0),D (0,2,2), E (0,0,0)∵AD ∥面BFC ,所以()f x =V A -BFC =13BFC S AE ∆⋅ ()114432x x ⋅⋅⋅-⋅ ()22882333x =--+≤,即2x =时()f x 有最大值为83.(2)设平面DBF 的法向量为()1,,n x y z =u v,∵AE=2, B (2,0,0),D (0,2,2),F (0,3,0),∴()2,3,0,BF =-u u u v BD =u u u v (-2,2,2),则1100n BD n BF ⎧⋅=⎪⎨⋅=⎪⎩u v u u u vu v u u u v ,即()()()(),,2,2,20,,2,3,00x y z x y z ⎧⋅-=⎪⎨⋅-=⎪⎩,2220230x y z x y -++=⎧⎨-+=⎩ 取x =3,则y =2,z =1,∴()13,2,1n u v=面BCF 的一个法向量为()20,0,1n =u u v则cos<12,n n u v u u v>=121214n n n n u v u u v u v u u v ⋅=⋅. 由于所求二面角D -BF -C的平面角为钝角,所以此二面角的余弦值为:-14【典例3】【北京市昌平区2020届模拟】如图,在长方体ABCD -A 1B 1C 1D 1中,E ,H 分别是棱A 1B 1,D 1C 1上的点(点E 与B 1不重合),且EH ∥A 1D 1. 过EH 的平面与棱BB 1,CC 1相交,交点分别为F ,G .(I )证明:AD ∥平面EFGH ;(II ) 设AB=2AA 1="2" a .在长方体ABCD -A 1B 1C 1D 1内随机选取一点.记该点取自几何体A 1ABFE -D 1DCGH 内的概率为p ,当点E ,F 分别在棱A 1B 1上运动且满足EF=a 时,求p 的最小值.【思路引导】 解法一:(I ) 证明:在长方体ABCD -A 1B 1C 1D 1中,AD ∥A 1D 1 又∵EH ∥A 1D 1,∴AD ∥EH. ∵AD ¢平面EFGH EH 平面EFGH ∴AD//平面EFGH.(II ) 设BC=b ,则长方体ABCD -A 1B 1C 1D 1的体积V=AB·AD·AA 1=2a 2b , 几何体EB 1F -HC 1G 的体积V 1=(1/2EB 1 ·B 1F )·B 1C 1=b/2·EB1·B 1 F ∵EB 12+ B 1 F 2=a 2∴EB 12+ B 1 F 2≤ (EB 12+ B 1 F 2)/2 = a 2 / 2,当且仅当EB1=B 1F=2a 时等号成立 从而V 1≤ a 2b /4 .故 p=1-V 1/V ≥22412a ba b-=78 解法二:(I ) 同解法一(II ) 设BC=b ,则长方体ABCD -A 1B 1C 1D 1的体积V=AB·AD·AA 1=2a 2b , 几何体EB 1F -HC 1G 的体积V 1=(1/2 EB1·B 1 F )·B 1C 1=b/2 EB1·B 1 F设∠B 1EF=θ(0°≤θ≤90°),则EB1=" a" cosθ,B 1 F ="a" sinθ 故EB1·B 1 F = a 2sinθcosθ=,当且仅当sin 2θ=1即θ=45°时等号成立.从而214a bV ≤ ∴p=1- V 1/V≥22412a ba b-=78,当且仅当sin 2θ=1即θ=45°时等号成立.所以,p 的最小值等于7/81. 【广东省佛山市第一中学2020届月考】如图,正方体1111ABCD A B C D -的棱长为a ,E F 、分别为AB BC 、上的点,且AE BF x ==.(1)当x 为何值时,三棱锥1B BEF -的体积最大? (2)求异面直线1A E 与1B F 所成的角的取值范围. 【思路引导】(1)首先得到体积函数,然后利用均值不等式确定取得最值时x 的值即可;(2)首先作出异面直线1A E 与1B F 所成的角,然后结合余弦定理求得角的余弦值取值范围,最后利用余弦值的范围确定异面直线1A E 与1B F 所成的角的取值范围. 【详解】 (1),当2ax =时,三棱锥1B BEF -的体积最大. (2)在AD 上取点H 使AH =BF =AE ,则,,,所以1HA E∠(或补角)是异面直线1A E 与1B F 所成的角;在Rt △1A AH 中,1A H =在Rt △1A AE 中,1A E =在Rt △HAE 中,HE ==,在△1HA E 中,222111112A H A E EH cosHA E A H A E +-=⋅ 222a a x=+, 因为0x a <≤,所以22222a x a a <+≤,222112a x a≤<+,1112cosHA E ≤<,1π03HA E <∠≤ 2.【安徽省安庆市2020届模拟】如图,△ABC 内接于圆O ,AB 是圆O 的直径,四边形DCBE 为平行四边形,DC ⊥平面ABC ,2,AB EB ==(1)求证:DE ⊥平面ADC ;(2)设AC x =,(x)V 表示三棱锥B ACE -的体积,求函数(x)V 的解析式及最大值. 【思路引导】(1)要证(1)要证DE ⊥平面ADC ,需证BC ⊥平面ADC ,需证DC BC BC AC ⊥⊥,,用综合法书写即可.(2)由(1)可知BE ⊥平面ABC ,所以体积为13ABC BE S ⨯, AC x BC EB ===,均值不等式求解最大值.详解:(1)证明:∵四边形DCBE 为平行四边形,∴CD ∥BE ,BC ∥DE . ∵DC ⊥平面ABC ,BC ⊂平面ABC ,∴DC ⊥BC . ∵AB 是圆O 的直径,∴BC ⊥AC ,且DC ∩AC =C . ∴BC ⊥平面ADC .∵DE ∥BC ,∴DE ⊥平面ADC ; (2)∵DC ⊥平面ABC ,∴BE ⊥平面ABC . 在Rt △ABE 中,AB =2,EB =3√.在Rt △ABC 中,∵AC =x ,BC =4−x 2−−−−−√(0<x <2). ∴S △ABC =12AC ⋅BC =12x ⋅4−x 2−−−−−√, ∴V (x )=VE −ABC =3√6x ⋅4−x 2−−−−−√,(0<x <2).∵x 2(4−x 2)⩽(x 2+4−x 22)2=4,当且仅当x 2=4−x 2,即x =2√时,取等号, ∴x =2√时,体积有最大值为3√3.3.【浙江省金华市十校2020届模拟】如图,在三棱锥P ABC -中,AB BC =,AP PC =,60ABC ∠=︒,AP PC ⊥,直线BP 与平面ABC 成30°角,D 为AC 的中点,PQ PC λ=u u u v u u u v,(0,1)λ∈.(Ⅰ)若PB PC >,求证:平面ABC ⊥平面PAC ;(Ⅰ)若PC PB <,求直线BQ 与平面PAB 所成角的正弦值的取值范围. 【思路引导】由题意可得直线BP 与平面ABC 所成角是PBD ∠,即30PBD ∠=︒.设2AC a =,则BD =,PD a =,由余弦定理得PB a =或2a .(Ⅰ)若PB PC >,则2PB a =,由勾股定理可得PD DB ⊥,又PD AC ⊥,据此可得PD ⊥平面ABC ,平面PAC ⊥平面ABC .(Ⅰ)若PB PC <,则PB a =,故PQ a =,BQ =,设Q h 是Q 到面PAB 的距离,C h 是C 到面PAB 的距离,则Q C h h λ=,由等体积法可得7C h a =,7Q h a λ=.设直线BQ 与平面PAB 所成角为α,则sin α=,据此可得直线BQ 与平面PAB 所成角的正弦值的取值范围为0,7⎛ ⎝⎭.试题解析:∵AB BC =,AP PC =,D 为AC 的中点,∴BD AC ⊥,PD AC ⊥,∴AC ⊥平面PBD , ∴直线BP 与平面ABC 所成角是PBD ∠,30PBD ∠=︒. 设2AC a =,则BD =,PD a =,由余弦定理得PB a =或2a .(Ⅰ)若PB PC >,则2PB a =,∴在PBD ∆中222PD DB PB +=.∴PD DB ⊥, 又PD AC ⊥,AC DB D ⋂=,∴PD ⊥平面ABC ,∴平面PAC ⊥平面ABC . (Ⅰ)若PB PC <,∴PB a =,∵PQ PC λ=u u u v u u u v,∴PQ a =,BQ =,设Q h 是Q 到面PAB 的距离,C h 是C 到面PAB 的距离,则Q C h h λ=,由等体积法:)2112323C aa a h ⋅=⋅,∴7C h a =,∴7Q h a λ=. 设直线BQ 与平面PAB 所成角为α,则HQsin BQα==a=7=.∵()0,1λ∈10,2⎛⎫ ⎪⎝⎭.∴0sin α<<故直线BQ 与平面PAB所成角的正弦值的取值范围为0,7⎛ ⎝⎭. 4.【北京市城六区2019届高三模拟】已知三棱锥P ABC -(如图1)的平面展开图(如图2)中,四边形ABCD的正方形,△ABE 和△BCF 均为正三角形,在三棱锥P ABC -中: (I)证明:平面PAC ⊥平面ABC ; (Ⅰ)求二面角A PC B --的余弦值; (Ⅰ)若点M 在棱PC 上,满足CMCP λ=,12[,]33λ∈,点N 在棱BP 上,且BM AN ⊥,求BN BP的取值范围.【思路引导】第一问取AC 中点O ,根据等腰三角形的性质求得PO AC ⊥,根据题中所给的边长,利用勾股定理求得PO OB ⊥,利用线面垂直的判定定理以及面面垂直的判定定理得到结果;第二问根据题中所给的条件建立空间直角坐标系,写出相应的点的坐标,求得面的法向量,利用法向量所成角的余弦值得出结果;第三问利用向量间的关系,利用向量垂直的条件,利用向量的数量积等于0,得出所求的比值μ与λ的关系式,利用函数的有关知识求得结果. (Ⅰ)方法1:设AC 的中点为O ,连接BO ,PO . 由题意PA PB PC ===,1PO =,1AO BO CO ===因为在PAC ∆中,PA PC =,O 为AC 的中点 所以PO AC ⊥,因为在POB ∆中,1PO =,1OB =,PB =所以PO OB ⊥因为AC OB O ⋂=,,AC OB ⊂平面ABC 所以PO ⊥平面ABC 因为PO ⊂平面PAC 所以平面PAC ⊥平面ABC 方法2:设AC 的中点为O ,连接BO ,PO .因为在PAC ∆中,PA PC =,O 为AC 的中点 所以PO AC ⊥,因为PA PB PC ==,PO PO PO ==,AO BO CO == 所以POA ∆≌POB ∆≌POC ∆ 所以90POA POB POC ∠=∠=∠=︒ 所以PO OB ⊥因为AC OB O ⋂=,,AC OB ⊂平面ABC 所以PO ⊥平面ABC 因为PO ⊂平面PAC 所以平面PAC ⊥平面ABC 方法3:设AC 的中点为O ,连接PO ,因为在PAC ∆中,PA PC =, 所以PO AC ⊥设AB 的中点Q ,连接PQ ,OQ 及OB . 因为在OAB ∆中,OA OB =,Q 为AB 的中点 所以OQ AB ⊥.因为在PAB ∆中,PA PB =,Q 为AB 的中点 所以PQ AB ⊥.因为PQ OQ Q ⋂=,,PQ OQ ⊂平面OPQ所以AB ⊥平面OPQ因为OP ⊂平面OPQ所以OP AB ⊥因为AB AC A ⋂=,,AB AC ⊂平面ABC所以PO ⊥平面ABC因为PO ⊂平面PAC所以平面PAC ⊥平面ABC(Ⅰ)由PO ⊥平面ABC ,OB AC ⊥,如图建立空间直角坐标系,则()0,0,0O ,()1,0,0C ,()0,1,0B ,()1,0,0A -,()0,0,1P 由OB ⊥平面APC ,故平面APC 的法向量为()0,1,0OB =u u u v 由()1,1,0BC =-u u u v ,()1,0,1PC =-u u u v设平面PBC 的法向量为(),,n x y z =v ,则由00n BC n PC ⎧⋅=⎨⋅=⎩u u u vu u u v 得:00x y x z -=⎧⎨-=⎩令1x =,得1y =,1z =,即()1,1,1n =vcos ,nOBn OB n OB ⋅===⋅u u u vv u u u v v u u u v v由二面角A PC B --是锐二面角,所以二面角A PC B --的余弦值为3(Ⅰ)设BN BP μ=u u u v u u u v ,01μ≤≤,则()()()1,1,01,0,11,1,BM BC CM BC CP λλλλ=+=+=-+-=--u u u u v u u u v u u u u v u u u v u u u v ()()()1,1,00,1,11,1,AN AB BN AB BP μμμμ=+=+=+-=-u u u v u u u v u u u v u u u v u u u v 令0BM AN ⋅=u u u u v u u u v得()()()11110λμλμ-⋅+-⋅-+⋅= 即1111λμλλ==-++,μ是关于λ的单调递增函数, 当12,33λ⎡⎤∈⎢⎥⎣⎦时,12,45μ⎡⎤∈⎢⎥⎣⎦, 所以12,45BN BP ⎡⎤∈⎢⎥⎣⎦。
立体几何中线段长度的最值问题
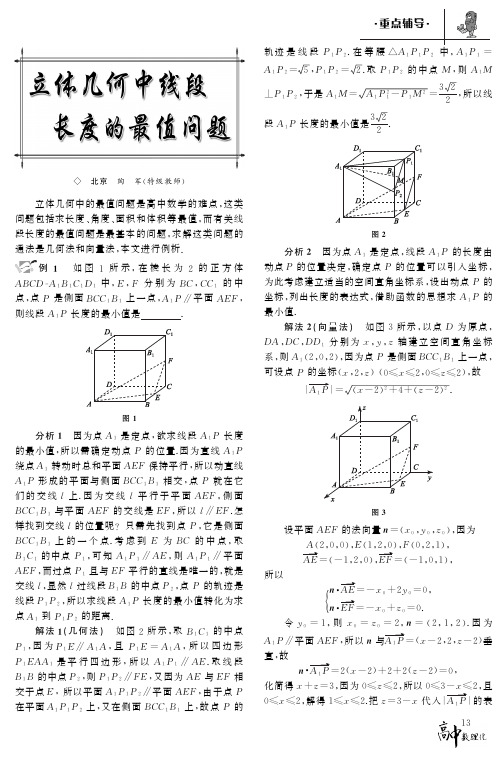
重点辅导Җ㊀北京㊀陶㊀军(特级教师)㊀㊀立体几何中的最值问题是高中数学的难点,这类问题包括求长度㊁角度㊁面积和体积等最值,而有关线段长度的最值问题是最基本的问题,求解这类问题的通法是几何法和向量法,本文进行例析.例1㊀如图1所示,在棱长为2的正方体A B C D GA 1B 1C 1D 1中,E ,F 分别为B C ,C C 1的中点,点P 是侧面B C C 1B 1上一点,A 1P ʊ平面A E F ,则线段A 1P 长度的最小值是.图1分析1㊀因为点A 1是定点,欲求线段A 1P 长度的最小值,所以需确定动点P 的位置.因为直线A 1P 绕点A 1转动时总和平面A E F 保持平行,所以动直线A 1P 形成的平面与侧面B C C 1B 1相交,点P 就在它们的交线l 上.因为交线l 平行于平面A E F ,侧面B C C 1B 1与平面A E F 的交线是E F ,所以l ʊE F .怎样找到交线l 的位置呢?只需先找到点P ,它是侧面B C C 1B 1上的一个点.考虑到E 为B C 的中点,取B 1C 1的中点P 1,可知A 1P 1ʊA E ,则A 1P 1ʊ平面A E F ,而过点P 1且与E F 平行的直线是唯一的,就是交线l ,显然l 过线段B 1B 的中点P 2,点P 的轨迹是线段P 1P 2,所以求线段A 1P 长度的最小值转化为求点A 1到P 1P 2的距离.解法1(几何法)㊀如图2所示,取B 1C 1的中点P 1,因为P 1E ʊA 1A ,且P 1E =A 1A ,所以四边形P 1E A A 1是平行四边形,所以A 1P 1ʊA E .取线段B 1B 的中点P 2,则P 1P 2ʊF E ,又因为A E 与E F 相交于点E ,所以平面A 1P 1P 2ʊ平面A E F ,由于点P 在平面A 1P 1P 2上,又在侧面B C C 1B 1上,故点P 的轨迹是线段P 1P 2.在等腰әA 1P 1P 2中,A 1P 1=A 1P 2=5,P 1P 2=2.取P 1P 2的中点M ,则A 1M ʅP 1P 2,于是A 1M =A 1P 21-P 1M 2=322,所以线段A 1P 长度的最小值是322.图2分析2㊀因为点A 1是定点,线段A 1P 的长度由动点P 的位置决定,确定点P 的位置可以引入坐标,为此考虑建立适当的空间直角坐标系,设出动点P 的坐标,列出长度的表达式,借助函数的思想求A 1P 的最小值.解法2(向量法)㊀如图3所示,以点D 为原点,D A ,D C ,D D 1分别为x ,y ,z 轴建立空间直角坐标系,则A 1(2,0,2),因为点P 是侧面B C C 1B 1上一点,可设点P 的坐标(x ,2,z )(0ɤx ɤ2,0ɤz ɤ2),故|A 1P ң|(x -2)2+4+(z -2)2.图3设平面A E F 的法向量n =(x 0,y 0,z 0),因为A (2,0,0),E (1,2,0),F (0,2,1),A E ң=(-1,2,0),E F ң=(-1,0,1),所以n A E ң=-x 0+2y 0=0,n E F ң=-x 0+z 0=0.{令y 0=1,则x 0=z 0=2,n =(2,1,2).因为A 1P ʊ平面A E F ,所以n 与A 1P ң=(x -2,2,z -2)垂直,故n A 1P ң=2(x -2)+2+2(z -2)=0,化简得x +z =3,因为0ɤz ɤ2,所以0ɤ3-x ɤ2,且0ɤx ɤ2,解得1ɤx ɤ2.把z =3-x 代入|A 1P ң|的表31重点辅导达式,整理得|A 1P ң|=2(x -32)2+92,x ɪ[1,2],故当x =32时,|A 1P ң|取得最小值322.例2㊀如图4所示,在棱长为2的正方体A B C D GA 1B 1C 1D 1中,E 为B C 的中点,点P 在线段D 1E 上,点P 到直线C C 1的距离的最小值为.图4分析1㊀求点P 到直线C C 1的距离的最小值,就是找点P 到直线C C 1的垂线段P Q 长度的最小值.求线段P Q 的长度涉及空间上两个动点长度的距离问题,不易处理.注意到C C 1ʅ平面A B C D ,P Q ʅC C 1,则P Q ʊ平面A B C D .因此,我们可以把P Q 正投影在平面A B C D 上,点P 在平面A B C D 上的正投影H 落在线段D E 上,点Q 在平面A B C D 上的正投影是点C ,于是P Q =H C ,求P Q 的最小值转化为在平面A B C D 上求定点C 与线段D E 上的动点H 之间距离的最小值,就是求定点C 到D E 的距离.解法1(几何法)㊀如图5所示,过点P 作P Q ʅC C 1,Q 为垂足,因为C C 1ʅ平面A B CD ,所以P Q ʊ平面A B C D ,过点P 作PH ʅDE ,H 为垂足,则PH ʅ平面A B C D ,所以PH ʊQ C ,且P Q ʊH C ,Q C ʅH C ,故四边形P Q C H 是矩形,P Q =H C ,在R t әC D E 中,当C H ʅD E 时,C H 长度最小,因为C E =1,C D =2,D E =5,所以C H =1ˑ25=255,故点P 到直线C C 1的距离的最小值为255.图5分析2㊀设点P 到直线C C 1的距离为P Q ,因为P ,Q 分别在线段D 1E 和C C 1上,故可以引入两个变量控制点P ,Q 的位置.设E P ң=λE D 1ң(0ɤλɤ1),C Q ң=μC C 1ң(0ɤμɤ1),根据正方体的特殊性建立适当的空间直角坐标系,利用向量的坐标运算推出点P ,Q 的坐标,进而用λ,μ表示P Q ң,利用P Q ң C C 1ң=0找出λ,μ的关系式,代入P Q 长度的表达式,转化为一元函数求最值.解法2(向量法)㊀如图6所示,以D 为原点,D A ,D C ,D D 1分别为x ,y ,z 轴建立空间直角坐标系,则D 1(0,0,2),E (1,2,0),C 1(0,2,2),C (0,2,0),E D 1ң=(-1,-2,2),由于点P 在线段D 1E 上,可设E P ң=λE D 1ң(0ɤλɤ1),即E P ң=(-λ,-2λ,2λ),由此得点P 的坐标为(,,).图6过点P 作P Q 垂直于C C 1,Q 为垂足,设点Q 的坐标(0,2,m ),P Q ң=(λ-1,2λ,m -2λ),C C 1ң=(0,0,2),因为P Q ңʅC C 1ң,所以P Q ң C C 1ң=0,即2(m -2λ)=0,m =2λ,P Q ң=(λ-1,2λ,0),|P Q ң|=(λ-1)2+(2λ)2+02=5(λ-15)2+45,λɪ[0,1].当λ=15,P Q 取得最小值255.综上所述,利用几何法求线段长度的最值,要点是先用立体几何知识确定动点的轨迹,再用平面几何知识求最值;利用向量法求线段长度的最值,要点是建立适当的坐标系,设出动点坐标,建立线段长度的表达式,借助向量知识把题目中的几何条件合理转化为代数条件,找到动点坐标的关系,把线段长度的表达式转化为一元函数,用函数的思想求最值.(作者单位:北京市怀柔区第一中学)41。
高中数学立体几何中的最值问题

高中数学立体几何中的最值问题在高中数学的学习中,立体几何一直是一个重点和难点,而其中的最值问题更是让许多同学感到头疼。
这类问题往往需要我们综合运用空间想象力、几何知识以及数学方法来求解。
接下来,让我们一起深入探讨立体几何中的最值问题。
一、常见类型及解法1、距离最值问题(1)两点间距离最值在立体几何中,求两点间距离的最值,常常需要我们将空间中的两点转化到同一平面内。
例如,在长方体中,求异面直线上两点的最短距离,就需要通过平移将其转化为共面直线,然后利用平面几何中的知识求解。
(2)点到直线距离最值求点到直线的距离最值时,通常要找到点在直线上的投影。
如果直线是某一平面的斜线,那么可以通过作垂线找到投影,再利用勾股定理计算距离。
(3)点到平面距离最值对于点到平面的距离最值,一般可以利用空间向量法。
先求出平面的法向量,然后通过向量的数量积来计算点到平面的距离。
2、面积最值问题(1)三角形面积最值在立体几何中,涉及三角形面积的最值问题,可能需要考虑三角形的边长关系或者角度大小。
例如,已知三角形的两边及其夹角,当夹角为直角时,面积最大。
(2)四边形面积最值对于四边形,如平行四边形,其面积可以表示为底边乘以高。
当底边长度固定时,高取得最大值时面积最大;或者当四边形的对角线相互垂直时,面积等于对角线乘积的一半。
3、体积最值问题(1)柱体体积最值对于柱体,如圆柱、棱柱,其体积等于底面积乘以高。
当底面积不变时,高最大则体积最大;反之,高最小时体积最小。
(2)锥体体积最值锥体体积为三分之一底面积乘以高。
在求解锥体体积最值时,需要关注底面积和高的变化。
二、例题分析例 1:在棱长为 2 的正方体 ABCD A1B1C1D1 中,E、F 分别是棱AB、BC 的中点,求点 A1 到直线 EF 的距离。
解:连接 A1C1、C1F、EF,因为 A1C1 平行于 EF,所以点 A1 到直线 EF 的距离等于点 A1 到直线 C1F 的距离。
立体几何的最值问题

立体几何最值问题立体几何是数学中的一个重要分支,它研究的是空间图形的性质和数量关系。
在立体几何中,我们经常遇到最值问题,即寻找某个量的最大值或最小值。
本文将介绍立体几何中最值问题的几个方面:1.立体几何位置关系立体几何中的位置关系是指空间中点、线、面之间的相对位置。
解决位置关系问题需要运用空间想象和逻辑推理。
在立体几何中最值问题中,位置关系往往与距离、角度等问题交织在一起,需要综合考虑多种因素。
2.立体几何中的距离立体几何中的距离是指空间中两点之间的直线距离,或者是点与线、线与面之间的距离。
在解决最值问题时,我们需要考虑如何利用距离公式来计算最短路径、最大距离等。
3.立体几何中的体积立体几何中的体积是指空间中封闭图形的体积,或者是两个平面图形之间的距离。
计算体积需要运用体积公式,而解决最大或最小面积问题则需要考虑如何调整图形的形状和大小。
4.立体几何中的最短路径立体几何中的最短路径问题是指寻找空间中两点之间的最短距离。
解决这类问题需要运用距离公式和几何定理,有时还需要借助对称、旋转等技巧。
5.立体几何中的最大/最小面积立体几何中的最大/最小面积问题通常涉及到平面图形在空间中的展开和折叠。
解决这类问题需要运用面积公式和平面几何定理,同时要注意图形的对称性和边长之间的关系。
6.立体几何中的角度问题立体几何中的角度问题是指空间中两条直线或两个平面之间的夹角。
解决这类问题需要运用角度公式和空间向量,同时要注意图形的对称性和边长之间的关系。
7.立体几何中的轨迹问题立体几何中的轨迹问题是指一个点或一条线在空间中按照一定规律移动所形成的轨迹。
解决这类问题需要运用轨迹方程和运动学原理,同时要注意轨迹的形状和大小随时间的变化情况。
立体几何第三讲 空间几何体得最值问题

分清定量与变量,然后根据变量的取值情况,利用函数法或平面几何的相关结论判断相应的
最值.如该题中确定三棱锥底面的面积最值是关键.
【玩转跟踪】在棱长为 1 的正方体 ABCD A1B1C1D1 中,点 P1, P2 分别是线段 AB 、BD1(不
包括端点)上的动点,且线段 P1P2 平行于 平面 A1 ADD1 ,则四面体 P1P2 AB 的体积的最大值
锥 P-AEF 的底面积和高,高为定值时,底面积最大,则体积最大.
【解析】因为 PA 平面 ABC, BC 平面 ABC,所以 PABC 又因为 BCAC, PA AC A ,所以 BC 平面 PAC,又 AF 平面 PAC,所以 BCAF , 又 AFPC, PC BC C ,所以 AF 平面 PBC,即 AFEF 。EF 是 AE 在平面 PBC 上的 射影,因为 AEPB ,所以 EFPB ,即 PE 平面 AEF。在三棱锥 P AEF 中, AP AB 2, AEPB ,
5
.
5
又 P 在 BD 上运动,且当 P 运动到点 O 时,PQ 最小,等于 OQ 的长为 2 5 ,也就是异面直 5
线 BD 和 SC 的公垂线段的长.故选 B. 2.几何体表面上的最短距离问题
【例 2】正三棱柱 ABC—A1B1C1 中,各棱长均为 2,M 为 AA1 中点,N 为 BC 的中点,则 在棱柱的表面上从点 M 到点 N 的最短距离是多少?并求之.
又∵ 0<α+β<π,∴(α+β)max=π-arctan 2 ,(α+β)min=π-arctan2 2 .
【迁移运用】
1.【西藏日喀则一中高三 10 月检测】已知正三C 的距离为1,点 是线段 的中点,过点 作球 的截面,则截面面
立体几何中的最值问题求解策略

化
中 , 面 积 最 小 的 是 一 个 四 棱 柱 , a 的 取 值 范 围 全 则
分别 变为 A ( , ) 3 5 ,故A ( , ) 0 5 、B ( , ) B 一 3 0 ,应
彝 辜
决的. 2 割 补 思 想
* ●’
参彝艟平单 位 :山 东省大 化 中 学 ) 移影晌 莱小 城 不啊量 芜 市凤 高级 ( 者 作
例 2 有 2 相 同的直三 棱柱 ( 图 2所示 ) 高 个 如 ,
甲
乙
圈 1
丙
) .
1 )如 图 1 甲, A c一 ̄( Bl )+B /A +B B C 一
错 解 由 A ( , ) B( , ) AB= O 12 、 24 得 B— O 一 A ( , ) ( ,) ( ,) 将 z一 3 一 0及 h 一 1 志 4 2 一 12 一 3 O , , 一 ,一 3代 人 平 移 / 1 A一何
.
乙 , c /AB+B )+AA A 一 ̄( c 一
一
.
I 十 得‘ 选 . 意{ ’ D z 故 : 一
,
= x+ h ’
I
,
l 一 , Y
平 移 公 式 揭 示 的 是 点 沿 着 向 量 平 移 前 后
丙 , 一 ̄( A1 c /AA +AD) +DC 一
另 一 个 是 乘 法 结 合 律 :n・ )・ v a・ 6・ ) ( 6 c/ = ( c.
立体几何最值问题求解的四大策略

1 棱 AB平行 于平 面 n 则 正 四 面体 上 的所有 点 在 平 , ,
是
析
.
c s , 定 区 间 ( , ) 有 f ( ) 0 则 函数 0 - 给 z一 7 O T , 1 < , z
当C / D/ a时 , 影 为 正 方 形 AD C , 时 射 B 此
,
过 E作 EHj BB 于 H , 以 _ 。 所
EF 一
面
√ ) (譬 √ + . ( 1 ) ++ = =
ABCDn 面 ABEF— AB, AB _BE, 以 BE _ 面 J 所 上 I
ABCD. 以 AB、 所 BC、 BE
图 4丙 ( A 沿 C 展 开 )
而使 问题 得 以解 决.
,.
例 2 如 图 3所 示 , 直 三 棱 柱 AB - B C 在 CA。
喜欢 读 书 , 等 于把 生活 中寂 寞 的 辰光 换 成 巨大 享 受 的 时刻 就
— —
孟 德 斯 鸠
中, AB — BC 一 , / 2,B 一 2 B ,
?
例 l 如 图 1所 示 , 四面 体 AB D 的棱 长 为 正 C
由 √。_1 . 令 数(一 面 a 内 的 射 影 构 成 的 图 形 面 积 的 取 值 范 围 于 一 + 函 厂) _ 1 /- , 可 x
 ̄ s , 厂( ) 一√ CS , f ( ) , /i 则 n 1 一1 O 令 z 一0得 z
能力.
( 者 单 位 . 京 市 第八 十 巾 晕 ) 作 北
◇彝 主翥喜 兰
的问题 , 可放入 正方体 中来考虑. 也 策 略 2 曲中求值 , 直处理 化
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何最值
A、
B、
C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
____________2、半径为4的球面上有A,B,C,D四点,且满足ABAC,ACAD,ADAB,则的最大值为____________3、某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为和的线段,则的最大值为()
A、
B、
C、4
D、4、在单位正方体ABCD-A的面对角线A上存在一点P使得AP+最短,则AP+的最小值为____________SDCQBAPO5、在正四棱锥S-ABCD中,SO⊥平面ABCD于O,SO=2,底面边长为,点P、Q分别在线段B
D、SC上移动,则P、Q两点的最短距离为()
A、
B、
C、2
D、
16、如图已知在中,,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,当AP=AB=2,,当变化时,三棱锥P-AEF体积的最大值为____________7、(xx•江西)如图,四棱锥P﹣ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.(1)求证:AB⊥PD;(2)若∠BPC=90,PB=,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.8、棱长为的正四面体内切一球,然后再正四面体和该球形成的空隙处各放一个小球,则这些小球的最大半径为__________。
