2019化学竞赛—结构化学—晶体结构与对称性
化学竞赛专题辅导资料——晶体结构

郴州市二中高一化奥班辅导资料——晶体结构(2008-05-28)【涉及概念和内容】根据《化学课程标准》和中学化学教材以及《物质结构与性质》选修教材,晶体结构涉及的内容包括:(1)基本概念:周期性有序排列、晶胞及晶胞类型、晶胞中粒子数的计算、配位数、空隙、堆积方式、晶格能、并置碓砌;(2)堆积方式:面心立方、六方、体心立方和简单立方堆积;(3)晶体种类和性质:金属晶体、离子晶体、分子晶体、原子晶体,自范性、各向异性、金属晶体的导电导热和延展性、X-射线衍射。
这些内容看似零碎,实际上它们有着密切的内在联系,了解和建立它们的关系,对于晶体结构的教与学,深刻理解晶体结构和性质,掌握核心、突出重点都是很重要的。
它们的联系可以用下面的结构表示,其中堆积类型是联系晶体基本概念、基本结构与不同晶体类型的结构和性质的桥梁。
面心立方最密堆积(A1)最密堆积六方最密堆积(A3)体心立方密堆积(A2)简单立方堆积金刚石型堆积(四面体堆积)(A4)一、晶体的结构1、晶体的概念晶体是质点(原子、分子、离子)在空间有规律周期性地重复排列,是具有规则的多面体固体物质。
2自范性:在一定条件下晶体能自动地呈现具有一定对称性的多面体的外形(晶体的形貌)。
非晶体不能呈现多面体的外形。
晶态石英的谱图非晶态石英的谱图3、晶体的点阵结构概念:在晶体内部原子或分子周期性地排列的每个重复单位的相同位置上定一个点,这些点按一定周期性规律排列在空间,这些点构成一个点阵。
点阵是一组无限的点,连结其中任意两点可得一矢量,将各个点阵按此矢量平移能使它复原。
点阵中每个点都具有完全相同的周围环境。
晶体结构= 点阵+ 结构基元结构基元:在晶体的点阵结构中每个点阵所代表的具体内容,包括原子或分子的种类和数量及其在空间按一定方式排列的结构。
(1)直线点阵(2)平面点阵(3)晶胞(晶胞是人为划定的,为平行六面体)空间点阵必可选择3个不相平行的连结相邻两个点阵点的单位矢量a,b,c,它们将点阵划分成并置的平行六面体单位,称为点阵单位。
高中化学竞赛【晶体的对称性】

晶面3
c
晶面2
晶面1
b a
晶面指标示例
例题: 1. 某一立方晶系晶体,晶胞的顶点位置全为
A占据,棱心为B占据, 体心为C占据。①写
出此晶体的化学组成; ②写出A、B、C的
(4)十四种空间点阵形式 立方晶系有立方简单点阵P (立方P ) 、立方
体心点阵I (立方I ) 、立方面心点阵F (立方F );四 方晶系只有四方简单点阵P (四方P ) 、四方体心 点阵I (四方I ); 正交晶系有正交P 、正交I 、正交 F 、正交C (或侧心A和B); 单斜晶系有单斜P 、 单斜C ; 三方、六方、三斜都只有素格子。可见, 晶体只有14种空间点阵型式。见下图。
晶体的对称性
1.晶体的宏观对称性 晶体的宏观对称性就是晶体外型的对称性。
也就是有限物体的对称性。
方铅矿
金绿宝石
(1)晶体的宏观对称元素: 由于习惯原因, 晶体宏观对称元素与分
子对称性中的对称元素名称、符号都不完全 相同。
对称元素 旋转轴n 反映面或镜面m 对称中心i
反轴 n
对应对称操作 旋转L(α) 反映M 倒反I 旋转倒反L(α) I
3.晶面和晶面指标 晶面:晶体中平面点阵所在的平面。 晶面指标: 晶面在三个晶轴上的倒易
截数的互质整数之比。记为: (h*k*l*) 晶面与晶面的交线称为晶棱, 晶棱与
直线点阵对应。
例如, 右图中晶面 1在3个晶轴上的截数 分别:1/2,∞,∞, 因此倒 易截数:2,0,0, 划成互质 整数比后成为: 1:0:0, 因此晶面1的晶面指标 是: (100)。
全国化学竞赛初赛讲义——晶体结构

全国化学竞赛初赛讲义——晶体结构晶体结构是化学竞赛中的重要内容之一、晶体是指由具有有序排列的原子,分子或离子组成的固态物质,具有规则的几何形状。
晶体结构的了解对于理解物质的性质和反应机理非常重要。
下面是晶体结构的讲义。
一、晶体结构的基本概念晶体的结构由最小的重复单元所组成,这个最小重复单元称为晶胞。
晶体结构中的重复单元之间的关系是平移关系,即晶胞通过平移操作得到整个晶体。
晶体结构可以分为离子晶体结构、共价晶体结构和金属晶体结构三种。
离子晶体由阳离子和阴离子组成,通常具有高熔点和硬度,如NaCl、CaF2等。
共价晶体由原子通过共价键相连形成,通常具有高熔点和硬度,如钻石、石墨等。
金属晶体由金属离子通过金属键相连形成,通常具有良好的导电性和延展性,如Cu、Al等。
二、晶体结构的表示方法1.点阵表示法:用数学点阵表示晶体中原子的相对位置关系。
有三种常见的点阵表示方法:简单立方点阵、面心立方点阵和体心立方点阵。
(1)简单立方点阵:晶胞内只含一个原子,每个原子都在晶体的角落上。
(2)面心立方点阵:晶胞内含有4个原子,每个原子都在晶体的角落和晶胞的中心。
(3)体心立方点阵:晶胞内含有2个原子,其中一个原子在晶体的角落上,另一个原子在晶胞的中心。
2.坐标表示法:用坐标系表示晶体中原子的位置。
在二维平面上,可以使用直角坐标系或斜坐标系表示晶体中原子的位置。
直角坐标系中,原子的位置可以用x和y两个坐标表示;斜坐标系中,原子的位置可以用a和b两个坐标表示。
在三维空间中,晶体中原子的位置通常用直角坐标系表示,即通过x、y和z三个坐标来确定原子的位置。
三、晶体的常见缺陷与晶体的生长晶体中常见的缺陷有点缺陷、线缺陷和面缺陷。
1.点缺陷:晶体中原子在其位置上发生的缺失、置换、插入或附加等现象。
(1)缺失缺陷:晶体中缺少一个原子。
(2)置换缺陷:晶体中一个原子被其他原子所替代。
(3)插入缺陷:晶体中多了一个原子。
(4)附加缺陷:晶体中多了一个原子,同时缺少一个原子。
晶体结构的对称性晶体结构的对称性

晶体结构的对称性-董成
不要混淆点阵点和原子
1. 2. 3.
阵点是在空间中无穷小的点。 原子是实在物体。 阵点不必处于原子中心。
晶体结构= 结构基元@点阵 晶体结构是在每 个点阵点上安放 一个结构基元。
晶体结构的对称性-董成
三维晶胞的原子计数
在晶胞不同位置的原子由不同数目 的晶胞分享: 顶角原子 1/8 棱上原子 1/4 面上原子 1/2 晶胞内部 1
{m [010]} (x、y, z) = (x, - y, z)
x' 1
y'
0
z'
0 0 0 x
1 0
y
z 0 1
晶体结构的对称性-董成
镜面类型和矩阵表示
关于对称平面(或镜面)σ的反映,可以平行于(vertical ,σv) 或 垂直于 (horizontal ,h) 主轴。 在二个C2轴之间角平分线的一个垂直平面叫作双面镜面,σd
晶体结构的对称性-董成
晶格
晶体结构的对称性-董成
晶体点阵与晶体对称性
在每个重复周期都选取一个代表点,就可以 用三维空间点阵来描述晶体的平移对称性。 而平移对称性是晶体最为基本的对称性。整 个点阵沿平移矢量 t=ua+vb+wc (u、v, w为任意整数) 平移,得到的新空间 点阵与平移前一样,称沿矢量t的平移为平移 对称操作。
晶体结构的对称性-董成
晶体点阵与晶体对称性
点阵是一组无限的点,连接其中任意两点可以得到一个矢 量,点阵按此矢量平移后都能复原。三维空间点阵是在三 维空间中点的无限阵列,其中所有的点都有相同的环境。 选任意一个阵点作为原点,三个不共面的矢量a, b和c作 为坐标轴的基矢,这三个矢量得以确定一个平行六面体如 下:
(整理)高中化学竞赛——晶体结构和性质
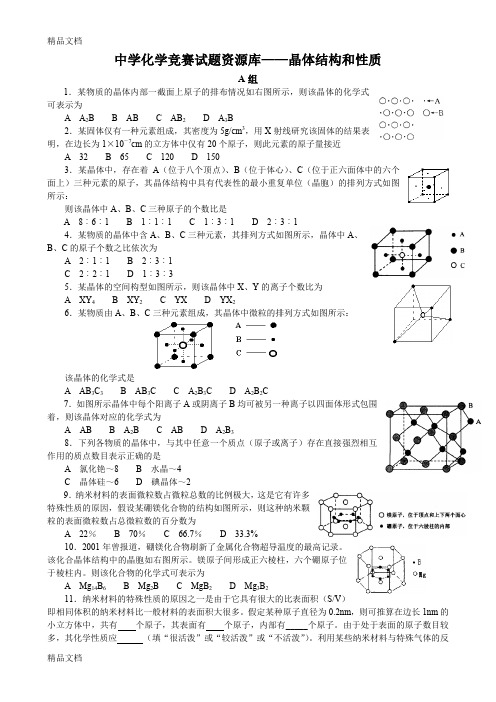
中学化学竞赛试题资源库——晶体结构和性质A组1.某物质的晶体内部一截面上原子的排布情况如右图所示,则该晶体的化学式可表示为A A2B B ABC AB2D A3B2.某固体仅有一种元素组成,其密度为5g/cm3,用X射线研究该固体的结果表明,在边长为1×10-7cm的立方体中仅有20个原子,则此元素的原子量接近A 32B 65C 120D 1503.某晶体中,存在着A(位于八个顶点)、B(位于体心)、C(位于正六面体中的六个面上)三种元素的原子,其晶体结构中具有代表性的最小重复单位(晶胞)的排列方式如图所示:则该晶体中A、B、C三种原子的个数比是A 8︰6︰1B 1︰1︰1C 1︰3︰1D 2︰3︰14.某物质的晶体中含A、B、C三种元素,其排列方式如图所示,晶体中A、B、C的原子个数之比依次为A 2︰1︰1B 2︰3︰1C 2︰2︰1D 1︰3︰35.某晶体的空间构型如图所示,则该晶体中X、Y的离子个数比为A XY4B XY2C YXD YX26.某物质由A、B、C三种元素组成,其晶体中微粒的排列方式如图所示:该晶体的化学式是A AB3C3B AB3C C A2B3CD A2B2C7.如图所示晶体中每个阳离子A或阴离子B均可被另一种离子以四面体形式包围着,则该晶体对应的化学式为A AB B A2BC ABD A2B38.下列各物质的晶体中,与其中任意一个质点(原子或离子)存在直接强烈相互作用的质点数目表示正确的是A 氯化铯~8B 水晶~4C 晶体硅~6D 碘晶体~29.纳米材料的表面微粒数占微粒总数的比例极大,这是它有许多特殊性质的原因,假设某硼镁化合物的结构如图所示,则这种纳米颗粒的表面微粒数占总微粒数的百分数为A 22%B 70%C 66.7%D 33.3%10.2001年曾报道,硼镁化合物刷新了金属化合物超导温度的最高记录。
该化合晶体结构中的晶胞如右图所示。
镁原子间形成正六棱柱,六个硼原子位于棱柱内。
2019化学竞赛—晶体结构出题模式及知识点分析—湖南师范大学化学院黄宏新152pdf

2019化学竞赛—晶体结构出题模式及知识点分析—湖南师范⼤学化学院黄宏新152pdf晶体结构出题模式及知识点分析湖南师范⼤学化学院黄宏新第⼀节点阵理论,布拉维格⼦及平移法的应⽤⼀. 晶体的定义: 微粒在空间作周期性分布.周期: ⼀个重复单位内的内容例画出如下图形的周期结构基元: ⼀个周期中的组成.点阵点: 将⼀个周期压缩成⼀个⼏何点, 表⽰它的⼏何位置.点阵: 由点阵点组成的图形.晶体结构=点阵+结构基元格⼦: 由相邻点阵点组成素向量, 由素向量组成格⼦.晶胞: 格⼦范围内的组成.晶胞=格⼦+结构基元结构基元=晶胞组成/晶胞周期数平移法五个⽤法: 1 画出晶胞; 2 判断点阵形式; 3 判断是否是晶胞; 4判断原⼦的位置; 5 判断原⼦的晶体环境⼆. ⼀维点阵及⼀维晶体例例三. 平⾯点阵1. 正当格⼦: 1对称性⾼, 2 点阵点少2. 平⾯点阵的四种对称类型和五种点阵形式(1) 正⽅格⼦晶胞参数平移法应⽤1:在已知图形中画晶胞(三步骤)1)在图形中选⼀个原⼦(最好是个数少的那种原⼦),然后在邻近找相同的原⼦,连接,假设为向量a,整个图形沿a 平移,如果图形重合,则向量a找成功;2)同法找到向量b;3)以a,b 为邻边作平⾏四边形。
例 1 (中国化学会2003年全国⾼中学⽣化学竞赛试题第6题12分)2003年3⽉⽇本筑波材料科学国家实验室⼀个研究⼩组发现⾸例带结晶⽔的晶体在5K下呈现超导性。
据报道,该晶体的化学式为Na0.35CoO2 ? 1.3H2O,具有……-CoO2-H2O-Na-H2O-……层状结构;在以“CoO2”为最简式表⽰的⼆维结构中,钴原⼦和氧原⼦呈周期性排列,钴原⼦被4个氧原⼦包围,Co-O键等长。
代表氧原⼦,以代表钴原⼦,画出CoO2层的结构,⽤粗线画出两种⼆维晶胞。
使⽤平移法的第⼀个⽤法,有:求出结构基元 (公式:结构基元=晶胞组成/晶胞周期数)(2) 六⽅格⼦例 2 ⽯墨的晶胞: 使⽤平移法的第⼀个⽤法,可以画出晶胞; 求出结构基元例 3⽂献中常⽤下图表达六⽅晶体氟磷灰⽯的晶体结构:该图是c轴投影图,位于图中⼼的球是氟,⼤球是钙,四⾯体是磷酸根(氧原⼦未画出)。
高中化学竞赛经典讲义——晶体结构

高中化学竞赛经典讲义——晶体结构晶体结构是高中化学竞赛中一个非常重要的知识点。
晶体是由一定数量的离子、分子或原子按照一定的几何排列方式所组成的固体,其最具有代表性的性质就是具有规则的几何形状。
晶体结构的了解对于理解晶体的性质、结构与合成具有重要意义。
晶体结构的揭示是通过实验技术以及理论研究来实现的。
其中最重要的实验手段是X射线衍射。
当X射线穿过晶体时,会产生衍射现象,出现一系列亮斑,这些亮斑的位置和强度依赖于晶体结构。
通过对衍射图像的解析,可以确定晶胞参数,揭示出晶体内部的几何排列。
理论上,可以使用动力学理论计算晶体的结构,得出一系列理论結构参数。
实验与理论的比较可以验证理论的正确性,并进一步完善理论模型。
晶体结构是有一定规律的,可以分为离子晶体和共价晶体两种类型。
离子晶体是由正离子和负离子通过离子键结合而成的晶体。
离子晶体的结构稳定,离子之间的排列有一定的规则。
若正离子与负离子的离子半径比较接近,离子晶体的结构会较紧密,例如氯化钠、氟化钙等。
若离子半径比差异较大,离子晶体的结构则会较为散松,例如氧化银、氧化铅等。
共价晶体是由原子通过共价键结合而成的晶体。
共价晶体的原子之间的键长和键角与几何排列有密切关系。
晶体结构可以通过晶胞参数来描述。
晶胞是晶体的最小重复单元,其正六面体的两边长度为a,与该边垂直的四棱面间的夹角为90°,而与该边相邻的两棱面间的夹角为120°。
晶胞参数a、b、c分别代表了晶体沿三个坐标轴方向的长度,而α、β、γ代表了晶体坐标轴之间的夹角。
晶体结构的描述还需要引入晶体结构中的间隙。
间隙是晶胞中没有原子、离子或分子占据的空隙,可以是正交的,也可以是六角形的。
晶胞中间隙的存在对于许多晶体性质有着重要影响,例如导电性、光学性质等。
为了更好的理解晶体结构,可以引入晶体结构分类的一些基本概念。
首先是晶格点的概念,晶格点是描述晶体排列的重要参考点。
晶格参数是晶体中两个晶格点之间的最短距离,而晶格的基元则是指两个相邻晶格点之间的最短距离。
结构化学晶体结构的对称性和基本定理

点击按钮观察动画.注意:反映滑移操作中
的“反映”是虚操作,可想象而难以实际表现, 故动画 中用幻影逗号的移动来模拟反映,请勿误解!
8.2.2 晶胞
设想把点阵放回晶体中去, 将把晶体切分成并置的平行六面 体小晶块,每个空间格子对应一 个小晶块. 这种小晶块就是晶胞, 是代表晶体结构的最小单元.
晶胞参数
NaCl型晶体
原子的分数坐标: A: 0 0 0
0 1/2 1/2 1/2 0 1/2 1/2 1/2 0 B: 1/2 0 0
0 1/2 0 0 0 1/2 1/2 1/2 1/2 结构基元: A-B (每个晶胞中有4个结构基元)
CsCl型晶体
原子的分数坐标: A: 0 0 0 B: 1/2 1/2 1/2
为什么要考虑带心格子?
立方面心格子,若按左图取素格子只能表现三方对称性;若取右图 所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖):
14种布拉维格子之一:立方简单(cP)
14种布拉维格子二:立方体心(cI)
14种布拉维格子三:立方面心(cF)
晶胞参数:
a、b、c α、β、γ
晶
胞
两
要
(1)晶胞的大小、型式
素
晶胞的大小可由晶胞参数确定,晶胞的型式是
指素晶胞或复晶胞.
(2)晶胞的内容
晶胞中原子的种类和位置. 表示原子位置要用 分数坐标.
分数坐标
晶胞中原子P 的位置用向量OP=xa+yb+zc代表. x、y、z
就是分数坐标,它们永远不会大于1.
14种布拉维格子之八:正交简单(oP)
14种布拉维格子之九:正交体心(oI)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有较高的结构稳定性。在自然界中也存在准晶。准晶材料
有许多应用,包括用于精细仪器耐用钢,不粘绝缘电线和
烹饪设备的制造。2011年,舍特曼因此项发现获诺贝尔化学
奖。
第七章-晶体结构
13
2019化学竞赛—结构化学—07晶体结构与对称性—四川省代表队培训讲义
玻璃体 Glasses
玻璃体
第七章-晶体结构
14
最小单位和平移向量:
第七章-晶体结构
26
结构基元与点阵
结构基元:晶体中重复的最小单位, 必须满足: 化学组成相同。 空间结构相同。 排列取向相同。 周围环境相同。
第七章-晶体结构
27
1. 一维周期性结构与直线点阵
第七章-晶体结构
28
2. 二维周期性结构与平面点阵
第七章-晶体结构
29
实例1: 石墨层抽取出平面点阵
研究快速凝固铝过渡金属合金。在这
项研究中,他发现二十面体相,从而 开创了准晶体的新领域。
第七章-晶体结构
12
1982年,舍特曼在美国霍普金斯大学工作时发现了准晶,
开始几年,舍特曼对晶体非周期性的解释遭到科学界的敌
视,莱纳斯·鲍林甚至说他在“胡说”,“没有准晶体,只
有准科学家。” 舍特曼研究小组的组长告诉他,“回去读
教科书”,然后“让他停止为团队‘带来耻辱’。”舍特
曼感到很沮丧。
瑞典皇家科学院的诺贝尔奖委员会说,“他的发现极具争
议性,”但他的工作“最终迫使科学界重新考虑他们对于
物质本质的看法。
后来,其他科学家开始确认并接受准晶存在的实证研究结
果。通过舍特曼的发现,其他几个研究小组得以合成类似
的准晶,发现这些材料具有较低的导热和导电性,同时具
晶体结构与对称性
物质的固态 晶态 玻璃态 液晶 准晶体 原子簇
2
2019化学竞赛—结构化学—07晶体结构与对称性—四川省代表队培训讲义
晶体 Crystal
金属晶体
晶体中金属原子的排列
第七章-晶体结构
3
2019化学竞赛—结构化学—07晶体结构与对称性—四川省代表队培训讲义
液晶 Liquid crystal
43
(3). 正当平面格子有5种型式:
60o
(a)
.(b)
(d)
(e)
(c)
图: 正当平面格子的5种型式 (a). 正方形 (b). 矩形 (c). 带心矩形 (d). 菱形 (e). 平行四边形
第七章-晶体结构
44
2. 空间格子
(1). 正当空间格子的选取标准: 含三个向量的平行六面体。 三个向量的交角尽可能是90º,使对称性尽可能高。 含点阵点尽可能少,体积尽可能小。
第七章-晶体结构
5
向列相结构(nematic)
向列相是最简单的液晶相,分子形状呈棒状,棒状分 子间互相错位平行,排列呈无序。在外力作用下发生流 动,并沿流动方向取向,互相穿越。 具有较高的比电阻、较低的粘度、正的铁电率异向性、 较高的化学和光化学稳定性,是液晶平面显示器(AMLCD)的良好材料 。
24
7.2 晶体的周期性结构与点阵
晶体的周期性结构用抽象的点阵方法描述
点阵点:将晶体中重复出现的最小单元用一个数 学上的点来代表。 点阵结构:整个晶体被抽象成的三维点阵阵列。 点阵的单位向量:连接任意相邻两点阵点作为单 位向量(a,b,c), 按单位向量平移能使三维点阵复原。
第七章-晶体结构
25
第七章-晶体结构
41
(1). 正当平面格子的选取标准: ➢平行四边形。 ➢尽可能是90º, 使对称性尽可能高。 ➢含点阵点尽可能少, 面积尽可能小。
(2). 平面格子含点阵点数的计算方法:
✓顶点为1/4; ✓棱心为1/2; ✓格内为1。
第七章-晶体结构
42
直线和平面点阵单位中点阵点的计算
第七章-晶体结构
例如:油酸铵
CH3(CH2)7CH=CH(CH2)7C OONH4
向列相液晶
第七章-晶体结构
6
近晶相结构smectic
近晶相结构接近结晶结构,分子形状呈棒状,垂直于 分子长轴方向,分子依靠所含官能团发生强相互作用, 相互平行排列成层状结构。
A.分子长轴垂直于层平面。 B.分子可层内活动,层间的运动困难。 C.分子层间可以相互滑动。 D.在各个方向都非常粘滞。
第七章-晶体结构
33
3. 三维周期性结构与空间点阵
第七章-晶体结构
34
实例3: 下列3类金属晶体结构抽象的点阵, 每一个原子 作为一个结构基元,抽象成一个点阵点。
1. Mn金属
点阵: 立方简单
2. Li Na K Cr Mo W…...
点阵: 立方体心
第七章-晶体结构
35
单个原子作为 一个结构基元
1966年丹尼尔∙舍特曼获以色列理工学 院机械工程理学士,1968年获材料工 程硕士学位,1972年获材料工程博士 学位。舍特曼教授后来成为俄亥俄州 赖特·帕特森空军基地航空航天研究实 验室的NRC研究员,在那里他花了三 年时间研究钛铝合金的微观结构和物 理冶金学。1975年他加入了以色列理 工学院材料工程系。1981年至1983年, 他在约翰斯·霍普金斯大学休假,在那 里他参与了国家统计局的合作方案,
3. Ni Pd Pt Cu Ag Au .……点阵: 立方 面心
立方简单(P) 立方体心(I)
立方面心(F)
第七章-晶体结构
36
实例4: 六方Mg晶体的点阵结构
1/3
六棱柱
单胞
c方向俯视图
1. 选取六棱柱的1/3为一单胞。
2. 六方Mg晶体不能将每个原子抽象为点阵点, 1和 2号两位置
的原子合为一点阵点。
第七章-晶体结构
47
为什么NaCl型晶胞要抽象成立方面心复格子(右图), 而不抽象成三方R素格子(左图红线所示)?对称性描述 晶体结构的重要性。
三方R素格子
立方面心复格子
第七章-晶体结构
48
7.4 晶胞
将结构基元放到点阵结构中,即得到晶体结构,空间点阵 把晶体切分成并置的平行六面体小晶块,每个空间格子 对应的小晶块就是晶胞, 晶胞是晶体结构的最小单元。
(2). 空间格子含点阵点数的计算方法: ✓顶点为1/8(为周围八个格子共用) ✓棱心为1/4(为周围四个格子共用) ✓面心为1/2(为周围二个格子共用) ✓格子内为1。
第七章-晶体结构
45
空间点阵单位中点阵点的计算
第七章-晶体结构
46
为什么六方格子选右图而不选左图?
1/3
六方格子
平行六面体, 不含重复单位, 体积最小。
@含有1的坐标原子不用写出, 因通过某些平移得到, 但只含分数的原子的坐标必须全部写出。
第七章-晶体结构
53
(0,0,0,), (1,0,0), (0,1,0),
(0,0,1),(1,1,0), (0,1,1), (1,0,1), (1,1,1)等8个顶点 均能通过(0,0,0,)平移得到, 故只写出(0,0,0)即可。体 心(1/2,1/2,1/2)必须单独写 出。
对应
第七章-晶体结构
49
晶胞参数
平行六面体单胞的晶胞 参数约定:
✓ a、b、c
✓α(b,c) ✓β(a,c) ✓γ(a,b) ✓ Z (分子数或原子数)
第七章-晶体结构
50
A. 晶胞的大小: 空间格子的单位向量的数值晶胞参数, 晶胞的大小可由晶胞参数确定。
B. 晶胞的型式: 素晶胞或复晶胞。 C. 晶胞内原子、原子基团或分子的排列: 原子的位置
液晶分类
A. 热致液晶(thermotropic LC): 液晶的光电效应受 温度条件控制。
B. 溶致液晶(lypotropic LC): 由一种溶质溶于一种极性 溶剂形成的液晶。典型的 溶质由一端为亲水基团, 另一端为疏水基团的双亲 分子构成。液晶的光电效 应受浓度条件控制。
液晶物质的外观
第七章-晶体结构
例如:对氧化偶氮苯甲醚。
CH3OC6H4(NO)=NC6H4OCH3
第七章-晶体结构
近晶相液晶
7
第七章-晶体结构
8
2019化学竞赛—结构化学—07晶体结构与对称性—四川省代表队培训讲义
准晶体 Quasicrystal
银铝准晶体
银铝原子的排列
第七章-晶体结构
9
准晶体( quasicrystals)-2011年诺贝尔化学奖
类似金属导电
┴ 半导体性导电
第七章-晶体结构
∥
17
石墨层结构
石墨单胞
第七章-晶体结构
18
实例3: 冰洲石双折射现象 ➢双折射现象:1669年巴尔托林用光束通过冰洲石时,发 现双影。
➢形成机制:晶体在两个方向上的折射率不同。
第七章-晶体结构
19
晶体的自范性
晶体生长的外形与晶体内部微观结构具有一致性。 在理想生长环境中能自发地形成规则的凸多面体外
3. 抽象的点阵结构为六方简单格子。
第七章-晶体结构
37
每一对Mg1-Mg2作为一个结构基元, 抽象出六方简单 点阵。
第七章-晶体结构
38
实例5: 石墨的点阵结构
1. 石墨晶体两相邻两层的结构是完全一样的, 在晶体中相错一单位向量, 第二层的C原子正对第一层的六员环的空位。 2. 红绿点是两不同位置的C, 是平面点阵点的取法,下层邻近的平面点阵 点对应的两C原子, 合为一点阵点。
六方简单
石墨晶体
素晶胞
第七章-晶体结构
39
7.3 点阵单位
晶体可以抽象成无限的点阵结构,从点阵中选取一个点阵 单位(即格子),当沿三个方向的单位向量平移,就能得到 点阵结构,即由点阵单位描述点阵结构。
