复变函数4 - 1 复数项级数和序列以及泰勒级数
合集下载
4.1复数项数列、复数项级数

级数收敛的必要条件
n =1
n =1
定理3:级数 n = (an + ibn ) 收敛的必要条件是
lim n = lim ( an + ibn ) = 0.
n →
n →
证明:由定理2及实数项级数收敛的必要条件可知
级数
n =1
n
收敛,则 级数
a
n =1
n
和 bn 都收敛;
n =1
n =1
n =1
n =1
所以当 an 与 bn 绝对收敛时, n 也绝对收敛.
2
同时有 an n ,bn n ,所以当 n 绝对收敛时,
a
n =1
n
n =1
与 bn 也绝对收敛.
推论:
n =1
n =1
n
n =1
n =1
绝对收敛的充要条件是级数 an 与 bn 也绝对收敛.
复变函数与积分变换
第一节 复数项级数
一、复数项数列
二、复数项级数
一、复数项数列
定义1: 设 n = 1,2,∙∙∙ 为一复数列,其中 = + , 又设
= +为一确定的复数.如果对于任意给定的 > 0,相应地总
能找到一个正数 , 使得当 > 时,不等式 − <
→∞
当n > 时,有 n − α < ,即 (n + ) − ( + ) < 成立,
从而有
所以
n − ≤ (n −) + ( − ) < ,
4-1复数项级数与幂级数
n0
n0
25
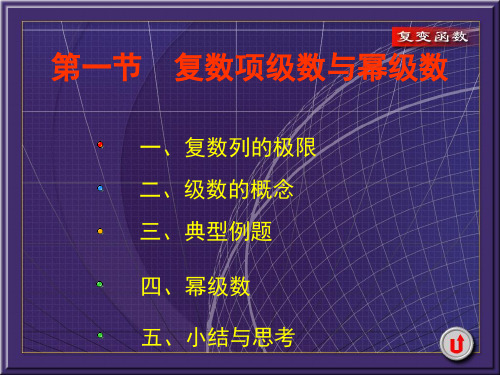
如果级数 cnz0n发散, 且如果| z || z0 | n0
用反证法, 设级数 cnzn反而收敛,则根据 n0
前面的结论可导出 cnz0n收敛,与所设 n0
矛盾. 因此只能是 cnzn发散 n0
26
2. 收敛圆和收敛半径 利用阿贝尔定理, 可以定出 幂级数的收敛范围, 对一个幂级数来说, 它的收敛 情况不外乎三种:
3
课堂练习:
下列数列是否收敛? 如果收敛, 求出其极限.
(1)
zn
1 1
ni ni
;
收敛到-1
(2)
zn
(1)n
n
i
; 1
不收敛
(3)
zn
1
e
ni 2
.
n
收敛到0
4
二、级数的概念
1.定义 设{n} {an ibn} (n 1,2,)为一复数列,
表达式
n 1 2 n
n1
称为复数项无穷级数.
34
更为重要的是代换(复合)运算
如果当| z | r时, f (z) an zn ,又设在 | z | R n0
内g(z)解析且满足 | g(z) | r,则当| z | R时,
f [g(z)] an[g(z)]n. n0
• 这个代换运算, 在把函数展开成幂级数时, 有着 广泛的应用.
35
n0
这种级数称为幂级数.
• 如果令za=z, 则(4.2.2)成为
cnz n , 这是
• (4.2.3)的形式, 为了方便, 今后n常0就(4.2.3)讨论
23
定理一(阿贝尔Abel定理)
如果级数 cnzn在z z0( 0)收敛,则对满足 n0
复变函数4-1

首页
上页
返回
下页
结束
铃
定理: 如果 | n |收敛,那么 也收敛,且
n 1
n 1 n
不等式 | n | | n | 成立
n 1 n 1
首页
上页
返回
下页
结束
铃
绝对收敛与条件收敛
定理 4.3 复级数(4.1)收敛的一个充分条件为级数
| a
n 1
n
n
1 解:(1) 因为 an 发散; n1 n1 n
1 bn n2 收敛Biblioteka n 1 n 1所以原级数发散
首页
上页
返回
下页
结束
铃
(2)因为
( 8i ) n 8 n , n! n!
8n 所以由正项级数的比值判别法知: 收敛, n1 n!
故原级数收敛, 且为绝对收敛.
(an a ) i (bn b)
an a bn b ,
所以 lim n .
n
首页
上页
返回
下页
结束
铃
定理:数列收敛的Cauchy准则
复数列 {n }(n 1, 2,) 收敛的充要条件是:
>0,N >0,当n N时,对p N :
那末 称为复数列{ n } 当 n 时的极限,
记作
lim n .
n
此时也称复数列{ n } 收敛于 .
首页 上页 返回 下页 结束 铃
复数列收敛的条件
定理 复数列 { n } {an ibn }( n 1, 2 ,) 收敛于 a ib 的充要条件是
复变函数4 - 1 复数项级数和序列以及泰勒级数幻灯片

w0
lim
n
zn
+
wn
z0 + w0
性质2 Cauchy收敛准则 zn z0
任意 0,存在N,使得 当m,
n>N时,| zm
zn |
6/16/2020
5
复数项级数
对于复数列 {z1,z2,…,zn,…},称
zn z1 z2 zn
n1
为复数项级数。部分和记为
n
Sn zk z1 z2 zn
| zn || |n
可知极限不存在。
6/16/2020
25
例2: 讨论数列{zn}的收敛性,其中
zn n , 为复数。
注:(3)用到了如下性质
lim zn z0 lim | zn || z0 |
n
n
这是因为
0 || zn | | z0 ||| zn z0 | 0
n 1
n 1
15
例1:判断如下数列的收敛性,若收敛,
求极限。(1)zn
( i )n,(2)zn 2
cos in。
6/16/2020
16
例1:判断如下数列的收敛性,若收敛,
求极限。(1)zn
( i )n,(2)zn 2
cos in。
分析与解:(1)由于 |i/2|<1,猜测{zn}的 极限为0
|
zn
n1
实数项级数 xn, yn 分别收敛于X和Y。
n1
n1
此时,S=X+iY
证明:由于Sn=Xn+iYn,可知 Sn S Xn X,Yn Y。
6/16/2020
10
定理:复数项级数 zn 绝对收敛
n1
实 数 项 级 数 xn , 都绝对收敛。
高等数学课件-复变函数与积分变换 第四章 级数

称为级数的部分和。
在收敛域D内
lim
n
Sn
(
z)
S
(
z
),
S ( z) 为级数的和函数。
二、幂级数
若 fn (z) Cn zn 或 fn (z) Cn (z z0 )n 时,
幂级数为
Cn zn 或
Cn (z z0 )n
n0
n0
定理4.7
Ab el 定理如果级数
Cn zn
n0
z z 在
z0
sin
z
k 0
(1)k z2k1
2k 1!
R
• 例5 将 cos z 在 z 0处展开成幂级数。
sin z 解: 将
两边对z求导
cos z
(1)k (2k 1)z2k
k 0
2k 1!
(1)k z2k
k 0
2k !
例6 arctan z 在 z 0 处展开成幂级数。
解:
arctan
z
b
二、复数项级数
定义4.2
z 设
为一复数列,表达式
n
zn z1 z2 zn
n1 为复数项级数,其前n项之和
Sn z1 z2 zn
为级数的部分和。 称级数收敛,
若
lim
n
Sn
S,
S称为级数的和,
记为
S zn
若
{Sn} 不收敛,则称级数是发散的
n1
n
n
n
Sn k an i bn 有
收敛,那么对满足
0
| z || z0 | 的z,
级数必绝对收敛。
如果在
z z 级数发散,那么对满足 0
第四章 复变函数的级数

n1 n!
解
因为
(8i )n
8n ,
n! n!
lim un1 r
u n n
r1时收敛, r1时发散
r 1时可能收敛或发散
所以由正项级数的比值判别法知:
8n 收敛,
n1 n!
8n1 n! 8n (n 1)!
n
8
1
0
故原级数收敛, 且为绝对收敛.
15
§2 复变函数项级数
n cn
lim( n ) p n n 1
=1
所以 R 1 1.
27
例2
级数
n0
zn,
n0
zn n2
,
n0
zn n
的收敛半径,
并讨论它们在收敛圆上的敛散性。
解:根据比值法,三个级数都有lim Cn1 1
n Cn
故收敛半径R 均为1, 收敛圆周均为 z 1
设 z z0 ( 0)时,级数 cn (z z0 )n 收敛;
n0
由Abel定理,级数在 z z0 内收敛。
设z z0 ( 0)时,级数 cn (z z0 )n发散.
n0
23
由Abel定理的推论,级数在 z z0 内发散。 y
cn (z1
z0 )n
0
因而存在正数M,使对所有的n,
有 cn(z1 z0 )n M , 19
n
n
故 cn(z z0 )n
cn (z1 z0 )n
z z0 z1 z0
M
z z0 z1 z0
.
复变函数与积分变换第4章4.1收敛数列与收敛级数

n
3
§4.1 复数项级数 第 一、收敛序列 四 章 2. 复数序列极限存在的充要条件 定理 设 zn xn i yn , a i , 则 lim z n a 的充要条件是 解 n P76 析 定理 lim x , lim y . n n n 函 4.1 n 数 zn 证明 必要性 “ ” 的 | zn - a | | yn - | 级 若 lim z n a , 则 e 0 , N , n 数 a | xn - | 表 当 n N 时,| zn - a | e , 示
即得级数 z n 收敛的充要条件是 x n 和 yn 都收敛。
9
§4.1 复数项级数 第 二、复数项级数 四 章 3. 复数项级数收敛的必要条件 定理 设 zn xn i yn , 则 z n 收敛的必要条件是 lim zn 0 . n 解 析 P79 函 证明 由于级数 z 收敛的充要条件是 x 和 y 都收敛, n n n 数 的 而实数项级数 x n 和 yn 收敛的必要条件是: 级 数 lim xn 0 , lim yn 0 等价于 lim zn 0 , 表 n n n 示 因此 z n 收敛的必要条件是 lim zn 0 .
1 n 1 zn 2 i 2 e n n
i
π n 2
§4.1 复数项级数 第 二、复数项级数 四 章 4. 复数项级数的绝对收敛与条件收敛 定义 (1) 若 | z n | 收敛,则称 z n 绝对收敛。 解 析 P79 (2) 若 | z n | 发散, z n 收敛,则称 z n 条件收敛。 函 数 的 定理 若 | z n | 收敛,则 z n 必收敛。 P80 定理4.4 级 2 2 | z | x y 证明 由 收敛, n n 收敛, n 数 表 2 2 2 2 | x | x y , | y | x y 又 示 n n n n n n,
3
§4.1 复数项级数 第 一、收敛序列 四 章 2. 复数序列极限存在的充要条件 定理 设 zn xn i yn , a i , 则 lim z n a 的充要条件是 解 n P76 析 定理 lim x , lim y . n n n 函 4.1 n 数 zn 证明 必要性 “ ” 的 | zn - a | | yn - | 级 若 lim z n a , 则 e 0 , N , n 数 a | xn - | 表 当 n N 时,| zn - a | e , 示
即得级数 z n 收敛的充要条件是 x n 和 yn 都收敛。
9
§4.1 复数项级数 第 二、复数项级数 四 章 3. 复数项级数收敛的必要条件 定理 设 zn xn i yn , 则 z n 收敛的必要条件是 lim zn 0 . n 解 析 P79 函 证明 由于级数 z 收敛的充要条件是 x 和 y 都收敛, n n n 数 的 而实数项级数 x n 和 yn 收敛的必要条件是: 级 数 lim xn 0 , lim yn 0 等价于 lim zn 0 , 表 n n n 示 因此 z n 收敛的必要条件是 lim zn 0 .
1 n 1 zn 2 i 2 e n n
i
π n 2
§4.1 复数项级数 第 二、复数项级数 四 章 4. 复数项级数的绝对收敛与条件收敛 定义 (1) 若 | z n | 收敛,则称 z n 绝对收敛。 解 析 P79 (2) 若 | z n | 发散, z n 收敛,则称 z n 条件收敛。 函 数 的 定理 若 | z n | 收敛,则 z n 必收敛。 P80 定理4.4 级 2 2 | z | x y 证明 由 收敛, n n 收敛, n 数 表 2 2 2 2 | x | x y , | y | x y 又 示 n n n n n n,
4-1复数项级数和幂级数

则 limr n cosn limr n sinn 0, lim n 0
n
n
n
20
(2) 若r 1, 则 n r n(cosn i sinn ),
则1
n
r -n[co(s - n)
i sin(- n )],
r-n[cosn - i sinn ],
则 limr-n 0,cosn ,sinn有界, n
称为该级数前n项的部分和.
24
n
Sn (z) f1(z) f2(z) fn(z)= fk (z) k 1
若对
D
内的
某一点
z0,
lim
n
Sn(z0 )
S(z0 )
存在,称 fn(z) 在 z0 收敛, 且S(z0 )为它的和.
n1
如果级数在D内处处收敛, 那末它的和一定
是 z 的一个函数 S(z)
n0
n0
f (z) g(z) anzn bnzn (an bn )zn ,
n0
n0
n0
f (z) g(z) ( anzn ) ( bnzn ),
n0
n0
(anb0 an1b1 a0bn )zn ,
n0
其中 z R, R min( r1, r2 )
32
定理4 设幂级数 cn(z z0 )n 的收敛半径为 R, 则
(1)
1 (1 i ),
n1 n
n
(2)
(1
1
i
)e n
n1
n
解
(1)
n1
1 (1 n
i )= n
n1
(
1 n
i n2
)
(8i)n
(3) n1 n!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z0
1 ) c z ( 1,利用 1 n 0 n 0
n n 0 n n
z n n n c z c z ( 向级数 c z n n0 z n 0 靠拢) n 0 n 0 n 0 0
n
z
z0
1 ) c z ( 1,利用 1 n 0 n 0
lim zn z0 lim | zn || z0 |
n n
这是因为
0 || zn | | z0 ||| zn z0 | 0
n+… 例3: 设| |<1,证明级数1+ +…+
收敛于 1 1
n+… 例3: 设| |<1,证明级数1+ +…+
收敛于 1 1 证明:先求部分和
可知数列 zn cos in 发散。
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n ,
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n , 分析与解:
类似于实数列情形,应该以1为临界
点分为三种情况: (1)| |<1,(2)| |=1,(3)| |>1
为复数。 zn n ,
| zn || | 1 ,可知数列{zn} (2)| |=1,
n
在单位圆上运动。设 =ei ,则 zn=ein。
当 =2k ,即 =1时,显然有 lim zn 1 。
| 当 k 2 ≠,
zn zn 1 || e
in
e
n i ( n 1)
| |1 |
由Cauchy收敛准则知极限不存在。
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n , (3)| |>1,此时有
| zn || |
n
可知极限不存在。
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n , 注:(3)用到了如下性质
敛,记作 S zn
n 1
n 1
若{Sn}发散,则称级数 zn 发散。
n 1
若
| z
n 1
n
| 收敛,称级数 zn 绝对收敛。
n 1
对应的实数项级数
x
n 1 n 1
n
x1 x2
xn
y
部分和
n
y1 y2
n
yn
xn yn
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n , (1)| |<1,此时
| zn || | 0
n
可知 lim zn 0
n
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n ,
| zn || | 1 ,可知数列{zn} (2)| |=1,
Abel定理:
若幂级数 cn z 在点 z0≠0 收敛,则
n
它在区域 D : {z | |z|<|z |} 绝对收敛, 0 即级数
n 0
c z
n n 1
n
在区域 D 收敛;
Abel定理:
若幂级数 cn z 在点 z0≠0 收敛,则
n
它在区域 D : {z | |z|<|z |} 绝对收敛, 0 即级数
n 1 n 1
例1:判断如下数列的收敛性,若收敛, i )n ( zn cos in。 ,(2) zn 求极限。(1) 2
例1:判断如下数列的收敛性,若收敛, i )n ( zn cos in。 ,(2) zn 求极限。(1) 2
分析与解:(1)由于 |i/2|<1,猜测{zn}的
n 1 n 1
n 1
此时,S=X+iY
证明:由于Sn=Xn+iYn,可知 Sn S Xn X,Yn Y。
定理:复数项级数 zn 绝对收敛 实 数 项 级 数 xn , 都绝对收敛。 n 1 n 1 yn
n 1
定理:复数项级数 zn 绝对收敛 实 数 项 级 数 xn , 都绝对收敛。 n 1 n 1 yn 证明:“ ”假设
极限为0
i n 1 | zn || ( ) | n 0 2 2
可知
lim zn 0
n
例1:判断如下数列的收敛性,若收敛, i )n ( zn cos in。 ,(2) zn 求极限。(1) 2
分析与解:(2)由余弦函数的定义
1 n n z n cos in (e e ) 2 ( n 0)
Sn 1
n 1
1 1
n
1 由例2, lim S n ,即 n 1
1 1 n 0
n
n+… 例3: 设| |<1,证明级数1+ +…+
收敛于 1 1
类似地,可证明当 | | 1 时,级数
n 2 1 n 0
例5: 求如下级数的收敛域
(n !) 2 n (1) n z n 1 n
解:由于
n 1 lim n ( n 1) n e cn 1 lim n c n
n
可知
因此,R=0,收敛域为{0}。
例5: 求如下级数的收敛域
1 z n (2) 2 ( ) 2 n 1 n
n
在单位圆上运动。
例2: 讨论数列{zn}的收敛性,其中
为复数。 zn n ,
| zn || | 1 ,可知数列{zn} (2)| |=1,
n
在单位圆上运动。设 =ei ,则 zn=ein。
当 =2k ,即 =1时,显然有 lim zn 1 。
n
例2: 讨论数列{zn}的收敛性,其中
复数项级数和序列
复数序列
复数列即有序的复数集
{zn}={z1,z2,…,zn,…}
称{zn}收敛于z0,若
lim | zn z0 | 0
记作
n
lim zn z0
n
复数列的极限归结为实数列的极限
lim zn z0 lim | zn z0 | 0
n n
n n 0 n n
由于级数
n 0 n
c z n收敛,可知 c z n 有界
n 0 n 0
1 M M 1 n 0
由Abel定理,只有三种情况 ☺ ☺
☺
n c z 幂级数 n 在整个复平面收敛 n 0
幂级数只在 z=0 处收敛
在圆 |z|=R外发散,在圆内收敛,在 圆周上单独讨论。 此时,称 |z|=R为收敛圆。
n 1
级数 zn
n 1
收敛。
n 1
性质:
1、
z 收敛
n
2、
z 收敛
n n 1
n 1
zk 0 {zk}有界;
> 0,存在N,使
得n>N时,
| zn 1 zn 2
3、
zn p |
(z
n 1
n
wn ) zn wn
n 1
| x |, | y
n
n
| 收
(| x
n 1
n 1
n 1
n
| | yn |) 收敛,由于
|zn|≤|xn|+|yn|,可知
| z
n 1
n
| 收敛。
定理:复数项级数 zn 绝对收敛 实 数 项 级 数 xn , 都绝对收敛。 n 1 n 1 yn 推论:复数项级数 zn 绝对收敛
X n xk x1 x2 Yn yk y1 y2
k 1 k 1 n
定理:复数项级数 zn 收敛于S 实数项级数 xn, yn 分别收敛于X和Y。
n 1 n 1
ห้องสมุดไป่ตู้
n 1
此时,S=X+iY
定理:复数项级数 zn 收敛于S 实数项级数 xn, yn 分别收敛于X和Y。
n 0
c z
n n 1
n 0
n
在区域 D 收敛;
n
若幂级数
c z
n
在点 z0≠0 发散,则
它在区域 K:{z | |z|>|z0|} 发散。
z n n n c z c z ( 向级数 c z n n0 z n 0 靠拢) n 0 n 0 n 0 0
n
z
n>N时,| zm
zn |
复数项级数
对于复数列 {z1,z2,…,zn,…},称
z
n 1
n
z1 z2
zn
为复数项级数。部分和记为
S n zk z1 z2
k 1
n
zn
收敛性:若 lim S n S ,则称级数 zn 收
n
lim | xn x0 | 0 n lim | y y | 0 n 0 n lim xn x0 n lim yn y0 n
性质1 线性性质
, C,lim zn z0, lim wn w0
n n n
收敛。因此收敛域为{z | |z| 2}。
例5: 求如下级数的收敛域
