复变函数与积分变换公式
复变函数与积分变换知识点总复习
解析函数 f (z) 的导数仍为解析函数, 它的 n阶
导数为:
f
(n)
( z0
)
n! 2πi
C
(z
f
(z) z0 )n1
dz
(n 1,2,)
其中C 为在函数 f (z) 的解析区域 D内围绕 z0 的
任何一条正向简单闭曲线, 而且它的内部全含于 D.
8.调和函数与解析函数的关系
调和函数
满足 Laplace
但u iv不是解析函数。
证明：
因为 u x
2x,
2u x 2
2,
u y
2 y,
2u y 2
2,
2u 2u 2 2 0,所以，u是调和函数。 x2 y2
同理 2v 6x2 y 2y3 , 2v 6x2 y 2y3 , x2 (x2 y2 )3 y2 (x2 y2 )3
2v x 2
解：u(x, y) a ln(x2 y2 ),v(x, y) arct an y ,则 x
u 2ax , u 2ay , v y , v x , x x2 y2 y x2 y2 x x2 y2 y x2 y2 在区域x 0内连续，且 u v , v u 在区域x 0上成立时，2a 1, x y x y 即，当a 1 时，函数f (z)在区域x 0内是解析的。
Байду номын сангаас
而 u y2, u 2xy, v 2xy, v x2,在复平面上
x
y
x
y
处处连续，当x y 0时满足C R方程，
故f (z)仅在(0,0)点可导，在复平面上处处不解析。
2）因为f (z) x2 iy,则u(x, y) x2, v(x, y) y,
复变函数与积分变换公式
复变函数与积分变换公式复变函数是指定义在复数域上的函数。
复变函数与实变函数有很多相似之处，但也有着一些独特的性质和应用。
在实际问题中，经常会遇到求解复变函数的积分问题。
积分变换是一种通过对函数进行积分计算来求得更简单或者更易求解的函数的方法。
本文将介绍复变函数以及积分变换公式。
一、复变函数的定义和性质复变函数的定义：复变函数通常可以表示为 f(z) = u(x,y) +iv(x,y)，其中 u(x,y) 和 v(x,y) 是实变量 x 和 y 的实函数，i 是虚数单位。
复变函数可以看作二元实函数的推广。
在复变函数的定义中，x 和 y 是自变量，而 u 和 v 是因变量。
复变函数的性质：复变函数具有以下性质：1.可微性：类似于实变函数中的导数，复变函数也有导数的概念，称为复导数。
如果复变函数f(z)在一些点z0处可导，则称f(z)在z0处可导。
2.全纯性：如果复变函数在一些区域上都可导，则称该函数在该区域上是全纯的。
3.古典解析性：如果复变函数在整个复平面上都可导，则称该函数是古典解析的。
4. 共轭性：对于复变函数 f(z) = u(x,y) + iv(x,y)，可以定义其共轭函数 f*(z) = u(x,-y) - iv(x,-y)。
共轭函数与原函数在实部上相等，虚部上相反。
5.奇函数和偶函数：如果复变函数f(z)满足f(-z)=-f(z)，则称f(z)是奇函数；如果f(-z)=f(z)，则称f(z)是偶函数。
积分变换通常是求解复变函数积分的一种方法。
常见的积分变换公式有：1.单连通域中的柯西定理：设f(z)在单连通域D上是全纯的，则对于D的任意闭合曲线C，有∫[C] f(z)dz = 0这个公式是复变函数积分计算的基础。
2. 柯西-Goursat 定理：设 f(z) 在连通域 D 上是全纯的，则对于D 的任意简单闭合曲线 C，有∫[C] f(z)dz = 0这个公式是柯西定理的推广形式，适用于连通域D。
复变函数与积分变换公式
复变函数复习提纲（一）复数的概念1.复数的概念：z = X ∙ iy , X, y 是实数,x = Rez,y=lmz.r=_i.中的幅角。
3）arg Z与arctan~y之间的关系如下:Xy当X 0, arg Z= arctan 丄；Xyy -0,arg Z= arctan 二! Xyy ：： O,arg Z= arctan -二J X4)三角表示：Z = Z(COS8 +isin0 ),其中日=argz；注：中间一定是“ +”号。
5)指数表示：Z = ZeF,其中V - arg z。
(二)复数的运算1.加减法：若Z I=X I iy1, z2=X2 iy2,贝廿z1二z2= x1二x2iy1- y22.乘除法：1)若z1 = x1 iy1, Z2 =X2 iy2,贝U狂h[N×2 一y$2i x2% x1y2 ；乙_ X1+ i y_ (x1 十i和X—i y_ XX y*y y x；。
XZ2 X2+ i% (对讪-X )i2y 2+2X222+ 2X222)若Z I=Iz I e i^,z2 =∣z2 e iθ ,则Z1Z2 = ZIll Z2 e i(t1也；3.乘幕与方根1)若Z= Z(COS J isin * n (CoS n i Sinn )= n e i"。
2）幅角：在Z=O时，矢量与X轴正向的夹角, 记为Arg Z （多值函数）；主值arg Z 是位于（-理,二］注：两个复数不能比较大小2.复数的表示2)若 Z = IZ(COSB+isinT)=∣ze i ^,则（三）复变函数1∙复变函数： w = f z ,在几何上可以看作把 Z 平面上的一个点集 D 变到W 平面上的一个点集 G的映射. 2 •复初等函数1）指数函数：e z =e x cosy isiny ,在Z 平面处处可导，处处解析；且 注：e z 是以2二i 为周期的周期函数。
（注意与实函数不同） 3）对数函数：LnZ=In z+i （argz + 2kιι） （k=0,±1,±2八）（多值函数）；主值：In Z = Inz+iargz 。
《复变函数与积分变换》 留数—计算规则
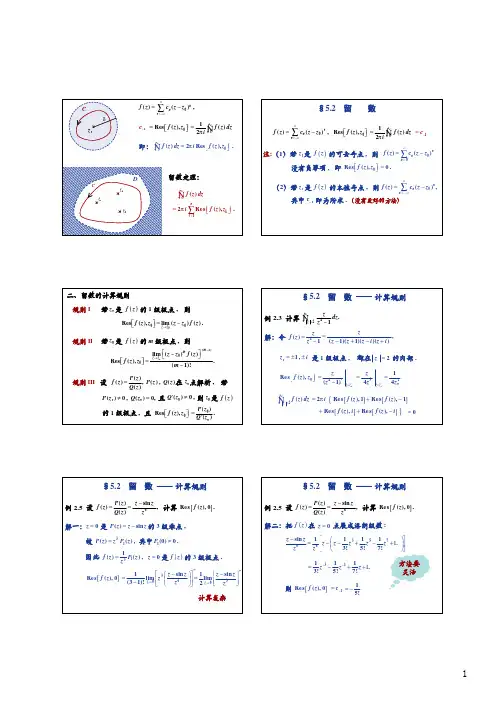
三、在 ∞ 点的留数 定义 2.2 设 ∞ 是 f ( z ) 的孤立奇点 , 则 f ( z ) 在 R < z < +∞ 内解析 ,
C 是 R < z < +∞ 内一条简单闭
y C
O
§5.2 留 数 —— 在 ∞ 点的留数
R
x
定理 2.2 若 f ( z ) 在 C U {∞} 上有有限个奇点：z1 ,L , z n , ∞ , 则
1 P ( z ) , z = 0 是 f ( z ) 的 3 级极点 . z3 1
解二：把 f ( z ) 在 z = 0 点展成洛朗级数 :
z − sin z 1 = 6 z6 z = 1 3 1 5 1 7 z − z − 3! z + 5! z − 7! z + L
O
1 = − c1 . ∫ C f ( z ) dz, 则 Res f ( z ) , ∞ 2π i Ñ
× zn
f ( z ) ,∞ . = − 2π i Res
§5.2 留 数 —— 在 ∞ 点的留数
规则 IV Res [ f ( z ), ∞ ] = − Res f ( )
(5)
假设 z0 是 f ( z ) 的 k 级极点 , k < m ,
f ( z ) = c− k ( z − z0 )
−k
+ L + c−1 ( z − z0 ) + c0 + c1 ( z − z0 ) + L
−1 m− k
( z − z0 )
0
m
f ( z ) = c− k ( z − z0 )
§5.2 留 数 —— 计算规则
复变函数与积分变换
C f ( z )dz lim 1 f ( k ) zk . n k
n
3.积分的性质
g 设 f ( z ) ， ( z ) 在曲线 C 上可积，则 C 1) C f ( z )dz C f ( z )dz ， 与 C 反向； 2) C Kf ( z )dz K C f ( z )dz，K 为常数；
习题：
1.设C是正向圆周z 1, 计算下列各积分的值。 dz dz dz 1 ） ; 2) ; 3) ; i z2 cos z c c c ( z )( z 2) 2 解：
dz 1) 0; z2 c dz 2) 0; cos z c 4i 3) 2i ; i i c ( z )( z 2) 2 i4 2 2 dz 1
z re i
z x iy
(5)代数表示:
5.运算 1)相等; 2)四则运算,及运算规律; 3)共轭运算,及运算规律; 4) z z r r [cos( ) i sin( )]
1 2 1 2 1 2 1 2
5)
z1 r 1 [cos(1 2 ) i sin(1 2 )] z2 r2 r i (1 2 ) 1e ． r2
2i
3.沿指定曲线计算下列各积分.
ez 1 ） z 2 dz, C : z 2 1; c ez 3) C ( z 1)( z 2) dz, C : z 3; eiz 3 2) 2 dz, C : z 2i ; z 1 2 c ez 4) 3 dz, C : z 2; C z
2 2
在区域x 0内连续，且 u v v u , 在区域x 0上成立时， 1, 2a x y x y 1 即，当a 时，函数f ( z )在区域x 0内是解析的。 2
复变函数-总结
所 以 vx,y1y22xy-1x2c. 于是
2
2
27
fzx2-y2xy i 1 2y22 xy-1 2x2 c
由f00( x y 0 0) c0 从而
fz x 2- y 2 x y i 1 2 y 2 2 x y - 1 2 x 2 1 - 2 i z 2
即为所求解析函数。
等价定义：
设 f (z) = u(x,y) + iv(x,y) , A = u0+iv0 , z0 = x0+iy0 ,
那么
lim f (z)
zz0
运算性质：
limu(x, Axyxyl im xxyy0000 v(x,
y) y)
u0 v0
.
( 1 ) li (f m ( z ) g ( z ) ) lifm ( z ) lig ( m z )
例题1 一调和函数 ux,yx2-y2xy,
求一解析函数 fzuiv使 f00.
解：〔法一〕 ux2xy,uy-2yx
由 C-R 方程 v y u x 2 x y v 2 x y d y
由 v x - u y 2x2 yy 12c y2x c 2 xy - x v x c2xyc-12xx2,c,
9
对复平面内任一
x3
点z, 用直线将z
除了复数的平面表 示方法外, 还可以
与N相连, 与球面
N(0,0,2r) 用球面上的点来表
相交于P点, 那么
示复数.
球面上除N点外
x3
的所有点和复平
面上的所有点有
P(x1,x2,x3)
一一对应的关系,
而N点本身可代
表无穷远点, 记 作 .这样的球面
复变函数与积分变换公式汇总
复变函数与积分变换公式汇总一、复变函数复变函数是将复数域上的变量映射到复数域上的函数。
形式上，复变函数可以表示为f(z) = u(x,y) + iv(x,y)，其中z = x + iy是自变量，u(x,y)和v(x,y)是实部和虚部函数。
复变函数的性质包括解析性、全纯性、调和以及实部虚部的关系等。
1.解析函数性质解析函数是复变函数的重要性质之一，它表示函数在其定义域内处处可导，并且其导数连续。
如果f(z)是定义在区域D上的函数，满足Cauchy-Riemann条件，则f(z)是该区域上的解析函数。
Cauchy-Riemann条件可以表示为：∂u/∂x=∂v/∂y,∂u/∂y=-∂v/∂x2.全纯函数性质全纯函数是解析函数的特殊情形，它在整个复平面上都有定义，并且是解析的。
全纯函数还有许多重要的性质，如Liouville定理、最大模原理等。
3.调和函数性质调和函数是复平面上的实函数，满足拉普拉斯方程(△u=∂²u/∂x²+∂²u/∂y²=0)。
调和函数在物理学中有广泛的应用，例如描述电势、热力学等现象。
4.实部虚部关系对于任意一个复变函数f(z)，其实部u(x,y)和虚部v(x,y)之间有一些重要的关系。
例如，如果f(z)是一个解析函数，则它的实部和虚部函数满足调和方程，并且u(x,y)和v(x,y)是共轭调和函数。
二、积分变换公式积分变换是对函数进行积分操作的数学工具，常用于求解微分方程、信号处理等问题。
常见的积分变换公式包括拉普拉斯变换和傅里叶变换等。
1.拉普拉斯变换拉普拉斯变换是一种广泛应用于信号分析和控制系统的积分变换方法。
定义域为半无穷区间的函数f(t)在复平面上进行拉普拉斯变换后得到一个复变函数F(s)，满足积分方程：F(s) = L[f(t)] = ∫[0,∞] f(t)e^(-st) dt2.拉普拉斯变换的性质拉普拉斯变换具有一些重要的性质，如线性性、位移性质、尺度变换、微分性质等。
复变函数与积分变换公式汇总
复变函数与积分变换公式汇总一、复变函数的基本概念和性质1. 复数集的定义：复数集是由实数和虚数构成的集合，形式为a + bi，其中a和b都是实数，i是虚数单位，满足i² = -12. 复变函数的定义：设有一个定义在平面上的函数f(z)，其中z = x + yi是平面上的点，x和y是实数。
如果对任意给定的z都有唯一确定的复数w与之对应，那么称函数f(z)是复数域上的一个函数。
3.复变函数的连续性：如果在z0处存在一个复数A，使得当z趋于z0时，函数f(z)趋于复数A，则称函数f(z)在点z0处连续。
4.复变函数的可导性：如果函数f(z)在z0处连续，并且当z趋于z0时，函数f(z)的导数存在有一个有限的极限L，则称函数f(z)在z0处可导，并记为f'(z0)=L。
二、复变函数的常用公式1. 欧拉公式：e^(iθ) = cosθ + isinθ2. 增补公式：sinh(x + iy) = sinh(x)cos(y) + isin(y)cosh(x)3.多项式的根公式：设P(z)=aₙzⁿ+aₙ₋₁zⁿ⁻¹+…+a₀是一个非常数多项式，aₙ≠0，则P(z)=0在复数域存在n个根。
4.共轭根公式：如果z是复数P(z)=0的根，则z^*也是复数P(z)=0的根。
5. 辐角公式：对于复数z = x + yi，其中x和y是实数，辐角θ = arctan(y/x)，其中-π < θ ≤ π。
6. 复数的模公式：对于复数z = x + yi，其中x和y是实数，模，z，= √(x² + y²)。
7. 三角和指数函数的关系：sinθ = (e^(iθ) - e^(-iθ))/(2i)，cosθ = (e^(iθ) + e^(-iθ))/28. 三角函数和指数函数的关系：sin(ix) = i sinh(x)，cos(ix) = cosh(x)。
三、复变函数的常用积分变换公式1.度量积分变换：对于复变函数f(z)，定义如下的度量积分变换公式：∫(f(z)dz) = ∫(f(z₁)dz₁ + f(z₂)dz₂ + … + f(zₙ)dzₙ)，(z₁,z₂,…,zₙ)为路径连续的点。
复变函数与积分变换重点公式归纳
复变函数与积分变换第一章 复变函数一、复变数和复变函数()()()y x iv y x u z f w ,,+== 二、复变函数的极限与连续极限 A z f z z =→)(lim 0连续 )()(lim 00z f z f z z =→第二章 解析函数一、复变函数),(),()(y x iv y x u z f w +==可导与解析的概念。
二、柯西——黎曼方程掌握利用C-R 方程⎪⎩⎪⎨⎧-==xy yx v u v u 判别复变函数的可导性与解析性。
掌握复变函数的导数：yx y x y y x x v iv iu u v iu y fi iv u x f z f +==-=+-=∂∂=+=∂∂=1)('三、初等函数重点掌握初等函数的计算和复数方程的求解。
1、幂函数与根式函数θθθθθin n n n n n e r n i n r i r z w =+=+==)sin (cos )sin (cos 单值函数nk z i n ner z w π2arg 1+== (k =0、1、2、…、n-1) n 多值函数2、指数函数：)sin (cos y i y e e w xz+==性质：（1）单值.（2）复平面上处处解析，zze e =)'(（3）以i π2为周期 3、对数函数ππk i z k z i z Lnz w 2ln )2(arg ln +=++== （k=0、±1、±2……）性质：（1）多值函数,（2）除原点及负实轴处外解析,（3）在单值解析分枝上:kk z z 1)'(ln =。
4、三角函数：2cos iz iz e e z -+= ie e z iziz 2sin --=性质：（1）单值 （2）复平面上处处解析 （3）周期性 （4）无界5、反三角函数（了解）反正弦函数)1(1sin 2z iz Ln iz Arc w -+== 反余弦函数 )1(1cos 2-+==z z Ln iz Arc w性质与对数函数的性质相同。
复变函数与积分变换概念公式
复变函数与积分变换概念公式一、复变函数复变函数是指定义在复平面上的函数，即函数的自变量和因变量均为复数。
复数可用标准形式表示为 z = x + yi，其中 x 和 y 分别表示实部和虚部。
复变函数可以将一个复数映射到另一个复数，即 f(z) = u(x, y) + iv(x, y)，其中 u 和 v 分别表示实部和虚部。
复变函数通常具有解析性，即满足柯西-黎曼方程，即：∂u/∂x=∂v/∂y∂u/∂y=-∂v/∂x复变函数的求导规则也与实变函数类似，可以通过对u和v分别对x和y求偏导得到。
复变函数的积分也可类似地进行，即将曲线积分转换为线积分，并利用格林公式等方法进行计算。
积分变换是指将一个函数通过积分的方式转换为另一个函数，常见的积分变换包括拉普拉斯变换、傅里叶变换和z变换等。
1.拉普拉斯变换拉普拉斯变换是一种将实函数转换为复函数的积分变换方法，可以用于求解微分方程和信号处理等问题。
拉普拉斯变换的定义为：F(s) = L{f(t)} = ∫[0,∞] f(t)e^(-st)dt其中 f(t) 为已知的函数，s 为复变量。
拉普拉斯变换具有线性性质，即 L{af(t) + bg(t)} = aF(s) + bG(s)，其中 a 和 b 为常数，f(t) 和g(t) 分别为待变换的函数。
2.傅里叶变换傅里叶变换是一种将复函数表示为基本正弦和余弦函数的线性组合的积分变换方法，主要用于信号处理和频谱分析等领域。
傅里叶变换的定义为：F(ω) = F{f(t)} = ∫[-∞,+∞] f(t)e^(-jωt)dt其中 f(t) 为已知的函数，ω 为角频率。
傅里叶变换也具有线性性质，即 F{af(t) + bg(t)} = aF(ω) + bG(ω)，其中 a 和 b 为常数，f(t) 和 g(t) 分别为待变换的函数。
3.z变换z变换是一种将离散信号表示为z的幂次的线性组合的积分变换方法，主要用于差分方程的求解和数字信号处理等领域。
复变函数与积分变换公式
复变函数与积分变换公式1.复数复数是由实数和虚数组成的数，记作z=a+bi，其中a和b都是实数，i是虚数单位，满足i2=-1。
复数的共轭是指将复数中的虚部取相反数，即z*=a-bi。
2.复变函数复变函数是定义在复平面上的函数，即将复数作为自变量和函数值的函数。
设f(z)是复变函数，其中z=x+iy是复数，x和y是实数，则f(z)可以表示为f(z)=u(x,y)+iv(xy)，其中u(xy)和v(xy)都是实函数，分别称为f(z)的实部和虚部。
3.欧拉公式欧拉公式是数学中的一个重要公式，它描述了复数和三角函数之间的关系。
欧拉公式可以表示为e^ix=cos(x)+isin(x)，其中e 是自然对数的底数，i是虚数单位，x是实数。
4.柯西-黎曼方程柯西-黎曼方程是描述复变函数的重要方程，它表明如果一个复变函数f(z)在某个区域内连续且可微分，那么它满足柯西-黎曼方程。
柯西-黎曼方程可以表示为:дu/дx=дv/дyдu/ду=-дv/дx其中u(xy)和v(xy)分别是f(z)的实部和虚部。
二、积分变换公式1.傅里叶变换傅里叶变换是一种重要的积分变换，它可以将一个函数在时间域内的积分转换为频率域内的积分。
傅里叶变换可以表示为:F(w)=∫f(t)e^(-jwt)dtf(t)=1/2π∫F(w)e^(jwt)dw其中F(w)是f(t)的傅里叶变换，f(t)是函数在时间域内的表示，w是频率，j是虚数单位。
2.拉普拉斯变换拉普拉斯变换是一种常用的积分变换，它可以将一个函数在时间域内的积分转换为复平面内的积分。
拉普拉斯变换可以表示为:F(s)=∫f(t)e^(-st)dtf(t)=1/2πj[F(s)e^(st)ds其中F(s)是f(t)的拉普拉斯变换，f(t)是函数在时间域内的表示，s是复数。
3.Z变换Z变换是一种离散的积分变换，它可以将一个离散函数在时间域内的积分转换为复平面内的积分。
Z变换可以表示为:F(z)=∑f(n)z^(-n)f(n)=1/2πj∫F(z)z^n-1dz其中F(z)是f(n)的Z变换，f(n)是离散函数在时间域内的表示，z是复数。
复变函数及积分变换重点公式归纳
复变函数及积分变换重点公式归纳复变函数是指定义在复数域上的函数，其自变量和函数值都是复数。
复变函数可以表示为两个实变量的函数，即f(z)=u(x,y)+iv(x,y)，其中u(x,y)和v(x,y)是实变量的函数。
复变函数的积分变换是指对复变函数进行积分变换，得到新的复变函数。
在复变函数的积分变换中，有一些重要的公式需要归纳，包括：1.度量公式：对于复变函数f(z)=u(x,y)+iv(x,y)，其微分形式为dz=dx+idy。
根据度量公式，有dx=\frac{1}{2}(dz+d\bar{z})，dy=\frac{1}{2i}(dz-d\bar{z})。
2.柯西-黎曼方程：对于复变函数f(z)=u(x,y)+iv(x,y)，满足柯西-黎曼方程的充要条件是u_x=v_y和u_y=-v_x。
3.柯西-黎曼积分定理：对于一个闭合曲线C，如果复变函数f(z)在C内解析（即在C内柯西-黎曼方程成立），那么有\oint_C f(z)dz=0。
4.柯西积分公式：对于一个有界区域D和在D内解析的复变函数f(z)，柯西积分公式为\oint_C \frac{f(z)}{z-a} dz=2\pi i f(a)，其中C是D内包围点a 的闭合曲线。
5.柯西积分公式的推广：对于一个有界区域D和在D内解析的复变函数f(z)，柯西积分公式的推广形式为\oint_C \frac{f(z)}{(z-a)^n} dz=2\pi i \frac{f^{(n-1)}(a)}{(n-1)!}，其中C是D内包围点a的闭合曲线。
6.柯西积分公式的应用：柯西积分公式可以用于计算复变函数的积分，如计算围道上的积分或者在无穷远处的积分等。
7.柯西主值公式：对于一个有界区域D和在D内解析的复变函数f(z)，柯西主值公式为\frac{1}{2\pi i}\int_C \frac{f(z)}{z-a} dz=PV\frac{1}{2\pii}\int_C \frac{f(z)}{z-a} dz=PVf(a)+\frac{1}{2}f(a)，其中PV表示柯西主值。
复变函数与积分变换公式
复变函数与积分变换公式复变函数是指定义在复数域上的函数。
在数学中，复变函数是研究复数平面上的函数性质的一个重要分支。
与实变函数不同的是，复变函数具有更多的性质和更复杂的变换规律。
在复变函数的研究中，积分变换公式是一个重要的工具，它可以用来计算复变函数的积分或者对其进行变换。
复变函数可以表示为f(z)=u(x,y)+iv(x,y)，其中z=x+iy表示复数，u(x,y)和v(x,y)表示实函数。
根据柯西—黎曼方程，对于复变函数f(z)来说，它满足以下条件：u(x,y)和v(x,y)都是可微的，且满足以下偏微分方程：∂u/∂x=∂v/∂y和∂u/∂y=-∂v/∂x这两个方程表明了复变函数的实部和虚部的偏导数之间的关系。
在复变函数的积分变换中，常用的方法包括柯西—黎曼积分公式和柯西—黎曼积分定理。
柯西—黎曼积分公式用于计算沿着闭合曲线的复变函数的积分，它表示为：∮f(z)dz = ∫[f(z)dz] = ∫[u(x,y)dx-v(x,y)dy] +i∫[v(x,y)dx+u(x,y)dy]其中，∮表示沿着闭合曲线的积分，[f(z)dz]表示该路径上的函数f(z)乘以微元dz的积分，u(x,y)和v(x,y)分别表示f(z)的实部和虚部。
柯西—黎曼积分定理是基于柯西—黎曼积分公式的一个重要定理，它表示了在闭合曲线内的函数积分等于该函数在闭合曲线上的积分。
根据柯西—黎曼积分定理，如果一个函数在一条围成的区域内是解析的（也就是满足柯西—黎曼方程），那么该函数在该区域内的积分等于零。
除了柯西—黎曼积分公式和柯西—黎曼积分定理，还有其他一些积分变换公式。
其中，常用的有拉普拉斯变换和傅里叶变换。
拉普拉斯变换是一种用于处理函数的积分变换方法，它将一个函数f(t)转换为另一个函数F(s)，其中F(s)是复平面上的一个函数。
拉普拉斯变换可以用来解决微分方程、积分方程以及控制系统的问题。
傅里叶变换是另一种常用的积分变换方法，它将一个函数f(t)转换为另一个函数F(ω)，其中F(ω)是复平面上的一个函数。
复变函数与积分变换重要知识点
sin2 z 0, cos2 z 0 在复数中均不成立。
3
复变函数与积分变换复习要点
2013 年 11 月中旬至 12 月中旬
shz ez ez , chz ez ez
双曲函数
2
2；
shz 奇函数， chz 是偶函数。 shz, chz 在 z 平面内解析，且 shz chz,chz shz
6 辐角：Argz 1 2k k为任意整数,其中把满足- 0 的0称为Argz的主值，
记作，0 = arg z. z 0 辐角的主值
arg
z
arctan
π, 2
arctan
y x
y
, x 0, x 0, y 0,
π, x 0, y
3! 5!
zn n!
zn (R ) n0 n!
(1)n z2n1 (2n 1)!
, (R )
cos z 1 z2 z4 (1)n z2n
2! 4!
(2n)!
1 1 z z2 (1)n zn ,| z | 1 1 z
如果我们定义
zn
1 zn
,
那么当
n
为负整数时,
上式仍成立.
棣莫佛公式：当 z 的模 r 1, 即 z cos i sin,
(cos i sin )n cos n i sin n.
方程 wn
z
的根：
w
n
z
1
rn
cos
复变函数与积分变换(第一章)
z1z2 r1ei1 r2ei2 r1r2ei (1 2 ) .
z1z2 rr 1 2 z1 z2
Arg( z1 z2 ) Argz1 Argz2 .
两个复数相乘，积的模等于各复 数的模的积，积的幅角等于这两 个复数的幅角的和.
z1z2 rr 1 2 z1 z2
(6)简单曲线、光滑曲线
设x(t)和y(t)是实变量t的两个实函数，它们在闭区 间[,]上连续，则由方程组 x x(t ) y y(t ) 或由复值函数 z (t ) x(t ) iy(t ) 定义的集合称为复平面上的一条曲线，上述方程称为 曲线的参数方程.点A=z() 和B=z()分别称为曲线的 起点和终点.如果当 t1 , t2 [ , ], t1 t2 时，有 z(t1 ) z(t2 ) ， 称曲线为简单曲线，也称为约当(Jordan)曲线. z ( ) z ( ) 的简单曲线称为简单闭曲线.
3 i 2eiπ / 6
复数乘法的几何意义
z1 r1 (cos1 i sin 1 ), z2 r2 (cos2 i sin 2 ).
z1 z2 r1 (cos 1 i sin 1 ) r2 (cos 2 i sin 2 ) r1 r2 ((cos 1 cos 2 sin 1 sin 2 ) i(sin 1 cos 2 cos 1 sin 2 )) r1r2 (cos(1 2 ) i sin(2 2 ))
a 0, ； (3) a ，则 a
a (4) a 0 ，则 ； 0
(5) , 的实部、虚部、幅角都无意义； (6)为了避免和算术定律相矛盾，对
0 , 0 , , 0
复变函数与积分变换重点公式归纳
复变函数与积分变换重点公式归纳复变函数是指变量为复数的函数，可以表示为f(z)=u(x, y)+iv(x, y)，其中z=x+iy，u(x, y)和v(x, y)为实数函数。
复变函数与实变函数（实数域上的函数）相比较，具有一些独特的性质和变换。
复变函数的基本性质有：1. 复变函数的可导性：复变函数的可导性与实变函数的可导性略有不同。
如果f(z)=u(x, y)+iv(x, y)在域D上的偏导数u_x、u_y、v_x、v_y都存在，并且满足柯西-黎曼方程（u_x=v_y，u_y=-v_x），则f(z)在D上可导。
2. 柯西-黎曼方程：对于复变函数f(z)=u(x, y)+iv(x, y)，满足柯西-黎曼方程的函数可以表示为全纯函数，也即f'(z)=u_x+iv_x存在。
复变函数的积分变换（Integral Transform）是通过对函数进行积分变换，得到新的函数表示形式。
常见的复变函数积分变换包括拉普拉斯变换、傅里叶变换、反傅里叶变换、正变换等。
以下是复变函数积分变换中的一些重点公式：1. 拉普拉斯变换（Laplace Transform）拉普拉斯变换将函数f(t)变换为F(s)（s为复数变量）的形式，公式表示为：F(s) = ∫[0,∞] e^(-st)f(t) dt2. 逆拉普拉斯变换（Inverse Laplace Transform）逆拉普拉斯变换将函数F(s)变换为f(t)的形式，公式表示为：f(t) = 1/2πi ∫[-i∞, i∞] e^(st)F(s) ds3. 傅里叶变换（Fourier Transform）傅里叶变换将函数f(t)变换为F(ω)（ω为频率）的形式，公式表示为：F(ω) = ∫[-∞,∞] e^(-iωt)f(t) dt4. 反傅里叶变换（Inverse Fourier Transform）反傅里叶变换将函数F(ω)变换为f(t)的形式，公式表示为：f(t)=1/2π∫[-∞,∞]e^(iωt)F(ω)dω5. 正变换（Forward Transform）正变换是指从时域到频域的变换，例如：拉普拉斯变换、傅里叶变换等。
复变函数与积分变换第3章复变函数的积分
23
如果将定理3.3的条件加强为“f ′(z)在D内连续”，则定理的证明就变得简 单，事实上，设z=x+iy,f(z)=u(x,y)+iv(x,y)，由f(z)在D内解析,可得
由f′(z)在D内连续，可知
均在D内连续，进而由Green公式可得
2021/7/30
24
其中 是以C为边界的闭区域，再由定理3.1得 单连通区域上的Cauchy积分定理还可进一步推广如下：
在闭圆
上连续，则
内解析，
2021/7/30
50
3.3.2解析函数的无穷可微性 定理3.11（Cauchy导数公式）在定理3.9的假设条件下，则对任 意正整数n和z∈D，有
2021/7/30
51
证 只证明n=1的情形，一般情况可用数学归纳法完成．
使得
取Δz≠0,且使得
则由Cauchy积分公式可得
2021/7/30
26
定理3.5对于单连通区域D内解析的函数f(z)，由式(3.4)所定义的F(z)在 D内解析，并且
证明只需证明 z∈D，有F′(z)=f(z)即可．由f(z)在D内的连续性，对
ε>0，可取δ>0充分小，使得
,并且对
，有2021/7/30 Nhomakorabea27
设
，由于积分与路径无关，则
其中从z到z+Δz的积分路径可选择为直线段（图3.7）．
4
图3.1
2021/7/30
5
其中
．记λ为所有小弧段 的弧长的最大者，当分点无限增多且λ→0
时，不论对C的分法如何，也不论对ξk的取法如何，和式Sn的极限都存在且等 于J，则称f(z)沿C从A到B可积，而称J为f(z)沿C从A到B的积分，记为
复变函数与积分变换重要公式集锦(第一篇1、2章)
第一篇 第一章 复数第一节 复数及其表示法 实部、虚部：x=Re z; y=Im z.辐角：θ=Arg z ； x=│z │cos θ；y=│z │sin θ，tg θ=y/x 数0是惟一的模为零而辐角没有定义的复数。
Arg z= arg z+2n π(n=0,±1, ±2,…)1 三角表示：⎩⎨⎧==θθsin rcos x r y z=r(cos θ+i sin θ)欧拉公式：e i θ=cos θ+isin θ 指数表示：z=re i θ,第二节 复数的运算及几何意义加法：z 1+z 2=(x 1+x 2)+i （y 1+y 2） 减法：z 1+z 2=(x 1-x 2)+i （y 1-y 2） 乘法：z 1z 2=(x 1x 2-y 1y 2)+i(x 1y 2+x 2y 1) 除法：)0(2222221122222212121≠+-+++=z y x y x iy y x x z zyxyx两个复数乘积的模等于它们模的乘积，两个复数乘积的辐角等于他们辐角的和。
2121212121)(ArgzArgz z z Arg z z r r z z +=⋅==复数z 的n 次幂2121212121)(ArgzArgz z z Arg z z r r z z -===z n =r n (cos n θ+isin n θ)(n 为正整数) 棣莫佛公式：（cos θ+isin θ）n=cos n θ+isin n θ两个复数商的模等于他们模的商，两个复数商的辐角等于分子与分母辐角的差。
复数的方根。
，的算术根，为其中1-n ,2,1,0k r r )2sin2(cosr z nnn=+++==nk i nk πθπθω共轭复数及其运算性质 iy -x z iy,x z =+= z=z 1）（rgz -z rg 2A A =）（z z 3=）（ 2zz z 4=）（2121z z z z 5±=±）（2121z z z z 6⋅=）（2121z z z z 7=⎪⎪⎭⎫ ⎝⎛）（.2,2x 8z z y z z -=+=）（关于复数模的重要公式)Re(2);Re(2212221221212221221z z z z z z z z z z z z -+=-++=+第三节 平面点集和区域邻域：在平面上以z0为中心，正数ρ为半径的圆内部的点集，称为点z0的ρ邻域。
大学高数复变函数与积分变换复习公式知识点
ℱ f nx ( j)n F()
4、积分性质
ℱ
x x0
f
xdx
1 F () j
ℱ
(
j
xn)
f
x
d
n F () d n
由 Fourier 变换的微分和积分性质，我们可以利用 Fourier 变换求解微积分方程。
四、卷积和卷积定理
f1(x) * f2 (x) f1( ) f2 (x )d
2、闭路积分： a) f zdz c
利用留数定理，柯西积分公式，高阶导数公式。
b) [u(x, y) iv(x, y)]dz c
三、柯西积分定理：
c f zdz 0
推论 1：积分与路径无关
f zdz z2 f (z)dz
c
z1
推论 2：利用原函数计算积分
z2 z1
f
(z)dz
F(z2 ) F(z1)
第四章 解析函数的级数
一、幂级数及收敛半径：
an (z b)n
n0
1、一个收敛半径为 R（≠0）的幂级数，在收敛圆内的和函数 f (z) 是解析函数，在这个收敛圆内，这
个展开式可以逐项积分和逐项求导，即有：
f 'z nan z bn n1
zb R
z f
0
z dz
n0
z
l an
大学高数复变函数与积分变换复习公式知识点
第一章 复变函数 一、复变数和复变函数
w f z ux, y ivx, y
二、复变函数的极限与连续
极限 lim f (z) A zz0
连续
lim f (z)
zz0
f (z0)
第二章 解析函数
一、复变函数 w f (z) u(x, y) iv(x, y) 可导与解析的概念。
复变函数与积分变换3.3Cauchy积分公式
设 f (z)
( 2 1)sin d , 求 f (i) 和 f (2 3i)
||2 z
解 由Cauchy积分公式和Cauchy积分定理，有
2πi(z2 1)sin z z 2
f (z)
0
z 2
f (i) 4πiz sin z 2πi(z2 1)cos z 4πsin i 4πisinh1 zi
C z z0
K z z0
K z z0
K z z0
2πi f (z0)
f (z) f (z0 ) dz K z z0
而
f (z) f (z0) d z f (z) f (z0) d s d s 2π
K f (z) f (z0) d z 0 K z z0
(3.3.1)
柯西积分公式
证明
由于 f (z)在z0 连续，任意给定 0, 必存在一个 0, 当0 z z0 时， 有 f (z) f (z0)
现以z0为中心，R 为半径作圆周K：z z0 R,
使其全部包含在C的内部，且 R ,
D
C K z0.R z
柯西积分公式
则有 f (z) dz f (z) dz f (z0) dz f (z) f (z0) dz
1
2）I
1
dz
(z 2) d z 2πi 1 2πi
|z1|1 4 ( z 1)( z 2)
z 1 |z1|1 4
z 2 z1
3)
1
1 1
(z 1)(z 2) z 2 z 1
1
dz
1 dz
1 dz
|z|3 (z 1)(z 2)
|z|3 z 2
|z|3 z 1
2πi 2πi 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
复变函数复习提纲(一)复数的概念1.复数的概念：z x iy =+，,x y 是实数, ()()Re ,Im x z y z ==.21i =-.注：两个复数不能比较大小. 2.复数的表示 1）模：z =2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值()arg z 是位于(,]ππ- 中的幅角。
3）()arg z 与arctanyx之间的关系如下： 当0,x > arg arctan yz x=；当0,arg arctan 0,0,arg arctan yy z x x y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩； 4）三角表示：()cos sin z z i θθ=+，其中arg z θ=；注：中间一定是“+”号。
5）指数表示：i z z e θ=，其中arg z θ=。
(二) 复数的运算1.加减法：若111222,z x iy z x iy =+=+，则()()121212z z x x i y y ±=±+±2.乘除法：1）若111222,z x iy z x iy =+=+，则()()1212122112z z x x y y i x y x y =-++；()()()()112211112121221222222222222222x iy x iy z x iy x x y y y x y x i z x iy x iy x iy x y x y +-++-===+++-++。
2）若121122,i i z z e z z eθθ==, 则()121212i z z z z e θθ+=；()121122i z z e z z θθ-= 3.乘幂与方根1） 若(cos sin )i z z i z e θθθ=+=，则(cos sin )n nn in z z n i n z e θθθ=+=。
2） 若(cos sin )i z z i z e θθθ=+=，则122cos sin (0,1,21)nk k z i k n n n θπθπ++⎛⎫=+=- ⎪⎝⎭（有n 个相异的值）（三）复变函数1．复变函数：()w f z =，在几何上可以看作把z 平面上的一个点集D 变到w 平面上的一个点集G 的映射.2．复初等函数 1）指数函数：()cos sin z xe ey i y =+，在z 平面处处可导，处处解析；且()z z e e '=。
注：ze 是以2i π为周期的周期函数。
（注意与实函数不同） 3） 对数函数： ln (arg 2)Lnz z i z k π=++(0,1,2)k =±±（多值函数）； 主值：ln ln arg z z i z =+。
（单值函数）Lnz 的每一个主值分支ln z 在除去原点及负实轴的z 平面内处处解析，且()1lnz z'=；注：负复数也有对数存在。
（与实函数不同） 3）乘幂与幂函数：(0)bbLnaa ea =≠；(0)b bLnzz e z =≠注：在除去原点及负实轴的z 平面内处处解析，且()1b b zbz-'=。
4）三角函数：sin cos sin ,cos ,t ,22cos sin iz iz iz iz e e e e z zz z gz ctgz i z z---+==== sin ,cos z z 在z 平面内解析，且()()sin cos ,cos sin z z z z ''==-注：有界性sin 1,cos 1z z ≤≤不再成立；（与实函数不同）4） 双曲函数 ,22z z z ze e e e shz chz ---+==； shz 奇函数，chz 是偶函数。
,shz chz 在z 平面内解析，且()(),shz chz chz shz ''==。
（四）解析函数的概念1．复变函数的导数 1）点可导：()0f z '=()()000limz f z z f z z∆→+∆-∆；2）区域可导： ()f z 在区域内点点可导。
2．解析函数的概念1）点解析： ()f z 在0z 及其0z 的邻域内可导，称()f z 在0z 点解析； 2）区域解析： ()f z 在区域内每一点解析，称()f z 在区域内解析； 3）若()f z 在0z 点不解析，称0z 为()f z 的奇点；3．解析函数的运算法则：解析函数的和、差、积、商（除分母为零的点）仍为解析函数；解析函数的复合函数仍为解析函数；（五）函数可导与解析的充要条件1．函数可导的充要条件：()()(),,f z u x y iv x y =+在z x iy =+可导⇔(),u x y 和(),v x y 在(),x y 可微，且在(),x y 处满足C D -条件：,u v u v x y y x∂∂∂∂==-∂∂∂∂ 此时， 有()u vf z i x x∂∂'=+∂∂。
2．函数解析的充要条件：()()(),,f z u x y iv x y =+在区域内解析⇔(),u x y 和(),v x y 在(),x y 在D 内可微，且满足C D -条件：,u v u v x y y x∂∂∂∂==-∂∂∂∂； 此时()u vf z i x x∂∂'=+∂∂。
注： 若()(),,,u x y v x y 在区域D 具有一阶连续偏导数，则()(),,,u x y v x y 在区域D 内是可微的。
因此在使用充要条件证明时，只要能说明,u v 具有一阶连续偏导且满足C R -条件时，函数()f z u iv =+一定是可导或解析的。
3．函数可导与解析的判别方法1）利用定义 （题目要求用定义，如第二章习题1）2）利用充要条件 （函数以()()(),,f z u x y iv x y =+形式给出，如第二章习题2） 3）利用可导或解析函数的四则运算定理。
（函数()f z 是以z 的形式给出，如第二章习题3）（六）复变函数积分的概念与性质1． 复变函数积分的概念：()()1lim nkkcn k f z dz f zξ→∞==∆∑⎰，c 是光滑曲线。
注：复变函数的积分实际是复平面上的线积分。
2． 复变函数积分的性质1）()()1ccf z dz f z dz -=-⎰⎰ （1c -与c 的方向相反）； 2） ()()()()[],,cccf zg z dz f z dz g z dz αβαβαβ+=+⎰⎰⎰是常数；3） 若曲线c 由1c 与2c 连接而成，则()()()12cc c f z dz f z dz f z dz =+⎰⎰⎰。
3．复变函数积分的一般计算法 1）化为线积分：()cccf z dz udx vdy i vdx udy =-++⎰⎰⎰；（常用于理论证明） 2）参数方法：设曲线c ： ()()z z t t αβ=≤≤，其中α对应曲线c 的起点，β对应曲线c 的终点，则()()[]()cf z dz f z t z t dt βα'=⎰⎰。
（七）关于复变函数积分的重要定理与结论1．柯西—古萨基本定理：设()f z 在单连域B 内解析，c 为B 内任一闭曲线，则()0cf z dz =⎰2．复合闭路定理： 设()f z 在多连域D 内解析，c 为D 内任意一条简单闭曲线，12,,n c c c 是c内的简单闭曲线，它们互不包含互不相交，并且以12,,n c c c 为边界的区域全含于D 内，则①()cf z dz ⎰()1,knk c f z dz ==∑⎰ 其中c 与kc均取正向；②()0f z dz Γ=⎰，其中Γ由c 及1(1,2,)c k n -=所组成的复合闭路。
3．闭路变形原理 ： 一个在区域D 内的解析函数()f z 沿闭曲线c 的积分，不因c 在D 内作连续变形而改变它的值，只要在变形过程中c 不经过使()f z 不解析的奇点。
4．解析函数沿非闭曲线的积分： 设()f z 在单连域B 内解析，()G z 为()f z 在B 内的一个原函数，则()()()212112(,)z z f z dz G z G z z z B =-∈⎰说明：解析函数()f z 沿非闭曲线的积分与积分路径无关，计算时只要求出原函数即可。
5。
柯西积分公式：设()f z 在区域D 内解析，c 为D 内任一正向简单闭曲线，c 的内部完全属于D ，0z 为c 内任意一点，则()()002c f z dz if z z z π=-⎰6．高阶导数公式：解析函数()f z 的导数仍为解析函数，它的n 阶导数为()()()0102(1,2)()!n n c f z i dz f z n z z n π+==-⎰其中c 为()f z 的解析区域D 内围绕0z 的任何一条正向简单闭曲线，而且它的内部完全属于D 。
7．重要结论：12,010,()n ci n dz n z a π+=⎧=⎨≠-⎩⎰。
（c 是包含a 的任意正向简单闭曲线） 8．复变函数积分的计算方法1）若()f z 在区域D 内处处不解析，用一般积分法()()()[]cf z dz f z t z t dt βα'=⎰⎰2）设()f z 在区域D 内解析， ● c 是D 内一条正向简单闭曲线，则由柯西—古萨定理，()0cf z dz =⎰●c 是D 内的一条非闭曲线，12,z z 对应曲线c 的起点和终点，则有()()()()2121z cz f z dz f z dz F z F z ==-⎰⎰3）设()f z 在区域D 内不解析● 曲线c 内仅有一个奇点：()()()()()0001022()!cn n c f z dz i f z z z f z i dz f z z z n ππ+⎧=⎪-⎪⎨⎪=⎪-⎩⎰⎰（()f z 在c 内解析）● 曲线c 内有多于一个奇点：()cf z dz ⎰()1knk c f z dz ==∑⎰（ic 内只有一个奇点kz）或：()12Re [(),]nkk cf z dz i s f z z π==∑⎰（留数基本定理）● 若被积函数不能表示成()1()n o f z z z +-，则须改用第五章留数定理来计算。
（八）解析函数与调和函数的关系1．调和函数的概念：若二元实函数(,)x y ϕ在D 内有二阶连续偏导数且满足22220x yϕϕ∂∂+=∂∂，(,)x y ϕ为D 内的调和函数。
2．解析函数与调和函数的关系● 解析函数()f z u iv =+的实部u 与虚部v 都是调和函数，并称虚部v 为实部u 的共轭调和函数。