传输矩阵方法
【国家自然科学基金】_传输矩阵方法_基金支持热词逐年推荐_【万方软件创新助手】_20140801
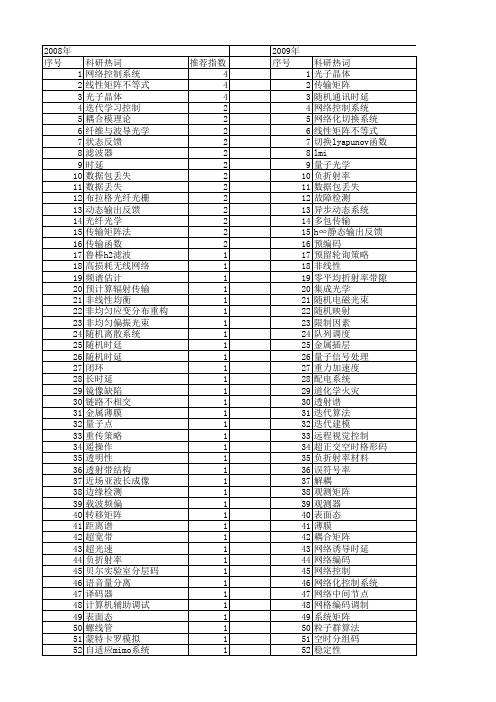
稀疏表示 稀疏脏数据 稀疏 磁电垒 磁光纤光栅 磁光传感器 矩阵方法 矩阵几何解 矩量法 瞬态电磁响应 相干光学 电磁波反射 电磁极化转换 电导率 电光开关 生物认证 牛顿法 爆炸指数法 热辐射 灵敏度 激光技术 源载耦合 波矢过滤 正交幅度调制 次地表层 极化度 有限域 有效折射率法 最小路法 最大距离可分码 最大比合并 时域积分方程 时变时延 无线传感器网络 数据传输 数据丢包 数字用户线 散射强度 提升格式 指数稳定性 性能分析 快速时变信道 微带双通带带通滤波器 张量方法 异质结构 开关频率 开关时间 建模 广义网络控制系统 并列运行机组 带吸收态的有限状态马尔可夫链 左手材料 嵌入式零树小波 小波变换
推荐指数 4 4 4 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 光子晶体 传输矩阵 随机通讯时延 网络控制系统 网络化切换系统 线性矩阵不等式 切换lyapunov函数 lmi 量子光学 负折射率 数据包丢失 故障检测 异步动态系统 多包传输 h∞静态输出反馈 预编码 预留轮询策略 非线性 零平均折射率带隙 集成光学 随机电磁光束 随机映射 限制因素 队列调度 金属插层 量子信号处理 重力加速度 配电系统 道化学火灾 透射谱 迭代算法 迭代建模 远程视觉控制 超正交空时格形码 负折射率材料 误符号率 解耦 观测矩阵 观测器 表面态 薄膜 耦合矩阵 网络诱导时延 网络编码 网络控制 网络化控制系统 网络中间节点 网格编码调制 系统矩阵 粒子群算法 空时分组码 稳定性
传输线矩阵解.

输线方程 一次特征参数
L,C
通解 二次特征参数
W LC ,
L Z0 C
边界条件 确定A1 ,A2
工作参数
, Z,
传输线一般解法
一、传输线段的矩阵解
在上面讨论中已给我们一个重要启示:传输线的 各种应用都可以归结为一段长度?为l的传输线段, 不管是短路、开路或任意负载。
传输线段起到变换的作用,而矩阵理论恰恰是表 征这种变换的最好数学工具。因此,产生了传输线 段的矩阵解思想。
C
U (l)
I
(l )
j
cos 1 sin Z0
jZ0 sin
cos
U (0)
I
(0)
(5-8)
方程(5-8)称为传输线段矩阵。可以说,只需记住这一
矩阵,即可给出大部分传输线公式。我们再一次注意
到推导矩阵(5-8)过程中没有利用任何边界条件。正因
(5-3)
L
dI dz
sJ(s)
I (0)
一、传输线段的矩阵解
I(l)
I(0)
U (l)
U (0)
zl
0
图5-1 传输线段坐标
代入式(5-2),有
sV (s) jLI(s) U(0) jCV (s) sJ(s) I(0)
(5-4)
一、传输线段的矩阵解
jZ0
Xl
Z0
1
Xl Z0
tan tan
令,tanl
Xl Z0
即可导出
Z(z) jZ0 tan( l )
(5-12)
第11次 第六章 微波网络 ABCD矩阵 传输矩阵
二端口网络
1. ABCD与S的关系:
P207给出了详细证明,207的第三行、第四行有错,将a2-b2改为b2-a2,由物理含义 明白错误的原因。
1 A B CZ D 2 ( AD BC ) 0 1 Z0 [S ] 1 1 2 A B CZ 0 D A B CZ 0 D Z0 Z0
T11 T 21
Anhui University
二、二端口T矩阵的特性
1.对称网络: 2.互易网络:
S11 S22 T21 T12 S12 S21 T11T22 T12T21 1
P209 (6.6.5)式有误
3.便于级联运算:
T T 1 T 2 T N
(a)串联阻抗: 1
cos l (c)均匀传输线: j sin l Z0
Z 0 1
(b)并联导纳: 1
jZ 0 sin l cos j sin cos l Z0 jZ 0 sin cos
三、二端口网络的性质:
ABCD参数不仅适用于二端口网络的级联,而且很方便的表示二端口网络得各种特性:
1. 阻抗和反射特性:
在微波电路的分析和综合中,常用 ABCD 参量来表示电路的各种性能指标,如若在网 络输出端的端口2连接负载阻抗为ZL,则其输入端的端口1的输入阻抗为:
V1 A B V2 V1 AV2 BI 2 I C D I I CV DI 2 1 1 2 2
B
Z0 D
Anhui University
传输矩阵方法

(b ) ky kx ky kx ky kx
图1.Dirac点K 附近波矢圆上单层(左),双层(中)和三层(右)石墨烯 的赝自旋矢量旋转图.图中单层赝自旋旋转一次,双层赝自旋旋转 两次而三层旋转三次.第一行表示导带中赝自旋矢量,第二行表示 价带中赝自旋矢量,其方向正好与导带中的方向相反.
2 2
假定势垒边缘相当陡峭且在晶格尺度上光滑,则不引起 能 谷 间 散 射,那 么 我 们 只 需 研 究 一 个 能 谷K 的 散 射. 由 于 势 函 数 与 坐 标y 无 关,则 粒 子 的 波 函 数 可 写 为ψ (r ) = ψ (x)eiky y .二维矩阵表示中, 对无势垒区域的波函数的x分 量满足本征值方程 2 0 (kx − iky )2 ψ1 (x) ψ1 (x) =E − 2m (kx + iky )2 0 ψ2 (x) ψ2 (x) (5) 这里E 是费米能.式(5)可写为下面的两个微分方程 d + ky dx d − ky dx 由(6)(7)消去ψ2 (x)有 d2 2 − ky dx2
其中nJ = −(cos(Jφ), sin(Jφ))表示赝自旋极化轴,在二维 波矢平面上的极化角φ = arctan(ky /kx ),波矢k与动量p与 的 关 系 为p = k.赝 自 旋 矢 量σ = (σx , σy )是 两 维 泡 利 矩 阵.在 上 面 的 表 示 中, J 表 示 石 墨 烯 的 层 数,也 叫 手 性 自由度,它联系各层的电子密度,比如对单层J = 1,对双 层J = 2,等等.
以后的研究进一步指出J 可表示赝自旋在倒空间的缠 绕数.这里赝自旋矢量描述粒子两分量波函数的相对相 位,J 表示当电子波矢绕狄拉克点作一次完全旋转时赝自旋 矢量经历的旋转次数.正如图1所示,在k空间对单层石墨烯 它是厄米和么正算符,本征值为±1.不存在质量项时,螺旋 当波矢绕Dirac点K 旋转一周,赝自旋矢量的方向σ 也旋转 1
传输矩阵在物理学

传输矩阵在物理学中的前沿应用2013261021 李霄强传输矩阵在物理学中的前沿应用2013261021 李霄强传输矩阵法(TMM) 就是将麦克斯韦方程组转换为传输矩阵的形式, 应用传输矩阵进行分析的方法。
为了了解传输矩阵的前沿应用,我查找并阅读了几篇关于传输矩阵应用的文献,这些都是使用传输矩阵解决问题。
列如《传输矩阵法在行波管内部反射引起的增益波动计算中的应用》、《光纤光栅法布里-珀罗腔的V-I传输矩阵法研究》及《用传输矩阵法研究微波波段准一维同轴光子晶体能隙结构》。
在《传输矩阵法在行波管内部反射引起的增益波动计算中的应用》一文中,研究者分析了由于行波管慢波结构制造误差引入的多个不连续点对小信号增益的影响. 行波管内部反射对增益波动的影响, 须采用考虑反射波的四阶模型进行分析, 用传输矩阵法对节点处的自左至右入射和自右至左入射两种散射类型建立传输矩阵, 研究在不同空间电荷参量下, 慢波电路的单个反射节点以及慢波电路的皮尔斯速度参量b 和增益参量C 的多个随机分布不连续性对行波管小信号增益的影响。
即通过传输矩阵可以将一个层面上的电磁波幅值与紧邻的另一个层面的电磁波幅值联系起来,如果知道了第一段入射波分布, 就可以利用传输矩阵法计算最后一段电磁波分布,将第一段电磁波幅值与最后一段电磁波幅值联系起来, 通过求解边界条件, 就可以求任一段电磁波幅值,也可以求出行波管的增益。
在《光纤光栅法布里-珀罗腔的V-I传输矩阵法研究》中,研究者要进行光纤光栅法布里-珀罗腔反射光谱特性的分析,由于目前对于结构简单的光栅构成的法布里-珀罗腔的特性分析多采用偶合模理论。
但对于复杂结构的光栅,由于难以得到解析解,一般采用四阶的龙格-库塔方法进行数值求解或采用多层膜法进行分析计算。
这两种方法都可以保证分析精度,但求解速度较慢。
要快速实时获得光器件、光通信系统以及光传感系统的特性,由于庞大的运算量而引起耗费时间过长成为突出问题。
第五章 微波网络基础 传输(ABCD)矩阵(转移矩阵)

B1 V2 I D1 2
V2 A2 I C 2 2
B2 V3 D2 I 3
V1 A1 I C 1 1
B1 A2 D1 C2
B2 V3 M个二端口网络级联 [ A] [ A1 ][ A2 ] [ AM ] D2 I 3
I1 D I2
V2 0
2
(端口2短路)
传输矩阵应用
传输矩阵的应用——二端口网络的级联
I1
+ -
I2
V1
I3
A1 B1 C D 1 1
二端口网络1
+ -
V2
A2 B2 C D 2 2
二端口网络2
+ -
V3
V1 A1 I C 1 1
传输矩阵参量计算
变压器:
传输矩阵与阻抗矩阵之间的关系
阻抗矩阵线性方程组
V1 Z11 V Z 2 21
A
B
注意负号意义!
Z12 I1 I Z 22 2
I1Z11 Z11 / Z 21 I1Z 21
V1 I1Z11 I 2 Z12 V2 I1Z 21 I 2 Z 22
若网络是互易的, Z12 Z 21
I1 D I2
I 2 Z 22 / Z 21 Z 22 / Z 21 I2 V 0
2
AD BC 1
11
二端口网络
二端口网络——微波电路中最常见
衰减器
移相器 匹配器 滤波器 ……
12
失配损耗 耗散损耗
V1 AV2 BI 2 I1 CV2 DI 2
传输散射矩阵
\ S21 =
Z 01 (1 + GL )(1 + S11 ) Z 02 j (1- GL )
Z 02 - Z 01 Z 02 S11 = 2 Z 0 + Z 01 Z 02
Z 02 - Z 0 GL = Z 02 + Z 0
而
? S21
2Z0 Z01Z02 Z01 2Z0 Z02 - j =- j 2 2 Z02 Z0 + Z01Z02 Z0 + Z01Z02
对于对称二端口网络,若从网络的端口1和2看入时网络 是相同的,则必有S11=S22,可得:
T21 = - T12
对于互易二端口网络( S12 S 21 ),T参数应满足
T11T22 - T12T21 = 1
S11 S 21 S12 T12 / T22 S 22 1 / T22 T11 (T12T21 / T22 ) T21 / T22
T11 (T12T21 / T22 ) T21 / T22
上式中同样要求 T22 0
2. 用S矩阵表示T矩阵
T11 T12 (S11 S 22 S12 S 21 ) / S 21 T T S 22 / S 21 21 22
S11 / S 21 1 / S 21
即
轾 轾 T11 T12 T11 A T12 A 犏 = 犏 犏 犏 T21 T22 T21 A T22 A 臌 臌
轾 T11B 犏 犏 T21B 臌
T12 B T22 B
用矩阵表示:
[T ] [T ]1[T ]2
对于N级级联二端口网络的T矩阵等于各单个二端口网络 T矩阵的乘积。
轾 T11 犏 犏 T21 臌
行波电极微带线的传输abcd矩阵

一、概述行波电极微带线是一种常用的电磁波传输线路结构,广泛应用于微波集成电路、天线阵列、射频系统等领域。
行波电极微带线的传输abcd 矩阵是描述其传输特性的重要参数,对于设计和分析微带线电路具有重要的意义。
二、行波电极微带线的基本原理行波电极微带线是由微带线和两根电极组成的,电极分布沿微带线的方向呈周期性分布,利用电磁波在微带线和电极之间的耦合传输信号。
微带线部分起到传输电磁波的作用,而电极部分起到了调制电波和传输电波的作用。
行波电极微带线的传输abcd矩阵描述了其在不同频率下对电磁波的传输特性。
三、行波电极微带线的传输abcd矩阵计算方法行波电极微带线的传输abcd矩阵可以利用多种方法来进行计算,主要包括理论分析、仿真计算和实验测试。
其中理论分析是基于电磁场方程和原理进行推导和计算,仿真计算是利用电磁场仿真软件进行数值模拟和计算,实验测试是通过实际的电路板搭建和测试获得。
四、行波电极微带线的传输abcd矩阵的影响因素行波电极微带线的传输abcd矩阵是受到多种因素影响的,主要包括微带线的几何结构、材料特性、电极的设计参数等。
其中微带线的介质常数、电导率和电极结构的尺寸是影响传输abcd矩阵的重要因素。
五、行波电极微带线的传输abcd矩阵在电路设计中的应用行波电极微带线的传输abcd矩阵在电路设计中具有重要的应用价值,可以用于分析电磁波在微带线中的传输特性、设计微带线的匹配网络、优化电路性能等方面。
通过对传输abcd矩阵的分析和计算,可以指导实际电路设计中的优化和改进。
六、结论行波电极微带线的传输abcd矩阵是描述其传输特性的重要参数,对于设计和分析微带线电路具有重要的意义。
通过深入研究行波电极微带线的传输abcd矩阵,可以指导微带线的设计和优化,推动微波集成电路、天线阵列、射频系统等领域的发展。
希望通过本文的介绍,读者对行波电极微带线的传输abcd矩阵有更深入的理解,为相关领域的研究和应用提供参考和指导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cheng Yanfu, 2012.9.18
摘要: 本文研究有质量手性费米子和非手性费米子的势垒遂穿.重点讨论手性费米子在势垒中的运动特征,对反 “Klein遂穿”给出直观解释,并比较无手性费米子的遂穿行为. 1. 引言 费米子就是自旋为半整数的粒子,比如自旋为1/2的电 子就是最典型的费米子.电子通过势垒的遂穿是量子力 学中的基本问题,满足薛定谔方程的非相对论电子通过势 垒时透射概率随势垒的高度和宽度指数衰减.因此电子完 全通过极高和极宽势垒的现象被认为是完全不可能的,然 而1929年Klein发现[2] 满足Dirac方程的相对论电子可以完 全遂穿势垒,这个效应叫Klein遂穿. 对Klein遂穿的理解来自量子场论.势垒具有很强的电 势从而排斥电子而吸引正电子,导致在势垒内部产生正电 子态,它的能量与势垒外面的电子匹配,越过势垒的电子和 正电子的波函数连续导致高遂穿效应.这里电子和正电子 密切联系,并由Dirac方程的不同分量来描述,这种性质通 常叫电荷共轭对称.虽然这个解释能完全说明Klein遂穿,但 要从实验上观察这个现象存在很大困难,即相对论电子的 完全遂穿要求势垒高度大于粒子的Compton波长,产生如 此势垒要求电场E > 1016 V/cm.以现在的技术手段几乎 不可能产生如此大的电场,因此这个效应从实验上不可能 被观察,所以人们一直把这个现象称为Klein佯谬.2004年石 墨烯的发现预言了两维无质量Dirac电子的Klein遂穿[4] ,并 且极容易地从实验上观察到这个效应[5] ,从而真正解决 了Klein佯谬问题. 石墨烯是具有两个原子基(通常叫子格A和B)的二维晶 体薄片.石墨烯蜂巢结构由两个三角布拉维晶格组成,因此 载流子除了通常的电子自旋外(本文忽略),还有与子格自旋 度相联系的赝自旋.因为子格赝自旋,人们把波函数写为子 格空间的Dirac双旋量,并且引入粒子的手性,即单层石墨烯 中的准粒子是无质量手性费米子.后来发现在多层石墨烯 系统中也能推广手性概念,即准粒子为有质量的手性费米 子.有质量手性粒子通过势垒的行为与非手性粒子存在很 大差异, 它们垂直通过势垒前者表现为反Klein遂穿,后者 出现振荡遂穿.本文讨论重点讨论有质量手性粒子,通过其 在势垒中的传播来理解手性概念,并比较非手性粒子通过 势垒的遂穿行为. 2. 赝自旋与手性 手性概念最初出现在高能物理中,它与粒子的螺旋性 紧密联系.螺旋算符η ˆ定义为粒子的自旋s对传播方向p的投 影, p·s η ˆ= (1) |p| 算符与狄拉克-哈密顿量对易,因此与哈密顿量有共同的本 征函数,这时我们把螺旋算符和手性看成相等. 比如质量近 似为零的中微子为左手粒子,即它们的自旋与它们的动量 反平行,反中微子是右手粒子,它的自旋与动量平行. 单层石墨烯中的准粒子是无质量狄拉克费米子,由石墨 烯的晶格结构引入赝自旋σ .赝自旋来自晶格的两个不等价 子格A和B,因此可像自旋粒子一样引入手性(螺旋性).因此 石墨烯中准粒子的手性也可像方程(1)一样定义为赝自旋 在动量方向的投影[6] ,这里只要把自旋算符s改为赝自旋算 符σ 即可. 对有质量的狄拉克粒子,需要推广无质量粒子的手性概 念.比如对多层菱形堆叠石墨烯系统,两能带低能哈密顿量 近似为 HJ = ε(p)σ · nJ = ε(p)[cos(Jφ)σx + sin(Jφ)σy ] (2)
2 2
假定势垒边缘相当陡峭且在晶格尺度上光滑,则不引起 能 谷 间 散 射,那 么 我 们 只 需 研 究 一 个 能 谷K 的 散 射. 由 于 势 函 数 与 坐 标y 无 关,则 粒 子 的 波 函 数 可 写 为ψ (r ) = ψ (x)eiky y .二维矩阵表示中, 对无势垒区域的波函数的x分 量满足本征值方程 2 0 (kx − iky )2 ψ1 (x) ψ1 (x) =E − 2m (kx + iky )2 0 ψ2 (x) ψ2 (x) (5) 这里E 是费米能.式(5)可写为下面的两个微分方程 d + ky dx d − ky dx 由(6)(7)消去ψ2 (x)有 d2 2 − ky dx2
2 2 qx + qy =s
如 果D以nm为 单 位,方 程(16)中 双 曲 函 数 的 变 量q 量 级 达 到107 ,则T 以指数方式衰减很快,几乎完全没有透射. 双层石墨烯在电子正入射时完全没有透射,这通常叫 反Klein效应.从波的边界条件可知正入射时a = b = 0,即势 垒区域只有渐消波通道,这种情况下与Schrodinger粒子通 过势垒指数衰减完全相同.当然对斜入射粒子,势垒中传输 通道是行波和渐消波的混合,渐消波产生指数衰减,而向前 和向后的行波通过Fabry-Perot干涉产生共振透射.
2 2
ψ2 (x) =
2
2mE
2
ψ1 (x), ψ2 (x)
(6) (7)
ψ1 (x) =
2mE
2
ψ1 =
2mE
2
2
ψ1 ≡ k 4 ψ1
(8)
0
(kx − iky )2 0
方程(8)的解为行波解exp(±ikx x)或者指数增长(衰减)的渐 (3) 消波解exp(±κx x).把行波解ψ1 (x) = e±ikx x 代入(8)式有
2mE 2 2 k 2 = kx + ky =s 2 , 对K 点附近的低能哈密顿量只需作替换ky → −ky 即可.由 于我们研究的散射不考虑能谷混合, 今后只考虑对K 能谷 这里s表示能带指标,E > 0, s = +1,E < 0, s = −1.即双层 的散射. 石墨烯能量色散为二次关系,正如图2所示的抛物线
以后的研究进一步指出J 可表示赝自旋在倒空间的缠 绕数.这里赝自旋矢量描述粒子两分量波函数的相对相 位,J 表示当电子波矢绕狄拉克点作一次完全旋转时赝自旋 矢量经历的旋转次数.正如图1所示,在k空间对单层石墨烯 它是厄米和么正算符,本征值为±1.不存在质量项时,螺旋 当波矢绕Dirac点K 旋转一周,赝自旋矢量的方向σ 也旋转 1
2mE 双层石墨烯系统的载流子是有质量手性费米子,它通 2 κ2 = k2 x − ky = s 2 过势垒的行为与非手性粒子完全不同.下面考虑有质量手 性粒子通过方势垒的遂穿. 假定能量为E 的入射手性费米 这里 2 2 2 2 子—电子—从左边以角度φ入射到宽为D高为V0 的方势垒 κ2 x = k + ky = k (1 + sin φ) 上,如图2所示.如果势垒沿x为矩形并沿y 轴无限长,则分段 即κx = k 1 + sin2 φ.那么由(7)则赝自旋渐消波函数第二 常数势函数可表示为 分量为 V 0 < x < D 0 2 κx − ky V (x) = (4) ψ = s e±κx x = sh1 e±κx x 0 2 其它区域. k 2
k
k kx
I
II
III
其中波矢k = 2m|E |/ ,kx = k cos φ, ky = k sin φ.把旋量 波函数写为两分量形式,则波函数的x分量为 1 e±ikx x , ψ (x) = (10) −se±2iφ 同理对渐消波有
图2.上图粒子通过高为V0 ,宽为D的方势垒,以及双层石墨烯的抛 物线能量色散.下图表示k空间费米圆及各区域波矢与散射角.
一次,对双层石墨烯赝自旋矢量经历两次旋转,对三层石墨 烯则经历三次旋转. 手性算符定义为η ˆ = σ · nJ ,可知手性 算符和哈密顿量有共同的本征函数. 赝自旋矢量σ 与极化 轴平行或者反平行依赖手性算符的本征值.对无隙能带赝 自旋只在(kx , ky )平面上,导带中赝自旋矢量与极化轴平行 而价带中赝自旋矢量与极化轴反平行,正如图1所示.图1中 第一行表示导带中赝自旋矢量的取向而第二行表示价带中 赝自旋的取向,正好与导带中方向相反. 2. 两维有质量手性粒子的势垒遂穿 两维有质量手性粒子最简单的模型出现在双层石墨 烯中.双层石墨烯由两个单层碳原子耦合而成,它的每层都 为蜂巢结构,每层都有两个不等价碳原子A和B. 两层间不 同堆叠构成不同的双层系统,天然石墨剥离产生的双层系 统为Bernal堆叠,即上层的A2 原子正好在下层B1 原子的顶 上.在多层石墨烯低能哈密顿量中,我们取J = 2,且ε(p) = p2 /2m,这里有效质量m ≈ 0.054me [15] ,me 为祼电子质量.那 么在能谷K 点附近哈密顿量为 p H2 = − (σx cos 2φ + σy sin 2φ) 2m =− 2m (kx + iky )2
从方程(10)和(11)得到波函数中与坐标无关的两分量旋 量|χs (k) 由赝自旋决定,它是手性算符η ˆ = σ · n的本征函 数,即满足本征值方程η ˆ|χs (k ) = s|χs (k ) .从这里我们可以 看到对K 能谷手性指标就是能带指标s.赝自旋矢量σ 与极 化轴n平行或者反平行就由s决定,它在粒子通过势垒时起 重要作用. 如果是势垒区域,我们取波矢q = 2m|V0 − E |/ ,然后 把无势垒区域波矢k, κ和能量E 替换为q, λ和E − V0 ,即有关 系
2m(E − V0 )
2
2 , λ2 x − qy = s
2m(E − V0 )
2
V0
V
V
双层石墨烯通过势垒的Klein效应由其手性决定.对K 能 谷手性指标与能带指标相同,即导带手性为+1,赝自旋方 向 与 波 矢 方 向 相 同;价 带 手 性 为−1,赝 自 旋 与 波 矢 方 向 相 反. 粒 子 通 过 势 垒 界 面 要 求 赝 自 旋 守 恒.比 如 对 正 入 射(ky = 0),赝自旋只有x分量σx ,赝自旋守恒使图4中只能 出现细黑箭头所允许的传输过程,即单层石墨烯中只允 许出现透射传输,双层石墨烯中只允许出现反射传输.所 以双层石墨烯势垒区域不可能出现行波模,即只有渐消 这里考虑只有电子行波入射,反射有行波和渐消波.在0 < 模,也就是说势垒区域的空穴波矢不是实波矢−k 而是虚波 x < D的势垒区域同时存在左右行波和渐消波,则 矢q = ik . 4. 两维有质量无手性粒子的势垒遂穿 1 1 eiqx x + b e−iqx x ψII (x) =a 为了与有质量手性粒子的势垒遂穿进行比较,这里我们 −s e−2iθ −s e2iθ 只能考虑非手性载流子无隙半导体,这有可能在某种异质 [16] 1 1 λ x − λ x e x + d e x , + c (13) 结构中实现 .这个系统的哈密顿量为 s h2 s /h2 2 d2 d2 ˆc = − (17) H + 2 2 2m dx dy 其中h2 = ( 1 + sin2 θ − sin θ)2 .同理x > D的无势垒区域 只有右行波和衰减的渐消波 我们还是取势函数在y 方向平移不变,则波函数ψ (x, y ) = ψ (x)eiky y .由波函数满足的本征值方程有 1 1 ikx x −κx x ψIII (x) = t1 e + t2 e , (14) 2 −se2iφ s/h1 d2 2 − ky − = Eψ (x) (18) 2m dx2 上述系数r1 , r2 , a, b, c, d, t1 , t2 都为复振幅,我们要求波函数 和其导数在x = 0和x = D连续可得出这些系数,在计算过 即 程中取s = 1, s = −1. 在任意入射角φ下并不能得到透射 d2 2mE 2 − ky ψ (x) = − 2 ψ (x), (19) 系数的解析解,它需要用数值解来完成. 2 dx 而正入射时,φ = θ = 0,我们能求出透射系数的解析表 设传播波解为ψ (x) = e±ikx x ,那么由(19)有 示 t1 = 4ikq exp(−ikD) (q + ik )2 exp(−qD) − (q − ik )2 exp(qD) (15) 3
