人教版数学五年级下册长方体和正方体的表面积的体积整理复习
第三单元 长方体和正方体的体积 2023-2024学年五年级数学下册重难点知识点(人教版)
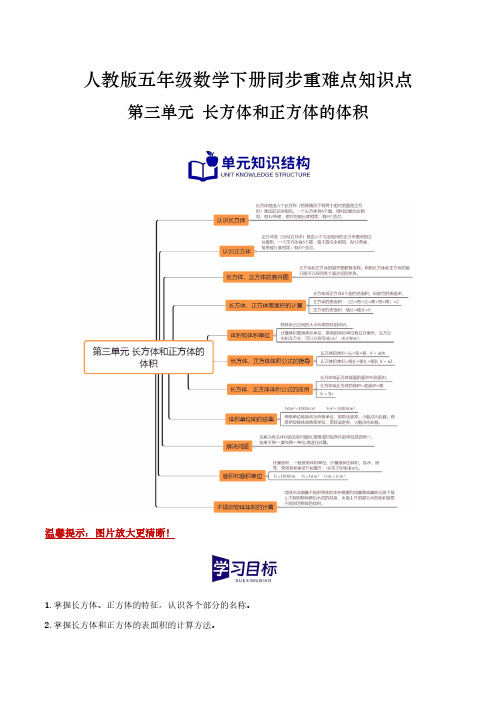
人教版五年级数学下册同步重难点知识点第三单元长方体和正方体的体积温馨提示:图片放大更清晰!1.掌握长方体、正方体的特征,认识各个部分的名称。
2.掌握长方体和正方体的表面积的计算方法。
3.理解体积的概念,掌握体积单位及体积单位之间的进率,能正确进行单位的换算。
4.掌握长方体和正方体体积的计算方法。
5.掌握容积的意义、容积单位间的进率及容积单位与体积单位的换算。
6.会计算不规则物体的体积。
重点:1.长方体、正方体的特征。
2.长方体、正方体表面积和体积的计算方法。
难点:用公式解决生活中的实际问题。
知识点一:认识长方体长方体是由六个长方形(特殊情况下有两个相对的面是正方形)围成的立体图形。
一个长方体有6个面,相对的面完全相同;有12条棱,相对的棱长度相等;有8个顶点。
知识点二:认识正方体正方体是(也叫立方体)是由六个完全相同的正方形围成的立体图形。
一个正方体有6个面,每个面完全相同;有12条棱,每条棱长度相等;有8个顶点。
知识点三:长方体、正方体的展开图长方体和正方体的展开图都有多种。
利用长方体和正方体的展开图可以探究各个面之间的关系。
知识点四:长方体、正方体表面积的计算长方体或正方体6个面的总面积,叫做它的表面积。
长方体的表面积:(长×宽+长×高+宽×高)×2正方体的表面积:棱长×棱长×6知识点五:体积和体积单位物体所占空间的大小叫做物体的体积。
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm³、dm³和m³。
知识点六:长方体、正方体体积公式的推导长方体的体积=长×宽×高 V = abh正方体的体积=棱长×棱长×棱长 V = a3知识点七:长方体、正方体体积公式的应用长方体或正方体底面的面积叫底面积。
长方体或正方体的体积=底面积×高V = Sh知识点八:体积单位间的进率1dm³=1000cm ³ 1m³=1000dm³高级单位转换成为低级单位,用乘法进率,小数点向右移;低级单位转化成高级单位,用除法进率,小数点向左移。
人教版五年级数学下册第3单元《长方体和正方体的表面积》综合复习练习题(含答案)

人教版五年级数学下册第3单元《3.2长方体和正方体的表面积》综合复习练习题(含答案)一、填空题1.把一个棱长2dm的正方体切成两个相等的长方体,表面积增加了( )。
2.如图是有许多棱长1厘米的立方体堆积而成,它的表面积是.3.有7个分开摆放的棱长1cm的小正方体,把它们搭成一个几何体(如下图),表面积比原来减少了( )cm2。
4.一个包装箱上的连乘式子如右图所示,它表示这个包装箱的( )是185mm,( )是150mm,( )是230mm。
这个包装箱的表面积是( )cm2。
5.把一个棱长为4dm的正方体切成棱长为2dm的小正方体,可以得到_____个小正方体.它们的表面积之和比原来的大正方体的表面积增加_____.二、判断题6.如图是长方体的表面展开图,与⑥相对的面是③。
( )7.图形是由7个棱长1厘米的正方体拼成的,它的表面积是24平方厘米。
( )8.正方体的棱长扩大5倍,它的表面积就扩大125倍。
( )9.如果一个长方体长3米,宽2米,高1.2米,它的表面积是24平方米..10.两个长方体的表面积相等,它们的形状一定相同。
( )三、选择题11.如图,沿虚线把长方体木料刚好锯成2个同样的正方体,这样表面积比原长方体增加了32cm2,原来长方体木料的表面积是()cm2。
A.64 B.128 C.160 D.32012.一个长方体,底面周长为8dm的正方形,侧面展开也是一个正方形,这个长方体的表面积是()dm3.A.32 B.64 C.72 D.12813.“仁、义、礼、智、信、孝”是我国的传统美德,小明将这六个字写在一个正方体的六个面上,下图是这个正方体的平面展开图,在原正方体中和“孝”相对的字是()。
A.礼B.智C.仁D.义14.下面两个立体图形,甲的表面积()乙的表面积。
A.大于B.等于C.小于D.无法比较15.把三个棱长为2厘米的正方体拼成一个长方体,这个长方体的表面积是()平方厘米.A.72 B.64 C.56 D.48四、解决问题16.水泥厂要制作10根长方体铁皮通风管,管口是边长30厘米的正方形,管子长2米。
人教版五年级数学下册期末 巧求长方体、正方体的表面积和体积 专项试卷附答案

人教版五年级数学下册方法技能分类评价3.巧求长方体、正方体的表面积和体积一、认真审题,填一填。
(每小题4分,共20分)1.在( )里填上合适的单位。
一辆大客车车厢的体积约为50( )。
电脑机箱的体积约为50( )。
一个牛奶盒的表面积约是128( )。
一个游泳池的墙壁面积约是360( )。
2.用36个棱长为1 cm的小正方体,可以摆成一个长6 cm,宽2 cm,高( )cm的长方体。
3.如右图,一块2.5 m长的方钢,把它沿虚线截成2段,表面积增加了60 cm2,则原来这块方钢的体积是( )cm3。
4.一个长20 cm、宽12 cm、高8 cm的长方体铁块的体积是( )cm3;把它熔铸成底面积是10 cm2,高是8 cm的小长方体铁块,可熔铸成( )个。
5.把2个表面积都是24 dm2的正方体拼成一个长方体,如果给这个长方体的表面涂色,涂色部分的面积( )dm2。
二、仔细推敲,选一选。
(每小题4分,共16分)1.做一节长120 cm,宽和高都是10 cm的长方体通风管,至少需要铁皮( )cm2。
A.5000B.4900C.4800D.26002.用5个相同的小正方体搭出三个不同的几何体,比较这三个几何体的表面积,下面说法正确的是( )。
①②③A.图①的表面积最大B.图②的表面积最大C.图③的表面积最大D.三个几何体的表面积一样大3.有大、小两个正方体,大正方体的表面积是小正方体表面积的4倍,大正方体的体积是小正方体体积的( )倍。
A.16B.8C.12D.94.棱长为1 m的正方体可以切成( )个棱长为1 cm的小正方体。
A.100B.10000C.100000D.1000000三、求下面物体的表面积和体积。
(12分)四、聪明的你,答一答。
(共52分)1.图①是一种茶叶包装盒,把这样的4盒茶叶按图②的摆放方式放入一个礼品袋中。
(1)这个礼品袋的占地面积最少是多少?(6分)(2)做这个礼品袋最少需要多少平方厘米的硬纸板?(接口处不计)(8分)(3)这个礼品袋的体积最小是多少?(8分)2.有一块长方形铁皮,长45 cm、宽30 cm,在四个角上分别剪去面积相等的正方形后折成一个深5 cm的无盖收纳盒,求这个收纳盒的容积。
人教版五年级下册数学第三单元长方体和正方体整理与复习课件

长方体 正方体
长方体或正 方体12条棱
长的总和
棱长总和=(长+宽+高) ×4
棱长总和=棱长×12
常用单位
厘米 分米
米
深化知识
形体
定义
表面积 计算公式
常用单位
长方体 正方体
长方体或正方 体6个面的总
面积
S=(长×宽+长×高+ 宽×高) ×2
S=棱长×棱长×6
平方厘米 平方分米
平方米
深化知识
形体
定义
的长 方体
深化知识 对应训练1
1.填空。 (1)长方体有( 6 )个面,相对的面( 完全相同 )。可能这几个面
都是长方形,也有可能有( 2 )个面是( 正方形 )。 (2)长方体有( 8 )个顶点。 (3)长方体有( 12 )条棱,相对的棱长度( 相等 )。
深化知识
(4)长方体的棱可以分成( 3 )组,每组有( 4 )条。 (5)相交于一个顶点的三条棱的长度分别叫做长方体的( 长 )、
这个包装箱的表面积是: 0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4 =1.66(m2) 答:至少要用1.66m2的硬纸板。
0.4m
深化知识
3. 一个玻璃鱼缸的形状是正方体,棱长 3dm。制作这个鱼缸时至少需要玻璃 多少平方分米? (上面没有盖。)
3×3×5=45(dm2) 答:制作这个鱼缸时至少需要玻璃45dm2。
知识梳理
长 方 体 正 方 体
长方体、正方体的特征 长方体、正方体的表面积 长方体、正方体的体积
面
棱
顶点 意义 计算
意义 单位、进率 计算
深化知识
1 长方体正方体的认识
人教版五年级数学下册第三单元-长方体和正方体整理与复习PPT课件

22
22
2、新建的篮球馆要铺设3cm厚的木质地板,已知该 馆的长36m,宽20m,铺设它至少需要用多少方木 材?
3cm=0.03m 36×20×0.03 =720×0.03 =21.6(m3) 答:铺设它至少需要用21.6m3木材。
23
23
24 24
学温 而故 时而 习知 之新
部分资料从网络收集整 理而来,供大家参考,
表面积
体积
容积
意义
计算 方法
长方体或正方体 6个面的总面积
物体所占空 间的大小
容器所能容 纳物体体积 的大小
S长=2ab+2ah+2bh V长=abh
=(ab+ah+bh) ×2 S正=a2×6
V正=a3
同体积
V=sh (从里面量)
常用计 m²dm² 量单位 cm²
m³dm³ cm³
m³dm³cm³ L ml
12
12
ห้องสมุดไป่ตู้
5、体积单位间的进率都是1000 。 (×) 6、把一个正方体的橡皮泥捏成一个长方体后 虽然它的形状变了,但是它所占的空间大小不 变。(√ ) 7、正方体的棱长扩大2倍,它的体积就扩大6 倍。(× )
2021最新人教版数学五年级下册长方体和正方体的体积《整理与复习》优质课件

3 长方体和正方体
3 长方体和正方体的体积
整理和复习
人教版数学五年级下册
1
体积的意义和体积单位:
物体所占空间的大小叫做物体的体积。 计量体积要用体积单位,常用的体积单位有立方 厘米、立方分米和立方米,可以分别写成 cm ³、 dm ³和 m ³。
2
长方体和正方体体积计算公式:
9
7. 算一算。
4³= 64 4×3 = 12 4+4+4 = 12
8²= 64 8×2 = 16 8+8 = 16
10
8. 建筑工地要挖一个长 50m、宽 30m、深 50cm的 长方体土坑,一共要挖出多少方的土? 50cm = 0.5m 50×30×0.5 = 1500×0.5 = 750(m³)= 750方 答:一共要挖出 750方的土。
50800cm³ 6.039m² 1500dm
5080dm³ 603900cm² 15m
5080000cm³ 60.39m² 150dm
27
7. 一个长方体的无盖水族箱,长是 6 m,宽是 60 cm,
高是 1.5 m。这个水族箱占地面积有多大?需要用多
少平方米的玻璃?它的体积是多少? 60 cm = 0.6 m 6×0.6 = 3.6(m²)
答:这面墙一共用了 36000 块积木。
25
5. 学校运来 7.6m³,铺在一个长 5 m、宽 38dm的沙 坑里,可以铺多厚?
38dm = 3.8m 7.6÷(5×3.8)
= 7.6÷19
= 0.4(m) 答:可以铺 0.4m厚。
26
6. 请你圈出每组数据中与其他数据不相等的那个数。
(1)5.08m³ (2)6039dm² (3)1500cm
人教版五年级数学下册长方体和正方体知识点归纳

人教版五年级数学下册长方体和正方体知识点归纳长方体和正方体是五年级数学下册的重要内容之一。
它们是立体几何中常见的几何体形状,具有特定的性质和特征。
本文将对人教版五年级数学下册关于长方体和正方体的知识点进行归纳。
一、长方体的定义和特征长方体是一种具有六个矩形面的立体几何体,其中相对的面两两平行且面积相等。
它的特征包括:1. 六个面都是矩形,相对的面两两平行且面积相等;2. 每个面的边长两两相等;3. 所有的顶点都是直角。
二、长方体的性质和运算长方体具有以下性质和运算:1. 面的个数:长方体有6个面;2. 顶点的个数:长方体有8个顶点;3. 边的个数:长方体有12条边;4. 表面积:长方体的表面积等于所有面的面积之和,可通过计算每个面的长乘以宽再乘以2,然后将六个面的面积相加得到;5. 体积:长方体的体积等于底面的面积乘以高,可通过计算底面的长乘以宽再乘以高得到。
三、正方体的定义和特征正方体是一种具有六个正方形面的立体几何体,每条边的长度相等。
它的特征包括:1. 六个面都是正方形,每个面的边长相等;2. 相邻面之间的夹角都是直角。
四、正方体的性质和运算正方体具有以下性质和运算:1. 面的个数:正方体有6个面;2. 顶点的个数:正方体有8个顶点;3. 边的个数:正方体有12条边;4. 表面积:正方体的表面积等于所有面的面积之和,可以通过计算一个面的边长的平方再乘以6得到;5. 体积:正方体的体积等于底面的边长的立方,可通过计算边长的立方得到。
五、长方体和正方体的应用长方体和正方体在生活和实际问题中有广泛的应用,例如:1. 房间的体积:我们可以将房间看作一个长方体,通过测量长度、宽度和高度,计算房间的体积,从而确定房间的空间大小;2. 体育器材:篮球、足球、乒乓球等体育器材往往具有正方体或长方体的形状,了解它们的形状特征和性质,有助于更好地认识和使用它们;3. 包装箱的运输:考虑到方便和安全,一些物品在运输过程中会被装在长方体或正方体的包装箱中,了解包装箱的体积和表面积有助于合理选择箱子和运输方式。
人教版数学五年级下册-03长方形和正方形-04整理和复习-教案02

长方体和正方体复习教案问题研究:通过引导学生经历对长方体和正方体的知识系统化的整理,培养学生能综合运用所学的知识和技能解决实际问题的能力。
教学内容:人教版五年级下册第三单元的内容教学目标:知识与技能目标:加深对长方体正方体的形体特征的认识,分清表面积和体积的概念,能熟练地掌握形体的表面积和体积(容积)的计算,解决一些实际问题。
过程与方法目标:通过引导学生讨论探索、合作交流,建立初步的空间观念,发展形象思维。
培养学生知识的自我总结能力。
情感态度与价值观目标:通过解决实际问题,让学生感受到数学与生活的密切相关,使学生形成积极参与数学教学活动,并积极与人合作获得成功的体验,树立学好数学的信心与勇气。
教学重点:帮助学生梳理长方体、正方体知识,使之系统化。
理解体积和表面积的意义,并运用公式解决实际问题。
教学难点:培养学生综合运用所学知识解决实际问题的能力。
教学过程:第一课时课前3分钟口算。
0.75+0.8= 0.13×4= 2.4-0.8=8.5×100=16.7-0.92-1.08=一、呈现目标。
1、导入课题。
课件出示长方体,问:你还记得长方体的哪些知识?2、出示目标。
今天我们一起来复习长方体的面、棱及表面积的计算与应用。
二、回顾知识。
1、出示问题,整理知识。
①长方体有多少个面?各是什么形状?相对的两个面有什么特点?②长方体有多少条棱?相对的棱长短怎样?怎样求长方体的棱长总和?③长方体有多少个顶点?④从不同的角度观察长方体,做多能看到几个面?⑤什么叫做长方体的表面积?怎样计算它们的表面积?三、综合练习。
1、填空。
(1)长方体有()个面,()条棱,()个顶点。
()面积相等,()棱长相等。
(2)长方体中相交与一个顶点的三条棱分别叫做长方体的(),(),()。
(3)求加工一个长方体油箱要用多少铁皮,是求这个油箱的()。
(4)要求用一根多长的铁丝正好可以做一个长6cm、宽5cm、高3cm的长方体框架,就是要求这个长方体的()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宽是14厘米
剪去正方形的 长
宽
高
体积
边长
3
14 8
3
336
剪拼长方体礼盒
正方形边长 是4厘米
宽是14厘米
剪去正方形的 长
宽
边长
4
12 6
长是20厘米
高
体积
4
288
剪去正方形 长
的边长
20
1
18
2
16
3
14
4
12
5
10
6
8
剪拼盒子
宽
高
14
12
1
10
2
8
3
6
4
4
5
2
6
体积
216 320 336 288 200 96
哪个长方体礼盒装得多?
4
序号 4
8 15
长 15 宽8
8
15
高
?
体积
反思一下
➢ 刚才我们是怎么解决这些问题的? ➢ 解决这些问题过程中,您有什么发现?
剪拼长方体礼盒
一张长是20厘米,宽是14厘米长方形的纸,从四 个角剪去一个的正方形(边长为整厘米数),用 剩下的纸折成一个小纸盒。 (1)如果剪去正方形边长是1、2、3、4厘米,那 么折成纸盒的体积分别是多少?
5 15
单位:cm
4 号礼盒
8 15
8 15
单位:cm
学习要求
➢ 第一步:独立思考。根据信息,你想到的 是怎样的长方体,容积(体积)是多少?
➢ 第二步:组内讨论。按顺序交流自己的方 法,可以画一画,更要说说为什么;
➢ 第三步:集体交流。最好你的想法教会别 人来说,你说别人的方法。
哪个长方体礼盒装得多? 单位:cm
用数学·做环保
➢ 寻找身边不同的茶叶礼盒。 ➢ 你有什么发现? ➢ 你对这些包装有何想法? ➢ 请从数学和环保节能的角度提出
意见?
用数学·做环保
如果你的意见没有得到别人的回应,可以用中 秋节月饼的包装为题材再试试。
课堂小结
今天的学习你有什么收获? 解决问题的过程中有什么感受? 还想到了什么新问题?
长方体、正方体表面积、体积练习课
新华小学 向宗勤
包装礼盒
单位:cm
10
15
20
至少需要多大的包装纸? 1张包装纸够吗?
70
20
1400 > 1300
包装礼盒
单位:cm
把两个完全一样的正方体包装在一起,至 少需要多大的包装纸?
10
10
10 10
10 10
包装礼盒
单位:cm
把2个完全一样的长方体包装在一起,至 少需要多大的包装纸?
(2)剪去越大,盒子的容积怎么变?
剪拼长方体礼盒
正方形边长 是1厘米
长是20厘米
宽是14厘米
剪去正方形的 长
宽
高
边长
1
18 12
1
体积 216
剪拼长方体礼盒
正方形边长 是2厘米
长是20厘米
宽是14厘米
剪去正方形的 长
宽
高
边长
2
16 10
2
体积 320
剪拼长方体礼盒
正方形边长 是3厘米
长是20厘米
1
8 10
6 10
6 8
8 10
6 10
6 8
序号 1
长 10
宽8
高
6
体积 480
哪个长方体礼盒装得多? 单位:cm
2
10 20
10 20
5 10
5 10
序号 2
长 20
宽 10
高
5
体积 1000
哪个长方体礼盒装得多? 单位:cm
3
8 15
5 15
序号 3
长 15
宽8
高
5
体积 600
单位:cm
20 30 15
20 30 15
哪个长方体礼盒装得多?
C
A
B
E D
求什么? 怎么求?
单位:cm
哪个长方体礼盒装得多?
➢ 请你根据现有的信息来判断礼盒的大小?
1 号礼盒
单位:cm
8 10
6 10
6 8
8 10
6 10
6 8
2 号礼盒
10 20
10 20
5 10
5 10
单位:cm
3 号礼盒
8 15
